Логарифмы mathprofi: Свойства логарифмов / Библиотека МатПрофи.ком

Содержание

Логарифмы примеры решения задач, формулы и онлайн калькуляторы

Содержание:

Логарифм произведения, сумма логарифмов
Логарифм частного, разность логарифмов
Логарифм степени
Логарифм корня
Разложение в ряд Маклорена натурального логарифма
Решение логарифмических уравнений
Решение логарифмических неравенств

Логарифмы (Логарифмирование) активно используются в решении задач, так как значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.

Перед изучением примеров решения задач советуем изучить теоретический материал по логарифмам, прочитать определения и все свойства логарифмов.

Логарифм произведения, сумма логарифмов

Теоретический материал по теме — логарифм произведения.

Пример

Задание. Представить $\log _{5} 6$ в виде суммы логарифмов.

Решение. $\log _{5} 6=\log _{5}(2 \cdot 3)=\log _{5} 2+\log _{5} 3$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Упростить $\log _{5} 4+\log _{5} 3$

Решение. $\log _{5} 4+\log _{5} 3=\log _{5}(4 \cdot 3)=\log _{5} 12$

Логарифм частного, разность логарифмов

Теоретический материал по теме — логарифм частного.

Пример

Задание. Известно, что $\log _{5} 2=a$, а $\log _{5} 3=b$. Выразить $\log _{5} \frac{2}{3}$ через $a$ и $b$.

Решение. $\log _{5} \frac{2}{3}=\log _{5} 2-\log _{5} 3=a-b$

Пример

Задание. Вычислить значение выражения $\log _{5} 10-\log _{5} 2$

Решение. {2}-x-2=0 \Rightarrow x_{1}=2, x_{2}=-1$$

Второй корень не принадлежит ОДЗ, а значит решение $x=2$

Ответ. $x=2$

Пример

Задание. Решить уравнение $\ln (x+1)=\ln (2 x-3)$

Решение. Находим ОДЗ:

$$\left\{\begin{array}{l} x+1>0 \\ 2 x-3>0 \end{array} \Rightarrow\left\{\begin{array}{l} x>-1 \\ 2 x>3 \end{array} \Rightarrow\left\{\begin{array}{l} x>-1 \\ x>\frac{3}{2} \end{array} \Rightarrow\left(\frac{3}{2} ;+\infty\right)\right.\right.\right.$$

Решаем уравнение $x+1=2 x-3: x=4 \in$ ОДЗ.
Итак, решением исходного логарифмического уравнения также является это значение.
Ответ. $x=4$

Решение логарифмических неравенств
Теоретический материал по теме — логарифмические неравенства.
Пример
Задание. Решить неравенство $\log _{0,5}(x-1)>-1$
Решение. {-1}$   или   $x-1<2 \Rightarrow x<3$
В пересечении с ОДЗ получаем, что $x \in(1 ; 3)$
Ответ. $x \in(1 ; 3)$
Пример
Задание. Решить неравенство $\log _{5} 5>\log _{5} x$
Решение. Данное неравенство равносильно системе:
$$\left\{\begin{array}{l} 5>x, \\ x>0 \end{array} \Rightarrow\left\{\begin{array}{l} x0 \end{array} \Rightarrow x \in(0 ; 5)\right.\right.$$

Ответ. $x \in(0 ; 5)$
Читать первую тему — формулы и свойства логарифмов, раздела логарифмы.
Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами. Теория 11 класс онлайн-подготовка на Ростелеком Лицей |

Подготовка к ЕГЭ по математике

Эксперимент
Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами.
Теория
Конспект урока
На предыдущих уроках мы обсуждали показательную функцию, решение показательных уравнений и неравенств.

Определение логарифма

Когда мы обсуждали решение показательных уравнений, то нам всегда удавалось представить обе части в виде степеней с одинаковыми основаниями.

Но вполне логично, что может возникнуть ситуация, когда это сделать не удастся. Например, решить уже рассмотренными методами уравнение не получится, так как 5 мы пока не умеем представлять в виде степени с основанием 2.
С другой стороны, мы обсуждали тот факт, что показательная функция принимает любое положительное значение. Поэтому, в какой-то точке значение функции должно равняться 5.
Фактически, мы столкнулись с ситуацией, похожей на извлечение корня – мы точно знали, что есть число, квадрат которого равен 2, но не могли записать его доступными нам методами. В том случае мы поступили следующим образом: ввели новое понятие «корень» и операцию извлечение корня, которая была обратна возведению в степень.
Возвращаясь к нашей проблеме, нам придётся поступить аналогично. Обозначим степень, в которую надо возвести 2, чтобы получить 5, как – логарифм пяти по основанию 2.
То есть, определение логарифма следующее: для . То есть, логарифм показывает: в какую степень необходимо возвести основание логарифма (), чтобы получилось подлогарифмическое выражение ().
Рассмотрим простейшие примеры вычисления логарифмов:
1) , так как .
2) , так как .
3) , так как .
4), так как .

Особые виды логарифмов

Существует два специальных вида логарифмов: десятичный и натуральный.

Десятичный логарифм – это логарифм с основанием 10. Он обозначается следующим образом: .
Натуральный логарифм – это логарифм с основанием (напомним, что ). Он обозначается следующим образом: .

Основное логарифмическое тождество

Исходя из определения логарифма , легко получить следующее свойство, которое называется основным логарифмическим тождеством. Для этого достаточно подставить вторую формулу в первую. В результате получаем: .

Это выражение называется основным логарифмическим тождеством.

Свойства логарифмов

Давайте сформулируем ещё несколько основных свойств логарифмов ().

1)    (т.к. ),
2)
3)
4)
5) Формула перехода к новому основанию:
6)    (т.к. )
7)    (т.к. )
На этом уроке мы с вами сформулировали определение логарифма, основное логарифмическое тождество и свойства логарифма.
В практической части урока мы научимся вычислять различные логарифмы, а также преобразовывать выражения, содержащие логарифмы.
Полезные ссылки:
1)      Алгебра 11 класс: «Понятие логарифма»
2)      Алгебра 11 класс: «Понятие логарифма. Простейшие задачи»
3)      Алгебра 11 класс: «Свойства логарифмов. Логарифм произведения и частного»
4)      Алгебра 11 класс: «Свойства логарифмов.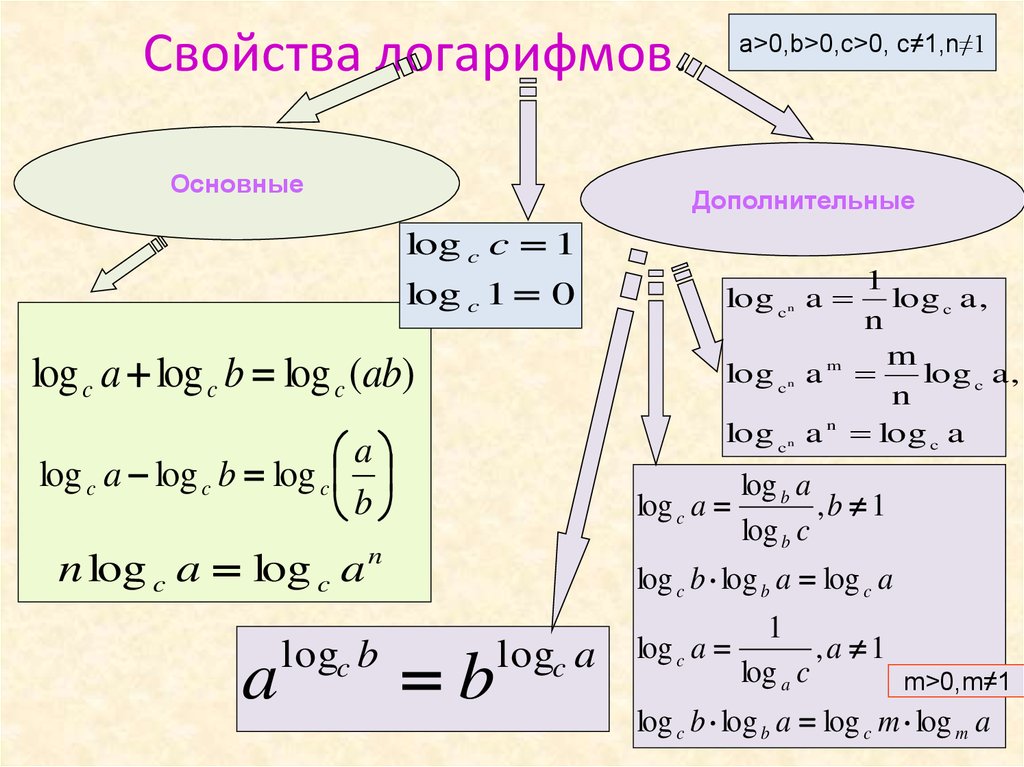 Логарифм степени»
5)      Алгебра 11 класс: «Свойства логарифмов. Решение более трудных задач»
6)      Алгебра 11 класс: «Переход к новому основанию логарифма»
7)      Алгебра 11 класс: «Переход к новому основанию логарифма. Решение задач»

Видеоурок: Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами. Теория по предмету Алгебра за 11 класс.
Оценка для обучения в презентации в классе в элементарной математике
Оценка обучения в начальной математической презентации классной комнаты
Реклама
1 из 68
Top Clyd Slide
Скачать для чтения в автономном режиме
PowerPoint из «оценки для обучения в элементар Математический класс»
Реклама
Реклама
Оценка для обучения в начальной математической презентации
Представлено Таней Брейбрук, B.Ed. Электронная почта: [email protected] Следите за новостями в Твиттере: @MathProfile Найти нас на Facebook
Цели семинара Общие ожидания учащихся: Учащийся будет готов попробовать одну новую оценку стратегию в своем математическом классе в течение следующих четырех недель. Конкретные ожидания учащихся: 1. Учащийся обсудит, какую оценку за обучение есть и нет. 2. Учащийся поймет выводы исходящие из исследований. 3. Учащийся исследует различные оценочные задания. 4. Учащийся увидит множество рубрик для конкретные математические задачи. 5. Учащийся увидит различные способы записи сохранение.

Исследования Блэк, Пол и Дилан Уильям. «Внутри черного ящика: повышение Стандарты через оценивание в классе». Фи Дельта Каппан (октябрь 1998 г.): 139–148. Стиггинс, Ричард. «Оценка, уверенность учащихся и школа Успех.» Фи Дельта Каппан (ноябрь 1999 г.): 191–198. Гланфилд, Флоренс, Уильям С. Буш, Джин Керр Стенмарк. Оценка по математике: практическое пособие для классов K-2. Рестон, Вирджиния: Национальный совет учителей математики, 2003. Хуинкер, ДеЭнн. Образец оценки по математике: Дошкольный класс 2. Рестон, Вирджиния: Национальный совет Учителя математики, 2006. Образование Альберты. Переосмысление оценивания в классе с помощью Цель в уме: оценка для обучения, оценка как Обучение, оценка обучения. Эдмонтон, AB: Альберта Образование, 2006.
Картинка показывает 2-й издание, которое был опубликован в 2011. Стиггинс, Ричард, Джудит А. Артер, Ян Чаппиус и Стивен Чаппиус. Оценивание в классе для обучения учащихся: выполнение Правильно — правильно использовать. Портленд, Орегон: тренинг по оценке Институт, 2004. Учебный институт оценки http://www.assessmentinst.com

Три больших вопроса / Семь стратегий (из Stiggins, Arter, J. Chappius & S. Chappius: Classroom Assessment for Student Learning) КУДА Я ИДУ? Стратегия 1: Предоставьте четкое и понятное видение цели обучения. Стратегия 2: Используйте примеры и модели сильной и слабой работы. ГДЕ Я СЕЙЧАС? Стратегия 3: Предлагайте регулярные описательные отзывы. Стратегия 4: Научите учащихся оценивать себя и ставить цели. КАК Я МОГУ ЗАКРЫТЬ ПРОБЕЛ? Стратегия 5: Планируйте уроки так, чтобы они фокусировались на одном аспекте качества за раз. Стратегия 6: Научите студентов целенаправленному повторению. Стратегия 7. Вовлеките учащихся в самоанализ и позвольте им отслеживать и поделиться своим обучением.

Стратегия 1: Дайте четкое и понятное видение цели обучения. Мы учимся… имена наших одноклассников. Мы учимся… предсказать закрытые слова. Мы учимся… правильно написать дату. Мы учимся… на что рассчитывать при добавлении. Мы учимся… как определить, есть ли число является нечетным или четным.

Мы учимся… как найти площадь форма.
Математические задачи Я могу… √ решать задачи с помощью календаря √ пропустить счет: 2, 3, 4, 5, 10, 25 и 100 √ показать номер -с использованием подсчетов -с материалами -с использованием картинок -использование чисел -различными способами √ читать трехзначные числа √ читать числовые слова √ представлять число в виде различных уравнений √ сравнить числа √ расставь числа по порядку √ найти ошибки в числах, которые идут по порядку √ оценка √ обсудить информацию с гистограммы
гр. 2 примера основных вопросов Какие числа мы можем использовать, чтобы говорить о позиции? Какие числа используются для пропуска счета: -2, -5, -10? Какими способами можно представить двузначные числа? Как можно сравнивать и упорядочивать двузначные числа? Как мы можем оценить количество объектов? Как дни связаны с неделями и месяцами?

Учимся называть месяцы года. Мы учимся соотносить количество месяцев с годом. 1. Напишите месяц, который идет ПОСЛЕ. март сентябрь 2. Напишите месяц, который идет ДО. июнь август 3. Напишите месяц, который идет МЕЖДУ. Октябрь Декабрь Май Июль 4. В каком положении находится каждый месяц? (1-й, 2-й, 3-й, 4-й, …) сентябрь февраль 5. Напишите тот месяц, который находится в каждой позиции. 4-й 8-й 6. Сколько месяцев в году? 7. Если сейчас октябрь, а мой день рождения в апреле, сколько еще месяцев до моего дня рождения? 8. Какой месяц наступает через 3 месяца после марта? 9. Какой месяц наступает за 6 месяцев до января? 10. Если твоей младшей сестре два с половиной года, сколько это месяцев?

Стратегия 2: Используйте примеры и модели сильной и слабой работы.
Приведите примеры и не примеры: четных чисел ПРИМЕРЫ НЕ ПРИМЕРЫ Студент А: 2, 4, 6, 8, 10 1, 3, 5, 7, 9 Студент Б: 743, 321, 568, 75 904, 772, 547, 329 Студент C: 6 824 3 265 Другие возможные задания  треугольники, определенные события, острые углы, повторяющийся узор ABCC
«Визуальная рубрика» (Энн Дэвис)
Стратегия 3: Предлагайте регулярные описательные отзывы Образование Альберты. Переосмысление оценивания в классе с учетом цели: Оценка для обучения, Оценка как обучение, Оценка обучения. Эдмонтон, Альберта: Образование Альберты, 2006.
Категории инструмента оценки математического профиля по уровням обучения 1—9 КЛАСС Представлять числа Место подсчета значений Оценка шаблонов сложения и вычитания Геометрия измерения равенств 2 КЛАСС—12 разрядов Представлять числа Место подсчета значений Оценка шаблонов сложения и вычитания Геометрия измерения равенств Графики календаря и анализ данных Решение проблем 3 КЛАСС—15 разрядов Представлять числа Место подсчета значений Оценка Сложение и вычитание Умножение и деление Дроби Образцы Уравнения Измерение календаря времени Геометрия Графики и анализ данных Решение проблем

КЛАСС 4—14 разряды Представлять числа, размещать значения, добавлять и вычитать Умножение и деление дробей Шаблоны Уравнения Время Геометрия календарных измерений Решение проблем с графиками и анализом данных 5 КЛАСС—12 разрядов Представление чисел Оценка умножения и деления Дроби Десятичные шаблоны Уравнения Измерение Геометрия Графики и анализ данных Вероятность и решение проблем неопределенности 6 КЛАСС—13 разрядов Представление чисел Оценка операций с целыми числами Дроби, отношения и проценты Образцы Уравнения Измерение Преобразования геометрии Графики и анализ данных Случайность и решение проблем неопределенности

Чтение и интерпретация графика профиля
Рубрики Ван де Валле, Джон А. и ЛуЭнн Х. Ловин. Обучение, ориентированное на студента Математика: классы К-3. Бостон, Массачусетс: Пирсон Образование, Inc., 2006.
Показать и поделиться проектом
Стратегия 4: Научите учащихся оценивать себя и ставить цели. Отделение католической школы Лосиного острова Второй класс, созданный Кэрри Анака, Мишель Байсен и Дженна де Врис
Стратегия 5: Уроки дизайна, чтобы сосредоточиться на одном аспекте качества за раз. ~ решение проблем  обучение различным стратегиям и/или способам записи ответов по одному ~ основные факты об использовании философии/метода Силы Десяти (обучать таким стратегиям, как двойное и двойное плюс один; визуализация; -9, потом -8) ~ задачи производительности
Стратегия 6: Научите студентов целенаправленному пересмотру.
Возможные темы включают: -2-значные числа (73 и 93) -формы (квадратные и треугольник) -операции (умножение и разделение) -меры измерения (килограмм и грамм)
Стратегия 7: Вовлекайте учащихся в самоанализ и позволяйте им отслеживать и поделиться своим обучением. Название диаграммы основных фактов: Этот график показывает, что я… Перечислите 2 стратегии, которые вы использовали, чтобы стать лучше в безумные минуты. 1. 2. Напишите предложение, в котором сравните свои баллы, используя слово «больше». Напишите предложение, в котором сравните свои баллы, используя слово «меньше».
Другие идеи для саморефлексии и обмена знаниями… Журналы обучения / математические журналы Выходные карты Фотографии манипулятивной работы Студенческая конференция
Портфели
Запись и отчетность
В небольшой группе обсудите… Как будет то, что вы видели и слышали на этом занятии повлияли на ваше преподавание?
Обучающие цепочки Можно использовать «Я могу…» или «Я узнал…» Может использоваться для измерения индивидуального или группового прогресса
Общие ожидания учащихся: Учащийся будет готов попробовать одну новую оценку стратегию в своем математическом классе в течение следующих четырех недель. Заключительная мысль…
Примечания редактора
Сфотографируйте мою форму дня с целями обучения.
Объявление
PGI410188-41010064DO/ME (20202) — Tecnologias em Ensino e Aprendizagem
Путь к странице
К сожалению, запрошенный файл не найден
90 002 Дополнительная информация об этой ошибке
Перейти к… Перейти к…Programa discip Tecn Ensino e AprendПлан курса на 2020 год.2Введение в курс — PPSSРасписаниеКомната для наших встреч Доска объявлений только учителемПредставления членов группыСоциальный форумLang Learning with Tech by StanleyВеб-сайт для книги Обзоры книгиСтатьи, главы и т. д. Chapelle 2008Публикации Селсо ТумолоCurso Especializ Educação na Cultura DigitalTPaCK16 Principles for Games — James Paul Geedigital storyЦифровая историяInstructionsThe DilemmaBrain Gain глава 1Present — Recap on PrenskyThe Shallows, глава 7Present — Recap on The ShallowsThe Shallows — bookThe Social DilemmaVideos on PrenskyVideo s on CarrОбсуждение прироста мозгов, ПренскиОбсуждение мелководья, автор Карр Обсуждая социальную дилеммуНазначить №1 — 19 февраляСлайды для презентацийИнструкцииЗВОНИТЕ: определения, escopo e abrangência Tecnologias digitais ensino línguas Зачем звонить ЗВОНИТЕ CALLТехнологии на английском языке: панорама.
No related posts.