Логарифмы с одинаковым основанием как делить: Деление логарифмов | Логарифмы

Действия с логарифмами. Постигаем азы!

        На прошлом занятии мы познакомились с понятием логарифма и порешали несколько несложных примеров на определение и смысл логарифма. Для начального знакомства. )

        Теперь настал черёд более тесного знакомства с логарифмами и, соответственно, решения более серьёзных примеров. Начнём мы с ограничений в логарифмах.

Ограничения в логарифмах.

        Как и у любого математического понятия, у логарифма тоже есть свои свойства и фишки. Именно о них мы сейчас и будем разговаривать. И в первую очередь это ограничения в логарифмах. До сих пор мы с вами знали лишь два жёстких ограничения в математике:

        — нельзя делить на ноль;

        — нельзя извлекать корень чётной степени из отрицательного числа.

        С этого момента к этим двум добавляются дополнительные ограничения в логарифмах.

        Для начала запишем определение логарифма в самом общем виде. Через буквы.

        log_ab = c

        Напоминаю, что это равенство означает всего лишь решение показательного уравнения

        a^c = b.

        И всё.

        А теперь подумаем, любым ли числом может быть a? Пусть, к примеру, a = 1. Тогда получается забавная штука: единица в любой степени равна единице… И каким бы ни было число c, числа a и b останутся единичками. Та же самая история и с нулём. Не подходят эти числа в качестве основания…

        Отрицательные числа — очень вредные и капризные. В одну степень их можно возводить, а в другую — нельзя. Вот и поступили математики с ними, как со всеми капризными — вовсе исключили из рассмотрения.

        В результате у нас получилось такое ограничение на основание:

        a > 0,    a ≠ 1.

        А каким может быть число b? Давайте подумаем: если заведомо положительное основание a возвести любую степень c, то какое число мы в итоге получим? Верно, положительное число и получим!

        Отсюда ещё одно ограничение на аргумент логарифма:

        b > 0.

        Вот и все ограничения. Число c (значение логарифма) может быть совершенно любым.

        Конечно, при решении безобидных числовых примеров на логарифмы эти ограничения практически никак не сказываются. Зато когда столкнётесь с логарифмическими уравнениями и неравенствами, вы про эти ограничения ещё не раз вспомните! А если не вспомните, то я вам напомню. И буду напоминать при каждом удобном случае.) Ибо эти ограничения очень (!) важны при решении уравнений и неравенств. Про ОДЗ помните? Вот, то-то и оно…

Свойства логарифмов.

        Итак, с ограничениями на логарифмы разобрались. Пора переходить на следующий уровень и знакомиться со свойствами логарифмов. Вот они:

        Здесь всюду b>0 и c>0, а также a>0, a≠1.

        Вот такой вот джентльменский набор. Ни много ни мало.) Теперь кратенько пробежимся по каждому из этих свойств. Чтобы ясно было, откуда ноги растут, как говорится.)

        Начнём с первого свойства:

        Обычно это свойство именуют особо — основным логарифмическим тождеством. Откуда же оно берётся? Запишем снова уже до боли знакомое нам равенство:

        log_ab = c

        Из самого определения логарифма мы с вами знаем, что, если число а (основание) возвести в степень c (показатель), то получим число b:

        a^c = b

        А теперь подумаем, чему же равно у нас число c? Да вот же оно:

        с = log_ab

        Подставим это выражение в предыдущее равенство и получим как раз то, что нам и требуется:

        «И зачем нам такая странная перетасовка?» — спросите вы.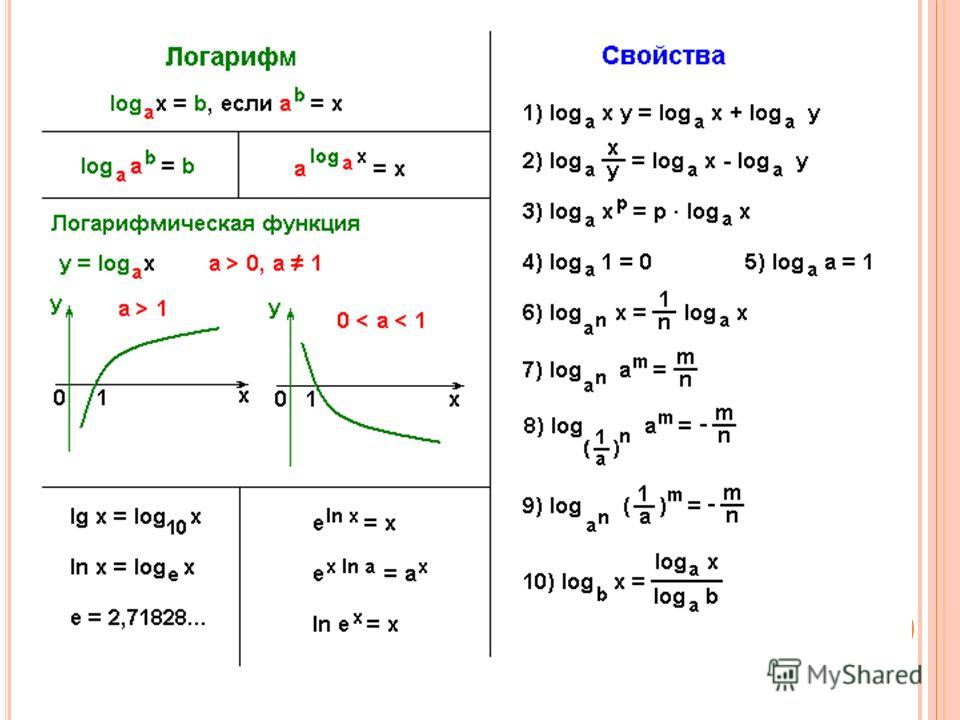 А затем, что многоэтажное выражение превращается в элементарное b! Полезная формула.) Это единственная формула, где логарифм стоит в показателе степени.

        Следующая группа формул (2-3):

        Думаю, тут комментарии излишни. Всё прямо из определения логарифма следует.) И даже примеры разбирались. В предыдущем материале. Кому всё-таки непонятно, применяем старый добрый способ — словесную расшифровку. Проверено, помогает.)

        Переходим к следующей группе формул (4-5):

        Коротко эти формулы называются логарифм произведения и логарифм частного (дроби).

        А вот с их доказательствами вопрос похитрее будет.) Эти два свойства проистекают из обычного умножения и деления степеней с одинаковым основанием. Как именно? Мы с седьмого класса помним, что при перемножении двух степеней с одинаковым основанием показатели степеней складываются, а при делении — вычитаются:

        Для доказательства, например, четвёртой формулы (логарифм произведения) придётся ввести вспомогательные обозначения:

        m = log_ab  

        и 

        n = log_ac.

        До конца доказывать эти две формулы я не буду. Как продолжить доказательство? Подставьте выражения для m и n в формулу умножения степеней и воспользуйтесь основным логарифмическим тождеством (формула №1). Попробуйте! Очень полезно.)

        Кстати, прошу обратить внимание: данные формулы справедливы только при одинаковых основаниях! Если основания разные, то, скорее всего, преобразования более мудрёные…

        Идём дальше. Следующая группа формул (6-7) — это формулы, позволяющие избавляться от степеней в аргументе или в основании логарифма:

        Смысл их тоже прост. Если аргумент логарифма возводится в степень, то показатель степени n можно вынести наружу и приписать перед логарифмом. То же самое происходит и тогда, когда в степень возводится основание логарифма, только показатель степени переворачивается. Эти две полезные формулы избавляют нас от степеней в аргументе/основании. Если это мешает, конечно. Это понятно.)

        Осталась последняя формула №8:

        Это — так называемая формула перехода к новому основанию. Самая трудная для запоминания формула. Поэтому народ частенько и ленится её запоминать… А вы запомните. Не сочтите за труд.) Когда она применяется? А когда основания логарифмов — разные.) Скажем, в примере куча логарифмов по основанию 3 и затесался один логарифм по основанию 7. Его и менять надо. На тройку.) Мы с этой формулой крепко подружимся. И примеры тоже порешаем.) В соответствующем уроке.

        Вот такой вот перечень формул и свойств. Их вполне достаточно, чтобы уверенно решать примеры на логарифмы любого уровня сложности. Эти формулы нужно не просто помнить, но и уметь применять. Причём в обоих направлениях — как слева направо, так и справа налево.

        Ещё не помешало бы знать, что такое десятичный логарифм и что такое натуральный логарифм.

        Десятичный логарифм — это просто логарифм по основанию 10:

        log₁₀b = lg b

        В написании десятичного логарифма всего лишь пропадает буковка «о».

        Натуральный логарифм (хотя чего уж в нём такого натурального) — это логарифм по основанию e. Иррациональному числу «e».

        e = 2,71828182845…

        Что это за загадочное число, узнаете и поймёте, когда поступите в институт. В курсе матанализа.) В школьной математике это число практически не встречается, зато в высшей — сплошь и рядом.)

        Обозначается натуральный логарифм вот так:

        log_eb = ln b

        Логарифмы по этим основаниям хотя и имеют своё особое написание, но ни по определению, ни по свойствам ничем не отличаются от обычных логарифмов, скажем, по основанию два. Или три. И решаются точно так же.

        Итак, будем считать, что необходимая теоретическая база подготовлена. Переходим к практике.)

Начальный уровень. Немного формул. Немного дробей. Немного степеней.

        На этом уровне мы:

        — впрямую используем определение логарифма,

        — впрямую используем самые простые свойства логарифмов.

        Мыслей здесь особых не нужно. Главное — память и внимательность. Итак, читаем, смотрим, вникаем.

        Пример 1

        Вычислить:

        Решение примера вытекает непосредственно из определения и смысла логарифма. В какой степени 1/3 даёт 1/27? В кубе, конечно. То есть, в третьей степени.

        Ответ: 3.

        Следующий пример:

        Пример 2

        Всё то же самое, только дроби десятичные. Ну и что? Опять напрямую пользуемся определением логарифма: в какой степени 0,3 даст 0,09? В квадрате, разумеется! Или во второй степени. )

        Ответ: 2.

        И ещё один примерчик на дроби:

        Пример 3

        А вот тут некоторые могут и зависнуть. Почему? Потому что связь между 0,5 и 1/128 визуально просматривается плохо. Что делать?

        Что-что… Да к обычным дробям перейти! Вот вам и первый практический совет:

        Если в одном примере смешались в кучу разные типы дробей, то переходим к обыкновенным дробям.

         Этот приём, между прочим, работает не только в логарифмах, но и в других смежных темах — в показательных выражениях, в корнях.

        В нашем примере 0,5 = 5/10 = 1/2. Ну и как? Связь между 1/2 и 1/128 легче углядеть? Естественно! 1/128 — это 1/2 в седьмой степени.

        Ответ: 7

        Что? Забыли, что 128 — это 2 в седьмой степени? Срочно повторить степени!

        Следующий пример:

        Пример 4

        Прямое применение формулы разности логарифмов:

        И как вам? Оба логарифма по отдельности ровно не считаются, зато через формулу разности — отлично!

        Ответ: 1

        Ещё пример:

        Пример 5

        А вот здесь складывать по формуле нельзя: основания разные — тройка и двойка. А формула — штука жёсткая. Раз требуются одинаковые основания, значит, так и надо.

        Но тут ничего хитрого нет: оба логарифма считаются ровно.

        Ответ: 10.                     

        Не каждый, правда, догадается, что 243 — это 3 в пятой степени, а 32 — это 2 в пятой… Но тут дело уже не в логарифмах, дело в степенях!

        Вот вам и второй практический совет.

        Степени популярных чисел надо знать. В лицо!

        Конечно, возвести двойку в седьмую степень или тройку в пятую может каждый. Не в уме, так хотя бы на черновике. Но это умение слабо помогает в работе с логарифмами, да. А вот сообразить, какое число и в какой степени скрывается за числом 128 или 243 — это уже совсем другое дело. Почувствуйте разницу, что называется!

        Поскольку умение распознавать степени в лицо пригодится не только на этом уровне, но и на следующих, вот вам небольшое задание:

        Определить, какими степенями и каких чисел являются числа:

        4; 8; 16; 27; 32; 36; 49; 64; 81; 100; 125; 128; 216; 243; 256; 343; 512; 625; 729; 1024.

        Ответы (вразброс, естественно):

        27²; 2¹⁰; 3⁶; 7²; 2⁶; 9²; 3⁴; 4³; 10²; 2⁵; 3⁵; 7³; 16²; 2⁷; 5³; 2⁸; 6²; 3³; 2⁹; 2⁴; 2²; 4⁵; 25²; 4⁴; 6³; 8²; 9³.

        Да-да! Не удивляйтесь, что ответов побольше, чем заданий. Например, 2⁸, 4⁴ и 16² — это всё 256.

        А теперь я настоятельно рекомендую взять любой учебник по школьной математике и порешать оттуда простейшие примеры на логарифмы. Порешали? Хоть что-то получилось? Тогда будем считать, что начальный уровень вы прошли. Переходим на следующий уровень.

Почти все формулы. Почти все степени. Поиск «братьев по степени».

        На этом уровне применяем почти все формулы работы с логарифмами. Кроме последней формулы перехода к новому основанию. А также закрепляем наши навыки работы со степенями.

        Поехали расширять наши возможности!

        Пример 6

        Вот тут прямое применение определения логарифма не годится: из четвёрки 128 простым возведением в степень никак не сделаешь. И формулы логарифмов непонятно как употреблять… Не беспокойтесь, сейчас всё получится.)  При маленьком условии, что вы узнали в лицо число 128. Да! Это 2 в седьмой степени! Так и запишем:

        log₄128 = log₄2⁷

        Вот и одна из формул (третья снизу) приходит на помощь. Та, где показатель степени ставится множителем перед логарифмом:

        log_axⁿ = n·log_ax

        Вот и выносим семёрку за наш логарифм. Пишем:

        log₄2⁷ = 7log₄2

        Что дальше? Дальше осталось вспомнить, что 4 = 2². Верно!

        7log₄2 = 7log₂²2

        Вот и ещё одна формулка в дело просится!) Вторая снизу, где в степень возводится основание логарифма. Только в этом случае при вынесении показателя наружу его надо перевернуть: 1/n.

        Записываем:

        Ответ: 3,5

        Вот так вот! А если бы мы не узнали в числе 128 степень двойки, то так и застряли бы на этом, в общем-то несложном примере…

        А теперь мы вплотную подошли к одному весьма и весьма полезному приёму в работе с логарифмическими и показательными выражениями. Приём этот называется «поиск братьев». Братьев по степени. И по разуму тоже.) Суть этого полезного приёма заключается в тщательном осмотре примера и распознавании одного и того же числа в разных степенях.

        Этот приём (шифровка одного и того же числа в разных степенях) — очень популярный приём в логарифмах! Да и в показательных уравнениях и неравенствах тоже. Например, числа 27 и 243 — родные братья! Да, 243 из 27 прямым возведением в натуральную степень никак не получить, но зато они — родня по тройке! Так как 27 = 3³, а 243 = 3⁵. В разобранном только что примере родственниками оказались 4 и 128. По числу 2. В общем, идея понятна, да?

        И зачем всё это нужно — распознавать степени и родственников? А затем, что примеры от этого проще становятся! И формулы свойств логарифмов сразу высвечиваются.) Особенно важно получить в примере одинаковые основания у логарифмов, ибо чем больше одинаковых значков в примере и меньше разных, тем лучше. И не нужно здесь применять формулу перехода к новому основанию: зачем же из пушки по воробьям палить.?)

        Следующий пример на братьев (или сестёр):

        Пример 7

        Вычислить:

        В примере стоит сумма логарифмов, но основания логарифмов разные — тройка и девятка. Стало быть, применять напролом формулу суммы логарифмов нельзя. Но! Первый логарифм уже считается ровно, получится просто тройка:

        log₃27 = log₃3³ = 3

        А со вторым логарифмом что? Из девятки 27 возведением в целую степень не получишь! Но зато 9 и 27 — родня! По тройке.) Самое время вспомнить, что:

        9 = 3²

        Что ж, поработаем отдельно со вторым логарифмом. Перейдём в основании от девятки к тройке. Поможет нам такое преобразование или нет — неизвестно. Но что-то делать всё-таки надо, правда? Итак, преобразовываем второй логарифм по второй (снизу) формуле — выносим степень из основания за логарифм:

        Осталось лишь сложить 3 (первый логарифм) и 3/2 (второй логарифм)

        Ответ: 4,5

        Так, с близкой роднёй разобрались. Идём дальше. Иногда пример может не соответствовать в точности формуле, а может быть лишь похожим на одну из формул. И наша задача — сначала преобразовать пример под ту или иную формулу. Как, например, этот:

        Пример 8

        Напоминаю, что запись lg означает просто логарифм по основанию 10. И всё.)

        Итак, основания логарифмов уже одинаковые — десятка. Ну прям напрашивается формула суммы логарифмов! А н-е-ет, не катит! Двойка во втором слагаемом всё портит. Коэффициент, понимаешь.) А формула применима только к чистым логарифмам, безо всяких коэффициентов. Но горевать рано! Мы эту двойку сейчас ликвидируем. Безопасно для примера.) Мы её внутрь логарифма загоним. Как? Всё по той же формуле логарифма от степени:

        log_axⁿ = n·log_ax

        Здесь как раз тот случай, когда формулу надо применять справа налево. Ни в одной другой теме школьной математики нельзя вот так красиво избавляться от мешающих коэффициентов, а в логарифмах — пожалуйста! Итак, избавляемся от двойки перед вторым логарифмом:

        2lg5 = lg5² = lg25

        Вот так. Осталось лишь сложить два логарифма по формуле логарифма произведения (опять же в применении справа налево). Вот и складываем:

        lg4 + lg25 = lg(4́·25) = lg100 = 2

        Напоминаю, что десятичные логарифмы формулу ничуть не портят, ибо они по своим свойствам ничем не отличаются от обычных!    

        Ответ: 2

        Вот вам и третий практический совет.

        Любую степень можно записать множителем перед логарифмом. И наоборот — любой числовой коэффициент можно спрятать внутрь логарифма. Если он мешает, конечно.

       Ну что, вот и состоялась наше более близкое знакомство с логарифмами! Осталось теперь с ними крепко подружиться. На следующем уровне и в следующем уроке.)

        Традиционные примеры для самостоятельного решения.

        Вычислить:

        Ответы (вразнобой): 0; 1; 2; 3; 

Как решать логарифмы егэ.

В этом видеоуроке мы рассмотрим решение довольно серьезного логарифмического уравнения, в котором не просто требуется найти корни, но и отобрать те из них, которые лежат на заданном отрезке.

Задача C1. Решите уравнение. Найдите все корни этого уравнения, принадлежащие промежутку.

Замечание по поводу логарифмический уравнений

Однако из года в год ко мне приходят ученики которые пытаются решать вот такие, прямо скажем, непростые уравнения

В результате многие начинают опасаться этой темы, а то и вовсе считать себя тупыми. Так вот, запомните: если у вас не получается решить такое уравнение, это совершенно не значит, что вы — тупые. Потому что, например, вот с таким уравнением вы справитесь практически устно:

log 2 x = 4

А если это не так, вы сейчас не читали бы этот текст, поскольку были заняты более простыми и приземленными задачами. Конечно, кто-то сейчас возразит: «А какое отношение это простейшее уравнение имеет к нашей здоровой конструкции?» Отвечаю: любое логарифмическое уравнение, каким бы сложным оно ни было, в итоге сводится вот к таким простейшим, устно решаемым конструкциям.

Разумеется, переходить от сложных логарифмических уравнений к более простым нужно не с помощью подбора или танцев с бубном, а по четким, давно определенным правилам, которые так и называются —

И именно об этих правилах мы будем говорить в сегодняшнем уроке. Поехали!

Решение логарифмического уравнения в задаче C1

Итак, решаем уравнение:

В первую очередь, когда речь заходит о логарифмических уравнениях, вспоминаем основную тактику — если можно выразиться, основное правило решения логарифмических уравнений. Заключается оно в следующем:

Теорема о канонической форме. Любое логарифмическое уравнение, что бы в него не входило, какие бы логарифмы, по какому бы основанию, и что бы в себе не c одержали, обязательно нужно привести к уравнению вида:

log a f (x ) = log a g (x )

Если мы посмотрим на наше уравнение, то заметим сразу две проблемы:

1. Слева у нас стоит сумма двух чисел , одно из которых вообще не является логарифмом.
2. Справа стоит вполне себе логарифм, однако в его основании стоит корень. А у логарифма слева — просто 2, т.е. основания логарифмов слева и справа различаются.

Итак, мы составили этакий список проблем, которые отделяют наше уравнение от того канонического уравнения , к которому нужно привести любое логарифмическое уравнение в процессе решения. Таким образом, решение нашего уравнения на данном этапе сводится к тому, чтобы устранить описанные выше две проблемы.

Любое логарифмическое уравнение решается быстро и легко, если свести его к канонической форме.

Сумма логарифмов и логарифм произведения

Давайте действовать по порядку. Сначала разберемся с конструкцией, которая стоит слева. Что мы можем сказать про сумму двух логарифмов? Давайте вспомним замечательную формулу:

log a f (x ) + log a g (x ) = log a f (x ) · g (x )

Но стоить учесть, что в нашем случае первое слагаемо вообще не является логарифмом. Значит, нужно представить единицу в виде логарифма по основанию 2 (именно 2, потому что слева стоит логарифм по основанию 2). Как это сделать? Опять вспоминаем замечательную формулу:

a = log b b a

Здесь нужно понимать: когда мы говорим «Любое основание b », то подразумеваем, что b все-таки не может быть произвольным числом. Если мы вставляем какое-то число в логарифм, на него сразу накладываются определенные ограничения , а именно: основание логарифма должно быть больше 0 и не должно быть равно 1. Иначе логарифм просто не имеет смысла. Запишем это:

0

Давайте посмотрим, что происходит в нашем случае:

1 = log 2 2 1 = log 2 2

Теперь перепишем все наше уравнение с учетом этого факта. И сразу же применяем другое правило: сумма логарифмов равна логарифму произведения аргументов. В итоге получим:

Мы получили новое уравнение. Как видим, оно уже гораздо ближе к тому каноническому равнению, к которому мы стремимся. Но есть одна проблема, мы записали ее в виде второго пункта: у наших логарифмов, которые стоят слева и справа, разные основания . Переходим к следующему шагу.

Правила вынесения степеней из логарифма

Итак у логарифма, который стоит слева, основание просто 2, а у логарифма, который стоит справа, в основании присутствует корень. Но и это не является проблемой, если вспомнить, что из оснований из аргументов логарифма можно выносить в степень. Давайте запишем одно из этих правил:

log a b n = n · log a b

Переведя на человеческий язык: можно выносить степень из основания логарифма и ставить ее спереди в качестве множителя. Число n «мигрировало» из логарифма наружу и стало коэффициентом спереди.

С тем же успехом мы можем вынести степень из основания логарифма. Выглядеть это будет так:

Другими словами, если вынести степень из аргумента логарифма, эта степень также пишется в качестве множителя перед логарифмом, но уже не в виде числа, а в виде обратного числа 1/k .

Однако и это еще не все! Мы можем объединить две данные формулы и почить следующую формулу:

Когда степень стоит и в основании, и в аргументе логарифма, мы можем сэкономить время и упростить вычисления, если сразу же вынести степени и из основания, и из аргумента. При этом то, что стояло в аргументе (в нашем случае это коэффициент n ), окажется в числителе. А то, что было степенью у основания, a k , отправится в знаменатель.

И именно эти формулы мы сейчас будем применять для того, чтобы свести наши логарифмы к одному и тому же основанию.

Прежде всего, выберем более-менее красивое основание. Очевидно, что с двойкой в основании намного приятней работать, чем с корнем. Таким образом, давайте попробуем привести второй логарифм к основанию 2. Давайте выпишем этот логарифм отдельно:

Что мы можем здесь сделать? Вспомним формулу степени с рациональным показателем. Другими словами, мы можем записать в корни в качестве степени с рациональным показателем. А затем выносим степень 1/2 и из аргумента, и из основания логарифма. Сокращаем двойки в коэффициентах в числителе и знаменателе, стоящих перед логарифмом:

Наконец, перепишем исходное уравнение с учетом новых коэффициентов:

log 2 2(9x 2 + 5) = log 2 (8x 4 + 14)

Мы получили каноническое логарифмическое уравнение. И слева, и справа у нас стоит логарифм по одному и тому же основанию 2. Помимо этих логарифмов никаких коэффициентов, никаких слагаемых ни слева, ни справа нет.

Следственно, мы можем избавиться от знака логарифма. Разумеется, с учетом области определения. Но прежде, чем это сделать, давайте вернемся назад и сделаем небольшое уточнение по поводу дробей.

Деление дроби на дробь: дополнительные соображения

Далеко не всем ученикам понятно, откуда берутся и куда деваются множители перед правым логарифмом. Запишем еще раз:

Давайте разберемся, что такое дробь. Запишем:

А теперь вспоминаем правило деления дробей: чтобы разделить на 1/2 нужно умножить на перевернутую дробь:

Разумеется, для удобства дальнейших вычислений мы можем записать двойку как 2/1 — и именно это мы наблюдаем в качестве второго коэффициента в процессе решения.

Надеюсь, теперь всем понятно, откуда берется второй коэффициент, поэтому переходим непосредственно к решению нашего канонического логарифмического уравнения.

Избавление от знака логарифма

Напоминаю, что сейчас мы можем избавиться от логарифмов и оставить следующее выражение:

2(9x 2 + 5) = 8x 4 + 14

Давайте раскроем скобки слева. Получим:

18x 2 + 10 = 8x 4 + 14

Перенесем все из левой части в правую:

8x 4 + 14 − 18x 2 − 10 = 0

Приведем подобные и получим:

8x 4 − 18x 2 + 4 = 0

Можем разделить обе части этого уравнения на 2, чтобы упростить коэффициенты, и получим:

4x 4 − 9x 2 + 2 = 0

Перед нами обычное биквадратное уравнение , и его корни легко считаются через дискриминант. Итак, запишем дискриминант:

D = 81 − 4 · 4 · 2 = 81 − 32 = 49

Прекрасно, Дискриминант «красивый», корень из него равен 7. Все, считаем сами иксы. Но в данном случае корни получатся не x , а x 2 , потому что у нас биквадратное уравнение. Итак, наши варианты:

Обратите внимание: мы извлекали корни, поэтому ответов будет два, т.к. квадрат — функция четная . И если мы напишем лишь корень из двух, то второй корень мы просто потеряем.

Теперь расписываем второй корень нашего биквадратного уравнения:

Опять же, мы извлекаем арифметический квадратный корень из обеих частей нашего уравнения и получаем два корня. Однако помните:

Недостаточно просто приравнять аргументы логарифмов в канонической форме. Помните об области определения!

Итого мы получили четыре корня. Все они действительно являются решениями нашего исходного уравнения. Взгляните: в нашем исходном логарифмическом уравнении внутри логарифмов стоит либо 9x 2 + 5 (эта функция всегда положительна), либо 8x 4 + 14 — она тоже всегда положительна. Следовательно, область определения логарифмов выполняется в любом случае, какой бы корень мы не получили, а это значит, что все четыре корня являются решениями нашего уравнения.

Прекрасно, теперь переходим ко второй части задачи.

Отбор корней логарифмического уравнения на отрезке

Отбираем из наших четырех корней те, которые лежат на отрезке [−1; 8/9]. Возвращаемся к нашим корням, и сейчас будем выполнять их отбор. Для начала предлагаю начертить координатную ось и отметить на ней концы отрезка:

Обе точки будут закрашенные. Т.е. по условию задачи нас интересует заштрихованный отрезок. Теперь давайте разбираться с корнями.

Иррациональные корни

Начнем с иррациональных корней. Заметим, что 8/9

Из этого следует, что корень из двух не попадает в интересующий нас отрезок. Аналогично мы получим и с отрицательным корнем: он меньше, чем −1, т. е. лежит левее интересующего нас отрезка.

Рациональные корни

Остается два корня: x = 1/2 и x = −1/2. Давайте заметим, что левый конец отрезка (−1) — отрицательный, а правый (8/9) — положительный. Следовательно, где-то между этими концами лежит число 0. Корень x = −1/2 будет находиться между −1 и 0, т.е. попадет в окончательный ответ. Аналогично поступаем с корнем x = 1/2. Этот корень также лежит на рассматриваемом отрезке.

Убедиться, что число 8/9 больше, чем 1/2, можно очень просто. Давайте вычтем эти числа друг из друга:

Получили дробь 7/18 > 0, а это по определению означает, что 8/9 > 1/2.

Давайте отметим подходящие корни на оси координат:

Окончательным ответом будут два корня: 1/2 и −1/2.

Сравнение иррациональный чисел: универсальный алгоритм

В заключении хотел бы еще раз вернуться к иррациональным числам. На их примере мы сейчас посмотрим, как сравнивать рациональные и иррациональные величины в математике. Для начала по между ними вот такую галочку V — знак «больше» или «меньше», но мы пока не знаем, в какую сторону он направлен. Запишем:

Зачем вообще нужны какие-то алгоритмы сравнения? Дело в том, что в данной задаче нам очень повезло: в процессе решения возникло разделяющее число 1, про которое мы точно можем сказать:

Однако далеко не всегда вы с ходу увидите такое число. Поэтому давайте попробуем сравнить наши числа «в лоб», напрямую.

Как это делается? Делаем то же самое, что и с обычными неравенствами:

1. Сначала, если бы у нас где-то были отрицательные коэффициенты, то мы умножили бы обе части неравенства на −1. Разумеется, поменяв при этом знак . Вот такая галочка V изменилась бы на такую — Λ.
2. Но в нашем случае обе стороны уже положительны, поэтому ничего менять не надо. Что действительно нужно, так это возвести обе части в квадрат , чтобы избавится от радикала.

Если при сравнении иррациональных чисел не удается с ходу подобрать разделяющий элемент, рекомендую выполнять такое сравнение «в лоб» — расписывая как обычное неравенство.

При решении это оформляется вот таким образом:

Теперь это все легко сравнивается. Дело в том, что 64/81

Все, мы получили строгое доказательство, что все числа отмечены на числовой прямой х правильно и именно в той последовательности, в которой они должны быть на самом деле. Вот к такому решению никто не придерется, поэтому запомните: если вы сразу не видите разделяющее число (в нашем случае это 1), то смело выписывайте приведенную выше конструкцию, умножайте, возводите в квадрат — и в итоге вы получите красивое неравенство. Из этого неравенства точно будет понятно, какое число больше, а какое — меньше.

Возвращаясь к нашей задаче, хотелось бы еще раз обратить ваше внимание на то, что мы делали в самом начале при решении нашего уравнения. А именно: мы внимательно посмотрели на наше исходное логарифмическое уравнение и попытались свести его к каноническому логарифмическому уравнению. Где слева и справа стоят только логарифмы — без всяких дополнительных слагаемых, коэффициентов спереди и т. д. Нам нужны не два логарифма по основанию a или b , именно логарифм, равный другому логарифму.

Кроме того, основания логарифмов также должны быть равны. При этом если уравнение составлено грамотно, то с помощью элементарных логарифмических преобразований (сумма логарифмов, преобразование числа в логарифм и т. д.) мы сведем это уравнение именно к каноническому.

Поэтому впредь, когда вы видите логарифмическое равнение, которое не решается сразу «в лоб», не стоит теряться или пробовать подобрать ответ. Достаточно выполнить следующие шаги:

1. Привести все свободные элементы к логарифму;
2. Затем эти логарифмы сложить;
3. В полученной конструкции все логарифмы привести к одному и тому же основанию.

В результате вы получите простое уравнение, которое решается элементарными средствами алгебры из материалов 8—9 класса. В общем, заходите на мой сайт, тренируйтесь решать логарифмы, решайте логарифмические уравнения как я, решайте их лучше меня. А у меня на этом все. С Вами был Павел Бердов. До новых встреч!

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
• если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.

Сбор и использование персональной информации

Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.

От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.

Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.

Какую персональную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу персональную информацию:

• Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
• Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
• Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.

Защита персональной информации

Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.

Логарифмические уравнения. Продолжаем рассматривать задачи из части В ЕГЭ по математике. Мы с вами уже рассмотрели решения некоторых уравнений в статьях « » , « » . В этой статье рассмотрим логарифмические уравнения. Сразу скажу, что никаких сложных преобразований при решении таких уравнений на ЕГЭ не будет. Они просты.

Достаточно знать и понимать основное логарифмическое тождество, знать свойства логарифма. Обратите внимание на то, то после решения ОБЯЗАТЕЛЬНО нужно сделать проверку — подставить полученное значение в исходное уравнение и вычислить, в итоге должно получиться верное равенство.

Определение :

Логарифмом числа a по основанию b называется показатель степени, в который нужно возвести b, чтобы получить a.

Например:

Log 3 9 = 2, так как 3 2 = 9

Свойства логарифмов:

Частные случаи логарифмов:

Решим задачи. В первом примере мы сделаем проверку. В последующих проверку сделайте самостоятельно.

Найдите корень уравнения: log 3 (4–x) = 4

Так как log b a = x b x = a, то

3 4 = 4 – x

x = 4 – 81

x = – 77

Проверка:

log 3 (4–(–77)) = 4

log 3 81 = 4

3 4 = 81 Верно.

Ответ: – 77

Решите самостоятельно:

Найдите корень уравнения: log 2 (4 – x) = 7

Найдите корень уравнения log 5 (4 + x) = 2

Используем основное логарифмическое тождество.

Так как log a b = x b x = a, то

5 2 = 4 + x

x =5 2 – 4

x = 21

Проверка:

log 5 (4 + 21) = 2

log 5 25 = 2

5 2 = 25 Верно.

Ответ: 21

Найдите корень уравнения log 3 (14 – x) = log 3 5.

Имеет место следующее свойство, смысл его таков: если в левой и правой частях уравнения имеем логарифмы с одинаковым основанием, то можем приравнять выражения, стоящие под знаками логарифмов.

14 – x = 5

x = 9

Сделайте проверку.

Ответ: 9

Решите самостоятельно:

Найдите корень уравнения log 5 (5 – x) = log 5 3.

Найдите корень уравнения: log 4 (x + 3) = log 4 (4x – 15).

Если log c a = log c b, то a = b

x + 3 = 4x – 15

3x = 18

x = 6

Сделайте проверку.

Ответ: 6

Найдите корень уравнения log 1/8 (13 – x) = – 2.

(1/8) –2 = 13 – x

8 2 = 13 – x

x = 13 – 64

x = – 51

Сделайте проверку.

Небольшое дополнение – здесь используется свойство

степени ().

Ответ: – 51

Решите самостоятельно:

Найдите корень уравнения: log 1/7 (7 – x) = – 2

Найдите корень уравнения log 2 (4 – x) = 2 log 2 5.

Преобразуем правую часть. воспользуемся свойством:

log a b m = m∙log a b

log 2 (4 – x) = log 2 5 2

Если log c a = log c b, то a = b

4 – x = 5 2

4 – x = 25

x = – 21

Сделайте проверку.

Ответ: – 21

Решите самостоятельно:

Найдите корень уравнения: log 5 (5 – x) = 2 log 5 3

Решите уравнение log 5 (x 2 + 4x) = log 5 (x 2 + 11)

Если log c a = log c b, то a = b

x 2 + 4x = x 2 + 11

4x = 11

x = 2,75

Сделайте проверку.

Ответ: 2,75

Решите самостоятельно:

Найдите корень уравнения log 5 (x 2 + x) = log 5 (x 2 + 10).

Решите уравнение log 2 (2 – x) = log 2 (2 – 3x) +1.

Необходимо с правой стороны уравнения получить выражение вида:

log 2 (……)

Представляем 1 как логарифм с основанием 2:

1 = log 2 2

log с (ab) = log с a + log с b

log 2 (2 – x) = log 2 (2 – 3x) + log 2 2

Получаем:

log 2 (2 – x) = log 2 2 (2 – 3x)

Если log c a = log c b, то a = b, значит

2 – x = 4 – 6x

5x = 2

x = 0,4

Сделайте проверку.

Ответ: 0,4

Решите самостоятельно: Далее необходимо решить квадратное уравнение. Кстати,

корни равны 6 и – 4.

Корень «– 4″ не является решением, так как основание логарифма должно быть больше нуля, а при » – 4″ оно равно « – 5». Решением является корень 6. Сделайте проверку.

Ответ: 6.

Решите самостоятельно:

Решите уравнение log x –5 49 = 2. Если уравнение имеет более одного корня, в ответе укажите меньший из них.

Как вы убедились, никаких сложных преобразований с логарифмическими уравнениями нет. Достаточно знать свойства логарифма и уметь применять их. В задачах ЕГЭ, связанных с преобразованием логарифмических выражений, выполняются более серьёзные преобразования и требуются более глубокие навыки в решении. Такие примеры мы рассмотрим, не пропустите! Успехов вам!!!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Предварительное исчисление по алгебре — Логарифмическое вычитание и деление с одинаковыми основаниями

Вопрос задан 2 года, 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 409 раз

$\begingroup$

Я заржавел в логарифмах. Каков подход к такой проблеме? Любые подсказки будут оценены.

Я думаю, что вычитание числителя и знаменателя может стать делением, так как основания одинаковы? 9b$ понадобится здесь. Затем вы можете сделать \начать{выравнивать*} \ гидроразрыва {\ log_2 24 — \ гидроразрыва 12 \ log_2 72} {\ log_3 18 — \ гидроразрыва 13 \ log_3 72} знак равно \frac{\log_2 24 — \log_2 \sqrt{72}} {\log_3 18 — \log_3 \sqrt[3]{72}} \\ знак равно \ гидроразрыва {\ log_2 \ гидроразрыва {24} {\ sqrt {72}}} {\ log_3 \ гидроразрыва {18} {\ sqrt [3] {72}}} \\ знак равно \ гидроразрыва {\ log_2 \ гидроразрыва {24} {3 \ кв. 8}} {\ log_3 \ гидроразрыва {18} {2 \ sqrt [3] {9}}} \\ знак равно \ гидроразрыва {\ log_2 \ гидроразрыва {8} {\ sqrt 8}} {\ log_3 \ гидроразрыва {9} {\ sqrt [3] {9}}} \\ знак равно \frac{\log_2 8 — \log_2 \sqrt 8} {\log_3 92 \справа)} \\ &\quad{}= \frac{3\log_2 2 + \log_2 3 — \frac{1}{2} \left( 3\log_2 2 + 2\log_2 3 \right)}{\log_3 2 + 2\log_3 3 — \frac{1}{3} \left( 3\log_3 2 + 2\log_3 3 \right)} \\ &\quad{}= \frac{3 + \log_2 3 — \frac{1}{2} \left( 3 + 2\log_2 3 \right)}{\log_3 2 + 2 — \frac{1}{3 } \влево( 3\log_3 2 + 2 \вправо)} \\ &\quad{}= \frac{3 + \log_2 3 — \frac{3}{2} — \log_2 3 }{\log_3 2 + 2 — \log_3 2 — \frac{2}{3}} \\ &\quad{}= \frac{3 — \frac{3}{2}}{2 — \frac{2}{3}} \cdot \frac{6}{6} \\ &\quad{}= \frac{18-9q)} = \log_q(p)$

$\endgroup$

$\begingroup$

Да, вычитания могут стать делением, а дроби могут стать корнями плюс $\log_a b =\frac 1 {\log_b a}$

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Умножение и деление логарифмов — Математика средней школы

• Войти
• Биографии репетитора
• Подготовка к тесту

  СРЕДНЯЯ ШКОЛА

  • ACT Репетиторство
  • SAT Репетиторство
  • Репетиторство PSAT
  • ASPIRE Репетиторство
  • ШСАТ Репетиторство
  • Репетиторство STAAR

  ВЫСШАЯ ШКОЛА

  • Репетиторство MCAT
  • Репетиторство GRE
  • Репетиторство по LSAT
  • Репетиторство по GMAT

  К-8

  • Репетиторство AIMS
  • Репетиторство по HSPT
  • Репетиторство ISEE
  • Репетиторство ISAT
  • Репетиторство по SSAT
  • Репетиторство STAAR

  Поиск 50+ тестов

• Академическое обучение

  репетиторство по математике

  • Алгебра
  • Исчисление
  • Элементарная математика
  • Геометрия
  • Предварительный расчет
  • Статистика
  • Тригонометрия

  Репетиторство по естественным наукам

  • Анатомия
  • Биология
  • Химия
  • Физика
  • Физиология

  иностранные языки

  • французский
  • немецкий
  • Латинский
  • Китайский мандарин
  • Испанский

  начальное обучение

  • Чтение
  • Акустика
  • Элементарная математика

  прочее

  • Бухгалтерия
  • Информатика
  • Экономика
  • Английский
  • Финансы
  • История
  • Письмо
  • Лето

  Поиск по 350+ темам

• О
  • Обзор видео
  • Процесс выбора наставника
  • Онлайн-репетиторство
  • Мобильное обучение
  • Мгновенное обучение
  • Как мы работаем
  • Наша гарантия
  • Влияние репетиторства
  • Обзоры и отзывы
  • Освещение в СМИ
  • О преподавателях университета

Звоните прямо сейчас, чтобы записаться на обучение:

(888) 888-0446

Все ресурсы по математике для старших классов

8 Диагностические тесты 613 практических тестов Вопрос дня Карточки Learn by Concept

Справка по математике для старших классов » Алгебра II » Математические отношения и основные графики » Логарифмы » Упрощение логарифмов » Умножение и деление логарифмов

Упростить .

Возможные ответы:

Правильный ответ:

Объяснение:

Использование свойств журналов. Объяснение:

Вызов правила журнала: 

В данном конкретном случае  и . Таким образом, наш ответ .

Отчет Ошибка

Используйте свойства логарифмов для решения следующего уравнения:

Возможные ответы:

No Real Solutions

. Правильная Ответ: 9000

111111211212129000

1111112121212 9000

111.

Объяснение:

Поскольку основания журналов одинаковы, а логарифмы добавлены, аргументы можно перемножать. Затем упростим правую часть уравнения:

Логарифм может быть преобразован в экспоненциальную форму:

Фактор Уравнение:

Хотя есть два раствора для уравнения, логарифмы не могут быть отрицательными. Поэтому единственным реальным решением является .

Сообщить об ошибке

Что из следующего представляет собой упрощенную форму ?

Возможные ответы:

Правильный ответ:

Объяснение:

Правило сложения логарифмов следующее: 

.

В качестве приложения к этому.

Сообщить об ошибке

Упростите выражение, используя логарифмические тождества.

Возможные ответы:

Выражение не может быть упрощено0005

Объяснение:

Логарифм дроби равен логарифму числителя минус логарифм знаменателя.

Если мы встретим два логарифма с одинаковым основанием, мы, вероятно, сможем их объединить. В этом случае мы можем использовать инверсию приведенного выше тождества.

Сообщить об ошибке

Уведомление об авторских правах

Посмотреть репетиторов

Owen E
Сертифицированный репетитор

Канзасский университет, бакалавриат, английский язык. Канзасский университет, магистр, TESOL.

Посмотреть репетиторов

Джесси
Сертифицированный репетитор

Центральный Вашингтонский университет, бакалавр искусств, биология, общие.

Посмотреть репетиторов

Мэллори
Сертифицированный репетитор

Университет друзей, бакалавр наук, преподавание в начальной школе. Государственный университет Уичито, магистр образования, образование…

Все ресурсы по математике для старших классов

8 диагностических тестов 613 практических тестов Вопрос дня Карточки Learn by Concept

Как вы делите бревна?

Подразделение. Правило при делении двух значений с одинаковым основанием заключается в вычитании показателей степени. Следовательно, правилом деления является вычитание логарифмов. Лог частного — это разница логов.

Этот закон говорит нам, как сложить два логарифма. Сложение журнала A и журнала B дает логарифм произведения A и B, то есть журнал AB. В расчетах используется одно и то же основание, в данном случае 10. … Одна и та же база, в данном случае e, используется во всех вычислениях.

Еще вопрос, как умножать и делить бревна?

Правило состоит в том, что вы сохраняете базу и добавляете показатели степени. Помните, что логарифмы — это показатели степени, и при умножении вы будете складывать логарифмы. Лог продукта – это сумма логов.

Кроме того, является ли журнал журналом B? Законы применимы к логарифмам по любому основанию, но одно и то же основание должно использоваться во всех вычислениях. … Добавление журнала A и журнала B приводит к логарифму произведения A и B, то есть к журналу AB.

Соответственно лог лог можно взять? Логарифм является обратным показателем степени. … Это соотношение позволяет удалить логарифмы из уравнения, возведя обе части в тот же показатель степени, что и основание логарифма. Если уравнение содержит более одного логарифма, они должны иметь одинаковое основание, чтобы это работало.

Какие 4 закона логарифмов?

– Существует четыре следующих математических формулы логарифмирования: ● Закон правила произведения:
– loga (MN) = loga M + loga N. ● Закон правила частного:
– лога (M/N) = лога М – лога N. ● Степенной закон правила:
– IogaMn = n йога М. ● Изменение основного закона правила:

Что такое второй закон логарифмов?

Второй Закон. журнал A — журнал B = журнал. A. B. Итак, вычитание журнала B из журнала A дает журнал A.

Каковы правила логарифмирования?

Правило или особый случай Формула
——————— ——————-
Произведение ln(xy)=ln(x)+ln(y)
Частное ln(x/y)=ln(x )−ln(y)
Логарифм мощности ln(xy)=yln(x)
Логарифм e ln(e)=1

Какова характеристика журнала?

Целая часть десятичного логарифма называется характеристикой, а неотрицательная десятичная часть называется мантисса. Допустим, log 39,2 = 1,5933, тогда 1 — характеристика, а 5933 — мантисса логарифма. Если лог. 009423 = – 3 + .

Как умножить бревна?

По какому правилу умножаются два значения с одинаковым основанием вместе (x2 * x3)? Правило состоит в том, что вы сохраняете базу и добавляете показатели степени. Помните, что логарифмы — это показатели степени, и при умножении вы будете складывать логарифмы. Лог продукта – это сумма логов.

Как найти ограничения логарифмической функции?

Законы логарифмов: основание b в логарифмической функции должно быть положительным. Для экспонент это условие гарантировало, что выходы bx всегда были положительными. Для логарифмов это ограничение, согласно которому входные данные всегда должны быть положительными. Логарифмы живут полностью справа от оси Y.

Как найти правило логарифмической функции?

Поскольку eln(x/y)=eln(x)−ln(y), мы можем заключить, что правило отношения для логарифмов имеет вид ln(x/y)=ln(x)−ln(y). (Этот последний шаг мог бы следовать, например, из логарифмирования обеих частей eln(x/y)=eln(x)−ln(y), как мы сделали на последнем шаге для правила произведения.)

Какие два типа логарифмов существуют?

Узнав о логарифмах, мы можем отметить, что основанием логарифмической функции может быть любое число, кроме 1 и нуля. Однако есть еще два специальных типа логарифмов, которые часто используются в математике. Это десятичный логарифм и натуральный логарифм.

Каковы характеристики логарифмических функций?

имеют некоторые общие характеристики. Логарифмические функции являются взаимно однозначными функциями. график проходит тест горизонтальной линии на функциональную инверсию. график асимптотичен по отношению к оси y — подходит очень, очень близко к оси y, но в данном случае не касается ее и не пересекает ее.

Как решить логарифмическое умножение?

Просмотреть видео на YouTube

Как найти домен и область значений логарифмической функции?

Таким образом, областью определения логарифмической функции y=logbx является множество положительных действительных чисел, а областью значений является множество действительных чисел.