Теория функций комплексного переменного. Поле комплексных чисел, страница 6
Математика \ Математика
11 Основные функции комплексной переменной
Напомним определение комплексной экспоненты – . Тогда
— разложение в ряд Маклорена. Радиус сходимости этого ряда равен +∞, значит комплексная экспонента аналитична на всей комплексной плоскости и
(exp z)’=exp z; exp 0=1. (2)
Первое равенство здесь следует, например, из теоремы о почленном дифференцировании степенного ряда.
11.1 Тригонометрические и гиперболические функции
Синусом комплексного переменного называется функция
Косинус комплексного переменного есть функция
Гиперболический синус комплексного переменного определяется так:
Гиперболический косинус комплексного переменного — это функция
Отметим некоторые свойства вновь введеных функций.
A. Если x∈ ℝ , то cos x, sin x, ch x, sh x∈ ℝ .
Б. Имеет место следующая связь тригонометрических и гиперболических функций:
cos iz=ch z; sin iz=ish z, ch iz=cos z; sh iz=isin z.
В. Основные тригонометрическое и гиперболическое тождества:
cos2z+sin2z=1; ch2z-sh2z=1.
Доказательство основного гиперболического тождества.
Основное тригонометрическое тождество следует из оновного гиперболического тождества при учете связи тригонометрических и гиперболических функций (см. свойство Б)
Г Формулы сложения:
В частности,
Д. Для вычисления производных тригонометрических и гиперболических функций следует применить теорему о почленном дифференцировании степенного ряда. Получим:
(cos z)’=-sin z; (sin
z)’=cos z; (ch z)’=sh z; (sh z)’=ch z.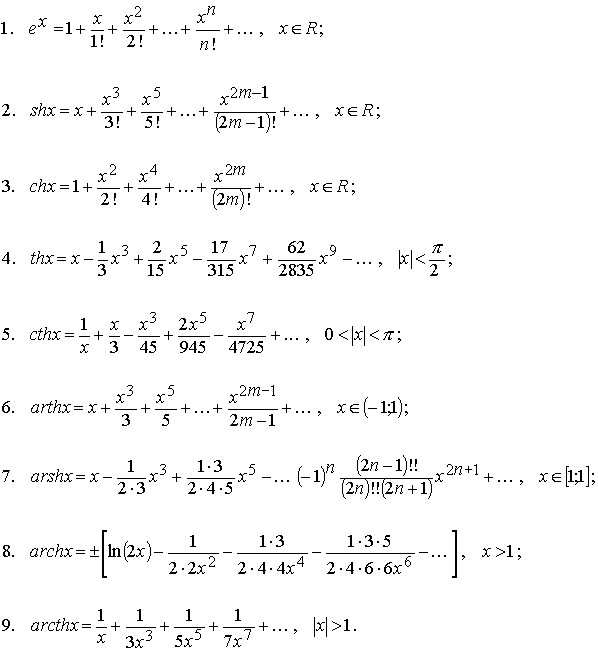
Е. Функции cos z, ch z четны, а функции sin z, sh z нечетны.
Ж. (Периодичность) Функция ez периодична с периодом 2π i. Функции cos z, sin z периодичны с периодом 2π , а функции ch z, sh z периодичны с периодом 2πi. Более того,
Применяя формулы суммы, получаем
З. Разложения на действительную и мнимую части:
Если однозначная аналитическая функция f(z) отображает биективно область D на область G, то D называется областью однолистности.
И. Область Dk={ x+iy | 2π k≤ y<2π (k+1)} для любого целого k является областью однолистности функции ez, которая отображает ее на область ℂ* .
Доказательство. Из соотношения (5) следует инъективность
отображения exp:Dk→ ℂ
. Пусть w — любое ненулевое комплексное число. Тогда, решая уравнения ex=|w|
и
eiy =w/|w| с действительными переменными x и y (y выбираем из
полуинтеравала [2πk, 2π (k+1))), получим z=x+iy∈Dk
такое, что exp z=w.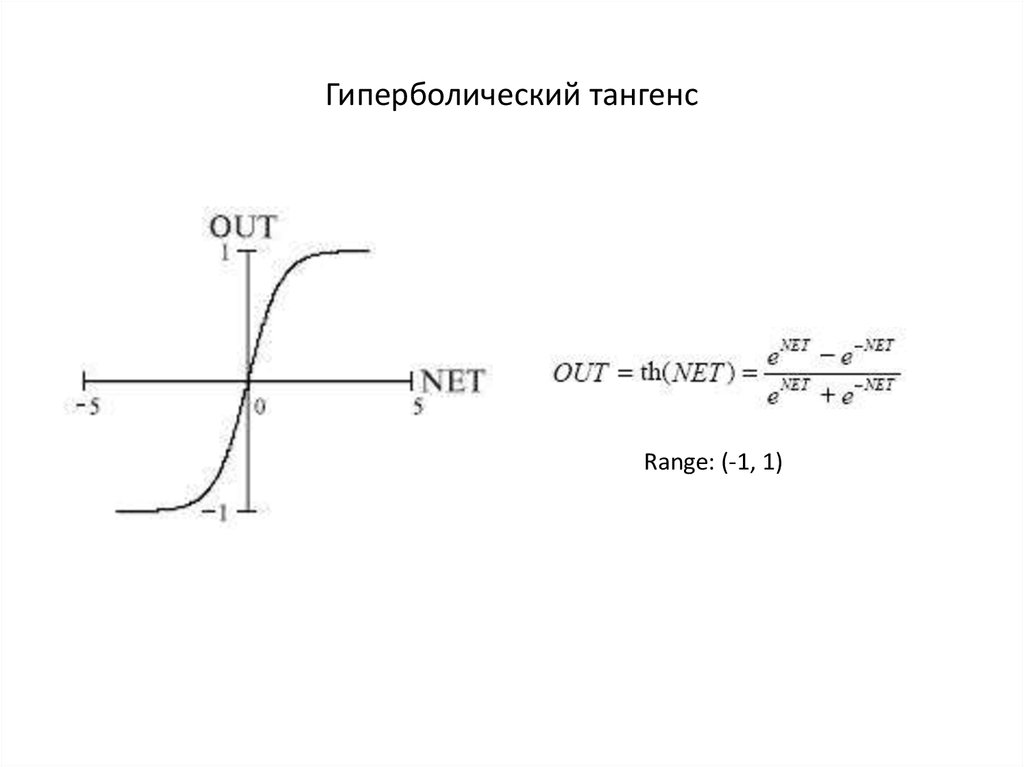 Сюръективность доказана.
Сюръективность доказана.
Следствием предыдущего свойства является
К. Область значений. Область значений функций cos z, sin z, ch z, sh z есть все поле комплексных чисел.
Л. Нули Решением уравнения sin z=0 является множество {πk | k∈ ℤ } . Нули функции cos z — множество { π /2+πk | k∈ ℤ } . Нулями функции sh z является множество { πki | k∈ ℤ} , а нули функции ch z — множество { π/2i+πki | k∈ ℤ } .
Доказательство. Имеет место соотношения sin z=0 тогда и только тогда, когда eiz -e-iz =0 Это равносильно соотношению e2iz =0, что дает 2iz=2πik. Окончательно, z=2πk (k∈ ℤ ). Аналогично доказываются утверждения для остальных функций.□
Функция tg z=sin z /cos z называется тангенсом, а функция th z= sh z/ ch z называется гиперболическим тангенсом. Производные тангенсов вычисляются c использованием известного правила «производная отношения»:
(tg z)’=1/cos2z , (th z)’= 1/ch2z .
Область допустимых значений тангенса tg z есть многосвязная область ℂ \{π /2+πk | k∈ ℤ }
12 Аргумент комплексного числа
Главным значением аргумента ненулевого комплексного числа z назовем то единственное действительное число 𝜑 ∈ [0,2π ), для которого z /| z| =exp(i𝜑 ). Обозначаем главное значение аргумента как arg z.
Всевозможные решения уравнения exp(i𝜑 )= z /| z| относительно переменной 𝜑, т.е. множество {arg z+2π k ∣ k∈ ℤ } назовем аргументом комплексного числа z и обозначим Arg z. Таким образом Arg z — многозначная функция.
Скачать файл
Гиперболические функции — Математика — 11 класс
Бюджетное муниципальное общеобразовательное учреждение
«Школа № 31»
Школьная Академия Наук «Созвездие»
СЕКЦИЯ
математики, информатики, физики
Доклад
На тему «Некоторые практические приложения гиперболических функций»
Выполнила учитель математики
Кряквина Лилия Низамитдиновна
г.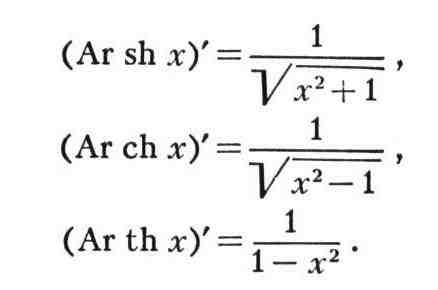 Ростов-на-Дону
Ростов-на-Дону
2019 г.
Оглавление
стр.
Введение………………………………………………………………3
Результаты исследования…………………………………………….5
Выводы…………………………………………………………………9
Приложение…………………………………………………………..10
Литература……………………………………………………………13
1. Введение
Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени.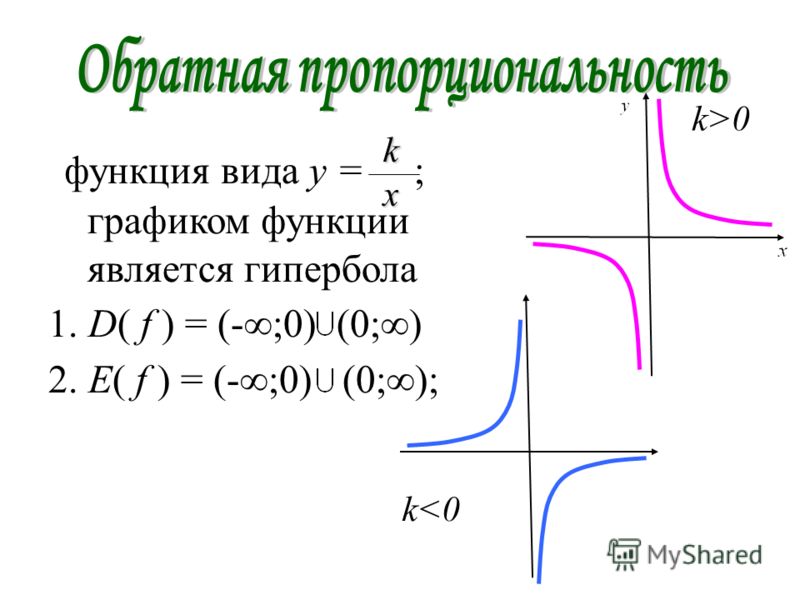 Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы1.
Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы1.
Современная математика рассматривает гиперболические функции, как пары экспоненциальной функции, но Риккати исследовал их свойства, используя только геометрические свойства гиперболы х² — y² = 1 или 2xy = 1. Он использовал геометрические методы, хотя он был знаком с работами Эйлера, предшествовавших выходу книги Риккати.
Над гиперболическими функциями Риккати работал вместе с Джироламо Саладини. Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.
Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.
Цель данной работы – изучить гиперболические функции и их применение.
В задачи работы входит изучение следующих вопросов:
1. Раскрыть понятие о гиперболических функциях.
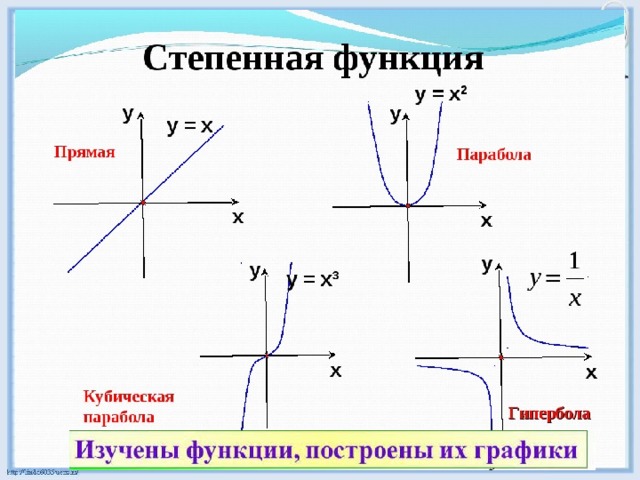
2. Изучить основные свойства и графики гиперболических функций.
3. Рассмотреть применение гиперболических синуса и косинуса при решении уравнения с параметром.
Актуальность темы заключается в том, что прикладной характер гиперболических функций достаточно широк (применение в физике, информатике, архитектуре).
Новизна темы базируется на оригинальном, нестандартном методе решения уравнения с параметром. Кроме того, в работе предоставлен материал, выходящий за рамки школьного курса.
Кроме того, в работе предоставлен материал, выходящий за рамки школьного курса.
2. Результаты исследования. 2.1. Понятие гиперболических функций
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями2.
Гиперболические функции задаются следующими формулами:
гиперболический синус:
гиперболический косинус:
гиперболический тангенс:
гиперболический котангенс:
,
Иногда также определяются гиперболические секанс и косеканс:
,
.
Ввиду соотношения гиперболические функции дают параметрическое представление гиперболы x2 − y2 = 1 ( , ). При этом аргумент t = 2S, где S — площадь криволинейного треугольника, взятая со знаком «+», если сектор лежит выше оси OX, и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
При этом аргумент t = 2S, где S — площадь криволинейного треугольника, взятая со знаком «+», если сектор лежит выше оси OX, и «−» в противоположном случае. Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
2.2. Свойства гиперболических функций
Важные тождества
Чётность:
Формулы сложения:
Формулы двойного угла:
Формулы понижения степени
2. 3 Примеры применения гиперболических функций при решении задач
Задание Доказать тождество
Доказательство По определению
Подставим эти выражения в левую часть заданного равенства:
Что и требовалось доказать.
Задание Найти приближенное значение
Решение По определению , подставляем значение , получим
В последнее выражение подставим значение экспоненты :
Ответ
Пример использования гиперболических функций при решений уравнений с параметрами.
П ример 3
Найти корни уравнения .
Решение
Пусть , тогда ; , . Исходное уравнение равносильно уравнению
; ;
; .
Имеем = b; Введем переменную
Таким образом, получили .
Найдем дискриминант уравнения: .
Если
0.
При .
;
.
Ответ:
3. Выводы
Выводы
Представленный в работе материал нетривиален и полезен для приложений. Выше рассмотренные гиперболические функции имеют большую практическую значимость, поскольку их использование является важным в физике, архитектуре, информатике. Гиперболические функции часто встречаются в теории относительности. Однородная веревка или цепочка, свободно подвешенная за свои концы, приобретает форму графика функции (в связи с чем график гиперболического косинуса иногда называют цепной линией). Это обстоятельство используется при проектировании арок, поскольку форма арки в виде перевёрнутой цепной линии наиболее удачно распределяет нагрузку. Гиперболический тангенс используют в качестве функции активации в нейронных сетях. Гиперболические функции используются при сжатии информации. Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций.
В работе показан оригинальный приём решения уравнения с параметром, позволяющий достаточно сложное уравнение свести к стандартному квадратному уравнению с параметром. Естественно, что это даёт хороший опыт работы с заданиями повышенного уровня сложности.
4. Приложения
Графики гиперболических функций даны на рис. 1.
Рисунок 1.
Гиперболические функции в компьютерных программах
Гиперболические функции представлены следующим набором:
sinh — гиперболический синус;
cosh — гиперболический косинус;
tanh — гиперболический тангенс;
sech — гиперболический секанс;
csch — гиперболический косеканс;
coth — гиперболический котангенс.
Примеры применения гиперболических функций представлены ниже:
На рис. 2 сверху представлены графики гиперболического синуса, косинуса и тангенса. По ним можно судить о поведении этих функций.
2 сверху представлены графики гиперболического синуса, косинуса и тангенса. По ним можно судить о поведении этих функций.
Рис. 2. Графики основных гиперболических и обратных гиперболических функций
5. Литература
Бугров Я.С., Никольский С.М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 2004.
Ильин В. А., Позняк Э. Г. Основы математического анализа: В 2-х ч. Часть I: Учеб. для вузов. — 7-е изд. — М.: ФИЗМАТЛИТ, 2004.
Казимиров Н.И. Математический анализ. Конспект лекций для специальности «Физика». — Петрозаводск, 2002.
Начало математического анализа: Учеб.-метод. пособие / Авт.-сост.: А.Я. Алеева, Ю.Ю. Громов, О.Г. Иванова, А.В. Лагутин. — Тамбов: Изд-во Тамб. гос. техн. ун-та, 2001
Стахов A.П. Обобщенные Золотые Сечения и новый подход к геометрическому определению числа // Украинский математический журнал, 2004, том 56, № 8.
Стахов А.П. Формула Кассини // М.: «Академия Тринитаризма», Эл № 77-6567, публ.12542, 01.11.2005.
Владимиров Ю.С. Метафизика. – M.: Бином, 2002.
Бугров Я. С., Никольский С. М. Высшая математика. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. — Москва: Наука, 1998г.
Шерватов В.Г. Гиперболические функции. Государственное издательство технико – теоретической литературы.М.2003г.
1 Начало математического анализа: Учеб.-метод. пособие / Авт.-сост.: А.Я. Алеева, Ю.Ю. Громов, О.Г. Иванова, А.В. Лагутин. — Тамбов: Изд-во Тамб. гос. техн. ун-та, 2001. С. 193.
2 Аксёнов А.П. Математический анализ. Интегралы, зависящие от параметра. Двойные интегралы. Криволинейные интегралы. Учебное пособие. — СПб.: Изд-во «НЕСТОР», 2000. С. 163.
| Гиперболические функции Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Дальнейшее исследование свойств гиперболических функций было проведено Ламбертом. Риккати применял для гиперболических функций обозначения Sh и Ch. В дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой. Например, в Энциклопедии Брокгауза и Эфрона используются обозначения sinhyp, coshyp, в русскоязычной литературе закрепились обозначения sh, ch, в англоязычной закрепились sinh,cosh.Гиперболические функции часто встречаются при вычислении различных интегралов. Некоторые интегралы от рациональных функций и от функций, содержащих радикалы, довольно просто выполняются с помощью замен переменных с использованием гиперболических функций. Гиперболические функции задаются следующими формулами:
(в англоязычной литературе обозначается sinh(x))
(в англоязычной литературе обозначается tanh(x))
, Иногда также определяются
В связи с особенностями написания операторов гиперболических функций в русском языке появился ряд жаргонных наименований этих функций. Простейшее (и наиболее распространённое) словообразование использует уточняющую приставку «гипер-» к названиям тригонометрических функций. Также существуют такие жаргонные названия:
sh(x), ch(x), th(x), cth(x) Геометрическое определение Ввиду соотношения ch²t-sh²t=1, гиперболические функции дают параметрическое представление гиперболы x2 − y2 = 1 (x=cht, y=sht). При этом аргумент t = 2S, где S — площадь криволинейного треугольника OQR, взятая со знаком «+», если сектор лежит выше оси OX, и «−» в противоположном случае. Связь с тригонометрическими функциями Гиперболические функции выражаются через тригонометрические функции от мнимого аргумента. . . sin (х) = Im(e) cos(x) = Re(e), где e ix = cos (x) + i sin(x). Функция Гудермана, названная в честь Кристофа Гудермана (1798—1852), связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел. Она определяется как Имеют место также следующие тождества: , , , , Важные тождества
Неравенства При всех выполняется: , Разложение в степенные ряды (Ряд Лорана) Здесь B2n — числа Бернулли. Обратные гиперболические функции Читаются ареа… (-синус и т. д.) — от лат. «area» — «площадь». — обратный гиперболический синус, гиперболический арксинус, ареасинус: — обратный гиперболический косинус, гиперболический арккосинус, ареакосинус. — обратный гиперболический тангенс, гиперболический арктангенс, ареатангенс. — обратный гиперболический котангенс, гиперболический арккотангенс, ареакотангенс. — обратный гиперболический секанс, гиперболический арксеканс, ареасеканс. — обратный гиперболический косеканс, гиперболический арккосеканс, ареакосеканс. Связь между некоторыми обратными гиперболическими и обратными тригонометрическими функциями: где i — мнимая единица. Эти функции имеют следующее разложение в ряд: В зарубежной литературе обратные гиперболические функции часто обозначают посредством знака минус первой степени: например, пишут как (причём обозначает другую функцию — ), и т. Каталог: rest -> eratos жүктеу/скачать 261 Kb. Достарыңызбен бөлісу: |
Гиперболические функции — значение, формулы, примеры
Гиперболические функции определяются в математике аналогично тригонометрическим функциям. Как следует из названия, график гиперболической функции представляет собой прямоугольную гиперболу, и ее формулу часто можно увидеть в формулах гиперболы. Они определяются с помощью гиперболы вместо единичного круга, как в случае тригонометрии. Гиперболические функции аналогичны тригонометрическим функциям, но выводятся из гиперболы, как тригонометрические функции выводятся из единичного круга.
Гиперболические функции выражаются через показательную функцию e x . Существует шесть гиперболических функций: sinh x, ch x, tanh x, coth x, sech x, csch x. В этой статье мы определим эти гиперболические функции и их свойства, графики, тождества, производные и т. д. вместе с некоторыми решенными примерами.
В этой статье мы определим эти гиперболические функции и их свойства, графики, тождества, производные и т. д. вместе с некоторыми решенными примерами.
| 1. | Что такое гиперболические функции? |
| 2. | Гиперболическое значение |
| 3. | Формулы гиперболических функций |
| 4. | Графики гиперболических функций |
| 5. | Область и диапазон гиперболических функций |
| 6. | Свойства гиперболических функций |
| 7. | Идентификаторы гиперболических триггеров |
| 8. | Дифференцирование и интегрирование гиперболических функций |
| 9. | Обратные гиперболические функции |
| 10. | Часто задаваемые вопросы о гиперболических функциях |
Что такое гиперболические функции?
Как обычная тригонометрическая функция определяется для окружности или на ней, так и гиперболическая функция определяется для гиперболы. В обычной тригонометрии мы использовали синус, косинус и другие функции. Точно так же для гиперболических функций мы используем sinh, cosh, tanh, coth, sech и csch. Как и в обычной тригонометрической функции, мы знаем, что координаты точек на единичной окружности равны (cos θ, sin θ), аналогично в гиперболических функциях (ch θ, sh θ) образует правую половину равносторонней гиперболы.
В обычной тригонометрии мы использовали синус, косинус и другие функции. Точно так же для гиперболических функций мы используем sinh, cosh, tanh, coth, sech и csch. Как и в обычной тригонометрической функции, мы знаем, что координаты точек на единичной окружности равны (cos θ, sin θ), аналогично в гиперболических функциях (ch θ, sh θ) образует правую половину равносторонней гиперболы.
Эти функции могут быть решениями различных линейных дифференциальных уравнений, кубических уравнений и уравнения Лапласа. Шесть основных гиперболических функций:
- Гиперболический синус или синус x
- Гиперболический косинус или кош x
- Гиперболический тангенс или тангенс x
- Гиперболический косеканс или косеканс x
- Гиперболический секанс или sech x
- Гиперболический котангенс или кот x
Гиперболическое значение
Гиперболические функции определяются аналогично тригонометрическим функциям. У нас есть шесть основных гиперболических функций, а именно sh x, ch x, th th, coth x, sech x и cosech x. Они могут быть выражены как комбинация экспоненциальной функции. Эти функции выводятся с использованием гиперболы точно так же, как тригонометрические функции выводятся с использованием единичной окружности.
Они могут быть выражены как комбинация экспоненциальной функции. Эти функции выводятся с использованием гиперболы точно так же, как тригонометрические функции выводятся с использованием единичной окружности.
Формулы гиперболических функций
Гиперболические функции определяются через алгебраические выражения, включающие экспоненциальную функцию (e x ) и его обратные экспоненциальные функции (e -x ), где e — постоянная Эйлера. Давайте посмотрим все их формулы одну за другой:
- Sinh x: это нечетная часть экспоненциальной функции. Алгебраическое выражение для функции гиперболического синуса:
sh x = (e x — e -x )/2 - Cosh x: это четная часть экспоненциальной функции. Алгебраическое выражение для функции гиперболического косинуса:
ch х = (e х + е -х )/2 - Tanh x: tanh x = sh x/cosh x = (e x — e -x )/(e x + e -x )
- Coth x: coth x = ch x/sinh x = (e x + e -x )/(e x — e -x )
- Sech x: sech x = 1/cosh x = 2/(e x + e -x )
- Кщ х: кщ х = 2/(е х — е -х )
Графики гиперболических функций
График гиперболической функции, синонимичной своему названию, представляет собой прямоугольную гиперболу, и ее формулу часто можно увидеть в формулах гиперболы. Ниже приведена схема графиков различных гиперболических функций:
Ниже приведена схема графиков различных гиперболических функций:
Область и диапазон гиперболических функций
Глядя на график гиперболической функции, мы можем определить ее область определения и область значений. Области и диапазоны этих функций приведены в следующей таблице:
| Гиперболическая функция | Домен | Диапазон |
|---|---|---|
| х | (-∞, +∞) | (-∞, +∞) |
| шпон х | (-∞, +∞) | [1, ∞) |
| танх x | (-∞, +∞) | (-1, 1) |
| ткань x | (-∞ , 0) У (0 , + ∞) | (-∞ , — 1) У (1 , +∞) |
| сек х | (-∞, +∞) | (0 , 1] |
| сч х | (-∞, 0) У (0, +∞) | (-∞, 0) У (0, +∞) |
Свойства гиперболических функций
Свойства гиперболических функций аналогичны свойствам тригонометрических функций.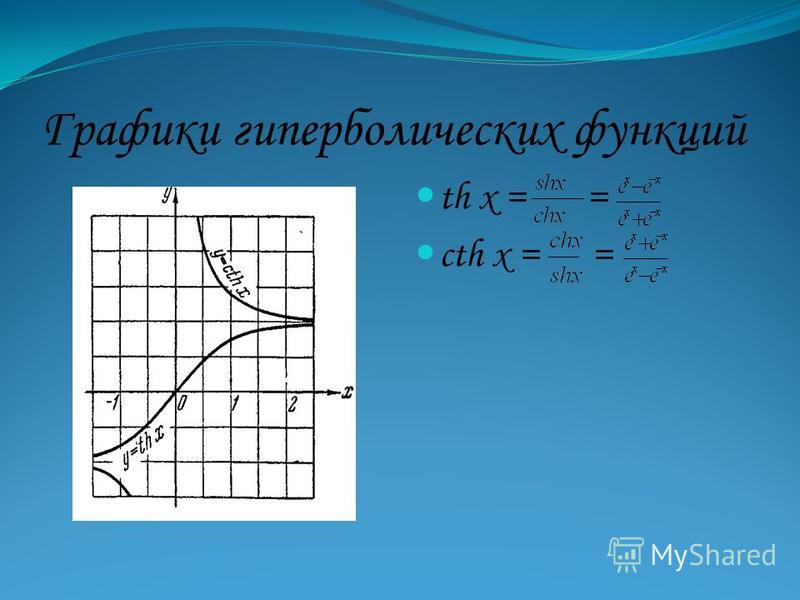 Рассмотрим некоторые важные свойства этих функций, которые используются для решения различных математических задач.
Рассмотрим некоторые важные свойства этих функций, которые используются для решения различных математических задач.
- грех (-х) = – грех (х)
- кош (-х) = кош (х)
- танх (-х) = — танхх
- столб (-x) = — столб x
- сек (-х) = сек х
- csc (-x) = — csch x
- штрих 2x = 1 + 2 шв 2 (x) = 2 штрих 2 x — 1
- ch 2x = ch 2 x + sin 2 x
- синх 2x = 2 синхх х шикх
Гиперболические функции также могут быть выведены из тригонометрических функций с комплексными аргументами:
- sin x = — i sin(ix)
- кош х = cos(ix)
- танх x = — i тан(ix)
- кровать х = я кровать (ix)
- сек х = сек(икс)
Идентификаторы гиперболических триггеров
Гиперболические тригонометрические тождества аналогичны тригонометрическим тождествам и могут быть лучше поняты снизу. Правило Осборна гласит, что тригонометрические тождества могут быть преобразованы в гиперболические тригонометрические тождества при полном расширении с точки зрения интегральных степеней синусов и косинусов, что включает изменение синуса на синус, косинуса на кош.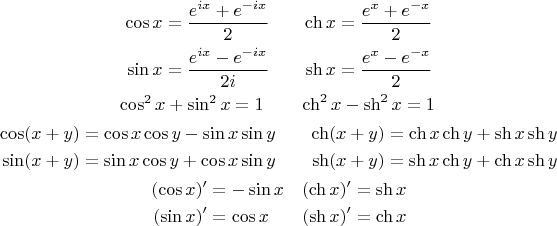 Следует заменить знак каждого члена, содержащего произведение двух синхов.
Следует заменить знак каждого члена, содержащего произведение двух синхов.
- sh x – sh y = 2 ch [(x+y)/2] sh [(x-y)/2]
- sin x + sh y = 2 sinh [(x+y)/2] ch[(x-y)/2]
- ch x + ch y = 2 ch [(x+y)/2] ch[(x-y)/2]
- ch x – ch y = 2 sh [(x+y)/2] sh [(x-y)/2])
- 2 sin x ch y = sh (x + y) + sh (x — y)
- 2 ch x sh y = sh (x + y) – sh (x – y)
- 2 sin x sh y = ch (x + y) – ch (x – y)
- 2 кош х кош у = кош (х + у) + кош (х – у)
- sh(x ± y) = sh x ch y ± ch x sh y
- ch(x ± y) = ch x ch y ± sh x sh y
- тангенс (х ± у) = (тангенс х ± тангенс у)/ (1 ± танс кс танс у)
- coth(x ± y) = (coth x coth y ± 1)/(coth y ± coth x)
- ш 2 х — ш 2 х = 1
- танх 2 х + сек 2 х = 1
- ткань 2 x — csch 2 x = 1
Интегралы и производные гиперболических функций
Производная и интеграл гиперболической функции аналогичны производной и интегралу тригонометрической функции. В отличие от производной тригонометрических функций, мы можем наблюдать изменение знака у производной гиперболической секущей функции. Производные и интегралы гиперболических функций приведены в следующей таблице:
В отличие от производной тригонометрических функций, мы можем наблюдать изменение знака у производной гиперболической секущей функции. Производные и интегралы гиперболических функций приведены в следующей таблице:
| Гиперболическая функция | Производная | Интеграл |
|---|---|---|
| х | кош х | кош х + С |
| шпон х | синх х | синх х + С |
| танх x | сек 2 х | пер(ш х) + С |
| ткань x | -csch 2 x | пер(синх х) + C |
| сек х | -сечь х. Танх х | арктан(синх х) + C |
| сч х | -csch х. х | лн(танх (х/2)) + С |
Обратные гиперболические функции
Обратная гиперболическая функция называется обратной гиперболической функцией. Например, если x = sh y, то y = sh -1 x — функция, обратная гиперболическому синусу. Обратные гиперболические функции, выраженные через логарифмические функции, показаны ниже:
Например, если x = sh y, то y = sh -1 x — функция, обратная гиперболическому синусу. Обратные гиперболические функции, выраженные через логарифмические функции, показаны ниже:
- sh -1 x = ln (x + √(x 2 + 1))
- кош -1 х = ln (х + √(х 2 — 1))
- танх -1 х = пер [(1 + х)/(1 — х)]
- coth -1 x = ln [(x + 1)/(x — 1)]
- сек -1 х = пер [{1 + √(1 — х 2 )}/x]
- csch -1 x = ln [{1 + √(1 + x 2 )}/x]
Важные замечания по гиперболическим функциям
- Существует шесть гиперболических функций, а именно: sh x, cosh x, tanh, x, coth x, sech x, csch x.
- Для гиперболы определена гиперболическая функция.
- Гиперболические тождества аналогичны тригонометрическим тождествам.
Похожие темы
- танх x
- Гипербола
- Калькулятор гиперболы
Часто задаваемые вопросы о гиперболических функциях
Что такое гиперболические функции
в математике? Гиперболические функции определены для гиперболы. График гиперболической функции, синонимичной ее названию, представляет собой прямоугольную гиперболу, а формулу гиперболической функции часто можно увидеть в формулах гиперболы. Гиперболические функции аналогичны тригонометрическим функциям, но выводятся из гиперболы, как тригонометрические функции выводятся из единичного круга.
График гиперболической функции, синонимичной ее названию, представляет собой прямоугольную гиперболу, а формулу гиперболической функции часто можно увидеть в формулах гиперболы. Гиперболические функции аналогичны тригонометрическим функциям, но выводятся из гиперболы, как тригонометрические функции выводятся из единичного круга.
Каковы основные шесть гиперболических функций?
Существует шесть гиперболических функций, а именно:
- Гиперболический синус, sinh x
- Гиперболический косинус, cosh x
- Гиперболический тангенс, tanh x
- Гиперболический котангенс, coth x
- Гиперболический секанс, sech x
- Гиперболический косеканс, csch x
Какие формулы формулы гиперболических функций?
Формулы для основных гиперболических функций:
- sh x = (e x — e -x )/2
- кош х = (е х + е -х )/2
- танх x = (e x — e -x )/(e x + e -x )
- coth x = (e x + e -x )/(e x — e -x )
- сек х = 2/(е х + е -х )
- сч х = 2/(е х — е -х )
Что такое дифференциация гиперболических функций?
Производные гиперболических функций:
- d(sinx x)/dx = ch x
- d(ш х)/дх = ш х
- d(тангенс x)/dx = сек 2 x
- d(coth x)/dx = — cosech 2 x
- d(sech x)/dx = — sech x.
 tanh x
tanh x - d(козех x)/dx = — козех x.coth x
Что такое обратные гиперболические функции?
Список обратных гиперболических функций:
- sinh -1 x = ln (x + √(x 2 + 1))
- кош -1 х = ln (х + √(х 2 — 1))
- танх -1 х = пер [(1 + х)/(1 — х)]
- coth -1 x = ln [(x + 1)/(x — 1)]
- sech -1 x = ln [{1 + √(1 — x 2 )}/x]
- csch -1 x = ln [{1 + √(1 + x 2 )}/x]
Сколько существует гиперболических функций?
Существует шесть основных гиперболических функций, а именно sh x, ch x, th th, coth x, sech x, csch x.
Что такое идентификаторы гиперболических триггеров?
Гиперболические тригонометрические тождества представляют собой формулы гиперболических функций, которые аналогичны тригонометрическим функциям. Вот некоторые из гиперболических тригонометрических тождеств:
- sh(x ± y) = sh x ch y ± chx sh y
- ch(x ± y) = ch x ch y ± sh x sh y
- тангенс (х ± у) = (тангенс х ± тангенс у)/ (1 ± танс кс танс у)
- coth(x ± y) = (coth x coth y ± 1)/(coth y ± coth x)
- ш 2 х — ш 2 х = 1
- танх 2 х + сек 2 х = 1
- ткань 2 x — csch 2 x = 1
- sin x – sh y = 2 ch [(x+y)/2] sinh [(x-y)/2]
- sin x + sh y = 2 sinh [(x+y)/2] ch[(x-y)/2]
- ch x + ch y = 2 ch [(x+y)/2] ch[(x-y)/2]
- ch x – ch y = 2 sh [(x+y)/2] sh [(x-y)/2])
- 2 sin x ch y = sh (x + y) + sh (x — y)
- 2 ch x sh y = sh (x + y) – sh (x – y)
- 2 sin x sh y = ch (x + y) – ch (x – y)
- 2 кош х кош у = кош (х + у) + кош (х – у)
Почему гиперболические функции называются гиперболическими?
Гиперболические функции называются гиперболическими, потому что они выводятся и определяются из гиперболы точно так же, как тригонометрические функции выводятся из единичной окружности. График гиперболической функции представляет собой прямоугольную гиперболу.
График гиперболической функции представляет собой прямоугольную гиперболу.
В чем разница между гиперболическими функциями и тригонометрическими функциями?
Основное различие между тригонометрическими и гиперболическими функциями заключается в том, что тригонометрические функции определяются из единичной окружности x 2 + y 2 = 1, а гиперболические функции получаются из гиперболы x 2 — y 2 = 1 , Еще одно различие между ними состоит в том, что гиперболические функции не являются периодическими, как тригонометрические функции.
Формула гиперболических функций – определение, график и решенные вопросы
Гиперболические функции относятся к экспоненциальным функциям, обладающим сходными свойствами с тригонометрическими функциями. Эти функции аналогичны тригонометрическим функциям в том смысле, что они называются так же, как и тригонометрические функции, с добавлением буквы «h» к каждому имени. Они имеют такое же отношение к гиперболе, как тригонометрические функции к окружности.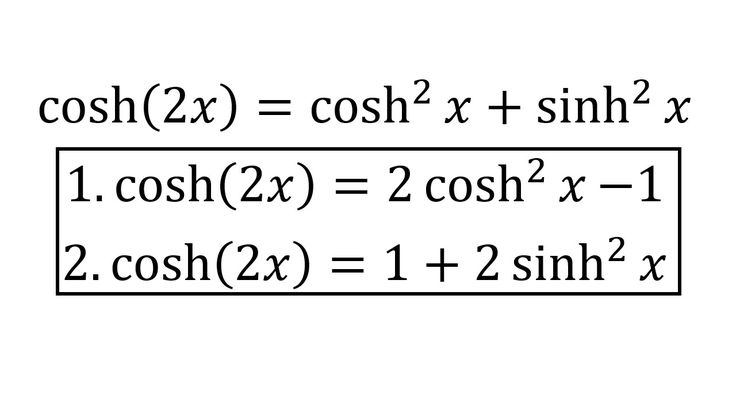 Таким образом, они вместе известны как гиперболические функции, а по отдельности называются гиперболическим синусом, гиперболическим косинусом и так далее. Помимо моделирования, их можно использовать в качестве решений некоторых типов дифференциальных уравнений в частных производных. В этой статье мы собираемся обсудить формулу гиперболических функций, общее уравнение гиперболы, стандартное уравнение гиперболы, формулу гиперболы, тригонометрические гиперболические формулы.
Таким образом, они вместе известны как гиперболические функции, а по отдельности называются гиперболическим синусом, гиперболическим косинусом и так далее. Помимо моделирования, их можно использовать в качестве решений некоторых типов дифференциальных уравнений в частных производных. В этой статье мы собираемся обсудить формулу гиперболических функций, общее уравнение гиперболы, стандартное уравнение гиперболы, формулу гиперболы, тригонометрические гиперболические формулы.
Общее уравнение гиперболы / Стандартное уравнение гиперболы
Гипербола — это плоская кривая, образованная точкой, движущейся так, что разница расстояний от двух фиксированных точек постоянна. Две фиксированные точки являются фокусами, а середина отрезка, соединяющего фокусы, является центром гиперболы. Поперечная ось — линия, проходящая через фокусы. Сопряженная ось — это линия, проходящая через центр и перпендикулярная поперечной оси.
Вершины гиперболы — это точки, в которых гипербола пересекает поперечную ось. 2с — расстояние между двумя фокусами. Расстояние между двумя вершинами равно 2а. 2a s также является длиной поперечной оси. Длина сопряженной оси равна 2b. Значение b равно.
2с — расстояние между двумя фокусами. Расстояние между двумя вершинами равно 2а. 2a s также является длиной поперечной оси. Длина сопряженной оси равна 2b. Значение b равно.
(Изображение будет обновлено в ближайшее время)
(Изображение будет обновлено в ближайшее время)
Эксцентриситет гиперболы
Гипербола, где разности всех точек на множестве плоскостей из двух неподвижных точек постоянна.
Проще говоря, расстояние от фиксированной точки на плоскости имеет постоянный коэффициент, больший, чем расстояние от фиксированной точки на плоскости.
Поэтому эксцентриситет гиперболы всегда больше 1, т. е. e > 1
Общее уравнение гиперболы или стандартное уравнение гиперболы обозначается как значения a и b являются длинами большой и малой полуосей соответственно. 9{2}}}a\]
9{2}}}a\]
Обсудим тригонометрические гиперболические формулы.
Гиперболический синус x | Sinh X: (E x -E -x )/2 |
9008
9008 9008-X )/2 -E -x )/2 -E -X )/2 -E -X 8)/2 9000 -E -X). Cosh x : (e x + e- x )/2 | |
Гиперболический тангенс x | Tanh x: sinh x/ cosh x = (e x − e -x ) / (e x + e -x ) |
The Hyperbolic cotangent of x | Coth x: ch x/ sh x = (e x + e -x ) / (e x − e -x ), где 0 x не равно |
Гиперболический секанс x | Sech x: 1/ ch x = 2/ (E x + E -x ) |
Гиперболический космос x | CSCH X: 1/ SINH X = 2/20088 CSCH x: 1/ SINH X = 2/77777777777777777 годы X 7. |
График, показывающий разницу между функциями Sin(x) и Sinh (x)
(Изображение скоро будет обновлено)5 Изображение скоро будет обновлено)
График, показывающий разницу между функциями Cos(x) и Cosh (x)
(изображение будет обновлено в ближайшее время)
(изображение будет обновлено в ближайшее время)
График, показывающий разницу между функциями Tan(x) и Tanh (x)
(изображение будет обновлено в ближайшее время)
Обновлено в ближайшее время)
Связь между гиперболическими функциями (тригонометрические гиперболические формулы)
| |||||
| 1/TANH X = COSH X/SINH X | ||||
| |||||
| |||||
| |||||
| |||||
| 1/SINH X | ||||
5. COSH 2 X —SINH 9007 2 | 5. COSH 2 X —SINH 2 5. COSH 2 x —SINH 2 5. COSH 2 x —SINH 2 .0013 6. Sech 2 x −tanh 2 x 1 | ||||
7. | 1 |
Формулы сложения
sinh (x+y)=sinh x ch y + ch x sh y
ch (x+y)= ch x ch y + sh x sh y
907 х+у) = (тангенс х + тангенс у) / 1+тангенс х. танх танх (х-у) = (танх х — танх у) / 1-танх х. tanh y
coth (x+y) =(coth x. coth y+1) / coth y. coth x
coth (x-y) = (coth x. coth y-1) / coth y. Coth x
Тригонометрические идентичности
SINH (−x) = −SINH (X)
COSH (−x) = COSH (X)
COSH (−x) = COSH (X)
COSH (−x) = COSH (x)
(−x) = Cosh (x)
.
 tanh(x)
tanh(x)coth(−x) = −coth(x)
sech(−x) = sech(x)
csch(−x) = −csch(x)
Вопросы, требующие решения
1. Получите дополнительные тождества для sin h (x) ) и cos h (x+y).
В тождестве tanh (x+y)= (tanh x + tanh y)/1+tanh x. tanh y
Решение: tanh x(x+y) = sh (x+y)/ ch (x+y)
Так как sh (x+y) = sh x ch y + ch x sh y
ch ( x+y) равно ch x ch y + sh x sh y
=\[\frac{sinx x\ ch y + sh y\ ch x}{ch x\ ch y + sh x\ sh y}\]
Деление числителя и знаменателя на ch x и ch y,
= \[\frac{sin x / ch x\ +\ sh y / ch x}{1 + sh x / ch x\ .\ sh y / ch y}\]
=\[\frac{tanh x\ +\ tanh y}{1 + tanh x\ tanh y}\]
2.
 Что такое гиперболические функции?
Что такое гиперболические функции?Все мы знаем о тригонометрических функциях, которые определяются на окружности или для нее так же, как и гипербола, мы используем гиперболическую функцию. Обычно мы используем синус, косинус и другие функции в тригонометрии. Аналогичным образом для гиперболы мы используем csch, sech, sinh, tan h, coth и cosh. Опять же, в нормальной тригонометрии мы знаем, что точки координат на единице окружности равны (sin Φ, cos Φ) аналогичным образом (sinn Φ, cos Φ) образуют правую половину равносторонней гиперболы для гиперболических функций.
Уравнение Лапласа, дифференциальные уравнения и кубические уравнения имеют различные решения из-за гиперболической функции. Существует шесть из этих функций, которые приведены ниже:
SINH X или гиперболический синус.
Coth x или гиперболический котангенс
Sech x или гиперболический секанс
Гиперболические функции Значение
Аналогичным образом гиперболические функции определяются как тригонометрические функции.
 А именно sh x, tan h x, coth x, sech x, cosech x и ch x являются основными шестью функциями гиперболы. Комбинация экспоненциальных функций выражается для гиперболических функций. Точно так же, как тригонометрические функции выводятся с использованием окружности единицы измерения, гиперболические функции выводятся с использованием гиперболы.
А именно sh x, tan h x, coth x, sech x, cosech x и ch x являются основными шестью функциями гиперболы. Комбинация экспоненциальных функций выражается для гиперболических функций. Точно так же, как тригонометрические функции выводятся с использованием окружности единицы измерения, гиперболические функции выводятся с использованием гиперболы.Формулы гиперболических функций
9{-x}\], где она известна как постоянная Эйлера; благодаря этому мы можем определить гиперболические функции.Тождества гиперболических функций
Как мы знаем, тождества тригонометрических функций аналогичны тождествам гиперболических функций и могут быть лучше поняты из объяснения ниже. Правило Осборна гласит, что при правильном и полном расширении с точки зрения интегральных степеней косинусов и синусов, которое включает изменение положения косинуса на кош и снова синуса на h, тождества тригонометрических функций могут быть изменены или преобразованы в тождества гиперболических функций.
 {-1} x\], то x = sh y является инверсией синуса гиперболических функций. Выразим обратную гиперболическую функцию через логарифм функции. Точно так же, как обратная гипербола используется по-другому, наоборот, тригонометрические функции полезны в некоторых интегрированиях, исчислениях. Существуют некоторые ограничения на домен, чтобы сделать функции один к одному из каждого, а домены — результирующие и обратные функции их диапазонов.
{-1} x\], то x = sh y является инверсией синуса гиперболических функций. Выразим обратную гиперболическую функцию через логарифм функции. Точно так же, как обратная гипербола используется по-другому, наоборот, тригонометрические функции полезны в некоторых интегрированиях, исчислениях. Существуют некоторые ограничения на домен, чтобы сделать функции один к одному из каждого, а домены — результирующие и обратные функции их диапазонов.Важные замечания по гиперболическим функциям
Cosh x, coth x, csch x, sh x, sech x и tanh x — это шесть гиперболических функций.
Для гиперболы мы определяем гиперболическую функцию.
Тождества тригонометрических функций аналогичны тождествам гиперболических функций.
6.9: Расчет гиперболических функций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2527
- Гилберт Стрэнг и Эдвин «Джед» Герман
- OpenStax
Цели обучения
- Применять формулы для производных и интегралов гиперболических функций.

- Применить формулы для производных обратных гиперболических функций и связанных с ними интегралов.
- Опишите общие прикладные условия контактной кривой.
Ранее мы познакомились с гиперболическими функциями и некоторыми их основными свойствами. В этом разделе мы рассмотрим формулы дифференцирования и интегрирования для гиперболических функций и их обратных функций.
Производные и интегралы гиперболических функций 9{−x}] \\[4pt] &=\cosh x. \end{align*} \nonumber \]
Аналогично,
\[\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
Мы суммируем формулы дифференцирования для гиперболических функций в таблице \(\PageIndex{1}\).
Таблица \(\PageIndex{1}\): производные гиперболических функций \(f(x)\) \(\dfrac{d}{dx}f(x)\) \(\шп х\) 92\, х\) \(\text{sech} х\) \(−\text{sech}\, x \tanh x\) \(\text{csch} х\) \(−\text{csch}\, x \coth x\) Давайте сравним производные гиперболических функций с производными стандартных тригонометрических функций.
 Сходства много, но и различий тоже. Например, производные функций синуса совпадают:
Сходства много, но и различий тоже. Например, производные функций синуса совпадают:\[\dfrac{d}{dx} \sin x=\cos x \nonumber \]
и
\[\dfrac{d}{dx} \sinx x=\cosh x. \nonumber \]
Производные функций косинуса, однако, отличаются знаком:
\[\dfrac{d}{dx} \cos x=-\sin x, \nonumber \]
но
\ [\dfrac{d}{dx} \cosh x=\sinh x. \nonumber \]
Продолжая изучение гиперболических функций, мы должны помнить об их сходствах и различиях со стандартными тригонометрическими функциями. Эти формулы дифференцирования гиперболических функций непосредственно приводят к следующим интегральным формулам. 92)+С. \end{выравнивание*}\]
б. Пусть \(u=\ch x\). Затем \(du=\sinh x\,dx\) и
\[\begin{align*} \int \tanh x \,dx &=\int \dfrac{\sinh x}{\cosh x}\ ,dx \\[4pt] &=\int \dfrac{1}{u}du \\[4pt] &=\ln|u|+C \\[4pt] &= \ln|\cosh x|+C .\end{align*}\]
Обратите внимание, что \(\cosh x>0\) для всех \(x\), поэтому мы можем исключить знаки абсолютного значения и получить
\[\int \tanh x \ ,dx=\ln(\cosh x)+C.
 \nonumber \]
\nonumber \]Упражнение \(\PageIndex{2}\)
Оцените следующие интегралы: 92(3x) \, dx=\dfrac{\tanh(3x)}{3}+C\)
Вычисление обратных гиперболических функций
Глядя на графики гиперболических функций, мы видим, что при соответствующих ограничениях диапазона все они имеют обратные функции. Большинство необходимых ограничений диапазона можно различить при внимательном изучении графиков. Области и диапазоны обратных гиперболических функций приведены в таблице \(\PageIndex{2}\).
Таблица \(\PageIndex{2}\): домены и области значений обратных гиперболических функций 9х)+С\) Приложения
Одним из физических приложений гиперболических функций является подвеска кабелей. Если кабель одинаковой плотности подвешен между двумя опорами без какой-либо нагрузки, кроме собственного веса, кабель образует кривую, называемую контактной сетью . Высоковольтные линии электропередач, цепи, висящие между двумя столбами, и нити паутины образуют контактную сеть.
Рисунок \(\PageIndex{3}\): Цепи между этими столбами имеют форму контактной сети. (кредит: модификация работы OKFoundryCompany, Flickr) На следующем рисунке показаны цепи, свисающие с ряда столбов.
На следующем рисунке показаны цепи, свисающие с ряда столбов.Гиперболические функции могут использоваться для моделирования контактных сетей. В частности, функции вида \(y=a\cdot \cosh(x/a)\) являются цепными. На рисунке \(\PageIndex{4}\) показан график \(y=2\cosh(x/2)\).
Рисунок \(\PageIndex{4}\): Функция гиперболического косинуса образует контактную сеть.Пример \(\PageIndex{5}\): использование контактной сети для определения длины кабеля ≤15\), где \(x\) измеряется в футах. Определите длину кабеля (в футах). 9{15}_{−15}\\[4pt] &=10\left[\sinh\left(\dfrac{3}{2}\right)-\sinh\left(-\dfrac{3}{2} \right)\right]\\[4pt] &=20\sinh \left(\dfrac{3}{2}\right) \\[4pt] &≈42,586\,\text{ft.} \end{align *}\]
Упражнение \(\PageIndex{5}\):
Предположим, что подвесной трос имеет форму \(15 \cosh (x/15)\) для \(−20≤x≤20\). Определите длину кабеля (в футах).

- Ответить
\(52,95\) футов
Ключевые понятия
- Гиперболические функции определяются в терминах экспоненциальных функций.
- Почленное дифференцирование дает формулы дифференцирования для гиперболических функций. Эти формулы дифференцирования порождают, в свою очередь, формулы интегрирования.
- При соответствующих ограничениях диапазона все гиперболические функции имеют обратные значения.
- Неявное дифференцирование дает формулы дифференцирования для обратных гиперболических функций, которые, в свою очередь, приводят к формулам интегрирования.
- Наиболее распространенными физическими приложениями гиперболических функций являются расчеты, связанные с контактными сетями.
Глоссарий
- Контактная сеть
- кривая в виде функции \(y=a\cdot\cosh(x/a)\) является контактной; трос одинаковой плотности, подвешенный между двумя опорами, принимает форму контактной сети
Эта страница под названием 6.




 Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
Это определение аналогично определению тригонометрических функций через единичную окружность, которое тоже можно построить подобным образом.
 д.
д. tanh x
tanh x e -x ), где x не равно 0.
e -x ), где x не равно 0.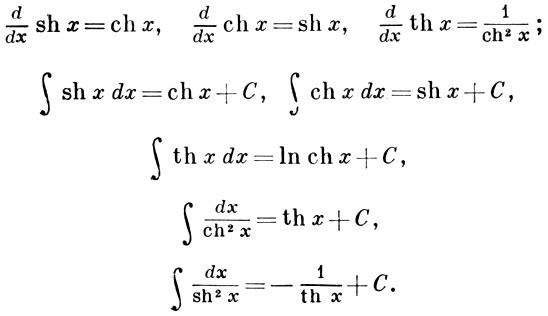 0005
0005 Coth 2 x−csch 2 x
Coth 2 x−csch 2 x tanh(x)
tanh(x)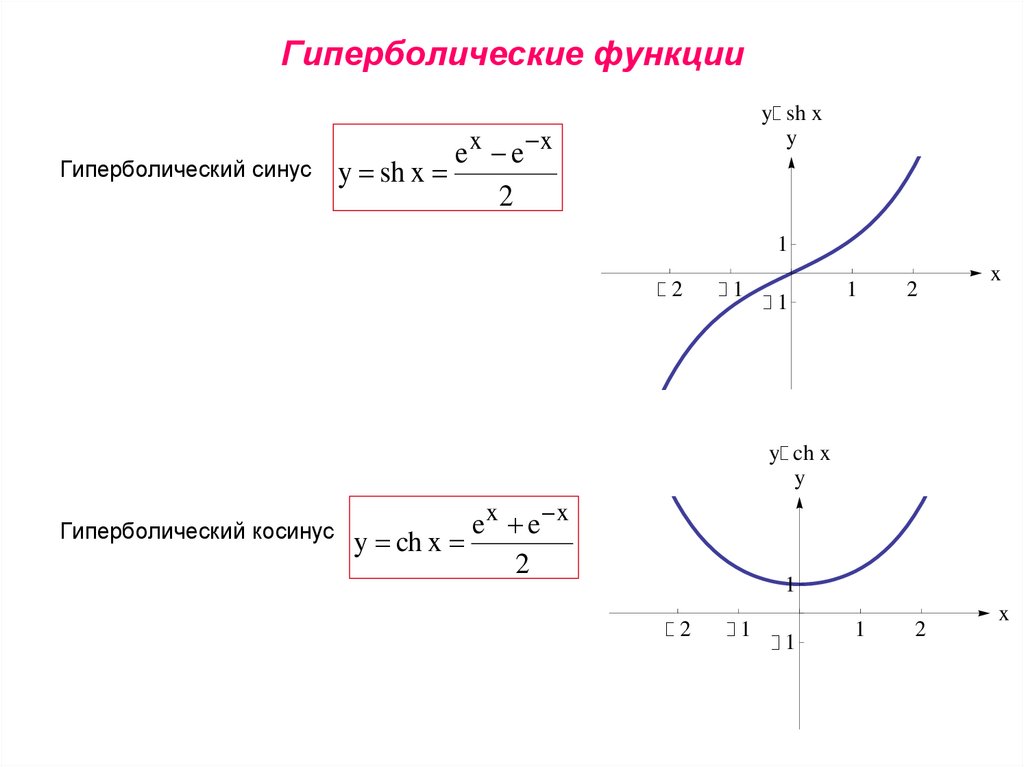 Что такое гиперболические функции?
Что такое гиперболические функции?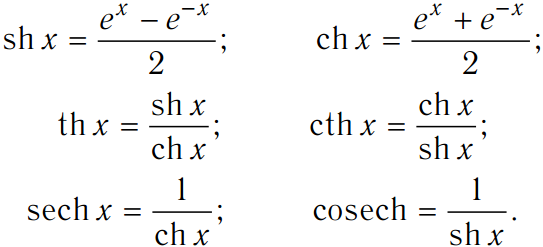 А именно sh x, tan h x, coth x, sech x, cosech x и ch x являются основными шестью функциями гиперболы. Комбинация экспоненциальных функций выражается для гиперболических функций. Точно так же, как тригонометрические функции выводятся с использованием окружности единицы измерения, гиперболические функции выводятся с использованием гиперболы.
А именно sh x, tan h x, coth x, sech x, cosech x и ch x являются основными шестью функциями гиперболы. Комбинация экспоненциальных функций выражается для гиперболических функций. Точно так же, как тригонометрические функции выводятся с использованием окружности единицы измерения, гиперболические функции выводятся с использованием гиперболы. {-1} x\], то x = sh y является инверсией синуса гиперболических функций. Выразим обратную гиперболическую функцию через логарифм функции. Точно так же, как обратная гипербола используется по-другому, наоборот, тригонометрические функции полезны в некоторых интегрированиях, исчислениях. Существуют некоторые ограничения на домен, чтобы сделать функции один к одному из каждого, а домены — результирующие и обратные функции их диапазонов.
{-1} x\], то x = sh y является инверсией синуса гиперболических функций. Выразим обратную гиперболическую функцию через логарифм функции. Точно так же, как обратная гипербола используется по-другому, наоборот, тригонометрические функции полезны в некоторых интегрированиях, исчислениях. Существуют некоторые ограничения на домен, чтобы сделать функции один к одному из каждого, а домены — результирующие и обратные функции их диапазонов.
 Сходства много, но и различий тоже. Например, производные функций синуса совпадают:
Сходства много, но и различий тоже. Например, производные функций синуса совпадают: \nonumber \]
\nonumber \] На следующем рисунке показаны цепи, свисающие с ряда столбов.
На следующем рисунке показаны цепи, свисающие с ряда столбов.
