Интегральная теорема Муавра-Лапласа — Студопедия
Поделись с друзьями:
Интегральная теорема Муавра-Лапласа позволяет вычислить вероятность того, что число успехов в схеме Бернулли заключено между m1 и m2 (при )
,
где , .
Неопределенный интеграл не выражается через элементарные функции. Для его вычисления используются таблицы функций Лапласа
.
Тогда искомая вероятность вычисляется по формуле
Приближенными формулами Лапласа пользуются в случае, если . Если же npq < 10, то эти формулы приводят к довольно большим погрешностям.
Задание 3. Пусть вероятность появления события A при одном испытании равна p = 0,37. Найти вероятность того, что при n = 100 испытаниях событие A появится от m1 = 30 до m2 = 45
Решение.
a. Сначала выполните задание, используя таблицу функции Лапласа.
1.
2.
Значения функций Лапласа выбираются из таблицы ЭУМК, контент, тема 12, приложение 2.
Введите исходные данные задания n = 100, p = 0,37, q, m1 = 30, m2 = 45 и выполните вычисления , как показано на рис. 19.
Рис. 19. Исходные данные с вычисленными значениями x2 и x1
По вычисленным значениям x2 и x1 найдите в таблице – контент, тема 12, приложение 2 значения функций Лапласа и . Внесите их в ячейки F55 и G55 как показано на рис. 20. В ячейке F57 вычислите вероятность
Рис. 20. В ячейке F57 показан результат вычисления вероятности , полученный с использованием таблиц функции Лапласа
b.
Вычисление вероятности в Excel выполняется с использованием функции НОРМРАСП, что позволяет обойтись без таблиц функции Лапласа.
Функции Лапласа связана с функцией НОРМРАСП следующим соотношением
Поместите в ячейку F59 формулу , где , вычисленная ранее и находящаяся в ячейке F53, как показано на рис. 21.
В ячейку G59 поместите формулу , в ячейке G53 находится
В ячейку F60 поместите конечную формулу вычисления вероятности
Рис. 21. В ячейке F60 показан результат вычисления вероятности , полученный с использованием функцией НОРМРАСП
с. Этот же результат можно получить, используя функцию БИНОМРАСП, как показано на рис. 22.
Рис. 22. В ячейке F62 показан результат вычисления вероятности , полученный с использованием функции
БИНОМРАСП(x2; n; p;1) – БИНОМРАСП(x1; n; p;1)
Сравните все полученные результаты и сделайте выводы.
Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями:
Повторение испытаний.
Наивероятнейшее число наступления события. Производящая функция4.1. Формула Бернулли
Если производится несколько испытаний, причем вероятность события в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события .
В разных независимых испытаниях событие может иметь либо различные вероятности, либо одну и ту же вероятность. Будем далее рассматривать лишь такие независимые испытания, в которых событие имеет одну и ту же вероятность.
Ниже воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми.
Пусть производится независимых
испытаний, в каждом из которых событие может
появиться либо не появиться. Условимся считать, что вероятность события в
каждом испытании одна и та же, а именно равна р.
Следовательно, вероятность ненаступления события в
каждом испытании также постоянна и равна .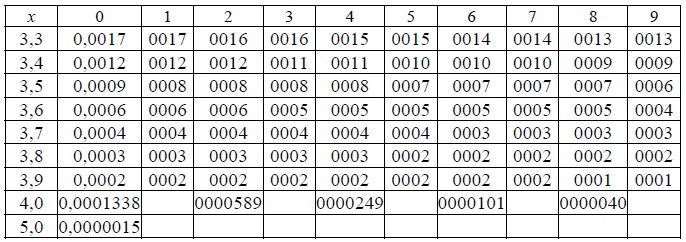
Поставим перед собой задачу вычислить вероятность того, что при испытаниях событие осуществится ровно раз и, следовательно, не осуществится раз.
Важно подчеркнуть, что не требуется, чтобы событие повторилось ровно к раз в определенной последовательности. Например, если речь идет о появлении события три раза в четырех испытаниях, то возможны следующие сложные события: , , , . Запись означает, что в первом, втором и третьем испытаниях событие наступило, а в четвертом испытании оно не появилось, т.е. наступило противоположное событие ; соответственный смысл имеют и другие записи.
Искомую вероятность обозначим . Например, символ означает вероятность того, что в пяти испытаниях событие появится ровно 3 раза и, следовательно, не наступит 2 раза.
Поставленную задачу можно решить с помощью так называемой формулы Бернулли.
Вывод формулы Бернулли. Вероятность одного сложного
события, состоящего в том, что в испытаниях
событие наступит
раз
и не наступит раз,
по теореме умножения вероятностей независимых событий равна .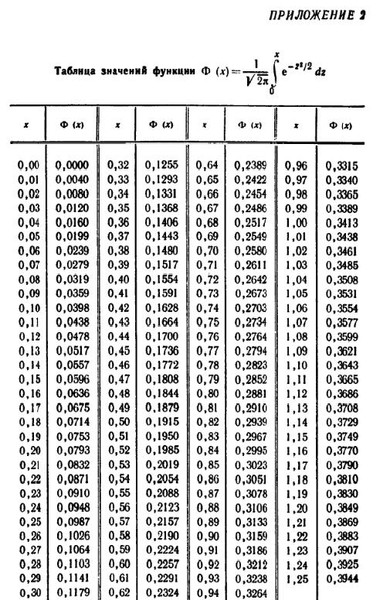
Таких сложных событий может быть столько, сколько можно составить сочетаний из элементов
по элементов,
т. е. .
Так как эти сложные события несовместны, то по теореме сложения вероятностей
несовместных событий искомая вероятность равна сумме вероятностей всех возможных
сложных событий. Поскольку же вероятности всех этих сложных событий одинаковы,
то искомая вероятность (появления раз
события в
испытаниях)
равна вероятности одного сложного события, умноженной на их число:
или
Полученную формулу называют формулой Бернулли.
Пример 4.1. Вероятность того, что расход электроэнергии в продолжение одних суток не превысит установленной нормы, равна
Найти вероятность того, что в ближайшие 6 суток расход электроэнергии в течение 4 суток не превысит нормы.
Решение.
Вероятность нормального расхода электроэнергии в продолжение каждых из 6 суток
постоянна и равна .
Следовательно, вероятность перерасхода электроэнергии в каждые сутки также
постоянна и равна .
Искомая вероятность по формуле Бернулли равна
4.2. Локальная теорема Лапласа
Выше была выведена формула Бернулли, позволяющая вычислить вероятность того, что событие появится в испытаниях ровно раз. При выводе мы предполагали, что вероятность появления события в каждом испытании постоянна. Легко видеть, что пользоваться формулой Бернулли при больших значениях достаточно трудно, так как формула требует выполнения действий над громадными числами. Например, если , , , то для отыскания вероятности надо вычислить выражение
где
Правда, можно несколько упростить вычисления, пользуясь специальными таблицами логарифмов факториалов. Однако и этот путь остается громоздким и к тому же имеет существенный недостаток: таблицы содержат приближенные значения логарифмов, поэтому в процессе вычислений накапливаются погрешности; в итоге окончательный результат может значительно отличаться от истинного.
Естественно возникает вопрос: нельзя ли вычислить
интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается,
можно.
Заметим, что для частного случая, а именно для , асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольного , отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь, иногда называют теоремой Муавра-Лапласа.
Доказательство локальной теоремы Лапласа довольно сложно, поэтому мы приведем лишь формулировку теоремы и примеры, иллюстрирующие ее использование.
Теорема 4.1. (Локальная теорема Лапласа). Если вероятность появления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в испытаниях ровно раз, приближенно равна (тем точнее, чем больше ) значению функции
при
Имеются таблицы, в которых помещены значения функции
соответствующие положительным
значениям аргумента .
Для отрицательных значений аргумента пользуются теми же таблицами, так как
функция четна,
т. е. .
Итак, вероятность того, что событие появится в независимых испытаниях ровно раз, приближенно равна
где
Пример 4.2. Найти вероятность того, что событие наступит ровно 80 раз в 400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,2.
Решение. По условию, ; ; ; Воспользуемся асимптотической формулой Лапласа:
Вычислим определяемое данными задачи значение :
По таблице приложения 1 находим .
Искомая вероятность
Формула Бернулли приводит примерно к такому же результату (выкладки ввиду их громоздкости опущены):
Пример 4.3. Вероятность поражения мишени стрелком при одном выстреле . Найти вероятность того, что при 10 выстрелах стрелок поразит мишень 8 раз.
Решение. По условию, ; ; ; . Воспользуемся асимптотической формулой Лапласа:
Вычислим определяемое данными задачи значение :
По таблице приложения 1 находим .
Искомая вероятность
Формула Бернулли приводит к иному результату, а именно
Столь значительное расхождение ответов объясняется тем, что в настоящем примере имеет малое значение (формула Лапласа дает достаточно хорошие приближения лишь при достаточно больших значениях ).
4.3. Интегральная теорема Лапласа
Вновь предположим, что производится испытаний, в каждом из которых вероятность появления события постоянна и равна . Как вычислить вероятность того, что событие появится в испытаниях не менее и не более раз (для краткости будем говорить «от до раз»)? На этот вопрос отвечает интегральная теорема Лапласа, которую мы приводим ниже, опустив доказательство.
Теорема 4.2. Если вероятность наступления события в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие появится в испытаниях от до раз, приближенно равна определенному интегралу
(4. |
1)где
и
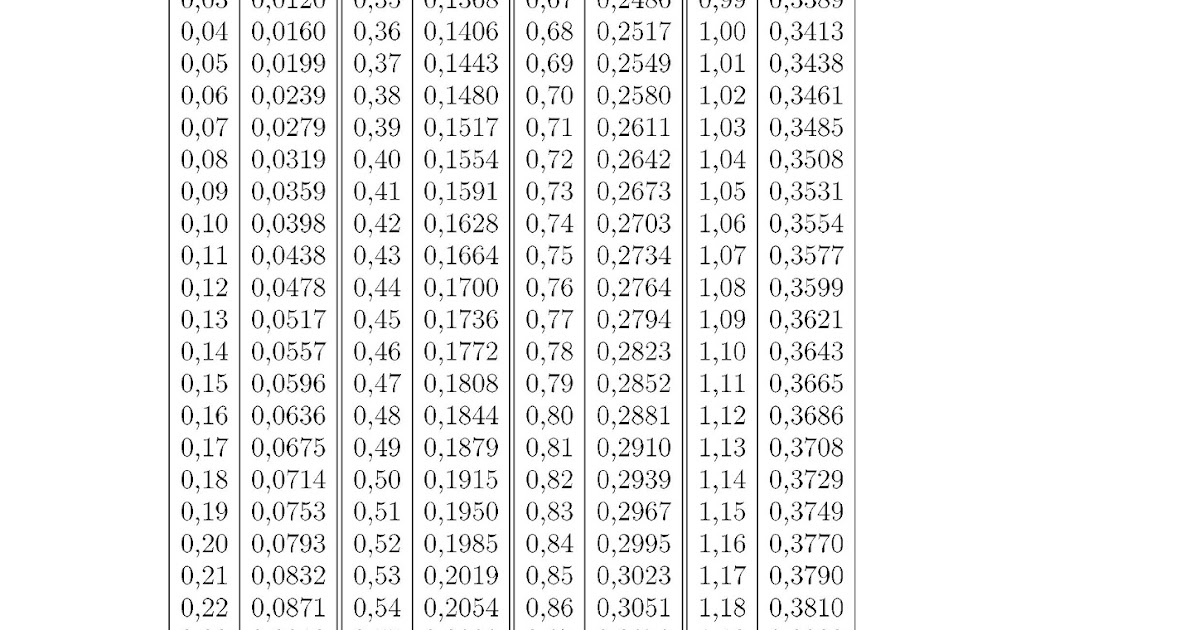
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами, так как неопределенный интеграл не выражается через элементарные функции. Таблица для интеграла
приведена в конце лекционного материала (см. приложение 2). В таблице даны значения функции для положительных значений и для ; для пользуются той же таблицей, т.к. функция нечетна, т.е.
В таблице приведены значения интеграла лишь до , так как для можно принять . Функцию часто называют функцией Лапласа.
Для того чтобы можно было пользоваться таблицей функции Лапласа, преобразуем соотношение (4.1) так:
Итак, вероятность того, что событие появится в независимых испытаниях от до раз,
где
и
Приведем пример, иллюстрирующий применение интегральной теоремы Лапласа.
Пример 4.
4.
Вероятность того, что деталь не прошла проверку ОТК, равна .
Найти вероятность того, что среди 400 случайно отобранных деталей окажется
непроверенных от 70 до 100 деталей.
Решение. По условию, ; ; ; ; . Воспользуемся интегральной теоремой Лапласа:
Вычислим нижний и верхний пределы интегрирования:
Таким образом, имеем
По таблице приложения 2 находим:
Искомая вероятность
Замечание 4.1. Обозначим через число появлений события при независимых испытаниях, в каждом из которых вероятность наступления события постоянна и равна . Если число изменяется от до , то дробь
изменяется от
Следовательно, интегральную теорему Лапласа можно записать и так:
Эта форма записи используется ниже.
4.4. Вероятность отклонения относительной частоты от постоянной вероятности в независимых испытаниях
Вновь будем считать, что производится независимых
испытаний, в каждом из которых вероятность появления события постоянна
и равна .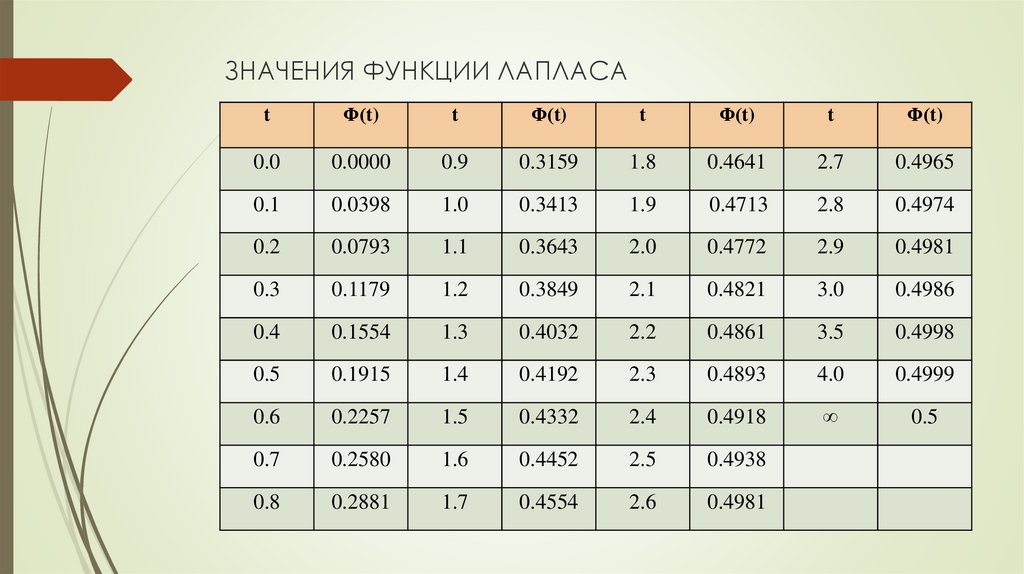
Поставим перед собой задачу найти вероятность того, что отклонение относительной частоты от постоянной вероятности по абсолютной величине не превышает заданного числа . Другими словами, найдем вероятность осуществления неравенства
(4.2) |
Эту вероятность будем обозначать так:
Заменим неравенство (4.2) ему равносильными:
или
Умножая эти неравенства на положительный множитель
получим неравенства, равносильные исходному:
Воспользуемся интегральной теоремой Лапласа в форме, указанной в замечании 4.1. Положив
и
имеем
Наконец, заменив неравенства, заключенные в скобках, равносильным им исходным неравенством, окончательно получим
Итак, вероятность осуществления неравенства
приближенно равна значению удвоенной функции Лапласа при
Пример 4.
5.
Вероятность того, что деталь не стандартна, .
Найти вероятность того, что среди случайно отобранных 400 деталей относительная
частота появления нестандартных деталей отклонится от вероятности по
абсолютной величине не более чем на 0,03.
Решение. По условию, ; ; ; . Требуется найти вероятность
Пользуясь формулой
имеем
По таблице приложения 2 находим . Следовательно,
Итак, искомая вероятность приближенно равна 0,9544.
Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей в каждой, то примерно в 95,44% этих проб отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит 0,03,
Пример 4.6.
Вероятность того, что деталь не стандартна, .
Найти, сколько деталей надо отобрать, чтобы с вероятностью, равной 0,9544, можно
было утверждать, что относительная частота появления нестандартных деталей
(среди отобранных) отклонится от постоянной вероятности по
абсолютной величине не более чем на 0,03.
Решение. По условию,
Требуется найти .
Воспользуемся формулой
В силу условия
Следовательно,
По таблице приложения 2 находим .
Для отыскания числа получаем уравнение . Отсюда искомое число деталей .
Смысл полученного результата таков: если взять достаточно большое число проб по 400 деталей, то в 95,44% этих проб относительная частота появления нестандартных деталей будет отличаться от постоянной вероятности по абсолютной величине не более чем на 0,03, т.е. относительная частота заключена в границах от до . Другими словами, число нестандартных деталей в 95,44% проб будет заключено между 28 (7% от 400) и 52 (13% от 400).
Если взять лишь одну пробу из 400 деталей, то с большой уверенностью можно ожидать, что в этой пробе будет нестандартных деталей не менее 28 и не более 52. Возможно, хотя и маловероятно, что нестандартных деталей окажется меньше 28 либо больше 52.
4.
5. Наивероятнейшее число появлений события в независимых испытаниях
Число (наступления события в независимых испытаниях, в каждом из которых вероятность появления события равна ) называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях раз, превышает (или, по крайней мере, не меньше) вероятности остальных возможных исходов испытаний.
Наивероятнейшее число определяют из двойного неравенства
причем:
а) если число — дробное, то существует одно наивероятнейшее число ;
б) если число — целое, то существует два наивероятнейших числа, а именно: и
в) если число — целое, то наивероятнейшее число .
4.6. Производящая функция
Ранее рассматривались испытания с одинаковыми вероятностями появления события; рассмотрим испытания, в которых вероятности появления события различны.
Пусть производится независимых
испытаний, причем в первом испытании вероятность появления события равна
,
во втором — ,…,
в -м
испытании — ;
вероятности непоявления события соответственно
равны ;
–
вероятность появления события в
испытаниях
ровно раз.
Производящей функцией вероятностей называют функцию, определяемую равенством
Вероятность того, что в независимых испытаниях, в первом из которых вероятность появления события равна , во втором и т.д., событие появится ровно раз, равна коэффициенту при в разложении производящей функции по степеням . Например, если , то
Здесь коэффициент при равен вероятности того, что событие появится ровно два раза в двух испытаниях; коэффициент при равен вероятности того, что событие появится ровно один раз; коэффициент при , т. е. свободный член равен вероятности того, что событие не появится ни одного раза.
Заметим, что если в различных испытаниях появляются различные события (в первом испытании событие во втором — событие и т.д.), то изменяется лишь истолкование коэффициентов при различных степенях . Например, в приведенном выше разложении коэффициент определяет вероятность появления двух событий и .
[1] Функцию называют асимптотическим приближением функции , если
Эластичная сжатие с компрессионной повязкой Law Law
Связанные ресурсы: Fluid Flow
Эластичный сжатие повязки Laplace’s Law
Гидравлический и пневматический меню
что внутри трубчатой конструкции изменение давления, необходимое для растяжения, пропорционально поверхностному натяжению стенки и обратно пропорционально ее радиусу. Другими словами, структура с большим радиусом и низким поверхностным натяжением требует минимального изменения давления, чтобы вызвать дальнейшее расширение, однако структура с меньшим радиусом и высоким поверхностным натяжением требует значительного давления.
Согласно закону Лапласа давление медицинской подповязки прямо пропорционально натяжению повязки, но обратно пропорционально радиусу кривизны конечности, на которую она наложена. теоретическое соотношение между натяжением T бинта (сила, необходимая для растяжения бинта, которая определяется механическими свойствами бинта и прикладываемым растяжением), местной кривизной r c конечности и локально приложенным давление, P,
определяется законом Лапласа.
Ур. 1
Закон Лапласа для цилиндра
P = T / r c
где
T = упругое натяжение (фунт-сила/дюйм, Н/мм)
r c = локальная кривизна
Уравнение Лапласа, используемое для прогнозирования давления под бандажом, получено из формулы, описанной независимо Томасом Юнгом (1773-1829) и Пьером Симоном де Лапласом (1749-1827) в 1805 году. Это определяет взаимосвязь между градиентом давления на замкнутой эластичной мембране или сфере жидкой пленки и натяжением в мембране или пленке. более строгие формулы:
Ур. 2
Для сфер
P α — P β = 2 γ / r
Ур. 2а
Для сфер
γ = (стр. α — стр β ) R / 2
, где
P α = Внутреннее давление
P β = давление Внешнее
P β = давление Внешнее
P β = давление Внешнее
P β = давление. или пленка
r = радиус кривизны
Ур. 3
Для цилиндров
P α — P β = γ / r
Ур. 3а
Для цилиндров
γ = ( P α — P β ) r
Уравнение показывает, что давление внутри сферической поверхности всегда больше, чем давление снаружи, но эта разница уменьшается до нуля, когда радиус становится бесконечным (когда поверхность ровная). Напротив, перепад давления увеличивается, если радиус становится меньше и стремится к бесконечности, как r стремится к нулю. Однако уравнение нарушается до того, как r достигнет нуля, поэтому на практике такой ситуации не возникает.
В качестве альтернативы модуль упругости бандажа (K) может быть определен экспериментально и по спецификации и выражается в Н/мм, определяется по формуле;
Ур. 2
Модуль упругости бандажа
K = F / [W ( L f — L i ) / L i ]
Ур. 3
Сила, приложенная с известным
Модуль упругости бинта
F = K [W ( L f — L i ) / L i ]
где
K = модуль упругости бандажа фунты/дюйм (Н/мм) — аналогично жесткости пружины
1
F = сила растяжения бинта, фунт-сила (Н)
W = ширина бинта, дюймы (мм)
L f = длина натянутого бинта, дюймы (мм)
L i = исходная длина, дюймы (мм)
Таблица 1, Механические свойства выбранных эластичных бинтов
| Эластичный бинт | Модуль продольной упругости (Н/мм) | Сила растяжения = 1,3 (Н/мм) |
| Бифлекс ® 16 (B16) | 0,23 | 0,070 |
| Бифлекс ® 17 (B17) | 0,44 | 0,13 |
Таблица 2. Единицы преобразования
| Параметр | Когерентный блок | Альтернативный блок | Коэффициент преобразования |
| Давление | Паскаль | мм рт.ст. | 0,0075 |
| Сила | Ньютон | кгс | 0,102 |
| Длина | Метр | Сантиметр | 100 |
| Радиус | Окружность | 2 π r = (2 x 3,142 r ) |
Использование несвязанных единиц также означает, что постоянные
Компрессионные бинты в основном классифицируются как эластичные и неэластичные. Эластичные компрессионные бинты (Таблица 3) классифицируются в зависимости от уровня давления, оказываемого на угол средней ноги. Повязки класса 3а обеспечивают легкое сжатие 14–17 мм рт.ст., умеренное сжатие (18–24 мм рт.ст.) обеспечивается повязками класса 3b, а повязки типа 3с обеспечивают сильное сжатие от 25 до 35 мм рт.ст. Повязки сверхвысокой компрессии 3-го типа (до 60 мм рт. ст.) используются нечасто, поскольку создаваемое очень высокое давление снижает кровоснабжение кожи. Следует отметить, что примерно 30–40 мм рт. Компрессионные чулки обеспечивают поддержку при лечении ТГВ и варикозного расширения вен, а также для предотвращения венозных язв на ногах. Они классифицируются как легкая поддержка (Класс 1), средняя поддержка (Класс 2) и сильная поддержка (Класс 3).
Таблица 3, Классификация эластичных бинтов
| Класс | Тип бандажа | Функция повязки |
| 1 | Легкий, соответствующий | Применяют очень низкое давление под повязкой и используются для удержания повязок на месте. |
| 2 | Световая опора | Прикладывают умеренное давление под повязкой и используются для предотвращения отека или для лечения язв смешанной этиологии. |
| 3а | Легкая компрессия | Произведите давление в диапазоне 14–17 мм рт. ст. на лодыжку. |
| 3б | Умеренное сжатие | Произведите давление в диапазоне 18–24 мм рт. ст. на лодыжку. |
| 3с | Высокое сжатие | Произведите давление в диапазоне 25–35 мм рт. ст. на лодыжку. |
| 3Д | Сверхвысокая степень сжатия | Давление до 60 мм рт. ст. на лодыжку. |
Внимание! Если давящая повязка слишком туго накладывается на конечность, давящая повязка превращается в жгут. Жгут перекрывает кровоснабжение артерий. Как только это кровоснабжение прекращается, ткани, отделенные от богатого кислородом кровотока, такие как нервы, кровеносные сосуды и мышцы, могут быть необратимо повреждены и привести к потере конечности. Этот документ не является заменой медицинского работника, поэтому вам следует проконсультироваться со своим врачом по поводу правильного использования и применения эластичного компрессионного бинта.
Этот документ не является медицинским справочником. Позвоните своему врачу, если:
- У вас есть боль, онемение или покалывание
- Ваши пальцы на ногах или пальцах становятся другого цвета
- Ваша повязка промокает
- Обертка помята или сложена
- Повязка трется о кожу или сползает вниз
- Жидкость просачивается из пораженного участка наружу повязки
Родственные
- Сосуд высокого давления, тонкостенная окружность и уравнение продольных напряжений и калькулятор
- Уравнение Клаварино для толстостенных цилиндров из пластичного материала Калькулятор и формула
- Артериальное давление измеряется с помощью революционной технологии | Новости машиностроения
- Толстостенные цилиндрические сосуды под давлением Уравнения и калькулятор
- Уравнение Ламса Толстостенные цилиндры Формула и калькулятор
- Расчет внешнего давления в сосуде под давлением
- Таблица стандартных размеров и спецификаций труб Данные таблицы
Ссылки
Экспериментальное исследование давления
Наносится на голень резинкой
Компрессионный бинт
Анналы биомедицинской инженерии
Журнал биомедицинских
Инженерное общество
Фанетт Шассан, Фредерик Мартен,
Пьер Бадель, Рейнальд Конверт, Паскаль
Giraux & Jérôme Molimard
Современный текстиль для компрессии ран
С. Раджендран С. К. Ананд Редактор главы С. Раджендран, в Advanced Textiles for Wound Care (Second Edition),
2019
Стив Томас,
кандидат наук
Директор
Лаборатория испытаний хирургических материалов
Больница принцессы Уэльской, Бридженд, Уэльс
май 2002 г.
Генератор случайных чисел — Руководство NumPy v1.24
Генератор обеспечивает доступ к
широкий спектр дистрибутивов, и служил заменой RandomState . Основное различие между
два заключается в том, что Generator полагается на дополнительный BitGenerator для
управлять состоянием и генерировать случайные биты, которые затем преобразуются в
случайные значения из полезных распределений. BitGenerator по умолчанию, используемый Генератор это PCG64 . БитГенератор
можно изменить, передав созданный экземпляр BitGenerator в Generator .
- numpy.random.default_rng ( семя = нет )
Создайте новый генератор с помощью BitGenerator по умолчанию (PCG64).
- Параметры:
- seed {None, int, array_like[ints], SeedSequence, BitGenerator, Generator}, необязательный
Seed для инициализации
BitGenerator. Если нет, то свежий, непредсказуемая энтропия будет вытягиваться из ОС. Еслиintилипередано array_like[ints], затем оно будет передано вSeedSequenceдля получения начального состоянияBitGenerator. Можно также пройти в экземпляреSeedSequence. Кроме того, при передачеBitGeneratorон будет обернутГенератор. Если передатьГенератор, он будет возвращен без изменений.
- Возвращает:
- Генератор
Инициализированный объект генератора.
Примечания
Если
семянне являетсяBitGeneratorилиGenerator, новымBitGeneratorсоздается экземпляр. Эта функция не управляет глобальным экземпляром по умолчанию.Примеры
default_rng— рекомендуемый конструктор для класса случайных чиселГенератор. Вот несколько способов, которыми мы можем построить случайную генератор чисел с использованиемdefault_rngи классаGenerator.Здесь мы используем
default_rngдля генерации случайного числа с плавающей запятой:>>> импортировать numpy как np >>> rng = np.random.default_rng(12345) >>> напечатать(rng) Генератор (PCG64) >>> rfloat = rng.random() >>> плыть 0,22733602246716966 >>> тип(rfloat) <класс 'плавающий'>
Здесь мы используем
default_rngдля генерации 3 случайных целых чисел от 0 (включительно) и 10 (эксклюзивно):>>> импортировать numpy как np >>> rng = np.random.default_rng(12345) >>> rints = rng.integers(low=0, high=10, size=3) >>> ринц массив([6, 2, 7]) >>> тип(ринц[0]) <класс 'numpy.
int64'>
Здесь мы указываем начальное число, чтобы получить воспроизводимые результаты:
>>> импортировать numpy как np >>> rng = np.random.default_rng(seed=42) >>> напечатать(rng) Генератор (PCG64) >>> arr1 = rng.random((3, 3)) >>> обр1 массив([[0,77395605, 0,43887844, 0,85859792], [0,69736803, 0,09417735, 0,97562235], [0,7611397, 0,78606431, 0,12811363]])Если мы выйдем и перезапустим наш интерпретатор Python, мы увидим, что мы генерировать те же самые случайные числа снова:
>>> импортировать numpy как np >>> rng = np.random.default_rng(seed=42) >>> arr2 = rng.random((3, 3)) >>> обр2 массив([[0,77395605, 0,43887844, 0,85859792], [0,69736803, 0,09417735, 0,97562235], [0,7611397, 0,78606431, 0,12811363]])
- класс numpy.random.Generator ( bit_generator )
Контейнер для BitGenerators.
Генераторпредоставляет ряд методов для генерации случайных числа, взятые из различных вероятностных распределений. В дополнение к
аргументы, специфичные для дистрибутива, каждый метод принимает аргумент ключевого слова размер , по умолчанию None. Если размер равенNone, то одиночный значение генерируется и возвращается. Если размер является целым числом, то одномерный возвращается массив, заполненный сгенерированными значениями. Если размер является кортежем, затем массив с этой формой заполняется и возвращается.Функция
numpy.random.default_rngсоздаст экземпляр генераторBitGenerator.Нет гарантии совместимости
Генераторне дает гарантии совместимости версий. В в частности, по мере развития лучших алгоритмов битовый поток может меняться.- Параметры:
- bit_generator BitGenerator
BitGenerator для использования в качестве основного генератора.
См. также
-
default_rng Рекомендуемый конструктор для
Генератор.
Примечания
Модуль Python stdlib
randomсодержит генератор псевдослучайных чисел с помощью ряда методов, аналогичных тем, которые доступны вГенератор. Он использует Mersenne Twister, и этот генератор битов может получить доступ, используяMT19937.Генератор, помимо того, что Поддержка NumPy имеет то преимущество, что предоставляет гораздо большее количество распределения вероятностей на выбор.Примеры
>>> из генератора импорта numpy.random, PCG64 >>> rng = Генератор (PCG64()) >>> rng.standard_normal() -0,203 # случайный
Доступ к BitGenerator
| Получает экземпляр генератора битов, используемый генератором |
Простые случайные данные
| Возвращает случайные целые числа от младшего (включительно) до старшего (исключительно) или, если endpoint=True, младшего (включительно) до старшего (включительно). |
| Возвращает случайные числа с плавающей запятой в полуоткрытом интервале [0,0, 1,0). |
| Генерирует случайную выборку из заданного массива |
| Возврат случайных байтов. |
Перестановки
Способы случайной перестановки последовательности
| Изменение массива или последовательности на месте путем перетасовки их содержимого. |
| Произвольная перестановка последовательности или возврат переставленного диапазона. |
| Произвольно переставить x вдоль оси оси . |
В следующей таблице приведены сведения о поведении методов.
метод | копия/на место | обработка оси |
|---|---|---|
перемешивание | на месте | как бы 1д |
перестановка | копия | как бы 1д |
перестановка | либо (используйте ‘out’ на месте) | независимый от оси |
В следующих подразделах содержится более подробная информация о различиях.
На месте против копии
Основное отличие Generator.shuffle от Generator.permutation заключается в том, что Generator.shuffle работает на месте, а Generator.permutation возвращает копию.
По умолчанию Generator. возвращает копию. Для работы на месте с permuted Generator.permuted , передайте тот же массив в качестве первого аргумента и как
значение параметра из . Например,
>>> rng = np.random.default_rng()
>>> x = np.arange(0, 15).reshape(3, 5)
>>> х
массив([[ 0, 1, 2, 3, 4],
[5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> y = rng.permuted(x, axis=1, out=x)
>>> х
массив([[ 1, 0, 2, 4, 3], # случайный
[6, 7, 8, 9, 5],
[10, 14, 11, 13, 12]])
Обратите внимание, что когда задано из , возвращаемое значение равно из :
>>> у есть х Истинный
Обработка параметра оси
Важным отличием этих методов является способ обработки оси . параметр. И Generator.shuffle , и Generator.permutation относятся к
вводится как одномерная последовательность, а параметр оси определяет
какое измерение входного массива использовать в качестве последовательности. В случае
двумерный массив, axis=0 фактически переупорядочивает строки
массив и axis=1 переупорядочивает столбцы. Например
>>> rng = np.random.default_rng()
>>> x = np.arange(0, 15).reshape(3, 5)
>>> х
массив([[ 0, 1, 2, 3, 4],
[5, 6, 7, 8, 9],
[10, 11, 12, 13, 14]])
>>> rng.permutation(x, axis=1)
массив([[ 1, 3, 2, 0, 4], # случайный
[6, 8, 7, 5, 9],
[11, 13, 12, 10, 14]])
Обратите внимание, что столбцы были переставлены «навалом»: значения внутри каждый столбец не изменился.
Метод Generator.permuted обрабатывает параметр оси аналогично
как к этому относится numpy.sort . Каждый срез вдоль заданной оси перемешивается
независимо от других. Сравните следующий пример использования Generator.permutation в приведенном выше примере Generator.permutation :
>>> rng.permuted(x, axis=1)
массив([[ 1, 0, 2, 4, 3], # случайный
[5, 7, 6, 9, 8],
[10, 14, 12, 13, 11]])
В этом примере значения в каждой строке (т. е. значения вдоль axis=1 ) были перемешаны независимо друг от друга. Это не «масса»
перетасовка столбцов.
Перетасовка последовательностей, отличных от NumPy
Generator.shuffle работает с последовательностями, отличными от NumPy. То есть, если дано
последовательность, которая не является массивом NumPy, она перемешивает эту последовательность на месте.
Например,
>>> rng = np.random.default_rng() >>> a = ['A', 'B', 'C', 'D', 'E'] >>> rng.shuffle(a) # перемешать список на месте >>> а ['B', 'D', 'A', 'E', 'C'] # случайный
Распределения
| Взять образцы из бета-версии. |
| Выбрать образцы из биномиального распределения. |
| Выбрать образцы из распределения хи-квадрат. |
| Выбрать образцы из распределения Дирихле. |
| Выбрать образцы экспоненциального распределения. |
| Взять образцы из F-распределения. |
| Взять образцы из гамма-распределения. |
| Взять образцы из геометрического распределения. |
| Взять образцы из распределения Гамбеля. |
| Выбрать образцы из гипергеометрического распределения. |
| Выбрать образцы из распределения Лапласа или двойного экспоненциального распределения с указанным местоположением (или средним значением) и масштабом (распадом). |
| Взять образцы из логистической сети. |
| Выбрать образцы из логарифмически нормального распределения. |
| Выбрать образцы из логарифмического ряда распределения. |
| Выбрать образцы полиномиального распределения. |
| Создание переменных из многомерного гипергеометрического распределения. |
| Произвести случайные выборки из многомерного нормального распределения. |
| Выбрать образцы из отрицательного биномиального распределения. |
| Выбрать образцы из нецентрального распределения хи-квадрат. |
| Взять образцы из нецентрального F-распределения. |
| Произвести случайные выборки из нормального (гауссовского) распределения. |
| Взять образцы из распределения Парето II или Ломакса заданной формы. |
| Взять образцы из распределения Пуассона. |
| Выбирает выборки в [0, 1] из распределения мощности с положительным показателем степени a — 1. |
| Выбрать образцы из распределения Рэлея. |
| Выбрать образцы из стандартного распределения Коши с модой = 0. |
| Возьмите образцы из стандартного экспоненциального распределения. |
| Взять образцы из стандартного гамма-распределения. |
| Выбрать образцы из стандартного нормального распределения (среднее=0, стандартное отклонение=1). |