6.2. Локальная и интегральная теоремы Лапласа
Выше мы рассмотрели формулу Бернулли,
которая позволяет находить вероятность
появления события в 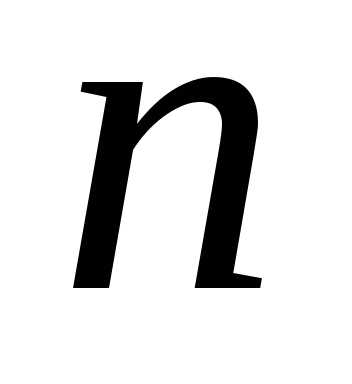 испытаниях
испытаниях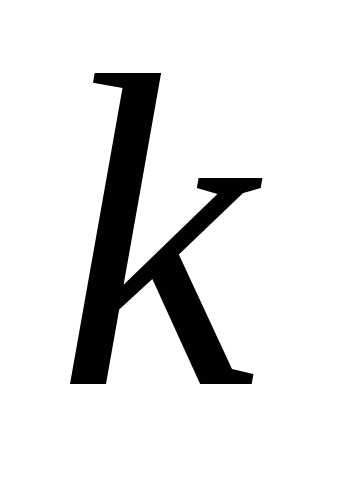 раз. Эту формулу удобно использовать в
тех случаях, когда число испытаний
раз. Эту формулу удобно использовать в
тех случаях, когда число испытаний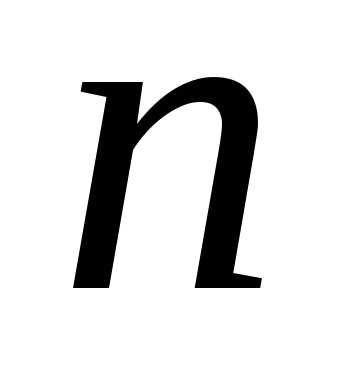 невелико. Если же, например, надо найтиP50(30), то в этом
случае сталкиваемся с вычислением
невелико. Если же, например, надо найтиP50(30), то в этом
случае сталкиваемся с вычислением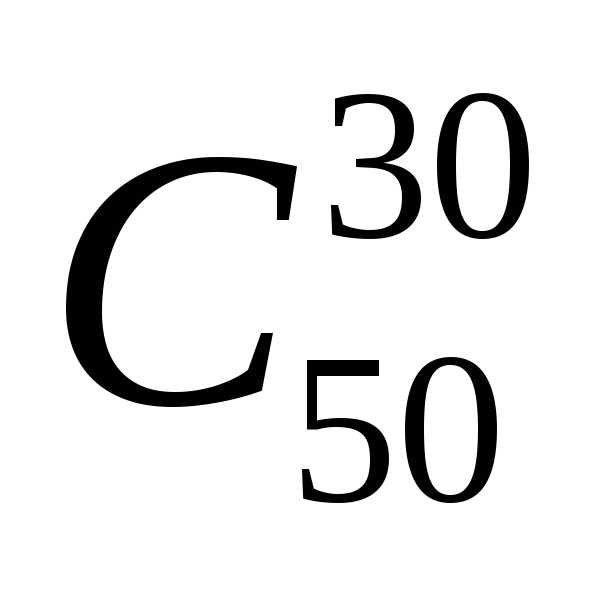 .
Но даже не все современные калькуляторы
могут вычислить это значение. При
использовании стандартной записи числа
приходится делать округления, отбрасывая
значащие цифры, что приводит в процессе
вычислений к накоплению погрешностей.
.
Но даже не все современные калькуляторы
могут вычислить это значение. При
использовании стандартной записи числа
приходится делать округления, отбрасывая
значащие цифры, что приводит в процессе
вычислений к накоплению погрешностей.
Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается можно. Локальная теорема Лапласа дает асимптотическую формулу, которая позволяет приближенно найти вероятность появления события ровно kраз вnиспытаниях, если число испытаний достаточно велико.
Заметим, что для частного случая, а именно для p=1/2, асимптотическая формула была найдена в 1730 г. Муавром; в 1783 г. Лаплас обобщил формулу Муавра для произвольногоp, отличного от 0 и 1. Поэтому теорему, о которой здесь идет речь иногда называют теоремой Муавра – Лапласа.
Мы приведем только формулировку этой теоремы, опуская ее доказательство.
Теорема 6.1 (локальная теорема Лапласа).
Если вероятность pпоявления событияAв каждом испытании постоянно и отличается от нуля и единицы, то вероятностьP
n(k) того, что событиеAпоявится вnиспытаниях ровноkраз, приближенно равна (тем точнее, чем большеn):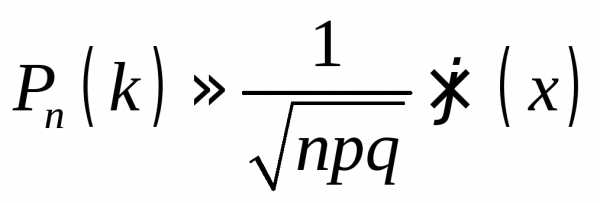 ,
где
,
где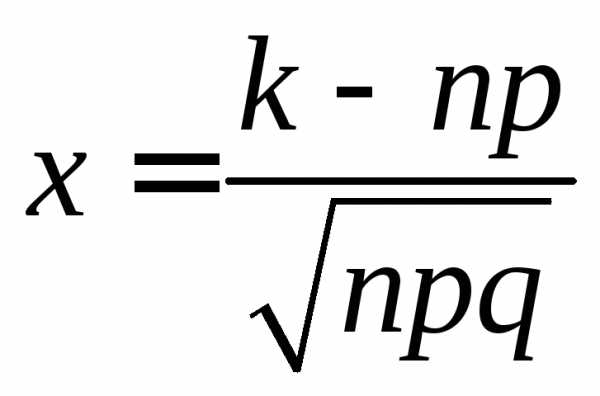 .
(6.2)
.
(6.2)
Функция 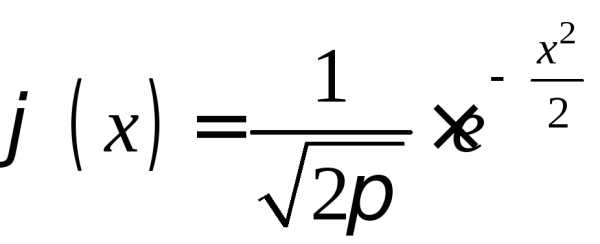 называется малой функций Лапласа.
Значения функции(x),
соответствующие положительному значению
аргумента
называется малой функций Лапласа.
Значения функции(x),
соответствующие положительному значению
аргумента ,
определяется из соответствующей таблицы.
Для отрицательных значений аргумента
пользуются той же таблицей, так как(x)
четная функция, т.е.
.
,
определяется из соответствующей таблицы.
Для отрицательных значений аргумента
пользуются той же таблицей, так как(x)
четная функция, т.е.
.
Вновь предположим, что производится 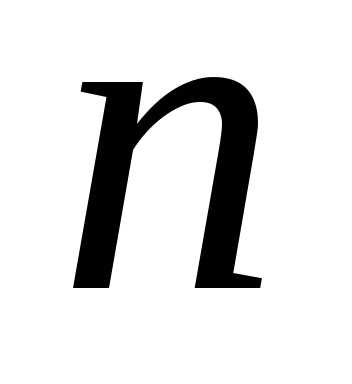 испытаний, в каждом из которых вероятность
появления события
испытаний, в каждом из которых вероятность
появления события
 появится вnиспытаниях
не менее
появится вnиспытаниях
не менее и не более
и не более раз (для краткости будем говорить «от
раз (для краткости будем говорить «от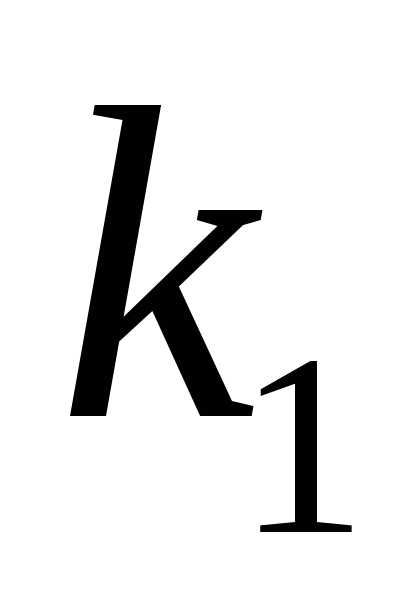 до
до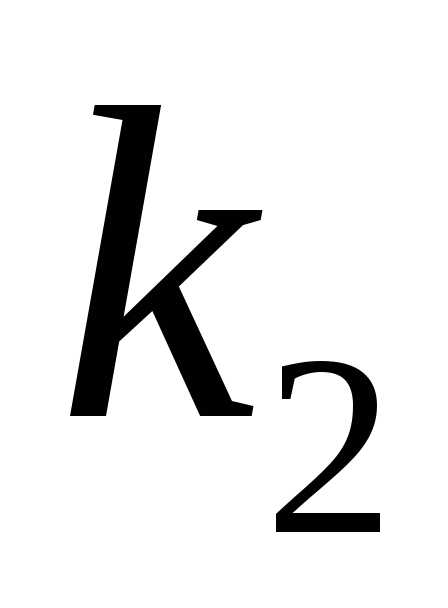 раз»)? На этот вопрос отвечает интегральная
теорема Лапласа, которую мы приводим,
опустив доказательство.
раз»)? На этот вопрос отвечает интегральная
теорема Лапласа, которую мы приводим,
опустив доказательство.Теорема 6.2 (интегральная теорема Лапласа).
Если вероятность  появления события
появления события
 появится вnиспытаниях
от
появится вnиспытаниях
от до
до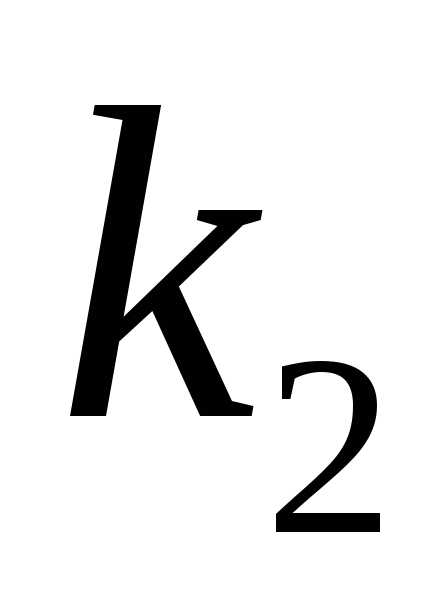 раз, приближенно равна:
раз, приближенно равна:, где. (6.3)
Функция 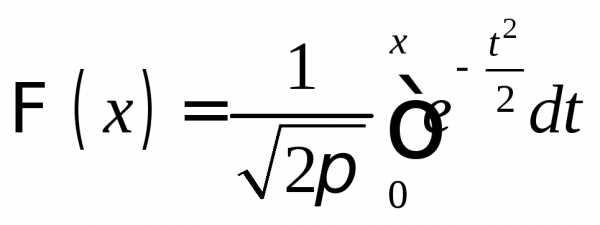 называется функций Лапласа. Значения
функции(x),
соответствующие положительному значению
аргумента
называется функций Лапласа. Значения
функции(x),
соответствующие положительному значению
аргумента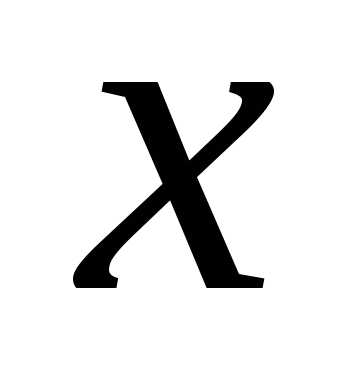 и
и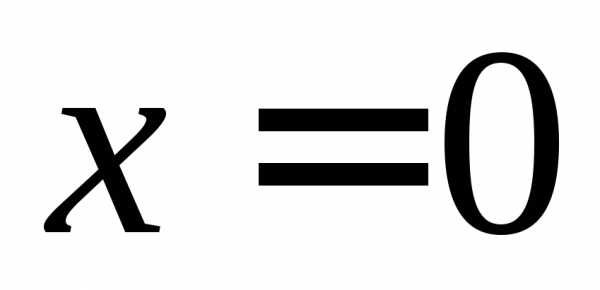 ,
определяется из соответствующей таблицы.
Для отрицательных значений аргумента
можно пользоваться той же таблицей, так
как(
,
определяется из соответствующей таблицы.
Для отрицательных значений аргумента
можно пользоваться той же таблицей, так
как(
 .
При
.
При можно принять.
можно принять.Замечание. Локальной и интегральной теоремами Лапласа на практике удобно пользоваться в случае, если npq>10. Если же npq<10, то эти формулы приводят к большим погрешностям.
Пример 6.4.Вероятность появления событияAв каждом из 900 независимых испытаний равнаp=0,8. Найти вероятность того, что событиеAпроизойдет:
а) 750 раз;
б) не менее 710 раз и не более 740 раз.
Решение.а) Из условия следует, чтоn=900,k=750,p=0,8, поэтомуq=0,2. Посколькуnpq=9000,80,2=144>10, то можно воспользоваться локальной теоремой Лапласа.
Находим x:
.
По таблице значений функции находим (2,5)=0,0175.
Согласно локальной теореме Лапласа получаем искомую вероятность:
.
б) Из условия следует, что n=900,k1=710,k2=740,p=0,8, поэтомуq=0,2. Находимx1иx2:
;
.
По таблице значений функции Лапласа, учитывая нечетность функции, определяем
(x1)=(0,83)=0,2967;
(x2)=(1,67)=0,4525.
Согласно интегральной теореме Лапласа получаем искомую вероятность:
.
studfiles.net
Локальная и интегральная теоремы Лапласа — Мегаобучалка
Пусть производится n одинаковых независимых испытаний с вероятностью появления события в каждом испытании, равной p. Тогда вероятность частоты m наступления события А определяется, как было показано ранее по формуле Бернулли:
.
Вычисление по этой формуле трудно практически осуществить при n > 20.
В таких случаях применяют асимптотическую формулу, позволяющую найти указанную вероятность. Теорема, выражающая эту формулу, носит название локальной теоремы Муавра – Лапласа.
Теорема. Если производится n одинаковых испытаний, в каждом из которых вероятность появления события равна p, то вероятность того, что данное событие появится m раз, определяется по формуле
, где ; .
Эта теорема дает приближение биномиального закона распределения к нормальному при p, значительно отличающемся от нуля и единицы.
Задача. Для мастера определенной квалификации вероятность изготовить деталь отличного качества равна 0,75. За смену он изготовил 400 деталей. Найти вероятность того, что в их числе 250 деталей отличного качества.
Решение: По условию n = 400, p = 0,75 , q = 0,25 и m = 280, откуда npq = 75, х = –2,3095.
По таблицам (t) найдем (–2,31) = (2,31) = 0,0277. Искомая вероятность равна Р = 0,0032.
Интегральная теорема Лапласа
Для вычисления вероятности того, что частота m, подчиненная биномиальному закону распределения, заключена между данными значениями и , применяют интегральную теорему Лапласа, выраженную асимптотической формулой. Формулу, выражающую интегральную теорему Лапласа, можно получить из закона нормального распределения.
Теорема. Пусть вероятность р наступления события А в каждом испытании постоянна и 0 < p < 1. Тогда вероятность того, что событие А появится в n испытаниях от до раз, приближенно равна определенному интегралу
= ,
где , и .
При больших значениях n наиболее вероятная частота совпадает с математическим ожиданием частоты. Поэтому для нахождения вероятности того, что абсолютная величина отклонения частоты от наиболее вероятной частоты не превосходит заданного числа > 0, используют приближенное равенство:
.
Формула Пуассона
Если вероятность события р (или q) в отдельном испытании близка к нулю, то даже при большом числе испытаний n, но небольшой величине произведения np (меньше 10), применяют асимптотическую формулу Пуассона
,
где .
Задача. Некоторое электронное устройство выходит из строя, если откажет определенная микросхема. Вероятность ее отказа в течение 1 ч работы устройства равна 0,004. Какова вероятность того, что за 1000 ч работы устройства придется пять раз менять микросхему?
Решение: По условию, n = 1000, p = 0,004, а = 1000 • 0,004 = 4 < 10. Для нахождения вероятности P1000(5) воспользуемся формулой Пуассона, так как условия ее применения выполнены. Имеем
0,1582.
Задача. На факультете насчитывается 1825 студентов. Какова вероятность того, что 1 сентября является днем рождения одновременно четырех студентов факультета?
Решение: Вероятность того, что день рождения студента 1 сентября, равна р = 1/365. Так как р = 1/365 – мала , n = 1825 – велико и l = n • р = 1825 × (1/365) = 5 £ 10, то применяем формулу Пуассона:
.
megaobuchalka.ru
Page Title
13Локальная и интегральная теоремы Лапласа.
Теоремы Муавра-Лапласа. На практике приближенные формулы Муавра-Лапласа применяются в случае, когда
Локальная теорема Муавра-Лапласа. Если вероятность появления события А в каждом из n независимых испытаний равна одной и той же постоянной р=const (0<р<1), то вероятность того, что во всех этих испытаниях событие А появится ровно k раз, приближенно вычисляется формулой:
, (4.8)
где: , — кривая Гаусса.
Таблицы значений функции даны в приложениях к учебникам по теории вероятностей
Интегральная теорема Муавра-Лапласа. Пусть вероятность появления события А в каждом из n (n→∞) независимых испытаний равна одной и той же постоянной р (0<р<1), то вероятность того, что во всех этих испытаниях событие А появится не менее k1 и не более k2 раз, приближенно вычисляется формулой:
, (4.9)
где
— функция Лапласа,
,
Значения аргументов функции Лапласа для х Î[0,5] даны в приложениях к учебникам по теории вероятностей (Приложение 2 настоящего методического пособия), для x>5 F(x)=1/2.Функция нечетная — F(x)= F(-x).
examhack.narod.ru
