определение, примеры, представления, координатная прямая
Данная статья посвящена теме «Действительные числа». В статье дается определение действительных чисел, иллюстрируется их положение на координатной прямой, рассматриваются способы задания действительных чисел числовыми выражениями.
Определение действительных чисел
Целые и дробные числа вместе составляют рациональные числа. В свою очередь, рациональные и иррациональные числа составляют действительные числа. Как дать определение, что такое действительные числа?
Определение 1Действительные числа — это рациональные и иррациональные числа. Множество действительных чисел обозначается через R.
Данное определение можно записать иначе с учетом следующего:
- Рациональные числа можно представить в виде конечной десятичной дроби или бесконечной периодической десятичной дроби.
- Иррациональные числа представляют собой бесконечные непериодические десятичные дроби.

Действительные числа — числа, которые можно записать в виде конечной или бесконечной (периодической или непериодической) десятичной дроби.
Действительные числа — это любые рациональные и иррациональные числа. Приведем примеры таких чисел: 0; 6; 458; 1863; 0,578; -38; 265; 0,145(3); log512.
Нуль также является действительным числом. Согласно определению, существуют как положительные, так и отрицательные действительные числа. Нуль является единственным действительным числом, которое не положительно и не отрицательно.
Еще одно название для действительных чисел — вещественные числа. Эти числа позволяют описывать значение непрерывно меняющейся величины без введения эталонного (единичного) значения этой величины.
Координатная прямая и действительные числа
Каждой точке не координатной прямой соответствует определенное и единственное действительное число. Иными словами, действительные числа занимают всю координатную прямую, а между точками кривой и числами присутствует взаимно-однозначное соответствие.
Представления действительных чисел
Под определение дейситвительных чисел попадают:
- Натуральные числа.
- Целые числа.
- Десятичные дроби.
- Обыкновенные дроби.
- Смешанные числа.
Также действительные числа часто представляются в виде выражений со степенями, корнями и логарифмами. Сумма, разность произведение и частное действительных чисел также являются действительными числами.
Значение любого выражения, составленного из действительных чисел, также будет являться действительным числом.
Например, значения выражений sin23π·e-285·10log32 и tg676693-8π32 — действительные числа.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Навигация по статьям
Предыдущая статьяВычитание целых чисел
Следующая статья
Рациональные числа
- Арифметические операции над действительными числами
- Взаимно обратные числа
- Вычитание десятичных дробей
- Вычитание натуральных чисел
- Вычитание натуральных чисел
- Все темы по математике
- Курсовые работы
- Рефераты
- Контрольные работы
- Отчет по практике
- Эссе
Узнать подробнее
ПЛАСТИНЧАТЫЙ ТЕПЛООБМЕННИК В Компас А Бумага теплообменник кожухотрубчатый
Вид работы:
Чертёж
Выполнена:
27 июня 2022 г.

Стоимость:
2 400 руб
Заказать такую же работу
Математические модели инфодемии
Заказать такую же работу
Нужно рассчитать теплообменник
Вид работы:
Контрольная работа
Выполнена:
28 апреля 2022 г.

Стоимость:
3 600 руб
Заказать такую же работу
Задания прикреплены
Вид работы:
Контрольная работаВыполнена:
21 января 2022 г.

Стоимость:
1 400 руб
Заказать такую же работу
Особенности исторической застройки Красноярска от появления острога до конца века
Вид работы:
Реферат
Выполнена:
27 декабря 2021 г.

Стоимость:
1 000 руб
Заказать такую же работу
по Строительным материалам
Вид работы:
Решение задач
Выполнена:
30 ноября 2021 г.

Стоимость:
1 100 руб
Заказать такую же работу
Смотреть все работы по чертежам в компас
Урок 8. иррациональные числа. понятие действительного числа. сравнение действительных чисел — Алгебра — 7 класс
Алгебра
7 класс
Урок № 8
Иррациональные числа. Понятие действительного числа.
Сравнение действительных чисел
Перечень вопросов, рассматриваемых в теме:
- Иррациональные числа.

- Понятие действительного числа.
- Абсолютная величина (модуль) числа.
- Сравнение действительных чисел.
Тезаурус:
Число, которое можно записать в виде конечной или бесконечной периодической десятичной дроби, называют рациональным.
Бесконечная периодическая десятичная дробь – это бесконечная дробь, у которой одна цифра или группа цифр повторяются. Повторяющаяся группа цифр называется периодом и записывается в скобках.
Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным числом.
Рациональные и иррациональные числа называются действительными числами.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
Рассмотрим положительную бесконечную непериодическую дробь 0,10110111011110…
После запятой записаны группы единиц, разделённые нулём. Эта дробь не может быть десятичным разложением какого – либо рационального числа.
Её называют иррациональным (нерациональным) числом.
Иррациональное число – бесконечная непериодическая десятичная дробь.
Примеры иррациональных чисел:
0,010010001…
-17,1234567…
Самое знаменитое иррациональное число π = 3,1415926…
Понятие действительного числа:
Рациональные и иррациональные числа называют действительными.
Таким образом, любое действительное число можно представить в виде бесконечной (периодической или непериодической) десятичной дроби.
Если дробь периодическая – число рациональное.
Если дробь непериодическая – число иррациональное.
Число, образованное цифрами до запятой, называют целой частью, после запятой дробной частью.
Для записи произвольной бесконечной десятичной дроби, отличной от нуля, пользуются буквами:
α0,α1 α2 α3… αn…, причем хотя бы одна из цифр отлична от нуля.
Противоположные числа
Противоположные числа отличаются только знаками:
α0, α1, α2, α3,… αn…, и — α0,α1, α2, α3,… αn…,
Обозначают: а, если а положительное число,
-а, если а отрицательное число.
Абсолютная величина числа (модуль) числа
Абсолютной величиной числа (модулем) действительного числа называют:
- само число а, если а – положительное
- 0, если а = 0
- число -а, если а – отрицательное число.

Обозначается: а, если а > 0,
|а| = 0, если а = 0,
-а, если а < 0.
Примеры:
а = 0,10110111… |а| = 0,10110111…
b = -2,1234567…… |b| = 2,1234567…
c = 0,(0) |c| = 0
Сравнение действительных чисел.
Правило 1.
Два действительных числа равны, если они имеют одинаковые знаки и их абсолютные величины имеют одинаковые целые и дробные части.
Правило 2.
Отрицательное число меньше 0 и меньше любого положительного числа.
Число 0 меньше любого положительного числа.
Правило 3.
Если целые части положительных чисел разные, то больше то, у которого целая часть больше.
Если целые части положительных чисел одинаковые, то больше то, у которого цифра в наименьшем разряде дробной части больше.
Из двух отрицательных чисел больше то, у которого абсолютная величина меньше.
Сравнение чисел обозначают с помощью знаков: > = <
Разбор решения заданий тренировочного модуля.
Задача 1.
Изобразите числовые множества с помощью кругов Эйлера.
Определите, какому множеству принадлежат числа: 2,(3) и 2,1234?
Решение:
Число 2,(3) принадлежит множествам рациональных и действительных чисел.
Число 2,1234 принадлежит множествам иррациональных и действительных чисел.
Задача 2.
Сравните числа:
- 0,(27) > 0,2727, т. к. 0,(27) = 0,272727…
- -3,(5) < -3,(4), т. к. абсолютная величина первого числа меньше.
- 8,273273 > 8,(27), т. к. 8,273 и 8,272, первая отличная цифра в третьем разряде больше.
Все ли иррациональные числа действительные числа да или нет? – Обзоры Вики
Да. Иррациональные числа определяются как те действительные числа, которые не являются рациональными.
Отсюда, почему каждое иррациональное число не является действительным числом? Таким образом, каждое иррациональное число является действительным числом. … Поскольку никакое отрицательное значение не может быть квадратным корнем натурального числа, поэтому каждая точка на числовой прямой не может быть в форме u221am, где m — натуральное число.
… Поскольку никакое отрицательное значение не может быть квадратным корнем натурального числа, поэтому каждая точка на числовой прямой не может быть в форме u221am, где m — натуральное число.
Является ли каждое действительное число рациональным или иррациональным? Это действительные числа, которые мы не можем записать как отношение pq, где p и q — целые числа, при этом q≠0. По факту, каждое действительное число является либо рациональным числом, либо иррациональным числом. Никакое число не может быть одновременно рациональным и иррациональным!
Кроме того, каждое ли иррациональное число является рациональным числом? «Является каждый иррациональный рациональное число?» Нет. Рациональные числа — это те, которые могут быть выражены как отношение (доля) двух целых чисел; иррациональные числа — это те, которые не могут быть выражены таким образом. Между этими двумя категориями нет пересечения.
Всякое ли натуральное число является действительным числом? Да, цель не каждое действительное число является натуральным числом. Натуральные числа — это набор целых положительных чисел {1, 2, 3,…}, которые также являются действительными числами. Однако действительные числа также включают отрицательные числа, дроби и т. д., ни одно из которых не является натуральным числом.
Натуральные числа — это набор целых положительных чисел {1, 2, 3,…}, которые также являются действительными числами. Однако действительные числа также включают отрицательные числа, дроби и т. д., ни одно из которых не является натуральным числом.
Что такое каждое иррациональное число?
иррациональное число, любое действительное число, которое не может быть выражено как частное двух целых чисел. Например, среди целых чисел и дробей нет числа, равного квадратному корню из 2. … Каждое иррациональное число может быть выражено как бесконечное десятичное расширение без регулярно повторяющихся цифр или групп цифр.
Является ли каждое целое число действительным числом? Мы знаем, что целые числа не включают десятичные числа. Иррациональное число определяется как число, которое не может быть выражено в виде дробей. … Каждое целое число реальное число и Рациональное число, но не иррациональные числа и натуральные числа. Следовательно, каждое целое число является действительным числом и рациональным числом.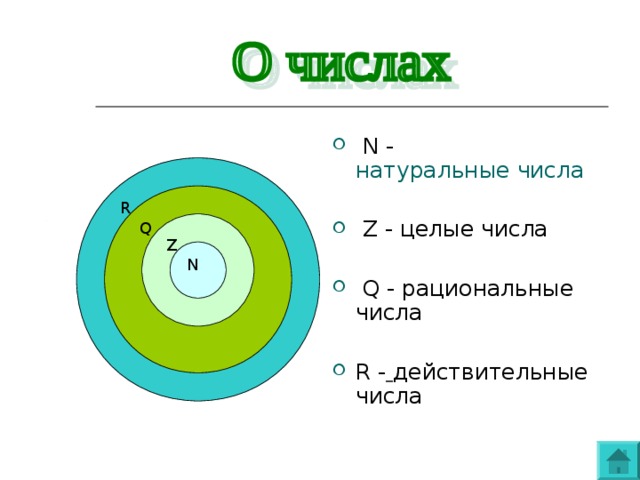
Как иррациональные числа используются в реальной жизни? Инженерные револьверы по конструированию вещей для реальной жизни и несколько вещей, таких как обработка сигналов, расчет силы, спидометр и т. д. использовать иррациональные числа. Исчисление и другие области математики, в которых используются эти иррациональные числа, широко используются в реальной жизни. Иррациональные числа используются косвенно.
Что такое каждое рациональное число?
Каждое рациональное число целое число.
Также является ли каждое иррациональное число целым числом? Поскольку иррациональные числа не могут быть выражены как отношение двух целых чисел, отсюда следует, что иррациональные числа не могут быть целыми числами, и наоборот.
Каждое ли число является рациональным числом?
Поскольку любое целое число можно представить как отношение двух целых чисел, все целые числа являются рациональными числами. Помните, что все счетные числа и все целые числа тоже целые, а значит, они тоже рациональны.
Что такое действительные и рациональные числа? Рациональными считаются числа, которые можно представить в виде отношения двух целых чисел, причем знаменатель не равен нулю. Действительные числа – это те, которые может быть представлен на действительной числовой прямой. … не может быть выражено как отношение двух целых чисел, как рациональные числа, но может быть представлено в прямой числовой строке.
Как действительные числа используются в реальной жизни?
Большинство чисел, с которыми мы работаем каждый день, являются действительными числами.. К ним относятся все деньги в вашем кошельке, статистика, которую вы видите в спорте, или измерения, которые мы видим в поваренных книгах. Все эти числа можно представить в виде дроби (нравится нам это или нет).
Каковы примеры действительных чисел?
В математике действительное число — это значение непрерывной величины, которое может представлять расстояние вдоль линии. Реальные числа включают как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2,7, 8/2.5, 7) и иррациональные числа, такие как √XNUMX, π и т. д., являются действительными числами.
Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2,7, 8/2.5, 7) и иррациональные числа, такие как √XNUMX, π и т. д., являются действительными числами.
Всякое ли целое число является рациональным числом? Рациональное число — это число, которое может быть выражено в виде p/q, где q не должно быть равно 0… Но это не целое число, а десятичное. Таким образом, рациональное число может быть или не быть целым числом, но каждое целое число является рациональным числом.
Реально или рационально? Число рациональное (записывается как отношение двух целых чисел), но оно также реальные . Все рациональные числа также являются действительными числами.
…
| Тип десятичной дроби | Рациональный или иррациональный | Примеры |
|---|---|---|
| Нагрузочный | Рациональный | 0.25 (золото) 1.3 (золото) |
| Непрерывный и повторяющийся | Рациональный | 0. 66… (золото) 3.242424… (золото) 66… (золото) 3.242424… (золото) |
Что такое действительные числа и недействительные числа?
Реальные числа могут быть положительными или отрицательными.и включите число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел. Мнимые числа — это числа, которые невозможно определить количественно, например квадратный корень из -1.
Что такое недействительные числа? Чай числа не действительные, а мнимые называются недействительными или недействительными числами. Недействительные числа не могут быть представлены на числовой прямой. I. Комплексные числа: 4+i5 , где «i» представляет йоту, которая равна √−1 .
Как найти настоящие числа?
Абсолютное значение числа — это его расстояние от нуля на числовой прямой. Действительные числа — это числа, которые не являются мнимыми, то есть все числа, кроме квадратного корня из -1 и бесконечности. Чтобы найти абсолютное значение действительного числа, найдите его расстояние от нуль в числовой строке.
Что такое рациональное и иррациональное число? Рациональные числа – это те числа, которые целые и может быть выражено в виде x/y, где и числитель, и знаменатель являются целыми числами, тогда как иррациональные числа — это те числа, которые не могут быть выражены дробью. … Иррациональные числа включают surds и специальные числа, такие как π.
Что такое рациональное и иррациональное число на примере?
Рациональное число — это число, которое можно представить в виде P/Q, где P и Q — целые числа, а Q ≠ 0. Но иррациональное число нельзя записать в виде простых дробей. ⅔ это пример рациональных чисел, тогда как √2 — иррациональное число.
Почему каждое рациональное число является действительным числом? Верно или ложно? Ага это правда….
Что такое действительное число в математике?
действительное число, в математике, количество, которое может быть выражено в виде бесконечного десятичного разложения. … Действительные числа включают положительные и отрицательные целые числа и дроби (или рациональные числа), а также иррациональные числа.
Что такое рациональные и иррациональные числа? Рациональные числа — это числа, которые можно представить в виде дроби или части целого числа.. (примеры: -7, 2/3, 3.75) Иррациональные числа — это числа, которые нельзя представить в виде дроби или отношения двух целых чисел. Нет конечного способа выразить их. (примеры: √2, π, е)
Что такое реальное число 10-го класса?
Реальные числа просто комбинация рациональных и иррациональных чисел, в системе счисления. В общем, над этими числами можно производить все арифметические действия, и их можно представить в числовой строке.
404 Cтраница не найдена
Размер:
AAA
Цвет: C C C
Изображения Вкл. Выкл.
Обычная версия сайта
Найти ближайший филиал Версия для слабовидящих Версия для слабовидящих
КАМЕНСК-УРАЛЬСКИЙ
АГРОПРОМЫШЛЕННЫЙ ТЕХНИКУМ
Сохраняя традиции, вместе создаем будущее!
Не хватает прав доступа к веб-форме.
Выше сщщбщение успешно отправлено.
-
Сведения об ОО
- Основные сведения
- Структура и органы управления
- Документы
- Образование
- Образовательные стандарты
- Руководство. Педагогический состав
- Педагогический состав
- МТО и оснащенность ОП
- Стипендия и иные виды материальной поддержки
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приёма (перевода)
- Противодействие коррупции
- Бесплатная юридическая помощь
- Награды, достижения ОО
- Инновационная деятельность
- Доступная среда
- Международное сотрудничество
-
Летопись техникума
- Страницы летописи
- Руководители
- Нам есть у кого учиться
- Педагоги техникума
- Наша гордость — выпускники
- Достижения
- СМИ о техникуме
- Хранители нашей истории
-
Абитуриентам
- Прием 2022
- Дни открытых дверей
- Специальности/профессии
- Общежитие
- Правила и условия приема
- Документы для поступления
- Подать заявление онлайн
- Студенческая жизнь
- Приемная комиссия
- Мониторинг подачи заявлений и документов
- Зачисление
- Фото-экскурсия
- Инклюзивное образование
- Целевое обучение
-
Студентам
- Расписание
- Заочное отделение
- Документы
- Студенческая жизнь
- Государственная итоговая аттестация
- Центр профориентологии
- Стипендия и иные виды материальной поддержки
- Спорт
- Конференции и олимпиады
- Советы психолога
- Сайты преподавателей
- ЕГЭ для студентов учреждений СПО
- Воспитательная работа
- Целевое обучение
- Выпускникам
-
Сотрудникам
- Документы
- Методическая служба
-
Родителям
- Телефонный справочник
- Информация для Родителей
- Специальности / профессии
- Главная
- ›
- uploads
- ›
- about_the_university
- ›
- 14_sistema-distantsionnogo-obucheniya
- ›
- raspisanie-na-05-09-2020g-subbota
определение и сравнение • BUOM
Автор: редакционная команда Indeed
30 апреля 2021 г.
Категории чисел показывают, насколько некоторые группы чисел отличаются или похожи на другие группы чисел. Некоторые из этих категорий перекрываются и включают в себя подмножества друг друга, потому что они имеют схожие характеристики, в то время как другие категории уникальны и не пересекаются. Действительные числа и целые числа принадлежат к двум различным категориям чисел. В этой статье мы обсудим, что такое действительные числа, что такое целые числа, действительные числа и целые числа, а также сравним действительные и целые числа на диаграмме.
Что такое действительное число?
Вещественное число — это любое число на числовой прямой, которое включает в себя подмножества чисел, включая натуральные, целые, целые, рациональные и иррациональные числа. Проще говоря, все числа являются действительными числами, за исключением мнимых чисел, которые представляют собой набор комплексных чисел, которые когда-то считались невозможными для вычисления.
Вы можете разделить действительные числа на две категории, рациональные числа и иррациональные числа. Вы можете дополнительно разделить категорию рациональных чисел на подмножество целых чисел, которые содержат подмножество, целые числа; который содержит подмножество натуральных чисел. Существует множество наглядных пособий и диаграмм того, как работают эти категории и подмножества чисел. Если вы хотите найти один в Интернете, вы найдете его легко.
Вы можете дополнительно разделить категорию рациональных чисел на подмножество целых чисел, которые содержат подмножество, целые числа; который содержит подмножество натуральных чисел. Существует множество наглядных пособий и диаграмм того, как работают эти категории и подмножества чисел. Если вы хотите найти один в Интернете, вы найдете его легко.
Вот определения чисел, из которых состоят все действительные числа:
Иррациональные числа
Иррациональное число — это действительное число, которое нельзя записать в виде простой дроби. Числа, которые вы не можете записать в виде дроби, — это десятичные числа, которые продолжаются вечно без повторяющегося шаблона.
Например, некоторые известные иррациональные числа:
Число пи, или «π», является иррациональным числом, потому что это десятичная дробь, которая продолжается бесконечно, не повторяясь, и вы не можете записать ее в виде дроби.
Квадратный корень из двух, или «√2», — это еще одна бесконечная десятичная дробь, которая никогда не повторяется.

Число Эйлера, или «е», — это десятичная дробь без шаблона или конца.
Золотое сечение, или «φ», — это еще одна десятичная дробь без конца и без видимой закономерности.
Рациональное число
Рациональное число — это число, которое можно записать как отношение двух целых чисел, или, другими словами, как простую дробь. Рациональные числа включают подмножества: целые числа, целые числа и натуральные числа.
Например, следующие числа являются рациональными числами:
Десятичное число 2,5 можно записать как дробь 6/2.
Дробь 0,33 — это повторяющаяся десятичная дробь, которую можно записать как дробь 1/3.
Целое число -4 также можно записать в виде дроби -4/1.
Целое число 32 также можно записать в виде дроби 32/1.
Натуральное число 1 также можно записать в виде дроби 1/1.
Целые числа
Целое число — это положительное или отрицательное целое число без дробной или десятичной части. Целые числа включают подмножества, целые числа и натуральные числа.
Целые числа включают подмножества, целые числа и натуральные числа.
Например, следующие числа являются целыми:
Отрицательное число, -16
Целое число, 0
Счетное число, 57
Целые числа
Целое число — это положительное целое число без дробной или десятичной части. Целые числа включают подмножество натуральных чисел. Целые числа представляют целые объекты без каких-либо частей или фрагментов.
Например, следующие числа являются целыми числами:
Целое число, 0
Целое число, 1258
Натуральное число, 7
Натуральные числа
Натуральное число иногда также называют «счетным числом» и оно похоже на целое число, за исключением того, что вы не включаете ноль в набор. Если бы вы естественным образом начали подсчитывать количество предметов в сумке, вы бы начали с единицы, а не с нуля.
Например, следующие числа являются натуральными числами:
Натуральное число, 1
Натуральное число 513
Натуральное число 3 482 389.

Что такое целое число?
Целое число — это положительное или отрицательное целое число без дробной или десятичной части. Целые числа представляют собой подмножество действительных чисел и включают в себя целые числа подмножества и натуральные числа. Обычно целые числа представляются как: «-3, -2, -1, 0, 1, 2, 3», поскольку это показывает, что числа бесконечны в любом направлении, целые числа и содержат число ноль.
Целые числа имеют следующие характеристики:
Целые числа положительны, поэтому вы видите их в правой части числовой строки, а положительные целые числа имеют более высокое значение, чем их отрицательные аналоги или противоположности.
Целые числа отрицательны, поэтому вы видите их в левой части числовой строки, а отрицательные целые числа имеют меньшее значение, чем их положительные аналоги или противоположности.
Есть одно целое число — ноль — нейтральное, то есть ни положительное, ни отрицательное, и вы видите его в центре числовой прямой.

Целые числа не имеют фрагментов, то есть это целые числа без дробных или десятичных частей.
Действительные числа против целых чисел
Целые числа являются действительными числами, но не все действительные числа являются целыми числами. Вот некоторые отличия:
Действительные числа включают целые числа, но также включают рациональные, иррациональные, целые и натуральные числа.
Целые числа — это тип вещественных чисел, который включает в себя только положительные и отрицательные целые числа и натуральные числа.
Действительные числа могут включать дроби из-за рациональных и иррациональных чисел, но целые числа не могут включать дроби.
Действительные числа обладают «свойством наименьшей верхней границы», или полнотой, но целые числа не обладают этим свойством.
Таблица сравнения целых и действительных чисел
Вот таблица, которая поможет вам легче сравнивать целые числа с действительными числами:
Параметры сравнения Целые числа Действительные числа Происхождение Арбермут Холст изобрел систему счисления целых чисел в 1563 году. Слово целое имеет латинские корни 16-го века, означая целое или неповрежденное. Рене Декарт ввел термин «действительный» в 17 веке для описания всех чисел, которые не считались мнимыми числами. Классификация Математики классифицируют целые числа только как целые числа и их отрицательные числа. Математики классифицируют действительные числа как рациональные числа, иррациональные числа, целые числа, целые числа и натуральные числа. Счетность Целые числа могут образовывать счетное бесконечное множество. Нотационный символ «Z» представляет собой набор всех целых чисел. Действительные числа могут образовывать неисчисляемое бесконечное множество. «R» представляет собой набор всех действительных чисел. Представление в числовой строке Целые числа в числовой строке — это все целые числа и их отрицательные числа. Действительные числа на числовой прямой — это любая точка на числовой прямой. Наличие дробей или десятичных знаков Дробное или десятичное число не является целым числом. Дробное или десятичное число является действительным числом.
Слово целое имеет латинские корни 16-го века, означая целое или неповрежденное. Рене Декарт ввел термин «действительный» в 17 веке для описания всех чисел, которые не считались мнимыми числами. Классификация Математики классифицируют целые числа только как целые числа и их отрицательные числа. Математики классифицируют действительные числа как рациональные числа, иррациональные числа, целые числа, целые числа и натуральные числа. Счетность Целые числа могут образовывать счетное бесконечное множество. Нотационный символ «Z» представляет собой набор всех целых чисел. Действительные числа могут образовывать неисчисляемое бесконечное множество. «R» представляет собой набор всех действительных чисел. Представление в числовой строке Целые числа в числовой строке — это все целые числа и их отрицательные числа. Действительные числа на числовой прямой — это любая точка на числовой прямой. Наличие дробей или десятичных знаков Дробное или десятичное число не является целым числом. Дробное или десятичное число является действительным числом.
Поиск материала «Числа рациональные и иррациональные, Нивен А., 1966» для чтения, скачивания и покупки
Ниже показаны результаты поиска поисковой системы Яндекс. В результатах могут быть показаны как эта книга, так и похожие на нее по названию или автору.
Search results:
- Числа рациональные и иррациональные | Нивен А., Яглом…
Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами
Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала.Автор книги — известный американский специалист по теории чисел. Скачать книгу бесплатно (djvu, 3.86 Mb) | Читать «Числа рациональные и иррациональные».
bookscat.
 org
org - А. нивен. числа рациональные и иррациональные…
А. НИВЕН. ЧИСЛА РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ Москва: «Мир», 1966 #книги_math_досуг. Аннотация издательства: Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и…
vk.com
-
Купить эту книгу
- Канцтовары
Канцтовары: бумага, ручки, карандаши, тетради. Ранцы, рюкзаки, сумки. И многое другое.
my-shop.ru
- А. НИВЕН числа РАШИОНАЛЬНЫЕ ИРРАШИОНАЛЬНЫЕ 3 1415 9
3.
 (Действительные) алгебраические числа. 4. Числа, допускающие построение 5. Рациональные числа.
(Действительные) алгебраические числа. 4. Числа, допускающие построение 5. Рациональные числа.ikfia.ysn.ru
- Числа рациональные и иррациональные — Нивен А. — быстро…
Числа рациональные и иррациональные.djvu. Читать онлайн. Нивен А. (посмотреть).
klex.ru
- Нивен А. Числа рациональные и иррациональные. — 1966
Нивен А. Числа рациональные и иррациональные / пер. с англ. В. В. Сазонова ; под ред. И. М. Яглома. — М. : Мир, 1966.
Рациональные числа. 33§ 1. Определение рациональных чисел 36§ 2. Конечные и бесконечные десятичные дроби 39§ 3. Различные способы формулировки и доказательства предложений 45§ 4. Периодические десятичные дроби 50§ 5. Всякую конечную десятичную дробь можно представить в виде периодической десятичной дроби 53§ 6.
 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7Действительные числа образуются всеми рациональными и иррациональными числами и являются основной числовой системой в математике. Любое геометрическое рассуждение, касающееся длин, площадей или объемов, сразу приводит к действительным числам.
b-ok.xyz
- Числа рациональные и иррациональные » Litgu.ru…
Название: Числа рациональные и иррациональные Автор: Нивен Айвен Издательство: Мир Год: 1966 Формат: PDF/Djvu Страниц: 201 Размер: 24.3 MB Язык: Русский. Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру.

litgu.ru
- А. нивен. числа рациональные и иррациональные…
А. НИВЕН. ЧИСЛА РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ Москва: «Мир», 1966 #книги_math_досуг. Аннотация издательства: Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое.
vk.com
- Числа рациональные и иррациональные
Название: Числа рациональные и иррациональные Автор: Нивен Айвен Издательство: Мир Год: 1966 Страниц: 201 Формат: PDF, DJVU Размер: 24,3 МБ Качество: Отличное. Числа рациональные и иррациональные — Эта книга посвящена одному из основных понятий математики — понятию действительного числа.
 Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе…
Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе…bookskeeper.ru
- Скачать Нивен А. Числа рациональные и иррациональные [PDF]
Нивен А. Числа рациональные и иррациональные. Файл формата pdf. размером 4,80 МБ.
Дополнительные главы», содержащие классическое изложение понятий и результатов математической логики с элементами теории множеств, теории алгоритмов и оснований математики….
eruditor.io
- А. нивен. числа рациональные и иррациональные…
А. Нивен. Числа рациональные и иррациональные.
vk.
 com
com - Скачать Числа рациональные и иррациональные — Нивен…
Нивен А. Числа рациональные и иррациональные. Формат: Электронная/бумажная книга Жанр: Теория чисел Автор(ы): Нивен А. Название: Числа рациональные и иррациональные Издательство: Мир Город: Москва Год: 1966. Аннотация: Эта книга посвящена одному из основных понятий математики — понятию действительного числа.
dislyget.ru
- Числа рациональные и иррациональные | Нивен Айвен
Нивен Айвен. Скачать книгу бесплатно (djvu, 4.40 Mb) | Читать «Числа рациональные и иррациональные».
bookscat.org
- Числа рациональные и иррациональные | Нивен А. | download
A НИВЕН ЧИСЛА РАЦИОНАЛЬНЫЕ и ИРРАиИОНАЛЬНЫЕ 3-4 7С= 3 1Л15927.
 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7Действительные числа образуются всеми рациональными и иррациональными числами и являются основной числовой системой в математике. Любое геометрическое рассуждение, касающееся длин, площадей или объемов, сразу приводит к действительным числам.
b-ok.cc
- Скачать Нивен А. Числа рациональные и иррациональные…
Нивен А. Числа рациональные и иррациональные. Файл формата djvu. размером 3,00 МБ.
Чтобы скачать этот файл зарегистрируйтесь и/или войдите на сайт используя форму сверху.
eruditor.io
- Скачать книгу Числа рациональные и иррациональные — Нивен.
 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7Действительные числа образуются всеми рациональными и иррациональными числами и являются основной числовой системой в математике. Любое геометрическое рассуждение, касающееся длин, площадей или объемов, сразу приводит к действительным числам.
b-ok.cc
- Числа рациональные и иррациональные
Числа рациональные и иррациональные. Айвен Нивен. Числа рациональные и иррациональные. Эта книга посвящена одному из основных понятий математики — понятию действительного числа. Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру.
 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7. Натуральные числа.
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7. Натуральные числа.СОВРЕМЕННАЯ МАТЕМАТИКА» Популярная серая АЙВЕН НИВЕН Числа рациональные и иррациональные Перевод с английского В, В, Сазонова Под редакцией И. М. Яглома ИЗДАТЕЛЬСТВО «МИР» Москва 1966.
b-ok.global
- Книга Числа рациональные и иррациональные (Нивен…
Читать онлайн книгу Числа рациональные и иррациональные автора Нивен А., Яглом И.М. (ред.)
bookree.org
- Числа рациональные и иррациональные — Нивен А.
Числа рациональные и иррациональные. Нивен А. | Математика. Эта книга посвящена одному из основных понятий математики — понятию действительного числа.
 Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала.
Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала.www.koob.ru
- Айвен Нивен «Числа рациональные и иррациональные«
] Книга двести тридцать вторая. Айвен Нивен «Числа рациональные и иррациональные» (Ivan Niven «Numbers: Rational and Irrational», 1961) М: Мир, 1966 г., 200 стр. От прошлой жизни осталась куча книг по математике — элементарной и не очень. Эта — из элементарных. Не читал раньше, почему бы и не. Тем более в ней доказывается существование трансцендентных чисел прямым лиувиллевским построением — даже не помню, знал ли я это доказательство раньше.

timur0.livejournal.com
- Числа рациональные и иррациональные | Нивен Айвен
Нивен Айвен. Скачать (djvu, 4.40 Mb) Читать.
www.bookfi.net
- Целые числа. Рациональные и иррациональные числа
Рациональные и иррациональные числа. Шилепина Надежда Ивановна. преподаватель. Новокузнецк, 2019. Что такое число. Число — основное понятие математики, используемое для количественной характеристики, сравнения, нумерации объектов и их частей.
Рациональные числа. Множество чисел, которое можно представить в виде ,называется множеством рациональных чисел и обозначается — Q первой буквой французского слова Quotient — «отношение».
multiurok.ru
- Нивен А., Числа рациональные и иррациональные.
 .
.Нивен А., Числа рациональные и иррациональные. Серия: Современная математика. 1966, изд-во: Мир, город: М., стр. : 198 с., обложка: Мягкая издательская обложка, формат: Обычный, состояние: Хорошее (следы влаги). Книга известного американского специалиста по теории чисел посвящена понятию действительного числа.
4. Иррациональные числа. 5. Значения тригонометрических и логарифмической функций. Приближение иррациональных функций рациональными. 7. Существование трансцендентных чисел.
www.gornitsa.ru
- Разница между рациональными и иррациональными числами…
Рациональные и иррациональные числа. Рациональное число – это такое число, которое можно записать в виде дроби с целыми числителем и знаменателем.
Иррациональное число – это число, которое невозможно записать в виде дроби с целыми числителем и знаменателем. Невозможно, потому что это бесконечные дроби, да еще и непериодические.
 Поэтому нет таких целых чисел, которые бы поделившись друг на друга, дали бы иррациональное число.
Поэтому нет таких целых чисел, которые бы поделившись друг на друга, дали бы иррациональное число.cos-cos.ru
- Числа: натуральные, целые, рациональные, иррациональные…
Рациональные числа — это целые числа и дроби. Любое рациональное число может быть представлено в виде периодической дроби.
Действительные числа – это все рациональные и все иррациональные числа. Множество действительных чисел обозначается латинской буквой R. Школьная алгебра Школьная геометрия.
sbp-program.ru
- Какие числа называются Иррациональные?
Просмотры. 43252. Определение иррациональных чисел. Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби: Оно может быть выражено в форме бесконечной
Множество иррациональных чисел договорились обозначать латинской буквой I.
 Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль. Если натуральное число n не является точным квадратом, т. е. n ≠ k2…
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль. Если натуральное число n не является точным квадратом, т. е. n ≠ k2…skysmart.ru
- Рациональные и иррациональные числа. Понятие…
Множество рациональных и иррациональных чисел составляют множество вещественных (действительных) чисел.
Это число, как и любое другое иррациональное число, изображается бесконечной непериодической десятичной дробью. Последовательностью десятичных приближений числа с недостатком называют последовательность конечных десятичных дробей, которая получится, если у числа отбросить все десятичные знаки, начиная, сначала с первого десятичного знака, затем со второго десятичного знака, потом с третьего…
www.resolventa.ru
- Числовая ось, рациональные, иррациональные числа
Такие числа называются иррациональными числами.
 Иррациональное число невозможно представить в виде Приведём примеры иррациональных чисел
Иррациональное число невозможно представить в виде Приведём примеры иррациональных чиселНапример, иррациональные числа. Множество иррациональных чисел обозначается буквой I. Арифметические действия над иррациональными числами и их свойства аналогичны рациональным числам. Множество, состоящее из рациональных и иррациональных чисел, называется множеством действительных чисел, которое обозначается буквой R.
www.evkova.org
- Рациональные и иррациональные числа, множество…
Множество рациональных чисел замкнуто, относительно операций сложения, вычитания, умножения и деления (исключая деление на 0). В алгебре говорят, что рациональные числа образуют поле. Иррациональные числа. Иррациональное число – это число, которое нельзя представить обыкновенной дробью m/n, где числитель m – целое число, а знаменатель n – натуральное число. Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.

reshator.com
На данной странице Вы можете найти лучшие результаты поиска для чтения, скачивания и покупки на интернет сайтах материалов, документов, бумажных и электронных книг и файлов похожих на материал «Числа рациональные и иррациональные, Нивен А., 1966»
Для формирования результатов поиска документов использован сервис Яндекс.XML.
Нашлось 13 млн ответов. Показаны первые 32 результата(ов).
Дата генерации страницы:
Классифицировать реальное число | Колледж Алгебра
Результаты обучения
- Запись целых чисел в виде рациональных чисел
- Определение рациональных чисел
- Классифицировать действительные числа по наборам
Числа, которые мы используем для счета или перечисления предметов, — это натуральных чисел : 1, 2, 3, 4, 5 и так далее. Мы описываем их в системе обозначений как {1, 2, 3, …}, где многоточие (…) указывает, что числа продолжаются до бесконечности. Натуральные числа, конечно же, также называются 9.0015 подсчет чисел . Всякий раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел. Набор из целых чисел — это набор натуральных чисел плюс ноль: {0, 1, 2, 3,…}.
Мы описываем их в системе обозначений как {1, 2, 3, …}, где многоточие (…) указывает, что числа продолжаются до бесконечности. Натуральные числа, конечно же, также называются 9.0015 подсчет чисел . Всякий раз, когда мы перечисляем членов команды, считаем монеты в коллекции или подсчитываем деревья в роще, мы используем набор натуральных чисел. Набор из целых чисел — это набор натуральных чисел плюс ноль: {0, 1, 2, 3,…}.
Набор из целых чисел добавляет противоположные натуральные числа к набору целых чисел: {…,-3, -2, -1, 0, 1, 2, 3,…}. Полезно отметить, что набор целых чисел состоит из трех различных подмножеств: отрицательных целых чисел, нуля и положительных целых чисел. В этом смысле положительные целые числа — это просто натуральные числа. Другой способ думать об этом состоит в том, что натуральные числа являются подмножеством целых чисел.
[латекс]\begin{align}&{\text{целые отрицательные}} && {\text{ноль}} && {\text{целые положительные}}\\&{\dots ,-3,-2,- 1,} && {0,} && {1,2,3,\dots }\\ \text{ }\end{align}[/latex]
Набор из рациональных чисел записывается как [латекс]\ left\{\frac{m}{n}|m\text{ и }{n}\text{ являются целыми числами, а }{n}\ne{ 0 }\right\}[/latex]. Обратите внимание на то, что из определения рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен 0. Мы также можем видеть, что каждое натуральное, целое и целое число является рациональным числом с знаменатель 1,
Обратите внимание на то, что из определения рациональные числа — это дроби (или частные), содержащие целые числа как в числителе, так и в знаменателе, а знаменатель никогда не равен 0. Мы также можем видеть, что каждое натуральное, целое и целое число является рациональным числом с знаменатель 1,
Поскольку это дроби, любое рациональное число также может быть представлено в десятичной форме. Любое рациональное число может быть представлено как:
- завершающая десятичная дробь: [латекс]\фракция{15}{8}=1,875[/латекс] или
- повторяющееся десятичное число: [латекс]\frac{4}{11}=0,36363636\dots =0.\overline{36}[/latex]
Мы используем линию, проведенную над повторяющимся блоком чисел, вместо многократного написания группы.
Пример: запись целых чисел в виде рациональных чисел
Каждое из следующих чисел запишите в виде рационального числа.
- 7
- 0
- –8
Показать решение
Попробуйте
Каждое из следующих чисел запишите в виде рационального числа.
- 11
- 3
- –4
Показать решение
Пример: Идентификация рациональных чисел
Запишите каждое из следующих рациональных чисел как завершающее или повторяющееся десятичное число.
- [латекс]-\dfrac{5}{7}[/латекс]
- [латекс]\dfrac{15}{5}[/латекс]
- [латекс]\dfrac{13}{25}[/латекс]
Показать решение
Иррациональные числа
В какой-то момент в далеком прошлом кто-то обнаружил, что не все числа являются рациональными числами. Строитель, например, мог обнаружить, что диагональ квадрата с единицей стороны равна не 2 и даже не [латекс]\фрак{3}{2}[/латекс], а чему-то другому. Или швейник мог заметить, что отношение длины окружности к диаметру рулона ткани чуть больше 3, но все же это не рациональное число. Такие числа называются 9.0015 иррационально , потому что их нельзя записать в виде дробей. Эти числа составляют набор из иррациональных чисел . Иррациональные числа не могут быть представлены в виде дроби от двух целых чисел. Невозможно описать этот набор чисел одним правилом, кроме как сказать, что число иррационально, если оно не рационально. Итак, мы пишем это, как показано.
Иррациональные числа не могут быть представлены в виде дроби от двух целых чисел. Невозможно описать этот набор чисел одним правилом, кроме как сказать, что число иррационально, если оно не рационально. Итак, мы пишем это, как показано.
{ч | h не является рациональным числом}
Пример: дифференцирование рациональных и иррациональных чисел
Определите, является ли каждое из следующих чисел рациональным или иррациональным. Если оно рационально, определите, является ли оно завершающим или повторяющимся десятичным числом.
- [латекс]\sqrt{25}[/латекс]
- [латекс]\dfrac{33}{9}[/латекс]
- [латекс]\sqrt{11}[/латекс]
- [латекс]\dfrac{17}{34}[/латекс]
- [латекс]0.3033033303333\точки[/латекс]
Показать решение
Попробуйте
Вещественные числа
Для любого числа n мы знаем, что n либо рационально, либо иррационально. Не может быть и того, и другого. Наборы рациональных и иррациональных чисел вместе составляют набор действительные числа . Как мы видели с целыми числами, действительные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа. Каждое подмножество включает дроби, десятичные числа и иррациональные числа в соответствии с их алгебраическим знаком (+ или –). Ноль не считается ни положительным, ни отрицательным.
Наборы рациональных и иррациональных чисел вместе составляют набор действительные числа . Как мы видели с целыми числами, действительные числа можно разделить на три подмножества: отрицательные действительные числа, ноль и положительные действительные числа. Каждое подмножество включает дроби, десятичные числа и иррациональные числа в соответствии с их алгебраическим знаком (+ или –). Ноль не считается ни положительным, ни отрицательным.
Действительные числа можно изобразить на горизонтальной числовой линии с произвольной точкой, выбранной как 0, с отрицательными числами слева от 0 и положительными числами справа от 0. Затем для обозначения каждого целого числа используется фиксированное единичное расстояние. (или другое базовое значение) по обе стороны от 0. Любое действительное число соответствует уникальной позиции на числовой прямой. Верно и обратное: каждое место на числовой прямой соответствует ровно одному вещественному числу. Это известно как переписка один на один. Мы называем это действительная числовая строка .
Мы называем это действительная числовая строка .
Строка действительных чисел
Пример: Классификация действительных чисел
Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное. Находится ли число слева или справа от 0 на числовой прямой?
- [латекс]-\dfrac{10}{3}[/латекс]
- [латекс]\sqrt{5}[/латекс]
- [латекс]-\sqrt{289}[/латекс]
- [латекс]-6\пи[/латекс]
- [латекс]0.615384615384\точки[/латекс]
Показать раствор
Попробуйте
Классифицируйте каждое число как положительное или отрицательное, а также как рациональное или иррациональное. Находится ли число слева или справа от 0 на числовой прямой?
- [латекс]\sqrt{73}[/латекс]
- [латекс]-11.411411411\точки [/латекс]
- [латекс]\dfrac{47}{19}[/латекс]
- [латекс]-\dfrac{\sqrt{5}}{2}[/латекс]
- [латекс]6.
 210735[/латекс]
210735[/латекс]
Показать решение
Наборы чисел как подмножества
Начав с натуральных чисел, мы расширили каждый набор, чтобы сформировать больший набор, а это означает, что существует отношение подмножества между наборами чисел, с которыми мы сталкивались до сих пор. Эти отношения становятся более очевидными, если рассматривать их в виде диаграммы.
Наборы цифр. N : множество натуральных чисел W : множество целых чисел I : множество целых чисел Q : множество рациональных чисел Q´ : множество иррациональных чисел
Общее примечание: наборы чисел
Набор из натуральных чисел включает числа, используемые для счета: [латекс]\{1,2,3,\точки\}[/латекс].
Набор из целых чисел — это набор натуральных чисел плюс ноль: [латекс]\{0,1,2,3,\точки\}[/латекс].
Набор из целых чисел добавляет отрицательные натуральные числа к набору целых чисел: [латекс]\{\dots,-3,-2,-1,0,1,2,3,\dots\}[ /латекс].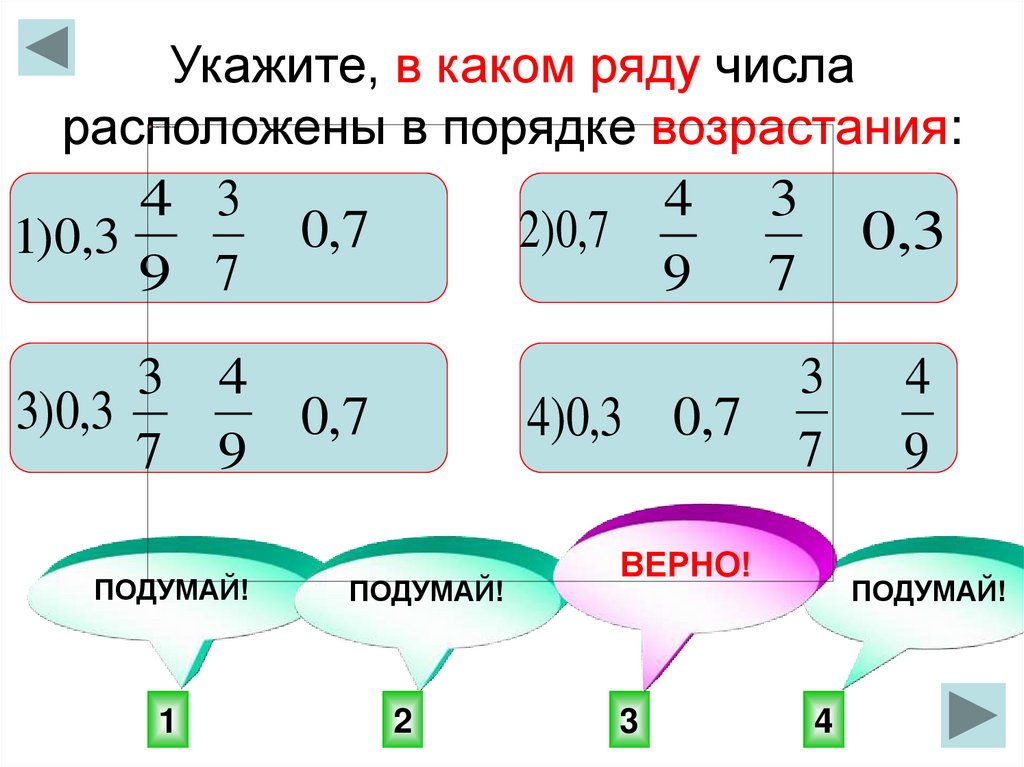
Набор из рациональных чисел включает дроби, записанные как [латекс]\{\frac{m}{n}|m\text{ и }n\text{ являются целыми числами, а }n\ne 0\}[/latex].
Набор из иррациональных чисел — это набор нерациональных, неповторяющихся и непрерывных чисел: [латекс]\{ч|ч\текст{ не является рациональным числом}\}[/латекс].
Пример: дифференцирование наборов чисел
Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и/или иррациональное число ( Q’ ).
- [латекс]\sqrt{36}[/латекс]
- [латекс]\dfrac{8}{3}[/латекс]
- [латекс]\sqrt{73}[/латекс]
- [латекс]-6[/латекс]
- [латекс]3.2121121112\точки [/латекс]
Показать решение
Попробуйте
Классифицируйте каждое число как натуральное число ( N ), целое число ( W ), целое число ( I ), рациональное число ( Q ) и/или иррациональное число ( Q’ ).
- [латекс]-\dfrac{35}{7}[/латекс]
- [латекс]0[/латекс]
- [латекс]\sqrt{169}[/латекс]
- [латекс]\sqrt{24}[/латекс]
- [латекс]4.763763763\точки [/латекс]
Показать решение
Внесите свой вклад!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Рациональные и иррациональные числа — математический обзор (видео и практика)
TranscriptFAQsPractice
Привет и добро пожаловать в это видео о рациональных и иррациональных числах!
Рациональные и иррациональные числа составляют систему действительных чисел . Эта диаграмма Венна показывает визуальное представление того, как классифицируются действительные числа.
Эта диаграмма Венна показывает визуальное представление того, как классифицируются действительные числа.
натуральных чисел составляют наименьшее подмножество, также известное как множество «счетных» чисел. Это все положительные недесятичные значения, начинающиеся с единицы. Целые числа — это натуральные числа плюс значение нуля. Набор чисел integer включает целые числа и все отрицательные недесятичные значения.
Рациональные числа включают наборы, показанные здесь, в дополнение к дробным значениям между ними.
Простой способ запомнить это — слово ratio в названии этой классификации. Все числа, входящие в набор рациональных чисел, можно записать в виде отношения целых чисел:
Если \(a\) и \(b\) являются целыми числами: рациональные числа могут быть записаны как \(\frac{a}{b}\), если \(b\neq 0\).
Ясно, что множество целых чисел можно записать в виде отношений, потому что любое целое число, деленное на 1, дает исходное целое число. Как показано здесь, целые числа могут быть выражены в виде дробей бесконечным числом способов.
Как показано здесь, целые числа могут быть выражены в виде дробей бесконечным числом способов.
Целое число 3 можно представить в виде дробей \(\frac{3}{1}\), \(\frac{6}{2}\), \(\frac{-24}{-8) }\)
Целое число -5 может быть представлено в виде следующих дробей \(\frac{-5}{1}\), \(\frac{5}{-1}\), \(\frac{-25 {5}\)
Целое число 0 может быть представлено в виде дробей \(\frac{0}{3}\), \(\frac{0}{-2}\), \(\frac{0}{123}\)
В качестве примечания, это не единственные дроби, которые приводят к этим целым числам, это лишь некоторые из множества существующих примеров.
Дроби также могут быть записаны в виде десятичных дробей. Например:
.1 эквивалентно \(\frac{1}{10}\), поскольку 1 находится в десятых десятичных разрядах
.13 эквивалентно \(\frac{13}{100} \) потому что 3 находится в сотых десятичных разрядах, а единица — в десятых десятичных разрядах
.
237 эквивалентно \(\frac{237}{1,000}\), потому что 7 находится в тысячных десятичных долях, и так далее.
Эти десятичные дроби можно записать в виде дробей, поэтому они считаются рациональными.
Другие десятичные числа имеют повторяющихся шаблонов. Они также считаются рациональными, поскольку могут быть выражены в виде дроби на основе следующего доказательства:
Повторяющаяся десятичная дробь \(2.\overline{17}\) представляет цифры \(2.1717171717\)…
Давайте попробуем это в качестве практической задачи.
Пусть \(x=2.\overline{17}\). Повторяющаяся десятичная дробь состоит из двух цифр, что представляет сотые доли.
Итак, давайте умножим обе части уравнения на 100:
В результате получится \(100x=217,17171717\)…, что равно \(217,17\) повторения.
Мы перемещаем десятичную дробь на две точки, потому что мы умножили на 100. Теперь давайте вычтем исходное уравнение из этого:
| \(100x\) | \ (= 217,171717 \)… | |
| \ ( — \) \ (x \) | \ (= 002. 171717 \)… 171717 \)… | |
| \) ( | ||
| \) ( | ||
| \)… | ||
| \)… | ||
| \)… | ||
| \)… | ||
| \)… ) |
Обратите внимание, что повторяющаяся часть десятичной дроби теперь удалена.
Решение для \(x\) дает \(x=\frac{215}{99}\).
Итак, \(99x\) равно \(215\). Обратите внимание, что повторяющаяся часть десятичной дроби теперь удалена. Решение для \(x\) приводит к делению обеих частей на \(99\): \(x = \frac{215}{99}\).
Это дробное представление \(x=2.\overline{17}\).
Это доказательство показывает, что повторяющиеся десятичные числа также считаются рациональными, поскольку их можно записать в виде дроби целых чисел. Если вы подключите это к своему калькулятору, вы получите что-то близкое, возможно, округленное, к 2,17 повторения.
Важно отметить, что не все десятичные знаки повторяются. Некоторые десятичные дроби имеют бесконечное число неповторяющихся цифр и, следовательно, не могут быть выражены как часть целых чисел. Эти типы действительных чисел классифицируются как иррациональный . Хотя в действительной системе счисления существует бесконечное количество иррациональных чисел, в математике чаще всего используются квадратные корни несовершенных квадратов, например, квадратный корень из 2, а также константы π и e. Обозначение иррациональных чисел позволяет повысить эффективность математических приложений.
Некоторые десятичные дроби имеют бесконечное число неповторяющихся цифр и, следовательно, не могут быть выражены как часть целых чисел. Эти типы действительных чисел классифицируются как иррациональный . Хотя в действительной системе счисления существует бесконечное количество иррациональных чисел, в математике чаще всего используются квадратные корни несовершенных квадратов, например, квадратный корень из 2, а также константы π и e. Обозначение иррациональных чисел позволяет повысить эффективность математических приложений.
Для геометрии вы можете вспомнить, что π = 3,14159… для бесконечности. Это получено из длины окружности любого круга и его диаметра. Поскольку десятичное значение неповторяющееся и бесконечное, мы используем приблизительное значение в математических приложениях. Бизнес-приложения, касающиеся непрерывного начисления процентов, используют иррациональное значение e, которое снова имеет приблизительное значение 2,718 для бесконечности.
Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Все ли целые числа рациональные?
A
Да, рациональное число — это любое число, которое можно представить в виде дроби. Все целые числа подходят под это определение.
Q
Рациональны ли отрицательные числа?
A
Да, большинство отрицательных чисел рациональны. Рациональное число — это любое число, которое можно представить в виде дроби. К ним относятся целые числа, дроби, десятичные дроби, которые заканчиваются, и десятичные дроби, которые повторяются. Положительное и отрицательное не влияют на рациональность.
Q
Все ли рациональные числа являются целыми числами?
A
Нет, не все рациональные числа являются целыми числами. К рациональным числам относятся все числа, которые заканчиваются или повторяются. Целое число — это любое число без дробной части, которое больше или равно нулю.
пр. 2,7 — рациональное число, но не целое.
Q
В чем разница между рациональными и иррациональными числами?
A
Разница между рациональными и иррациональными числами заключается в том, что рациональное число можно представить в виде точной дроби, а иррациональное число — нет. Рациональное число включает в себя любое целое число, дробь или десятичное число, которое заканчивается или повторяется. Иррациональное число — это любое число, которое нельзя превратить в дробь, то есть любое число, не подпадающее под определение рационального числа.
Практические вопросы
Вопрос №1:
Рационально ли число π?
Да
Нет
Иногда
Невозможно определить
Показать Ответ
Ответ:
Правильный ответ — нет. Пи (π) — иррациональное число, потому что это бесконечная десятичная дробь, которую нельзя упростить до точной дроби.
Скрыть ответ
Вопрос № 2:
Является ли \(1.\overline{3}\) рациональным числом?
Да
Нет
Иногда
Невозможно определить
Показать ответ
Ответ:
Правильный ответ — да. \(1.\overline{3}\) можно представить в виде дроби \(1\frac{1}{3}\), что означает, что оно рационально. Любое число, которое можно представить в виде дроби, считается рациональным.
Скрыть ответ
Вопрос № 3:
Какое из следующих чисел является примером рационального числа?
π
\(\sqrt{2}\)
4.17
\(4-\sqrt{7}\)
Показать ответ
Ответ:
9 Правильный ответ:
9 90. Это единственное число из этого списка, которое можно превратить в дробь, \(4\frac{17}{100}\).
Это единственное число из этого списка, которое можно превратить в дробь, \(4\frac{17}{100}\).
Скрыть ответ
Вопрос № 4:
Какое из следующих чисел является иррациональным?
\(\frac{17}{3}\)
13
\(2.\overline{97}\)
\(\sqrt{3}\)
Показать ответ
Ответ:
Правильный ответ: \(\sqrt{3}\). Квадратные корни несовершенных квадратов нерациональны, потому что они равны бесконечному десятичному числу, а это значит, что это число нельзя превратить в дробь.
Скрыть ответ
Вопрос № 5:
Является ли \(\frac{7}{9}\) рациональным?
Да
Нет
Иногда
Невозможно определить
Показать Ответ
Ответ:
Правильный ответ — да. Рациональное число — это любое число, которое можно превратить в дробь, а \(\frac{7}{9}\) — это дробь.
Рациональное число — это любое число, которое можно превратить в дробь, а \(\frac{7}{9}\) — это дробь.
Скрыть ответ
Вернуться к видео по основам арифметики
280645255557515712
Вещественное число, которое нельзя точно выразить как отношение двух целых чисел.
Произношение: /ɪˈræ.ʃə.nl ˈnʌm.bər/ Объяснение
Иррациональное число – это настоящий номер которое не может быть выражено как отношение двух целые числа. Поскольку Рациональное число это действительное число, которое можно выразить как отношение двух целых чисел, это означает, что любое действительное число либо рационально, либо иррационально, но не может быть и то, и другое.
В математике можно
представлять
номера способами, которые маскируют их настоящую личность. Например, квадратный корень
можно уменьшить до 2,
и поэтому не является иррациональным числом, даже если оно представлено
используя квадратный корень.
Например, квадратный корень
можно уменьшить до 2,
и поэтому не является иррациональным числом, даже если оно представлено
используя квадратный корень.
Примеры иррациональных чисел включают π , , а также .
Вот несколько примеров неиррациональных чисел: 5,2 , , 3 и .
Свойства иррациональных чисел
| Свойство | Описание |
|---|---|
| Непрерывность | Множество иррациональных чисел не является непрерывным множеством. |
| Дополнение | Сложение иррациональных чисел такое же, как сложение действительных чисел. |
| Закрытие в отношении дополнения | Множество иррациональных чисел , а не замкнуто относительно сложения так как + — = 0. 0 не является иррациональным числом. |
| Ассоциативное свойство дополнения | Множество иррациональных чисел ассоциативно относительно сложения. Так как все
иррациональные числа также являются действительными числами, а множество действительных чисел ассоциативно
по отношению к сложению ассоциативное свойство сложения относится к иррациональным
числа. Так как все
иррациональные числа также являются действительными числами, а множество действительных чисел ассоциативно
по отношению к сложению ассоциативное свойство сложения относится к иррациональным
числа. |
| Дополнительный идентификатор | Аддитивная идентичность для действительных чисел равна нулю. Ноль это а не в наборе иррациональных чисел. Множество иррациональных чисел не обладает свойством идентичность по отношению к дополнению. |
| Добавка, обратная | Аддитивная инверсия иррационального числа есть — а т.к. a + (- a ) = 0. Множество иррациональные числа обратимы относительно сложения. |
| Группа в отношении дополнения | Поскольку аддитивная идентичность иррациональных чисел сама по себе не является иррациональной число, набор иррациональных чисел , а не образует группу с относительно доп. |
| Умножение | Умножение иррациональных чисел такое же, как умножение действительных
числа. |
| Замыкание по умножению 903:50 | Множество иррациональных чисел , а не замкнуто относительно умножение с · = 2. 2 не является иррациональное число. |
| Ассоциативное свойство умножения | Множество иррациональных чисел ассоциативно относительно умножения. С все иррациональные числа также являются действительными числами, а множество действительных чисел равно ассоциативный по отношению к умножению, ассоциативное свойство умножения относится к иррациональным числам. |
| Мультипликативная идентичность | Мультипликативное тождество для действительных чисел равно единице. Один , а не в множество иррациональных чисел. Множество иррациональных чисел не обладает свойством тождества относительно умножения. |
| Мультипликативный обратный | Мультипликативная инверсия иррационального числа а это 1/ с ·
1/ a = 1, a ≠ 0. Множество иррациональных чисел равно
обратимым относительно умножения. Множество иррациональных чисел равно
обратимым относительно умножения. |
| Группа по умножению | Поскольку мультипликативное тождество иррациональных чисел само по себе не является иррациональное число, набор иррациональных чисел , а не образует группу относительно умножения. |
| Мощность | Мощность иррациональных чисел равна ℵ 1 = 2 ℵ0 . Множество иррациональных чисел несчетно. |
| Таблица 1: Свойства иррациональных чисел. | |
Доказательство существования иррациональных чисел
Первое доказательство существования иррациональных чисел приписывается пифагорейцу, представитель древнегреческой религии. Это происходит следующим образом:
| Шаг | Уравнения/диаграммы | Обсуждение | |||||
|---|---|---|---|---|---|---|---|
| 1 | Претензия | Предположим, что длина гипотенузы и длина катетов равнобедренного
оба прямоугольных треугольника являются рациональными числами. Так как отношение двух рациональных чисел можно уменьшить
к другому рациональному числу существует отношение двух целых чисел c : b , которые могут представлять
отношение любых двух рациональных чисел. 903:50 Так как отношение двух рациональных чисел можно уменьшить
к другому рациональному числу существует отношение двух целых чисел c : b , которые могут представлять
отношение любых двух рациональных чисел. 903:50 | |||||
| 2 | Пусть c : b будет отношением длины гипотенузы к катету равнобедренного прямоугольного треугольника, выраженные в наименьшие члены, где c и b оба являются целыми числами. С c : b выражается в наименьшем термины, c и б имеют № общих факторов. | ||||||
| 3 |
| Начните с теоремы Пифагора: A 2 + В 2 = С 2 . Затем замените
переменные из диаграммы на шаге 1. Замените б в для А и Б . Заменять c дюймов для С . Затем объедините похожие термины, чтобы получить
уравнение
2 б 2 = в 2 . Затем замените
переменные из диаграммы на шаге 1. Замените б в для А и Б . Заменять c дюймов для С . Затем объедините похожие термины, чтобы получить
уравнение
2 б 2 = в 2 . | |||||
| 4 | 2 б 2 = с 2 | Определение четного числа — это число, которое имеет 2 как фактор. С с 2 = 2 б 2 , 2 является фактором с 2 . Это означает, что c 2 — четное число. | |||||
| 5 | c четно. | Так как c 2 имеет коэффициент
из 2 и с 2 = с · с , c также должен иметь коэффициент
2. Итак, c четно. Итак, c четно. | |||||
| 6 | б нечетное. | Начиная с c : b находится в низшей условия, b имеет нет факторов общего с c . Так b может , а не иметь коэффициент 2. Это означает, что b должно быть нечетным. | |||||
| 7 | с = 2 г | Поскольку c четно, существует целое число и такие, что с = 2 у . | |||||
| 8 | 4 у 2 = 2 б 2 | Начиная с c 2 =
2 б 2 , заменитель
2 и в для с . Это дает уравнение
(2 y ) 2 = 2 б 2 . Расширьте показатель степени в левой части уравнения, чтобы получить
4 y 2 = 2 b 2 . Расширьте показатель степени в левой части уравнения, чтобы получить
4 y 2 = 2 b 2 . | |||||
| 9 | 2 у 2 = б 2 | Возьмем уравнение 4 y 2 = 2 б 2 и упростите. Это дает уравнение 2 y 2 = b 2 . | |||||
| 10 | b четно. | По аналогии с шагами 3 и 4, b должно быть четным. | |||||
| 11 | Противоречие | Так как b может ли не быть одновременно четным и
странно, есть противоречие. Это означает, что размеры как ноги, так и
гипотенузы равнобедренного прямоугольного треугольника не могут быть рациональными числами. Итак, число
это , а не , должно существовать рациональное число. | |||||
| Таблица 2: Доказательство существования иррациональных чисел. | |||||||
Ссылки
- МакАдамс, Дэвид Э.. Словарь всех математических слов, иррациональное число . Издание 2-го класса 20150108-4799968. стр. 103. Life is a Story Problem LLC. 8 января 2015. Купить книгу
Цитируйте эту статью как:
МакАдамс, Дэвид Э. Иррациональное число . 23.04.2019. Вся энциклопедия математических слов. ООО «Жизнь — это проблема истории». https://www.allmathwords.org/en/i/irrational.html.
Авторы изображений
- Все изображения и манипуляции принадлежат Дэвиду МакАдамсу, если не указано иное. Все изображения Дэвида МакАдамса защищены авторским правом © Life is a Story Problem LLC и находятся под лицензией Creative Commons Attribution-ShareAlike 4.0 International License.
История изменений
23. 04.2019:
04.2019:
Уравнения и выражения обновлены до нового формата.
(МакАдамс, Дэвид Э.)
22.03.2019:
Исправлена мультипликативная инверсия.
(МакАдамс, Дэвид Э.)
21.12.2018:
Пересмотрено и исправлено произношение МФА.
(МакАдамс, Дэвид Э.)
28.08.2018:
Исправлена орфография.
(МакАдамс, Дэвид Э.)
07.08.2018:
Словарные ссылки изменены на формат WORDLINK.
(МакАдамс, Дэвид Э.)
06. 08.2018:
08.2018:
Удалены битые ссылки, обновлена лицензия, реализована новая разметка, реализован новый протокол Geogebra.
(МакАдамс, Дэвид Э.)
03.03.2010:
Добавлен «Справочник», добавлен раздел о доказательстве существования иррациональных чисел.
(МакАдамс, Дэвид Э.)
13.08.2008:
Некоторые математические конструкции заменены изображениями. Добавлена проверка понимания
(МакАдамс, Дэвид Э.)
12.07.2007:
Первоначальная версия.
(МакАдамс, Дэвид Э.)
√4 — рациональное или иррациональное число?
Действительные числа, которые не могут быть выражены простой дробью, известны как иррациональных чисел. Его нельзя представить в виде отношения типа p/q, где p и q — целые числа, q≠0. Это несоответствие рациональных чисел. Иррациональные числа обычно записываются как R \ Q, где знак обратной косой черты означает «установить минус». Его также можно записать как R-Q, что представляет собой разницу между набором действительных и рациональных чисел.
Его нельзя представить в виде отношения типа p/q, где p и q — целые числа, q≠0. Это несоответствие рациональных чисел. Иррациональные числа обычно записываются как R \ Q, где знак обратной косой черты означает «установить минус». Его также можно записать как R-Q, что представляет собой разницу между набором действительных и рациональных чисел.
Вычисления, основанные на этих цифрах, немного сложнее. К иррациональным числам относятся √5, √11, √21 и так далее. Если такие числа используются в арифметических операциях, сначала должны быть оценены значения под корнем.
Что такое рациональные числа? Рациональные числа имеют форму p/q, где p и q — целые числа, а q ≠ 0. Из-за лежащей в основе структуры чисел, формы p/q, большинству людей трудно отличить дроби от рациональных чисел. Когда рациональное число делится, вывод находится в десятичной форме, которая может быть как оканчивающейся, так и повторяющейся. 3, 4, 5 и т. д. — некоторые примеры рациональных чисел, поскольку они могут быть выражены дробью как 3/1, 4/1 и 5/1.
Иррациональные числа — это любые числа, не являющиеся рациональными числами. Иррациональные числа могут быть представлены десятичными знаками, но не дробями, что означает, что они не могут быть представлены как отношение двух целых чисел. После запятой иррациональные числа имеют бесконечное количество неповторяющихся цифр.
Вещественное число, которое не может быть представлено как отношение целых чисел, называется иррациональным числом. Например, √2 — иррациональное число.
Десятичное расширение иррационального числа не заканчивается и не повторяется. Определение иррационального — это число, которое не имеет отношения или для которого нельзя установить отношение, то есть число, которое не может быть представлено никаким другим способом, кроме как с использованием корней. Иными словами, иррациональные числа нельзя представить в виде отношения двух целых чисел.
Примеры иррациональных чисел
√2, √3, √5 и т. д. — некоторые примеры иррациональных чисел, поскольку они не могут быть выражены в форме p ⁄ q. Число Эйлера, золотое сечение, π и т. д. также являются примерами иррациональных чисел. 1/0, 2/0, 3/0 и т. д. иррациональны, потому что дают нам неограниченные значения.
д. — некоторые примеры иррациональных чисел, поскольку они не могут быть выражены в форме p ⁄ q. Число Эйлера, золотое сечение, π и т. д. также являются примерами иррациональных чисел. 1/0, 2/0, 3/0 и т. д. иррациональны, потому что дают нам неограниченные значения.
Является ли число √4 рациональным или иррациональным?
Решение:
Иррациональные числа — это действительные числа, которые нельзя записать в виде p/q, где p и q — целые числа, а q≠0. Например, √2 и √3 и так далее иррациональны. Рациональное число — это любое число, которое можно записать в виде p/q, где p и q — целые числа, а q≠0.
Здесь данное число √4 равно 2; число 2 является целым числом, а целые числа всегда рациональны. Кроме того, его можно выразить в форме дроби как 2 ⁄ 1, что означает, что это рациональное число. Следовательно, √4 равно не иррациональное число .
Похожие вопросы
Вопрос 1: Является ли √5 рациональным или иррациональным числом?
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0.
Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √5 не может быть выражено в виде p/q. Кроме того, 5 является простым числом. Это означает, что число 5 не имеет пары и не делится на 2. Следовательно, √5 — иррациональное число.
Вопрос 2: Определите, является ли 4.152152…. является рациональным числом.
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число 4.152152…. имеет повторяющиеся цифры. Следовательно, 4,152152…. является рациональным числом.
Вопрос 3: Является ли √11 рациональным или иррациональным числом?
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0.
Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √11 не может быть выражено в виде p/q. Альтернативно, 11 — простое число. Это означает, что число 11 не имеет пары и не делится на 2. Следовательно, √11 — иррациональное число.
Вопрос 4: Определите, является ли 7,23 рациональным числом.
Ответ:
Рациональное число — это действительное число, имеющее форму p/q, где q≠0. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь заданное число, 7.23…. имеет конечные цифры. Следовательно, 7,23 — рациональное число.
Что такое иррациональные числа? | Живая наука
Живая наука поддерживается своей аудиторией. Когда вы покупаете по ссылкам на нашем сайте, мы можем получать партнерскую комиссию. Вот почему вы можете доверять нам.
Вот почему вы можете доверять нам.
Иррациональные числа — это числа, которые нельзя представить как отношение двух целых чисел. Это противоположно рациональным числам, таким как 2, 7, одна пятая и -13/9, которые могут выражаться и выражаются как отношение двух целых чисел. При выражении в виде десятичного числа иррациональные числа всегда идут после десятичной точки и никогда не повторяются.
Связанный: 9 самых больших существующих чисел
Кто вычислил иррациональные числа?
Греческому математику Гиппасу из Метапонта приписывают открытие иррациональных чисел в V веке до нашей эры, согласно статье Кембриджского университета . Говорят, что во время работы над отдельной задачей Гиппас наткнулся на тот факт, что равнобедренный прямоугольный треугольник, две стороны которого имеют длину 1 единицу, будет иметь гипотенузу, равную √2, что является иррациональным числом. 2.)
2.)
Легенда гласит, что Гиппас был брошен в море в награду за его великое открытие. Это потому, что он был членом пифагорейцев, квазирелигиозного ордена, которые верили, что «все есть число» и что вселенная состоит из целых чисел и их соотношений. Обеспокоенные открытием Гиппаса, группа приговорила его к смертной казни через утопление.
Связанный: Фотографии: Большие числа, определяющие Вселенную
Страх перед иррациональными числами позже утих, и в конце концов они были включены в математику. Вместе рациональные и иррациональные числа составляют число 9.1260 действительных чисел , которые включают любое число на числовой прямой и в которых отсутствует мнимое число i.
Большинство действительных чисел иррациональны. Немецкий математик Георг Кантор окончательно доказал это в 19 веке, показав, что рациональные числа счетны , а действительные числа несчетны. Это означает, что реальных больше, чем рациональных, согласно веб-сайту по истории, математике и другим темам от образовательного карикатуриста Чарльза Фишера Купера. Поскольку иррациональные числа — это все те действительные числа, которые не являются рациональными, иррациональные числа значительно перевешивают рациональные числа; они составляют все остальные несчетные действительные числа.
Поскольку иррациональные числа — это все те действительные числа, которые не являются рациональными, иррациональные числа значительно перевешивают рациональные числа; они составляют все остальные несчетные действительные числа.
Известные иррациональные числа:
Квадратный корень из 2
Несмотря на судьбу Гиппаса, √2 является одним из самых известных иррациональных чисел и иногда называется константой Пифагора, согласно веб-сайту Wolfram MathWorld .
Постоянная Пифагора равна 1,4142135623… (точки означают, что она продолжается вечно).
Все это может звучать теоретически, но число имеет и очень конкретное применение. Международные форматы бумаги включают √2. Международная организация по стандартизации (ИСО) 216 определение серии размеров бумаги A гласит, что длина листа, деленная на его ширину, должна составлять 1,4142. Это приводит к тому, что лист бумаги формата А1, разделенный пополам по ширине, дает два листа бумаги формата А2. Разделите лист формата А2 еще раз пополам, и вы получите два листа бумаги формата А3 и так далее.
Разделите лист формата А2 еще раз пополам, и вы получите два листа бумаги формата А3 и так далее.
Пи
Пи — это отношение длины окружности к ее диаметру. Математикам известно число пи со времен древних вавилонян, 4000 лет назад.
Пи равно 3,1415926535…
Некоторые фанаты числа Пи очень гордятся тем, что могут запомнить как можно больше цифр числа Пи. Суреш Кумар Шарма из Индии установил мировой рекорд в 2015 году, запомнив 70 030 цифр числа Пи, согласно мировому рейтингу числа Пи .
Phi
Phi также известен как золотое сечение . Его можно найти, взяв палку и разломив ее на две части; если соотношение между этими двумя частями такое же, как соотношение между общей палочкой и большим сегментом, говорят, что части находятся в золотом сечении.
Фи равняется 1,6180339887…
На протяжении столетий вокруг понятия фи накопилось множество преданий, например идея о том, что оно представляет совершенную красоту или может быть найдено повсюду в природе. Но большая часть этого неверна. Фи тесно связана с последовательностью Фибоначчи , еще одним источником многих заблуждений.
Но большая часть этого неверна. Фи тесно связана с последовательностью Фибоначчи , еще одним источником многих заблуждений.
e
Основание натуральных логарифмов названо e в честь своего тезки, швейцарского математика 18-го века Леонарда Эйлера.
e равно 2,7182818284…
Наряду с логарифмами, e появляется в уравнениях , включающих комплексных чисел и экспоненциальный рост. Подобно тому, как День Пи отмечается 14 марта (14 марта), г. и День отмечается 7 февраля (7 февраля) или 27 января (27 января), в зависимости от того, какую календарную систему вы используете.
Дополнительные ресурсы:
- В Академии Хана есть много полезных видеороликов, объясняющих иррациональные числа. Вот с чего начать: « Введение в рациональные и иррациональные числа.
Адам Манн — независимый журналист с более чем десятилетним стажем, специализирующийся на астрономии и физике. Он имеет степень бакалавра астрофизики Калифорнийского университета в Беркли.
 Его работы публиковались в New Yorker, New York Times, National Geographic, Wall Street Journal, Wired, Nature, Science и многих других изданиях. Он живет в Окленде, штат Калифорния, где любит кататься на велосипеде.
Его работы публиковались в New Yorker, New York Times, National Geographic, Wall Street Journal, Wired, Nature, Science и многих других изданиях. Он живет в Окленде, штат Калифорния, где любит кататься на велосипеде.Это может показаться скорее иррациональным, чем рациональным | Алекс Лин
Как иррациональных чисел больше, чем рациональных.
Photo by Danny Lines on UnsplashМир математики может быть довольно загадочным. В зависимости от того, куда смотреть, некоторые истины, кажется, просто бросают вызов нашей базовой интуиции.
Тот факт, что иррациональных чисел больше, чем рациональных, не имел для меня особого смысла. Вероятно, можно с уверенностью предположить, что оба набора бесконечны, так как же один набор может быть больше?
Сегодня мы исследуем, как исчисляемые и неисчисляемые бесконечности помогают нам прийти к этому, казалось бы, странному заключению.
Содержание
Фоновый контекст
Что происходит с действительными числами?
Как насчет рациональных чисел?
Собираем все вместе
Прежде чем мы погрузимся в сочную математику, давайте на минутку дадим определение паре терминов.

Что такое рациональные числа?
Любое число, которое может быть получено путем деления двух целых чисел (целых чисел) является рациональным.
Например, 10 разделить на 4 равно 2,5, поэтому 2,5 рационально. Деление на 1 тоже считается, поэтому все целые числа рациональны.
Что такое иррациональные числа?
Иррациональные числа противоположны рациональным. Любое число, которое не может быть получено путем деления двух целых чисел, является иррациональным.
Рассмотрим π. Хотя такие оценки, как 22/7, близки, мы никогда не сможем разделить два целых числа, чтобы получить точное значение π.
Вещественные числа
Любое число, которое вы можете нанести на числовую строку ниже, считается действительным.
Одномерная числовая линия, расширяющаяся в сторону отрицательной и положительной бесконечности.Комбинация всех рациональных и иррациональных чисел образует наши действительные числа. Однако мнимые числа и бесконечность не считаются реальными.

Наша цель — показать взаимосвязь между размерами рациональных и иррациональных множеств. Поскольку действительные числа являются объединением или комбинацией двух наборов, возможно, стоит попытаться на мгновение изучить действительные числа.
Насколько велики действительные числа?
Давайте сначала рассмотрим действительные числа от 0 до 1. Скажем, у нас есть набор, назовем его X, , который содержит всех действительных чисел в пределах нашего интервала.
Набор всех действительных чисел от 0 до 1.Наш набор явно бесконечен по размеру, поскольку он будет продолжать расширяться вниз.
Хотя наш набор содержит все возможные действительные числа от 0 до 1, я утверждаю, что мы всегда можем найти новое действительное число, которого нет в нашем наборе.
Начнем с изучения первого числа в наборе X. Мы построим новое число, увеличив значение первой цифры после запятой.
Создание нашего уникального реального номера из набора реальных номеров.
Обратите внимание, что наш новый номер уникален из первого значения набора X . Давайте продолжим развивать наше новое число, увеличив вторую цифру второго числа из набора X .
Создание нашего уникального реального номера из набора реальных номеров.Интересно… Наш новый номер уникален как из первых , так и из вторых значений нашего набора. Если мы продолжим повторять этот диагональный узор бесконечно, мы найдем уникальное действительное число, которого нет в нашем исходном наборе!
Продолжение диагонального узора показывает уникальное действительное число.На самом деле увеличение диагональных цифр было не единственным нашим вариантом. Мы могли бы добавить или вычесть любое число по диагонали, чтобы получить уникальное действительное значение.
Различные уникальные действительные числа и их операции.Итак, мы показали, что наш набор всех действительных чисел от 0 до 1 каким-то образом пропускает множество других действительных значений.
 Этот образец известен как диагональный аргумент Кантора.
Этот образец известен как диагональный аргумент Кантора.Как бы мы ни пытались подсчитать размер нашего набора, мы всегда будем упускать больше значений. Этот тип бесконечности и есть то, что мы называем неисчислимым.
Напротив, счетные бесконечности являются перечислимыми бесконечными множествами. Рассмотрим множество целых чисел — мы всегда можем подсчитать все целые числа, не пропуская ни одного значения.
Теперь мы знаем, что между 0 и 1 множество действительных чисел несчетно бесконечно. Отсюда следует, что множество всех действительных чисел также несчетно бесконечно.
Теперь рассмотрим рациональные числа. Мы надеемся, что определяя размер его множества, мы сможем пролить свет на наше доказательство.
С нашим новым пониманием счетных и несчетных бесконечностей, можем ли мы определить, возможно ли окончательно подсчитать все значения в множестве рациональных чисел?
Подсчет рациональных чисел
Рассмотрим это расположение положительных рациональных чисел.
Предложение по отображению всех рациональных чисел.
Увеличив числитель для каждого столбца и знаменатель для каждой строки, эта сетка в конечном итоге будет включать все положительные рациональные числа.
Теперь, можем ли мы найти способ абсолютного подсчета всех значений в нашей сетке?
Существует бесконечное количество строк и столбцов. Если бы мы попытались просто считать по каждой строке/столбцу, мы бы никогда не достигли «конца» первой строки/столбца. Таким образом, этого метода подсчета будет недостаточно.
Ну, если прямо поперек или вниз нельзя, то как насчет диагонали? Рассмотрим следующий способ обхода.
Подсчет сетки по диагоналиНачав с красного круга, мы можем пройти рациональные числа по диагональному пути, отмеченному зелеными стрелками. Бесконечно следуя этому зигзагообразному шаблону, мы можем увидеть, что в конечном итоге будут встречаться все положительные рациональные значения!
Мы можем применить тот же шаблон обхода, чтобы включить и отрицательные рациональные числа!
Включение отрицательного пути обходаЭтот путь обхода дает нам четкий метод подсчета размера рациональных чисел.
 Хотя мы будем считать до бесконечности, мы по крайней мере знаем, что не будет пропущенных рациональных значений.
Хотя мы будем считать до бесконечности, мы по крайней мере знаем, что не будет пропущенных рациональных значений.Как видим, множество рациональных чисел счетно бесконечно!
На данный момент мы знаем пару важных фактов.
- Вещественные числа неисчислимо бесконечны.
- Рациональные числа счетно бесконечны.
- Действительные числа представляют собой объединение множества рациональных и иррациональных чисел.
Если мы удалим все рациональные числа из нашего набора действительных чисел, у нас все равно останется несчетно бесконечное множество, состоящее только из иррациональных чисел. Следовательно, множество иррациональных чисел также несчетно бесконечно!
Поскольку несчетно бесконечные множества всегда больше счетно бесконечных множеств, мы можем в конце концов заключить, что иррациональных чисел больше, чем рациональных.
Вот оно! То, что начиналось как неинтуитивный факт, теперь помогло нам немного больше понять о бесконечностях и их различных размерах.





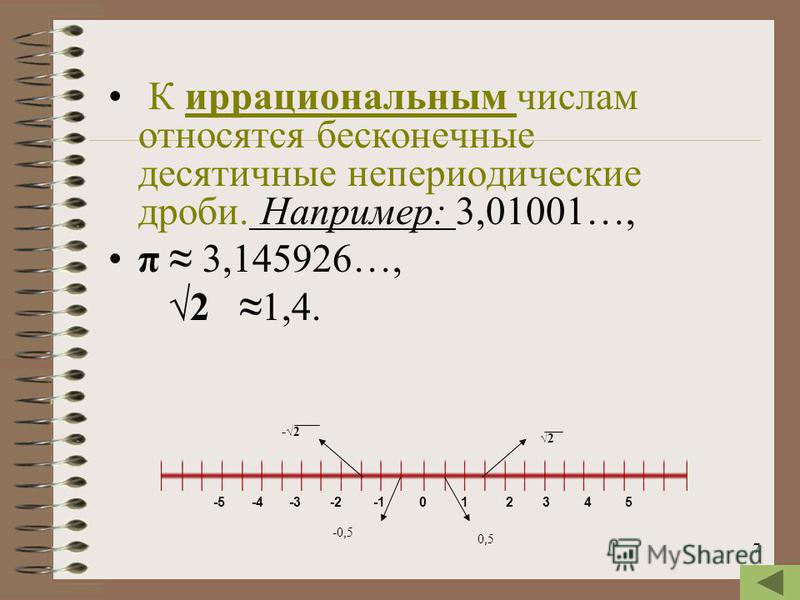






 (Действительные) алгебраические числа. 4. Числа, допускающие построение 5. Рациональные числа.
(Действительные) алгебраические числа. 4. Числа, допускающие построение 5. Рациональные числа. 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7
 Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе…
Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе… com
com 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7 718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7. Натуральные числа.
718 2818, 37 коп. kj 1. Комплексные числа 2. Действительные числа 3. (Действительные) алгебраические числа 4. Числа, допускающие построение 5. Рациональные числа 6. Целые числа 7. Натуральные числа.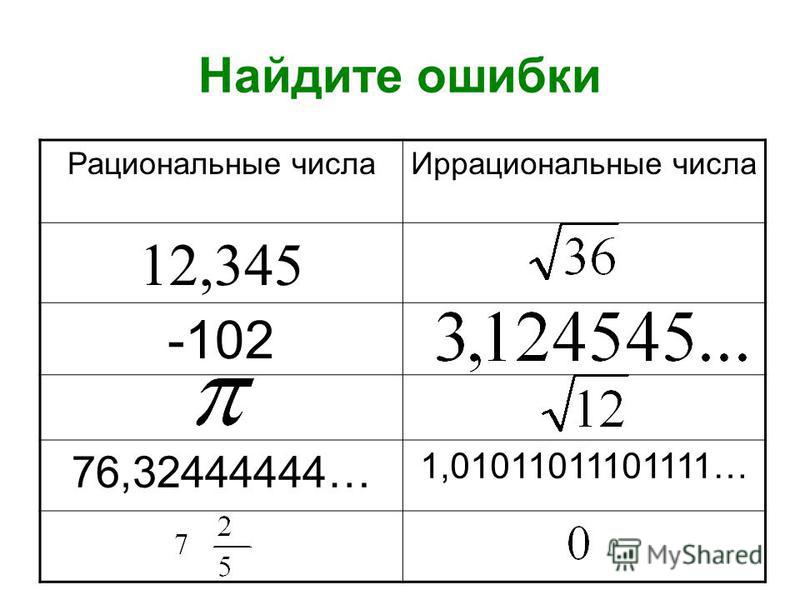 Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала.
Ученики старших классов (именно на них она в первую очередь и рассчитана) узнают из нее некоторые свойства чисел, о которых они раньше и не подозревали, и познакомятся с доказательствами теорем, принимаемых в школьном курсе алгебры на веру. Изложение очень простое и живое. Оно сопровождается рядом вопросов и задач, облегчающих активное усвоение материала.
 .
. Поэтому нет таких целых чисел, которые бы поделившись друг на друга, дали бы иррациональное число.
Поэтому нет таких целых чисел, которые бы поделившись друг на друга, дали бы иррациональное число. Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль. Если натуральное число n не является точным квадратом, т. е. n ≠ k2…
Действительныеили вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль. Если натуральное число n не является точным квадратом, т. е. n ≠ k2… Иррациональное число невозможно представить в виде Приведём примеры иррациональных чисел
Иррациональное число невозможно представить в виде Приведём примеры иррациональных чисел
 210735[/латекс]
210735[/латекс] 237 эквивалентно \(\frac{237}{1,000}\), потому что 7 находится в тысячных десятичных долях, и так далее.
237 эквивалентно \(\frac{237}{1,000}\), потому что 7 находится в тысячных десятичных долях, и так далее. Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √5 не может быть выражено в виде p/q. Кроме того, 5 является простым числом. Это означает, что число 5 не имеет пары и не делится на 2. Следовательно, √5 — иррациональное число.
Когда рациональное число разбивается, результатом является десятичное число, которое может быть как завершающим, так и повторяющимся десятичным числом. Здесь данное число √5 не может быть выражено в виде p/q. Кроме того, 5 является простым числом. Это означает, что число 5 не имеет пары и не делится на 2. Следовательно, √5 — иррациональное число.