Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Инструкция
Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например, круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 сантиметров.
Если надо найти площадь квадрата (S) по диаметру вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.
Если
 2 / 4 + 20*10/2», а нажать клавишу Enter.
2 / 4 + 20*10/2», а нажать клавишу Enter.Источники:
- как найти площадь окружности по диаметру
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов « окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Используйте какой-либо , чтобы рассчитать длину диаметра, если сделать это в уме не получается. Например, можно воспользоваться тем, который встроен в поисковую систему Nigma или Google — он математические операции, вводимые на «человеческом» . Например, если известная длина окружности составляет четыре метра, то для нахождения диаметра можно «по-человечески» попросить поисковик: «4 метра разделить на пи». Но если вы введете в поле поискового запроса, например, «4/пи», то поисковик поймет и такую постановку задачи. В любом случае ответом будет «1.27323954 метра».
Воспользуйтесь программным калькулятором Windows, если вам более привычны интерфейсы с обычными кнопками. Чтобы не искать ссылку на его запуск в глубинных уровнях главного меню системы, нажмите сочетание клавиш WIN + R, введите команду calc и нажмите клавишу Enter. Интерфейс этой программы очень незначительно отличается от обычных калькуляторов, поэтому операция деления длины окружности на число Пи вряд ли вызовет какие-либо затруднения.
Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.
Применительно к Земле не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».
Официальный диаметр Земли
Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.
Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.
Вычисление диаметра Земли
Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.
Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.
Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).
Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).
В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах. Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.
На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по – 40 007,86. Эратосфен лишь немного ошибся.
Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.
Источники:
- Как измерили Землю в 2019
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.

Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу.
 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R. - Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Для начала дадим определение радиуса. В переводе с латинского radius — это «луч, спица колеса». Радиус окружности — это отрезок прямой, соединяющий центр окружности с точкой, которая находится на ней. Длина данного отрезка — это значение радиуса. В математических расчётах для обозначения данной величины используют R.
Советы по нахождению радиуса:
- является отрезком прямой, проходящей через ее центр и соединяющей точки, лежащие на окружности, которые максимально удалены друг от друга.

- Длина закрытой кривой, которая образуется на плоскости — это длина окружности. Если вы знаете ее длину, то для нахождения радиуса окружности вы можете применить универсальную в своем роде формулу: R = L/(2*π), где L является длиной окружности, а π — константой, равной 3,14. Константа π представляет собой отношение длины окружности к длине ее диаметра, она одинакова для всех окружностей.
- Круг представляет собой геометрическую фигуру, являющуюся частью плоскости, ограниченной кривой — окружностью. В том случае, если вы знаете площадь какого либо круга, то радиус окружности может быть найден по специальной формуле R = √(S/π), где S является площадью круга.
- Радиус вписаной окружности (в квадрат) находится следующим образом: r = a/2, где а является стороной квадрата.
- Радиус описанной окружности (вокруг прямоугольника) вычисляют по формуле: R = √ (a2 + b 2)/2, где а и b являются сторонами прямоугольника.

- В том случае, если вы не знаете длину окружности, но знаете высоту и длину какого-либо ее сегмента, то вид формулы будет таков:
R = (4*h3 + L2)/8*h, где h является высотой сегмента, а L является его длиной.
Находим радиус окружности, вписанной в треугольник (прямоугольный). В треугольник, какой бы вид он не имел, может быть вписана лишь одна-единственная окружность, центр которой будет одновременно той точкой, где пересекаются биссектрисы его углов. имеет множество свойств, которые должны быть учтены, когда вычисляется радиус вписанной окружности. В задаче могут быть приведены различные данные, следовательно, требуется выполнить дополнительные вычисления, необходимые для ее решения.
Советы по нахождению радиуса вписанной окружности:
- Сначала нужно построить треугольник с теми размерами, которые уже были заданы в вашей задаче. Это необходимо делать, зная размеры всех трёх сторон или двух сторон и угла между ними. Так как размер одного угла вам уже известен, то в условии должны быть два катета.
 Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза — как с. Что касается радиуса вписанной окружности, то он обозначается как r.
Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза — как с. Что касается радиуса вписанной окружности, то он обозначается как r. - Для применения стандартной формулы определения радиуса вписанной окружности требуется найти все три стороны прямоугольного треугольника. Зная размеры всех сторон, вы сможете найти полупериметр треугольника из формулы: p = (a + b+ c)/2.
- Если вы знаете один угол и катет, то вам следует определить, прилежащий он или противолежащий. Если он прилежащий, то гипотенузу можно вычислить, используя теорему косинусов: c = a/cosCBA. Если он противолежащий, то тогда требуется воспользоваться c=a/sinCAB.
- Если у вас есть полупериметр, то вы можете определить радиус вписанной окружности. Вид формулы для радиуса будет таким: r=√(p-b)(p-a)(p-c)/p.
- Следует отметить, что найти радиус можно по формуле: r = S/p. Так что если вам известны два катета, то процедура вычисления будет более лёгкой. Гипотенуза, требуемая для полупериметра, может быть найдена по сумме квадратов его катетов.
 Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
Зачастую, когда школьник сдает выпускные экзамены в школе либо вступительные в какой-либо ВУЗ, ему необходимы определенные знания в области геометрии. Причем, задания бывают не такие уж сложные, просто нужно помнить базовые формулы, чтобы применить их в решении. Задачи, в которых необходимо найти радиус окружности, не являются исключением. В принципе, они достаточно просты в решении. В данной статье мы расскажем вам, как найти радиус окружности разными способами.
Находим радиус окружности, исходя из формул
Когда вы получаете задание на контрольной или на экзамене, в котором надо найти радиус окружности, в первую очередь необходимо проанализировать имеющиеся данные. Потому что именно от них будет зависеть ход решения в целом. Так, например, найти рассматриваемую величину можно, используя такие параметры: длину окружности, ее площадь, диаметр и др. Мы рассмотрим самые простые и часто встречающиеся способы решения задач, в которых радиус окружности является неизвестным.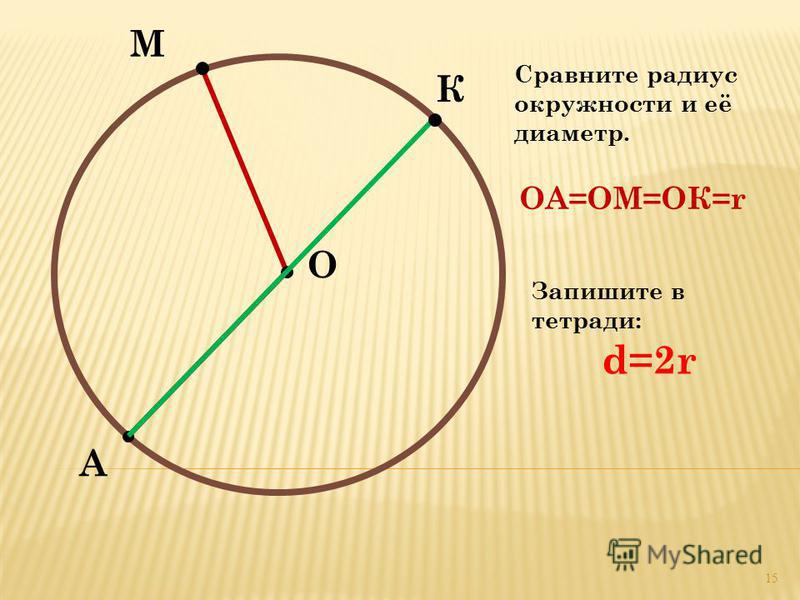
Все мы знаем, что радиусом окружности является длина от ее центра до какой-либо точки,которая расположена на самой окружности. В связи с этим, решения могут быть следующими:
- Когда вам в исходных данных задачи дан диаметр окружности, то решение здесь будет проще простого. Ведь нам известно, что диаметром является отрезок, который соединяет несколько точек на окружности, проходя при этом через ее центр. Из этого следует, что диаметр – это 2 радиуса. Тогда радиус мы находим по формуле: r=D/2, где r – это радиус окружности, а D, соответственно, ее диаметр. Например, диаметр по условию равен 32 см, тогда радиус мы вычисляем так: 32/2=16 см.
- Переходим к следующему способу решения. Допустим, вам в условии дана длина окружности. Выражаясь математическим языком, это так называемый периметр. Мы прекрасно знаем, что есть специальная формула нахождения длины окружности: P=2πr. Отсюда, мы можем вывести формулу радиуса: r=P/2π. Теперь рассмотрим это на примере. Допустим, по условию задачи вам дана длина окружности, равная 31,4 см, а π в математике – величина постоянная и всегда равна 3,14; тогда радиус находим следующим образом: 31,4/2*3,14=5 см.

- Теперь рассмотрим, как найти радиус окружности, если дана ее площадь. Формула площади окружности имеет такой вид: S=πr2. Отсюда находим формулу радиуса: r=√(S/π). Опять же рассмотрим все в цифровом исчислении. Пусть вам дана в условии задачи площадь, к примеру – 28,26 см2. Подставляем данные в выведенную нами формулу и получаем: √28,26/3,14=3 см.
Теперь вам не составит труда решить любую задачу с нахождением радиуса окружности. Главное – четко проанализировать исходные данные, а потом применить подходящую формулу, и можете считать себя великим математиком.
через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Инструкция
Сначала надо исходные данные к задаче. Дело в том, что ее условии не может быть явно сказано, какова радиуса окружности . Вместо этого в задаче может быть дана длина диаметра окружности . Диаметр окружности — отрезок, который объединяет между собой две противоположные точки окружности , проходя через ее центр. Проанализировав определения окружности , можно сказать, что длина диаметра удвоенной длине радиуса.
Теперь можно принять радиус окружности равным R. Тогда для длины окружности необходимо воспользоваться формулой:
L = 2πR = πD, где L — длина окружности , D — диаметр окружности , который всегда в 2 раза радиуса.
Обратите внимание
Окружность можно вписать в многоугольник, либо описать вокруг него. При этом, если окружность вписана, то она в точках касания со сторонами многоугольника будет делить их пополам. Чтобы узнать радиус вписанной окружности, нужно поделить площадь многоугольника на половину его периметра:
R = S/p.
Если окружность описана вокруг треугольника, то ее радиус находится по следующей формуле:
R = a*b*c/4S, где a, b, c — это стороны данного треугольника, S — площадь треугольника, вокруг которого описана окружность.
Если требуется описать окружность вокруг четырехугольника, то это можно будет сделать при соблюдении двух условий:
Четырехугольник должен быть выпуклым.
В сумме противоположные углы четырехугольника должны составлять 180°
Полезный совет
Помимо традиционного штангенциркуля, для начертания окружности можно применять и трафареты. В современных трафаретах включены окружность разных диаметров. Данные трафареты можно приобрести в любом магазине канцтоваров.
Источники:
- Как найти длину окружности?
Окружность — замкнутая кривая линия, все точки которой находятся на равном расстоянии от одной точки. Эта точка — центр окружности, а отрезок между точкой на кривой и ее центром называется радиусом окружности.
Инструкция
Если через центр окружности провести прямую линию, то ее отрезок между двумя точками пересечения этой прямой с окружностью называется диаметром данной окружности. Половина диаметра, от центра до точки пересечения диаметра с окружность — это радиус
окружности. Если окружность разрезать в произвольной точке, выпрямить и измерить, то полученная величина является длиной данной окружности.
Начертите несколько окружностей разным раствором циркуля. Визуальное сравнение позволяет сделать вывод, что больший диаметр очерчивает больший круг, ограниченный окружностью с большей длиной. Следовательно, между диаметром окружности и ее длиной существует прямо пропорциональная зависимость.
По физическому смыслу параметр «длина окружности» соответствует , ограниченного ломаной линией.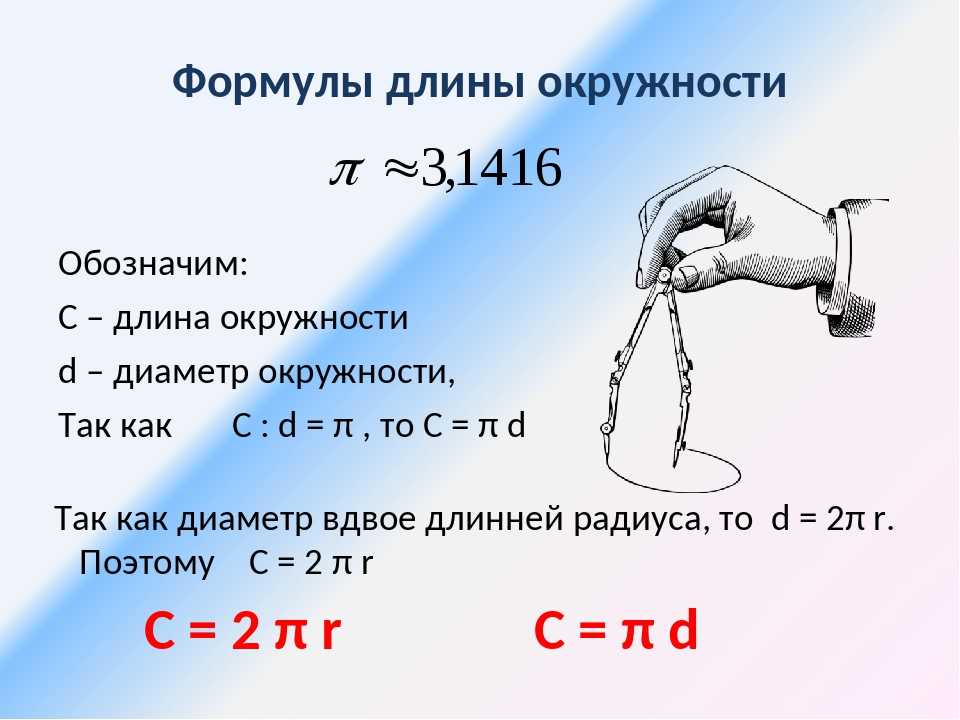 Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для окружности разделите ее длину на число π=3,14.
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению.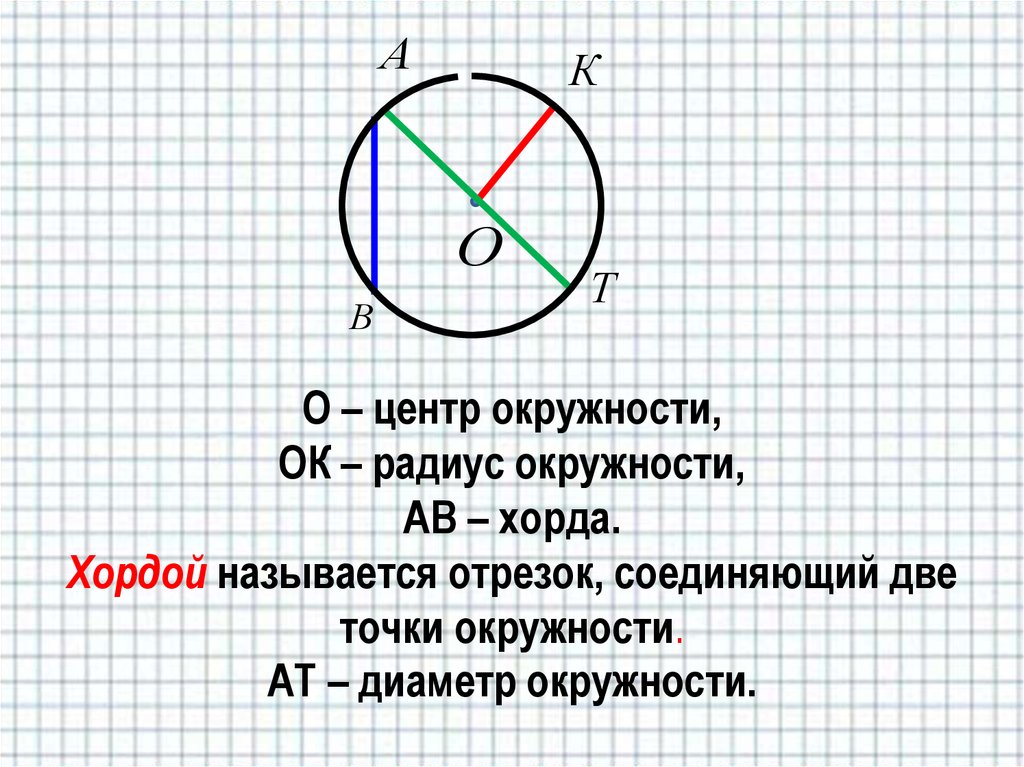 Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.

Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Как узнать длину окружности зная диаметр формула. Как рассчитать длину окружности, если не указан диаметр и радиус круга
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».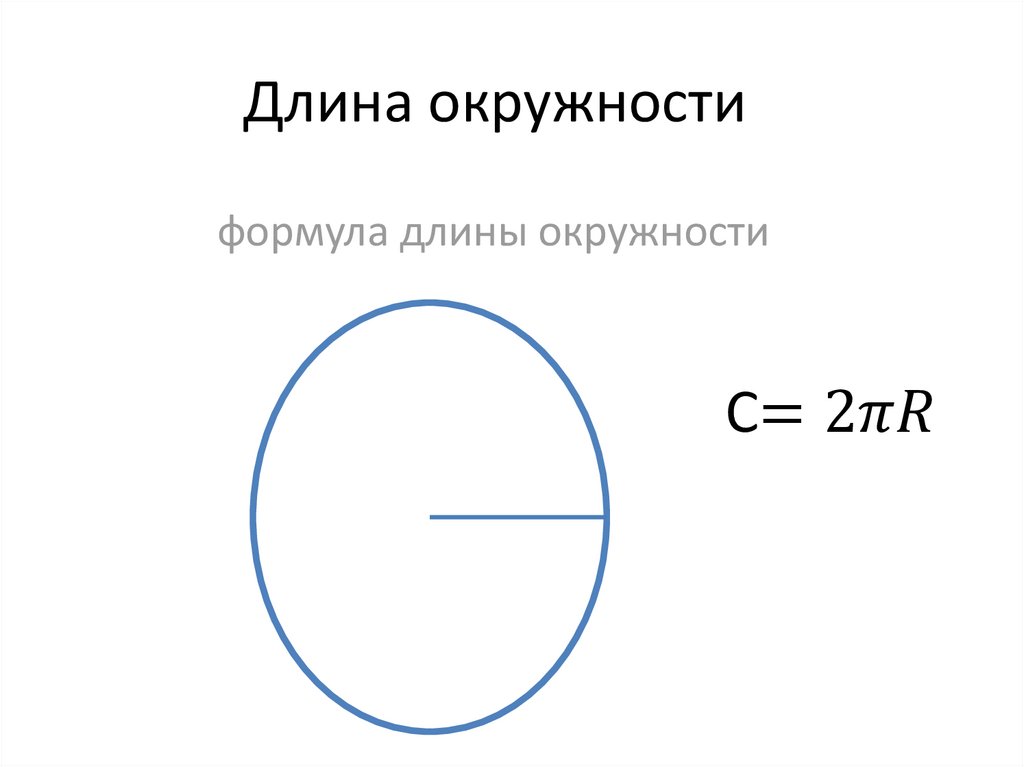
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра.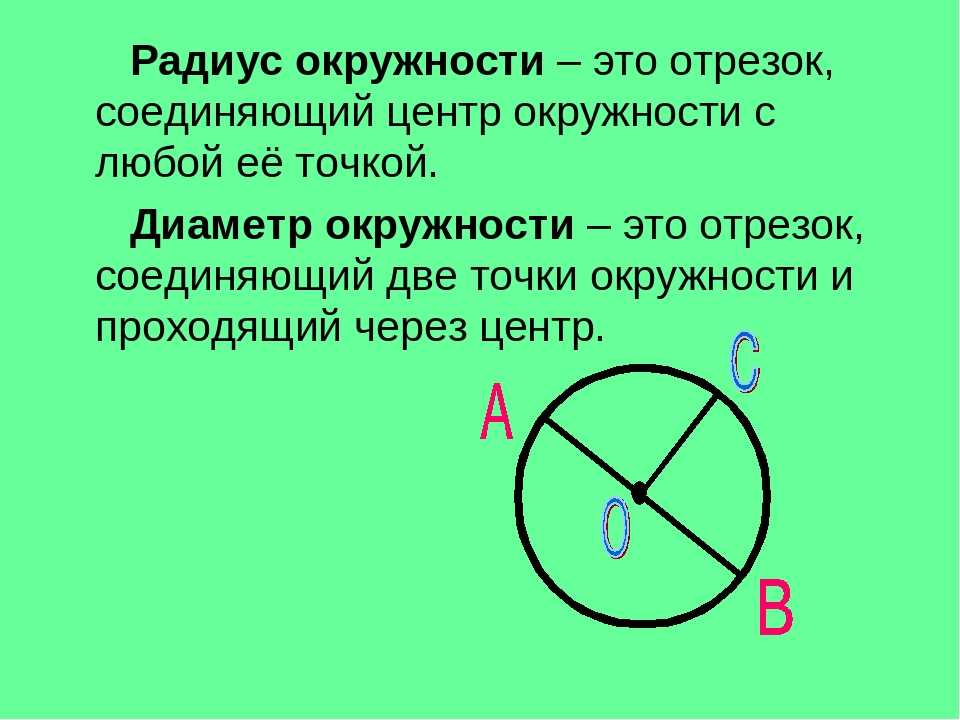 Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.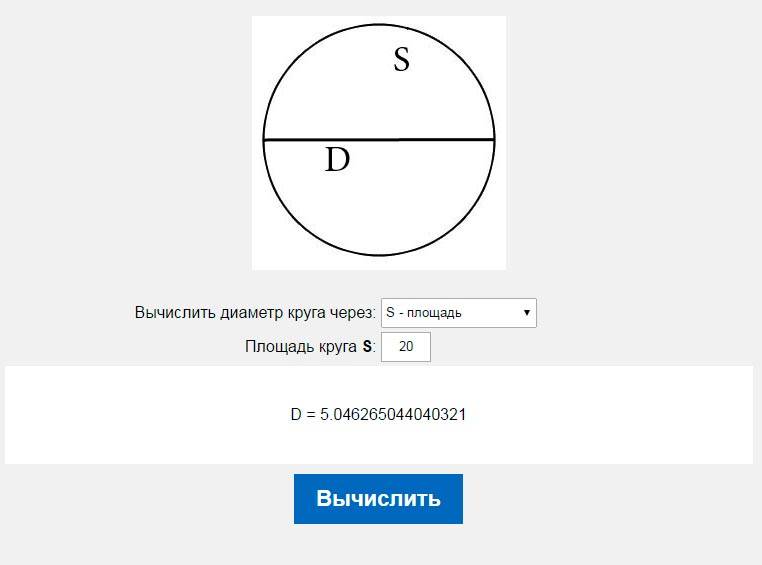
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.

- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр.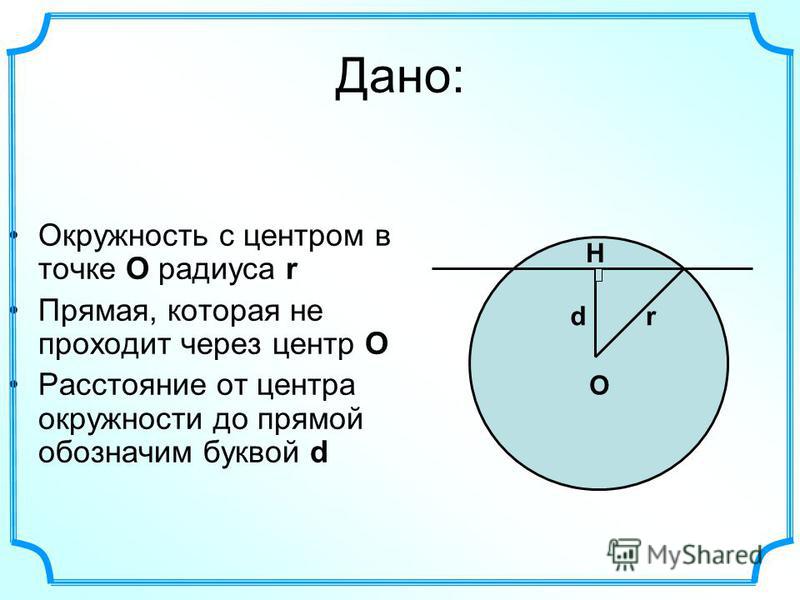 Для этого L нужно поделить на 2π или на π соответственно.
Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов.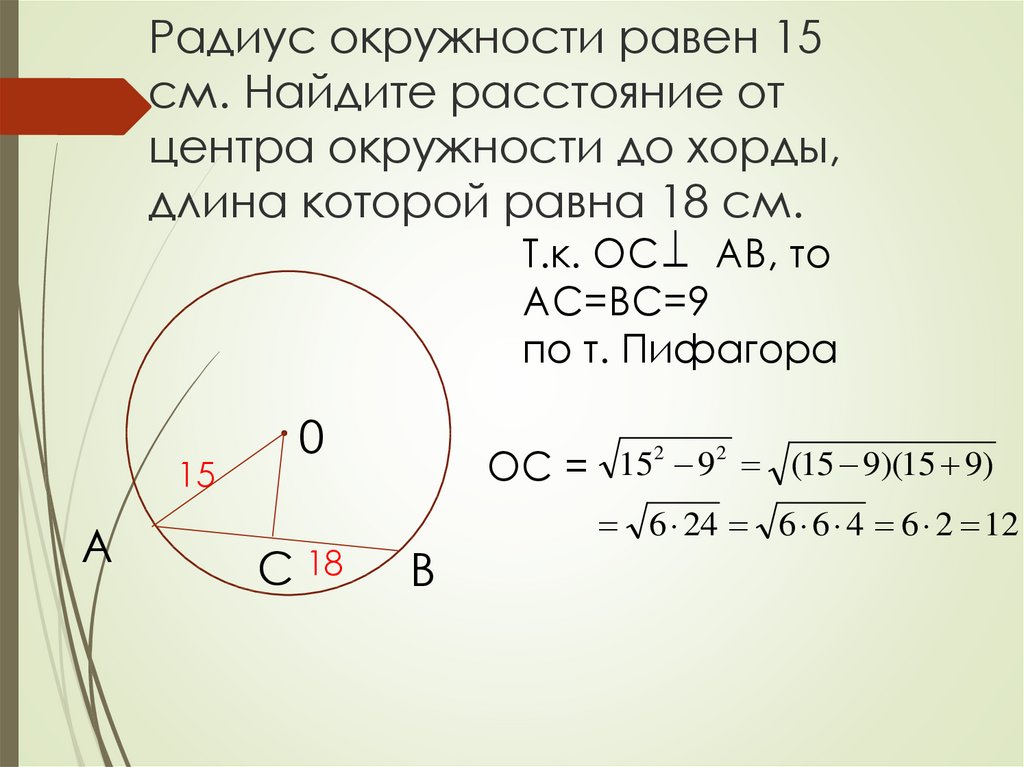 Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой.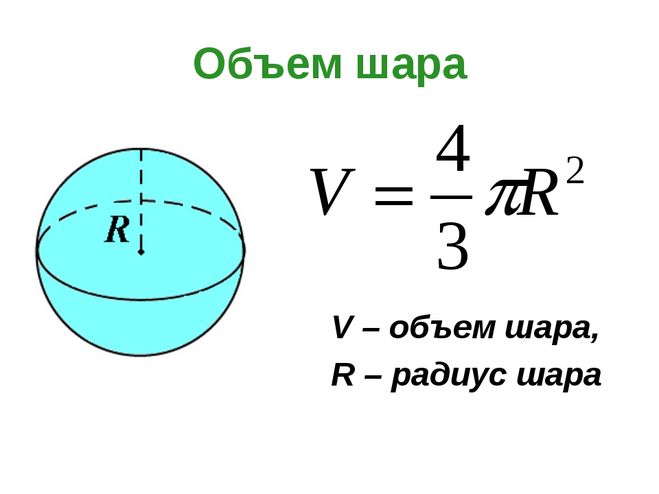 Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2.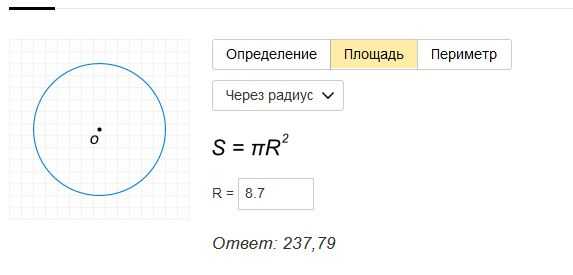 Найти площадь круга, если его диаметр равен 7 см.
Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.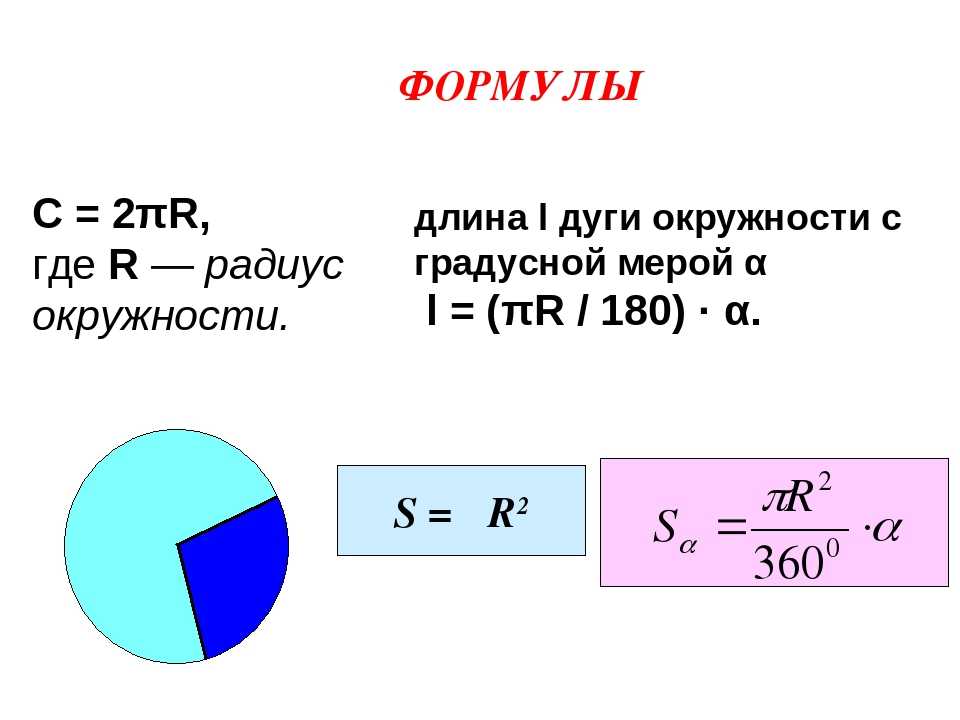
Как найти длину окружности зная радиус и диаметр: формула, как найти длину круга и разницу между величинами
Очень часто при решении школьных заданий по математике или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы, понятия и определения требуются для этого….
Содержание
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку. Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности.
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр. Он обозначается латинской буквой d.
- Окружность — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром.
 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности. Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях! Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r. Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два.
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r.
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. 2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
Это интересно! Первый признак равенства треугольников: доказательство
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга . Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см. Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Это интересно! Что такое биссектриса треугольника: свойства, связанные с отношением сторон
Длина окружности
Окружность, диаметр, хорда геометрия 7 класс
Заключение
Исходя из приведённых выше рассуждений, можно прийти к выводу, что никаких сложностей в задачах, связанных с нахождением всевозможных характеристик окружности, нет. Достаточно хорошо выучить понятия и формулы, а также уметь производить арифметические действия, причём все выражения выводятся друг из друга.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
Как найти окружность зная диаметр. Как найти длину окружности: через диаметр и радиус
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
теперь найдём длину окружности, умножив π на диаметр:
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. 2»).
2»).
Зная лишь длину диаметра окружности, можно вычислить не только площадь круга, но и площади некоторых других геометрических фигур. Это вытекает из того, что диаметры вписанных или описанных вокруг таких фигур окружностей совпадают с длинами их сторон либо диагоналей.
Инструкция
Если надо найти площадь (S) по известной длине его диаметра (D), умножайте число пи (π) на возведенную в длину диаметра , а результат делите на четыре: S=π ²*D²/4. Например, круга равен двадцати сантиметрам, то его площадь можно вычислить так: 3,14² * 20² / 4 = 9,86 * 400 / 4 = 986 сантиметров.
Если надо найти площадь квадрата (S) по диаметру вокруг него окружности (D), возводите длину диаметра в квадрат, а результат разделите пополам: S=D²/2. Например, если диаметр описанной окружности равен двадцати сантиметрам, то площадь квадрата можно вычислить так: 20² / 2 = 400 / 2 = 200 квадратных сантиметров.
Если площадь квадрата (S) нужно найти по диаметру вписанной в него окружности (D), достаточно возвести длину диаметра в квадрат: S=D². 2 / 4 + 20*10/2», а нажать клавишу Enter.
2 / 4 + 20*10/2», а нажать клавишу Enter.
Источники:
- как найти площадь окружности по диаметру
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Используйте какой-либо , чтобы рассчитать длину диаметра, если сделать это в уме не получается. Например, можно воспользоваться тем, который встроен в поисковую систему Nigma или Google — он математические операции, вводимые на «человеческом» . Например, если известная длина окружности составляет четыре метра, то для нахождения диаметра можно «по-человечески» попросить поисковик: «4 метра разделить на пи». Но если вы введете в поле поискового запроса, например, «4/пи», то поисковик поймет и такую постановку задачи. В любом случае ответом будет «1.27323954 метра».
Вопрос о диаметре земного шара не так прост, как может показаться на первый взгляд, ведь само понятие «земной шар» весьма условно. У настоящего шара диаметр всегда будет одинаковым, в каком бы месте ни был проведен отрезок, соединяющий две точки на поверхности сферы и проходящий через центр.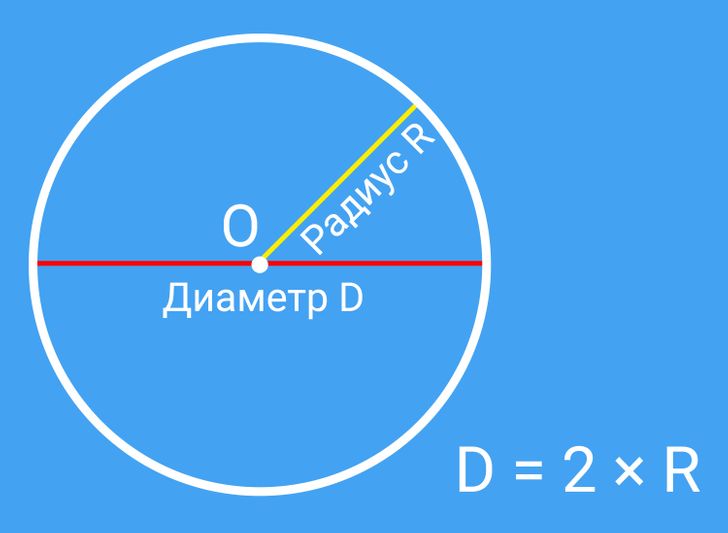
Применительно к Земле не представляется возможным, поскольку ее шарообразность далеко не идеальна (в природе вообще не бывает идеальных геометрических фигур и тел, они представляют собой абстрактные геометрические понятия). Для точного обозначения Земли ученым даже пришлось ввести специальное понятие – «геоид».
Официальный диаметр Земли
Величина диаметра Земли определяется тем, в каком месте его будут измерять. Для удобства за официально признанный диаметр принимаются два показателя: диаметр Земли по экватору и расстояние между Северным и Южным полюсами. Первый показатель равен 12 756,274 км, а второй – 12 714, разница между ними составляет немногим менее 43 км.
Данные числа не производят особого впечатления, они уступают даже расстоянию между Москвой и Краснодаром – двумя городами, расположенными на территории одной страны. Тем не менее, вычислить их было непросто.
Вычисление диаметра Земли
Диаметр планеты высчитывается по такой же геометрической формуле, как и любой другой диаметр.
Чтобы найти периметр окружности, необходимо умножить ее диаметр на число πи. Следовательно, для нахождения диаметра Земли нужно измерить ее окружность в соответствующем сечении (по экватору или в плоскости полюсов) и разделить ее на число πи.
Первым человеком, попытавшимся измерить окружность Земли, был древнегреческий ученый Эратосфен Киренский. Он обратил внимание, что в Сиене (ныне – Асуан) в день летнего солнцестояния Солнце находится в зените, освещая дно глубокого колодца. В Александрии же в этот день оно отстояло от зенита на 1/50 окружности. Из этого ученый сделал вывод, что расстояние от Александрии до Сиена составляет 1/50 окружности Земли. Расстояние между этими городами равно 5 000 греческим стадиям (приблизительно 787,5 км), следовательно, окружность Земли равна 250 000 стадий (примерно 39 375 км).
В распоряжении современных ученых имеются более совершенные средства измерения, но их теоретическая основа соответствует идее Эратосфена. В двух точках, расположенных в нескольких сотнях километров друг от друга, фиксируют положение Солнца или определенных звезд на небосводе и вычисляют разницу между результатами двух измерений в градусах.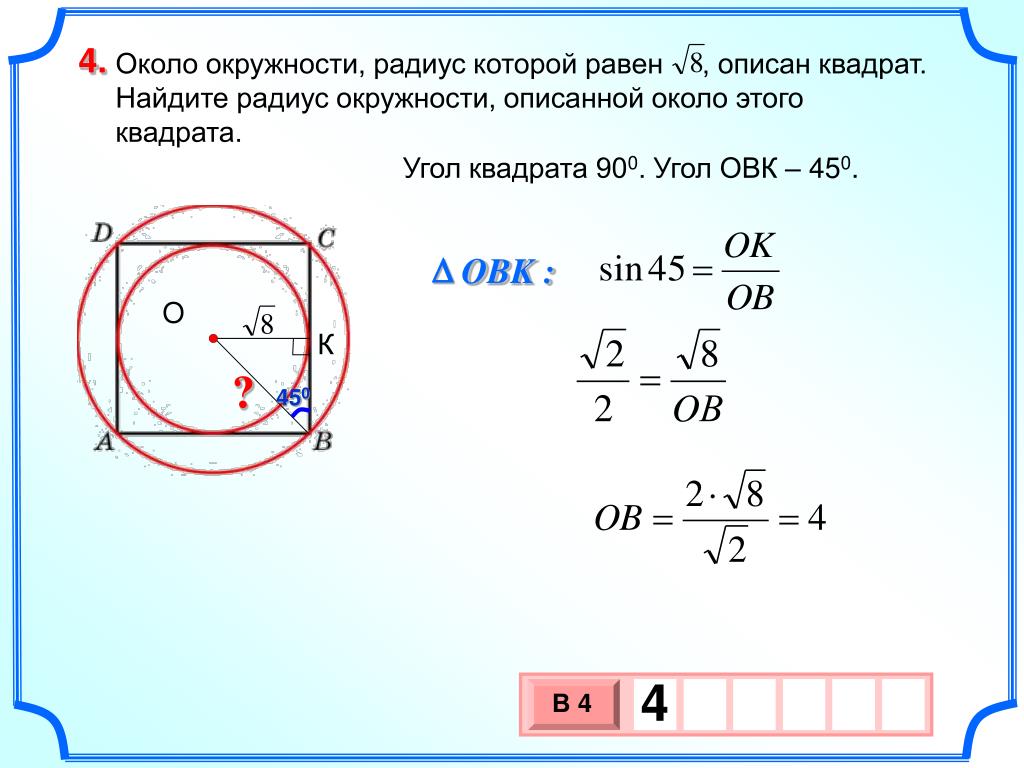 Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Зная расстояние в километрах, несложно вычислить длину одного градуса, а затем умножить ее на 360.
Для уточнения размеров Земли используется и лазерная дальнометрия, и спутниковые системы наблюдения.
На сегодняшний день считается, что окружность Земли по экватору составляет 40 075,017 км, а по – 40 007,86. Эратосфен лишь немного ошибся.
Величина и окружности, и диаметра Земли увеличивается из-за метеоритного вещества, постоянно выпадающего на Землю, но процесс этот идет очень медленно.
Источники:
- Как измерили Землю в 2019
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3. 14
14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Найти длину круга если средняя скорость. Составление системы уравнений
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.
- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
§ 117. Длина окружности и площадь круга.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис.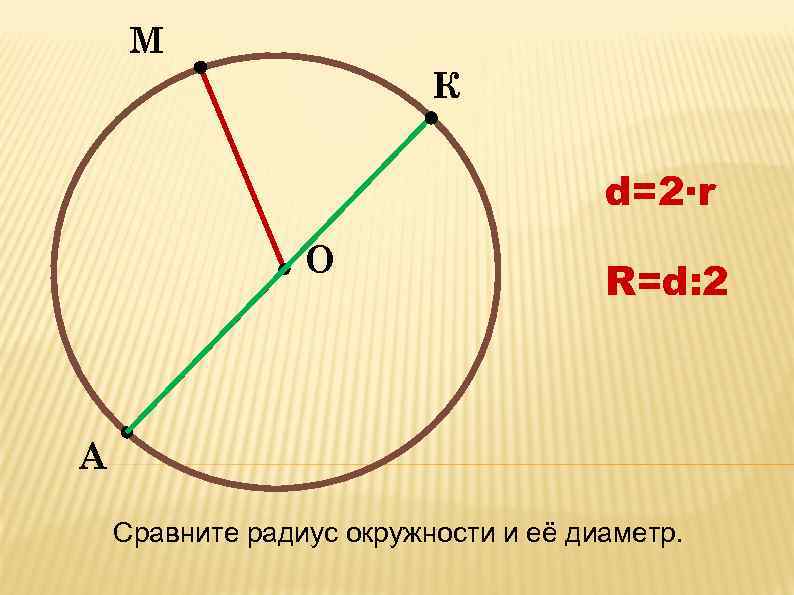 27).
27).
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).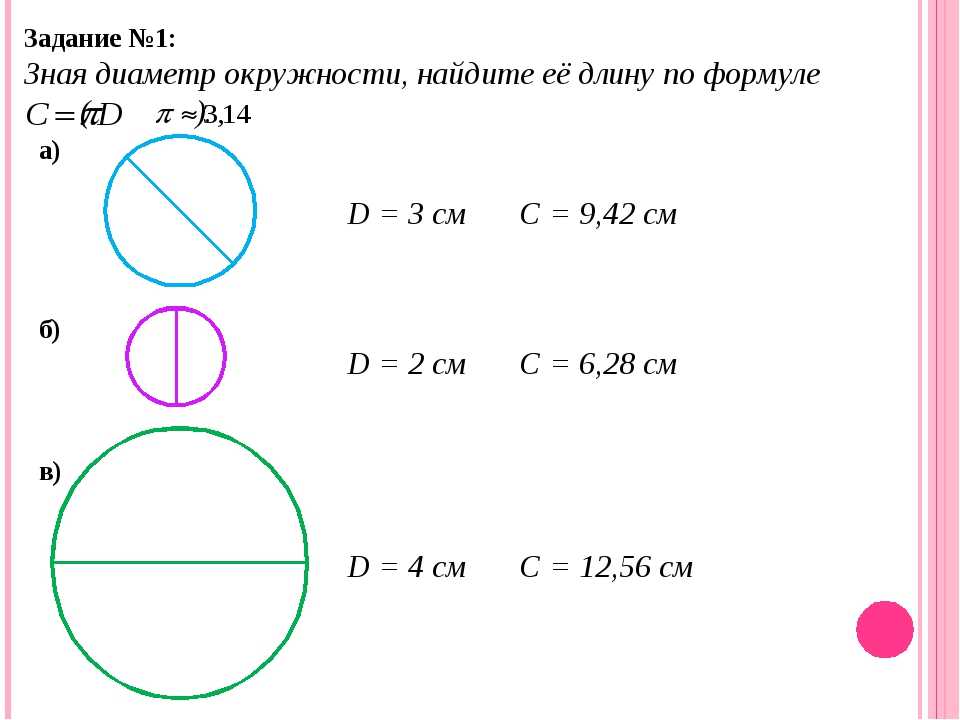
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).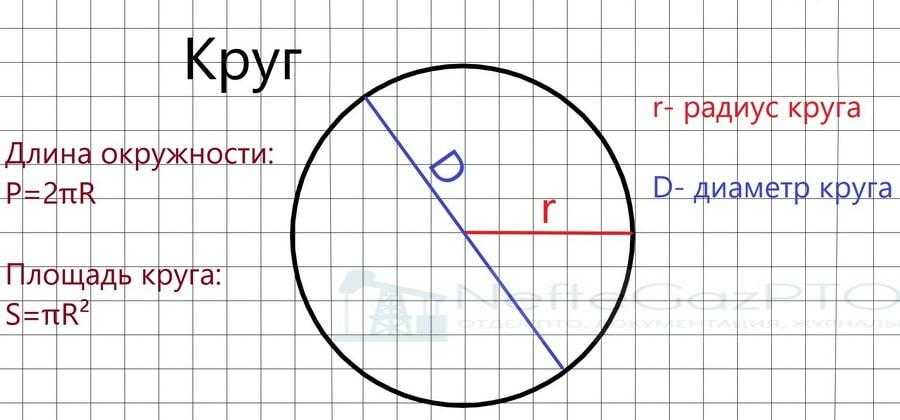
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н. И. Сырнева.
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение.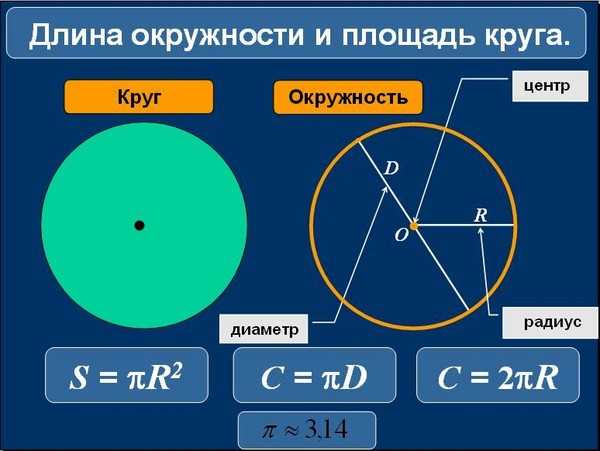 И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.
В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие. Узнать длину окружности, радиус которой равен 5 см.
Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
Ответ: l = 31,4 см.
Задача вторая
Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.
Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.
Ответ: r = 200 мм.
Задача третья
Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.
Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.
Ответ: d = 18 см.
Задача четвертая
Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.
Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ: l 1 = 18,84 см, l 2 = 31,4 см.
Задача пятая
Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?
Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.
Ответ: Белка пробегает 6,28 м.
- если известен диаметр окружности, то формула выглядит так L = ПD
- если известен радиус окружности, то формула имеет следующий вид L = 2Пr.
Формула длины окружности
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе. Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.

Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.
Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.
Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга. Она вас, при решении геометрических задач, еще не раз выручит.
Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,
Решение уравнений:
Геометрическая прогрессия:
Комбинаторика:
Решить химическое уравнение
Арифметическая прогрессия.

Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности
Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.
r — это радиус
D — диаметр
Приблизительно 3,14
Но окружность — это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.14.
Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.
Длину окружности можно найти одним из представленных способов:
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O », а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
π
≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π
,
Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π , мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если
её длина равна 56,52
дм.
(π
≈ 3,14
).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A » и «B ». Эти точки делят окружность на две части, каждую из которых называют дугой . Это синяя дуга «AB » и черная дуга «AB ». Точки «A » и «B » называют концами дуг .
Радиус круга – формула, определение
Радиус определяется как отрезок, соединяющий центр с границей круга или сферы. Длина радиуса остается неизменной от центра до любой точки на окружности круга или сферы. Это половина длины диаметра. Давайте узнаем больше о радиусе в этой статье.
| 1. | Что такое радиус? |
| 2. | Формулы радиуса |
| 3. | Радиус окружности |
| 4. | Как найти радиус окружности? |
5. | Уравнение радиуса окружности |
| 6. | Радиус сферы |
| 7. | Часто задаваемые вопросы о Radius |
Что такое радиус?
В геометрии радиус определяется как отрезок, соединяющий центр круга или сферы с его окружностью или границей. Это важная часть кругов и сфер, которая обычно обозначается аббревиатурой «r». Множественное число радиуса — « радиусов », которое используется, когда мы говорим о более чем одном радиусе одновременно. Наибольший отрезок в окружности или сфере, соединяющий любые точки, лежащие на противоположной стороне от центра, является диаметром, а длина радиуса составляет половину длины диаметра. Его можно выразить как d/2, где d — диаметр круга или сферы. Посмотрите на изображение круга, приведенное ниже, показывающее соотношение между радиусом и диаметром.
Теперь давайте изучим формулы радиуса, которые помогут вам вычислить его длину с учетом данной информации.
Формулы радиуса
Радиус круга и сферы можно рассчитать с помощью определенных формул, которые вы изучите в этом разделе. Здесь мы поговорим о формулах радиуса для окружности. Формула радиуса сферы обсуждается в разделе ниже.
Формула радиуса от диаметра: Диаметр представляет собой прямую линию, проходящую через центр и соединяющую точку на одном конце с точкой на другом конце окружности. Диаметр в два раза больше длины радиуса. Математически это записывается как диаметр = 2 × радиус. Это также самая длинная хорда окружности. Когда диаметр круга дан, тогда формула радиуса выражается как:
Радиус = Диаметр/2 или D/2 единиц
Формула радиуса из окружности: Периметр круга называется его окружностью. Это граница круга и может быть выражена формулой: C = 2πr единиц. Здесь C — длина окружности, r — радиус окружности, а π — константа, равная 3,14159.. Радиус равен отношению длины окружности к 2π. Формула радиуса с использованием длины окружности выражается следующим образом:
Формула радиуса с использованием длины окружности выражается следующим образом:
Радиус = Окружность/2π или C/2π единиц
Формула радиуса с площадью: Площадь круга – это пространство, занимаемое кругом. Связь между радиусом и площадью определяется формулой Площадь круга = πr 2 квадратных единиц. Здесь r — радиус, а π — константа, равная 3,14159. Формула радиуса с использованием площади круга выражается как:
Радиус = √(Площадь/π) единиц
Радиус окружности
Радиус — одна из важных частей окружности. Это расстояние от центра круга до любой точки на его границе. Другими словами, когда мы соединяем центр круга с любой точкой его окружности с помощью прямой линии, этот отрезок линии является радиусом этого круга. Круг может иметь более одного радиуса, потому что на его окружности бесконечное количество точек. Это означает, что круг имеет бесконечное число радиусов и все радиусы круга равноудалены от центра круга.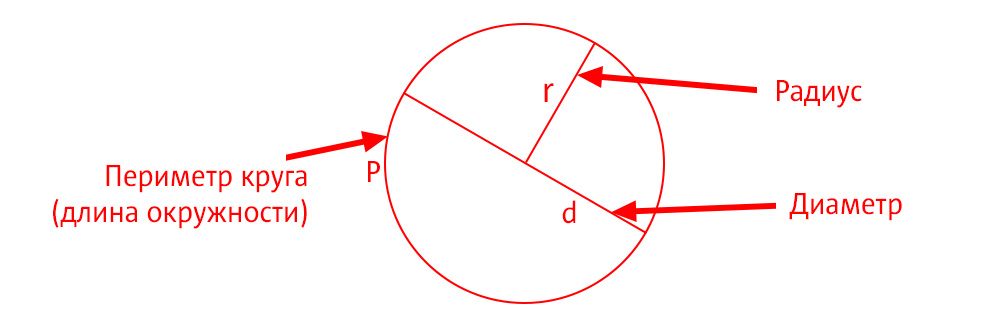 Размер круга меняется при изменении длины радиуса.
Размер круга меняется при изменении длины радиуса.
На приведенном ниже рисунке точки A, B, M, N, P, Q, X и Y лежат на границе окружности. Заметим, что эти точки равноудалены от центра O. Итак, все отрезки OA, OB, OM, ON, OY, OX, OP и OQ называются радиусами окружности. Обратите внимание, что OA = OB = OM = ON = OP = OQ = OX = OY.
Как найти радиус окружности?
Радиус круга можно найти с помощью трех основных формул радиуса, т.е. когда известны диаметр, площадь или длина окружности. Воспользуемся этими формулами, чтобы найти радиус окружности.
- Когда диаметр известен, формула Радиус = Диаметр/2.
- Если длина окружности известна, формула Радиус = Длина окружности/2π.
- Когда площадь известна, формула для радиуса: Радиус = ⎷(Площадь круга/π).
Например, если диаметр равен 24 единицам, то радиус равен 24/2 = 12 единицам. Если длина окружности равна 44 единицам, то ее радиус можно рассчитать как 44/2π. Отсюда следует, что (44×7)/(2×22) = 7 единиц. И, если площадь круга равна 616 квадратных единиц, то радиус равен ⎷(616×7)/22 = ⎷28×7 = ⎷196 = 14 единиц.
Отсюда следует, что (44×7)/(2×22) = 7 единиц. И, если площадь круга равна 616 квадратных единиц, то радиус равен ⎷(616×7)/22 = ⎷28×7 = ⎷196 = 14 единиц.
Уравнение радиуса окружности
Радиус уравнения окружности на декартовой плоскости с центром (h, k) определяется как (x − h) 2 + (y − k) 2 = r 2 . Здесь (x, y) — точки на окружности окружности, находящиеся на расстоянии «r» (радиус) от центра (h, k). Когда центр окружности находится в начале координат (0,0), уравнение окружности сводится к x 2 + y 2 = r 2 . Обратите внимание на схему окружности на декартовой плоскости, показанную ниже. Здесь координаты центра равны (0, b), а радиус окружности представлен буквой «r», соединяющей центр с точкой (x, y) на окружности. Итак, нам просто нужно подставить эти значения в приведенное выше уравнение, чтобы получить радиус уравнения окружности. Уравнение для нахождения радиуса этой окружности:0085 2 .
Радиус сферы
Сфера — трехмерная объемная фигура. Радиус сферы — это отрезок от центра до любой точки на границе сферы. Это определяющий фактор при рисовании сферы, так как ее размер зависит от ее радиуса. Как и в случае с кругом, внутри сферы могут быть нарисованы бесконечные радиусы, и все эти радиусы будут равны по длине. Чтобы вычислить объем и площадь поверхности сферы, нам нужно знать ее радиус. И мы можем легко вычислить радиус сферы по формулам ее объема и площади поверхности.
Радиус сферы от объема = 3 ⎷(3V)/4π единиц, где V представляет объем, а значение π приблизительно равно 3,14.
Радиус сферы с использованием площади поверхности = ⎷(A/4π) единиц, где A представляет собой площадь поверхности.
Используйте наш бесплатный онлайн-калькулятор радиуса сферы, чтобы рассчитать радиус с заданным объемом, площадью поверхности или диаметром сферы.
☛ Статьи по теме
Проверьте эти интересные статьи, связанные с радиусом и его формулами.
- Формула радиуса кривизны
- Сегмент круга
- Сектор круга
Часто задаваемые вопросы о радиусе окружности
Что такое радиус круга в геометрии?
Радиус окружности — это длина отрезка от центра до точки на окружности окружности. Обычно обозначается аббревиатурой «р». В круге может быть бесконечное количество радиусов, и длина всех этих радиусов будет одинаковой. Это половина диаметра круга.
Как диаметр связан с радиусом окружности?
Диаметр круга в два раза больше радиуса, или радиус равен половине диаметра. Связь между радиусом и диаметром можно выразить формулой: Диаметр = 2 × радиус. Используйте бесплатный онлайн-калькулятор радиуса, чтобы рассчитать радиус с заданным диаметром.
Как найти радиус окружности с помощью длины окружности?
Длина окружности и радиус связаны друг с другом, и их отношение можно выразить как Длина окружности = 2πR, где R — радиус. Итак, когда длина окружности известна, формула, используемая для расчета радиуса круга, выглядит следующим образом: Радиус = Окружность / 2π.
Что такое радиус кривой?
Радиус кривой или дуги — это радиус окружности, частью которой они являются. Когда длина хорды, определяющей основание (W), и высота, измеренная в середине основания дуги (H), даны, формула для нахождения радиуса: Радиус = (H / 2) + (W 2 / 8Н).
Что такое формула радиуса?
Радиус круга можно рассчитать с помощью различных формул. Соблюдайте следующие формулы для расчета радиуса:
- Когда диаметр известен, формула Радиус = Диаметр / 2.
- Когда длина окружности известна, формула для радиуса равна Окружность / 2π.
- Если площадь известна, формула Радиус = ⎷(Площадь круга / π).
Как рассчитать радиус окружности с помощью калькулятора?
Длина радиуса равна половине длины диаметра, который можно рассчитать с помощью онлайн-калькулятора Cuemath, просто введя любое заданное значение среди диаметра, окружности или площади круга.
Как найти радиус круга с площадью?
Если известна площадь круга, то формула для нахождения радиуса дается как Радиус = ⎷(A/π) единиц, где A – заданная площадь.
Определение диаметра окружности и расчет — Math Open Reference
r
Определение диаметра круга и калькулятор — Math Open ReferenceMath Open Reference
Главная Контакт О Тематический указатель
Расстояние по окружности через ее центр.
Попробуйте это Перетащите оранжевую точку. Синяя линия всегда будет диаметром круга.
Диаметр круга — это длина линии, проходящей через центр и касающейся двух точек на его краю. На рисунке выше перетащите оранжевые точки и убедитесь, что диаметр никогда не меняется.
Иногда слово «диаметр» используется для обозначения самой линии. В этом смысле вы можете увидеть «нарисуйте диаметр круга». В более позднем смысле это длина линии, поэтому его называют «диаметром круга 3,4 сантиметра».
Диаметр тоже есть
аккорд.
Хорда – это линия, соединяющая любые две точки окружности.
Диаметр – это хорда, проходящая через центр окружности.
Это самая длинная хорда любого круга.
Центр круга является серединой его диаметра. То есть делит его на две равные части, каждая из которых представляет собой радиус окружности. Радиус равен половине диаметра.
Если вы знаете радиус
Зная радиус окружности, диаметр можно рассчитать по формуле где:R радиус окружности
Если вы знаете длину окружности
Если известна длина окружности, то диаметр можно найти по формуле, где:
C это длина окружности
π это Пи, примерно 3,142
Если вы знаете район
Если известна площадь круга, диаметр можно найти по формуле, где:
A – площадь круга
π – число Пи, примерно 3,142.
Калькулятор
| Радиус | прозрачный | |
| Диаметр | прозрачный | |
| Зона | прозрачный | |
| Окружность | прозрачный | |
Используйте калькулятор выше, чтобы рассчитать свойства круга.
Введите любое отдельное значение, и остальные три будут рассчитаны. Например: введите диаметр и нажмите «Рассчитать». Будут рассчитаны площадь, радиус и окружность.
Точно так же, если вы введете область, радиус, необходимый для получения этой области, будет рассчитан вместе с диаметром и окружностью.
Связанные предметы
Радиус Радиус — это расстояние от центра до любой точки края. Как видно из рисунка выше, диаметр равен двум радиусным линиям, расположенным вплотную друг к другу, поэтому диаметр всегда в два раза больше радиуса. См. радиус круга
Окружность Окружность — это расстояние вокруг края круга. Видеть Окружность круга для получения дополнительной информации.
Что попробовать
- На рисунке выше нажмите «Сброс» и перетащите любую оранжевую точку. Обратите внимание, что диаметр имеет одинаковую длину в любой точке окружности.
- Нажмите «показать радиус». Перетащите оранжевую точку в конце линии радиуса.
 Обратите внимание, что радиус всегда равен половине диаметра.
Обратите внимание, что радиус всегда равен половине диаметра. - Снимите флажок «фиксированный размер». Повторите вышеописанное и обратите внимание, что радиус всегда равен половине диаметра независимо от размера круга.
Теорема Фалеса
Теорема Фалеса утверждает, что диаметр окружности содержит прямой угол в любую точку окружности. (см. рисунок справа).Независимо от того, где находится точка, треугольник образуется всегда прямоугольный треугольник. См. Теорему Фалеса для интерактивной анимации этой концепции.
Другие темы кружка
Общий
- Определение круга
- Радиус окружности
- Диаметр окружности
- Длина окружности
- Части круга (схема)
- Определение полукруга
- Касательная
- Секанс
- Аккорд
- Теорема о пересекающихся хордах
- Теорема о пересекающихся секущих длинах
- Теорема о пересекающихся секущих углах
- Площадь круга
- Концентрические окружности
- Кольцо
- Площадь кольца
- Сектор круга
- Площадь сектора круга
- Сегмент круга
- Площадь сегмента окружности (данный центральный угол)
- Площадь сегмента круга (данная высота сегмента)
Уравнения окружности
- Основное уравнение окружности (центр в начале координат)
- Общее уравнение окружности (центр в любом месте)
- Параметрическое уравнение окружности
Уголки по окружности
- Угол вписанный
- Центральный уголок
- Теорема о центральном угле
Дуги
- Дуга
- Длина дуги
- Измеритель угла дуги
- Смежные дуги
- Большая/малая дуги
- Перехваченная дуга
- Сектор круга
- Радиус дуги или сегмента при заданной высоте/ширине
- Стрела — высота дуги или сегмента
(C) 2011 Copyright Math Open Reference.
Все права защищены
Как вычислить длину окружности, если я знаю диаметр?
33 ответа
Джеймс Фитцджеральд ответил
Чтобы рассчитать это, вам нужна правильная формула. Формула длины окружности классифицируется как пи х диаметр. Его также можно записать как pi.d.
Окружность — это, по сути, расстояние или длина по окружности. _, правильно произносимое как пирог, является иррациональным числом, а это значит, что его нельзя записать в виде дроби. Поэтому, чтобы быть уверенным, хорошее приближение π равно 3,14 при использовании в конкретных формулах.
Круговая диаграмма, или число Пи, необходима для вычисления длины окружности. Убедитесь, что вы знаете, где находится центр круга. Вам нужно будет найти диаметр, который является линией, которая касается двух концов круга и центра.
Затем вы можете использовать эту линию соответственно или радиус вместе с π для вычисления длины окружности. Все, что вам нужно сделать, это умножить радиус на 2, чтобы получить диаметр.
Все, что вам нужно сделать, это умножить радиус на 2, чтобы получить диаметр.
Другие вещи, которые следует учитывать в круге, включают радиус, который представляет собой линию, которая касается внешней части круга и центра. Он не соприкасается более чем с одной частью внешней среды. Вы сможете заменить диаметр на это для альтернативной формулы. Чтобы получить радиус, вам нужно разделить диаметр на 2, чтобы получить радиус.
Есть две формулы и, учитывая, что вы уже знаете диаметр, то будет намного проще сделать окружность. В математических терминах длина окружности в алгебре описывается как:
C = π x диаметр
или
C = π x (2 x радиус)
поблагодарил автора.
выпалил это.
Оддман ответил
36*Pi ≈ 113,1
поблагодарил автора.
выпалил это.
Mainul Hussain ответил
113,04 дюйма, принимая pi=3,14
поблагодарил автора.
выпалил это.
Кэти Гарри ответила
Окружность на самом деле похожа на периметр круга. Формула нахождения длины окружности:
C = Pi x r 2
Где,
C = длина окружности
pi = 3,14
r = радиус
Нам дан диаметр. Радиус равен половине диаметра, поэтому:
Радиус = Диаметр
2
Радиус = 28
2
Радиус = 14 дюймов
Теперь вычислим длину окружности:
C = Pi x r 2
6 903,14 (14) 2
C = 3,14 x 196
C = 615,4 дюйма ——ОТВЕТ
поблагодарил автора.
выпалил это.
Кэти Гарри ответила
Формула для нахождения длины окружности:
C = 2 x pi x r
Где
C = длина окружности
r = радиус
pi = 3,14
Теперь у нас нет значение радиуса здесь, хотя оно используется в формуле.
Итак, нам нужно сначала найти радиус этой окружности. Радиус всегда вдвое меньше диаметра, поэтому:
радиус = диаметр/2
радиус = 11/2
радиус = 5,5 футов
Теперь найдем длину окружности:
C = 2 x pi x r
C = 2(3,14 x 5,5)
C = 2(17,27)
C = 34,54 фута
Следовательно, длина окружности этого круга равна 34,54 фута.
поблагодарил автора.
выпалил это.
Аноним ответил
25.13
поблагодарил автора.
выпалил это.
Анонимный ответил
Чтобы найти длину окружности, зная диаметр. Все, что вам нужно сделать, это умножить диаметр на пи (пи равно 3,14!!) и вы получили его. ХОРОШО ТЫ СДЕЛАЛА ЭТО!!!!
Формула:(пример) 3.14-pi
x 2-диаметр
»»»»»»’
6.28-длина окружности
поблагодарил автора.
выпалил это.
Робин Ротман ответила
Классическая формула для нахождения длины окружности C=2pi r или длина окружности равна 2 умножить на пи (пи равно 3,14) умножить на радиус. Радиус круга составляет половину диаметра, поэтому вы можете просто умножить диаметр на 3,14 (пи). Это ваша окружность.
поблагодарил автора.
выпалил это.
Аноним ответил
Для диаметра 36 дюймов
поблагодарил автора.
выпалил это.
Аноним ответил
25.13
поблагодарил автора.
выпалил это.
Оддман ответил
Да, и вы сможете, если умножите 8 см на число Пи.
окружность = 8*3,1416 см = 25,1328 см
поблагодарил автора.
выпалил это.
Аноним ответил
25.12
поблагодарил автора.
выпалил это.
Анонимный ответил
Если я сделаю круг диаметром 3 фута из 12-дюймовых кирпичей, сколько мне понадобится?
поблагодарил автора.
выпалил это.
янтарный Джон ответил
Длина окружности равна удвоенному произведению постоянной пи на радиус окружности.
Окружность = 2 * пи * радиус
Пи = 3,14
Диаметр = 2 * радиус
Радиус = диаметр/2 ед.
Окружность = 43,96 шт.
Требуемая длина окружности 43,96.
поблагодарил автора.
выпалил это.
Анонимный ответил
Да
поблагодарил автора.
выпалил это.
Аноним ответил
Какова площадь круга, длина окружности которого равна 8
поблагодарил автора.
выпалил это.
Аноним ответил
А 6.28
поблагодарил автора.
выпалил это.
Анонимный ответил
R=5
поблагодарил автора.
выпалил это.
Аноним ответил
2 раза диаметр равен окружности
поблагодарил автора.
выпалил это.
Анонимный ответил
100,48
поблагодарил автора.
выпалил это.
Аноним ответил
16м
поблагодарил автора.
выпалил это.
Анонимный ответил
34,54 фута
поблагодарил автора.
выпалил это.
Пэт Меррифилд ответил
Ближайший ответ, который у вас есть, d, поскольку я придумал 50,27.
поблагодарил автора.
выпалил это.
Анонимный ответил
Думаю, 2 X (круг) X r = длина окружности. Круг равен 3,14, а R — радиус, равный 1/2 диаметра.
поблагодарил автора.
выпалил это.
Аноним ответил
Если диаметр круга равен 8, длина окружности равна 25,1327:
Окружность = (Диаметр)(pi)
= Окружность = (8)(pi)
= Окружность = 25,1327 92
поблагодарил автора.
выпалил это.
Аноним ответил
Умножить диаметр на 3,14
поблагодарил автора.
выпалил это.
Аноним ответил
Умножить на 3
поблагодарил автора.
выпалил это.
Анонимный ответил
25.13
поблагодарил автора.
выпалил это.
Аноним ответил
Да помогите мне плз
поблагодарил автора.
выпалил это.
Мерил Харгривз ответила
Умножьте диаметр на пи (греческая буква!)
Значение приблизительно равно 22/7 или 3,1416 или даже точнее, в зависимости от того, что вам дали.
C= Pd или c=2Pr
(Нет символа пи!!)
поблагодарил автора.
выпалил это.
Майк Каталанотто-младший ответил
Периметр = пи (3,1416) x диаметр.
поблагодарил автора.
выпалил это.
Кёко Катаяма ответила
C = (pi) D; Вы делаете математику.
поблагодарил автора.
выпалил это.
Вам также может понравиться…
Ответить на вопрос
Измерение кругов
Блок № 4Измерение кругов
День 1
Изучение кругов. В качестве введения в решающие проблемы, связанные с цирками, связанные с цирками. диаметр и окружность.
Радиус — прямая линия, проходящая от центра круга к внешнему краю. Он равен половине расстояния по окружности.
Диаметр — прямая линия, которая проходит от одного края круга, проходит через центр круга и касается другой стороны. Это в два раза больше длины радиуса.
Окружность — это расстояние вокруг внешнего края окружности. Он примерно в 3 раза длиннее диаметра.
Он примерно в 3 раза длиннее диаметра.
Хорда — прямая, соединяющая любые две точки на окружности.
Дуга — участок окружности, лежащий между двумя концами хорды (каждая хорда образует две дуги).
День 2
ВЫЧИСЛЕНИЕ ОКРУЖНОСТИ Вчера мы узнали, что длина окружности примерно в три раза больше ее диаметра. При нахождении приблизительного ответа на вопрос мы используем символ (≈), чтобы указать, что ответ близок к правильному, но не совсем правильный.
Часто измерение окружности нецелесообразно или требуется более точная формула, чем «примерно в 3 раза». Сегодня студенты узнают точную формулу расчета расстояния по окружности (окружности) с использованием константы Пи
(π = 3,14).
Для получения дополнительной информации об истории и использовании числа π
в математике посетите следующую веб-ссылку: http://bit.ly/brYCsl
Формула для оценки приблизительной длины окружности: C = 3d, где C обозначает окружность, а d обозначает диаметр
Формула для расчета точной длины длины окружности круга – это C = πd, где C – длина окружности, – символ 3.14, а d – диаметр.
** Когда известен только радиус, вам нужно умножить его на 2 (2r = d), чтобы найти диаметр.
Если вы хотите найти забавную (но познавательную) песню, которая поможет вам запомнить длину окружности, число π и диаметр, перейдите по этой ссылке на веб-сайт Teachertube, в котором текст песни Томми Тутоне 86953o9 заменен на 3.14159. http://bit.ly/vWeyfR
Должен: 13 декабря
День 3 Средний обзор
Page 160-161 #1-7
. Повторные. и число 3, когда оценивается как .
Повторные. и число 3, когда оценивается как .
Не забудьте использовать число Пи (π) при вычислении точных ответов .
День 4
ОБЛАСТЬ РАСЧЕТАстр. 166-167 #4-9
Площадь фигуры показывает, сколько места она занимает.
При оценке площади круга мы используем формулу: A = 3r²
При расчете площади круга мы используем формулу: A = πr²
**1) Не забывайте всегда использовать квадратные единицы в ответах на вопросы о площади .
**2) Если в вопросе указан только диаметр, вам нужно не забыть разделить его на два, чтобы найти радиус.
День 5 Решение проблем, работая назад
19 декабря. работая в обратном порядке, начиная со значений, которые они знают, чтобы найти значения, которые они не знают. Чтобы работать в обратном направлении для решения задач измерения окружности, учащиеся должны хорошо понимать формулы для нахождения длины окружности и площади круга. Учащиеся также должны распознавать отношения радиуса, диаметра, окружности и/или площади в формуле.
работая в обратном порядке, начиная со значений, которые они знают, чтобы найти значения, которые они не знают. Чтобы работать в обратном направлении для решения задач измерения окружности, учащиеся должны хорошо понимать формулы для нахождения длины окружности и площади круга. Учащиеся также должны распознавать отношения радиуса, диаметра, окружности и/или площади в формуле.
При решении задач в обратном порядке полезно, если учащиеся следуют плану. Я рекомендую четырехэтапный план.
Шаг 1 — Внимательно прочитайте вопрос и скопируйте предоставленную информацию.
Если дана длина окружности, скопируйте формулу длины окружности (C = πd). Если дана площадь круга, скопируйте формулу площади (A = πr²).
Шаг 2 — Замените символы и переменные в формуле известными числами из вопроса.
Шаг 3 — Сгруппируйте числа по одну сторону знака равенства и переменные (буквы) по другую.
**Когда числа переходят на другую сторону знака равенства, выполняемая операция становится противоположной тому, что было в исходной части уравнения. Другими словами, если вы умножили число справа от знака равенства, вы разделите это число слева от знака равенства.
Другими словами, если вы умножили число справа от знака равенства, вы разделите это число слева от знака равенства.
Шаг 1. Скопируйте предоставленную информацию.
A = 283 м² π = 3,14 A = πr²
Шаг 2. Замените символы и переменные в формуле известными числами.
A = πr²
283 м² = (3,14) (r²)
Шаг 3. Сгруппируйте числа по одну сторону от знака равенства и переменные по другую.
a = πr²
283 м² = (3,14) (R²)
283 м² ÷ 3,14 = R²
Шаг 4 -Решите уравнение, чтобы найти неизвестную переменную
A = πr²
283 M² = (3,14) (R²)
44833333333 283 M² = (3,14) (R²) m² ÷ 3,14 = r²
90,13 = r² 0244 (квадратный корень из) 90,13 = r
8,49 м = r

ДЕНЬ 6 Обзор кругов
Page 174-175 #1-10
Запомните
#1-10
Запомните
#1-10
. Запомните
.
Всегда записывайте формулу для начала решения задачи.
Радиус = 1/2 диаметра (r = 1/2d) или диаметр в два раза больше радиуса (d = 2r)
Формула окружности C = πd
Нарисуйте круг диаметром (по всей окружности) 1
Тогда длина окружности (по всей окружности) равна 3.14159265… число известное как Пи
Пи (произносится как «пирог») часто пишется с использованием греческого символа π
.
Определение π:
Окружность
, разделенная на Диаметр
Окружности.
Длина окружности, деленная на диаметр круга, всегда равна π, независимо от того, насколько большой или маленький круг!
Чтобы помочь вам вспомнить, что такое π… просто нарисуйте эту диаграмму.
В поисках Пи самостоятельно
Нарисуйте круг или используйте что-то круглое, например тарелку.
Измерение по краю ( окружность ):
У меня 82 см
Измерение по кругу ( диаметр ):
У меня 26 см
Разделить:
82 см / 26 см = 3,1538…
Это довольно близко к π. Может быть, если бы я измерил более точно?
Использование Пи
Мы можем использовать π, чтобы найти Окружность, когда мы знаем Диаметр
Длина окружности = π × диаметр
Пример: Вы идете по кругу диаметром 100 м, какое расстояние вы прошли?
Пройденное расстояние = Окружность
= π × 100 м
= 314,159. .. м
.. м
= 314 м (с точностью до м)
Также мы можем использовать π, чтобы найти Диаметр, когда мы знаем Окружность
Диаметр = Окружность / π
Пример: Сэм измерил 94 мм по внешней стороне трубы… каков ее диаметр?
Диаметр = Окружность / π
= 94 мм / π
= 29,92… мм
= 30 мм (с точностью до миллиметра)
Радиус
Радиус равен половине диаметра, поэтому мы также можем сказать:
Для круга с радиусом из 1
Расстояние на полпути вокруг окружности равно π = 3,14159265…
Цифры
π примерно равно:
3.14159265358979323846…
Цифры идут беспорядочно.
π было рассчитано с точностью до 100 триллионов знаков после запятой, и все же нет шаблона в цифрах, см. Pi Normal.
Приблизительно
Быстрое и простое приближение числа π равно 22/7
22/7 = 3,1428571. ..
..
Но, как видите, 22/7 — это не совсем правильно . На самом деле π не равно отношению любых двух чисел, что делает его иррациональным числом.
Действительно хорошее приближение, лучше, чем 1 часть на 10 миллионов:
355/113 = 3,1415929…
(представьте «113355», косую черту в середине «113/355», затем переверните «355/113»)
Резюме:
| 22/7 | = | 3,14 28571… |
| 355/113 | = | 3.141592 9… |
| № | = | 3.14159265 … |
Запоминание цифр
Обычно я просто запоминаю «3.14159», но вы также можете посчитать буквы:
«Можно мне сегодня большой контейнер масла»
3 1 4 1 5 9 2 6 5
До 100 знаков после запятой
Вот число π с первыми 100 знаками после запятой:
3. 14159265358979323846264338327950288 14159265358979323846264338327950288 4197169399375105820974944592307816 406986704608998825380 |
Самостоятельное вычисление числа Пи
Существует много специальных методов, используемых для вычисления числа π, и вот один из них, который вы можете попробовать самостоятельно: он называется Нилакантха, серия (в честь индийского математика, жившего в 1444–1544 годах).
Это продолжается вечно и имеет следующую схему:
3 + 4 2×3×4 − 4 4×5×6 + 4 6×7×8 − 4 8×9×10 + …
(Обратите внимание на шаблон + и -, а также на шаблон чисел под строками.)
Это дает следующие результаты:
| Термин | Результат (до 12 знаков после запятой) |
|---|---|
| 1 | 3 |
| 2 | 3,166666666667 |
| 3 | 3. 133333333333 133333333333 |
| 4 | 3.145238095238 |
| … | … и т.д.! … |
Возьмите калькулятор (или используйте электронную таблицу) и посмотрите, сможете ли вы добиться лучших результатов.
День Пи
День Пи отмечается 14 марта. Март — 3-й месяц, поэтому он выглядит как 14 марта
5839,5050,5052,1745,2106,5473,5477,1744,3236,3237
Упражнение: Найдите приблизительное значение числа Пи
Column Pi (отношение длины окружности к ее диаметру)
Все окружности подобны, и «длина окружности, деленная на диаметр», дает одно и то же значение независимо от их радиуса. Эта величина представляет собой отношение длины окружности к ее диаметру и называется π (Пи). Эта константа появляется при вычислении площади круга и является типом иррационального числа, известного как трансцендентное число , которое не может быть выражено ни дробью, ни каким-либо подкоренным знаком, таким как квадратный корень, или их комбинацией. . Число имеет бесконечное количество знаков после запятой, а именно 3,14159.26535…, и теперь компьютеры вычислили его с точностью до 5 триллионов знаков после запятой.
. Число имеет бесконечное количество знаков после запятой, а именно 3,14159.26535…, и теперь компьютеры вычислили его с точностью до 5 триллионов знаков после запятой.
Длина окружности больше 6 от указанной на рисунке. Поскольку диаметр круга равен 2, число Пи больше 3.
Что касается значения π, древние цивилизации использовали свое собственное значение. Так как правильный шестиугольник, вписанный в окружность радиусом 1, имеет периметр 6, то получается, что число Пи больше 3. В Древнем Египте получили приближение
(примерно, 3,16)
путем размещения правильного восьмиугольника на окружности, а в древней Вавилонии использовали
.
Архимед в своей работе Kyklu metresis (мера окружности) пришел к выводу, что Пи удовлетворяет
.
В древней Индии мы можем найти пример использования =3,1622776 или
.
В Китае они использовали
или
или
для Pi.
В период Эдо в Японии, 9 г.0245 Jinkoki (1627) Ёсида Мицуёси использовал 3,16 для числа Пи, но поскольку люди признали, что это значение было неточным, в которые были рассчитаны более точные значения для Pi, начали развиваться. Ученые-васан, такие как Мурамацу Шигекиё, Секи Такакадзу, Камата Тошикиё, Такебе Катахиро и Мацунага Йошисуке, рассчитали более точные значения числа Пи и достигли результатов, которые можно сравнить с европейской математикой.
в Европе, Viete (1540-1603) обнаружила первую формулу, которая выражает π:
После этого Wallis (1616-1703) Формула:
. 1675) и Лейбниц (1646-1716) Формула:
Кроме того, Ньютон (1642-1727) и Эйлер (1707-1783) открыли ряд, который сходится быстрее, что позволило им вычислить значения числа Пи с большей точностью места. Если использовать соотношение
, обнаруженный Дж. Мачином (1680-1752),
, мы можем получить значение 3,14159 для π с точностью до пяти знаков после запятой с первыми 4 членами разложения Тейлора tan -1 . В недавнем компьютерном расчете , использовались следующие уравнения:
В недавнем компьютерном расчете , использовались следующие уравнения:
или
* tan -1 : Арктангенс. Обратная функция тангенса.
Вычисление Пи в Васане
В конце Санпо сёдзё появляется метод вычисления Пи. Подводя итог тому, что описано в книге, метод выглядит следующим образом: Предположим, исходное число = 3, 9.0003
Продолжайте до тех пор, пока не будет создана разница 100. Затем Пи получается путем сложения исходного числа, разности 1, разности 2, разности 3… и так далее. Переписывая это как математическое выражение, мы видим, что оно имеет следующую закономерность:
«Кю энсю хидзюцу киген» (Происхождение тайного искусства нахождения Пи) из Санпо сёдзё
Санпо сёдзё
В книге утверждается, что этот метод является прямым и ясным решением вычисления Пи без использования Kakujutsu или Kaiho (эволюция), но не объясняет, почему это формула для вычисления числа π.
Цифровые коллекции NDL
Эта формула аналогична формуле, описанной в Hoen sankei (1739) Мацунаги Ёсисуке. Формирование этой формулы также включено в Koshigen koutei (1819) Нинчжоу.
В эпоху Мэйдзи Кикути Дайроку опубликовал четыре статьи на английском языке, в которых вводил вычисление числа Пи в васан в Токио сугаку бусури гаккай кидзи Том. 7 (1896 г.). В первом трактате он представил вычисление в Sanpo kyuseki tsuko (1844) Хасэгавы Хирому и объяснил Enrikatsujutsu , тип исчисления, первоначально начатый Вада Ясуси (1787-1840) с западными расчетными формулами.
«Какова площадь круга диаметром 1?» from Sanpo kyuseki tsuko
Санпо Кюсэки Цуко
В этой книге
он получает площадь круга с диаметром 1 и находит Пи, разделив площадь на 4. В этом вычислении, используется.
Цифровые коллекции NDL
При увеличении n для (сумма степеней натуральных чисел),
верно; Хасэгава использует это, чтобы получить результат
Мы ничего не знаем о регулярности числа только из этого результата. Однако на самом деле между терминами существует связь. Каждый член определяется путем умножения предыдущего члена на правильную дробь следующим образом:
Однако на самом деле между терминами существует связь. Каждый член определяется путем умножения предыдущего члена на правильную дробь следующим образом:
Кикучи заметил, что такой ряд был тем, что К. Ф. Гаусс (1777-1855) назвал гипергеометрическим рядом . Гипергеометрическая серия определяется следующим образом:
Следовательно, Kikuchi доказал в следующей статье, что расчет
в Enri Shinko Wada Yasushi был эквивалентен
Hasegawa’s Calculation
Hasegawa’s Calculation
. на
и что Мацунага
был эквивалентен
.
В Васан, Секи Такакадзу, Такебе Катахиро и др. искали формулы для вычисления π 2 .
, выведенная Такебе, является первой формулой для вычисления Пи в истории Васана. С помощью этой формулы Такебе вычислил число π с точностью до 41 знака после запятой. В следующем трактате Кикучи вывел
В следующем трактате Кикучи вывел
, чтобы выразить квадрат s или дугу окружности со стрелой c и диаметром d , который был описан Ямадзи Нусидзуми в Kenkon no maki (c 1765), и доказано
, потому что
когда
.
Дуга, стрела и диаметр окружности
На рисунке часть окружности называется ko (дуга), отрезок AB называется gen (хорда), а отрезок PR — ya (сагитта). Диаметр PQ по-японски называется kei.
Когда мы рисуем хорду для дуги PB и сагитту для хорды и продолжаем повторять этот процесс с более короткими хордами, форма, полученная путем соединения этих хорд, приближается к форме круга. Таким образом, Ямадзи вычисляет s, длину дуги, когда диаметр равен d и длина сагитты c .
В последней статье он доказал, что
, полученное Адзимой Наонобу в Kohai jutsukai , может быть упрощено до
В следующем году Кикучи также написал статью, в которой представил метод вычисления длины дуга, созданная Такебе Катахиро в Tokyo Sugaku Butsuri Gakkai Kiji Vol.

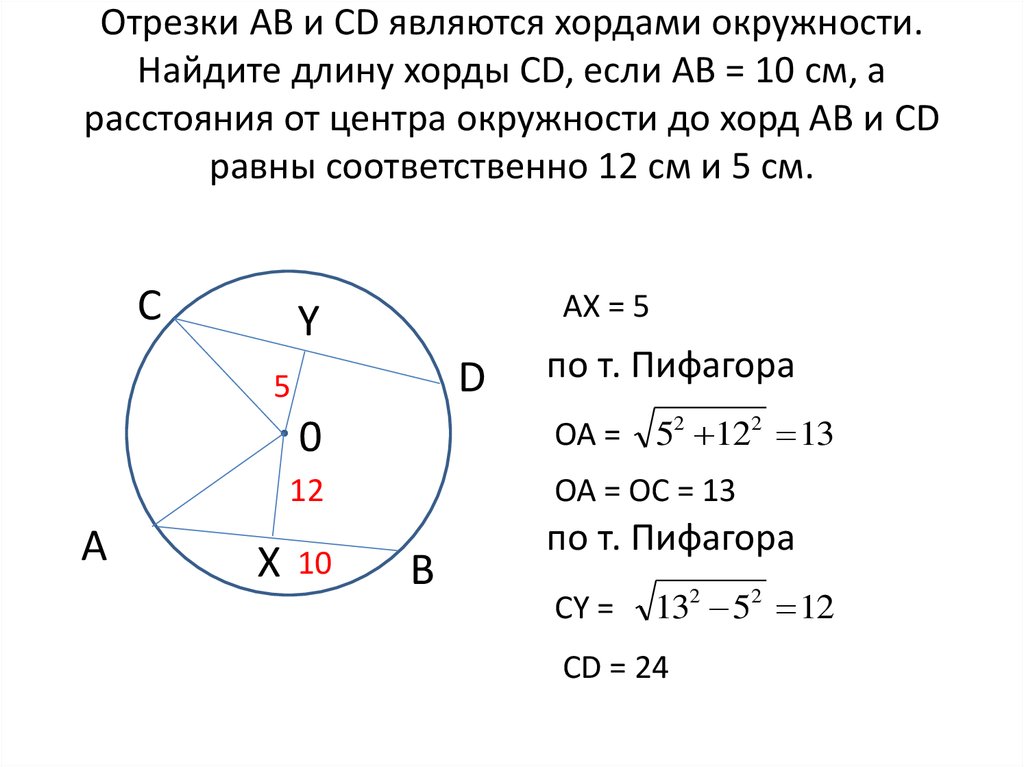
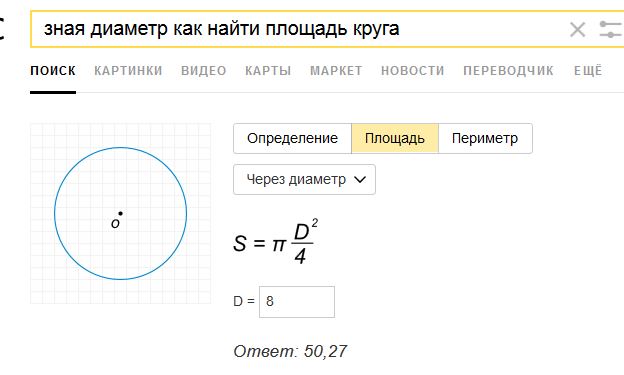 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R.

 Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза — как с. Что касается радиуса вписанной окружности, то он обозначается как r.
Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза — как с. Что касается радиуса вписанной окружности, то он обозначается как r. Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
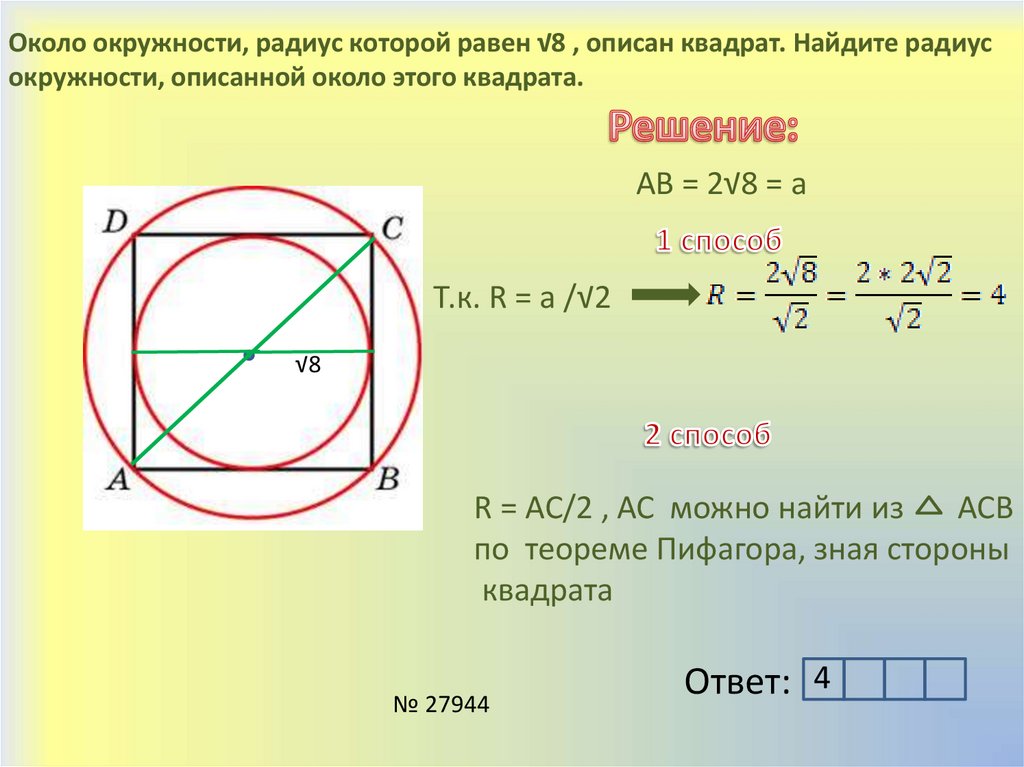
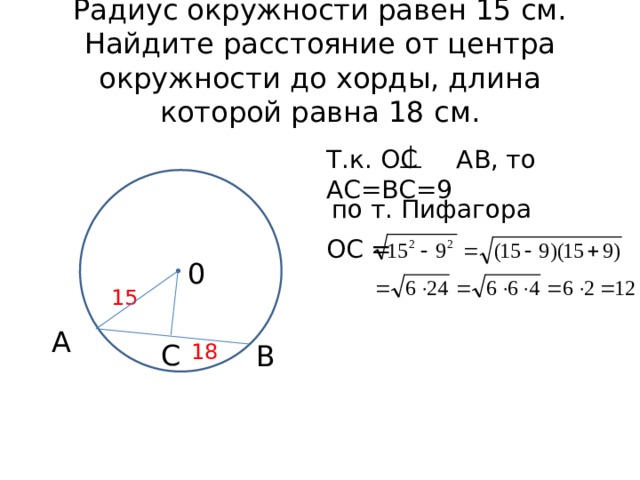
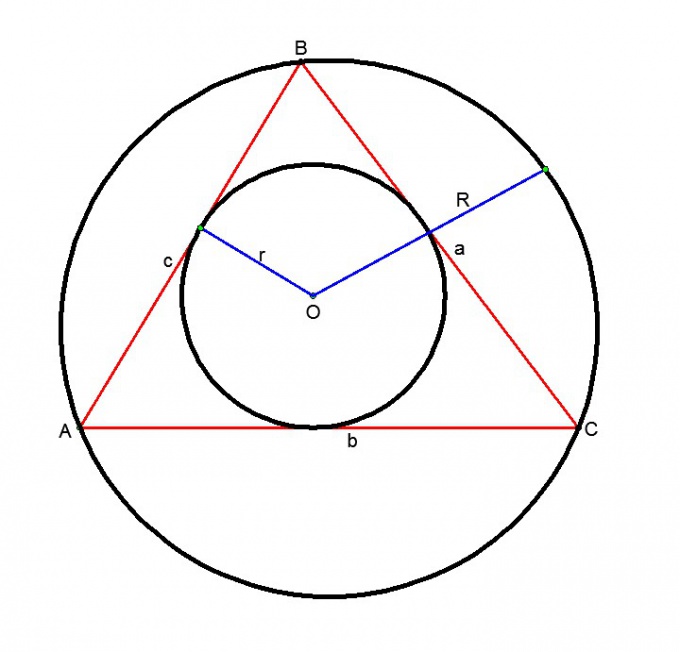 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l. 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
