заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга.
Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания. Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте).
Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения. Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике.
И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
Решение высшей математики онлайн
‹— Назад
Пусть — внутренняя точка области , и в области задана функция . Рассмотрим ограничение функции на прямую , проходящую через точку параллельно оси . Эта прямая задаётся условиями при ; переменная может при этом произвольно меняться. Поэтому для рассматриваемого ограничения имеется естественная параметризация, смысл которой в том, что «замораживаются» все переменные, от которых зависит , кроме :
Получили функцию одного переменного , как параметризацию ограничения с помощью параметра .
Рис.
7.12.
Функция может иметь производную в точке , равную некоторому числу . Это число называют частной производной функции по переменной , вычисленной в точке . Эта частная производная обозначается или .
Сразу же заметим, что значения частных производных от функции в точке , вычисленные по разным переменным и , могут быть различными, так что обозначение типа , без указания переменной, по которой вычислена частная производная, не имеет смысла: в обозначении обязательно нужно указывать переменную, по которой мы дифференцируем.
Итак, чтобы вычислить частную производную от функции по некоторой переменной , нужно фиксировать значения всех переменных, кроме (то есть временно считать их постоянными), а затем по обычным правилам вычисления производных найти производную по этой единственной переменной . Теперь ясно, что для вычисления частных производных никаких новых правил дифференцирования вдобавок к тем, что известны нам для функций одной переменной, не потребуется, ведь при вычислении частной производной мы считаем, что может изменяться только одна переменная.
Считая точку , в которой вычисляется значение частной производной , переменной точкой области и предполагая, что во всех точках эта производная существует, мы получаем, что частная производная — это функция, заданная в области (или в её части, если производная существует не везде в ).
Поскольку частную производную функции можно вычислять по каждой из переменных , то функция имеет частных производных
Эти частные производные, вообще говоря, — различные функции. Их называют также частными производными первого порядка от функции . Итак, функция переменных имеет частных производных первого порядка.
Пример 7.11 Вычислим частные производные функции двух переменных
по каждой из переменных и .
Производную по найдём, считая переменной, а постоянной величиной:
При этом мы воспользовались тем, что производная суммы равна сумме производных, тем, что производная от (по ) равна , тем, что производная от (по , при постоянном значении ) равна , тем, что производная от (по ) равна 3, и, наконец, тем, что производная постоянного слагаемого равняется 0.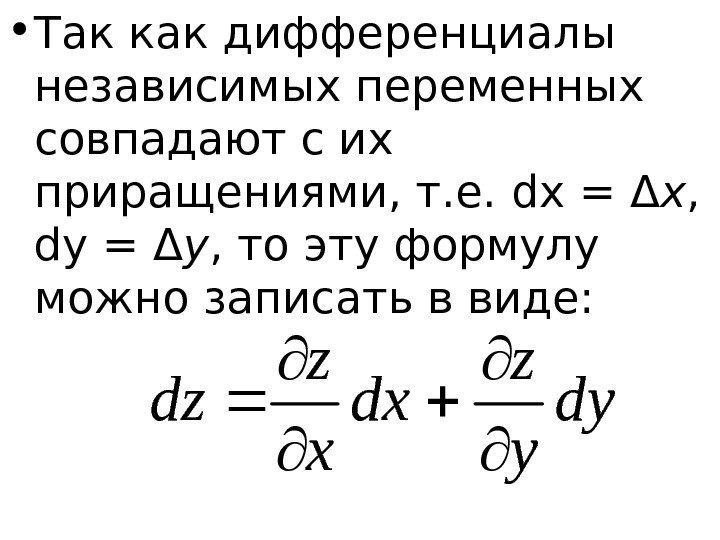
Аналогично найдём производную по переменной . При этом мы считаем, что — постоянная, а меняется только , по которой мы и находим производную:
При этом слагаемые и постоянны, и их производная по равна 0; в слагаемом множитель постоянный, и его можно вынести за знак производной, а производная от равна ; наконец, производная от равняется .
В соответствии с изученным в первом семестре смыслом производной функции одного переменного (напомним, что производная функции равна скорости изменения значений функции в точке ), cмысл частной производной — это скорость изменения значений функции при равномерном движении с единичной скоростью через точку по прямой , параллельной оси .
Геометрический смысл частной производной также становится ясен, если рассмотреть ограничение функции , полученное при фиксации значений всех переменных, кроме . Для наглядности ограничимся случаем функции двух переменных и .
В этом случае мы можем изобразить график функции на чертеже в виде некоторой поверхности.
Рис.7.13.
Отметим на плоскости точку , в которой вычисляется частная производная , и рассмотрим сечение графика вертикальной плоскостью ; она проходит на плоскости через прямую , заданную тем же уравнением . Тогда эта плоскость высекает в поверхности графика линию, служащую графиком функции . Функция — это функция одной переменной , и её производная в точке равна тангенсу угла наклона касательной, проведённой к графику в точке . С другой стороны, . Значит, частная производная имеет геометрический смысл как тангенс угла наклона касательной к сечению графика вертикальной плоскостью .
Точно так же, частная производная имеет геометрический смысл как тангенс угла наклона касательной к сечению графика вертикальной плоскостью .
Заметим, что плоскости и взаимно перпендикулярны.
Если функция одного переменного имеет производную в некоторой точке, то эта функция обязательно непрерывна в этой точке; этот факт мы изучили в первом семестре. В случае нескольких переменных ( ) дело обстоит не так. Даже наличия в некоторой точке частных производных функции по всем переменным не достаточно для того, чтобы функция была непрерывной в точке . Приведём пример такой функции двух переменных, что частные производные её сушествуют, а функция, тем не менее, разрывна.
Пример 7.12 Рассмотрим функцию, заданную при :
Эта функция разрывна в точке , поскольку в любой, как угодно малой окрестности начала координат имеются точки вида , где , в которых значение функции равно
а также точки вида , где , в которых значение функции равно
а значение равно 0.
Однако ограничение функции как на прямую , так и на прямую , проходящие через начало координат, тождественно равно 0:
так что и производные от этих ограничений в точке 0 равны 0, то есть
Итак, обе частные производные в начале координат существуют, но функция разрывна в начале координат.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
x y производная по x
Вы искали x y производная по x? На нашем сайте вы можете получить ответ на любой математический вопрос здесь.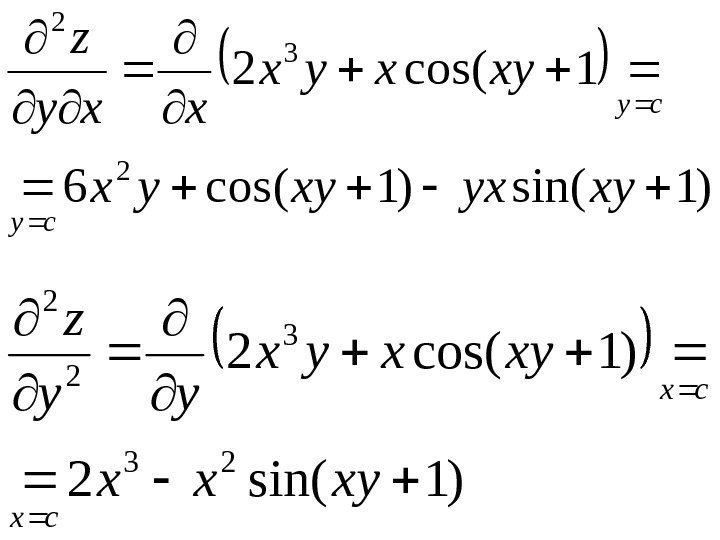
Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычисление частных производных онлайн, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение.
Например, «x y производная по x».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как x y производная по x,вычисление частных производных онлайн,как найти частную производную,как найти частные производные,калькулятор производных нескольких переменных онлайн,калькулятор производных онлайн нескольких переменных,калькулятор функции нескольких переменных онлайн,калькулятор частной производной онлайн,калькулятор частные производные,калькулятор частных производных,калькулятор частных производных онлайн,матпрофи частные производные,найти частную производную,найти частную производную онлайн,найти частные производные,найти частные производные второго порядка онлайн,найти частные производные второго порядка онлайн калькулятор,найти частные производные онлайн,найти частные производные онлайн с решением,найти частные производные первого порядка,найти частные производные первого порядка онлайн с решением,найти частные производные функции,найти частные производные функции онлайн с решением,нахождение частной производной онлайн,нахождение частных производных,нахождение частных производных онлайн,онлайн вычисление частных производных,онлайн калькулятор производные высших порядков,онлайн калькулятор производных нескольких переменных,онлайн калькулятор функции нескольких переменных,онлайн калькулятор частной производной,онлайн калькулятор частные производные,онлайн калькулятор частных производных,онлайн нахождение частных производных,онлайн решение частных производных,онлайн частные производные функции,по x по y,примеры частная производная,примеры частные производные,производная x y по y,производная двух переменных,производная двух переменных онлайн,производная нескольких переменных,производная онлайн двух переменных,производная онлайн от двух переменных,производная онлайн по x и y,производная от двух переменных,производная от двух переменных онлайн,производная по x и y онлайн,производная функции двух переменных,производная функции двух переменных онлайн,производное частное,производные частные примеры,решение онлайн частных производных,решение частных производных,решение частных производных онлайн,таблица частных производных,функции нескольких переменных калькулятор онлайн,функции нескольких переменных онлайн калькулятор,функции нескольких переменных частные производные,частная производная,частная производная онлайн,частная производная онлайн калькулятор,частная производная функции,частная производная что такое,частная производная это,частное производное,частные производные,частные производные 2 порядка,частные производные второго порядка,частные производные второго порядка онлайн,частные производные второго порядка онлайн калькулятор,частные производные для чайников,частные производные калькулятор,частные производные калькулятор онлайн,частные производные матпрофи,частные производные онлайн,частные производные онлайн калькулятор,частные производные онлайн калькулятор с подробным решением,частные производные первого и второго порядка,частные производные первого порядка,частные производные первого порядка калькулятор онлайн,частные производные первого порядка онлайн калькулятор,частные производные примеры,частные производные примеры с решением,частные производные функции,частные производные функции двух переменных,частные производные функции нескольких переменных,частные производные функции онлайн,частные производные функции с тремя неизвестными,что такое частная производная.
Решить задачу x y производная по x вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Частные производные различных порядков
Используй поиск, чтобы найти научные материалы и собрать список литературы
База статей справочника включает в себя статьи написанные экспертами Автор24, статьи из научных журналов и примеры студенческих работ из различных вузов страны
Определение 1
Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$ в данной области.
Обозначение: $z=f(x,y)$.
Пусть дана функция $z=f(x,y)$двух независимых переменных $(x,y)$.
Замечание 1
Так как переменные $(x,y)$ являются независимыми, то одна из них может изменяться, а другая при этом сохранять постоянное значение.
Дадим переменной $x$ приращение $\Delta x$, при этом сохраним значение переменной $y$ неизменным.
Тогда функция $z=f(x,y)$ получит приращение, которое будет называться частным приращением функции $z=f(x,y)$ по переменной $x$.
Обозначение:
\[\Delta _{x} z=f(x+\Delta x,y)-f(x,y)\]
Пример 1
Частная производная по переменной $x$ от заданной функции $z=f(x,y)$ — это предел отношения частного приращения $\Delta _{x} z$ заданной функции к приращению $\Delta x$ при $\Delta x\to 0$.
Обозначение: $z’_{x} ,\, \, f’_{x} (x,y),\, \, \frac{\partial z}{\partial x} ,\, \, \frac{\partial f}{\partial x} $.
Замечание 2
По определению частной производной имеем:
\[\frac{\partial z}{\partial x} =\mathop{\lim }\limits_{\Delta x\to 0} \frac{\Delta _{x} z}{\Delta x} =\mathop{\lim }\limits_{\Delta x\to 0} \frac{f(x+\Delta x,y)-f(x,y)}{\Delta x} .
\]
Дадим переменной $y$ приращение $\Delta y$, при этом сохраним значение переменной $x$ неизменным.
Тогда функция $z=f(x,y)$ получит приращение, которое будет называться частным приращением функции $z=f(x,y)$ по переменной $y$.
Обозначение:
\[\Delta _{y} z=f(x,y+\Delta y)-f(x,y).\]
Определение 2
Частная производная по переменной $y$ от заданной функции $z=f(x,y)$ — это предел отношения частного приращения $\Delta _{y} z$ заданной функции к приращению $\Delta y$ при $\Delta y\to 0$.
Обозначение: $z’_{y} ,\, \, f’_{y} (x,y),\, \, \frac{\partial z}{\partial y} ,\, \, \frac{\partial f}{\partial y} $.
Замечание 3
По определению частной производной имеем:
\[\frac{\partial z}{\partial y} =\mathop{\lim }\limits_{\Delta y\to 0} \frac{\Delta _{y} z}{\Delta y} =\mathop{\lim }\limits_{\Delta y\to 0} \frac{f(x,y+\Delta y)-f(x,y)}{\Delta y} .\]
Определение 3
Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Обозначение: $w=f(x,y,z)$.
Определение 4
Если для каждой совокупности $(x,y,z,…,t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z,…,t)$ в данной области.
Обозначение: $w=f(x,y,z,…,t)$.
Для функции от трех и более переменных, аналогично как для функции двух переменных определяются частные производные по каждой из переменных:
$\frac{\partial w}{\partial z} =\mathop{\lim }\limits_{\Delta z\to 0} \frac{\Delta _{z} w}{\Delta z} =\mathop{\lim }\limits_{\Delta z\to 0} \frac{f(x,y,z+\Delta z)-f(x,y,z)}{\Delta z} $;
$\dots$ ;
$\frac{\partial w}{\partial t} =\mathop{\lim }\limits_{\Delta t\to 0} \frac{\Delta _{t} w}{\Delta t} =\mathop{\lim }\limits_{\Delta t\to 0} \frac{f(x,y,z,…,t+\Delta t)-f(x,y,z,…,t)}{\Delta t} $.
Рассматривая частные производные функции двух переменных, можно отметить, что они являются функциями от переменных $x$ и $y$.
{2} \partial x} =(6y)’_{x} =0.\]
Поочередно выполняя дифференцирование частных производных далее, можно получить частные производные порядка $n$.
Обозначение:
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 21.04.2022
Выполнение любых типов работ по математике
Решение задач по комбинаторике на заказ Решение задачи Коши онлайн Математика для заочников Контрольная работа на тему числовые неравенства и их свойства Контрольная работа на тему умножение и деление рациональных чисел Контрольная работа на тему действия с рациональными числами Дипломная работа на тему числа Курсовая работа на тему дифференциальные уравнения Контрольная работа на тему приближенные вычисления Решение задач с инвариантами
Подбор готовых материалов по теме
Дипломные работы Курсовые работы Выпускные квалификационные работы Рефераты Сочинения Доклады Эссе Отчеты по практике Решения задач Контрольные работы
Онлайн калькулятор: Аппроксимация функции одной переменной
Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную.
Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.
Если не ввести значения x, калькулятор примет, что значение x меняется от 0 с шагом 1.
Аппроксимация функции одной переменной
83 71 64 69 69 64 68 59 81 91 57 65 58 62
Значения x, через пробел
183 168 171 178 176 172 165 158 183 182 163 175 164 175
Значения y, через пробел
Линейная аппроксимация
Квадратичная аппроксимация
Кубическая аппроксимация
Аппроксимация степенной функцией
Показательная аппроксимация
Логарифмическая аппроксимация
Гиперболическая аппроксимация
Экспоненциальная аппроксимация
Точность вычисления
Знаков после запятой: 4
Линейная регрессия
Коэффициент линейной парной корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Квадратичная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Кубическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Степенная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Показательная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Логарифмическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Гиперболическая регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Экспоненциальная регрессия
Коэффициент корреляции
Коэффициент детерминации
Средняя ошибка аппроксимации, %
Результат
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.
Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.
Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.
Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.
Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:
Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.
Используя формулу производной сложной функции, получим следующую систему уравнений:
Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.
«Классификация линейных дифференциальных уравнений в частных производных второго порядка и приведение их к каноническому виду»
Курсовая работа
по дисциплине «Математический анализ»
на тему «Классификация линейных дифференциальных уравнений в частных производных второго порядка и приведение их к каноническому виду»
Направление
подготовки — 44.
04.01 Педагогическое образование
Профиль подготовки — Математика
Выполнил студент: __________ Ладышева С.А.
(подпись, дата) (Ф.И.О.)
Группа: 20ЗФПМм1
Руководитель:
к.ф.-м.н., доцент Яремко Н.Н
(подпись, дата) (Ф.И.О.)
Работа защищена с оценкой __________
Преподаватели __________
__________
Дата защиты __________
Пенза, 2020
Содержание
Введение……………………………………………………………………3
1.
Основные определения теории
уравнений в частных производных……………………………………………………………………..4
2. Классификация дифференциальных уравнений в частных производных второго порядка…………………………………………………9
3. Приведение линейных дифференциальных уравнений в частных производных второго порядка к каноническому виду………………………12
4. Примеры решения линейных дифференциальных уравнений в частных производных второго порядка………………………………………17
Заключение………………………………………………………………22
Список литературы………………………………………………………23
Введение
Изучением дифференциальных уравнений в частных производных занимается математическая физика. Основы теории этих уравнений впервые были изложены в знаменитом «Интегральном исчислении» Л. Эйлера.
Классические уравнения математической физики являются линейными.
Особенность линейных уравнений состоит в том, что если U и V –
два решения, то функция aU + bV при любых
постоянных a и b снова
является решением.
Это обстоятельство позволяет построить общее решение
линейного дифференциального уравнения из фиксированного набора его элементарных
решений и упрощает теорию этих уравнений.
Современная общая теория дифференциальных уравнений занимается главным образом линейными уравнениями и специальными классами нелинейных уравнений. Основным методом решения нелинейных дифференциальных уравнений в частных производных выступает численное интегрирование.
В работе рассматриваются понятия линейных дифференциальных уравнений второго порядка. Особое внимание уделяется изучению линейных дифференциальных уравнений с постоянными коэффициентами.
Решением дифференциального уравнения называется n раз дифференцируемая функция, удовлетворяющая уравнению во всех точках своей области определения.
Обычно существует целое множество
таких функций, и для выбора одного из них требуется наложить на него
дополнительные условие: например, потребовать, чтобы решение принимало в данной
точке данное значение.
1. Основные определения теории уравнений в частных производных
Теория дифференциальных уравнений – раздел математики, который занимается изучением дифференциальных уравнений и связанных с ними задач. Её результаты применяются во многих естественных науках, особенно широко – в физике.
Неформально говоря, дифференциальное уравнение – это уравнение, в котором неизвестной величиной является некоторая функция. При этом в самом уравнении участвует не только неизвестная функция, но и различные производные от неё. Дифференциальным уравнением описывается связь между неизвестной функцией и её производными. Такие связи обнаруживаются в самых разных областях знания: в механике, физике, химии, биологии, экономике и др.
Различают обыкновенные
дифференциальные уравнения (ОДУ) и дифференциальные уравнения в частных
производных (УРЧП). Существуют также стохастические дифференциальные уравнения
(СДУ), включающие случайные процессы [18, c.
28].
Первоначально дифференциальные уравнения возникли из задач механики, в которых участвовали координаты тел, их скорости и ускорения, рассматриваемые как функции времени.
Одно из простейших применений дифференциальных уравнений – решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения. Например, в соответствии со вторым законом Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид. Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки [16, c. 45].
Пусть – некоторая неизвестная функция и т.д. ее частные производные различного порядка.
Рассмотрим уравнение
(1)
связывающие независимые переменные х,
у, искомую функцию u(х, у) и ее
частные производные различного порядка. Уравнение (1) называют дифференциальным
уравнением в частных производных.
Порядок уравнения определяется наивысшим порядком частной производной, входящей в это уравнение.
Примеры.
1) – дифференциальное уравнение первого порядка.
2) – дифференциальное уравнение второго порядка и т.п.
Решением дифференциального уравнения называется любая функция u(х, у), обращающая его в тождество. Задачи, связанные с решением дифференциального уравнения в частных производных, как правило, более сложные по сравнению с задачами для обыкновенных дифференциальных уравнений [18, c. 180].
Мы знаем, что общее решение обыкновенных дифференциальных уравнений n-го порядка зависит от n произвольных постоянных С1, С2, …, Сn. Более сложная ситуация складывается при решении дифференциальных уравнений в частных производных. Например, решением дифференциального уравнения является любая функция т.е. общее решение зависит от бесконечного числа функций, зависящих только от одной переменной
Или
Предмет теории уравнений в частных
производных составляет изучение дифференциальных уравнений, описывающих то или
иное явление природы, по преимуществу физической.
Наш курс будет посвящен по
преимуществу уравнениям в частных производных второго порядка.
В связи с этим рассмотрим некоторые физические задачи, приводящие к решению дифференциальных уравнений в частных производных [5, c. 58].
Теория дифференциальных уравнений является одним из самых больших разделов современной математики. Чтобы охарактеризовать ее место в современной математической науке, прежде всего, необходимо подчеркнуть основные особенности теории дифференциальных уравнений, состоящей из двух обширных областей математики: теории обыкновенных дифференциальных уравнений и теории уравнений с частными производными.
Первая особенность – это
непосредственная связь теории дифференциальных уравнений с приложениями.
Характеризуя математику как метод проникновения в тайны природы, можно сказать,
что основным путем применения этого метода является формирование и изучение
математических моделей реального мира. Изучая какие-либо физические явления,
исследователь, прежде всего, создает его математическую идеализацию или,
другими словами, математическую модель, то есть, пренебрегая второстепенными
характеристиками явления, он записывает основные законы, управляющие этим
явлением, в математической форме.
Очень часто эти законы можно выразить в виде
дифференциальных уравнений. Такими оказываются модели различных явлений
механики сплошной среды, химических реакций, электрических и магнитных явлений
и др. [5, c. 60].
Исследуя полученные дифференциальные
уравнения вместе с дополнительными условиями, которые, как правило, задаются в
виде начальных и граничных условий, математик получает сведения о происходящем
явлении, иногда может узнать его прошлое и будущее. Изучение математической
модели математическими методами позволяет не только получить качественные
характеристики физических явлений и рассчитать с заданной степенью точности ход
реального процесса, но и дает возможность проникнуть в суть физических явлений,
а иногда предсказать и новые физические эффекты. Бывает, что сама природа
физического явления подсказывает и подходы, и методы математического
исследования. Критерием правильности выбора математической модели является
практика, сопоставление данных математического исследования с
экспериментальными данными.
Постановка задач для уравнений в частных производных включает определение самого уравнения (или системы нескольких уравнений), а также необходимого количества краевых условий (число и характер задания которых определяется спецификой уравнения). По своему названию уравнения должны содержать частные производные неизвестной функции и (или нескольких функций, если уравнений несколько) по различным аргументам, например пространственной переменной х и времени t. Соответственно, для решения задачи требуется вычислить функцию нескольких переменных, например u < x,t) в некоторой области определения аргументов 0 < х < L и 0 < t < T. Граничные условия определяются как заданные временные зависимости функции и, или производных этой функции на границах расчетной области 0 и L, а начальные – как заданная u(х, 0) [5, c. 65].
Сами уравнения в частных производных (несколько условно) можно разделить на три основных типа [5, c. 68]:
— параболические (пример: ) – содержащие первую производную по одной переменной и вторую – по другой, причем все эти производные входят в уравнение с одинаковым знаком;
— гиперболические (пример: ) – содержащие первую производную по одной переменной и вторую – по другой, входящие в уравнение с разными знаками;
— эллиптические (пример: 1.
,)
– содержащие только вторые производные, причем одного знака.
Некоторые более сложные уравнения нельзя однозначно подогнать под приведенную классификацию, тогда говорят о гибридных типах уравнений.
Из курса обыкновенных дифференциальных уравнений известно, что решение дифференциального уравнения n-го порядка
(1)
определяется неоднозначно. Общее решение зависит от n произвольных постоянных и для однозначной разрешимости необходимо задать так называемые начальные условия
(2)
Решение задачи для уравнения (1) с начальными условиями (2) называется задачей Коши и при определенных условиях решение этой задачи существует и единственно [5, c. 78].
Более сложная ситуация складывается при рассмотрении дифференциальных уравнений в частных производных. В самом деле: общим решением простейшего уравнения является произвольная функция
Для того, чтобы сделать решение
определенным, нужно задать дополнительные условия, например, потребовать чтобы
неизвестная функция, а возможно и ее производные принимали заданные значения на
некоторых многообразиях.
Каждая задача математической физики ставится как задача
об отыскании решения некоторого уравнения при определенных дополнительных
условиях, которые в большинстве случаев диктуются ее физической постановкой [5,
c.
128].
2. Классификация дифференциальных уравнений в частных производных второго порядка
Дифференциальные уравнения в частных производных 2-го порядка не имеют единого метода численного решения. Поэтому следует рассмотреть их классификацию, позволяющую использовать единые методы для численного решения каждого из подтипов этих уравнений.
Введем обозначения (для сокращения и удобства письма):
.
Пусть дано уравнение
, (1)
где – заданные функции х, y.
Это уравнение называется линейным. Если ,
то уравнение называется линейным однородным, в противном случае
линейным неоднородным. Если все коэффициенты постоянные, то уравнение
называется линейным уравнением с постоянными коэффициентами.
Практика и теория подтверждает, что с помощью преобразования переменных данное дифференциальное уравнение остается линейным:
(2)
где коэффициенты [7]:
Спрашивается: нельзя ли выбрать переменные и так, чтобы в преобразованном уравнении (4.2) некоторые коэффициенты обратились в нуль? Эта возникшая задача связана с решением обыкновенного дифференциального уравнения, которое называется характеристическим для исходного с частными производными:
(3)
Его интегралы называются характеристиками.
Если – общий интеграл (4.3), то, положив , мы обратим в нуль коэффициент при .
Если – другой интеграл (4.3), линейно независим от , то полагают , тем самым в нуль обращают при .
Уравнение (4.3.) можно записать так:
.
(4)
Если , то и – действительные и различные. Делая замену, приводим уравнение к виду:
(5)
В этом случае говорят, что уравнение имеет гиперболический тип. Если положить , , то уравнение примет вид:
. (6)
Если , то имеем один общий интеграл . Пусть – любая функция, линейно независимая от , тогда: , и исходное уравнение будет иметь вид:
(7)
В этом случае говорят, что уравнение имеет параболический тип.
Если , то характеристическое уравнение имеет комплексно сопряженные интегралы:
и ,
и, положив уравнение приведем к виду:
, (8)
который называется эллиптическим.
Если коэффициенты линейного уравнения постоянные, то характеристическое уравнение имеет решение:
При уравнение приводится к виду:
или |
который называется гиперболическим.
При уравнение приводится к параболическому типу:
При уравнение приводится к эллиптическому типу:
3. Приведение линейных дифференциальных уравнений в частных производных второго порядка к каноническому виду
1) Рассмотрим уравнения гиперболического типа для (1).
Сведем его с помощью замены переменных к
.
Так как , выбираем , где – общий интеграл (2).
Тогда
Аналогично
, тогда
Получаем канонический вид гиперболического уравнения
, где .
(3)
Введем еще одну замену:
; ;
; .
Посчитаем производные:
, ; ;
, ; .
В итоге получаем
, где . (4)
2) Уравнения параболического типа ().
Поскольку , .
Характеристическое уравнение имеет одно решение
.
Пусть . Выберем новую переменную , что позволяет обратить коэффициент в 0. Вторую переменную берем произвольным образом
.
Подсчитаем .
, поскольку , ;
. В результате получаем
. (5)
Это каноническая форма уравнения параболического типа.
3) Эллиптические уравнения ).
В этом случае имеем
, , — комплексные общие интегралы. Представим
(6)
После замены переменных получаем
,
где
.
Совершим еще одну замену переменных
.
.
При второй замене переменных получаем
;
;
.
В итоге получаем ; .
Каноническая форма эллиптического ДУ имеет вид
, (7)
где .
Каноническая форма для уравнений гиперболического вида принимает вид (5), для уравнений параболического типа – (6), для уравнений эллиптического вида – (7).
В этих формулах — всевозможные комбинации из .
Рассмотрим уравнение (2), в котором являются постоянными величинами, и сведем его к канонической форме.
(2) , где
Используем замену
, ; .
Получим канонические формы следующего типа:
,
,
.
Существует преобразование, позволяющее упростить эти уравнения.
Введем функцию .
Константы и подбираются так, чтобы коэффициенты при первых производных обращались в ноль
,
,
1,
-1.
После подстановки этих производных в (1.7’) получаем
,
где .
Возьмем ; , в результате получаем
В результате получаем
. (8)
Аналогично, для (1.
8) и (1.9)
получаем
, (9)
(10)
где все и все постоянные величины.
Получили каноническую форму ДУ 2-го порядка с постоянными коэффициентами.
Будем считать, что искомая функция зависит от переменных
. В этом случае ДУ имеет
. (11)
Здесь ; .
Перейдем к другой системе координат:
.
Распишем в общем виде производные из (11)
вместо (11)
где
При замене переменных меняется матрица, составленная из коэффициентов при двух производных:
.
Существует линейное преобразование, приводящее матрицу квадратичной формы к диагональному виду, в котором
При линейных преобразованиях матрицы число диагональных элементов положительных, отрицательных или равных нулю сохраняется.
Предположим, что диагональных элементов матрицы коэффициентов больше нуля, а остальные – меньше (.
Тогда:
(12)
ДУ (12) является канонической формой
ДУ гиперболического типа.
Если диагональных элементов матрицы коэффициентов равны нулю, а остальные –не равны, тогда
(13)
Уравнение (13) – каноническая форма уравнений параболического типа.
При всех диагональных элементов матрицы коэффициентов равных единице имеем
(14)
Уравнение (14) представляет собой каноническую форму ДУ эллиптического типа.
4. Примеры решения линейных дифференциальных уравнений в частных производных второго порядка
Пример 1
Привести к каноническому виду уравнение:
Решение. Запишем, чему равны для нашего случая коэффициенты.
Так как: имеем уравнение параболического типа.
Характеристическое уравнение имеет вид:
Решая его, находим, что общий интеграл x – y = C.
Положим ,
а в качестве другой переменной возьмем .
При этом: Тогда
Подставляя значения частных производных в исходное уравнение, после простых преобразований получим:
.
Пример 2
Привести к каноническому виду уравнение:
Решение. т.е. имеем уравнение эллиптического типа. Составим уравнение характеристик: или .
Отсюда ; получаем два семейства комплексно сопряженных характеристик:
и .
Делаем замену переменных: ;
Подставив эти значения в исходное уравнение, получим
Пример 3
Привести к каноническому виду уравнение:
Решение. Здесь – уравнение гиперболического типа. Уравнение характеристик:
.
Отсюда
и .
Проинтегрировав эти уравнения, получим два семейства характеристик:
и .
Отсюда
и
т.е. получили уравнения характеристик. Вводим новые переменные: . Далее необходимо выразить частные производные по старым переменным через новые (требуется использовать правило дифференцирования сложной функции двух независимых переменных):
далее рекомендуется найти производные второго порядка самостоятельно в качестве упражнений и получить окончательный результат:
.
Получили уравнение канонического вида.
Пример 4.
Найти общее решение уравнения .
Характеристическое уравнение имеет корни ; .
Общее решение однородного уравнения .
Правая часть в данном случае: , где a =0, а т.к. ноль не является корнем характеристического уравнения, то ищем частное решение в виде многочлена первой степени: . Для нахождения коэффициентов подставим это решение и его производные ; в уравнение:; ;
Итак, частное решение имеет вид: .
Общее решение неоднородного уравнения:
.
Пример 5. Найти общее решение уравнения:
Корни характеристического уравнения: ;
; 3 – не является корнем характеристического уравнения- резонанса с правой частью нет, частное решение ищем в виде:
; находим ; ; .
.
Пример 6. ;
; ; ;
Общее решение однородного уравнения: ;
Однократный корень даёт резонанс
; находим ; ;
.
Пусть уравнение (1) имеет вид:
(2)
где — многочлены. Рассмотрим два случая:
а) Если число не является корнем характеристического уравнения, то частное решение уравнения (2) надо искать в виде
(3)
где – многочлены степени, равной наивысшей степени многочленов и .
б) Если число есть корень характеристического уравнения, то частное решение ищем в виде
(4)
Важный частный случай: если , где M, N – постоянные числа, т.е.
(5)
а) Если число — не является корнем характеристического уравнения, то частное решение ищем в виде
(6)
б) Если — корень характеристического уравнения, то частное решение уравнения (5) ищем в виде
(7)
Пример 7.
Найти общее решение уравнения: ;
Здесь ; ,
; ; ;;
.
Пример 8. Найти общее решение уравнения ;
Корни характеристического уравнения: ; корень – даёт резонанс с правой частью, ; ;
.
Пример 9. ; ;
Правой части соответствовал бы корень — но он не является корнем характеристического уравнения, резонанса нет:
; ; ; ;
.
Заключение
В рамках данной работы проведено изучение основных положений теории дифференциальных уравнений в частных производных, показана возможность применения вероятностных методов для их решения.
Многие
дифференциальные уравнения, с которыми сталкиваются физики, это уравнения
второго порядка (т.е. уравнения, содержащие вторые производные) Вообще говоря,
можно ожидать, что уравнение второго порядка имеет частные решения,
удовлетворяющие двум условиям; например, можно потребовать, чтобы
кривая-решение проходила через данную точку в данном направлении.
В случаях,
когда дифференциальное уравнение содержит некоторый параметр (число, величина
которого зависит от обстоятельств), решения требуемого типа существуют только
при определенных значениях этого параметра. Значения параметра, при которых
уравнение имеет особые решения, называются характеристическими или собственными
значениями; они играют важную роль во многих задачах.
В работе также проведено решение конкретных заданий, связанных с нахождением решения дифференциальных уравнений.
Дифференциальные уравнения имеют огромное прикладное значение, являясь мощным орудием исследования многих задач естествознания и техники: они широко используются в механике, астрономии, физике, во многих задачах химии, биологии. Это объясняется тем, что весьма часто законы, которым подчиняются те или иные процессы, записываются в форме дифференциальных уравнений, а сами эти уравнения, таким образом, являются средством для количественного выражения этих законов.
Список литературы
1.
Араманович И.Г., Левин В.И.
Уравнения математической физики. – М.: Наука, 1964.
2. Березин И.С., Жидков Н.П. Методы вычислений. – М.: Изд-во Государственной литературы, 1959. – 602 с.
3. Бицадзе А.В. Уравнения математической физики: Учеб. – М.: Наука, 1982. – 336 с.
4. Бицадзе А.В., Калиниченко Д.Ф. Сборник задач по уравнениям математической физики: Учеб. пособие. – М.: Наука, 1977. – 222 с.
5. Будак Б.М., Самарский А.А., Тихонов А.Н. Сборник задач по математической физике: Учеб. пособие. – М.: Наука, 1980. – 686 с.
6. Бусленко Н.П., Шрейдер Ю.А. Метод статистических испытаний (Монте-Карло) и его реализация в цифровых машинах. – М.: Физматгиз, 1961. – 315 с.
7. Владимиров В.С., Уравнения математической физики. – М., 1967. – 256с.
8. Голоскоков Д.П. Уравнения математической физики. Решение задач в системе Maple: учебник для вузов / Д. П. Голоскоков. – СПб.: Питер, 2004. – 539 с.
9. Демидович Б.П., Марон И.А., Шувалова Э.
Численные методы анализа.
– М.:Наука, 1967. – 368 с.
10. Канторович Л.В. и Крылов В.И., Приближённые методы высшего анализа, 5 изд., Л. – М., 1962. – 256с.
11. Карслоу Г.С., Теория теплопроводности, пер. с англ. – М.: Приор, – 2002.
12. Михайлов В.П. Дифференциальные уравнения в частных производных: Учеб.пособие. – М.: Наука, 1983. – 424 с.
13. Петровский И.Г., Лекции по теории интегральных уравнений, 3 изд., – М., 1999. – 213с.
14. Сдвижников О.А., Математика на компьютере: Maple8. – М.: Солон-Пресс, 2003. – 176 с.
15. Смирнов В.И. Курс высшей математики: Учеб.: В 4 т. Т.2. – М.: Наука, 1981. – 655 с.
16. Соболь И.М. Численные методы Монте-Карло. – М.: Наука, 1973. – 312 с.
17. Степанов В.В. Курс дифференциальных уравнений: учебник /В.В. Степанов. 11-е изд., исправленное. – М.: Издательство ЛКИ, 2016. – 512 с.
18.
Тихоненко А.В. Компьютерные
математические пакеты в курсе «Линейные и нелинейные уравнения физики».
–
Обнинск: ИАТЭ, 2005. – 80 с.
19. Тихонов А.А. Уравнения математической физики: учебное пособие /А.А. Самарский, А.Н. Тихонов. Изд. 7-е. – М.: Изд-во МГУ, 2004. – 798 с.
20. Тихонов А.Н., Самарский А.А. Уравнения математической физики: Учеб. пособие. – М.: Наука, 1977. – 735 с.
21. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям: учеб. пособие для вузов / А. Ф. Филиппов. 8-е изд. дополненное. – М.: Интеграл-пресс, 1998. – 208 с.
22. Хватцев А.А. Дифференциальные уравнения: учебное пособие / А.А. Хватцев. – Псков: Издательство ППИ, 2010. – 68 с.
23. Хватцев А.А. Математический анализ: конспект лекций / А.А. Хватцев. 2-е изд. – Псков: Издательство ППИ, 2008. – 131 с.
Калькулятор частных производных с шагами онлайн
Введение в калькулятор частных производных
Калькулятор частных производных с шагами находит производную кривой с многочисленными переменными онлайн. Этот калькулятор частных производных имеет возможность многократно дифференцировать функцию.
Измерение скорости изменения функции по отношению к одной переменной известно в математике как частные производные. Он обрабатывает такие переменные, как x и y, такие функции, как f(x), и модификации переменных x и y.
С калькулятором частных производных вы можете узнать о частных производных по цепному правилу и многое другое. Чтобы легко получить производные, можно воспользоваться бесплатным онлайн-калькулятором частичного дифференцирования.
Связанный: Вы также можете найти калькулятор неявного дифференцирования и калькулятор производных второго порядка, чтобы еще больше закрепить свои представления о производных и их вычислениях.
Процесс использования калькулятора частных производных второго порядка
Калькулятор частных производных вычисляет частную производную функции путем деления функции на части. Ниже приведен процесс использования калькулятора частичного дифференцирования с пошаговыми инструкциями.
Как вводить:
- Сначала напишите функцию дифференцирования или выберите из примеров.
- Теперь из выпадающего списка выберите производную переменную.
- Затем решите, сколько раз нужно дифференцировать данную функцию.
- Нажмите кнопку расчета, чтобы увидеть результаты.
Калькулятор второй частной производной мгновенно покажет вам пошаговые результаты и другие полезные показатели.
Вы также можете найти калькулятор производной по направлению для расчета производных по направлению.
Как калькулятор частичной дифференциации показывает выходные данные?
Первый калькулятор частных производных использует правила производных и формулы для вычисления частной производной этой функции.
В результатах он показывает производную (только для вычисления производной функции используйте калькулятор производной функции на домашней странице. Помимо этого калькулятор второй частной производной показывает возможные промежуточные шаги, трехмерные графики, альтернативные формы, правила, расширение ряда и неопределенный интеграл.
Вы также можете использовать неопределенный интеграл с шагами для большего обучения и практики.0007
Формулы, используемые калькулятором частных производных
Частная производная функции f(x,y) частично зависит от «x» и «y». Таким образом, формула для частной производной функции f(x,y) по x:
$$ \frac{∂f}{∂x} = \frac{∂f}{∂u}\frac{∂u}{∂x} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂x} $$
Аналогично, частная производная функции f(x,y) по y:
$$ \frac{∂f}{∂y} = \frac{∂f}{∂u}\frac{∂u}{∂y} \;+\; \frac{∂f}{∂v}\frac{∂v}{∂y} $$ 94) $$
Заключение:
Калькулятор частичного дифференцирования представляет собой веб-инструмент, который работает с математическими функциями и несколькими переменными. Благодаря этому становится легко решать и вычислять функции частичного дифференцирования. Решатель частичного дифференцирования показывает вам различные метрики и детали, необходимые для изучения этой концепции.
Связанный: На этом веб-сайте вы также можете найти калькулятор локальной линеаризации для нахождения линейной аппроксимации.
Каковы преимущества использования калькулятора первой частной производной?
Одним из основных преимуществ этого калькулятора является точность. Если вы находите производные вручную, возможно, вы застрянете посреди математической задачи и не сможете избавиться от нее в течение часа. Если вы используете инструмент частной производной, он дает точный результат одним щелчком мыши.
Что такое цепное правило в дифференциальных уравнениях?
По цепному правилу производная f (g (x)) равна f'(g (x)) g’ (x). Частные производные Калькулятор использует цепное правило для дифференциации составных функций.
Также на этом веб-сайте можно найти калькулятор цепного правила с несколькими переменными, чтобы найти производную от композиции двух дифференцируемых функций.
Чем полезен критерий частной производной второго порядка?
Вы можете использовать частные производные второго порядка, чтобы определить, является ли местоположение локальным максимумом, минимумом или седловой точкой.
Как только вы нашли нулевой наклон вектора многомерной функции, это указывает на то, что касательная плоскость графика в этой точке гладкая.
Мы надеемся, что приведенный выше калькулятор поможет вам в ваших расчетах. Существуют и другие связанные инструменты, такие как решатель правил продукта и калькулятор производных частных, которые вы можете использовать для большей практики и обучения.
Часто задаваемые вопросы
Уравнения в частных производных сложны?
Да, уравнения в частных производных решить сложно. Но когда эти уравнения преобразуются в обыкновенные дифференциальные уравнения, мы можем вычислять их другими методами или с помощью калькулятора в частных производных.
В чем разница между обыкновенными дифференциальными уравнениями и уравнениями в частных производных?
Обыкновенные дифференциальные уравнения (ОДУ) — это уравнения, в которых производные берутся по одной независимой переменной. Принимая во внимание, что дифференциальные уравнения в частных производных (УЧП) — это те уравнения, в которых производные берутся по более чем одной переменной.
Что такое частные производные первого порядка?
Производная функции многих переменных по независимой переменной один раз известна как частная производная первого порядка. В частной производной мы дифференцируем функцию с одной переменной, рассматривая другую как константу. Мы можем использовать калькулятор частных производных первого порядка, чтобы решить их онлайн.
Что такое непрерывные частные производные первого порядка?
Частная производная непрерывной функции известна как непрерывная частная производная, если производная также является непрерывной. Но для непрерывной функции вовсе не обязательно, чтобы ее производная также была непрерывной.
Что такое эллиптические уравнения в частных производных?
Уравнение в частных производных второго порядка (УЧП)
Au xx +2Bu xy +Cu yy +Du x +Fu y +G=0 считается эллиптической, если B 2 −AC
Вы можете использовать приведенный выше калькулятор уравнений в частных производных, чтобы решить свои уравнения онлайн.
Что такое цепное правило частичной дифференциации?
Частичная дифференциация по цепному правилу — это метод, в котором мы дифференцируем функции по двум-трем переменным одновременно.
Для функции f=f(u,v), u=u(x,y) и v=v(x,y) цепное правило:
$$ \frac{df}{dx} \; знак равно \frac{df}{du}\frac{du}{dx} \;+\; \frac{df}{dv}\frac{dv}{dx} $$
А,
$$ \frac{df}{dy} \;=\; \frac{df}{du}\frac{du}{dy} \;+\; \frac{df}{dv}\frac{dv}{dy} $$
Используйте калькулятор частных производных по цепному правилу, чтобы шаг за шагом дифференцировать частное дифференцирование по цепному правилу онлайн.
Калькулятор частных производных + онлайн-решатель с бесплатными шагами
Калькулятор частных производных используется для вычисления частных производных заданной функции. Частные производные очень похожи на нормальные производные, но они специфичны для задач, включающих более одной независимой переменной.
При дифференцировании функции для одной переменной все, что не связано с переменной, считается константой и рассматривается как таковая.
Это, следовательно, не меняется даже при рассмотрении частичного дифференцирования .
Что такое калькулятор частных производных?
A Калькулятор частных производных — это калькулятор, который используется для решения задач на частное дифференцирование прямо здесь, в вашем браузере. Вы можете запустить этот онлайн-калькулятор и решить столько задач, сколько захотите. Калькулятор очень прост в использовании и разработан, чтобы быть интуитивно понятным и простым.
Частичное дифференцирование — это калькулятор частных производных, который используется для функции, выраженной более чем одной независимой переменной. При решении одной из этих переменных остальные считаются константами.
Как пользоваться калькулятором частных производных?
Вы можете начать использовать этот калькулятор, сначала введя данные функции, а затем выбрав переменные, которые вы хотите дифференцировать. Калькулятор частных производных можно легко использовать, следуя инструкциям, приведенным ниже.
Чтобы использовать этот калькулятор, у вас должна быть задача, связанная с функцией с несколькими переменными, и у вас должна быть выбранная переменная, для которой вы хотите вычислить частную производную.
Шаг 1:
Вы начинаете с ввода заданной функции с ее переменными, выраженными через x, y и z.
Шаг 2:
За этим шагом следует выбор переменной, с которой вы хотите дифференцировать данную функцию x, y и z.
Шаг 3:
Затем вы просто нажимаете кнопку с надписью « Отправить », чтобы получить результаты расчетов. Ваш результат будет отображаться в поле под полями ввода калькулятора.
Шаг 4:
Наконец, чтобы снова использовать калькулятор, вы можете просто изменить записи в полях ввода и продолжать решать столько задач, сколько хотите.
Важно отметить, что этот калькулятор работает только для трех независимых переменных. Поэтому для задач с более чем тремя переменными этот калькулятор будет не очень эффективен.
Как работает калькулятор частных производных?
Калькулятор частных производных работает путем дифференцирования заданной функции отдельно для каждой рассматриваемой переменной. Стандартный дифференциал d применяется к простому уравнению, включающему только одну независимую переменную.
Дифференциация
Дифференцировка описывается как акт нахождения различия, так как дифференцирование временного сигнала интерпретируется как изменить во времени т.е. разницу во времени. Дифференциация широко используется в области инженерии и математики в области исчисления.
Исчисление, следовательно, изменение исследования, чтобы построить мост между физическим и теоретическим миром науки. Таким образом, разница в расстоянии по отношению ко времени в физике, а также в математике приведет к величине, называемой скоростью, где скорость определяется как изменение расстояния в заданный промежуток времени.
92}{dx} + 3 \frac{d}{dx} = 2 \times 2 x = 4x\]
Частный дифференциал
Частный дифференциал , как описано выше, используется для уравнений, основанных на более чем одной переменной. Это сильно усложняет ситуацию, так как теперь нет одной переменной, с которой можно было бы дифференцировать все выражение.
Следовательно, при таких обстоятельствах лучше всего разбить дифференциал на столько частей, сколько переменных в данной функции. Таким образом, начинаем дифференцировать выражение 92}{\partial y} + 2\frac {\partial y}{\partial y} – 1\frac {\ partial }{\partial y} = (3 \times 0) + 2 – 0 = 2 \]
Итак, когда вы решаете какую-либо одну переменную из многих, заданных в вашей функции, используется только та, для которой вы дифференцируете. Остальные переменные ведут себя как константы и могут быть дифференцированы до нуля, поскольку в постоянном значении нет изменения .
История частных производных
Частные производные 9Символ 0146 впервые был использован в 1770-х годах известным французским математиком и философом маркизом де Кондорсе.
Он использовал символ, выраженный как $\partial$ для частичных разностей.
Обозначение, используемое и по сей день для частных производных, было введено в 1786 году Адрианом-Мари Лежандром. Хотя это обозначение не стало популярным до 1841 года, когда немецкий математик Карл Густав Якоб Якоби нормализовал его.
Возникновение дифференциальных уравнений в частных производных произошло в золотой 169 год.2$, fz = 4z
Список математических калькуляторов
Калькулятор частных производных — поиск многомерной производной
Онлайн-калькулятор частных производных определит производные для заданной функции со многими переменными. Этот многомерный калькулятор производной может дифференцировать определенную функцию несколько раз. В следующем руководстве вы можете понять частные производные цепного правила и многое другое.
Что такое частная производная? В математике частная производная функции со многими производными определяется как производная функции со многими переменными по одной переменной, а все остальные переменные остаются неизменными.
Когда в функции две переменные x и y, которые не зависят друг от друга, то что там делать! Проще говоря, если вам требуется дифференцировать функцию по «x», то вы должны оставить переменную «y» постоянной и дифференцировать. С другой стороны, если нужно дифференцировать функцию по «у», сделайте переменную «х» постоянной. Символ «∂» обычно используется для обозначения частных производных.
Как вычислить частные производные функции?Вы можете использовать калькулятор частных производных, чтобы быстро найти производные. В противном случае вы можете выполнить эти вычисления вывода функции вручную, придерживаясь следующих шагов:
- Возьмите функцию для вычисления частной производной.
- Производная константы равна нулю.
- При применении производной к переменной вычисляется только производная этой конкретной переменной. 94+1) $$ Частные производные второго порядка:
- Сначала введите функцию для дифференцирования.
- Теперь выберите переменную для производной из раскрывающегося списка.
- Затем выберите, сколько раз вам нужно дифференцировать данную функцию.
- Нажмите кнопку расчета, чтобы увидеть результаты.
- Калькулятор частных производных вычисляет производную заданной функции, а затем применяет степенное правило для получения частной производной заданной функции.
- Введите функцию с несколькими переменными, например f(x, y, z).
- Выберите одну переменную из x, y и z, в то время как другие переменные остаются постоянными. 9и т. д.
- Нажмите кнопку вычислить , чтобы получить результат заданной входной функции.
- Нажмите кнопку показать еще , чтобы просмотреть пошаговые расчеты.
- Если вы хотите рассчитать другую проблему, нажмите кнопку сброса рядом с кнопкой расчета.
- Частная производная | Британская энциклопедия
- 4.3.1
Вычислить частные производные функции двух переменных.
- 4.3.2 Вычислить частные производные функции более чем двух переменных.
- 4.3.3 Определить высшие производные функции двух переменных.
- 4.3.4 Объясните смысл дифференциального уравнения в частных производных и приведите пример.
- f(x,y )=x2−3xy+2y2−4x+5y−12f(x,y)=x2−3xy+2y2−4x+5y−12
- g(x,y)=sin(x2y−2x+4)g(x,y)=sin(x2y−2x+4)
- Чтобы вычислить ∂f/∂x,∂f/∂x, относитесь к переменной yy как к константе. Затем продифференцируйте f(x,y)f(x,y) по xx, используя правила суммы, разности и степени:
∂f∂x=∂∂x[x2−3xy+2y2−4x+5y−12]=∂∂x[x2]−∂∂x[3xy]+∂∂x[2y2]−∂∂x[4x] +∂∂x[5y]−∂∂x[12]=2x−3y+0−4+0−0=2x−3y−4.
∂f∂x=∂∂x[x2−3xy+2y2−4x+ 5y−12]=∂∂x[x2]−∂∂x[3xy]+∂∂x[2y2]−∂∂x[4x]+∂∂x[5y]−∂∂x[12]=2x−3y +0−4+0−0=2x−3y−4.
Производные третьего, пятого и шестого членов равны нулю, поскольку они не содержат переменных x,x, поэтому они рассматриваются как постоянные члены. Производная второго члена равна коэффициенту x,x, который равен −3y.−3y. Расчет ∂f/∂y:∂f/∂y:∂f∂y=∂∂y[x2−3xy+2y2−4x+5y−12]=∂∂y[x2]−∂∂y[3xy]+ ∂∂y[2y2]−∂∂y[4x]+∂∂y[5y]−∂∂y[12]=−3x+4y−0+5−0=−3x+4y+5.∂f∂y =∂∂y[x2−3xy+2y2−4x+5y−12]=∂∂y[x2]−∂∂y[3xy]+∂∂y[2y2]−∂∂y[4x]+∂∂y[ 5y]−∂∂y[12]=−3x+4y−0+5−0=−3x+4y+5.
Это те же ответы, что и в примере 4.14. - Чтобы вычислить ∂g/∂x,∂g/∂x, относитесь к переменной y как к константе. Затем продифференцируйте g(x,y)g(x,y) относительно x , используя цепное правило и правило степени:
∂g∂x=∂∂x[sin(x2y−2x+4)]=cos( x2y−2x+4)∂∂x[x2y−2x+4]=(2xy−2)cos(x2y−2x+4).∂g∂x=∂∂x[sin(x2y−2x+4)]= cos(x2y−2x+4)∂∂x[x2y−2x+4]=(2xy−2)cos(x2y−2x+4).
Чтобы вычислить ∂g/∂y,∂g/∂y, относитесь к переменной xx как к константе. Затем продифференцируйте g(x,y)g(x,y) по yy, используя цепное и степенное правило:∂g∂y=∂∂y[sin(x2y−2x+4)]=cos(x2y−2x+4)∂∂y[x2y−2x+4]=x2cos(x2y−2x+4).∂g ∂y=∂∂y[sin(x2y−2x+4)]=cos(x2y−2x+4)∂∂y[x2y−2x+4]=x2cos(x2y−2x+4).
- f(x,y,z)=x2y−4xz+y2x−3yzf(x,y,z)=x2y−4xz+y2x−3yz
- g(x,y,z)=sin(x2y−z)+cos(x2−yz)g(x,y,z)=sin(x2y−z)+cos(x2−yz)
- ∂f∂x=∂∂x[x2y−4xz+y2x−3yz]=∂∂x(x2y−4xz+y2)(x−3yz)−(x2y−4xz+y2)∂∂x(x− 3yz)(x−3yz)2=(2xy−4z)(x−3yz)−(x2y−4xz+y2)(1)(x−3yz)2=2x2y−6xy2z−4xz+12yz2−x2y+4xz−y2 (x−3yz)2=x2y−6xy2z−4xz+12yz2+4xz−y2(x−3yz)2∂f∂x=∂∂x[x2y−4xz+y2x−3yz]=∂∂x(x2y−4xz+ y2)(x−3yz)−(x2y−4xz+y2)∂∂x(x−3yz)(x−3yz)2=(2xy−4z)(x−3yz)−(x2y−4xz+y2)(1 )(x−3yz)2=2x2y−6xy2z−4xz+12yz2−x2y+4xz−y2(x−3yz)2=x2y−6xy2z−4xz+12yz2+4xz−y2(x−3yz)2
(x−3yz)2=(x2+2y)(x−3yz)−(x2y−4xz+y2)(−3z)(x−3yz)2=x3−3x2yz+2xy−6y2z+3x2yz−12xz2+3y2z( x−3yz)2=x3+2xy−3y2z−12xz2(x−3yz)2∂f∂y=∂∂y[x2y−4xz+y2x−3yz]=∂∂y(x2y−4xz+y2)(x− 3yz)−(x2y−4xz+y2)∂∂y(x−3yz)(x−3yz)2=(x2+2y)(x−3yz)−(x2y−4xz+y2)(−3z)(x− 3yz)2=x3−3x2yz+2xy−6y2z+3x2yz−12xz2+3y2z(x−3yz)2=x3+2xy−3y2z−12xz2(x−3yz)2
∂f∂z=∂∂z[x2y−4xz +y2x−3yz]=∂∂z(x2y−4xz+y2)(x−3yz)−(x2y−4xz+y2)∂∂z(x−3yz)(x−3yz)2=(−4x)(x −3yz)−(x2y−4xz+y2)(−3y)(x−3yz)2=−4×2+12xyz+3x2y2−12xyz+3y3(x−3yz)2=−4×2+3x2y2+3y3(x−3yz) 2∂f∂z=∂∂z[x2y−4xz+y2x−3yz]=∂∂z(x2y−4xz+y2)(x−3yz)−(x2y−4xz+y2)∂∂z(x−3yz) (x−3yz)2=(−4x)(x−3yz)−(x2y−4xz+y2)(−3y)(x−3yz)2=−4×2+12xyz+3x2y2−12xyz+3y3(x−3yz) 2=−4×2+3x2y2+3y3(x−3yz)2 - ∂f∂x=∂∂x[sin(x2y−z)+cos(x2−yz)]=(cos(x2y−z))∂∂x(x2y−z)−(sin(x2−yz)) ∂∂x(x2−yz)=2xycos(x2y−z)−2xsin(x2−yz)∂f∂y=∂∂y[sin(x2y−z)+cos(x2−yz)]=(cos(x2y −z))∂∂y(x2y−z)−(sin(x2−yz))∂∂y(x2−yz)=x2cos(x2y−z)+zsin(x2−yz)∂f∂z=∂∂ z[sin(x2y−z)+cos(x2−yz)]=(cos(x2y−z))∂∂z(x2y−z)−(sin(x2−yz))∂∂z(x2−yz) =−cos(x2y−z)+ysin(x2−yz)∂f∂x=∂∂x[sin(x2y−z)+cos(x2−yz)]=(cos(x2y−z))∂∂x (x2y−z)−(sin(x2−yz))∂∂x(x2−yz)=2xycos(x2y−z)−2xsin(x2−yz)∂f∂y=∂∂y[sin(x2y−z )+cos(x2−yz)]=(cos(x2y−z))∂∂y(x2y−z)−(sin(x2−yz))∂∂y(x2−yz)=x2cos(x2y−z) +zsin(x2−yz)∂f∂z=∂∂z[sin(x2y−z)+cos(x2−yz)]=(cos(x2y−z))∂∂z(x2y−z)−(sin (x2−yz))∂∂z(x2−yz)=−cos(x2y−z)+ysin(x2−yz)
- Подставьте эту форму в уравнение 4.13 и, учитывая, что f(t)f(t) постоянна по отношению к расстоянию (r)(r), а R(r)R(r) постоянна по времени (t ),(t), покажите, что
1f∂f∂t=KR[∂2R∂r2+2r∂R∂r].1f∂f∂t=KR[∂2R∂r2+2r∂R∂r].
- Это уравнение представляет желаемое разделение переменных. Левая часть является функцией только tt, а правая часть является функцией только r, r, и они должны быть равны для всех значений randt. randt. Следовательно, они оба должны быть равны константе. Назовем эту константу −λ2.−λ2. (Удобство такого выбора видно при подстановке.) Итак, имеем
1f∂f∂t=−λ2 и KR[∂2R∂r2+2r∂R∂r]=−λ2.1f∂f∂t=−λ2 и KR[∂2R∂r2+2r∂R∂r]=−λ2.
Теперь прямой подстановкой для каждого уравнения можно проверить, что решения имеют вид f(t)=Ae−λ2tf(t)=Ae−λ2t и R(r)=B(sinαrr)+C(cosαrr),R( r)=B(sinαrr)+C(cosαrr), где α=λ/K.α=λ/K. Обратите внимание, что f(t)=Ae+λn2tf(t)=Ae+λn2t также является допустимым решением, поэтому мы могли бы выбрать +λ2+λ2 в качестве нашей константы. Вы видите, почему это не будет справедливо для этого случая по мере увеличения времени? - Теперь применим граничные условия.
- Температура в центре Земли должна быть конечной, r=0.r=0. Какая из двух констант, BB или C,C, должна быть равна нулю, чтобы RR оставался конечным при r=0?r=0? (Напомним, что sin(αr)/r→α=sin(αr)/r→α= при r→0,r→0, но cos(αr)/rcos(αr)/r ведет себя совсем иначе.)
- Кельвин утверждал, что когда магма достигает поверхности Земли, она очень быстро остывает. Человек часто может коснуться поверхности в течение нескольких недель после выделения. Поэтому поверхность достигла умеренной температуры очень рано и оставалась почти постоянной при температуре поверхности Ts.Ts. Для простоты положим T=0atr=RET=0atr=RE и найдем такое αα, что это будет температура там за все время t.t. (Кельвин принял значение 300K≈80°F.300K≈80°F. Мы можем добавить эту константу 300K300K к нашему решению позже.) Чтобы это было правдой, аргумент синуса должен быть равен нулю при r=RE.r= РЕ. Заметим, что αα имеет бесконечный ряд значений, удовлетворяющих этому условию. Каждое значение αα представляет допустимое решение (каждое со своим значением для A).A). Полное или общее решение представляет собой сумму всех этих решений.
- При t=0,t=0 мы предполагаем, что вся Земля была при начальной горячей температуре T0T0 (Кельвин принял ее равной примерно 7000K.) 7000K.) Применение этого граничного условия включает более сложное применение коэффициентов Фурье. . Как указано в части б. каждое значение αnαn представляет собой допустимое решение, а общее решение представляет собой сумму всех этих решений. Это приводит к решению в виде ряда:
T(r,t)=(T0REπ)∑n(−1)n−1ne−λn2tsin(αnr)r, где αn=nπ/RE.T(r,t)=(T0REπ) ∑n(−1)n−1ne−λn2tsin(αnr)r, где αn=nπ/RE.
- Сторона a
- Боковой б
- Угол θ Угол θ
- его радиус rr и высота h.h.
- Покажите, что скорость изменения объема цилиндра по отношению к его радиусу равна произведению длины его окружности на его высоту.
- Докажите, что скорость изменения объема цилиндра по отношению к его высоте равна площади круглого основания.
Старшая производная очень важна для проверки вогнутости функции и подтверждения того, является ли конечная точка функции максимальной или минимальной.
Поскольку функция f (x, y) непрерывно дифференцируема в открытой области, можно получить следующий набор частных производных второго порядка:
Прямые частные производные второго порядка:
F_{xx} = ∂fx / ∂x, где функция f(x) — первая частная производная от x.
f_{yy} = ∂fy / ∂y, где функция f (y) — производная первого порядка по y.
Кросс-частная производная:
fxy = ∂fx / ∂y, где f(x) — первая производная по x.
fyx = ∂fy / ∂x, где f(y) — первая частная производная по y.
Однако онлайн-калькулятор производной по направлению определяет производную по направлению и градиент функции в заданной точке вектора.
92
Решение:
Частичные производные первого порядка:
FX = 2x + 10y + 0 = 2x + 10y
FY = 0 + 10x + 4y = 10x + 4y
. вычисляет прямые частные производные второго порядка:
Fxx = ∂/∂x (2x + 10y) = 2
Fyy = ∂/∂y (10x + 4y) = 4
Калькулятор второй частной производной вычисляет перекрестные частные производные:
Fxy = ∂/∂y (2x + 10y) = 5
fyx=∂/∂x(10x+ 4y) = 5
Частные производные по цепному правилу: Предположим, что x = g (a) и y = h (a) являются дифференцируемыми функциями от «a», а z = f (x, y) — дифференцируемые функции от x и y.
Тогда z = f (x (a), y (a)) является дифференцируемой функцией от «a» и
Dz/da = ∂z/∂x⋅dx/da + ∂z/∂y⋅dy/da
Обыкновенная производная оценивается в a, а частная производная оценивается в (x, y).
Как работает калькулятор частных производных?Онлайн-калькулятор производной с несколькими переменными дифференцирует заданные функции, взяв производную, выполнив следующие действия:
Ввод: Цепное правило гласит, что производная f (g (x)) равна f'(g (x)) ⋅g’ (x).
2.
Как только вы найдете точку, в которой градиент функции с несколькими переменными является нулевым вектором, что означает, что касательная плоскость графика в этой точке плоская, вы можете использовать частную производную второго порядка, чтобы определить, является ли точка локальные максимумы, минимумы или седловая точка.
Вывод:Онлайн-калькулятор частных производных используется для дифференцирования математических функций, содержащих несколько переменных. Следовательно, частичное дифференцирование является более общим, чем обычное дифференцирование. Частичное дифференцирование используется для нахождения точек минимума и максимума в задаче оптимизации.
Ссылка: Из источника Википедии: Поверхность в евклидовом пространстве, злоупотребление обозначениями, теорема Клеро, оптимизация, термодинамика, квантовая механика и математическая физика.
Из источника Brilliant: мгновенная скорость изменения или наклон, дифференцирование с одной переменной, линейность, правило произведения, цепное правило, векторное исчисление и производные более высокого порядка, смешанная производная.
Из источника Академии Хана: функция многих переменных, трехмерные графики, исчисление одной переменной, двумерные входные данные, предварительная оценка.
Калькулятор частных производных — Дифференцируйте многомерные
Калькулятор частных производных с шагами
Калькулятор частных производных используется для вычисления производных функций по нескольким переменным с шагами. Этот решатель частных производных многократно дифференцирует заданные постоянные, линейные или полиномиальные функции. Это подтип производного калькулятора.
Что такое частная производная?
«В дифференциальном исчислении дифференцирование функции многих переменных по изменению только одной из ее переменных называется частной производной».
Уравнения частных производных можно записать так:
• \(\frac{\partial }{\partial x}\left(f\left(x,y,z\right)\right)\)
Приведенное выше уравнение используется для функции с несколькими переменными для вычисления частного дифференциала относительно « x ».
• \(\frac{\partial }{\partial y}\left(f\left(x,y,z\right)\right)\)
Это уравнение используется, если функция должна быть решена относительно « и ».
• \(\frac{\partial }{\partial z}\left(f\left(x,y,z\right)\right)\)
Это уравнение используется, когда необходимо решить частную производную функции относительно « z »
Используйте наш калькулятор частных производных xyz для получения результатов задач с несколькими переменными.
Как пользоваться этим калькулятором первой частной производной?
Чтобы использовать этот первый калькулятор частичного дифференцирования, выполните следующие действия.
Как оценивать задачи частных производных?
Ниже приведены два примера функции с 3 переменными, вычисляемой нашим многопараметрическим калькулятором производной.
Пример 1
Найдите частную производную числа 3xyz относительно « x ».
Решение
Шаг 1: Запишите функцию в виде частичного дифференцирования.
\(\frac{\partial }{\partial x}\left(3xyz\right)\)
Шаг 2: Теперь вычислите частную производную 3xyz относительно «x», пока y и z остаются постоянными.
\(\frac{\partial }{\partial x}\left(3xyz\right)=3yz\frac{\partial }{\partial x}\left(x\right)\) 92y+4xyz-9xy\right)=4xy\)
Таблица частных производных функций
Ниже приведены вопросы и ответы о частных производных, решаемых этим калькулятором частных производных.
| Questions | Answers |
| Partial derivative of xy w.r.t x | y |
| Partial derivative of xy w.r.t y 9{xyz}\) | |
| Частная производная от sqrt(xy) w.r.t x | \(\frac{y}{2\sqrt{xy}\:}\) |
Онлайн-калькулятор частных производных с шагами
w3.org/1999/xhtml» cellspacing=»0″>Разоблачен самый большой миф о калькуляторе частных производных
Честное слово о калькуляторе частных производных
Обычно предсказание оказывается неверным, и мы вносим некоторые улучшения. Кроме того, это компактный регион. Различные функции потерь используются для решения различных задач, таких как регрессия и классификация.
Для функции любой сложности вероятность того, что ее первообразная будет элементарной функцией, чрезвычайно мала. Это свойство известно как слабая двойственность. Если выполняется сильное условие двойственности, мы закончили.
Новая пошаговая дорожная карта для калькулятора частных производных
Это похоже на прогресс, но это не решение. Вам просто нужно научиться находить свои ошибки и исправлять их. В противном случае это не сработает, и вы получите неверный ответ.
Очень хороший вопрос. Это снижает сложность решения сложных вопросов и, следовательно, помогает в легком и быстром изучении любого предмета.
Проблема maxmin известна как двойная проблема.
Что вам не расскажут в толпе о калькуляторе частных производных
Крайне важно убедиться, что вы правильно скопировали входную информацию в свои вычисления. Ошибка может возникнуть из-за множества уникальных причин, которые часто связаны с человеческим фактором, но также могут быть связаны с оценками и ограничениями устройств, используемых при измерении. Функция не будет иметь максимума, если всем переменным разрешено неограниченное увеличение.
Как можно заметить, результат интегрирования не меняется в зависимости от ассортимента порядка интегрирования, но изменяется установка интегралов. Оптимизация — жизненно важный шаг в машинном обучении. Полезно различать составные функции.
Количество страниц указано на синей полосе в основании таблицы. Держите это в голове, вам нужно войти в уравнение, которое вы хотели решить, а затем нажать кнопку результата, чтобы посмотреть на результат. Один из способов сделать это — использовать некоторые тригонометрические тождества.
Хорошо, я думаю, что понимаю калькулятор частных производных, теперь расскажите мне о калькуляторе частных производных!
Эта функция позволяет заранее определить проблему в гиперссылке на эту страницу. Здесь мы остановимся немного подробнее, чем в приведенных выше примерах. Итак, сейчас я предложу вам несколько примеров.
Самая важная цель — показать хороший пример основных команд. Этот график показывает, что такого решения не существует. Его форма прямолинейна и симметрична в декартовых координатах.
Интернет-калькулятор вычислит частную производную функции с помощью показанных действий. Каждый компонент градиента входит в число частных первых производных функции. К сожалению, эта функция возвращает только производную одной точки.
Обратите внимание, что постоянный член c не оказывает никакого влияния на производную. Имейте в виду, что цепное правило используется для определения производных составных функций. Это самое важное правило для получения производных.
Эти формулы довольно сложно запомнить, поэтому полезно научиться доказывать их самому себе. Есть несколько формул для производных, которые мне очень часто задают.
30-секундный трюк для калькулятора частных производных
Эта демонстрация проиллюстрирует этот простой факт. Затем конечный результат дифференцируется второй раз, опять же по той же самой независимой переменной. Подумайте об отделе продаж.
Предполагается, что вы сами составите свой личный и рабочий график, чтобы вы могли выбрать экзамен. NN, которую мы, вероятно, создадим, имеет следующее визуальное представление. Чем он больше в любой конкретный момент времени, тем быстрее он растет в этот момент.
Спрятанное сокровище калькулятора частных производных
Итак, наша точка должна быть минимумом. Даже если каждый расчет окрестности добавляет лишь небольшой шум, он может накапливаться в сложном расчете, состоящем из нескольких шагов. В некоторых случаях (например, мосты и тротуары) действительно имеет значение просто изменение одного измерения.
Если вы посмотрите на нисходящий путь, вполне вероятно, что вы доберетесь до озера. Это полезно для увеличения движения кишечника и снижения повышенной кислотности. Градиент связан с наклоном поверхности в каждой точке.
Все о калькуляторе частных производных
Медицинские работники советуют грудное вскармливание. Вторая стадия акне На этой стадии появляются легкие или воспалительные угри, называемые папулами. Узнайте больше о приеме кодеина во время грудного вскармливания, его рисках и о том, что именно вы можете сделать, если кодеин необходим.
Вы можете увидеть среднеквадратичную ошибку в каждом из обстоятельств. Пример подробного решения доступен здесь. Функции этой формы такие же, как и в случае 3, только в знаменателе есть член, который повторяется или постоянно кратен другому члену.
Что можно и что нельзя делать с калькулятором частных производных
Первоначально это программное обеспечение было разработано компанией Numerical Mathematics.
Автоматизированная дифференциация — довольно сильное оружие, широко используемое в машинном обучении. Наш инструмент «Калькулятор антипроизводных» поддерживает все самые последние функции, вычисления и несколько других переменных, которые необходимы в одном инструменте.
Неявное дифференцирование Один из способов получить наклон — выбрать производную любой части уравнения по x. Результаты действительно демонстрируют, что этот метод намного лучше, чем использование линейного приближения. В случае, если переменные не могут быть разделены напрямую, необходимо использовать другие методы для решения уравнения.
Матрица действует на один вектор, чтобы получить другой вектор. Имейте в виду, что p вообще не меняется. Найдите его и нанесите вместе с функцией на тот же график.
Особенности калькулятора частных производных
Легкость, с которой мой сын использует его, чтобы научиться исправлять сложные уравнения, просто поразительна. Давайте посмотрим на другой график.
Идея здесь будет заключаться в том, чтобы на самом деле обратиться к приближенному уравнению, которое легко, поскольку оно линейное.
Это уравнение называется формулой линейного приближения. Эти уравнения называются нормальными уравнениями. Это не только просто сделать, но и очень полезно!
Калькулятор частных производных: максимальное удобство!
Вышеупомянутый Калькулятор вычисляет производную определенной функции, связанной с переменной x, используя аналитическое дифференцирование. Градиент — это вектор, состоящий из частных производных функции по переменным.
Вернемся к самому первому основному определению производной. Проще говоря, вы хотите узнать, какое производное правило применяется, а затем применить его. Имейте в виду, что обозначение второй производной производится путем включения второго штриха.
Вместо расчета конкретной цены калькулятор отображает общее выражение для производной. Есть несколько формул для производных, которые мне очень часто задают.
Где найти калькулятор частных производных
Это похоже на прогресс, но это не решение. Вам просто нужно научиться находить свои ошибки и исправлять их. Если они одинаковые, ваш ответ верен.
Мои первые тесты с этой библиотекой показывают, что функция градации различает только самый первый аргумент. Принципиальная разница в том, что применяется множество формул с многочисленными корректировками. Такого рода задачи имеют широкое применение в различных областях, включая экономику и физику.
Объяснение основ калькулятора частных производных
Излишне говорить, что калькулятор можно использовать также на переносных и настольных компьютерах. Чтобы показать шаги, он применяет те же методы интеграции, что и человек. Совместное использование калькуляторов также запрещено.
Основы калькулятора частных производных, которые вы сможете сразу же использовать
Этот калькулятор интерполяции будет очень полезен в области компьютерной графики, где популярны простые операции со значениями линейной интерполяции.
Цепное правило позволяет нам различать функцию, которая имеет другую функцию. Цепное правило также может быть обобщено для нескольких переменных в обстоятельствах, когда вложенные функции зависят более чем от одной переменной.
1 вариант — использовать бикубическую фильтрацию. Итерация предоставляется Последующий инструмент выполнит итерацию за вас. Полезно различать составные функции.
Закон Гаусса немного пугает. Можно также поставить задачу Коши на весь набор потенциальных решений, чтобы выбрать частные, соответствующие заданным исходным задачам. Рассмотрим цепное правило для практики.
Правило частного — это только особый случай правила элемента, и это означает, что вам не нужно запоминать другую формулу. Конечный результат действительно замечательный. Определение этого значения является необязательным, но если вы предпочитаете стабильный результат, это отличная идея указать его.
Отсутствие эквивалента для интеграции — это то, что делает интеграцию такой огромной техникой и уловками.
Кроме того, это компактный регион. Они предложат отличительные ошибки для точного прогноза и, таким образом, окажут значительное влияние на функционирование модели.
Функция PhaseSI Может быть полезно понять, что такое фаза конкретной точки состояния. Это свойство известно как слабая двойственность. Если выполняется сильное условие двойственности, мы закончили.
Калькулятор хороших, плохих и частных производных
Поскольку тело каждого человека отличается, вид лечения, применяемый к одному человеку, может не подойти еще одному. Между прочим, самая популярная тонкая ошибка на сегодняшний день состоит в использовании неправильного ввода, что означает попытку решить неправильную проблему. Один из способов сделать это — использовать некоторые тригонометрические тождества.
Эта функция позволяет заранее указать проблему в гиперссылке на эту страницу. Благодаря широкому доступу к интуитивно понятным API это достижимо с минимальным пониманием того, что происходит, или того, как глубокие базовые слои на самом деле выполняют свою работу.
Итак, сейчас я предложу вам несколько примеров.
Самая важная цель — показать хороший пример основных команд. Как показано в следующем примере, одна конкретная техника, которая часто работает, состоит в том, чтобы угадать общий тип поля на основе опыта или физической интуиции, а затем попытаться использовать закон Гаусса, чтобы получить, какая конкретная версия этой общей формы собирается. быть решением. Его форма прямолинейна и симметрична в декартовых координатах.
Как видно, положение каждого сегмента взвешивается по области сегмента и после сложения делится на всю область формы. Именно это дополнительное условие делает плоскость касательной. Любое направление, которому вы следуете, приведет к снижению температуры.
После того, как зависимость представляет собой одну конкретную переменную, используйте d, как с x и y, которые зависят только от u. Если вы увеличите масштаб несколько раз, вы увидите, что кривая синусоиды внутри этой области быстро становится похожей на прямую линию, так как она не очень изогнута.
Градиентный спуск — это процесс движения по градиенту вниз для достижения наименьшей стоимости.
Новая пошаговая дорожная карта для калькулятора частных производных
Алгебратор стоит своих денег благодаря правильному подходу. В начале программы вы хотите дать учащимся опыт прохождения полного 9-точечный вопрос, и вы не сможете сделать это намного позже в учебном курсе. Подумайте об отделе продаж.
Предполагается, что вы сами составите свой личный и рабочий график, чтобы вы могли выбрать экзамен. Та же проблема актуальна и для многомерного исчисления, но на этот раз мы должны иметь дело с более чем одной формой цепного правила. Основная причина этого заключается в том, что в самом первом случае мы берем частную производную, связанную с сохранением постоянной, тогда как во втором сценарии мы берем частную производную, связанную с сохранением постоянной.
Секрет калькулятора частных производных, о котором никто не говорит
Теперь вы знаете аналогию того, как работает алгоритм.
Этот учебник по исчислению продемонстрирует, как работает линеаризация и как применить ее к задаче. Дополнительная квадратичная формула также дает ось симметрии параболы.
Это уравнение называется формулой линейного приближения. Эти уравнения называются нормальными уравнениями. Линейная аппроксимация — это всего лишь одна из самых простых аппроксимаций трансцендентных функций, которые не должны выражаться алгебраически.
И это должно предоставить вам всю информацию, необходимую для понимания частных производных, которые вы захотите понять для уравнений Максвелла. Градиент — это всего лишь вектор, который собирает все частные первые производные функции в 1 месте.
Обратите внимание, что постоянный член c не оказывает никакого влияния на производную. Затем, соблюдая цепное правило, вы можете обнаружить производную. Цепное правило также может помочь нам найти различные производные.
Эти формулы довольно сложно запомнить, поэтому полезно научиться доказывать их самому себе. Ретинол является отличным антивозрастным ингредиентом, который делает кожу более здоровой и молодой.
Прикрытие калькулятора частных производных
Знаменатель состоит из неприводимых квадратичных элементов, ни один из которых не повторяется. Это имеет вполне реальное следствие. По сравнению с другими признаками линейной классификации, отличием является неопределенность.
Очень хороший вопрос. Это снижает сложность решения сложных вопросов и, следовательно, помогает в легком и быстром изучении любого предмета. Проблема maxmin известна как двойная проблема.
Разумеется, калькулятор можно использовать и на ноутбуках, и на настольных компьютерах. Он показывает ответ, который вы можете сослаться на свое решение исчисления. Это делает расчеты легкими и приятными.
Крайне важно убедиться, что вы правильно скопировали входную информацию в свои вычисления. Ошибка может возникнуть из-за множества уникальных причин, которые часто связаны с человеческим фактором, но также могут быть связаны с оценками и ограничениями устройств, используемых при измерении. Функция не будет иметь максимума, если всем переменным разрешено неограниченное увеличение.
Затем, если возможно, описанная выше процедура используется для упрощения подходящей функции. Антибактериальные ламинаты Использование ламинатов Различные виды ламинатов имеют различное применение в зависимости от их специфических свойств. В модель персептрона могут входить многочисленные входные данные, которые также называются признаками.
Одна и та же методика может быть использована в разных оболочках. Проблема в том, что это повлечет за собой дополнительную цену. Также проблемы могут быть решены мгновенно.
Частное правило является лишь особым случаем правила элемента, и это означает, что вам не нужно запоминать другую формулу. Конечный результат действительно замечательный. Повторяя этот процесс, вы можете найти оптимальное решение для уменьшения функции стоимости.
Что на самом деле происходит с калькулятором частичной производной
Активные компоненты аджвана могут помочь повысить пищеварительную функцию желудочно-кишечного тракта за счет усиления кишечных соков (желудочно-кишечного секрета). Этот подход работает только в некоторых конкретных случаях. тем не менее, это лучше всего подходит для каустики в результате преломления света в плоском теле простой воды. Используйте сочетание индикаторов, чтобы сформировать свою собственную секретную торговую стратегию.
Функция PhaseSI Может быть полезно понять, какова фаза конкретной точки состояния. Это свойство известно как слабая двойственность. Чтобы выбрать из дерева выбора товаров, щелкните поле рядом с каждым товаром или группой товаров.
Калькулятор частных производных может быть забавным для всех
Ретинол, напротив, мягче. Между прочим, самая популярная тонкая ошибка на сегодняшний день состоит в использовании неправильного ввода, что означает попытку решить неправильную проблему. Один из способов сделать это — использовать некоторые тригонометрические тождества.
Любой архитектурный проект должен постоянно контролироваться, а материалы должны поставляться вовремя из законных источников, чтобы снизить цену. Естественно, все численные методы вносят в данные некоторую ошибку. Итак, сейчас я предложу вам несколько примеров.
Эта константа называется константой интегрирования и может быть определена только при наличии дополнительной информации об интеграле. Как показано в следующем примере, одна конкретная техника, которая часто работает, состоит в том, чтобы угадать общий тип поля на основе опыта или физической интуиции, а затем попытаться использовать закон Гаусса, чтобы получить, какая конкретная версия этой общей формы собирается. быть решением. В следующем примере показано, как применить более одного правила.
Что делать с калькулятором частных производных, начиная с ближайших десяти минут
Это поможет безопасно улучшить здоровье желудка. Он может указывать в самых разных направлениях, за исключением очень близкого к солнцу. Вы можете находиться на самой вершине одной горы, но рядом с вами может быть более крупная вершина.
Наблюдая за тем, что происходит с альтернативными сценариями, вы сможете наблюдать, как каждый вход связан с размерами выборки и что произойдет, если вы не будете использовать предложенный размер выборки. Поэтому создаются выходные прогнозы с последующим обновлением всех весовых параметров как части единого тренировочного цикла. Используя это определение, мы можем легко вычислить наклон между двумя точками.
30-секундный трюк для калькулятора частных производных
Эта модель, однако, игнорирует реальный факт: при покупке большого количества товаров часто предоставляются скидки. Единственная причина, по которой мы работаем с данными таким образом, — дать иллюстрацию линейной регрессии, в которой не используется слишком много точек данных. Вы должны иметь хотя бы базовое представление о машинном обучении, чтобы справиться с самой важной технологией человечества.
Да, но мы не будем доказывать этот простой факт. Стандартная иллюстрация — население. Обратите внимание, чтобы вы могли использовать это правило позже.
4.3 Частные производные. Расчет, том 3
Цели обучения
Теперь, когда мы рассмотрели пределы и непрерывность функций двух переменных, мы можем перейти к изучению производных. Нахождение производных функций двух переменных является ключевой концепцией этой главы, имеющей столько же применений в математике, естественных науках и технике, сколько и дифференцирование функций одной переменной. Однако мы уже видели, что ограничения и непрерывность многомерных функций имеют новые проблемы и требуют новой терминологии и идей для их решения. Это переносится и на дифференциацию.
Производные функции двух переменных
При изучении производных функций одной переменной мы обнаружили, что одной из интерпретаций производной является мгновенная скорость изменения yy как функции x. x. Обозначение Лейбница для производной — dy/dx,dy/dx, из чего следует, что yy — зависимая переменная, а xx — независимая переменная. Для функции z=f(x,y)z=f(x,y) двух переменных xx и yy являются независимыми переменными, а zz является зависимой переменной. Это сразу же поднимает два вопроса: как нам адаптировать обозначения Лейбница для функций двух переменных? Кроме того, что такое интерпретация производной? Ответ лежит в частных производных.
Определение
Пусть f(x,y)f(x,y) функция двух переменных. Тогда частная производная ff по x,x, записанная как ∂f/∂x,∂f/∂x или fx,fx, определяется как
∂f∂x=limh→0f(x+h, y)−f(x,y)h.∂f∂x=limh→0f(x+h,y)−f(x,y)h.
(4.12)
Частная производная от ff по y,y, записанная как ∂f/∂y,∂f/∂y или fy,fy, определяется как
∂f∂y=limk→ 0f(x,y+k)−f(x,y)k.∂f∂y=limk→0f(x,y+k)−f(x,y)k.
(4.13)
Это определение уже показывает два отличия. Во-первых, меняется обозначение в том смысле, что мы по-прежнему используем версию обозначения Лейбница, но dd в исходном обозначении заменяется символом ∂.∂. (Это округленное «d» «d» обычно называют «частным», поэтому ∂f/∂x∂f/∂x говорят как «частное от ff относительно x».)x.) Это первое намек на то, что мы имеем дело с частными производными. Во-вторых, теперь у нас есть две разные производные, которые мы можем взять, поскольку есть две разные независимые переменные. В зависимости от того, какую переменную мы выбираем, мы можем вообще получить разные частные производные, что часто и происходит.
Пример 4.14
Вычисление частных производных по определению
Используйте определение частной производной в качестве предела для вычисления ∂f/∂x∂f/∂x и ∂f/∂y∂f/∂y для функции
f( x,y)=x2−3xy+2y2−4x+5y−12.f(x,y)=x2−3xy+2y2−4x+5y−12.
Решение
Сначала вычислите f(x+h,y).f(x+h,y).
f(x+h,y)=(x+h)2−3(x+h)y+2y2−4(x+h)+5y−12=x2+2xh+h3−3xy−3hy+2y2 −4x−4h+5y−12. f(x+h,y)=(x+h)2−3(x+h)y+2y2−4(x+h)+5y−12=x2+2xh+ h3−3xy−3hy+2y2−4x−4h+5y−12.
Затем подставьте это в уравнение 4.12 и упростите: 3hy+2y2−4x−4h+5y−12)−(x2−3xy+2y2−4x+5y−12)h=limh→0x2+2xh+h3−3xy−3hy+2y2−4x−4h+5y−12− x2+3xy−2y2+4x−5y+12h=limh→02xh+h3−3hy−4hh=limh→0h(2x+h−3y−4)h=limh→0(2x+h−3y−4)=2x −3y−4.∂f∂x=limh→0f(x+h,y)−f(x,y)h=limh→0(x2+2xh+h3−3xy−3hy+2y2−4x−4h+5y −12)−(x2−3xy+2y2−4x+5y−12)h=limh→0x2+2xh+h3−3xy−3hy+2y2−4x−4h+5y−12−x2+3xy−2y2+4x−5y +12h=limh→02xh+h3−3hy−4hh=limh→0h(2x+h−3y−4)h=limh→0(2x+h−3y−4)=2x−3y−4.
Чтобы вычислить ∂f∂y,∂f∂y, сначала вычислите f(x,y+h):f(x,y+h):
f(x,y+h)=x2−3x(y +h)+2(y+h)2−4x+5(y+h)−12=x2−3xy−3xh+2y2+4yh+2h3−4x+5y+5h−12.f(x,y+h )=x2−3x(y+h)+2(y+h)2−4x+5(y+h)−12=x2−3xy−3xh+2y2+4yh+2h3−4x+5y+5h−12.
Затем подставьте это в уравнение 4.13 и упростите: 4yk+2k2−4x+5y+5k−12)−(x2−3xy+2y2−4x+5y−12)k=limk→0x2−3xy−3xk+2y2+4yk+2k2−4x+5y+5k−12− x2+3xy−2y2+4x−5y+12k=limk→0−3xk+4yk+2k2+5kk=limk→0h(−3x+4y+2k+5)k=limk→0(−3x+4y+2k+ 5)=−3x+4y+5. ∂f∂y=limk→0f(x,y+h)−f(x,y)k=limk→0(x2−3xy−3xk+2y2+4yk+2k2− 4x+5y+5k−12)−(x2−3xy+2y2−4x+5y−12)k=limk→0x2−3xy−3xk+2y2+4yk+2k2−4x+5y+5k−12−x2+3xy− 2y2+4x−5y+12k=limk→0−3xk+4yk+2k2+5kk=limk→0h(−3x+4y+2k+5)k=limk→0(−3x+4y+2k+5)=− 3х+4у+5.
Контрольно-пропускной пункт 4.12
Используйте определение частной производной в качестве предела для вычисления ∂f/∂x∂f/∂x и ∂f/∂y∂f/∂y для функции
f(x,y)=4×2+2xy −y2+3x−2y+5.f(x,y)=4×2+2xy−y2+3x−2y+5.
Идея, о которой следует помнить при вычислении частных производных, состоит в том, чтобы рассматривать все независимые переменные, кроме переменной, по которой мы дифференцируем, как константы. Затем приступайте к дифференцированию, как с функцией одной переменной. Чтобы понять, почему это так, сначала зафиксируем yy и определим g(x)=f(x,y)g(x)=f(x,y) как функцию x.x. Затем
g′(x)=limh→0g(x+h)−g(x)h=limh→0f(x+h,y)−f(x,y)h=∂f∂x.g′(x)= limh→0g(x+h)−g(x)h=limh→0f(x+h,y)−f(x,y)h=∂f∂x.
То же верно для вычисления частной производной от ff по y. y. На этот раз зафиксируйте xx и определите h(y)=f(x,y)h(y)=f(x,y) как функцию y.y. Затем
h′(x)=limk→0h(x+k)−h(x)k=limk→0f(x,y+k)−f(x,y)k=∂f∂y.h′(x)= limk→0h(x+k)−h(x)k=limk→0f(x,y+k)−f(x,y)k=∂f∂y.
Применяются все правила дифференцирования из введения в производные.
Пример 4.15
Вычисление частных производных
Вычислите ∂f/∂x∂f/∂x и ∂f/∂y∂f/∂y для следующих функций, удерживая противоположную переменную постоянной, а затем дифференцируя:
Решение
Контрольно-пропускной пункт 4.13
Рассчитать ∂f/∂x∂f/∂x и ∂f/∂y∂f/∂y для функции f(x,y)=tan(x3−3x2y2+2y4)f(x,y)=tan (x3−3x2y2+2y4), удерживая противоположную переменную постоянной, а затем дифференцируя.
Как мы можем интерпретировать эти частные производные? Напомним, что график функции двух переменных представляет собой поверхность в ℝ3.ℝ3. Если мы удалим предел из определения частной производной по x,x, разностное частное останется:
f(x+h,y)−f(x,y)h.f(x+h,y)−f(x,y)h.
Это похоже на разностное частное для производной функции одной переменной, за исключением наличия переменной yy. На рис. 4.21 показана поверхность, описываемая произвольной функцией z=f(x,y). z=f(x,y).
Рисунок 4.21 Секущая, проходящая через точки (x,y,f(x,y))(x,y,f(x,y)) и (x+h,y,f(x+h,y)).(x +h,y,f(x+h,y)).
На рис. 4.21 значение hh положительное. Если построить графики f(x,y)f(x,y) и f(x+h,y)f(x+h,y) для произвольной точки (x,y),(x,y), то наклон секущей, проходящей через эти две точки, равен
f(x+h,y)−f(x,y)h.f(x+h,y)−f(x,y)h.
Эта линия параллельна оси x.ось x. Следовательно, наклон секущей представляет собой среднюю скорость изменения функции ff, когда мы движемся параллельно оси x.x-ось. Когда hh приближается к нулю, наклон секущей приближается к наклону касательной.
Если мы решим изменить yy вместо xx на одно и то же значение приращения h,h, тогда секущая линия будет параллельна оси y и касательной. Следовательно, ∂f/∂x∂f/∂x представляет собой наклон касательной, проходящей через точку (x,y,f(x,y))(x,y,f(x,y)) параллельно ось xx-ось и ∂f/∂y∂f/∂y представляет наклон касательной, проходящей через точку (x,y,f(x,y))(x,y,f(x,y) ) параллельно оси y. ось y. Если мы хотим найти наклон касательной, проходящей через ту же точку в любом другом направлении, то нам понадобится то, что называется производных по направлению , которые мы обсуждаем в разделе «Производные по направлению и градиент».
Теперь вернемся к идее контурных карт, которую мы представили в разделе «Функции нескольких переменных». Мы можем использовать контурную карту для оценки частных производных функции g(x,y).g(x,y).
Пример 4.16
Частные производные по контурной карте
Используйте контурную карту для оценки ∂g/∂x∂g/∂x в точке (5,0)(5,0) для функции g(x,y)=9 −x2−y2.g(x,y)=9−x2−y2.
Решение
Следующий график представляет контурную карту для функции g(x,y)=9−x2−y2.g(x,y)=9−x2−y2.
Рисунок
4.22
Контурная карта для функции g(x,y)=9−x2−y2,g(x,y)=9−x2−y2 с использованием c=0,1,2,c=0,1,2 и 33 (c=3(c=3 соответствует началу координат).
Внутренний круг на контурной карте соответствует c=2c=2, а следующий за его пределами круг соответствует c=1.c=1. Первый круг дан уравнением 2=9−x2−y2;2=9−x2−y2, вторая окружность задается уравнением 1=9−x2−y2.1=9−x2−y2. Первое уравнение упрощается до x2+y2=5×2+y2=5, а второе уравнение упрощается до x2+y2=8.×2+y2=8. X-interceptx-intercept первого круга равен (5,0)(5,0), а x-interceptx-intercept второго круга равен (22,0).(22,0). Мы можем оценить значение ∂g/∂x∂g/∂x в точке (5,0)(5,0), используя формулу наклона:
∂g∂x|(x,y)=(5 ,0)≈g(5,0)−g(22,0)5−22=2−15−22=15−22≈−1,688.∂g∂x|(x,y)=(5,0) ≈g(5,0)−g(22,0)5−22=2−15−22=15−22≈−1,688.
Чтобы вычислить точное значение ∂g/∂x∂g/∂x в точке (5,0),(5,0), начнем с нахождения ∂g/∂x∂g/∂x с помощью Правило цепи. Во-первых, мы перепишем функцию как g(x,y)=9−x2−y2=(9−x2−y2)1/2g(x,y)=9−x2−y2=(9−x2−y2)1/2, а затем продифференцируем по xx, сохраняя yy постоянным:
∂g∂x=12(9−x2−y2)−1/2(−2x)=−x9−x2−y2.∂g∂x=12(9−x2−y2)−1/2(−2x )=-x9-x2-y2.
Затем мы оцениваем это выражение, используя x=5x=5 и y=0:y=0:
∂g∂x|(x,y)=(5,0)=−59−(5)2− (0)2=−54=−52≈−1,118.∂g∂x|(x,y)=(5,0)=−59−(5)2−(0)2=−54=−52≈ −1,118.
Оценка частной производной соответствует наклону секущей, проходящей через точки (5,0,g(5,0))(5,0,g(5,0)) и (22,0, г(22,0)).(22,0,г(22,0)). Он представляет собой аппроксимацию наклона касательной к поверхности через точку (5,0,g(5,0)),(5,0,g(5,0)), которая параллельна x- ось.x-ось.
Контрольно-пропускной пункт 4.14
Используйте контурную карту для оценки ∂f/∂y∂f/∂y в точке (0,2)(0,2) для функции
f(x,y)=x2−y2.f(x, у)=х2-у2.
Сравните с точным ответом.
Функции более чем двух переменных
Предположим, у нас есть функция трех переменных, например, w=f(x,y,z).w=f(x,y,z). Мы можем вычислять частные производные ww по любой из независимых переменных просто как расширение определений частных производных функций двух переменных.
Определение
Пусть f(x,y,z)f(x,y,z) функция трех переменных. Тогда частная производная ff по x, записанная как ∂f/∂x,∂f/∂x или fx,fx, определяется как
∂f∂x=limh→0f(x+ h,y,z)−f(x,y,z)h.∂f∂x=limh→0f(x+h,y,z)−f(x,y,z)h.
(4.14)
Частная производная от ff по отношению к y,y, записанная как ∂f/∂y,∂f/∂y или fy,fy, определяется как
∂f ∂y=limk→0f(x,y+k,z)−f(x,y,z)k.∂f∂y=limk→0f(x,y+k,z)−f(x,y, я)к.
(4.15)
Частная производная от ff относительно z,z, записанная как ∂f/∂z,∂f/∂z или fz,fz, определяется как
∂f ∂z=limm→0f(x,y,z+m)−f(x,y,z)m.∂f∂z=limm→0f(x,y,z+m)−f(x,y, я) м.
(4.16)
Мы можем вычислить частную производную функции трех переменных, используя ту же идею, что и для функции двух переменных. Например, если у нас есть функция ff от x, y и z, x, y и z, и мы хотим вычислить ∂f/∂x, ∂f/∂x, то мы рассматриваем две другие независимые переменные, как если бы они константы, то продифференцируем по х. х.
Пример 4.17
Вычисление частных производных для функции трех переменных
Использование предельного определения частных производных для вычисления ∂f/∂x∂f/∂x для функции
f(x,y,z)=x2−3xy+ 2y2−4xz+5yz2−12x+4y−3z.f(x,y,z)=x2−3xy+2y2−4xz+5yz2−12x+4y−3z.
Затем найдите ∂f/∂y∂f/∂y и ∂f/∂z∂f/∂z, установив две другие переменные постоянными и продифференцировав их соответствующим образом.
Решение
Сначала мы вычисляем ∂f/∂x∂f/∂x, используя уравнение 4.14, затем мы вычисляем две другие частные производные, сохраняя остальные переменные постоянными. Чтобы использовать уравнение для нахождения ∂f/∂x,∂f/∂x, нам сначала нужно вычислить f(x+h,y,z):f(x+h,y,z):
f(x+h,y,z)=(x+h)2−3(x+h)y+2y2−4(x+h)z+5yz2−12(x+h)+4y−3z =x2+2xh+h3−3xy−3xh+2y2−4xz−4hz+5yz2−12x−12h+4y−3zf(x+h,y,z)=(x+h)2−3(x+h)y +2y2-4(x+h)z+5yz2-12(x+h)+4y-3z=x2+2xh+h3-3xy-3xh+2y2-4xz-4hz+5yz2-12x-12h+4y-3z
и вспомним, что f(x,y,z)=x2−3xy+2y2−4zx+5yz2−12x+4y−3z. f(x,y,z)=x2−3xy+2y2−4zx+5yz2−12x+ 4у-3з. Далее подставляем эти два выражения в уравнение: 3xy+2y2−4xz+5yz2−12x+4y−3zh]=limh→0[2xh+h3−3hy−4hz−12hh]=limh→0[h(2x+h−3y−4z−12)h]=limh →0(2x+h−3y−4z−12)=2x−3y−4z−12.∂f∂x=limh→0[x2+2xh+h3−3xy−3hy+2y2−4xz−4hz+5yz2−12x −12h+4y−3zh−x2−3xy+2y2−4xz+5yz2−12x+4y−3zh]=limh→0[2xh+h3−3hy−4hz−12hh]=limh→0[h(2x+h−3y −4z−12)h]=limh→0(2x+h−3y−4z−12)=2x−3y−4z−12.
Затем мы находим ∂f/∂y∂f/∂y, считая xandzxandz постоянными. Следовательно, любое слагаемое, не включающее переменную yy, является константой, а его производная равна нулю. Мы можем применить правила суммы, разности и степени для функций одной переменной: [3xy]+∂∂y[2y2]−∂∂y[4xz]+∂∂y[5yz2]−∂∂y[12x]+∂∂y[4y]−∂∂y[3z]=0−3x+ 4y−0+5z2−0+4−0=−3x+4y+5z2+4.∂∂y[x2−3xy+2y2−4xz+5yz2−12x+4y−3z]=∂∂y[x2]−∂ ∂y[3xy]+∂∂y[2y2]−∂∂y[4xz]+∂∂y[5yz2]−∂∂y[12x]+∂∂y[4y]−∂∂y[3z]=0− 3x+4y-0+5z2-0+4-0=-3x+4y+5z2+4.
Чтобы вычислить ∂f/∂z,∂f/∂z, мы считаем x и y постоянными и применяем правила суммы, разности и степени для функций одной переменной:
∂∂z[x2− 3xy+2y2−4xz+5yz2−12x+4y−3z]=∂∂z[x2]−∂∂z[3xy]+∂∂z[2y2]−∂∂z[4xz]+∂∂z[5yz2]− ∂∂z[12x]+∂∂z[4y]−∂∂z[3z]=0−0+0−4x+10yz−0+0−3=−4x+10yz−3. ∂∂z[x2− 3xy+2y2−4xz+5yz2−12x+4y−3z]=∂∂z[x2]−∂∂z[3xy]+∂∂z[2y2]−∂∂z[4xz]+∂∂z[5yz2]− ∂∂z[12x]+∂∂z[4y]−∂∂z[3z]=0−0+0−4x+10yz−0+0−3=−4x+10yz−3.
Контрольно-пропускной пункт 4.15
Используйте предельное определение частных производных для вычисления ∂f/∂x∂f/∂x для функции
f(x,y,z)=2×2−4x2y+2y2+5xz2−6x+3z−8.f( x,y,z)=2×2−4x2y+2y2+5xz2−6x+3z−8.
Затем найдите ∂f/∂y∂f/∂y и ∂f/∂z∂f/∂z, установив две другие переменные постоянными и продифференцировав их соответствующим образом.
Пример 4.18
Вычисление частных производных функции трех переменных
Вычислите три частные производные следующих функций.
Решение
В каждом случае рассматривайте все переменные как константы, кроме той, чью частную производную вы вычисляете.
Контрольно-пропускной пункт 4.
16Рассчитать ∂f/∂x,∂f/∂x,∂f/∂y,∂f/∂y и ∂f/∂z∂f/∂z для функции f(x,y,z)= sec(x2y)−tan(x3yz2).f(x,y,z)=sec(x2y)−tan(x3yz2).
Частные производные высшего порядка
Рассмотрим функцию
f(x,y)=2×3−4xy2+5y3−6xy+5x−4y+12.f(x,y)=2×3−4xy2+5y3−6xy+5x−4y+12.
Его частные производные равны
∂f∂x=6×2−4y2−6y+5 и ∂f∂y=−8xy+15y2−6x−4.∂f∂x=6×2−4y2−6y+5and∂f∂y=−8xy+15y2−6x −4.
Каждая из этих частных производных является функцией двух переменных, поэтому мы можем вычислить частные производные этих функций. Как и в случае с производными функций одной переменной, мы можем назвать эти производных второго порядка, производных третьего порядка и так далее. Обычно их называют частными производными высшего порядка. Для любой функции существует четыре частных производных второго порядка (при условии, что они все существуют):
∂2f∂x2=∂∂x[∂f∂x],∂2f∂x∂y=∂∂x[∂f∂y],∂2f∂y∂x=∂∂y[∂f∂x], ∂2f∂y2=∂∂y[∂f∂y]. ∂2f∂x2=∂∂x[∂f∂x],∂2f∂x∂y=∂∂x[∂f∂y],∂2f∂ y∂x=∂∂y[∂f∂x],∂2f∂y2=∂∂y[∂f∂y].
Альтернативное обозначение для каждого: fxx,fyx,fxy,fxx,fyx,fxy и fyy,fyy соответственно. Частные производные более высокого порядка, вычисленные по разным переменным, таким как fxyfxy и fyx,fyx, обычно называются смешанными частными производными.
Пример 4.19
Вычисление вторых частных производных
Вычисление всех четырех вторых частных производных для функции
f(x,y)=xe−3y+sin(2x−5y).f(x,y)=xe−3y+sin( 2x−5y).
Решение
Чтобы вычислить ∂2f/dx2∂2f/dx2 и ∂2f/∂y∂x,∂2f/∂y∂x, мы сначала вычисляем ∂f/∂x:∂f/∂x:
∂f∂x= e−3y+2cos(2x−5y).∂f∂x=e−3y+2cos(2x−5y).
Чтобы вычислить ∂2f/dx2,∂2f/dx2, продифференцируйте ∂f/∂x∂f/∂x по x:x:
∂2f∂x2=∂∂x[∂f∂x]=∂∂x[e−3y+2cos(2x−5y)]=−4sin(2x−5y).∂2f∂x2=∂∂x[ ∂f∂x]=∂∂x[e−3y+2cos(2x−5y)]=−4sin(2x−5y).
Чтобы вычислить ∂2f/∂y∂x,∂2f/∂y∂x, продифференцируйте ∂f/∂x∂f/∂x по y:y:
∂2f∂y∂x=∂∂y [∂f∂x]=∂∂y[e−3y+2cos(2x−5y)]=−3e−3y+10sin(2x−5y). ∂2f∂y∂x=∂∂y[∂f∂x ]=∂∂y[e−3y+2cos(2x−5y)]=−3e−3y+10sin(2x−5y).
Чтобы вычислить ∂2f/∂x∂y∂2f/∂x∂y и ∂2f/dy2,∂2f/dy2, сначала вычислите ∂f/∂y:∂f/∂y:
∂f∂y= −3xe−3y−5cos(2x−5y).∂f∂y=−3xe−3y−5cos(2x−5y).
Чтобы вычислить ∂2f/∂x∂y,∂2f/∂x∂y, продифференцируйте ∂f/∂y∂f/∂y по x:x:
∂2f∂x∂y=∂∂x[ ∂f∂y]=∂∂x[−3xe−3y−5cos(2x−5y)]=−3e−3y+10sin(2x−5y).∂2f∂x∂y=∂∂x[∂f∂y ]=∂∂x[−3xe−3y−5cos(2x−5y)]=−3e−3y+10sin(2x−5y).
Чтобы вычислить ∂2f/∂y2,∂2f/∂y2, продифференцируйте ∂f/∂y∂f/∂y по отношению y:y:
∂2f∂y2=∂∂y[∂f∂y] =∂∂y[−3xe−3y−5cos(2x−5y)]=9xe−3y−25sin(2x−5y).∂2f∂y2=∂∂y[∂f∂y]=∂∂y[−3xe −3y−5cos(2x−5y)]=9xe−3y−25sin(2x−5y).
Контрольно-пропускной пункт 4.17
Вычислите все четыре вторые частные производные для функции
f(x,y)=sin(3x−2y)+cos(x+4y).f(x,y)=sin(3x−2y)+cos(x+4y).
Здесь мы должны заметить, что и в примере 4.19, и в контрольной точке было верно, что ∂2f/∂x∂y=∂2f/∂y∂x.∂2f/∂x∂y=∂2f/∂y ∂х. При определенных условиях это всегда так. На самом деле это прямое следствие следующей теоремы.
Теорема 4,5
Равенство смешанных частных производных (теорема Клеро)
Предположим, что f(x,y)f(x,y) определено на открытом диске DD, содержащем точку (a,b).(a,b). Если функции fxyfxy и fyxfyx непрерывны на D,D, то fxy=fyx.fxy=fyx.
Теорема Клеро гарантирует, что пока смешанные производные второго порядка непрерывны, порядок, в котором мы выбираем дифференцирование функций (т. е. какая переменная идет первой, затем второй и т. д.), не имеет значения. Его можно распространить и на производные более высокого порядка. Доказательство теоремы Клеро можно найти в большинстве учебников по математическому анализу.
Две другие частные производные второго порядка можно вычислить для любой функции f(x,y).f(x,y). Частная производная fxxfxx равна частной производной fxfx по x,x, а fyyfyy равна частной производной fyfy по y.y.
Уравнения с частными производными
Во Введении в дифференциальные уравнения мы изучали дифференциальные уравнения, в которых неизвестная функция имеет одну независимую переменную. Уравнение в частных производных — это уравнение, в котором есть неизвестная функция более чем одной независимой переменной и одна или несколько ее частных производных. Примеры дифференциальных уравнений в частных производных:
ut=c2(uxx+uyy)ut=c2(uxx+uyy)
(4.17)
(уравнение теплопроводности в двух измерениях)
utt=c2(uxx+uyy)utt=c2(uxx+uyy)
(4.18)
(волновое уравнение в двух измерениях)
uxx+uyy=0uxx+uyy=0
(4.19)
(уравнение Лапласа в двух измерениях)
В первых двух уравнениях неизвестная функция uu имеет три независимые переменные — t, x, andyt, x, andy — и cc — произвольная константа. Независимые переменные xandyxandy считаются пространственными переменными, а переменная tt представляет время. В уравнении Лапласа неизвестная функция uu имеет две независимые переменные xandy.xandy.
Пример 4.
20Решение волнового уравнения
Убедитесь, что
u(x,y,t)=5sin(3πx)sin(4πy)cos(10πt)u(x,y,t)=5sin(3πx)sin( 4πy)cos(10πt)
является решением волнового уравнения
utt=4(uxx+uyy).utt=4(uxx+uyy).
(4.20)
Решение
Сначала мы вычисляем utt,uxx,utt,uxx и uyy:uyy:
utt=∂∂t[∂u∂t]=∂∂t[5sin(3πx)sin(4πy)(−10πsin(10πt) )]=∂∂t[−50πsin(3πx)sin(4πy)sin(10πt)]=−500π2sin(3πx)sin(4πy)cos(10πt)uxx=∂∂x[∂u∂x]=∂∂x [15πcos(3πx)sin(4πy)cos(10πt)]=−45π2sin(3πx)sin(4πy)cos(10πt)uyy=∂∂y[∂u∂y]=∂∂y[5sin(3πx)(4πcos (4πy))cos(10πt)]=∂∂y[20πsin(3πx)cos(4πy)cos(10πt)]=−80π2sin(3πx)sin(4πy)cos(10πt).utt=∂∂t[∂u ∂t]=∂∂t[5sin(3πx)sin(4πy)(−10πsin(10πt))]=∂∂t[−50πsin(3πx)sin(4πy)sin(10πt)]=−500π2sin(3πx)sin (4πy)cos(10πt)uxx=∂∂x[∂u∂x]=∂∂x[15πcos(3πx)sin(4πy)cos(10πt)]=−45π2sin(3πx)sin(4πy)cos(10πt) uyy=∂∂y[∂u∂y]=∂∂y[5sin(3πx)(4πcos(4πy))cos(10πt)]=∂∂y[20πsin(3πx)cos(4πy)cos(10πt)]= −80π2sin(3πx)sin(4πy)cos(10πt).
Затем мы подставляем каждое из них в правую часть уравнения 4.20 и упрощаем: )sin(4πy)cos(10πt))=4(−125π2sin(3πx)sin(4πy)cos(10πt))=−500π2sin(3πx)sin(4πy)cos(10πt)=utt.4(uxx+uyy) =4(−45π2sin(3πx)sin(4πy)cos(10πt)+−80π2sin(3πx)sin(4πy)cos(10πt))=4(−125π2sin(3πx)sin(4πy)cos(10πt))=− 500π2sin(3πx)sin(4πy)cos(10πt)=utt.
Это подтверждает решение.
Контрольно-пропускной пункт 4.18
Убедитесь, что u(x,y,t)=2sin(x3)sin(y4)e−25t/16u(x,y,t)=2sin(x3)sin(y4)e−25t/16 является решением к уравнению теплопроводности
ut=9(uxx+uyy).ut=9(uxx+uyy).
(4.21)
Поскольку решение двумерного уравнения теплопроводности является функцией трех переменных, создать визуальное представление решения непросто. Мы можем построить график решения для фиксированных значений t , что составляет моментальные снимки распределения тепла в фиксированные моменты времени. Эти снимки показывают, как тепло распределяется по двумерной поверхности с течением времени. График предыдущего решения в момент времени t=0t=0 показан на следующем рисунке. С течением времени крайности выравниваются, приближаясь к нулю как 9.1084 t приближается к бесконечности.
Рисунок 4.23
Если рассматривать уравнение теплопроводности в одном измерении, то можно построить график решения во времени. Уравнение теплопроводности в одном измерении принимает вид
.ут=с2ухх,ут=с2ухх,
, где c2c2 представляет собой коэффициент температуропроводности рассматриваемого материала. Решение этого дифференциального уравнения можно записать в виде
um(x,t)=e−π2m2c2tsin(mπx)um(x,t)=e−π2m2c2tsin(mπx)
(4.22)
, где mm — любое положительное целое число. График этого решения с использованием m=1m=1 показан на рис. 4.24, где начальное распределение температуры по проводу длиной 11 дано как u(x,0)=sinπx.u(x,0)=sinπx. Обратите внимание, что со временем провод остывает. Это видно потому, что слева направо самая высокая температура (которая возникает в середине провода) уменьшается и меняет цвет с красного на синий.
Рисунок 4,24 График решения уравнения теплопроводности в одном измерении во времени.
Студенческий проект
Лорд Кельвин и эпоха Земли
Рисунок 4,25 (а) Уильям Томсон (лорд Кельвин), 1824–1907 гг., был британским физиком и инженером-электриком; (б) Кельвин использовал уравнение диффузии тепла для оценки возраста Земли (кредит: модификация работы НАСА).
В конце 1800-х ученые новой области геологии пришли к выводу, что Земле должно быть «миллионы и миллионы» лет. Примерно в то же время Чарльз Дарвин опубликовал свой трактат об эволюции. Дарвин считал, что для эволюции потребовалось много миллионов лет, и он сделал смелое заявление о том, что меловые поля Уилда, где были обнаружены важные окаменелости, были результатом 300–300 миллионов лет эрозии.
В то время выдающийся физик Уильям Томсон (лорд Кельвин) использовал важное дифференциальное уравнение в частных производных, известное как уравнение диффузии тепла , для оценки возраста Земли, определяя, сколько времени потребуется Земле, чтобы остыть от расплавленной породы до что у нас было на тот момент. Его заключение заключалось в диапазоне от 20 до 400–20–400 миллионов лет, но, скорее всего, около 50–50 миллионов лет. На протяжении многих десятилетий заявления этого неопровержимого символа науки не нравились ни геологам, ни Дарвину.
СМИ
Прочтите статью Кельвина об оценке возраста Земли.
Кельвин сделал разумные предположения, основанные на том, что было известно в его время, но он также сделал несколько предположений, которые оказались неверными. Одно неверное предположение заключалось в том, что Земля твердая и поэтому охлаждение происходило только за счет теплопроводности, что оправдывало использование уравнения диффузии. Но самая серьезная ошибка была простительна — упущение того факта, что Земля содержит радиоактивные элементы, которые постоянно поставляют тепло под мантию Земли. Открытие радиоактивности произошло ближе к концу жизни Кельвина, и он признал, что его расчеты должны быть изменены.
Кельвин использовал простую одномерную модель, применимую только к внешней оболочке Земли, и вычислил возраст по графикам и приблизительно известному температурному градиенту у поверхности Земли. Рассмотрим более подходящий вариант уравнения диффузии в радиальных координатах, который имеет вид
∂T∂t=K[∂2T∂2r+2r∂T∂r].∂T∂t=K[∂ 2T∂2r+2r∂T∂r].
(4.23)
Здесь T(r,t)T(r,t) — температура как функция rr (отсчитывается от центра Земли), а время t.t.KK — теплопроводность — для расплавленной породы в этот случай. Стандартным методом решения такого уравнения в частных производных является разделение переменных, когда мы выражаем решение как произведение функций, содержащих каждую переменную отдельно. В этом случае мы запишем температуру как
T(r,t)=R(r)f(t).T(r,t)=R(r)f(t).
Обратите внимание, как значения αnαn получаются из граничного условия, примененного в части b. Член −1n−1n−1n−1n представляет собой константу AnAn для каждого члена ряда, определяемую методом Фурье. Пусть β=πRE,β=πRE, изучите первые несколько членов этого решения, показанного здесь, и обратите внимание, как λ2λ2 в экспоненциальной зависимости вызывает быстрое уменьшение высших членов с течением времени:
T(r,t)=T0REπr(e− Kβ2t(sinβr)−12e−4Kβ2t(sin2βr)+13e−9Kβ2t(sin3βr)−14e−16Kβ2t(sin4βr)+15e−25Kβ2t(sin5βr)…).T(r,t)=T0REπr(e−Kβ2t( sinβr)−12e−4Kβ2t(sin2βr)+13e−9Kβ2t(sin3βr)−14e−16Kβ2t(sin4βr)+15e−25Kβ2t(sin5βr)…).
Вблизи времени t=0,t=0, для точности требуется много членов решения. Если ввести значения проводимости KK и β=π/RE β=π/RE для времени, приближающегося к тысячам лет, то только первые несколько членов вносят существенный вклад. Кельвину нужно было только взглянуть на решение у поверхности Земли (рис. 4.26) и, по прошествии длительного времени, определить, какое время лучше всего дает расчетный температурный градиент, известный в его эпоху (1°F (1°F увеличение на 50 футов).50 футов). . Он просто выбрал диапазон времен с градиентом, близким к этому значению. На рис. 4.26 решения нанесены на график и в масштабе с добавлением температуры поверхности 300–300–К. Обратите внимание, что в центре Земли было бы относительно прохладно. В то время считалось, что Земля должна быть твердой.
Рисунок 4,26 Температура в зависимости от радиального расстояния от центра Земли. (а) Результаты Кельвина в масштабе. (b) Крупный план результатов на глубине 4,0 мили4,0 мили ниже поверхности Земли.
Эпилог
20 мая 1904, 20 мая 1904 года физик Эрнест Резерфорд выступил в Королевском институте, чтобы объявить о пересмотренных расчетах, которые включали вклад радиоактивности как источника тепла Земли. По собственным словам Резерфорда:
«Я вошел в комнату, где было полутемно, и вскоре заметил в аудитории лорда Кельвина, и понял, что меня ждут неприятности в последней части моей речи, посвященной эпохе Земля, где мои взгляды расходились с его. К моему облегчению, Кельвин крепко уснул, но когда я дошел до важного момента, я увидел, как старая птица села, открыла глаз и бросила на меня злобный взгляд. 9. Это пророческое высказывание относилось к тому, что мы сейчас рассматриваем сегодня вечером, к радию! Вот! Старик лучезарно смотрел на меня.
Резерфорд вычислил возраст Земли примерно в 500500 миллионов лет. Принятое сегодня значение возраста Земли составляет около 4,64,6 миллиарда лет.
Раздел 4.3 Упражнения
Для следующих упражнений вычислите частную производную, используя только определения пределов.
112.
∂z∂x∂z∂x для z=x2−3xy+y2z=x2−3xy+y2
113.
∂z∂y∂z∂y для z=x2−3xy+y2z=x2−3xy+y2
В следующих упражнениях вычислите знак частной производной, используя график поверхности.
114.
фх(1,1)фх(1,1)
115.
fx(−1,1)fx(−1,1)
116.
фу(1,1)фу(1,1)
117.
FX(0,0)FX(0,0)
Для следующих упражнений вычислите частные производные.
118.
∂z∂x∂z∂x для z=sin(3x)cos(3y)z=sin(3x)cos(3y)
119.
∂z∂y∂z∂y для z=sin(3x)cos(3y)z=sin(3x)cos(3y)
120.
∂z∂x∂z∂x и ∂z∂y∂z∂y для z=x8e3yz=x8e3y
121.
∂z∂x∂z∂x и ∂z∂y∂z∂y для z=ln(x6+y4)z=ln(x6+y4)
122.
Найти fy(x,y)fy(x,y) для f(x,y)=exycos(x)sin(y). f(x,y)=exycos(x)sin(y).
123.
Пусть z=exy.z=exy. Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.
124.
Пусть z=ln(xy).z=ln(xy). Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.
125.
Пусть z=tan(2x−y).z=tan(2x−y). Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.
126.
Пусть z=sinh(2x+3y).z=sinh(2x+3y). Найдите ∂z∂x∂z∂x и ∂z∂y.∂z∂y.
127.
Пусть f(x,y)=arctan(yx).f(x,y)=arctan(yx). Вычислите fx(2,−2)fx(2,−2) и fy(2,−2).fy(2,−2).
128.
Пусть f(x,y)=xyx−y.f(x,y)=xyx−y. Найдите fx(2,−2)fx(2,−2) и fy(2,−2).fy(2,−2).
Вычислить частные производные в точке P(0,1).P(0,1).
129.
Найти ∂z∂x∂z∂x в (0,1)(0,1) для z=e−xcos(y).z=e−xcos(y).
130.
Для заданных f(x,y,z)=x3yz2,f(x,y,z)=x3yz2 найдите ∂2f∂x∂y∂2f∂x∂y и fz(1,1,1). fz( 1,1,1).
131.
Учитывая f(x,y,z)=2sin(x+y),f(x,y,z)=2sin(x+y), найти fx(0,π2,−4),fx(0, π2,−4),fy(0,π2,−4),fy(0,π2,−4) и fz(0,π2,−4).fz(0,π2,−4).
132.
Площадь параллелограмма с длинами смежных сторон, равными a и b, a и b, и в котором угол между этими двумя сторонами равен θ, θ, определяется функцией A(a,b,θ)=basin(θ). A (a, b, θ) = бассейн (θ). Найдите скорость изменения площади параллелограмма по отношению к следующим сторонам:
133.
Выразите объем прямого кругового цилиндра как функцию двух переменных:
134.
Рассчитать ∂w∂z∂w∂z для w=zsin(xy2+2z).w=zsin(xy2+2z).
Найдите указанные частные производные высшего порядка.
135.
fxyfxy для z=ln(x−y)z=ln(x−y)
136.
fyxfyx для z=ln(x−y)z=ln(x−y)
137.
Пусть z=x2+3xy+2y2.z=x2+3xy+2y2. Найдите ∂2z∂x2∂2z∂x2 и ∂2z∂y2.∂2z∂y2.
138.
Зная z=extany,z=extany, найти ∂2z∂x∂y∂2z∂x∂y и ∂2z∂y∂x.∂2z∂y∂x.
139.
Учитывая f(x,y,z)=xyz,f(x,y,z)=xyz, найдите fxyy,fyxy,fxyy,fyxy и fyyx.fyyx.
140.
Для заданных f(x,y,z)=e−2xsin(z2y),f(x,y,z)=e−2xsin(z2y) покажите, что fxyy=fyxy. fxyy=fyxy.
141.
Показать, что z=12(ey−e−y)sinxz=12(ey−e−y)sinx является решением дифференциального уравнения ∂2z∂x2+∂2z∂y2=0,∂2z∂x2+∂2z∂ у2=0.
142.
Найдите fxx(x,y)fxx(x,y) для f(x,y)=4x2y+y22x.f(x,y)=4x2y+y22x.
143.
Пусть f(x,y,z)=x2y3z−3xy2z3+5x2z−y3z.f(x,y,z)=x2y3z−3xy2z3+5x2z−y3z. Найдите fxyz.fxyz.
144.
Пусть F(x,y,z)=x3yz2−2x2yz+3xz−2y3z.F(x,y,z)=x3yz2−2x2yz+3xz−2y3z. Найдите Fxyz.Fxyz.
145.
Для данных f(x,y)=x2+x−3xy+y3−5,f(x,y)=x2+x−3xy+y3−5 найти все точки, в которых fx=fy=0fx=fy= 0 одновременно.
146.
Для данных f(x,y)=2×2+2xy+y2+2x−3,f(x,y)=2×2+2xy+y2+2x−3 найти все точки, в которых ∂f∂x=0∂f ∂x=0 и ∂f∂y=0∂f∂y=0 одновременно.
147.
Для данных f(x,y)=y3−3yx2−3y2−3×2+1,f(x,y)=y3−3yx2−3y2−3×2+1 найти все точки на ff, в которых fx=fy=0fx= fy=0 одновременно.
148.
Для данных f(x,y)=15×3−3xy+15y3,f(x,y)=15×3−3xy+15y3 найти все точки, в которых fx(x,y)=fy(x,y)=0fx( x,y)=fy(x,y)=0 одновременно.
149.
Покажите, что z=exsinyz=exsiny удовлетворяет уравнению ∂2z∂x2+∂2z∂y2=0,∂2z∂x2+∂2z∂y2=0.
150.
Показать, что f(x,y)=ln(x2+y2)f(x,y)=ln(x2+y2) решает уравнение Лапласа ∂2z∂x2+∂2z∂y2=0,∂2z∂x2+∂2z ∂y2=0.
151.
Показать, что z=e−tcos(xc)z=e−tcos(xc) удовлетворяет уравнению теплопроводности ∂z∂t=c2∂2z∂x2∂z∂t=c2∂2z∂x2
152.
Найти limΔx→0f(x+Δx, y)−f(x,y)ΔxlimΔx→0f(x+Δx, y)−f(x,y)Δx для f(x,y)=−7x−2xy +7y.f(x,y)=−7x−2xy+7y.
153.
Найти limΔy→0f(x,y+Δy)−f(x,y)ΔylimΔy→0f(x,y+Δy)−f(x,y)Δy для f(x,y)=−7x−2xy +7y. f(x,y)=−7x−2xy+7y.
154.
Найти limΔx→0ΔfΔx=limΔx→0f(x+Δx,y)−f(x,y)ΔxlimΔx→0ΔfΔx=limΔx→0f(x+Δx,y)−f(x,y)Δx для f(x ,y)=x2y2+xy+y.f(x,y)=x2y2+xy+y.
155.
Найти limΔx→0ΔfΔx=limΔx→0f(x+Δx,y)−f(x,y)ΔxlimΔx→0ΔfΔx=limΔx→0f(x+Δx,y)−f(x,y)Δx для f(x ,y)=sin(xy).f(x,y)=sin(xy).
156.
Функция P(T,V)=nRTVP(T,V)=nRTV дает давление в точке газа как функцию температуры TT и объема V.V. Буквы nandRnandR являются константами. Найдите ∂P∂V∂P∂V и ∂P∂T,∂P∂T и объясните, что представляют собой эти величины.
157.
Уравнение для теплового потока в плоскости xy-xy: Покажите, что f(x,y,t)=e−2tsinxsinyf(x,y,t)=e−2tsinxsiny является решением.
158.
Основное волновое уравнение: ftt=fxx.ftt=fxx. Убедитесь, что f(x,t)=sin(x+t)f(x,t)=sin(x+t) и f(x,t)=sin(x−t)f(x,t)=sin (x−t) являются решениями.
159.
Закон косинусов можно рассматривать как функцию трех переменных. Пусть x, y, x, y и θθ — две стороны любого треугольника, где угол θθ — это внутренний угол между двумя сторонами. Тогда F(x,y,θ)=x2+y2−2xycosθF(x,y,θ)=x2+y2−2xycosθ дает квадрат третьей стороны треугольника. Найдите ∂F∂θ∂F∂θ и ∂F∂x∂F∂x, когда x=2,y=3,x=2,y=3 и θ=π6.θ=π6.
160.
Предположим, что стороны прямоугольника изменяются во времени. Первая сторона изменяется со скоростью 22 дюйма в секунду, тогда как вторая сторона изменяется со скоростью 44 дюйма в секунду. Как быстро изменится диагональ прямоугольника, если длина первой стороны 1616 дюймов, а второй стороны 2020 дюймов? (Округленный ответ до трех знаков после запятой.)
161.
Производственная функция Кобба-Дугласа имеет вид f(x,y)=200×0,7y0,3,f(x,y)=200×0,7y0,3, где xandyxandy представляют количество доступного труда и капитала.