Использование и применение формул массы через плотность и объём
Физика — наука невероятно увлекательная, если разобраться, что там к чему. А формулы в ней отражают реальные физические процессы, только в цифрах. И если вы будете понимать, почему формула именно такова, то учиться будет много легче. Но все сразу рассказать невозможно, и сегодня мы разберемся, как произвести нахождение массы через плотность и объём.
Прежде, чем приступить к изучению формул массы, плотности и объёма, следует уточнить некоторые детали:
- Во-первых, объём вещества зависит от температуры. При нагревании твёрдое вещество расширяется, при низкой температуре уменьшается. Есть также особые моменты, как в случае с жидким водородом. Он не может существовать при высокой температуре, потому что превратится в газ.
- Во-вторых, разные организации и страны имеют свои стандарты условий, при которых проводятся измерения.
 Иными словами, числовой показатель плотности одного и того же вещества в разных странах будет отличаться. Поэтому, прежде чем утверждать, что показатели неверные или правильные, следует уточнить условия, при которых эти показатели были получены.
Иными словами, числовой показатель плотности одного и того же вещества в разных странах будет отличаться. Поэтому, прежде чем утверждать, что показатели неверные или правильные, следует уточнить условия, при которых эти показатели были получены. - В-третьих, помимо температуры, на фактор объёма могут влиять и такие показатели, как атмосферное давление. Оно особо важно при измерении плотности газов, так как на твёрдые вещества это практически не влияет.
Содержание:
- Формула и удивительная история её возникновения
- Обозначения и термины
- Примеры решения задач
- Зачем и кому нужно знать эти формулы
- Видео
Формула и удивительная история её возникновения
Самая обычная формула для большинства случаев имеет вид: m = pV , где m – масса тела, p и V – плотность вещества и его объём, занимаемый в пространстве соответственно. Можно, конечно, не заморачиваться и посчитать всё на онлайн-ресурсах, но знать формулу всё же полезно. Соответственно V = m / p , p = m / V .
Соответственно V = m / p , p = m / V .
Самое интересное – это то, что формулу нашёл мужик, который бегал голышом по улице и был при этом другом царя. Интересно? Тогда следующие три абзаца для вас.
Был в Древней Греции такой царь-тиран, как Гиерон II. Он начал подозревать, что его корону сделали не из чистого золота и ювелиры его облапошили. Но Гиерон не знал, как можно это доказать. Тогда он обратился к умнейшему человеку того времени – Архимеду. Получив приказ разобраться с делами государственной важности, Архимед день за днём стал искать решение вопроса.
Ох, и нелёгкая же задачка выпала учёному. Ведь на то время не было ни нужных формул, ни современных девайсов, ни гугла, чтобы быстренько найти решение. И вот однажды, придя в баню и погрузившись в неё, Архимед заметил, что выливающаяся вода равна по объёму тому, что погружено в воду.
Эврика! – Прокричал Архимед и нагишом поспешил в свою лабораторию проводить опыты. Учёный сложил все данные в своей голове и позже проделал следующий опыт: он взял корону и опустил её в воду. Затем он взял кусок золота такого же веса и опустил его также в воду. Объём вытесненной воды получился разным. Если бы корона была сделана из чистого золота, то её объём и слитка совпали. Это доказывало то, что ювелиры обманули царя. Кто бы мог подумать, что одно из величайших открытий появилось благодаря обманщикам, тирану и учёному.
Затем он взял кусок золота такого же веса и опустил его также в воду. Объём вытесненной воды получился разным. Если бы корона была сделана из чистого золота, то её объём и слитка совпали. Это доказывало то, что ювелиры обманули царя. Кто бы мог подумать, что одно из величайших открытий появилось благодаря обманщикам, тирану и учёному.
Обозначения и термины
Далее будет приведён список понятий и их определение в условиях понятий об измерениях плотности:
- Масса – плотность тела, помноженная на его объём, занимаемый в пространстве. Это также величина, определяющая силу воздействия гравитационного поля на объект.
- Объём – физическая величина, характеризующая количество пространства, занимаемое объектом.
- Плотность определяет то, какое количество вещества умещается в объёме при определённом весе в стандартных условиях.
- Нормальные/стандартные условия в разных организациях имеют свои значения.
 К таким условиям относятся температура окружающей среды, атмосферное давление и в отдельных случаях прочие параметры.
К таким условиям относятся температура окружающей среды, атмосферное давление и в отдельных случаях прочие параметры. - Атмосферное давление – понятие, применяемое больше для газов, так как на их объём имеет большое влияние, нежели на твёрдые вещества. Атмосферное давление можно определить как силу, с которой воздействует воздух на Землю под действием гравитационного поля.
- Температура – физический показатель степени нагрева вещества. Чем больше температура, тем больше объём тела.
Примеры решения задач
Прежде чем приступить к примерам, следует понимать, что если данные даны в килограммах и кубических сантиметрах, то нужно либо сантиметры перевести в метры, либо килограммы перевести в граммы. По такому же принципу надо переводить и остальные данные – миллиметры, тонны и так далее.
Задача 1. Найти массу тела, состоящего из вещества, плотность которого равна 2350 кг/м³ и имеет объём 20 м³. Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.
Применяем стандартную формулу и с лёгкостью находим значение. m = p*V= 2 350 * 20 = 47 000 кг.
Задача 2. Уже известно, что плотность чистого золота без примесей равна 19,32 г/см³. Найти массу драгоценной цепочки из золота, если объём составляет 3,7 см³. Воспользуемся формулой и подставим значения. p = m / V = 19,32/3,7 = 5,22162162 гр.
Задача 3. На склад поставили металл с плотностью 9250 кг/м³. Масса составляет 1,420 тонн. Нужно найти занимаемый металлом объём. Тут нужно сначала перевести либо тонны в килограммы, либо метры в километры. Проще будет воспользоваться первым методом. V = m / p = 1420/9250 = 0.153513514 м³.
Зачем и кому нужно знать эти формулы
В любой стране есть стандарты, по которым производится продукция. Неважно, какая это отрасль – пищевая, химическая или другая. Стандарты также могут быть мировыми. Так вот для того чтобы выпускаемая на заводах продукция соответствовала этим стандартам и нужны знания о плотности, массе и объёме.
Но зачем кому-то придерживаться чьих-то правил? Для начала, эти правила взяты не с потолка. К этому пришли разные бизнесмены со всего мира и нашли оптимальное решение, удовлетворяющее как производителей, так и конечных пользователей продукта. Если бы все выпускали продукцию как им вздумается, то людям было бы очень тяжело выбрать производителя. Ведь даже сейчас, со всеми стандартами и ГОСТами выбор просто огромный.
Кроме того, игнорируя физику и математику, можно выработать продукцию себе же в убыток или сделать продукцию, которая не оправдает ожиданий и будет выглядеть не так, как задумывал производитель. Есть и другие ситуации, где необходимы знания подобного рода – при подсчёте планируемого объёма, который займёт продукция на складе; вес продукции, которую нужно будет перевести и т.д.
Эти знания могут потребоваться инженерам, технологам, конструкторам и прочим профессиям, чья деятельность связана с физическими материалами. Конечно, для простого обывателя эти знания могут и не пригодиться. Однако, стоит вспомнить про случай с Архимедом и тогда вы поймёте, что знания – защита от обмана и настоящая сила!
Однако, стоит вспомнить про случай с Архимедом и тогда вы поймёте, что знания – защита от обмана и настоящая сила!
Видео
В видео очень подробно объясняется, как рассчитать массу и объем тела по его плотности.
формулы для расчета, пояснения, примеры / Справочник :: Бингоскул
Все замечали, что разные вещества, занимающие один объем, весят по-разному. Ведёрко воды весит меньше, чем песка или камней. Вес тела зависит от его плотности – концентрации вещества в единице объема. Рассмотрим связь между этими величинами, способы, как найти массу воды в физике, зная её объём.
Что такое плотность
Плотностью называется скалярная величина, определяющаяся как отношение массы вещества к занимаемому им объёму. Плотность – величина не постоянная, поэтому для многих веществ берётся усреднённое значение, измеренное в нормальных условиях. Так, например, плотность многих встречаемых в повседневной жизни тел зависит от внешних условий. Если говорить о зерне, древесине, грунте, песке, их единица объёма весит тем больше, чем вещество влажнее – в нём больше влаги.
Так, например, плотность многих встречаемых в повседневной жизни тел зависит от внешних условий. Если говорить о зерне, древесине, грунте, песке, их единица объёма весит тем больше, чем вещество влажнее – в нём больше влаги.
На плотность жидкостей заметное влияние оказывает температура: при охлаждении концентрация в единице объёма увеличивается, при нагревании вещество становится менее плотным.
Здесь есть исключения – вода. Её вес, вязкость достигают пика при температуре 4 °C, при охлаждении и нагревании они снижаются. Лёд получается легче, чем вода, поэтому он образовывается на поверхности водоёмов, на дно не опускается.
При измерении плотности пористых, сыпучих материалов указывается его:
- Насыпное значение – реальное, измеряемое без учёта пустот. Например, сыпучие крупы, щебень, известняк.
- Истинное – от занимаемого объёма отнимаются пустоты. Они определяются практическим путём, например, погружением тела в воду, или через ранее вычисленные коэффициенты.

Плотность при переходе вещества между фазовыми состояниями обычно изменяется скачкообразно, наибольшая разница наблюдается при испарении твёрдых веществ – сублимации.
Формула массы жидкости
Плотность в физике обозначается буквой греческого алфавита , измеряется в кг/м3. Зависит от массы тела и объёма, который занимает:
ρ= m : V, где:
- m – масса тела;
- V – объём.
Все ли знают, как найти массу газа через давление и занимаемый им объем? Для этого пользуются формулой Клапейрона-Менделеева:
pV = (m : M) * RT, где:
- p – давление газа;
- M и T– его молярная масса и температура;
- R – постоянная, равняется 8,314 Дж/(моль⋅К).
Для вычисления массы необходимо провести ряд математических операций: разделим обе части уравнения на ρV, затем – умножим на m, получим:
m = pVM : RT.
Рассмотрим, как найти объем детали, погруженной в жидкость, используя приведённую формулу.
Задачи
В ведро цилиндрической формы налили 5 л воды. Её уровень составил 0,4 м. После погружения в ведро тела уровень жидкости поднялся до 0,55 м. Определите его объём.
Дан объём воды: 5 л или 5000 см3, остальные величины переведём в сантиметры для простоты вычислений: 40 см, 55 см.
Объём цилиндра вычисляется по формуле: V = Sосн * H. Найдём площадь основания:
Sосн = V : H = 5000 : 40 = 125 см2.
Далее вычисляем занимаемый водой и деталью объём:
V = Sосн * H = 125 * 55 = 6875 см3.
Высчитываем разницу: 6875 – 5000 = 1875 см3.
Далее рассмотрим, как найти массу жидкости, зная её вес, объём.
Вычислим вес 5-литровой бутыли подсолнечного масла.
Объём известен – 0,005 м3, плотность подсолнечного масла принимают за 920 кг/м3.
Подставим значения в формулу:
m = V * ρ = 0,005 * 920 = 4,6 кг.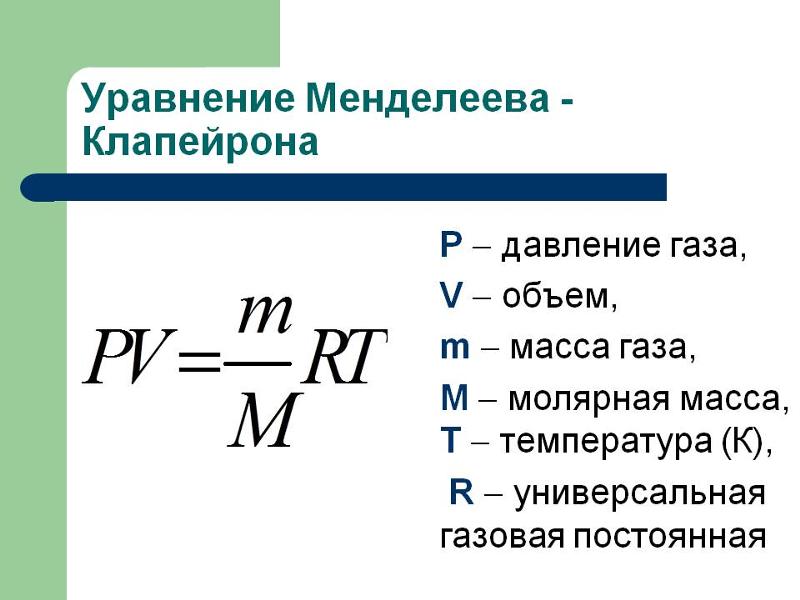
уравнений движения — Гиперучебник по физике
постоянное ускорение
Для точности этот раздел следует назвать «Одномерные уравнения движения при постоянном ускорении». Учитывая, что такое название было бы стилистическим кошмаром, позвольте мне начать этот раздел со следующей оговорки. Эти уравнения движения действительны только тогда, когда ускорение постоянно, а движение ограничено прямой линией.
Учитывая, что мы живем в трехмерной вселенной, в которой единственной константой являются изменения, у вас может возникнуть соблазн сразу пропустить этот раздел. Было бы правильно сказать, что ни один объект никогда не двигался по прямой с постоянным ускорением где-либо во Вселенной в любое время — ни сегодня, ни вчера, ни завтра, ни пять миллиардов лет назад, ни тридцать миллиардов лет в будущем. , никогда. Это я могу сказать с абсолютной метафизической уверенностью.
Так что же хорошего в этом разделе? Что ж, во многих случаях полезно предположить, что объект двигался или будет двигаться по траектории, которая в основном является прямой, и с почти постоянным ускорением; то есть любое отклонение от идеального движения можно по существу игнорировать.
Наша цель в этом разделе состоит в том, чтобы вывести новые уравнения, которые можно использовать для описания движения объекта с точки зрения его трех кинематических переменных: скорости ( v ), положения ( с ) и времени (). т ). Есть три способа их объединения: скорость-время, положение-время и скорость-положение. В таком порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин учить эти названия.
т ). Есть три способа их объединения: скорость-время, положение-время и скорость-положение. В таком порядке их также часто называют первым, вторым и третьим уравнениями движения, но нет веских причин учить эти названия.
Поскольку мы имеем дело с прямолинейным движением, направление будет обозначаться знаком — положительные величины указывают в одну сторону, а отрицательные — в противоположную. Определение того, какое направление является положительным, а какое отрицательным, совершенно произвольно. Законов физики изотропный ; то есть они не зависят от ориентации системы координат. Однако некоторые проблемы легче понять и решить, когда одно направление предпочтительнее другого. Пока вы последовательны в решении проблемы, это не имеет значения.
скорость-время
Соотношение между скоростью и временем является простым во время равноускоренного прямолинейного движения. Чем дольше ускорение, тем больше изменение скорости. Изменение скорости прямо пропорционально времени, если ускорение постоянно. Если скорость увеличивается на определенную величину за определенное время, она должна увеличиться вдвое на эту величину за удвоенное время. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы уже должны уметь видеть уравнение мысленным взором.
Если скорость увеличивается на определенную величину за определенное время, она должна увеличиться вдвое на эту величину за удвоенное время. Если объект уже стартовал с определенной скоростью, то его новая скорость будет равна старой скорости плюс это изменение. Вы уже должны уметь видеть уравнение мысленным взором.
Это самое простое из трех уравнений, которое можно вывести с помощью алгебры. Начните с определения ускорения.
| и = | ∆ по сравнению с |
| ∆ т |
Развернуть ∆ v до v − v 0 и сжать ∆ t до t .
| и = | v − v 0 |
| т |
Затем найдите v как функцию t .
v = v 0 + в [1]
Это первое уравнение движения . Он записывается как полином — постоянный член ( v 0 ), за которым следует член первого порядка ( на ). Поскольку старший порядок равен 1, правильнее называть его линейной 9.0010 функция.
Он записывается как полином — постоянный член ( v 0 ), за которым следует член первого порядка ( на ). Поскольку старший порядок равен 1, правильнее называть его линейной 9.0010 функция.
Символ v 0 [vee nought] называется начальной скоростью или скоростью a time t = 0. Его часто считают «первой скоростью», но это довольно наивный способ Опишите это. Лучшим определением было бы сказать, что начальная скорость — это скорость, которую имеет движущийся объект, когда он впервые становится важным в задаче. Скажем, метеор был замечен глубоко в космосе, и задача состояла в том, чтобы определить его траекторию, тогда начальная скорость, вероятно, была бы скоростью, которую он имел при первом наблюдении. Но если проблема заключалась в том, что тот же самый метеор сгорает при входе в атмосферу, то начальная скорость, вероятно, будет равна скорости, с которой он вошел в атмосферу Земли. Ответ на вопрос «Какова начальная скорость?» это «это зависит».
Символ v — это скорость через некоторое время t после начальной скорости. Ее часто называют конечной скоростью , но это не делает ее «последней скоростью» объекта. Возьмем случай с метеором. Какая скорость представлена символом v ? Если вы были внимательны, то должны были предвидеть ответ. Это зависит. Это может быть скорость метеора при прохождении мимо Луны, при входе в атмосферу Земли или при ударе о поверхность Земли. Это также может быть скорость метеорита, когда он находится на дне кратера. (в этом случае v = 0 м/с.) Любая из них является конечной скоростью? Кто знает. Кто-то мог извлечь метеорит из отверстия в земле и увезти его с собой. Это актуально? Вероятно, нет, но это зависит. Для такого рода вещей нет правил. Вы должны разобрать текст задачи на наличие физических величин, а затем присвоить значение математическим символам.
Последняя часть этого уравнения на представляет собой изменение скорости по сравнению с начальным значением. Напомним, что a — это скорость изменения скорости и что t — это время после некоторого начального события . Скорость раз время меняется. Если объект движется с ускорением 10 м/с 2 , через 5 с он будет двигаться на 50 м/с быстрее. Если бы он стартовал со скоростью 15 м/с, то его скорость через 5 с была бы…
Напомним, что a — это скорость изменения скорости и что t — это время после некоторого начального события . Скорость раз время меняется. Если объект движется с ускорением 10 м/с 2 , через 5 с он будет двигаться на 50 м/с быстрее. Если бы он стартовал со скоростью 15 м/с, то его скорость через 5 с была бы…
15 м/с + 50 м/с = 65 м/с
позиция-время
Перемещение движущегося объекта прямо пропорционально скорости и времени. Двигайся быстрее. Иди дальше. Двигайтесь дольше (как в более длительное время). Иди дальше. Ускорение усложняет эту простую ситуацию, поскольку теперь скорость также прямо пропорциональна времени. Попробуйте сказать это словами, и это прозвучит смешно. «Перемещение прямо пропорционально времени и прямо пропорционально скорости, которая прямо пропорциональна времени». Время является двойным фактором, что делает смещение пропорциональным квадрату времени. Автомобиль, ускоряющийся в течение двух секунд, преодолеет в четыре раза большее расстояние, чем автомобиль, ускоряющийся всего за одну секунду (2, Автомобиль, ускоряющийся в течение трех секунд, преодолеет в девять раз большее расстояние (3 2 = 9).
Автомобиль, ускоряющийся в течение трех секунд, преодолеет в девять раз большее расстояние (3 2 = 9).
Если бы это было так просто. Этот пример работает только тогда, когда начальная скорость равна нулю. Перемещение пропорционально квадрату времени, когда ускорение постоянно, а начальная скорость равна нулю. Правильное общее утверждение должно было бы учитывать любую начальную скорость и то, как скорость изменялась. Это приводит к ужасно беспорядочному заявлению о пропорциональности. Смещение прямо пропорционально времени и пропорционально квадрату времени при постоянном ускорении. Говорят, что функция, которая является одновременно линейной и квадратичной, равна 9.0009 квадратичный , что позволяет нам значительно сжать предыдущее утверждение. Перемещение является квадратичной функцией времени при постоянном ускорении
Заявления о пропорциональности полезны, но не так универсальны, как уравнения. Мы до сих пор не знаем, каковы константы пропорциональности для этой задачи. Один из способов выяснить их — использовать алгебру.
Один из способов выяснить их — использовать алгебру.
Начните с определения средней скорости.
| v = | ∆ с |
| ∆ т |
Развернуть ∆ s до s − s 0 и сжать ∆ t до t .
| v = | с — с 0 |
| т |
Решите для положения.
с = с 0 + вт [а]
Чтобы продолжить, нам нужно прибегнуть к небольшому трюку, известному как теорема о средней скорости или правило Мертона . Я предпочитаю последнее, поскольку это правило можно применить к любой величине, изменяющейся с одинаковой скоростью, а не только к скорости. Правило Мертона было впервые опубликовано в 1335 году в Мертон-колледже в Оксфорде английским философом, математиком, логиком и вычислителем Уильямом Хейтсбери (1313–1372). Когда скорость изменения величины постоянна, ее среднее значение находится посередине между конечным и начальным значениями.
Когда скорость изменения величины постоянна, ее среднее значение находится посередине между конечным и начальным значениями.
v = ½( v + v 0 ) [4]
Подставьте первое уравнение движения [1] в это уравнение [4] и упростите, чтобы исключить v .
| V = ½ [( V 0 + в )+ V 0 ] V = ½ (2 V 999999913 699999999999999999699999999999999999669 69 66999. 69 69 69 69 . v = v 0 + ½ в [б] |
Теперь замените [b] на [a], чтобы исключить и [vee bar].
s = s 0 + ( v 0 + ½ в ) t
И, наконец, найдите s как функцию t .
с = с 0 + v 0 t + ½ в 3 0 2 Это второе уравнение движения . Символ s 0 [эсс ноль] часто рассматривается как начальная позиция . Символ s — это позиция некоторое время t позже. Вы можете назвать это конечной позицией , если хотите. Изменение положения (∆ s ) называется перемещением или расстоянием (в зависимости от обстоятельств), и некоторые люди предпочитают писать второе уравнение движения так. ∆ s = v 0 t + ½ в 2 [2] Каждое из первых двух уравнений движения описывает одну кинематическую переменную как функцию времени. Объединение этих двух утверждений приводит к третьему — тому, что не зависит от времени. Подстановкой должно быть очевидно, что… Это утверждение особенно важно для безопасности вождения. Когда вы удваиваете скорость автомобиля, вам потребуется в четыре раза больше расстояния, чтобы его остановить. Утройте скорость, и вам понадобится в девять раз больше расстояния. Это хорошее практическое правило, которое следует запомнить. Концептуальное введение завершено. Пришло время вывести формальное уравнение. Объедините первые два уравнения вместе таким образом, чтобы исключить время как переменную. v = v 0 + в [1] решить на время… и затем подставляем во второе уравнение движения… с = с 0 + v 0 t + ½ в 2 2 0005 вот так… Сделайте квадрат скорости объекта, и все готово. V 2 = V 0 2 +2 A ( S — S 0 ) [3] Это третье уравнение движения . Еще раз, символ s 0 [ess nought] – это начальная позиция , а s – позиция через какое-то время от до . Если вы предпочитаете, вы можете написать уравнение, используя ∆ s — изменение положения , смещение , или расстояние в зависимости от ситуации. v 2 = v 0 2 + 2 a ∆ с [3] Более сложный способ вывести это уравнение — начать со второго уравнения движения в такой форме… ∆ с = v 0 t + ½ в 2 [2] и решить его на время. ½ в 2 + v 0 t − ∆ с = 0 и сравните его с общей формой квадратичного уравнения. ax 2 + bx + c = 0 Решения этого уравнения дает знаменитое уравнение… Замените символы в общем уравнении эквивалентными символами из нашего перестроенного второго уравнения движения… 3 5) немного почистить… , а затем подставьте его обратно в первое уравнение движения. v = v 0 + в [1] Вещи отменяются, и мы получаем это… v = ±√( v 0 2 + 2 a ∆ s ) Подровняйте обе стороны и готово. v 2 = v 0 2 + 2 a ∆ с [3] Теперь это было не так уж плохо, не так ли? Исчисление — сложная математическая тема, но оно значительно упрощает вывод двух из трех уравнений движения. По определению ускорение есть первая производная скорости по времени. Возьмите операцию в этом определении и отмените ее. Опять же по определению, скорость есть первая производная положения по времени. В отличие от первого и второго уравнений движения, нет очевидного способа вывести третье уравнение движения (которое связывает скорость с положением) с помощью вычислений. Первое уравнение движения связывает скорость со временем. По сути, мы вывели его из этой производной… Второе уравнение движения связывает положение со временем. Это произошло от этой производной… Третье уравнение движения связывает скорость с положением. По логике это должно происходить от производной, которая выглядит так… Но чему это равно? Ну ничего по определению, но, как и все величины, оно равно самому себе. Это также равно самому себе, умноженному на 1. Мы будем использовать специальную версию 1 ( dt dt ) и специальную версию алгебры (алгебра с бесконечно малыми). Следующий шаг, разделение переменных. Безусловно, умное решение, и оно было не намного сложнее, чем первые два вывода. [закрыть] В чем разница между двумя одинаковыми объектами, движущимися с разной скоростью? Почти все знают, что тот, кто движется быстрее (тот, у кого больше скорость), пройдет дальше, чем тот, кто движется медленнее, за то же время. Удвоение скорости означает удвоение пройденного расстояния за заданный промежуток времени. Удвоение скорости также означало бы сокращение вдвое времени, необходимого для преодоления заданного расстояния. Если вы немного разбираетесь в математике, эти утверждения будут значимыми и полезными. (Символ v используется для обозначения скорости из-за связи между скоростью и скоростью, которая будет вскоре обсуждаться.) Объединение этих двух правил дает определение скорости в символической форме. Не нравятся символы? Тогда вот еще один способ определить скорость. Скорость скорость изменения расстояния со временем. Чтобы вычислить скорость объекта, мы должны знать, как далеко он ушел и сколько времени потребовалось, чтобы туда добраться. «Дальше» и «ранее» соответствуют «быстрее». Допустим, вы поехали на машине из Нью-Йорка в Бостон. Расстояние по дороге составляет примерно 300 км (200 миль). Если поездка занимает четыре часа, какова была ваша скорость? Применение приведенной выше формулы дает… Это ответ, который дает нам уравнение, но насколько он верен? Было ли 75 км/ч 91 777 скоростью автомобиля 91 778? Да, конечно, это было… Ну, может быть, я предполагаю… Нет, это не могла быть скорость . Черта между и указывает на среднее или среднее значение, а символ ∆ (дельта) указывает на изменение. Прочитайте это как «Vee bar — это дельта-эсс над дельта-тройником». Это количество мы рассчитали для нашей гипотетической поездки. Напротив, спидометр автомобиля показывает его мгновенную скорость , то есть скорость, определяемую за очень небольшой интервал времени — мгновение. или на языке исчисления скорость есть первая производная расстояния по времени. Если вы не занимались исчислением, не парьтесь слишком сильно с этим определением. Есть и другие, более простые способы определения мгновенной скорости движущегося объекта. На графике расстояние-время скорость соответствует наклону, и, таким образом, мгновенная скорость объекта с непостоянной скоростью может быть найдена по наклону линии, касательной к его кривой. Чтобы вычислить скорость объекта, нам нужно знать, как далеко он ушел и сколько времени потребовалось, чтобы добраться туда. Тогда мудрый человек спросил бы… Что вы подразумеваете под как далеко ? Вам нужно расстояние или смещение ? Мудрый человек, когда-то давно Ваш выбор ответа на этот вопрос определяет, что вы рассчитываете — скорость или скорость. А для любителей исчисления… Скорость и скорость связаны почти так же, как связаны расстояние и перемещение. Смещение измеряется по кратчайшему пути между двумя точками, и его величина всегда меньше или равна расстоянию. Мгновенная скорость объекта равна величине его мгновенной скорости. v = | против | Скорость говорит вам, насколько быстро. Скорость говорит вам, как быстро и в каком направлении. Скорость и скорость измеряются в одних и тех же единицах измерения. Единицей расстояния и перемещения в СИ является метр. Этот прибор редко используется за пределами научных и академических кругов. Большинство людей на этой планете измеряют скорость в километров в час (км/ч или км/ч). Соединенные Штаты являются исключением в том, что мы используем более старую миль в час (миль/ч или миль в час). Давайте определим коэффициенты преобразования, чтобы мы могли связать скорость, измеренную в м/с, с более привычными единицами измерения. Десятичные значения, показанные выше, точны до четырех значащих цифр, но дробные значения следует рассматривать только как эмпирические правила (1 км/ч на самом деле больше похож на 2 7 м/с, чем 1 4 м/с и 1 миль/ч больше похоже на 4 9 м/с, чем на 1 29005 9000). Отношение любой единицы расстояния к любой единице времени является единицей скорости. Иногда скорость объекта описывается относительно скорости чего-то другого; желательно какое-то физическое явление.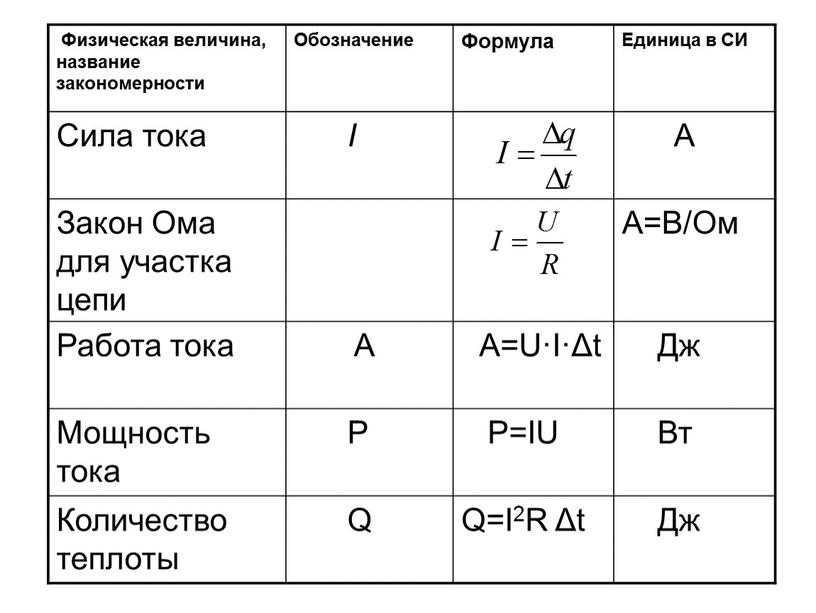 Он записывается как многочлен — постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ в 3 2 2 ) ). Поскольку высший порядок равен 2, правильнее называть его квадратичным .
Он записывается как многочлен — постоянный член ( s 0 ), за которым следует член первого порядка ( v 0 t ), за которым следует член второго порядка (½ в 3 2 2 ) ). Поскольку высший порядок равен 2, правильнее называть его квадратичным . скорость-позиция
 По сути…
По сути… метод 1
 Самый простой способ сделать это — начать с первого уравнения движения…
Самый простой способ сделать это — начать с первого уравнения движения… т = v − v 0 и с = с 0 + v 0 ⎛
⎜
⎝ v − v 0 ⎞
⎟
⎠ + ½ и ⎛
⎜
⎝ v − v 0 ⎞ 2
⎟
⎠ и и с — с 0 = vv 0 — v 0 2 + v 2 − 2 vv 0 + v 0 2 и 2 и 2 а ( с — S 0 ) = 2 ( В.  2 )
2 ) 2 a ( s − s 0 ) = v 2 − v 0 2 метод 2
 Это непростая задача, так как уравнение квадратное. Переставьте термины вот так…
Это непростая задача, так как уравнение квадратное. Переставьте термины вот так… x = − b ± √( b 2 − 4 ac ) 2 а т = − v 0 ± √[ v 0 2 — 4(½ a )(−∆ s 2(½ и ) т = − v 0 ± √( v 0 2 + 2 a ∆ s ) и 
v = v 0 + a ⎛
⎜
⎝ − v 0 ± √( v 0 2 + 2 a ∆ s ) ⎞
⎟
⎠ и математические выводы
 Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость. Это дает нам уравнение скорость-время. Если предположить, что ускорение постоянно, мы получим так называемое первое уравнение движения [1].
Вместо того, чтобы дифференцировать скорость, чтобы найти ускорение, интегрируйте ускорение, чтобы найти скорость. Это дает нам уравнение скорость-время. Если предположить, что ускорение постоянно, мы получим так называемое первое уравнение движения [1]. и = дв = а дт в ⌠
⎮
⌡ дв v 0 = т ⌠
⎮
⌡ а дт 0 v — v 0 = по v = v 0 + в [1]  Отменить эту операцию. Вместо того, чтобы дифференцировать положение, чтобы найти скорость, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положение-время для постоянного ускорения, также известное как -секундное уравнение движения [2].
Отменить эту операцию. Вместо того, чтобы дифференцировать положение, чтобы найти скорость, интегрируйте скорость, чтобы найти положение. Это дает нам уравнение положение-время для постоянного ускорения, также известное как -секундное уравнение движения [2]. v = дс = в дт дс = ( v 0 + в ) dt с ⌠
⎮
⌡ дс с 0 = т ⌠
⎮
⌡ ( v 0 + в ) dt 0 с — с 0 = v 0 t + ½ в 2 с = s 0 + v 0 t + ½ в 2 [2] 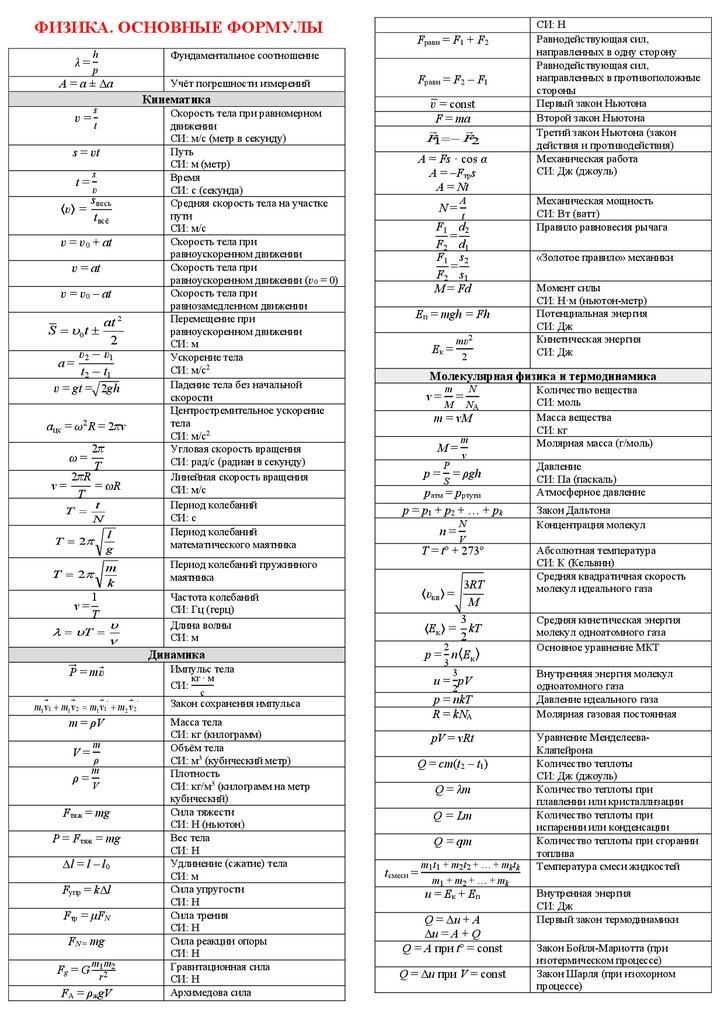 Мы не можем просто реконструировать это из определения. Нам нужно сыграть довольно изощренный трюк.
Мы не можем просто реконструировать это из определения. Нам нужно сыграть довольно изощренный трюк. дв = a дт дс = против дт дв = ? дс  Посмотрите, что происходит, когда мы это делаем. Получаем одну производную, равную ускорению ( dv dt ) и другую производную, равную обратной скорости ( dt ds ).
Посмотрите, что происходит, когда мы это делаем. Получаем одну производную, равную ускорению ( dv dt ) и другую производную, равную обратной скорости ( dt ds ). дв = дв 1 дс дс дв = дв дт дс дс дт дв = дв дт дс дт дс дв = и 1 дс v  Соберите похожие вещи и интегрируйте их. Вот что мы получаем, когда ускорение постоянно…
Соберите похожие вещи и интегрируйте их. Вот что мы получаем, когда ускорение постоянно… = в дв = и в ⌠
⎮
⌡ в дв v 0 = с ⌠
⎮
⌡ и с 0 ½( v 2 − v 0 2 ) = a ( с — с 0 ) v 2 = v 0 2 + 2 a ( с − с 0 ) [3]  Однако на самом деле это работало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно сложным. Мы бы вернулись к использованию алгебры только для того, чтобы сохранить рассудок. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сохранить.
Однако на самом деле это работало только потому, что ускорение было постоянным — постоянным во времени и постоянным в пространстве. Если бы ускорение каким-либо образом менялось, этот метод был бы неудобно сложным. Мы бы вернулись к использованию алгебры только для того, чтобы сохранить рассудок. Не то чтобы в этом что-то не так. Алгебра работает, а здравомыслие стоит сохранить. v = v 0 + на [1] + с = s 0 + v 0 t + ½ в 2 [2] = v 2 = v 0 2 + 2 a ( с — с 0 ) [3] Скорость и скорость – Гиперучебник по физике
скорость
 Либо так, либо вам скажут, что тот, кто движется быстрее, доберется до места раньше, чем тот, кто медленнее. Какой бы ни была скорость, она включает в себя и расстояние, и время. «Быстрее» означает «дальше» (большее расстояние) или «скорее» (меньше времени).
Либо так, либо вам скажут, что тот, кто движется быстрее, доберется до места раньше, чем тот, кто медленнее. Какой бы ни была скорость, она включает в себя и расстояние, и время. «Быстрее» означает «дальше» (большее расстояние) или «скорее» (меньше времени).
v = с т ☞ Это не окончательное определение. v = с ≈ 300 км = 75 км/ч т 4 часа  Если только вы не живете в мире, где автомобили имеют какой-то исключительный круиз-контроль и транспортные потоки регулируются каким-то идеальным образом, ваша скорость во время этого гипотетического путешествия, безусловно, должна была варьироваться. Таким образом, число, рассчитанное выше, не равно 9.1777 скорость автомобиля, это средняя скорость за весь путь. Чтобы подчеркнуть этот момент, уравнение иногда модифицируют следующим образом…
Если только вы не живете в мире, где автомобили имеют какой-то исключительный круиз-контроль и транспортные потоки регулируются каким-то идеальным образом, ваша скорость во время этого гипотетического путешествия, безусловно, должна была варьироваться. Таким образом, число, рассчитанное выше, не равно 9.1777 скорость автомобиля, это средняя скорость за весь путь. Чтобы подчеркнуть этот момент, уравнение иногда модифицируют следующим образом… v = ∆ с ∆ т  В идеале этот интервал должен быть как можно ближе к нулю, но на самом деле мы ограничены чувствительностью наших измерительных приборов. Мысленно, однако, можно представить вычисление средней скорости за все меньшие интервалы времени, пока мы не вычислим мгновенную скорость. Эта идея записывается символически как…
В идеале этот интервал должен быть как можно ближе к нулю, но на самом деле мы ограничены чувствительностью наших измерительных приборов. Мысленно, однако, можно представить вычисление средней скорости за все меньшие интервалы времени, пока мы не вычислим мгновенную скорость. Эта идея записывается символически как… v = лим ∆ t →0 ∆ с = дс ∆ т дт  Мы займемся этим позже в этой книге.
Мы займемся этим позже в этой книге. скорость
 Скорость — это скаляр, а скорость — это вектор. Скорость получает символ v (курсив), а скорость получает символ v (жирный шрифт). Средние значения получают полосу над символом.
Скорость — это скаляр, а скорость — это вектор. Скорость получает символ v (курсив), а скорость получает символ v (жирный шрифт). Средние значения получают полосу над символом. средняя
скорость v = ∆ с ∆ т мгновенная
скорость v = лим ∆ t →0 ∆ с = дс ∆ т дт средняя
скорость v = ∆ с ∆ т мгновенная
скорость v = лим ∆ t →0 ∆ с = д с ∆ т дт  Величина смещения приближается к расстоянию, когда расстояние приближается к нулю. То есть расстояние и смещение фактически одинаковы (имеют одинаковую величину), когда исследуемый интервал «небольшой». Поскольку скорость основана на расстоянии, а скорость основана на смещении, эти две величины фактически одинаковы (имеют одинаковую величину), когда временной интервал «небольшой» или, говоря языком исчисления, величина средней скорости объекта приближается. его средняя скорость по мере приближения интервала времени к нулю.
Величина смещения приближается к расстоянию, когда расстояние приближается к нулю. То есть расстояние и смещение фактически одинаковы (имеют одинаковую величину), когда исследуемый интервал «небольшой». Поскольку скорость основана на расстоянии, а скорость основана на смещении, эти две величины фактически одинаковы (имеют одинаковую величину), когда временной интервал «небольшой» или, говоря языком исчисления, величина средней скорости объекта приближается. его средняя скорость по мере приближения интервала времени к нулю. ∆ t → 0 ⇒ против → | против | шт.
 Единицей времени в СИ является секунда. Единицей скорости и скорости в СИ является отношение двух — 9.0009 метр в секунду .
Единицей времени в СИ является секунда. Единицей скорости и скорости в СИ является отношение двух — 9.0009 метр в секунду . ⎡
⎢
⎣ м = м ⎤
⎥
⎦ с с 1 км/ч = 1 км 1000 м 1 час 1 час 1 км 3600 с 1 км/ч = 0,2777… м/с ≈ ¼ м/с 1 035
1 миля 1609 м 1 час 1 час 1 миля 3600 с 1 миль в час = 0,4469… м/с ≈ ½ м/с 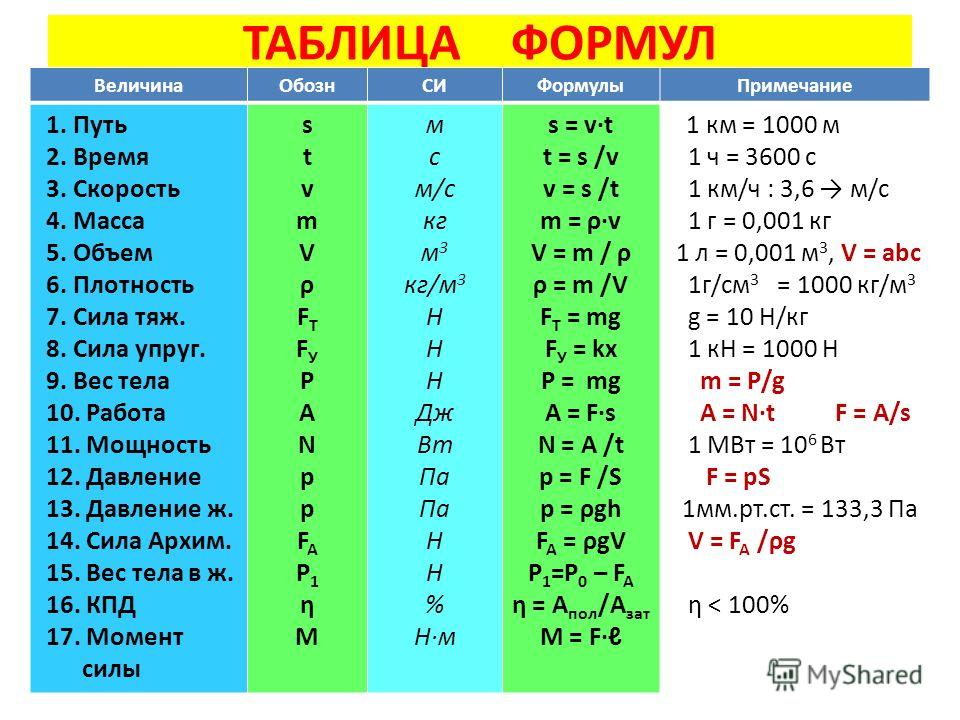
 Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с.
Более поздние модели также могли записывать с половиной этой скорости (7½ дюймов в секунду), затем с половиной этой скорости (3¾ дюймов в секунду), а затем с половиной этой скорости (1⅞ дюймов в секунду). Когда формулировался стандарт аудиокассет, было решено, что последнего из этих значений будет достаточно для нового носителя. Один дюйм в секунду по определению равен 0,0254 м/с. Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом.
Простое деление показывает, что эта скорость примерно вдвое превышает скорость звука или 2,0 Маха, что является исключительно быстрым. Для сравнения, Боинг 777 развивает крейсерскую скорость 248 м/с (555 миль в час) или 0,8 Маха, что только кажется медленным по сравнению с Конкордом. Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas .
Они лежат на окраинах наблюдаемой Вселенной и с невероятной скоростью уносятся от нас. Самые далекие квазары удаляются от нас почти на 0,9в. Кстати, символ c был выбран не потому, что скорость света является универсальной константой (которой она и является), а потому, что это первая буква латинского слова, обозначающего быстроту — celeritas . м/с км/ч устройство, событие, явление, процесс 10 −9 ~10 −8 континентальных пластин, рост волос, рост ногтей 10 −4 человеческие сперматозоиды 10 −3 улиток 0,013 0,045 розлив кетчупа из бутылки 10 −1 ленивцы, черепахи, черепахи 0,65–1,29 2,34–4,64 тараканы 1 3,6 нервные импульсы, немиелиновые клетки 1 3,6 океанские течения 0,06–1,14 0,22–4,10 ламантинов 1,3 4,8 человек, типичный темп ходьбы 2,391 8. 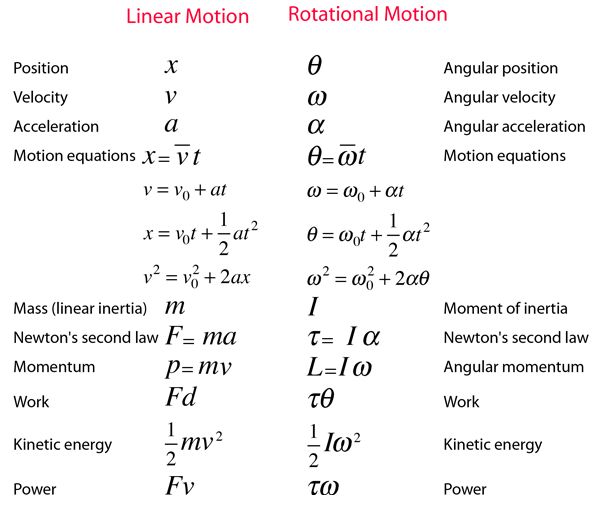 608
608 самый быстрый человек: плавание (Сезар Сьело) 8 30 максимальная комфортная скорость лифта 10 40 дельфины, морские свинки, киты 10 40 падающие капли дождя 10.422 37,520 самый быстрый человек: бег (Усэйн Болт) 12 43 волна стадиона 12 44 пробка для шампанского 15.223 54.803 самый быстрый человек: катание на коньках (Павел Кулижников) 20 70 кролики, зайцы, лошади, борзые, тунец, акулы 30 100 типичное ограничение скорости на автостраде 33 118 гепардов 34,42 123,9 самый быстрый человек: поле для софтбола (Моника Эбботт) 40 140 падающий град 42,47 152,9 самый быстрый человек: метание летающего диска (Саймон Лизотт) 46,98 169,1 самый быстрый человек: бейсбольное поле (Арольдис Чепмен) 55 200 предельная скорость типичного парашютиста 70.  8217
8217 254,958 самый быстрый человек: катание на лыжах (Иван Оригон) 73,06 263 самый быстрый человек: подача в теннисе (Сэм Грот) 80 290 сапсан в пикировании 82 295 очень быстрый мяч для гольфа 82.211 296,00 самый быстрый человек: велосипедист (Дениз Коренек Мюллер) 33–83 120–300 ураган, максимальная устойчивая скорость ветра 30–90 105–330 торнадо, максимальная устойчивая скорость ветра 100 360 нервные импульсы, миелинизированные клетки 113,2 407,5 максимальный порыв приземного ветра (остров Барроу, Австралия) 118,3 426 самый быстрый человек: победа в бадминтоне (Мадс Пилер Колдинг) 124,22 447,19 самый быстрый дорожный автомобиль (Koenigsegg Agera RS) 142,89 511,11 самый быстрый корабль (Дух Австралии) 159,7 574,8 самый быстрый поезд (Train à Grande Vitesse) 168,249 605,697 самый быстрый мотоцикл (Top 1 Ack Attack) 200 700 цунами 250 900 коммерческий реактивный самолет 331 1 190 скорость звука в воздухе, СТП 340 1 225 скорость звука в воздухе на уровне моря 341. 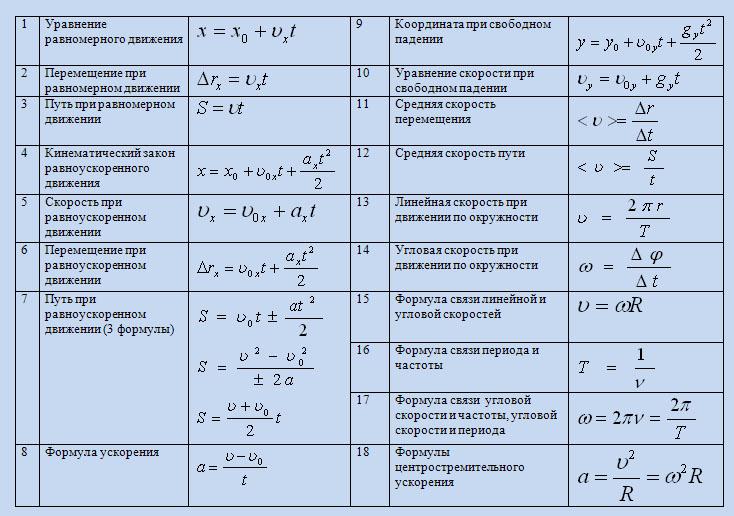

 Иными словами, числовой показатель плотности одного и того же вещества в разных странах будет отличаться. Поэтому, прежде чем утверждать, что показатели неверные или правильные, следует уточнить условия, при которых эти показатели были получены.
Иными словами, числовой показатель плотности одного и того же вещества в разных странах будет отличаться. Поэтому, прежде чем утверждать, что показатели неверные или правильные, следует уточнить условия, при которых эти показатели были получены. К таким условиям относятся температура окружающей среды, атмосферное давление и в отдельных случаях прочие параметры.
К таким условиям относятся температура окружающей среды, атмосферное давление и в отдельных случаях прочие параметры.