Масштабы чертежей — Чертежик
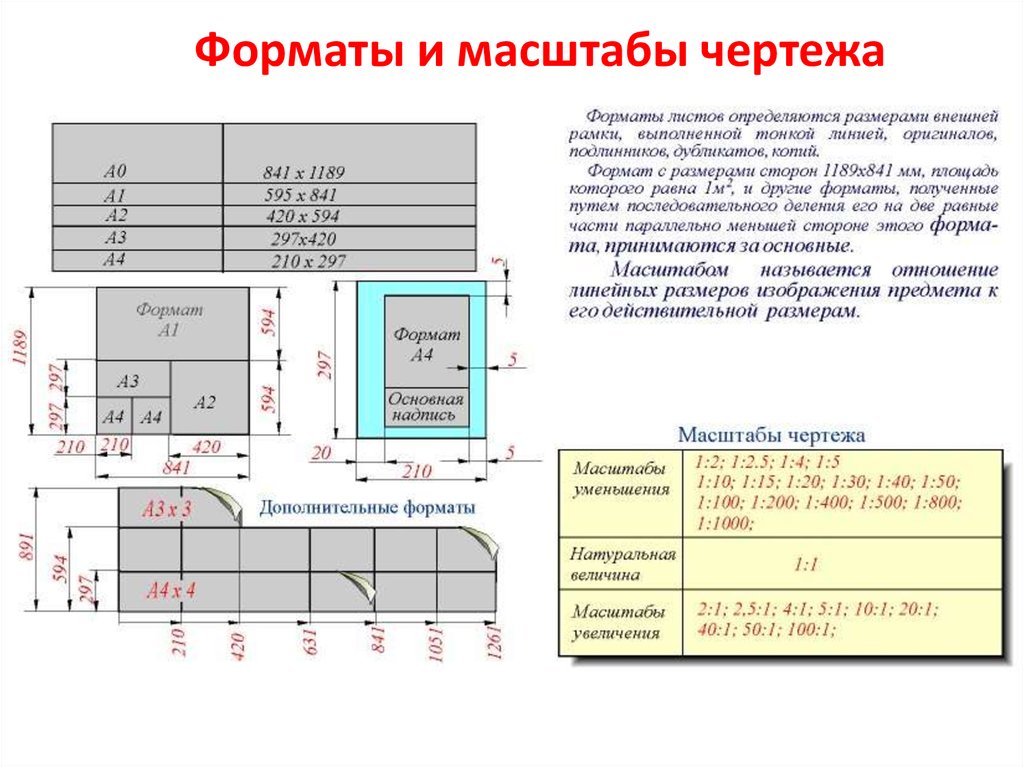
Масштабы чертежей. Масштабом называется отношение линейных размеров изображения предмета на чертеже к действительным размерам предмета.
Масштабы чертежей бывают численные, линейные, поперечные (десятичные) и угловые (пропорциональные).
Численный масштаб обозначается дробью, которая показываем кратность увеличения или уменьшения размеров изображения на чертеже. Численный масштаб обозначается дробью, которая показываем кратность увеличения или уменьшения размеров изображения на чертеже.
Графические масштабы на чертежеВ зависимости от сложности и величины изображения, ею назначения, стадии проектирования на чертежах применяются:
1.) Масштабы уменьшения: 1:2; 1 :2,5; 1:4; 1 : 5; 1 : 10; 1 : 15; 1:20; 1:25; 1 : 40; 1:50; 1:75; 1: 100; 1:200; 1:400; 1:500; 1:800; 1:1000.
(
Пример: допустим дана длина 5000 мм. Необходимо начертить в масштабе 1:100, то чертится отрезок размером 50 мм.)
При проектировании генеральных планов крупных объектов допускается применять масштабы: 1:2000; 1:5000; 1: 10000; 1:20000; 1:25000; 1: 50000.
2.) Масштабы увеличения: 2:1; 2,5:1; 4:1; 5:1; 10:1; 20:1; 40:1; 50:1; 100: 1.
Пример: допустим дана длина 50 мм. Необходимо начертить в масштабе 2:1, то чертится отрезок длиной 100 мм.)
В необходимых случаях допускается применять масштабы увеличения 100-n : I. где n — целое число.
3.) Натуральная величина: 1:1.(пример: длина детали 10 мм.
, соответственно, чертим линию размером 10мм. )
Масштаб должен указываться на всех чертежах, кроме некоторых строительных, а также чертежей, воспроизводимых путем клиширования или фотографирования.
Если на листе все чертежи выполнены в одном масштабе, то его значение проставляют в соответствующей графе основной надписи по типу 1:1; 1:2; 2:1 и т. д. Если на одном листе помещены чертежи разного масштаба, то масштаб указывают под названием соответствующего чертежа но типу М1:1; М1:2 и т. д.
Линейный масштаб на чертеже имеет вид линии с делениями, означающими какую-нибудь меру длины, например метр, километр и т.п. Линейные масштабы удобны тем, что с их помощью можно без вычисления определять по чертежу действительные размеры. По линейному масштабу отсчет размеров можно про-изводим.
Поперечный масштаб, позволяющий измерять размеры на чертеже с точностью до 0,01 принятой единицы длины, применяется в топографическом черчении.
Угловые (пропорциональные) маштабы применяют для построения изображений в уменьшенном или увеличенном в несколько раз виде.
Угловым масштабом целесообразно пользоваться, когда масштаб чертежа неопределенный 1 : n, где n может быть любое целое или дробное число и при ограниченном количестве размеров на чертеже.
Применение масштабов смотрите в примерах чертежей и в разделе чтение сборочного чертежа
«Масштаб 1:2, 1:5, 1:10, 1:100. Построение отрезков». 5-й класс
- Кивва Валентина Евгеньевна, учитель математики
Разделы: Математика, Коррекционная педагогика
Класс: 5
Задачи:
- Ознакомить с понятием масштаба;
- закрепить умение переводить из одной меры в другую; расширить знания о масштабе, придать им практическую направленность;
- корригировать и развивать устную и письменную речи;
- воспитывать интерес к предмету, бережное отношение к окружающему миру.
I
. Организация учащихся на урок.II. Устный счет.
- Однажды проводился конкурс красоты среди насекомых.
- Хотите узнать, какое из насекомых стало победителем?
- Оно спряталось под листочком, на котором ответ – четное число.
| 6 × 6 | 72 : 8 |
| + 24 | + 11 |
| — 20 | : 4 |
| : 8 | × 8 |
| 5 | 40 |
– Какое число является четным?
– Королева красоты – божья коровка.
– Что украшает красную спинку божьей коровки?
– Сколько точек у нее на спинке?
Задание 2
Закончить запись: Слайд 3
- 70 см = … дм;
- 47 м = … дм;
- 120 дм = … м.
2. Игра “Задачи от королевы красоты” Слайд 4
- Одна божья коровка 5 точечная, а другая – 15 точечная. Во сколько раз больше точек у одной коровки, чем у другой?
- На 8 листочках по 3 божьи коровки. Сколько всего божьих коровок?
- Красных божьих коровок 32, а желтых в 4 раза меньше. Сколько жёлтых божьих коровок?
- У одной божьей коровки на спинке 6 точек, а у другой на 8 точек больше. Сколько точек у второй божьей коровки?
Потрудились с божьей коровкой, а теперь отгадайте самое большое наземное животное.
Слайд 5
В зоопарке можно встретить,
Его не можешь не заметить,
Он огромен и силен
С хоботом, конечно … (слон)
3.
Подготовка к новому материалу. Слайд 6
Рост слона к 30 годам составляет
350 см = … м … дм (300 см + 50 см = 3 м 5 дм)
Уши слона, если измерить, то длина и ширина одинаковая и составляет:
7 дм 6 см= … см (70 см + 6 см = 76 см)
Если бы у слона не стирались и не обламывались бивни, они могли бы вырасти до таких размеров:
6 м = … дм (60 дм)
Из-за бивней слонов уничтожают и Африканские слоны занесены в Красную книгу. (Подчеркнуть на экране красным пером это выражение).
III. Физическая минутка.
Слайд 7
IV. Работа с новым материалом.
Слайд 8
Мы потрудились и с божьей коровкой, и со слоном. Посмотрите на них внимательно.
Такого ли размера они в природе?
Что использовал художник для изображения каждого из них?
ПЕЙЗАЖ
МАСШТАБ
ОРНАМЕНТ
Почему? Докажи.
Найдем это понятие в учебнике (с.
193, № 935). Слайд 9
Например, отрезок 30 см. Можем ли мы его начертить в ученической тетради?
Уменьшим его длину в два раза и построим отрезок в 2 раза короче, то есть длиной 15 см.
В таком случае говорят, что отрезок изображен в масштабе один к двум.
Как мы это запишем, найдите в учебнике.
Задача. Слайд 10
Божья коровка за 10 мин проползла 10 см. Изобразите ее путь в тетради в масштабе 1 : 2.
Запомните:
Размеры на чертеже записывают независимо от масштаба изображения.
Учебник: с. 193, №936 (1, 3). Слайды 11, 12
Масштаб может быть разным: М 1:2, М 1:5, М 1:10, М 1:100.
Это значит, что размеры уменьшаются соответственно в 2, 5, 10, 100 раз. Слайд 13
1) Открыли учебник на с. 194, №937. Слайд 14
Решаем в тетради, потом решение проверяем на слайде:
20 см : 5 = 4 см
2) с. 194, №938. Слайд 15
Решение этой задачи завершаем построением двух отрезков:
20 см : 5 = 4 см
15 см : 5 = 3 см
3) с.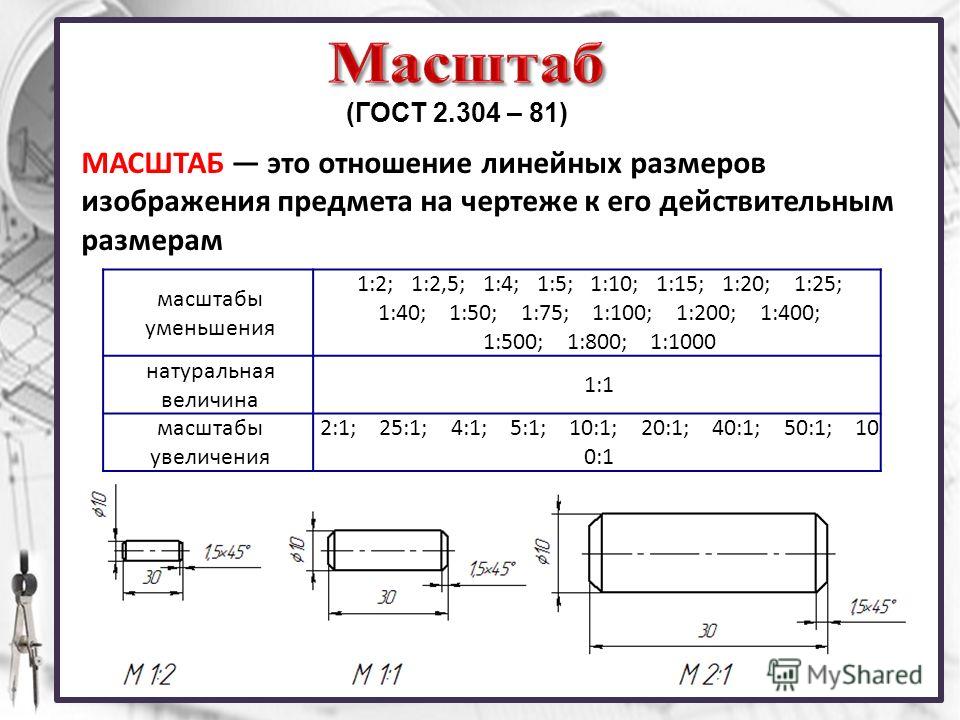
194, №939.
Решение и построение выполнить в тетради, а потом сравнить с экраном Слайд 16
4) с. 194, №940. Слайд 17
Решение:
- 4 м = 400 см;
- 3 м = 300 см;
- 400 : 100 = 4 см;
- 300 : 100 = 3 см.
Чертеж к задаче выполнить самостоятельно.
V. Итог урока
Выставление оценок.
VI. Домашнее задание
с. 194, №941 Слайд 18
VII. Список литературы
Приложение 2.
Масштабы, используемые в технических чертежах
••• Принадлежности для рисования. изображение от mashe с сайта Fotolia.com
Обновлено 7 августа 2017 г.
Автор: Кэролайн Энрайт
Рисунки в натуральную величину показывают реальный размер объекта. Если объект слишком мал или слишком велик, чтобы отобразить его в полном масштабе, дизайнер увеличивает или уменьшает его масштаб.
Технические чертежи рисуются в масштабе, чтобы инженеры, архитекторы и строители могли создавать объекты на чертеже в точном соответствии со спецификациями. При чтении масштабов число слева соответствует размеру на чертеже; число справа — это реальный размер.
Весы инженера-строителя
Весы инженера-строителя используются для проектирования крупных проектов, таких как дороги, мосты и водопроводы. В зависимости от проекта 1 дюйм на шкале может соответствовать 100 футам в реальной жизни. Шкала инженера-строителя делит 1 дюйм на равные десятичные единицы 10, 20, 30, 40, 50, 60 и 80. Планы, нарисованные в масштабе 10, могут иметь такие масштабы, как 1 дюйм = 10 футов, 1 дюйм = 100 футов. Шкала 20 используется для таких масштабов, как 1 дюйм = 2 фута, 1 дюйм = 20 футов и 1 дюйм = 200 футов. Независимо от того, используете ли вы масштаб 10, 20 или 50, значения увеличиваются на кратные 10. Так, например, чертеж в масштабе 50 может использовать масштаб 1 дюйм = 5 футов, 1 дюйм = 50 футов, 1 дюйм.
= 500 футов.
Архитекторские весы
Архитекторские весы преобразуют дюймы в футы и всегда показывают Х дюймов = 1 фут 0 дюймов. Масштаб 1/4 дюйма = 1 фут 0 дюймов означает, что 1/4 дюйма на чертеже равняется 1 футу в реальном здании — или нарисовано в размере 1/48. Другими словами, размер чертежа составляет 1/48 размера реального здания или проекта. Масштаб архитектора используется для составления планов крупных и мелких проектов. К ним относятся здания и сооружения, а также внутренние и внешние размеры помещений, стен, дверей и окон.
Метрическая шкала
Метрическая шкала использует миллиметры в качестве основного измерения. Полный размер в метрической шкале показан как 1:1. Полумасштаб 1:2. Полезно думать об этом так, как будто одна единица на чертеже равна двум единицам на объекте. Небольшой объект можно увеличить на бумаге и нарисовать в масштабе 2:1. Это означает, что рисунок объекта в два раза больше, чем сам объект.
Дизайнеры используют увеличенный масштаб, например двойной масштаб, для объектов, которые слишком малы, чтобы нарисовать их в натуральную величину с какой-либо значимой деталью. Общие метрические масштабы: 1:100, 1:50, 1:20, 1:10 и 1:5. Например, масштаб 1:50 равен одной пятидесятой (1/50) полного размера, или 1 миллиметр на чертеже равен 50 миллиметрам в действительности.
Статьи по теме
Ссылки
- Государственный университет Сан-Диего: основы рисования
- Управление пожарной охраны США: использование масштабов архитектора в 1992 году. Ее работа включает в себя выступления руководителей, годовые отчеты, статьи в газетах и журналах, информационные бюллетени и модули онлайн-обучения. Энрайт имеет степень магистра наук в области корпоративных связей с общественностью Северо-Западного университета и степень бакалавра гуманитарных наук в области американских исследований Университета Нотр-Дам.
Фотографии
Принадлежности для рисования.
изображение Маше с сайта Fotolia.comЧто такое Масштаб? Значение, формула, примеры
Вы когда-нибудь наблюдали, как вы можете посмотреть на карту, и она покажет вам точное местоположение места? Что бы вы делали, если бы у вас не было карты? Что ж, возможно, вам придется лететь высоко над землей и посмотреть, какой путь ведет к месту назначения! Но это не обязательно. Вы видите, как строитель берет проект дома и превращает его в реальную вещь?
Все это возможно благодаря математическому понятию масштабного коэффициента. Масштабный коэффициент можно описать как параметр, который используется для увеличения или уменьшения размеров фигур в двухмерной и трехмерной геометрии. С его помощью можно создавать похожие фигуры, но других размеров.
Что такое масштабный коэффициент?
Масштабный коэффициент определяется как отношение масштаба данного исходного объекта к масштабу нового объекта, являющегося его представлением, но другого размера (большего или меньшего).
Например, если у нас есть прямоугольник со сторонами 2 см и 4 см, мы можем увеличить его, умножив каждую сторону на число, скажем, 2. Новая фигура, которую мы получим, будет похожа на исходную фигуру, но все ее размеры будет в два раза больше исходного прямоугольника. Здесь число 2 будет называться коэффициентом масштабирования.
Обратите внимание, что масштабный коэффициент изменяет только размеры или длины сторон фигур, но не изменяет меры углов.
Как работает коэффициент масштабирования?
При описании увеличения необходимо указать, насколько увеличена форма. Например, масштабный коэффициент 3 означает, что новая фигура в три раза больше исходной.
Если коэффициент масштабирования представляет собой дробь, форма будет меньше. Это называется редукцией. Следовательно, коэффициент масштабирования 1/2 означает, что новая форма составляет половину исходной формы.
Как найти масштабный коэффициент?
Масштабный коэффициент можно определить, указав новые и исходные размеры.
- Коэффициент масштабирования = размер новой формы/размер исходной формы
Однако при использовании коэффициентов масштабирования необходимо понимать два термина: увеличение и уменьшение масштаба. Посмотрите на рисунки ниже, чтобы понять это лучше.
Масштабирование
Масштабирование означает увеличение маленькой формы до большой. Масштабный коэффициент для увеличения всегда больше 1.
Уменьшение масштаба
Уменьшение масштаба означает, что большое число уменьшается до малого. Масштабный коэффициент для уменьшения всегда меньше 1,9.0003
Использование коэффициента масштабирования
Масштабирование объектов — отличный способ визуализировать большие объекты реального мира в небольшом пространстве или увеличить мелкие объекты, чтобы их было легче увидеть!
Масштабный коэффициент используется для следующих целей:
- Нарисуйте подобную фигуру в геометрии.
- Создайте масштабную модель.
- Создание чертежей и масштабных планов машин и архитектуры.
- Сократите огромные земли в маленькие кусочки бумаги, как карту.
- Помогите архитекторам, машиностроителям и дизайнерам работать с моделями объектов, которые слишком велики, чтобы их можно было удержать, если они соответствуют их реальному размеру.
Решенные примеры
Пример 1. Найдите масштабный коэффициент, когда квадрат со стороной 4 см увеличивается, чтобы получился квадрат со стороной 8 см.
Решение : Формула масштабного коэффициента:
Масштабный коэффициент = размер новой формы/размер исходной формы
Следовательно, масштабный коэффициент для данного увеличения равен
Масштабный коэффициент = 8/4
Масштабный коэффициент = 2
Следовательно, квадрат был увеличен с масштабным коэффициентом 2,9.0003
Пример 2. Треугольник со сторонами 3 см, 4 см и 5 см был увеличен в 4 раза. Каковы размеры нового треугольника?
Решение :
Размеры новой формы = Масштабный коэффициент ✕ Размеры исходной формы
Следовательно, размеры нового треугольника будут в 4 раза больше исходных.
Итак, новые размеры 12 см, 16 см и 20 см.
Пример 3. Если круг радиусом 3 см уменьшить до круга радиусом 1 см, каков масштабный коэффициент для этого уменьшения?
Решение : Мы знаем, что,
Масштабный коэффициент = размер новой формы/размер исходной формы
Радиус исходного круга = 3 см
Радиус нового круга = 1 см для этого сокращения = 1/3
Практические задачи
2
3
4
5
Правильный ответ: 3
Масштабный коэффициент = размер новой формы / размер исходной формы куба
12 см,
Длина края нового куба = 36 см.
Итак, масштабный коэффициент для этого увеличения = 3$\frac{1}{2}$
$\frac{1}{3}$
$\frac{1}{4}$
$ \frac{1}{5}$
Правильный ответ: $\frac{1}{4}$
Мы знаем, что Масштабный коэффициент = размер новой формы/размер исходной формы Радиус исходной сферы = 20 см, Радиус новой сферы = 5 см. Таким образом, масштабный коэффициент для этого сокращения = $\frac{20}{5}$ = 4 см2 см
1/5 см
5 см
10 см
Правильный ответ: 2 см
Размеры новой формы = Масштабный коэффициент ✕ Размеры исходной формы
Следовательно, размеры нового квадрата будут в 2 раза больше исходных.
изображение Маше с сайта Fotolia.com
