Обратная матрица пример: 1.3.4. Примеры решения задач по теме «Обратная матрица»

1.3.4. Примеры решения задач по теме «Обратная матрица»

Задача 1.

Найти обратную матрицу для матрицы

И проверить выполнение условий ­А А-1 = А-1А = Е.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

Убедимся, что матрица А – невырожденная. ΔА = 1·4 — 2·(-1) ≠ 0, следовательно, А-1 существует.

Вычислим алгебраические дополнения к элементам А:

Применим способ вычисления обратной матрицы:

.

Не забудьте, что обратная матрица образована из алгебраических дополнений к элементам Транспонированной матрицы!

Найдем произведения ­А А-1 и А-1А:

Таким образом, найденная матрица А-1 отвечает определению обратной матрицы.

Ответ: .

Задача 2.

Найти обратную матрицу для матрицы

.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

Следовательно, матрица А невырожденная, и обратная матрица существует.

Вычислим алгебраические дополнения к элементам матрицы А:

Обратная матрица имеет вид:

Ответ: .

Задача 3.

Найти обратную матрицу для матрицы

.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

Вычислим определитель матрицы А разложением по первому столбцу:

.

Следовательно, обратная матрица для матрицы А существует.

Найдем алгебраические дополнения к элементам матрицы А:

Значит,

.

Ответ: .

Задача 4.

Найти обратную матрицу для матрицы

.

Указание

Убедитесь, что матрица А – невырожденная, и примените способ вычисления обратной матрицы.

Решение

.

Ответ:

Задача 5.

При каких X, Y, Z матрица

Является обратной к матрице

Указание

Необходимым условием того, что В = А-1, является требование АВ = Е.

Решение

Проверим невырожденность матрицы А:

Необходимым условием того, что В = А-1, является требование АВ = Е.

Найдем АВ:

Для того, чтобы выполнялось условие АВ = Е, X, Y, Z должны быть решением системы уравнений

Проверим, будет ли равно единичной матрице произведение ВА:

Значит, при найденных значениях X

, Y, Z В = А-1.

Ответ: X = -3, Y = -3, Z = 4.

< Предыдущая		Следующая >

Как найти обратную матрицу: формула, пример

В данной публикации мы рассмотрим, что такое обратная матрица, а также на практическом примере разберем, как ее можно найти с помощью специальной формулы и алгоритма последовательных действий.

• Определение обратной матрицы
• Алгоритм нахождения обратной матрицы

Определение обратной матрицы

Для начала вспомним, что из себя представляют обратные значения в математике. Допустим, у нас есть число 7. Тогда обратное ему будет равняться 7^-1 или ¹/₇. Если умножить данные числа, в результате получится один, т.е. 7 · 7^-1 = 1.

Почти то же самое и с матрицами. Обратной называется такая матрица, умножив которую на исходную, мы получим единичную. Обозначается она как A^-1.

A · A^-1 = E

Алгоритм нахождения обратной матрицы

Для нахождения обратной матрицы нужно уметь вычислять определитель матрицы, а также иметь навыки выполнения определенных действий с ними.

Сразу отметить, что найти обратную можно только для квадратной матрицы, а делается это по формуле ниже:

|A| – определитель матрицы;
A^T_M – транспонированная матрица алгебраических дополнений.

Примечание: если определитель равен нулю, то обратной матрицы не существует.

Пример
Давайте найдем для матрицы A ниже обратную ей.

Решение
1. Для начала найдем определитель заданной матрицы.

2. Теперь составим матрицу миноров, которая имеет те же самые размеры, что и исходная:

Нам нужно выяснить, какие числа должны стоять на месте звездочек. Начнем с верхнего левого элемента матрицы. Минор к нему находится путем зачеркивания строки и столбца, в котором он находится, т.е. в обоих случаях под номером один.

Число, которое останется после зачеркивания, и является требуемым минором, т.е. M₁₁ = 8.

Аналогичным образом находим миноры для оставшихся элементов матрицы и получаем такой результат.

3. Определяем матрицу алгебраических дополнений. Как их посчитать для каждого элемента мы рассмотрели в отдельной публикации.

Например, для элемента a₁₁ алгебраическое дополнение считается так:

A₁₁ = (-1)¹⁺¹ · M₁₁ = 1 · 8 = 8

4.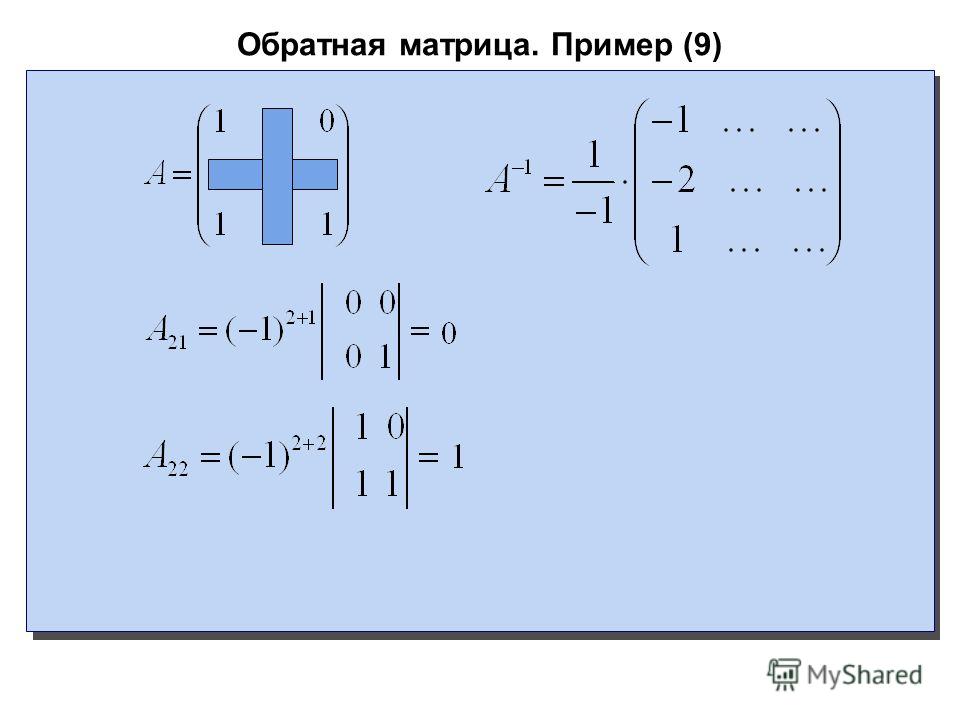 Выполняем транспонирование полученной матрицы алгебраических дополнений (т. е. поменяем столбцы и строки местами).

5. Остается только воспользоваться формулой выше, чтобы найти обратную матрицу.

Ответ можем оставить в таком виде, не деля элементы матрицы на число 11, так как в этом случае получится некрасивые дробные числа.

Проверка результата

Чтобы убедиться в том, что мы получили обратную исходной матрицу, мы можем найти их произведение, которое должно равняться единичной матрице.

В результате мы получили единичную матрицу, значит все сделали верно.

Обратная матрица с использованием миноров, кофакторов и адьюгата

Примечание: также ознакомьтесь с инверсией матрицы с помощью операций со строками и матричным калькулятором

 

Мы можем вычислить обратную матрицу:

• Шаг 1: расчет матрицы миноров,
• Шаг 2: затем превратите это в матрицу кофакторов,
• Шаг 3: затем Адъюгат и
• Шаг 4: умножьте это на 1/Определитель.

Но лучше всего это объяснить на примере!

Пример: найти обратное число A:

А =

302 20-2 011

Требуется 4 шага. Это все простая арифметика, но ее много, так что постарайтесь не ошибиться!

Шаг 1: Матрица миноров

Первым шагом является создание «Матрицы несовершеннолетних». На этом шаге больше всего вычислений.

Для каждого элемента матрицы:

• игнорировать значения в текущей строке и столбце
• вычислить определитель остальных значений

Поместите эти детерминанты в матрицу («Матрица миноров»)

Определитель

Для матрицы 2×2 (2 строки и 2 столбца) определитель прост: ad-bc

Подумай о кресте: Синий означает положительный (+объявление), Красный означает отрицательный (-bc)

(Сложнее для матрицы 3×3 и т.

д.)

Расчеты

Вот два первых и два последних вычисления « Матрицы несовершеннолетних » (обратите внимание, как я игнорирую значения в текущей строке и столбцах и вычисляю определитель, используя оставшиеся значения):

А вот и расчет для всей матрицы:

Шаг 2: Матрица кофакторов

Это просто! Просто примените «шахматную доску» минусов к «Матрице миноров». Другими словами, нам нужно изменить знак чередующихся ячеек, например:

.

Шаг 3: Сопряжение (также называемое сопряженным)

Теперь «Транспонировать» все элементы предыдущей матрицы… другими словами поменять их местами по диагонали (диагональ остается прежней):

Шаг 4: Умножение на 1/Определитель

Теперь найдите определитель исходной матрицы. Это не так уж сложно, потому что мы уже вычислили определители меньших частей, когда делали «Матрицу миноров».

Использование:

Элементы верхнего ряда: 3, 0, 2
Второстепенные элементы верхнего ряда: 2, 2, 2

Получаем такой расчет:

Определитель = 3×2 − 0×2 + 2×2 = 10

Ваш ход: попробуйте за любую другую строку или столбец , вы также должны получить 10.

Теперь мы умножаем Adjugate на 1/Определитель, чтобы получить:

Готово!

Сравните этот ответ с тем, что мы получили на обратной матрице с помощью элементарных операций со строками. Это то же самое? Какой метод вы предпочитаете?

Большие матрицы

Точно такие же шаги для больших матриц (например, 4×4, 5×5 и т. д.), но вау! требуется много вычислений.

Для матрицы 4×4 нам нужно вычислить 16 определителей 3×3. Поэтому часто проще использовать компьютеры (такие как Matrix Calculator).

Заключение

• Для каждого элемента вычислить определитель значений, не входящих в строку или столбец
  , чтобы составить Матрицу миноров
• Применить шахматную доску минусов, чтобы составить матрицу кофакторов
• Транспонировать , чтобы сделать Adjugate
• Умножить на 1/Определитель , чтобы получить обратное

 

2617, 2618, 8500, 8501, 8502, 8503, 8504, 8505, 8506, 8507

Обратная матрица с использованием элементарных операций со строками (Гаусса-Жордана)

Также называется методом Гаусса-Жордана.

Это интересный способ найти обратную матрицу:

Поиграйте со строками (сложение, умножение или замена) пока не сделаем Matrix A в матрицу идентичности I

И ТАКЖЕ внося изменения в матрицу идентичности, она волшебным образом превращается в обратную!

«Элементарные операции со строками» — это простые вещи, такие как добавление строк, умножение и замена… но давайте посмотрим на примере:

Пример: найдите инверсию «А»: матрица A и запишите ее рядом с матрицей идентичности I:

(это называется «расширенная матрица»)

Матрица идентичности

«Матрица идентичности» является матричным эквивалентом числа «1»:

Матрица идентичности 3×3

• Это «квадрат» (имеет такое же количество строк, как и столбцов),
• У него 1 с по диагонали и 0 с везде.
• Его символ — заглавная буква I .

 

Теперь мы делаем все возможное, чтобы превратить «А» (матрицу слева) в матрицу идентичности. Цель состоит в том, чтобы в матрице А было 1 с по диагонали и 0 с в другом месте (идентификационная матрица) … и правая сторона приходит в движение, и на ней также выполняются все операции.

Но мы можем делать только эти «Элементарные операции со строками» :

• поменять местами строк
• умножьте или разделите каждый элемент в строке на константу
• заменить строку на добавить или вычесть из нее кратное другой строке

И мы должны сделать это до Whate Row , например,:

СТАРЬ С A Далее I

Добавить строку 2 до строки 1

. ряд 1 на 5,

 

Затем возьмите 2 раза первую строку и вычтите ее из второй строки,

 

Умножьте вторую строку на -1/2,

 

Теперь поменяйте местами вторую и третью строку,

 

Наконец, вычтите третью строку из второй строки,

Готово!

 

И матрица A была превращена в матрицу идентичности . ..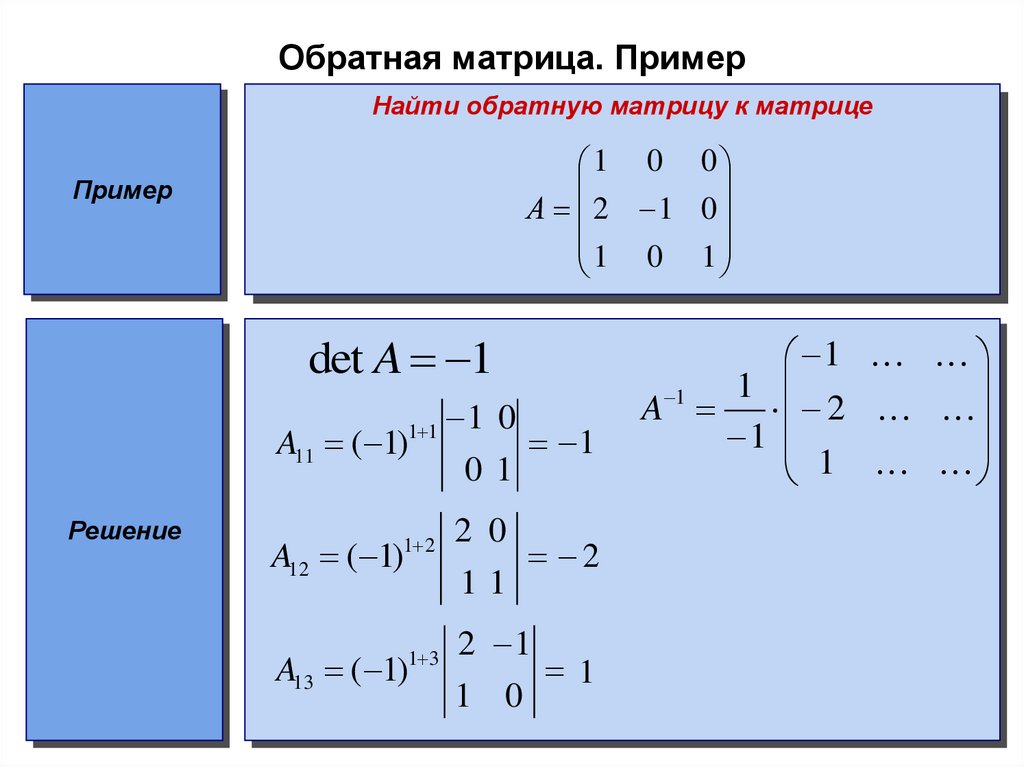

… и в то же время матрица идентичности превратилась в

A ^-1

5 DONE 90! Как по волшебству, и так же весело, как решать любую головоломку.

И обратите внимание: нет «правильного способа» сделать это, просто продолжайте играть, пока не добьетесь успеха!

(Сравните этот ответ с ответом, который мы получили при обращении к матрице с использованием миноров, кофакторов и сопряжения. Это то же самое? Какой метод вы предпочитаете?)

Большие матрицы

Мы можем сделать это с большими матрицами, для например, попробуйте эту матрицу 4×4:

Начните так:

Посмотрите, сможете ли вы сделать это самостоятельно (я бы начал с деления первой строки на 4, но вы делаете это по-своему).

Вы можете проверить свой ответ с помощью Калькулятора матриц (используйте кнопку «inv(A)»).