6 класс. Математика. Никольский. Учебник. Ответы к стр. 10
Отношения, пропорции, проценты
Масштаб
Ответы к стр. 10
21. Что показывает численный масштаб:
а) 1 : 100; б) 1 : 1000; в) 1 : 20 000.
а) расстояние на карте в 100 раз меньше расстояния на местности;
б) расстояние на карте в 1000 раз меньше расстояния на местности;
в) расстояние на карте в 20 000 раз меньше расстояния на местности.
22. Определите численный масштаб, если известно, что 1 см на плане (географической карте) изображает отрезок длиной:
а) 10 см; б) 50 см; в) 6 дм; г) 10 м;
д) 100 м; е) 1 км; ж) 6 км; з) 10 км.
а) 1 : 10;
б) 1 : 50;
в) 1 : 60, так как 6 дм = 60 см;
г) 1 : 1000, так как 10 м = 1000 см;
д) 1 : 10 000, так как 100 м = 10 000 см;
е) 1 : 100 000, так как 1 км = 100 000 см;
ж) 1 : 600 000, так как 6 км = 600 000 см;
з) 1 : 1 000 000, так как 10 км = 1 000 000 см.
23. Расстояние между двумя городами равно 200 км. Определите расстояние между изображениями этих городов на карте, если численный масштаб карты равен:
а) 1 : 1 000 000; б) 1 : 200 000; в) 1/5000000.
а) 200 км = 20 000 000 см
1 : 1 000 000 = 1/1000000
20 000 000 см • 1/1000000 = 20000000/1000000 см = 20 см
О т в е т: 20 см.
б) 200 км = 20 000 000 см
1 : 200 000 = 1/200000
20 000 000 см • 1/200000 = 20000000/200000 см = 100 см
О т в е т: 100 см.
в) 200 км = 20 000 000 см
20000000 см • 1/5000000 = 20000000/5000000 см = 4 см
О т в е т: 4 см.
24. Масштаб карты равен 1/50000. Определите расстояние на местности, если на карте оно равно:
а) 1 см; б) 5 см; в) 22 см; г) 37 мм; д) 1 1/5 дм; е) 146 мм.
а) 1 см : 1/50000 = 1 см • 50000/1 = 50 000 см = 500 м
О т в е т: 500 м.
б) 5 см : 1/50000 = 5 см • 50000/1 = 250 000 см = 2500 м = 2 км 500 м
О т в е т: 2 км 500 м.
в) 22 см : 1/50000 = 22 см • 50000/1 = 1 100 000 см = 11 000 м = 11 км
О т в е т: 11 км.
г) 37 мм = 37/10 см
37/10 см : 1/50000 = 37/10 см • 50000/1 = 37•50000/10 см = 37 см•5000/1 = 185 000 см = 1850 м = 1 км 850 м
О т в е т: 1 км 850 м.
д) 1 1/5 дм = 6/5 дм = 6/5 • 10 см = 6•10/5 см = 60/5 см = 12 см
12 см : 1/50000 = 12 см • 50000/1 = 600 000 см = 6000 м = 6 км
О т в е т: 6 км.
е) 146 мм = 146/10 см = 73/5 см
73/5 см : 1/50000 = 73/5 см • 50000/1 = 73•50000/5 см = 73 см•10000/1 = 730 000 см = 7300 м = 7 км 300 м
О т в е т: 7 км 300 м.
25. План комнаты имеет вид прямоугольника со сторонами 40 мм и 31 мм. Определите длину и ширину комнаты, если численный масштаб плана равен 1 : 200.
1 : 200 = 1/200
Длина α = 40 мм : 1/200 = 40 мм • 200/1 = 8000 мм = 800 см = 8 м
Ширина b = 31 мм : 1/200 = 31 мм • 200/1 = 6200 мм = 620 см = 6 м 20 см
О т в е т: длина α = 8 м, ширина b = 6 м 20 см.
26. Огород имеет вид прямоугольника, длина которого 340 м, а ширина 220 м. Какие размеры будет иметь изображение этого огорода на плане, выполненном в масштабе 1 : 500?
Какие размеры будет иметь изображение этого огорода на плане, выполненном в масштабе 1 : 500?
1 : 500 = 1/500
Длина α = 340 м • 1/500 = 340/500 м = 34/50 м = 17/25 м = 1700/25 см = 68 см
Ширина b = 220 м • 1/500 = 220/500 м = 22/50 м = 11/25 м = 1100/25 см = 44 см
Ответ: длина изображение на плане α = 68 см, ширина изображения на плане b = 44 см.
27. Прямоугольник со сторонами 12 см и 6 см изображает на плане поле, занятое под овёс. Определите масштаб плана, если бóльшая сторона поля имеет длину 360 м. Определите меньшую сторону поля.
Масштаб М = 12 см : 360 м = 12 см : 36 000 см = 12/36000 = 1/3000 = 1 : 3000
Ширина b = 6 см : 1/3000 = 6 см • 3000/1 = 18 000 см = 180 м
О т в е т: масштаб 1 : 3000, ширина поля b = 180 м.
28. Используя план местности (рис. 2) определите:
а) расстояние от А до B;
б) расстояние от А и от B до моста через реку;
в) расстояние от B до смешанного леса.
а) 1 : 10 000 = 1/10000
расстояние на плане от А до B примерно 70 мм = 7 см
расстояние на местности от А до B: s = 7 см : 1/10000 = 7 см • 10000/1 = 70 000 см = 700 м.
О т в е т: от А до В 700 м.
б) 1 : 10000 = 1/10000
расстояние на плане от А до моста через реку примерно 20 мм = 2 см
расстояние на плане от В до моста через реку примерно 50 мм = 5 см
расстояние на местности от А до моста через реку: s = 2 см : 1/10000 = 2 см • 10000/1 = 20 000 см = 200 м
расстояние на местности от В до моста через реку: s = 5 см : 1/10000 = 5 см • 10000/1 = 50 000 см = 500 м.
О т в е т: от А до моста 200 м, от В до моста 500 м.
в) 1 : 10000 = 1/10000
расстояние на плане от B до смешанного леса примерно 15 мм = 15/10 см = 3/2 см
расстояние на местности от B до смешанного леса: s = 3/2 : 1/10000 = 3/2 • 10000/1 = 30000/2 = 15 000 см = 150 м.
О т в е т: от В до смешанного леса 150 м.
Ответы по математике. 6 класс. Учебник. Никольский С.М., Потапов М.К., Решетников Н.Н., Шевкин А.В.
Математика. 6 класс
Trojden | Масштаб: Герасимова Т. П.
1. Зачем нужен масштаб? Ни один географический объект, например реку, мост, посёлок, невозможно изобразить на топографическом плане в натуральную величину. В древности люди рисовали уменьшенные изображения местности, на которых разные участки уменьшались произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т. д. Чтобы план был более точным, необходимо все расстояния уменьшать в одинаковое число раз с сохранением всех пропорций, делать изображение в масштабе.
В древности люди рисовали уменьшенные изображения местности, на которых разные участки уменьшались произвольно, в разной степени. Поэтому старинные чертежи местности не дают возможности понять, например, каково расстояние между берегами реки, чему равна длина реки и т. д. Чтобы план был более точным, необходимо все расстояния уменьшать в одинаковое число раз с сохранением всех пропорций, делать изображение в масштабе.
Масштаб показывает, во сколько раз расстояния на плане уменьшены по сравнению с расстояниями на местности.
Длина школьного здания на плане (рис. 7) в 1000 раз меньше, чем в действительности. Это означает, что на данном плане все расстояния уменьшены в 1000 раз.
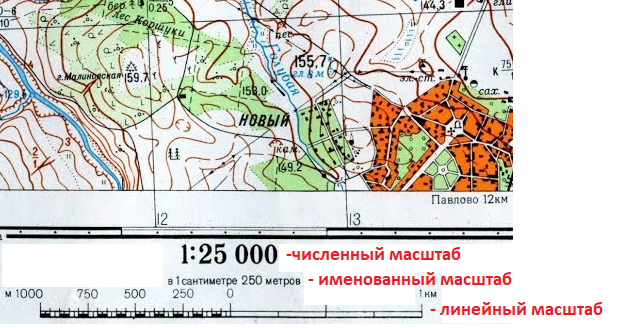
2. Численный и именованный масштабы. Масштаб подписывают по-разному. В виде числа масштаб изображается, например, так: 1:100 (это означает, что 1 см плана заменяет 100 см на местности). Это численный масштаб. 100 см — это 1 м, поэтому можно просто написать: в 1 см — 1м. Масштаб, записанный в таком виде, — именованный масштаб.
Масштаб, записанный в таком виде, — именованный масштаб.
Рис. 7. План школьного двора
ЗАДАНИЯ. 1. Запишите численный и именованный масштабы плана, если местность на нём уменьшена в 200 раз; в 500 раз; в 2000 раз. 2. Во сколько раз уменьшены расстояния на планах с масштабами 1:25, в 1 см — 50 м? На плане с каким масштабом объекты изображены наиболее крупно? 3. Во сколько раз уменьшена местность на планах на форзаце 1 и в атласе? Какому расстоянию на местности соответствуют расстояния в 1 см, 2 см, 10 см на этих планах? 4. Численный масштаб плана — 1:5000. Запишите этот масштаб в виде именованного масштаба. 5*. Определите численный масштаб плана, на котором расстояние от магазина до школы равно 5 см, если на местности это расстояние составляет 100 м.
3. Линейный масштаб. Обычно на планах, кроме численного и именованного масштабов, помещают линейный масштаб. Он представляет собой линию, разделённую на равные отрезки (см. рис. 7). Отрезки справа от 0 показывают, какому расстоянию на местности соответствуют расстояния на плане в 1 см, 2 см и т. д. Отрезок слева от 0 разделён на равные мелкие части. Зная расстояние на местности, которому соответствует большой отрезок, и количество мелких отрезков, можно вычислить, какому расстоянию на местности соответствует каждый мелкий отрезок. Например, длина большого отрезка слева от 0 на рисунке 7 равна 10 м. Этот отрезок разделён на 5 мелких частей, значит, длина одной такой части составляет 10 м : 5 = 2 м.
рис. 7). Отрезки справа от 0 показывают, какому расстоянию на местности соответствуют расстояния на плане в 1 см, 2 см и т. д. Отрезок слева от 0 разделён на равные мелкие части. Зная расстояние на местности, которому соответствует большой отрезок, и количество мелких отрезков, можно вычислить, какому расстоянию на местности соответствует каждый мелкий отрезок. Например, длина большого отрезка слева от 0 на рисунке 7 равна 10 м. Этот отрезок разделён на 5 мелких частей, значит, длина одной такой части составляет 10 м : 5 = 2 м.
Линейный масштаб позволяет измерять расстояния на плане при помощи циркуля-измерителя.
При помощи линейного масштаба можно определять длину кривых линий, например реки, дороги. Для этого надо отметить на полоске бумаги небольшое расстояние или установить небольшой раствор между иглами циркуля-измерителя и перемещать бумагу с отметкой или циркуль вдоль измеряемой линии, считая число перестановок. Определив при помощи линейного масштаба длину одного «шага» в метрах и умножив её на число перестановок, мы получим длину кривой линии.
4. Выбор масштаба. Масштаб выбирают в зависимости от величины территории, которую надо показать на плане. Например, надо изобразить участок размером 6×6 км. Масштаб в 1 см — 10 м не годится, потому что это расстояние изображается линией в 600 см, т. е. в 6 м. Удобнее взять масштаб: в 1 см — 300 м. При таком масштабе расстояние в 6 км будет соответствовать линии в 20 см.
ПРАКТИКУМ НА МЕСТНОСТИ (выполняется по группам)
Цель: изобразить здание школы в масштабе.
Оборудование: планшет (лист фанеры или картона с приколотым на него листом бумаги формата А4), карандаш, линейка, рулетка.
Ход работы
- 1. Выберите масштаб, в котором вы будете изображать школу (рекомендуемый масштаб: 1 : 1000 или 1 : 2500).
- 2. С помощью рулетки определите длину своего шага в сантиметрах. Переведите сантиметры в метры.
- 3. Измерьте шагами длину каждой стены школы в метрах.
- 4.
 Переведите метры в сантиметры и изобразите здание школы на планшете.
Переведите метры в сантиметры и изобразите здание школы на планшете. - 5. Подпишите численный и именованный масштабы, в которых изображена школа.
- 6. Оформите работу и сдайте её учителю.
ВОПРОСЫ И ЗАДАНИЯ
1. Для чего нужен масштаб? Что он показывает? 2. Какие виды масштабов существуют? Приведите пример численного масштаба. Переведите его в именованный масштаб. 3. Масштаб плана 1:3000. Какому расстоянию на местности соответствует участок плана длиной: а) 10 см; б) 5 см; в) 2 см? 4*. Изобразите в виде линии расстояние 100 м в масштабах: а) в 1 см — 10 м; б) в 1 см — 200 м; в) 1:2500. 5*. Во сколько раз расстояние на местности больше, чем на плане, если местность изображена в масштабах: а) 1:25 000; б) в 1 см — 5 м? Какой из этих масштабов крупнее? 6. По плану на форзаце 1 определите: а) расстояние от отдельно стоящего дерева до сарая; б) расстояние от пруда до начала оврага; в) длину ручья, впадающего в реку Нару.
Предыдущая
СтраницаСледующая
СтраницаОглавление
BestMaths
Карта представляет собой чертеж в масштабе .
Чертежи в масштабе используются на многих работах такими людьми, как дизайнеры, строители и инженеры, чтобы показать план более крупного объекта.
Чертеж в масштабе имеет ту же форму , но другой размер , что и исходный объект.
Чертеж в масштабе имеет масштаб , который представляет собой соотношение, показывающее, как размер чертежа связан с истинным размером объекта.
Масштаб = длина чертежа: истинная длина
Способы написания шкал| В соотношении | 1 см : 1 км |
| В виде уравнения | 1 см = 1 км |
| Прописью | от 1 см до 1 км |
Счетные весы
Это чертеж Магазина камней в Кери Кери. | Это фотография Магазина камней в Кери Кери. |
Длина рисунка около 3 см.
Настоящее здание имеет длину около 30 метров.
Таким образом, масштаб:
3 см : 30 м | = | 3 см : 3000 см |
= | 1 см : 1000 см | |
= | 1 : 1000 |
Это означает, что реальное здание в 1000 раз больше, чем на чертеже в масштабе.
Обратите внимание, что соотношение в шкале обычно записывается в самой простой форме.
Карты
Масштабы, указанные для карт, часто рассчитываются из соотношения с различными единицами измерения. В этих двух примерах используются карты Австралии и Новой Зеландии.
Расстояние по Австралии от города на западном побережье до Брисбена на восточном побережье составляет около 4050 км. То же самое расстояние, измеренное на этой карте Австралии в распечатанном виде, составляет около 9 см. Следовательно, масштаб этой карты .9 см : 4050 км = 1 см : 450 км = 1 см : 45 000 000 см = 1 : 45 000 000 | |
Протяженность Новой Зеландии от мыса Рейнга на севере Северного острова до Блаффа на юге Южного острова составляет около 1500 км. То же самое расстояние, измеренное на этой карте Новой Зеландии в распечатанном виде, составляет около 15 см. Таким образом, масштаб этой карты 15 см : 1500 км = 1 см : 100 км = 1 см : 10 000 000 см = 3 1 : 10 0000005 |
Пример 1 | Пример 2 | Пример 3 | |||||||||
| Упрощение шкалы 5 мм : 100 см | Масштаб карты 1 : 1000. Два места на карте находятся на расстоянии 25 см друг от друга. Каково реальное расстояние между двумя точками? | Длина автобуса 20 метров. На плане в масштабе 1 : 100 какой длины будет автобус? | |||||||||
Ответить
| Ответить Для масштаба 1 : 1000 1 см на карте равен 1000 см 25 см эквивалентно 25 × 1000 см = 25 000 см= 250 метров | Ответить Для масштаба 1 : 100 1 метр на плане равен 100 метрам. |

 Переведите метры в сантиметры и изобразите здание школы на планшете.
Переведите метры в сантиметры и изобразите здание школы на планшете.