Мат ожидание случайной величины: Математическое ожидание и дисперсия случайной величины

4.3.5. Математическое ожидание и дисперсия

Глава 4. Комбинаторика

4.3.

4.3.5.

Пусть мы измеряем случайную величину N раз, например, десять раз измеряем скорость ветра и хотим найти среднее значение. Как связано среднее значение с функцией распределения?

Будем кидать игральный кубик большое количество раз. Количество очков, которое выпадет на кубике при каждом броске, является случайной величиной и может принимать любые натуральные значения от 1 до 6. Среднее арифметическое выпавших очков, подсчитанных за все броски кубика, тоже является случайной величиной, однако при больших N оно стремится ко вполне конкретному числу – математическому ожиданию M_x.

В данном случае M_x = 3,5.

Каким образом получилась эта величина? Пусть в N испытаниях раз выпало 1 очко, раз – 2 очка и так далее. Тогда При N → ∞ количество исходов, в которых выпало одно очко, Аналогично, Отсюда

Модель 4.5. Игральные кости

	Предположим теперь, что мы знаем закон распределения случайной величины x, то есть знаем, что случайная величина x может принимать значения x1, x2, …, xk с вероятностями p1, p2, …, pk. Математическое ожидание M x случайной величины x равно

Математическое ожидание случайной величины часто обозначается как <x>. Записи <x> и M_x эквивалентны.

Пример 1

Найти математическое ожидание числа очков, которые выбьет первый стрелок в предыдущем примере.

Показать решение

Математическое ожидание не всегда является разумной оценкой какой-нибудь случайной величины. Так, для оценки средней заработной платы разумнее использовать понятие медианы, то есть такой величины, что количество людей, получающих меньшую, чем медиана, зарплату и большую, совпадают.

	Медианой случайной величины называют число x1/2 такое, что p (x < x1/2) = 1/2.

Другими словами, вероятность p₁ того, что случайная величина x окажется меньшей x_1/2, и вероятность p₂ того, что случайная величина x окажется большей x_1/2, одинаковы и равны 1/2. Медиана определяется однозначно не для всех распределений.

Вернёмся к случайной величине x, которая может принимать значения x₁, x₂, …, x_k с вероятностями p₁, p₂, …, p_k.

	Дисперсией случайной величины x называется среднее значение квадрата отклонения случайной величины от её математического ожидания:

Используя вероятности p_i того, что величина x принимает значения x_i, эту формулу можно переписать следующим образом:

	Среднеквадратическим отклонением случайной величины x называется корень квадратный из дисперсии этой величины:

Пример 2

В условиях предыдущего примера вычислить дисперсию и среднеквадратическое отклонение случайной величины x.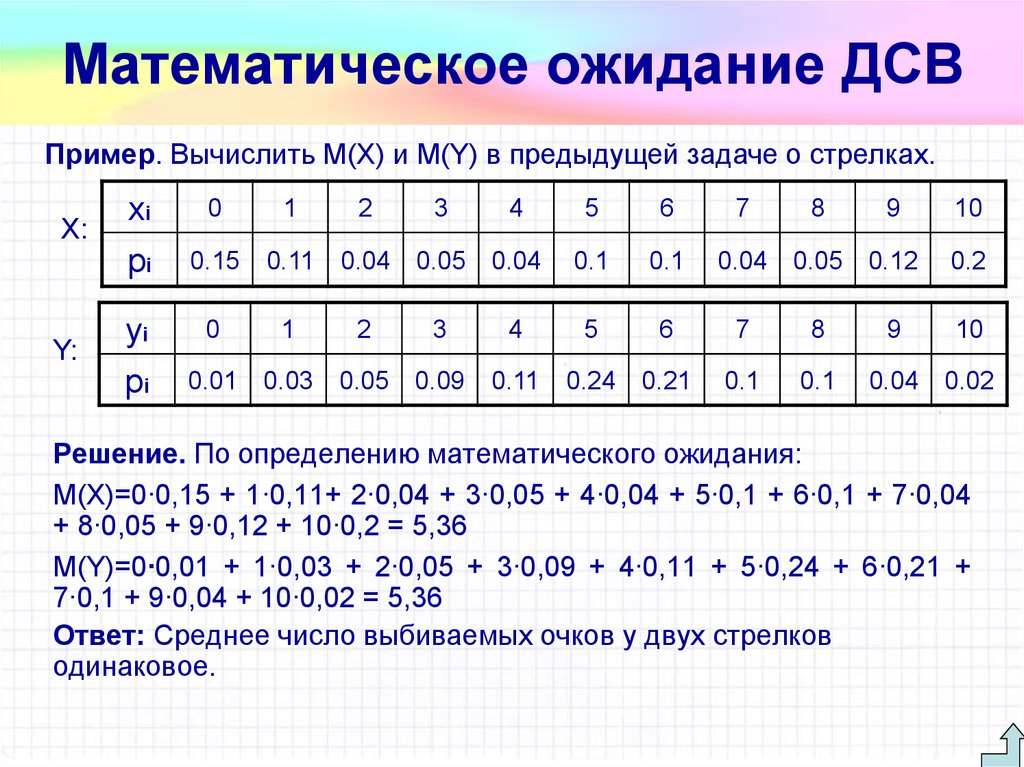

Показать решение

Модель 4.6. Стрельба в мишень

Пример 3

Найти распределение вероятности числа очков, выпавших на кубике с первого броска, медиану, математическое ожидание, дисперсию и среднеквадратичное отклонение.

Показать решение

Свойства математического ожидания Математическое ожидание суммы независимых случайных величин равно сумме их математических ожиданий: Mx + y = Mx + My. Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: Mx · y = Mx · My.

 

Пример 4

Найти математическое ожидание суммы и произведения очков, выпавшей на двух кубиках.

Показать решение

Свойства дисперсии Дисперсия суммы независимых случайных величин равно сумме дисперсий: Dx + y = Dx + Dy.

 

Пример 5

Найти математическое ожидание и дисперсию суммы очков, выпавших при бросании кубика N раз.

Показать решение

 

Дисперсия случайной величины связана с математическим ожиданием квадрата этой случайной величины следующим соотношением:

Доказательство
 



Главная   Онлайн учебники   База репетиторов России   Тренажеры по математике   Подготовка к ЕГЭ 2017 онлайн
Циклевочные машины в аренду Аренда и прокат легковых автомобилей в Москве, Рено, Хендай,Hyundai, Ауди atlant-parket. ru Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия. А также: online подготовка к ЕГЭ на College.ru, библиотека ЭОРов и обучающие программы на Multiring.ru.

22. Математическое ожидание случайной величины

Пусть задан закон распределения случайной величины x.

X	Х1	Х2	Х3	¼	Хn
P	P1	P2	P3	¼	Pn

Математическое ожидание МX (или М(x)) случайной величины x определяется формулой

Рассмотрим пример. Пусть в некотором магазине, торгующем электробытовой техникой, получены статистические данные о числе проданных холодильников в каждый день месяца (условно считаем, что месяц состоит из 30 рабочих дней). Эти данные собраны в таблицу

Количество проданных холодильников	0	1	2	3	4	5
Число дней, в которые было продано столько холодильников	3	7	8	9	2	1

По этой таблице легко подсчитать число холодильников, проданных в магазине за месяц: 0*1+1*7+2*8+3*9+4*2+5*1 = 63. Чтобы подсчитать среднее число холодильников, продававшихся в один день месяца, нужно эту сумму разделить на 30, в результате получим 2,1. Если в приведенной таблице каждое число второй строки поделить на 30, то получится последовательность дробей

,

Каждая из которых представляет собой так называемую Относительную частоту, с которой в данный месяц появлялся приведенный в верхней строке объём продаж. Очевидно, что если просуммировать все произведения чисел, стоящих в первой строке таблицы, на их относительные частоты, то получится то же среднее число продававшихся в один день холодильников:

Если бы в последней формуле относительные частоты рассчитывались не для одного месяца, а для существенно большего срока, то при некоторых условиях (например, при отсутствии кризисных явлений, существенно влияющих на спрос населения на дорогостоящие товары) эти относительные частоты можно было бы считать довольно близкими к вероятностям соответствующих значений объёма продаж. Таким образом, приходим к выводу, что математическое ожидание случайной величины – это в некотором смысле её среднее значение. Следует отметить, что случайная величина может вообще не принимать значения, равного её математическому ожиданию. Так, например, случайная величина, принимающая только значения 1 и –1, каждое – с вероятностью 0,5, имеет математическое ожидание, равное нулю.

Пример. Найти математическое ожидание случайной величины, заданной законом распределения

X	1	0
Р	P	Q

Здесь p + q = 1.

Mx = 1×р + 0×q = р

Свойства математического ожидания.

1. Если случайная величина x принимает одно и то же значение при всех исходах случайного эксперимента, то есть x º С, то её математическое ожидание равно С.

2. Если МX = А, и K – константа, то М(KX) = KMX (математическое ожидание случайной величины, умноженной на число, равно математическому ожиданию случайной величины, умноженному на это число).

3. Если МX = А, и K – константа, то М(K + X) = K + MX (математическое ожидание суммы случайной величины и числа равно сумме этого числа и математического ожидания случайной величины).

Выведем формулу для математического ожидания суммы двух случайных величин x и h, определённых на одном и том же пространстве элементарных исходов и заданных законами распределения

X	Х1	¼	XN		H	Y1	¼	Yk
Р		¼			Р		¼

М(x + h) = (Х1 + У1)Р((x = Х1) ∩ (h = У1))+ (Х2 + У1)Р((x = Х2) ∩ (h = У1)) +¼
+(ХI + УJ)Р((x = ХI) ∩ (h = УJ)) + ¼ + (ХN + УK)Р((x = ХN) ∩ (h = УK))

Очевидно, что сумма в правой части последней формулы содержит Nk Слагаемых.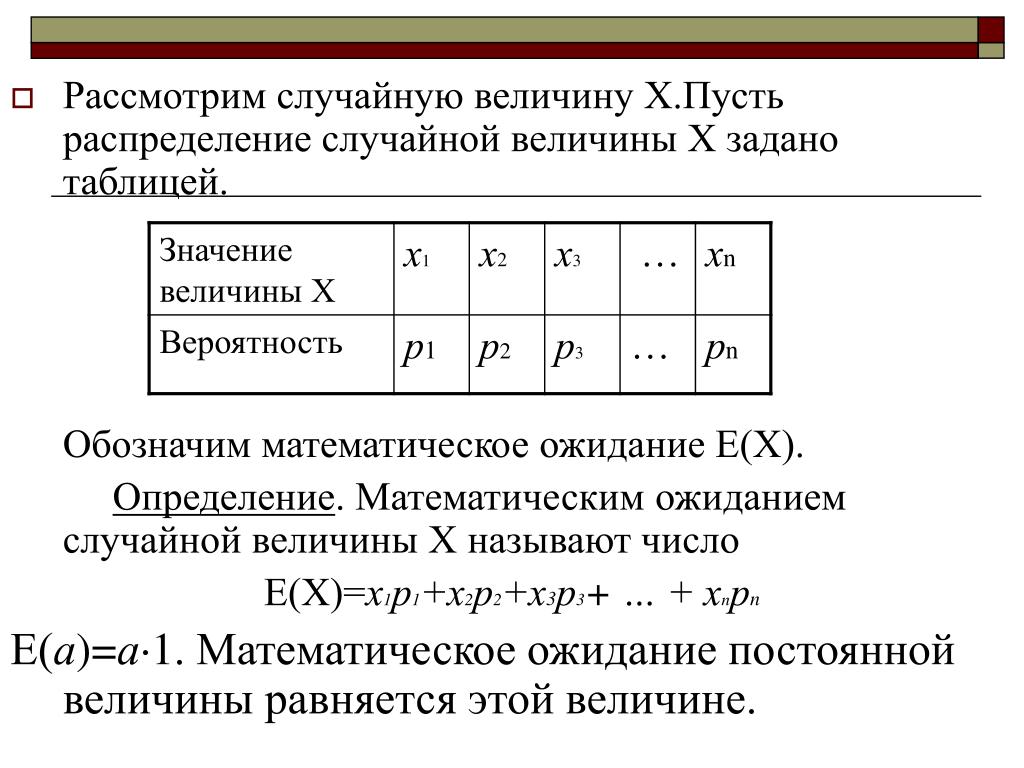 Преобразуем эту сумму следующим образом:

М(x + h) = Х1 Р((x=Х1)∩(h=У1)) + Х1 Р((x=Х1)∩(h=У2)) +¼+Х1 Р((x=Х1)∩(h=УK)) + + Х2Р((x=Х2)∩(h=У1)) + Х2Р((x=Х2)∩(h=У2)) +¼ + Х2Р((x=Х2)∩(h=УK)) + ¼

+ ХNР((x=ХN)∩(h=У1)) + ХNР((x=ХN)∩(h=У2)) +¼ + ХNР((x=ХN)∩(h=УK)) +

+ У1Р((x=Х1)∩(h=У1)) + У1Р((x=Х2)∩(h=У1)) +¼ + У1Р((x=ХN)∩(h=У1)) +

+ У2Р((x=Х1)∩(h=У2)) + У2Р((x=Х2)∩(h=У2)) +¼ + У2Р((x=ХN)∩(h=У2)) + ¼

+ УKР((x=Х1)∩(h=УK)) + УKР((x=Х2)∩(h=УK)) +¼ + УKР((x=ХN)∩(h=УK)) =

= Х1(Р((x=Х1)∩(h=У1)) + Р((x=Х1)∩(h=У2)) +¼ + Р((x=Х1)∩(h=УK))) +

+ Х2(Р((x=Х2)∩(h=У1)) + Р((x=Х2)∩(h=У2)) +¼ + Р((x=Х2)∩(h=УK))) +¼ +

+ ХN(Р((x=ХN)∩(h=У1)) + Р((x=ХN)∩(h=У2)) +¼ + Р((x=ХN)∩(h=УK))) +

+ У1(Р((x=Х1)∩(h=У1)) + Р((x=Х2)∩(h=У1)) +¼ + Р((x=ХN)∩(h=У1))) +

+ У2(Р((x=Х1)∩(h=У2)) + Р((x=Х2)∩(h=У2)) +¼ + Р((x=ХN)∩(h=У2))) + ¼

+ УK(Р((x=Х1)∩(h=УK)) + Р((x=Х2)∩(h=УK)) +¼ + Р((x=ХN)∩(h=УK))) =

= Х1Р(x=Х1) + Х2Р(x=Х2) +¼+ ХN Р(x=ХN) +

+ У1Р(h=У1) + У2Р(h=У2) +¼+ У1Р(h=У1) = MX + MH

При выводе этой формулы использован очевидный факт, что, например, событие x=Х1 можно представить в виде объединения несовместных событий (x=Х1)∩(h=У1), (x=Х1)∩(h=У2), ¼, (x=Х1)∩(h=УN).

Пример.

Заданы N Одинаково распределённых случайных величин x1, x2, ¼, xN с законом распределения

XI	1	0
P	P	Q

Найти математическое ожидание суммы этих случайных величин.

Решение.

M() = = Np

Теорема.

Если случайные величины x и h независимы, то

М(xh) = МX×МH

Доказательство.

Если заданы законы распределения двух независимых случайных величин x и h

X

Х1

¼

Xi

¼

XN

H

Y1

¼

Yj

¼

Yk

Р

¼

¼

Р

¼

¼

То математическое ожидание произведения этих случайных величин можно представить следующим образом:

М(xh) =  =

= Х1+Х2+¼+ ХI¼+ ХN =

= Х1MH + Х2MH + ¼+ ХIMH¼+ ХNMH = MH= МX×МH

< Предыдущая		Следующая >

26.

Математическое ожидание непрерывной случайной величины и его свойства

Математическим ожиданием  непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

При этом, конечно, предполагается, что несобственный интеграл сходится.

Все свойства такие же, как и для дискретных случ величин

(1. Математическое ожидание постоянной величины равно самой постоянной: M(C) = C.      2. Постоянный множитель можно выносить за знак математического ожидания: M(CX) = CM(X).      3. Математическое ожидание суммы нескольких случайных величин равно сумме математических ожиданий слагаемых: M(X+Y+Z) = M(X)+M(Y)+M(Z).      4. Математическое ожидание произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий: M(XYZ) = M(X)M(Y)M(Z). Все эти свойства имеют большое практическое значение.)

27. Дисперсия непрерывной случайной величины и её свойства. Среднее квадратическое отклонение св.

Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

Все свойства такие же, как и для дискретных случ величин(1. Дисперсия постоянной величины С равна нулю : D ( C ) = 0.        2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат : D ( CX ) = C ²D ( X ).        3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин:            D ( X+Y+Z ) = D ( X )+D ( Y )+D ( Z ).        4. Дисперсия суммы постоянной величины и случайной — равна дисперсии случайной величины: D ( C+X ) = D ( X ).      Дисперсию обозначают также как s ² с нижним индексом, обозначающим соответствующую случайную величину или без него.)

Средним квадратичным отклонением называется квадратный корень из дисперсии.

28. Начальные и центральные моменты случайных величин. Выражение мат.Ожидания и дисперсии св через моменты.

Начальным моментом k-го порядка случайной величины называется математическое ожидание k-й степени случайной величины , то есть .

Центральным моментом k-го порядка случайной величины называется величина , определяемая формулой .

На основе закона распределения альтернативно распределенной случайной величины получить выражение для математического ожидания биномиально распределенной случайной величины.

Альтернативно распределенная случайная величина: неуспех успех

Хi	0	1
P	q	p

M(Xi)=0*q + !*p = p

X = X1+X2+…+Xn

M(X) = M(X1+X2+…+Xn) = M(X1)+M(X2)+…+M(Xn) = n*p

M(X) = n*p – для биномиального закона

На основе закона распределения альтернативно распределенной случайной величины получить выражение для дисперсии биномиально распределенной случайной величины.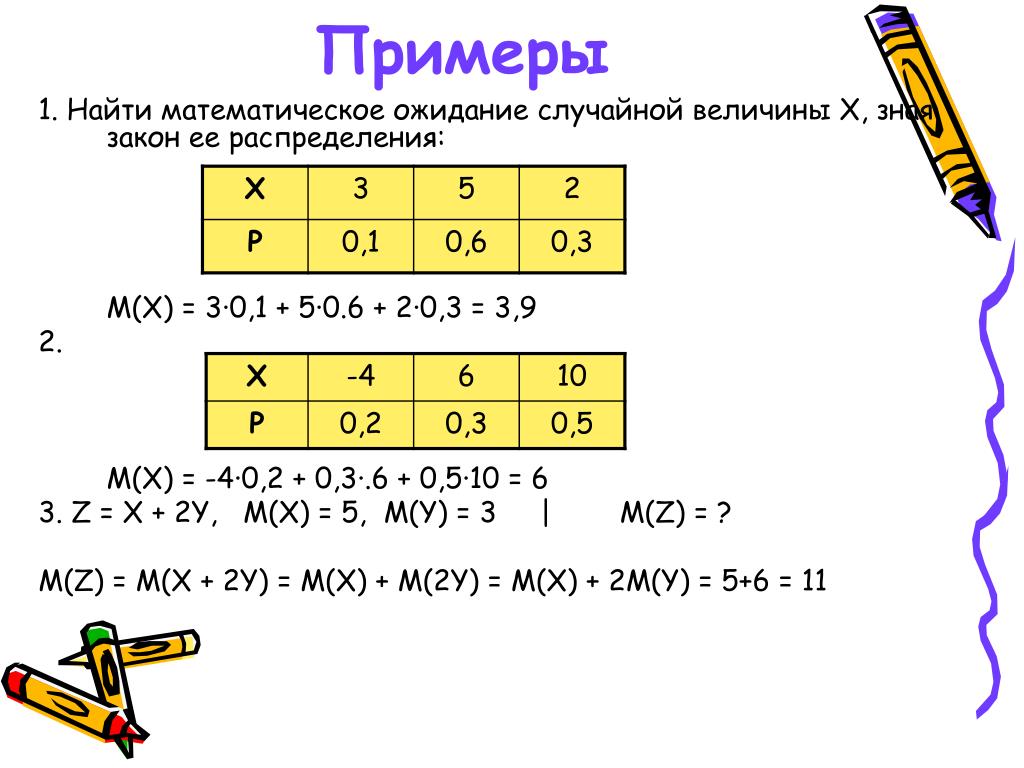 2 = p*(1-p) = p*q

X = X1+X2+…+Xn

D(X) = D(X1+X2+…+Xn) = D(X1)+D(X2)+…+D(Xn) = n*p*q — для биномиального закона

29. Нахождение вероятности попадания случайной величины в заданный интервал через , через , через ряд распределения. Вероятность принять конкретное числовое значение для дискретной и непрерывной случайной величины.

вероятность того, что случайна величина Х примет значение, заключенное в интервале (a, b), равна приращению функции распределения на этом интервале:

P(a<X<b)=F(b)-F(a)

Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), определяется равенством:

b

P(a<X<b)=∫f(x)dx

А

Через ряд распределения посмотрите задачу №260 Гмурмана, там на примере написано и несложно, если что я завтра объясню)

Вероятность того, что непрерывная случайная величина примет одно определенное значение, например х1, равна нулю:

P(X= х1)=0

Ожидаемое значение случайных величин — простое объяснение | by Soner Yıldırım

Ожидаемое значение случайной величины представляет собой средневзвешенное значение всех возможных значений переменной. Под весом здесь понимается вероятность того, что случайная величина примет определенное значение.

Каково ожидаемое значение длины моркови? Случайной величиной здесь является длина моркови. В этом посте я объясню, как ответить на этот вопрос.

Фото Чарльза Делювио на Unsplash

Прежде чем перейти к деталям, мы должны провести различие между дискретными и непрерывными случайными величинами.

• Дискретные случайные величины принимают конечное или счетно бесконечное множество значений. Количество дождливых дней в году является дискретной случайной величиной.
• Непрерывные случайные величины принимают несчетно бесконечно много значений. Например, время, которое требуется от вашего дома до офиса, является непрерывной случайной величиной. В зависимости от того, как вы ее измеряете (минуты, секунды, наносекунды и т. д.), она принимает бесчисленное множество значений.

Начнем с очень простой дискретной случайной величины X, которая принимает только значения 1 и 2 с вероятностью 0,4 и 0,6 соответственно.

Примечание : Сумма вероятностей должна равняться 1, потому что мы рассматриваем все значения, которые может принимать эта случайная величина.

Ожидаемое значение этой случайной величины, обозначенное E[X],

Если бы вероятности 1 и 2 были одинаковыми, то ожидаемое значение было бы равно 1,5. Формула для ожидаемого значения дискретной случайной величины:

Вы можете подумать, что эта переменная принимает только значения 1 и 2, и как может ожидаемое значение быть чем-то другим? Рассмотрим более широкий охват. Допустим, мы выбираем 10 значений из этой случайной величины. Общее ожидаемое значение будет равно 16 (6 умножить на 2 и 4 умножить на 1).

Давайте сделаем немного более сложный пример. Представьте, что вы проходите тест, в котором есть 4 вопроса с несколькими вариантами ответов. Каждый вопрос оценивается в 10 баллов и имеет 4 варианта ответа.

Вы случайно выбираете ответ, даже не читая вопросы. Каково ожидаемое значение баллов, которые вы наберете в этом тесте? Вы можете ответить на этот вопрос без каких-либо сложных вычислений.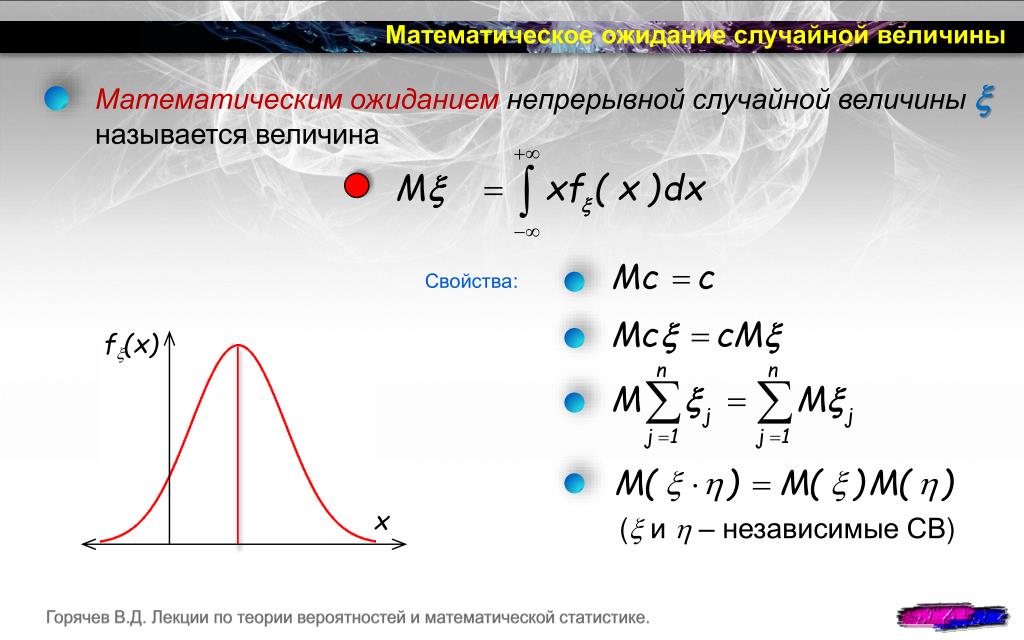 Так как вариантов 4, вероятность выбора правильного ответа равна 0,25. Есть 4 вопроса, поэтому вы, вероятно, правильно ответите на 1 вопрос (1 x 0,25), что дает 10 баллов.

Давайте также найдем ожидаемое значение с помощью формулы и посмотрим, получим ли мы тот же результат. Мы можем правильно ответить на 0, 1, 2, 3 или 4 вопроса. Таким образом, у нас есть дискретная случайная величина, которая принимает значения 0, 10, 20, 30 и 40. Ниже я вычислил вероятности каждого случая и записал баллы, заработанные в каждом случае.

Изображение автора Изображение автора

Ожидаемое значение рассчитывается путем умножения точки (xi) и вероятности получения этой точки (p(xi)) и их сложения. Если вы на самом деле продолжите вычисления, вы увидите, что результат равен 10.

Ожидаемое значение непрерывной случайной величины вычисляется по той же логике, но другими методами. Поскольку непрерывные случайные величины могут принимать несчетно бесконечно много значений, мы не можем говорить о переменной, принимающей конкретное значение. Мы скорее сосредоточимся на диапазонах значений.

Для расчета вероятности диапазонов значений используются функции плотности вероятности (PDF). PDF — это функция, определяющая вероятность того, что случайная величина примет значение в определенном диапазоне.

Вот PDF непрерывной случайной величины, которая равномерно распределена между 5 и 10. Ось x содержит все возможные значения, а ось y показывает вероятность значений.

Равномерно распределенная непрерывная случайная величина от 5 до 10 (Изображение автора)

Поскольку переменная имеет равномерное распределение, вероятность одинакова для всех значений. Площадь под всей PDF должна быть равна 1. Для приведенного выше PDF площадь составляет 0,2 x (10–5), что равно 1. Не каждая PDF представляет собой прямую линию. Как правило, площадь вычисляется путем взятия интеграла PDF.

Ожидаемое значение этой случайной величины равно 7,5, что легко увидеть на графике. Однако лучше выучить формулу, поскольку не каждый PDF-файл так прост, как приведенный выше.

Формула для ожидаемого значения непрерывной переменной:

На основе этой формулы ожидаемое значение рассчитывается, как показано ниже.

Изображение автора

Давайте сделаем немного более сложный пример. Рассмотрим следующую PDF непрерывной случайной величины X.

Изображение автора

Мы попробуем подойти к ожидаемому значению с другой точки зрения. Вероятность того, что переменная примет значение 0, равна 0. Вероятность продолжает увеличиваться по мере увеличения значения и в конечном итоге достигает наибольшей вероятности при значении 8.

Если бы это была однородная случайная величина, ожидаемое значение было бы равно 4. Поскольку вероятность увеличивается по мере увеличения значения, ожидаемое значение будет выше 4.

Если вы представляете этот PDF-файл как треугольный однородный лист металла или любого другого материала, ожидаемое значение представляет собой координату x координаты центр масс.

Функция PDF, представленная этой линией, равна f(x) = 0,03125x. Если посчитать, ожидаемое значение окажется 5,33.

Изображение автора

Ожидаемое значение — это простое, но очень фундаментальное понятие в статистике и вероятности. Чтобы закрепить ваше понимание, я предлагаю сделать несколько примеров самостоятельно. Тогда вы готовы идти!

Спасибо, что прочитали. Пожалуйста, дайте мне знать, если у вас есть какие-либо отзывы.

Все изображения созданы автором, если не указано иное.

Ожидаемое значение

Горячая математика

В распределение вероятностей , средневзвешенное возможных значений случайной величины с весами, заданными их соответствующими теоретическими вероятностями, называется ожидаемое значение , обычно представленный Е ( Икс ) .

Ожидаемое значение информирует о том, чего ожидать от эксперимента «в долгосрочной перспективе», после многих испытаний. В большинстве случаев такого значения в пространстве выборки может и не быть.

Формула средневзвешенного значения для ожидаемого значения дается путем умножения каждого возможного значения для случайная переменная вероятностью того, что случайная величина примет это значение, и суммированием всех этих произведений. Это можно записать как

Е ( Икс ) знак равно ∑ Икс я п ( Икс я ) ,

куда Икс я охватывает все возможные значения случайной величины, и п ( Икс я ) — соответствующая теоретическая вероятность.

Е ( Икс ) также называется средним значением распределения вероятностей, потому что оно говорит, чего ожидать в « долгосрочная перспектива «- то есть после многих испытаний.

Пример:

Когда вы бросаете кубик, вам платят $ 1 для нечетного числа и $ 2 для четного числа. Найдите ожидаемую сумму денег, которую вы получите за один бросок кости.

образец пространства эксперимента { 1 , 2 , 3 , 4 , 5 , 6 } .

В таблице показано распределение вероятностей для одного броска игральной кости и сумма, которая будет выплачена за каждый результат.

Рулон ( Икс )	1	2	3	4	5	6
Вероятность	1 6	1 6	1 6	1 6	1 6	1 6
Сумма ($)	1	2	1	2	1	2

Используйте формулу средневзвешенного значения.

Е ( Икс ) знак равно 1 ( 1 6 ) + 2 ( 1 6 ) + 1 ( 1 6 ) + 2 ( 1 6 ) + 1 ( 1 6 ) + 2 ( 1 6 ) знак равно 1 6 + 2 6 + 1 6 + 2 6 + 1 6 + 2 6 знак равно 96 знак равно 1,5

Итак, ожидаемое значение равно $ 1,50 . Другими словами, в среднем вы получаете $ 1,50 за рулон.

Случайные величины — среднее значение, дисперсия, стандартное отклонение

Случайная величина представляет собой набор возможных значений из случайного эксперимента.

Пример: Подбрасывание монеты: может выпасть орел или решка.

Присвоим им значения Головы=0 и Решки=1 и у нас есть Случайная переменная «X»:

Итак:

• У нас есть эксперимент (как подбрасывание монеты)
• Мы даем значений каждому событию
• Набор значений является случайной величиной

Узнайте больше о случайных величинах.

Среднее значение, дисперсия и стандартное отклонение

Пример: Бросание одного

нечестного игрального кубика

Ради интереса представьте себе взвешенный кубик (мошенничество!), чтобы у нас были следующие вероятности:9 1

31212 2 3 4 5 6 0,1 0,1 0,1 0,1 0,1 0,5

 

Среднее или ожидаемое значение: μ

Когда мы знаем вероятность p каждого значения x , мы можем вычислить ожидаемое значение (среднее) X:

μ = Σxp

Примечание: Σ — это сигма-нотация, означающая суммирование.

Чтобы рассчитать ожидаемое значение:

• умножьте каждое значение на его вероятность
• суммировать их

Продолжение примера:

x	1	2	3	4	5	6
р	0,1	0,1	0,1	0,1	0,1	0,5
опыт	0,1	0,2	0,3	0,4	0,5	3

μ = Σxp = 0,1+0,2+0,3+0,4+0,5+3 = 4,5

Ожидаемое значение равно 4,5

Примечание: это средневзвешенное значение: значения с более высокой вероятностью вносят больший вклад в среднее значение.

 

 

Дисперсия: Var(X)

Дисперсия:

Var(X) = Σx ² p − μ ²

Чтобы вычислить дисперсию:

• возведите каждое значение в квадрат и умножьте на его вероятность
• суммируем их и получаем Σx ² p
• , затем вычтите квадрат ожидаемого значения μ ²

Продолжение примера:

x	1	2	3	4	5	6
р	0,1	0,1	0,1	0,1	0,1	0,5
x 2 р	0,1	0,4	0,9	1,6	2,5	18

Σx ² p = 0,1+0,4+0,9+1,6+2,5+18 = 23,5

Var(X) = Σx ² P- μ ² = 23,5- 4,5 ² = 3,25

Дисперсия 3,25

Стандартное отклонение: σ

. Стандартное отклонение- квадратный корень варианта:

σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ = σ =. X)

Продолжение примера:

x	1	2	3	4	5	6
р	0,1	0,1	0,1	0,1	0,1	0,5
x 2 р	0,1	0,4	0,9	1,6	2,5	18

σ = √Var(X) = √3,25 = 1,803. ..

Стандартное отклонение равно 1,803…

 

Давайте еще один пример!

(Обратите внимание, что на этот раз мы запускаем таблицу вниз, а не вдоль.)

Вы планируете открыть новый ресторан McDougals Fried Chicken и нашли следующую статистику для похожих ресторанов:

Процент	Годовой доход
20%	$50 000 Убыток
30%	$0
40%	$50 000 Прибыль
10%	$150 000 Прибыль

Используя это как вероятностей для прибыли вашего нового ресторана, какова ожидаемая стоимость и стандартное отклонение?

 

Случайная переменная X = «возможная прибыль».

Сумма xp и x ² p :

Вероятность p	Прибыль (тыс. долл. США) x	хп	x 2 стр
0,2	-50	-10	500
0,3	0	0	0
0,4	50	20	1000
0,1	150	15	2250
Σр = 1		Σхр = 25	Σx 2 р = 3750

 

μ = Σxp = 25

Var(X) = Σx ² p − μ ²
= 3750 − 25 ²
= 3750 − 625
= 3125

σ = √3125 = 56 (to ближайшее целое число)

Но помните, что это тысячи долларов, поэтому:

• μ = 25 000 долларов
• σ = 56 000 долларов США

Таким образом, вы можете ожидать заработать 25 000 долларов, но с очень большим возможным отклонением.

Попробуем еще раз, но с гораздо большей вероятностью для $50 000:

Пример (продолжение):

Теперь с различными вероятностями (значение $50 000 имеет высокую вероятность 0,7 сейчас):

Вероятность p	Прибыль (тыс. долл. США) x	хп	x 2 стр
0,1	-50	-5	250
0,1	0	0	0
0,7	50	35	1750
0,1	150	15	2250
Σр = 1	Сумма:	Σхр = 45	Σx 2 р = 4250

 

μ = Σxp = 45

Var(X) = Σx ² p − μ ²
= 4250 — 45 ²
= 4250 — 2025
= 2225

σ = √2225 = 47 (к ближнему целу

σ = 47 000 долларов США

Среднее значение теперь намного ближе к наиболее вероятному значению.