Калькулятор дробей
Что такое дроби?
Дробь – это число, которое состоит из нескольких одинаковых частей — долей единицы, а также из одной ее части.
Обыкновенная дробь выглядит так:
В математической записи дроби число, которое находится выше черты — называется числителем, а число, которое расположено ниже — называется знаменателем. Оно показывает то, на сколько долей разделили единицу.
Первое число является делимым, а второе число служит делителем. Обыкновенные дроби могут образовывать поле рациональных чисел, если они будут с целыми числителями и ненулевыми знаменателями. Они показывают количество долей, на которые делится единица.
Математические дроби начинают изучать в школе. В основном в 5 или в 6 классах. Но также дроби очень часто используются в дальнейшей школьной и затем в вузовской программах.
История дробей
Русское слово «дробь», как и его аналоги в других языках, происходит от латинского слова «fractura» с арабским происхождением и означает в переводе: ломать или дробить.
Основы теории обыкновенных дробей заложили греческие и индийские математики. Слова числитель и знаменатель ввёл в оборот греческий математик Максим Плануд.
Позже дроби появляются в Европейской математике, например, у Фибоначчи в 1202 году. Поначалу европейские математики оперировали только с обыкновенными дробями, а в астрономии — с шестидесятеричными. В Европе первые десятичные дроби ввёл Иммануил Бонфис около 1350 года, но широкое распространение они получили только после появления сочинения Симона Стевина «Десятая» (1585).
В России, начиная с древней Руси, дроби именовали долями. А в первых отечественных учебниках по математике дроби назывались ломаными числами. Термин «дробь», как аналог латинского «fractura», впервые используется в «Арифметике» Магницкого в 1703 году как для обыкновенных, так и для десятичных дробей.
Виды дробей
Дроби бывают нескольких видов:
- обыкновенные;
- смешанные и простые;
- правильные и неправильные;
- десятичные;
- в виде процентов.
Обыкновенная дробь
Обыкновенная дробь имеет вид a/b. Число a — здесь будет являться числителем дроби, а число b — будет знаменателем.
Примеры:
- 1/2
- 6/5
- 3/1
- 7/15
Правильные и неправильные
Правильной называется дробь, у которой числитель (модуль числителя) меньше модуля знаменателя.
Пример, правильной дроби: 3/4, так как 3<4.
Неправильная дробь, наоборот, имеет числитель, который по модулю больше чем знаменатель.
Пример, неправильной дроби: 4/3, так как 4>3.
Простые и смешанные
Простая дробь содержит только числитель и знаменатель. Например, 4/3.
Смешанная дробь содержит целое число и дробь, и понимается как сумма этого числа и дроби. Например, 1 и 1/3.
Неправильную дробь всегда можно сделать смешанной, то есть выделить в ней целые части.
Десятичная дробь
Десятичная дробь — это запись дроби, в которой знаменатель не дан в явном виде, но понимается как целое число, степень десяти (напр.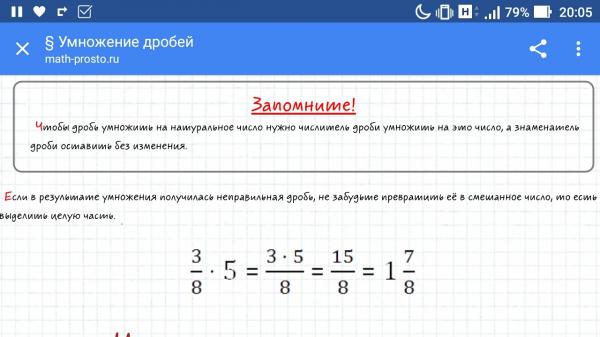
10, 100, 1000 и др).
Десятичная дробь записывается через запятую в строку таким образом, чтобы отделить дробную часть от целой части. Вот так:
- 0,7 – ноль целых и 7 десятых (7/10).
- 5,42 – пять целых и 42 сотых (42/100).
- 9,245 – девять целых и 245 тысячных (245/1000).
В виде процентов
Дробь в виде процентов — это когда при переводе десятичной дроби в проценты, ее необходимо умножить на 100. Запись производится с запятыми.
Например, 0,023 = 0,023 * 100% = 2,3%
Для того чтобы перевести проценты в десятичные дроби, следует разделить число процентов на 100.
Что нужно знать, чтобы работать с дробями?
Что переводить дроби из одного вида в другой и выполнять различные операции над дробями, надо знать несколько терминов.
Наименьшее общее кратное (НОК) для нескольких чисел — это наименьшее натуральное число, которое делится на каждое из этих чисел.
Наименьший общий знаменатель – это НОК, которое рассчитывается для знаменателей двух и более дробей.
Как найти наименьший общий знаменатель?
Чтобы это понять, необходимо рассмотреть следующий пример двух дробей:
1/20 и 3/14
Если нужно привести дроби с разными знаменателями к общему наименьшему знаменателю, следует найти наименьшее общее кратное (НОК) знаменателей этих дробей.
Знаменатель первой дроби равен 20.
Его нужно разложить его на простые множители: 20=2⋅5⋅2.
Далее также разложить 2 знаменатель дроби 14 на простые множители: 14 = 7*2.
Убираем повторяющиеся множители у знаменателя второй дроби и получаем:
НОК (14,20) = 2*5*2*7 = 140.
В итоге общий наименьший знаменатель равняется 140.
Как привести дробь к общему знаменателю?
Берем первую дробь 1/20 и умножаем ее на 7, чтобы прийти к 140. Для этого умножаем числитель и знаменательно на 7 и получаем:
А вторую дробь теперь следует умножить на 10 таким же образом:
Общим наибольшим делителем (НОД) нескольких чисел является самое большее целое натуральное число, на которое эти самые числа делятся без остатка.
- Для этого действия необходимо целую часть умножать на знаменатель дробной части.
- После этого полученный результат сложить с числителем дробной части. То, что получилось в итоге, и будет числителем новой дроби, а сам знаменатель при этом останется без изменений.
Операции над дробями
С дробями можно совершать различные арифметические операции.
➕ Сложение
Для сложения дробей с разными знаменателями сначала нужно найти знаменатель, который является общим. После этого нужно к общему знаменателю привести дроби. Хорошо, если это будет наименьший знаменатель.
Далее — выполнить сложение дробей, где под суммой числителей подписать общий знаменатель.
В конце, если возможно, сократить полученную дробь.
Например:
➖ Вычитание
Здесь потребуется из числителя уменьшаемого отнять числитель вычитаемого, а сам знаменатель при этом оставить без изменений.
Так, чтобы сделать вычитание из дроби, следует сначала вычесть числители, а все одинаковые знаменатели оставлять прежними.
Например:
✖ Умножение
Для этого умножаются числители и записывается результат, как числитель дроби.
Далее, умножаются знаменатели и записывается результат, как знаменатель дроби.
Например:
➗ Деление
Здесь следует числитель первой дроби умножить на знаменатель второй дроби. После чего записать полученное произведение в числитель новой дроби.
Знаменатель первой дроби умножается на числитель второй дроби. Далее записывается произведение, как знаменатель новой дроби.
Например:
📏 Сокращение
Это действие получается тогда, когда необходимо разделить числитель и знаменатель на одинаковое число, но которое не может быть равно 0.
В итоге получается равную дробь, имеющая меньший знаменатель и числитель.
Чтобы сократить дробь, необходимо в определенной последовательности проверять, на что делятся знаменатель и числитель. В случае, когда находится общий делитель, то сокращать именно на него.
Значительно упростит сокращение раскладывание знаменателя и числителя на множители.
Например:
❓ Вопросы и ответы
А также советуем обратить внимание на некоторые часто задаваемые вопросы про дроби и ответы на них.
Какие дроби называются простыми?
Простые дроби — это те, которые записываются в виде 2-ух целых чисел, определенных скошенной или горизонтальной прямой. Например: 1/4,1/2.
Какие дроби называются десятичными?
Когда в знаменателях стоят 10, 100, 1000 и т.д. и степень числа 10, то дроби имеют название — десятичные.
Какие дроби называются правильными?
Правильные дроби те, у которых модуль знаменателя больше модуля числителя.
Какие дроби называются неправильными?
org/Answer»>Неправильные дроби те, у которых модуль числителя меньше, чем модуль знаменателя.Как разделить дробь на дробь?
Нельзя делить на 0.
Если делить на 1 — будет такое же число.
Если делить 0 на любое число, получится 0.
Какая дробь называется положительной?
Когда она больше 0.
Какая дробь называется отрицательной?
Когда перед положительной дробью ставится знак «–».
Что такое степени с дробями?
Степени с дробями приводятся к знаменателю так же, как и рациональные дроби. Нужно найти дополнительный множитель и умножить на него знаменатель и числитель дроби.
При этом дополнительный множитель подбирать так, чтобы он не обращался в 0 для исходящего выражения.
Как пользоваться калькулятором дробей?
Калькулятор, решающий дроби, позволяет переводить дроби и производить самые простые операции типа сложения, вычитания, умножения, деления.
Для этого нужно заполнить соответствующие поля для дробей и нажать кнопку «Вычислить».
Поделитесь в соцсетях
Если понравилось, поделитесь калькулятором в своих социальных сетях: вам нетрудно, а проекту полезно для продвижения. Спасибо!
Есть что добавить?
Напишите своё мнение, комментарий или предложение.
Калькулятор дробей
При помощи калькулятора дробей вы легко сможете: сложить дроби, вычесть дроби, умножить дроби и разделить дроби онлайн. Калькулятор выводит результат с решением, что даст вам возможность легко освоить операции с дробями. При заполнении полей используйте целые, неотрицательные числа, а, чтобы задать знак дроби воспользуйтесь кнопкой «+/−».
Сложение и вычитание дробей с разными знаменателями
Приведем пример, сложим две смешанные дроби
Чтобы сложить дроби с разными знаменателями, необходимо привести эти дроби к неправильному виду. Чтобы привести дробь к неправильному виду, необходимо знаменатель оставить прежним, а в числитель записать как сумму, где первое слагаемое — это произведение целой части и знаменателя, а второе слагаемое – числитель.
=
(7 · 5) + 6
7
=
и вторая дробь
=
(9 · 3) + 5
9
=
Далее необходимо привести дроби к общему знаменателю. Существует несколько способов, чтобы привести дроби к общему знаменателю, мы рассмотрим самый простой. Общим знаменателем будет произведение знаменателей первой и второй дроби. Далее необходимо будет числитель первой дроби умножить на знаменатель второй дроби, а числитель второй дроби умножить на знаменатель первой дроби.
+
=
41 · 9
7 · 9
+
32 · 7
7 · 9
=
+
Теперь, когда дроби имеют общий знаменатель их числители можно сложить.
369 + 224
63
=
В ответе получилась несократимая дробь, поэтому просто приведем дробь к смешанному виду, то есть выделим целую часть. Для этого необходимо, поделить числитель дроби на знаменатель.
593 : 63 = 9 (остаток 26)
9 — целая часть
26 — числитель
63 — знаменатель
=
= 9.412698
Запишем пример целиком:
+
=
(7 · 5) + 6
7
+
(9 · 3) + 5
9
=
+
=
41 · 9
7 · 9
+
32 · 7
7 · 9
=
+
=
369 + 224
63
=
=
= 9.412698
При вычитании дробей, необходимо выполнить все те же действия, что и при сложении дробей, только уже числители дробей нужно не складывать, а вычитать. Вычтем две дроби из примера на сложение:
−
=
(7 · 5) + 6
7
−
(9 · 3) + 5
9
=
−
=
41 · 9
7 · 9
−
32 · 7
7 · 9
=
−
=
369 − 224
63
=
=
= 2.
301587
Сложение и вычитание дробей с одинаковыми знаменателями
При сложении и вычитании дробей с одинаковыми знаменателями, уже нет необходимости приводить такие дроби к общему знаменателю. Единственное что нужно сделать, это если одна из дробей имеет смешанный вид, то ее нужно будет привести к неправильному виду, то есть записать без целой части.
Приведем пример сложим две дроби с одинаковыми знаменателями, одна из которых имеет смешанный вид:
+
=
(16 · 4) + 1
16
+
=
+
=
65 + 7
16
=
=
9 · 8
2 · 8
=
=
= 4.5
Обратите внимание, что получившуюся дробь семьдесят две шестнадцатых можно сократить, для этого необходимо разделить числитель и знаменатель на восемь, либо записать числитель как произведение 9 · 8, а знаменатель как 2 · 8, в данном случае 8 сократятся и мы получим дробь девять вторых.
Умножение и деление дробей
Умножим две дроби
Чтобы умножить две дроби с разными знаменателями, нужно перемножить их числители и знаменатели.
В нашем примере первая дробь имеет смешанный вид, поэтому сначала необходимо эту дробь привести к неправильному виду, а затем выполнить умножения числителей и знаменателей.
×
=
(8 · 15) + 3
8
×
=
×
=
123 · 4
8 · 5
=
=
123 · 4
10 · 4
=
=
= 12.3
После умножения числителей и знаменателей получилась дробь четыреста девяносто две сороковых, данную дробь можно сократить, если разделить числитель и знаменатель на 4, либо записать числитель как сто двадцать три умножить на четыре, а знаменатель, как десять умножить на четыре. И также как в предыдущих примерах приводим дробь к смешанному виду, 123 : 10 = 12 (остаток 3), 12 — целая часть, 3 – числитель, 10 – знаменатель.
Деление дробей равносильно умножению первой дроби на обратную дробь второй дроби, проще говоря необходимо у второй дроби поменять числитель и знаменатель местами.
Дальнейшие вычисления аналогичны правилам умножения дробей, рассмотренным выше
÷
=
×
=
5 · 3
7 · 9
=
=
5 · 3
21 · 3
=
= 0.
238095
Калькулятор уравнений для целых чисел и дробей
Калькулятор уравнений для целых чисел и дробей
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
03.2004 
11.2001 
01.2004 
06.2004 
Я действительно рекомендую программу.Рациональное число в виде дроби
Учеба Математика Алгебра
Этот онлайн-калькулятор записывает рациональное число в виде дроби (отношение двух целых чисел) по формуле бесконечной геометрической прогрессии.
Когда вы начинаете изучать геометрические последовательности, вы можете столкнуться с задачей, сформулированной так:
Запишите рациональное число 0,58333… как отношение двух целых чисел.
Конечно, в этом примере задачи нас фактически просят преобразовать повторяющееся десятичное число в дробь. Действительно, для решения этой задачи требуется формула бесконечного геометрического ряда.
Этот калькулятор использует эту формулу, чтобы узнать числитель и знаменатель для данного повторяющегося десятичного числа. Решение и формулы описаны под калькулятором.
Обратите внимание, что в приведенной выше задаче повторяющаяся десятичная дробь неформально представлена многоточием (три точки…). На самом деле существует несколько условных обозначений для представления повторяющихся десятичных дробей, но ни одно из них не принято повсеместно. Например, в США обозначение представляет собой горизонтальную линию (винкулум) над повторяющимися цифрами, а в некоторых частях Европы обозначение заключается в заключении повторяющихся цифр в круглые скобки. Калькулятор поддерживает два способа ввода повторяющегося десятичного числа: 0,58333… и 0,58(3) 9.0014
Рациональное число как отношение двух целых чисел
Рациональное число
Отношение двух целых чисел
Повторяющееся десятичное число
Цитата из Википедии: это десятичная представление числа, цифры которого являются периодическими (повторяют свои значения через равные промежутки времени), а бесконечно повторяющаяся часть не равна нулю.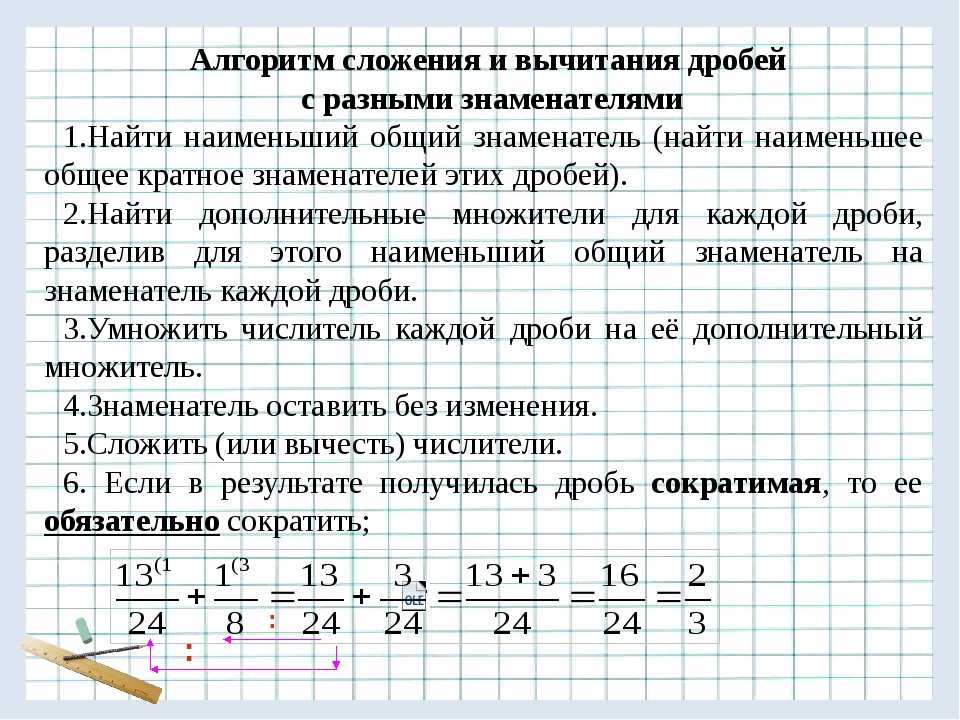
Бесконечно повторяющаяся последовательность цифр называется 9.0011 повторить или повторить . Если повторение равно нулю, это десятичное представление называется конечным десятичным числом, а не повторяющимся десятичным числом. Можно показать, что число рационально тогда и только тогда, когда его десятичное представление повторяется или заканчивается (т. е. имеет конечное количество цифр или начинает повторять конечную последовательность цифр). А рациональное число, по определению, — это любое число, которое может быть выражено как частное или дробь p/q двух целых чисел, числителя p и ненулевого знаменателя q.
Если у нас есть завершающая десятичная дробь, мы можем использовать конвертер дробей в десятичную и десятичную дробь. В случае повторяющегося десятичного числа расчет становится немного сложнее. И здесь нам помогут геометрические последовательности. Давайте воспользуемся приведенным выше примером и преобразуем рациональное число (мы знаем, что оно рационально, потому что его десятичное представление повторяется) 0,58333.