Математический пример сложный: Сложные примеры по математике, которые вгоняют в краску неучей

Зачем сложные примеры по математике решать взрослому человеку

Метки

Математика Наука Саморазвитие Ум Школа

Дружить с математикой нужно каждому человеку. И даже если этот предмет непросто давался в школе, его основы следует хорошо усвоить. Ведь базовые математические знания пригодятся в любой сфере жизни. Но чтобы любые расчеты давались легко, с цифрами следует работать как можно чаще. И даже порой решать сложные примеры по математике.

Поэтому сегодня редакция «Так Просто!» предложит несколько простых на вид, но запутанных примеров. Для кого-то такие задания окажутся легкими, но тот, кому трудно давалась математика на школьных уроках, может столкнуться с трудностями. Получится ли всё решить правильно?

GettyImages

1. Первым делом предлагаем разобраться с примером, где собраны одни девятки. Разве может такое задание оказаться сложным? Может, если в одном примере собраны сразу все основные математические операции. Да если еще и не каждый помнит, что в каком порядке следует выполнять. Попробуй справиться без ошибок.

2. В качестве второго задания окажется пример, который состоит только из троек. Однако тут математических операций еще больше, а потому легко запутаться и что-то посчитать неправильно. Справишься без калькулятора, чтобы дать правильный ответ?

3. И напоследок предлагаем любопытные уравнения, из которых следует понять, каким значениям равны A, B и C. Постарайся в уме разобраться с каждым уравнением, чтобы понять, какое число скрывается за вопросительным знаком. Это не так сложно, как кажется.
   

   View this post on Instagram

   A post shared by Antoha (@7second2)

Подсказки и решения

1. Если вспомнить основные правила, о которых много говорили учителя математики, то сможем несколько упорядочить наш пример. А тогда и решить его будет уже совсем не сложно: 9 + (9 / 9) + (9 * 9) – 9 = 9 + 1 + 81 – 9 = 82.

   GettyImages

2. Хотя во втором примере есть скобки, но они призваны скорее запутать читателя. Ведь каждую математическую операцию тут можно проводить в порядке написания. А потому 3 / 3 (3 * 3) * 3 / 3 + 3 = 1 * 9 * 3 / 3 + 3 = 27 / 3 + 3 = 9 + 3 = 12.
3. В первую очередь понимаем, что A = 39 / 3 = 13. Тогда B = (25 + 13) / 2 = 38 / 2 = 19. И в таком случае C = 50 – 6 – 19 = 25. И теперь нам легко решить последний пример 13 + 19 + 25 = 57.

   GettyImages

Получилось без ошибок справиться с каждым заданием? Или у тебя оказались другие числа? Расскажи в комментариях, удалось ли справиться с каждым заданием и какие ответы получились.

Фото в статье Getty Images

Поделиться

«Сложные примеры», которые разделили Сеть на два лагеря

Познавательное

18 Янв 2022

С первых лет школы на уроках математики нам рассказывают о том, как выполнять те или иные действия, а главное — в каком порядке их нужно решать. Но со временем это всё забывается. Именно из-за этого в Сети разгораются споры из-за, казалось бы, элементарных задач. Эти самые «сложные примеры» мы сегодня и рассмотрим…

«Сложные примеры» из социальных сетей

Недавно в Твиттере опубликовали математический пример на несколько действий, из-за которого люди разделились на два больших лагеря. Одни стали утверждать, что нет в нём ничего сложного, а другие и вовсе говорить, что здесь может быть два решения. Для начала официально заявляем: в математике не бывает двух правильных ответов. К единственно верному ответу можно дойти разными способами, но ответ всё равно будет один.

© Depositphotos

Итак, тот самый пример выглядел следующим образом:

2 + 5 (8 – 5) = ?

© Depositphotos

Перед тем как подойти к ответу, скажем, что огромное количество людей попыталось ответить на этот вопрос. Среди них, к примеру, оказался актер Тайка Вайтити.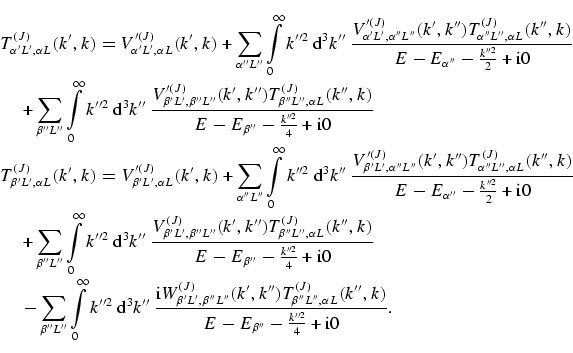 То ли мужчина вовсе не силен в математике, то ли он решил пошутить, но у него получился ответ 3. Если честно, мне даже понять трудно, как к нему можно было прийти.

Посмотреть эту публикацию в Instagram

Публикация от Синема Парк & Формула Кино (@kinoteatr.official)

Что касается правильного ответа, то, конечно, сначала нужно выполнить действие в скобках. Потом, по математическим правилам, идет умножение (знак перед скобками упущен), а в конце стоит прибавить два. В общем, 5 умножаем на 3 и прибавляем 2. Получили 17. Это и есть правильный ответ, а вовсе не 21, который стал вторым по популярности вариантом.

Немного логики

Еще одна интересная задачка требует скорее логических размышлений, нежели знаний правил. В общем, внимательно взгляни на картинку и дай ответ: какое время должны показать последние часы?

Посмотреть эту публикацию в Instagram

Публикация от Zanna k. (@zannakovalevskaja)

Если ты присмотришься, то поймешь, что вторые часы переведены на 1 час и 10 минут назад по отношению к первым. Третьи — на 1 час и 20 минут по отношению ко вторым. Четвертые — на 1 час и 30 минут по отношению к третьим. Соответственно, на пятых часах должно быть на 1 час и 40 минут меньше, чем на четвертых. Правильный ответ: 5 часов и 35 минут.

Логика и арифметика

Перед тобой, казалось бы, странные равенства. Но суть их в том, что тебе нужно найти закономерность между слагаемыми и суммой.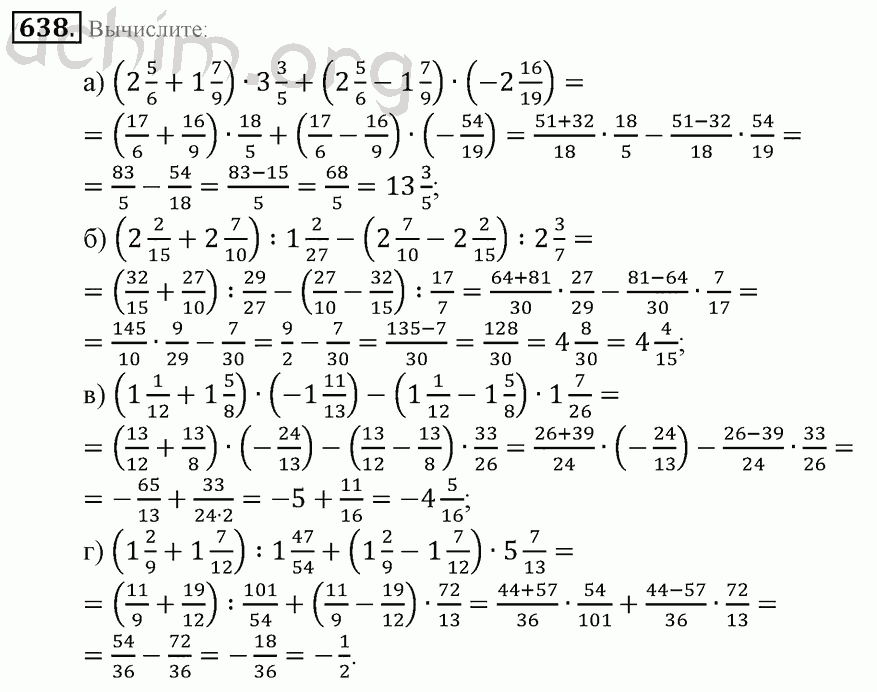

Присмотрись внимательно и ответь, что нужно записать вместо вопросительного знака?

Посмотреть эту публикацию в Instagram

Публикация от Zanna k. (@zannakovalevskaja)

Дело в том, что сначала нужно вычесть из первого слагаемого второе. А потом найти их сумму. Два полученных числа объединяем в одно и получаем правильный ответ. Так что в итоге 10 – 6 = 4, а 10 + 6 = 16. Так что правильный ответ — 416.

© Depositphotos

Искренне надеемся, что наши задачки были для тебя слишком простыми. Непременно напиши в комментариях, справился ли ты со всеми из них. Если нет, не расстраивайся, школьная программа понемногу улетучивается из памяти, так что мы помогли тебе ее немного вспомнить!

Поделиться

задачи логика математика

Автор статьи

Редакция «Boom»

Редакция Boom — это неутомимые искатели крутых видео, о которых хочется рассказать всей планете. Каждый день мы знакомим любимого читателя с невероятными событиями и интригующими жизненными историями. Наша задача — делать скучный мир веселее, а лучшие видеоролики со всего мира помогают нам в этом.

2 = -1 . (Другими словами, i — это квадратный корень из -1 .) Действительное число a называется действительной частью комплексного числа, а действительное число b — мнимая часть. Например, 3 + 2i — это комплексное число, имеющее действительную часть 3 и мнимую часть 2 . Комплексные числа часто используются в прикладной математике, теории управления, анализ сигналов, гидродинамика и другие области.

Использование #

Комплексное число создается с помощью функции math.complex . Эта функция принимает:

• два числа, представляющие действительную и мнимую части значения,
• одна строка, содержащая комплексное значение в форме a + bi , где a и b соответственно представляют действительную и мнимую части комплексного числа.
• объект со свойствами относительно и im для реального и мнимого часть значения или два свойства r и phi , содержащие полярные координаты комплексного значения. Функция возвращает объект Complex .

Синтаксис:

 math.complex(re: число) : Комплекс
math.complex(re: число, im: число): Комплекс
math.complex(комплекс: Комплекс) : Комплекс
math.complex({re: Number, im: Number}): Комплекс
math.complex({r: число, phi: число}) : Комплекс
math.complex({абс: число, аргумент: число}) : Комплекс
math.complex(str:string): сложный
 

Примеры:

 const a = math.complex(2, 3) // Комплекс 2 + 3i
a.re // Номер 2
a.im // Номер 3
const b = math.complex('4 - 2i') // Комплекс 4 - 2i
b.re = 5 // Число 5
б // Комплекс 5 - 2и
 

Расчеты #

Большинство функций math.js поддерживают комплексные числа. Комплексные и действительные числа можно использовать вместе.

 const a = math. complex(2, 3) // Комплекс 2 + 3i
const b = math.complex('4 - 2i') // Комплекс 4 - 2i
math.re(a) // Число 2
math.im(a) // Число 3
math.conj(a) // Комплекс 2 - 3i
math.add(a, b) // Комплекс 6 + i
math.multiply(a, 2) // Комплекс 4 + 6i
math.sqrt(-4) // Комплекс 2i
 

API #

Объект Complex , созданный math.complex , содержит следующие свойства и функции:

complex.re #

Число, содержащее действительную часть комплексного числа. Можно прочитать и заменить.

complex.im #

Число, содержащее мнимую часть комплексного числа. Можно прочитать и заменить.

complex.clone() #

Создать клон сложного числа.

сложный.равный(другой) #

Проверить, равно ли комплексное число другому комплексному значению.

Два комплексных числа равны, если их действительная и мнимая части равны. равный.

complex.neg() #

Возвращает комплексное число с действительной и мнимой частями, равными по величине, но противоположными по знаку текущему комплексному числу.

complex.conjugate() #

Возвращает комплексное число с равной действительной и мнимой частями, равными по величине, но противоположными по знаку текущему комплексному числу.

complex.inverse() #

Возвращает комплексное число, обратное текущему комплексному числу.

complex.toVector() #

Получить векторное представление текущего комплексного числа. Возвращает массив размера 2.

complex.toJSON() #

Возвращает JSON-представление комплексного числа с подписью {mathjs: 'Complex', re: число, im: число} . Используется при сериализации комплексного числа, см. Сериализация.

комплекс.toPolar() #

Получить полярные координаты комплексного числа, возврат объект со свойствами r и phi .

complex.toString() #

Возвращает строковое представление комплексного числа, отформатированное как a + bi , где a — действительная часть, а b — мнимая часть.

complex.format([precision: number]) #

Получить строковое представление комплексного числа, в формате a + bi , где a — действительная часть, b — мнимая часть. Если определена точность, значение единиц будет округлено до указанного количество цифр.

Доступ к следующим статическим методам можно получить с помощью math.Complex

Complex.fromJSON(json) #

Восстановление комплексного числа из объекта JSON. Принимает Объект {mathjs: 'Complex', re: number, im: number} , где свойство mathjs не является обязательным. Используется при десериализации комплексного числа, см. Сериализация.

Complex.fromPolar(r: number, phi: number) #

Создать комплексное число из полярных координат.

Complex.compare(a: Complex, b: Complex) #

Возвращает результат сравнения двух комплексных чисел:

• Возвращает 1, если действительная часть a больше, чем действительная часть b
• Возвращает -1, если действительная часть a меньше, чем действительная часть b
• Возвращает 1, когда действительные части равны и мнимая часть a больше, чем мнимая часть b
• Возвращает -1, когда действительные части равны а мнимая часть числа a меньше мнимой части числа b
• Возвращает 0, если действительная и мнимая части равны.

Пример:

 const a = math.complex(2, 3) // Комплекс 2 + 3i
const b = math.complex(2, 1) // Комплекс 2 + 1i
math.Complex.compare(a,b) // возвращает 1
//создать из json
const c = math.Complex.fromJSON({mathjs: 'Complex', re: 4, im: 3}) // Комплекс 4 + 3i
 

Что такое комплексное сопряжение в математике?

В математике каждое комплексное число (двухкомпонентное число, состоящее из вещественного числа, добавленного к мнимому числу) имеет комплексно-сопряженное число. Это комплексное сопряжение будет иметь ту же действительную часть, а мнимая часть будет иметь ту же величину, но противоположный знак. Комплексное число может быть представлено выражением a + bi , а его комплексно-сопряженное число может быть представлено выражением a — bi , где a и b — действительные числа, а i — мнимое число (в частности, квадратный корень из минус 1).

Несмотря на наличие мнимых компонентов, комплексно-сопряженные числа используются для описания физических реалий. Использование комплексных сопряжений работает, несмотря на наличие мнимых компонентов, потому что при перемножении двух компонентов получается действительное число. Что касается их математических приложений, комплексно-сопряженные числа используются для рационализации комплексных чисел. Репетиторство по математике — отличный способ помочь учащимся понять сложные сопряженные числа, поскольку они также необходимы для нахождения амплитуды полярной формы комплексного числа.

Компонент действительного числа 

Каждое комплексное число содержит компонент действительного числа, добавленный к компоненту мнимого числа. В выражении a + bi, a — это составляющая вещественного числа .

Компонент мнимого числа

Мнимое число определяется как любое число, которое при возведении в квадрат дает действительное отрицательное число. Это может быть переформулировано в других терминах для упрощения. Мнимое число — это любое действительное число, умноженное на квадратный корень из отрицательной единицы (-1).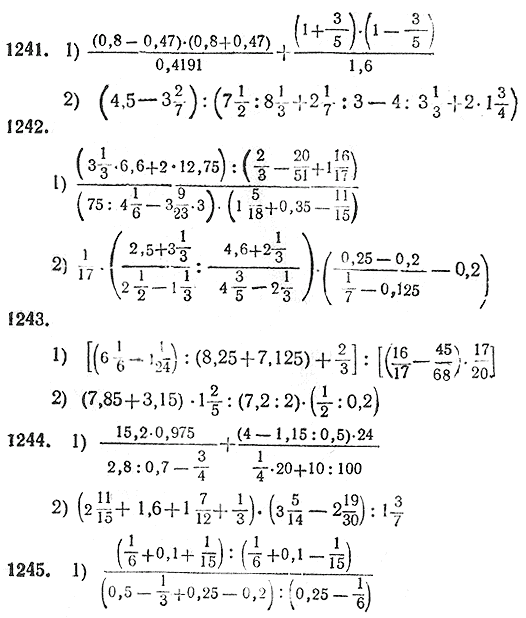 В этой форме комплексно-сопряженная пара чисел может быть записана как y = a+bi и ӯ = a–bi, где «i» — это квадратный корень из -1. Чтобы различить два значения y, одно из них обычно пишется с чертой над буквой ӯ, хотя иногда используется звездочка.

Хотя их величины равны, знак одной из мнимых составляющих в паре комплексно-сопряженных чисел противоположен знаку другой.

Откуда взялись комплексные числа?

Основная идея о том, что комплексное число существует в системе счисления, содержащей действительные числа и мнимые числа, возникла у математика Джероламо Кардано в 1545 году, хотя многие другие математики также внесли свой вклад в концепцию комплексных чисел, например, Каспер Вессель в 179 году.9.

Считается, что самое раннее упоминание квадратного корня из отрицательного числа (т. е. мнимого числа) появилось в работе древнегреческого математика Героя Александрийского. Несмотря на долгую историю комплексных чисел, сегодня они применяются по-разному, в том числе при умножении.

Умножение двух комплексно-сопряженных чисел

Чтобы продемонстрировать, что умножение двух комплексно-сопряженных чисел дает действительный результат, рассмотрим пример y = 7+2i и ӯ = 7–2i. Умножение их вместе дает yӯ = 49+14i–14i–4i2 = 49+4 = 53. Такой реальный результат комплексно-сопряженного умножения важен, особенно при рассмотрении систем на атомном и субатомном уровнях. Часто математические выражения для крошечных физических систем включают мнимую составляющую. Это особенно важно в квантовой механике, которая является неклассической физикой очень малых.

Уравнения в квантовой механике

В квантовой механике характеристики физической системы, состоящей из частицы, описываются волновым уравнением. Эти уравнения раскрывают все, что можно узнать о частице в ее системе. Часто волновые уравнения содержат мнимую составляющую. Умножение уравнения на его комплексно-сопряженное дает физически интерпретируемую «плотность вероятности». Характеристики частицы могут быть определены путем математического манипулирования этой плотностью вероятности.

‍»Вероятность рождения»

Например, использование плотности вероятности важно для дискретного спектрального излучения атомов. Это применение плотности вероятности называется «вероятностью Борна» в честь немецкого физика Макса Борна. Тесно связанная статистическая интерпретация того, что измерение квантовой системы даст определенные конкретные результаты, называется правилом Борна. Макс Борн получил Нобелевскую премию по физике 1954 года за свою работу в этой области. К сожалению, попытки вывести правило Борна из других математических выводов привели к неоднозначным результатам.

Какие профессии используют комплексные числа?

Есть несколько очевидных профессионалов, которые используют комплексные числа, в том числе ученые, инженеры и, конечно же, математики. Физики, квантовые физики и инженеры-электрики также регулярно используют комплексные числа. И есть другие, менее очевидные профессии, которые полагаются на комплексные числа. Интересно, что аналитики продаж и экономисты регулярно используют комплексные числа в своей работе.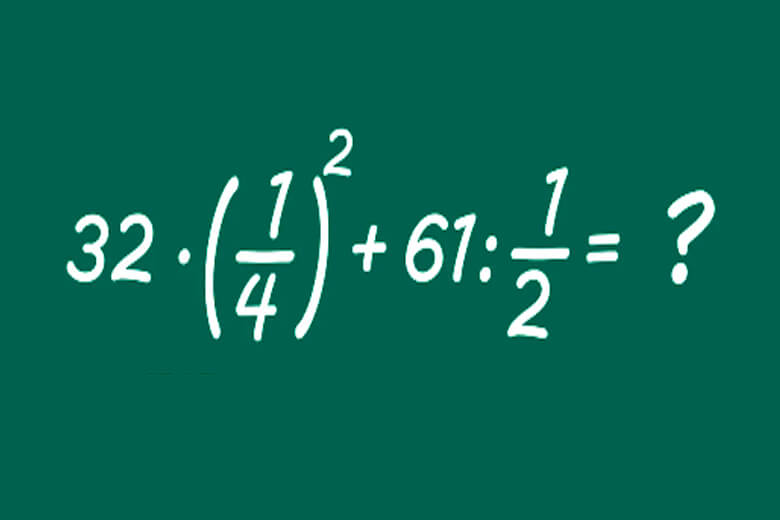

Комплексные числа также могут использоваться при обработке сигналов для поиска определенных заметок с помощью программного обеспечения для редактирования аудио. Они также участвуют в анализе цепей переменного тока. Комплексные числа часто используются при расчетах тока, напряжения и сопротивления в цепях переменного тока. Затем эти данные можно использовать для расчета разницы между двумя блоками питания переменного тока с течением времени. Как упоминалось выше, комплексные числа играют важную роль в квантовой механике — разделе физики, изучающем движения и взаимодействия между субатомными частицами.

Это всего лишь несколько примеров того, как комплексные числа (и комплексно-сопряженные числа) используются в практических, реальных целях. Для учащихся важно иметь четкое представление о комплексных числах и связанных с ними темах, потому что они необходимы для самых разных профессий. Математические задачи, связанные с комплексными числами, также могут появляться на некоторых вступительных экзаменах в колледж.

Используют ли старшеклассники сложное спряжение?

Усвоит ли старшеклассник комплексное спряжение, зависит от того, какие уроки математики преподаются в конкретной школе. Классы часто варьируются от штата к штату, поэтому трудно точно сказать, чему будут учить в классах старшей школы. Часто сложные сопряженные числа преподаются в Алгебре 1 или Алгебре 2. Однако комплексные сопряженные числа не ограничиваются только курсами алгебры, поскольку преподаватели могут обсуждать действительные и мнимые числа в различных контекстах.

Как правило, алгебру I преподают ученикам девятого класса или отличникам восьмого класса. Некоторые учащиеся могут сдавать Алгебру 2 в младших классах средней школы.

Комплексные числа входят в тест SAT?

Большая часть раздела SAT Math посвящена числам, операциям, алгебре, функциям, геометрии, измерениям, анализу данных, статистике и вероятности. При этом есть шанс, что концепция комплексных чисел может появиться на SAT в одном или двух вопросах. Чтобы быть хорошо подготовленным, рекомендуется иметь четкое представление о комплексных числах и комплексно-сопряженных числах, прежде чем сдавать SAT.

Есть много компонентов, которые работают вместе, чтобы дать правильный ответ по математике, поэтому учащимся важно знать, как выполнять определенные процедуры и как использовать определенные методы в различных математических предметах. Может быть трудно определить, о чем спрашивается вопрос SAT, если учащийся не обладает глубокими знаниями в нескольких разделах математики. Один из лучших способов подготовиться к вступительным экзаменам в колледж и добиться успеха — работать с репетитором. Репетитор может адаптировать свои инструкции к конкретным потребностям ученика. Вопреки тому, что некоторые могут подумать, репетиторы могут принести большую пользу всем учащимся, независимо от того, борются ли они с определенными понятиями или они преуспевают в классе и нуждаются в чем-то более сложном.

Чем могут помочь репетиторы по математике для учащихся

Хотя некоторым математика может даваться легко, существует множество математических тем, которые могут сбить с толку школьников и студентов колледжей. Математика — сложный, многогранный предмет. Некоторые понятия могут показаться сложными, но опытный репетитор по математике может помочь. Репетитор может помочь учащимся, предоставляя индивидуальную помощь и инструкции — в зависимости от того, какую услугу репетиторства выберет родитель или ученик. Некоторые компании предлагают только общие уроки, основанные на государственной учебной программе и стандартизированных тестах, в то время как другие предлагают гораздо более индивидуальный подход. Лучшие репетиторские услуги сначала выявляют сильные и слабые стороны студента, а затем основывают репетиторские занятия на его учебных потребностях и текущей успеваемости.

Модель обучения для учащихся основана на индивидуальных уроках, которые призваны помочь учащимся освоить наиболее сложные для них понятия, которые им необходимо усвоить для занятий или экзаменов. Процесс подключения к репетитору Learner очень прост. Во-первых, родители отвечают на вопросы об академическом образовании своего ребенка и его уникальных потребностях. Затем они назначают звонок академическому тренеру, чтобы определить цели и задачи обучения своего ребенка. Наконец, Learner подберет для каждого ребенка подходящего репетитора. Первое занятие с Learner всегда бесплатно, так что это отличная возможность попробовать репетиторство и посмотреть, подходит ли оно вам.

Ученик понимает, что у каждого ученика свой стиль обучения, уникальный образ мышления и академические устремления. Работа с опытным тьютором — отличный способ дать учащимся конкретную прямую обратную связь об их успеваемости. Репетиторство — это также отличный способ поощрить учащихся и укрепить их уверенность в себе при изучении новых и незнакомых тем, таких как сложные сопряжения.

Имейте в виду, что репетиторы предназначены не только для студентов, которым нужна дополнительная академическая помощь. Репетиторство также является отличным ресурсом для студентов, которые преуспевают в учебе. Репетиторы могут поощрять этих учеников к творческому мышлению, давать им дополнительную практику, а также расширять и бросать им вызовы, выходящие за рамки школьной программы.

Ищете индивидуальные занятия по математике? Поговорите с нашим академическим консультантом, чтобы получить индивидуальное соответствие с вашим онлайн-репетитором по математике сегодня!

Часто задаваемые вопросы

Сложные сопряжения могут быть запутанной темой. Вот некоторые распространенные вопросы и ответы о комплексных сопряжениях и связанных с ними темах.

Что такое квадратный корень из комплексного числа?

Квадратный корень из комплексного числа можно определить по формуле. Квадратный корень из натурального числа состоит из пар, а квадратный корень из комплексного числа использует x и y для представления действительных чисел.

Что такое сложная плоскость в математике?

Комплексная плоскость — это плоскость, образованная комплексными числами. Комплексная плоскость имеет ось x, которая называется действительной осью и образована действительными числами. Комплексная плоскость также имеет ось Y, которая называется мнимой осью, потому что она образована мнимыми числами.