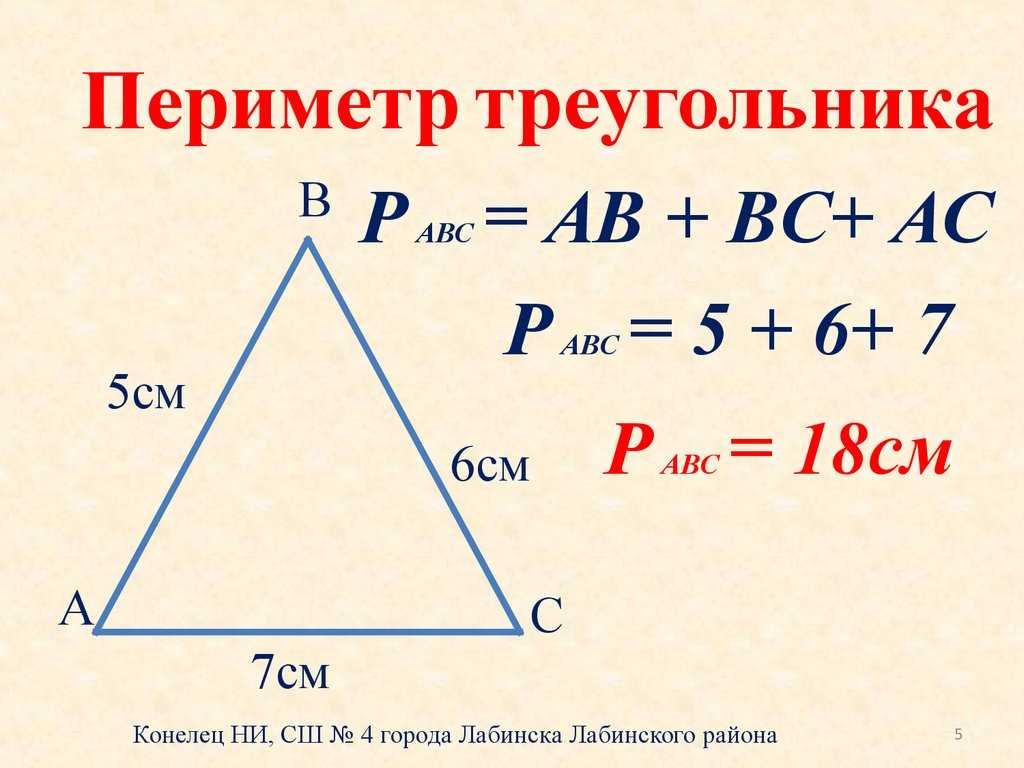
Стр 6. № 2. ГДЗ Математика 3 класс Часть 2. Моро М.И. Помогите найди периметр треугольника – Рамблер/класс
Стр 6. № 2. ГДЗ Математика 3 класс Часть 2. Моро М.И. Помогите найди периметр треугольника – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Найди периметр треугольника со сторонами длиной 10 см, 14 см, 9 см.
90:30 5∙20- 16 7• (42-34) 0∙ 1 = 12
80 : 40 74-60 : 2 (36 + 36) : 9 0 : 5∙20
ответы
10 + 14 + 9 = 33 см — периметр треугольника.
Ответ: 33 см.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
5 класс
Репетитор
Химия
Алгебра
похожие вопросы 5
Укажи знак сравнения. ГДЗ 3 класс математика Моро Часть 1 стр 81 тест вариант 2 задание 5
Решаем вот тест. Может кто уже сталкивался, ваш ответ?
Укажи знак сравнения, который надо поставить, чтобы получить верную запись: (Подробнее…)
ГДЗ3 классМатематикаМоро М.И.
Задание 2. Lesson 16 Part 2.Unit 1.Биболетова М.З.Welcome to GreenSchool!.Английский язык.3 класс.ГДЗ
Lesson 16 Part 2.Unit 1.Биболетова М.З.Welcome to GreenSchool!.Английский язык.3 класс.ГДЗКто сможет составить диалог ?
Твой друг, ученик лесной школы, пришёл к тебе в гости. Угости его. Разыграй с (Подробнее…)
ГДЗАнглийский язык3 классБиболетова М. З.
ЕГЭ Математика 11 класс. Ященко И. В. Тренировочная работа 57 Вопрос 12 Найдите среднюю скорость автомобиля.
Привет! Совсем потухла башка при ответе на подобный вопрос…помогите, пожалуйста…
Первую треть трассы автомобиль ехал со скоростью (Подробнее…)
ЕГЭМатематикаЯщенко И.В.Семенов А.В.11 класс
Task 19. Lesson 31. Travelling and Transport. Английский язык. 4 класс. И.Н. Верещагина ГДЗ
Выручайте! Накидайте предложения по заданию.
Write 5 sentences using present perfect and 5 sentences using past indefinite (Подробнее…)
ГДЗАнглийский языкВерещагина И.Н.4 класс
Task 1. Lesson 32. Travelling and Transport. Английский язык. 4 класс. И.Н. Верещагина ГДЗ
Lesson 32. Travelling and Transport. Английский язык. 4 класс. И.Н. Верещагина ГДЗ
Ребята, можете подсказать как выразить сомнения и несогласие по заданию
Last summer Bob (a boaster) staved at the Kina’s Hotel in (Подробнее…)
ГДЗАнглийский языкВерещагина И.Н.4 класс
Что такое периметр треугольника и как его найти
Оглавление
Время чтения:: 3 минуты
1 033
Основные определения
Наверное, каждый из нас сталкивался с треугольником. Это могло быть в школе, вузах, колледжах, на работе, во время помощи детям. Треугольник – это одна из самых простых геометрических фигур, но в то же время она выполняет очень важную роль. Множество свойств хранит треугольник. Но сегодня не будем вдаваться в подробности, а поговорим про периметр и порешаем задачи по нахождению его.
Если мы отметим на плоскости 3 точки и проведём к ним линии, то как раз получим треугольник.
Понятия
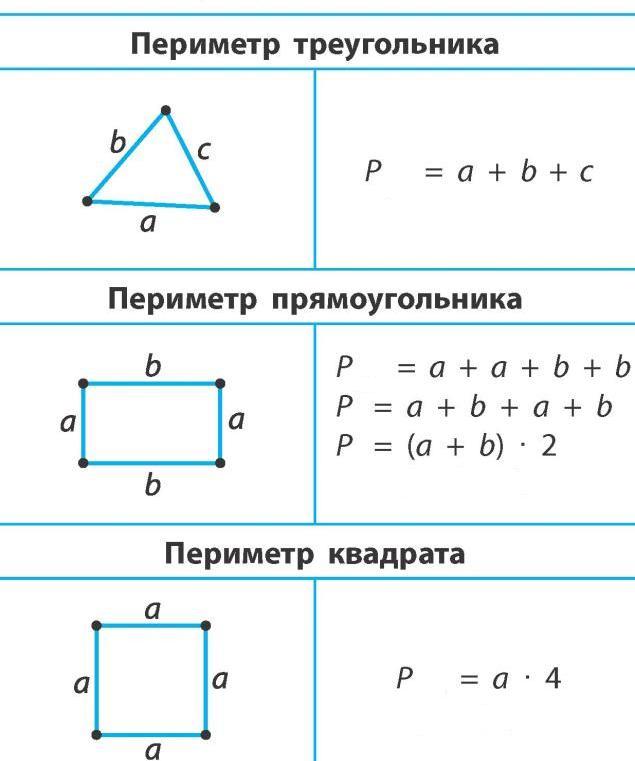
Треугольник – это геометрическая фигура, состоящая из трёх точек, которые соединены отрезками – сторонами. В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
В зависимости от отношений между сторонами фигуры, то они бывают равносторонними, разносторонними и равнобедренными (р/б – равнобедренный, р/с – равносторонний).
Вершины треугольника – это точки, где соединяются 2 стороны фигуры.
Р/б треугольник – это треугольник у которого две стороны равны, но не равны третьей.
Р/с треугольник – это треугольник, у которого все стороны равны между собой.
Разносторонний треугольник – это треугольник, у которого все стороны не равны между собой.
Прямоугольный треугольник — это треугольник, у у которого один угол равен 90о. Самая длинная сторона называется гипотенузой, а две другие катетами.
Формула нахождения периметра
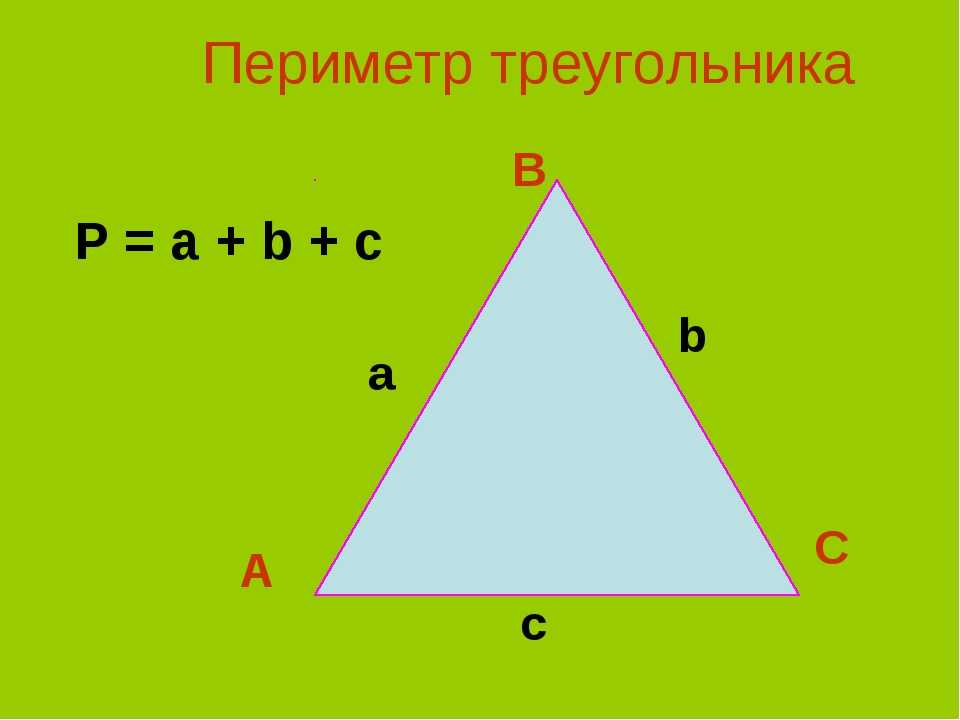
Из определения следует, что периметр геометрической фигуры – это сумма длин всех сторон, и треугольник не стал исключением. Общая формула имеет вид: Р = а + b + с. Периметр будет обозначаться Р. а, b и с — стороны треугольника. Решим задачу №1.
а, b и с — стороны треугольника. Решим задачу №1.
Задача 1
Пусть нам дан треугольник со сторонами 13 см, 15 см, 12 см. Нужно найти периметр данного треугольника.
Решение: \[P=13+15+12=40\] см.
Ответ: 40 см.
Периметр разностороннего треугольника
В прошлой задаче мы как раз нашли периметр разностороннего треугольника. Решим похожую задачу №2
Задача 2
Дан треугольник со сторонами 25 дм, 30 дм, 15 дм. Найдите периметр треугольника. Ответ выразите в метрах.
Решение:
P = 30 + 25 + 15 = 70 дм
70 : 10 = 7 м
Ответ: 7 м.
Периметр равнобедренного треугольника
Так как в р/б треугольнике 2 стороны равны (боковые), то формулу нахождения можно представить как: P = 2a + b. Решим 2 задачи.
Задачи 3 — 4
Дан равнобедренный треугольник АВС с биссектрисой, проведённой к основанию и равной 4 см, а также с боковой
стороной, равной 5 см. Найдите периметр данного треугольника.
Решение:
Так как ВН – биссектриса р/б треугольника АВС, то она является как высотой, так и медианой. {2}=225-81=144\]см
{2}=225-81=144\]см
ДК = √144 = 12 см.
Так как СК — высота в р/б треугольнике, проведённая к основанию, то она является медианой, следовательно, ДВ = ДК + КВ = 12 + 12 = 24 см.
Р = ДС + СВ + ДВ = 15 + 15 + 24 = 54 см.
Ответ: 54 см.
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Периметр равностороннего треугольника
А это один из самых “хороших” треугольников, его ещё называют правильным, так как все стороны и углы равны между собой. Формула нахождения периметра будет иметь вид: P = 3a.
Задачи 5 — 6
Дан равносторонний треугольник со стороной а = 13. Найдите периметр этого треугольника.
Решение:
Р = 3а = 3 * 13 = 39
Ответ: 39.
В равностороннем треугольнике АВС есть стороны: АВ = АС = СВ = 15 см, Найдите периметр данного треугольника.
Решение:
Р = 3АВ = 15 * 3 = 45 см. {2}=144+81=225 \mathrm{~см}\]
{2}=144+81=225 \mathrm{~см}\]
СВ = √225 = 15 см
S = (АС * АВ) : 2 = (9 * 12) : 2 = 54 см
P = 15 + 9 + 12 = 36 см
Ответ: 36 см; 54 см.
Оценить статью (87 оценок):
Поделиться
Федор Разовский — Кандидат математических наук
Популярные статьи
Выполнение любых работ по математике
Площадь и периметр треугольника
Введение
В этой статье мы узнаем все о треугольниках. Начав с определения и свойств фигуры, мы учимся на интуитивном уровне, прежде чем, наконец, измерим размеры фигуры по ее сторонам и площадь, занимаемую треугольником. При этом мы также попробуем несколько примеров, которые помогут нам в обучении.
Что такое треугольник?
Треугольник по определению является фигурой с тремя сторонами . Когда мы думаем о треугольнике, мы можем ассоциировать его с дорожными знаками, пирамидами, флагами и даже музыкальными инструментами!
В геометрическом выражении треугольник состоит из набора трех прямых или сторон , трех внутренних углов , образованных сторонами, и трех вершин , которые являются пересечениями линий, образующих треугольник.
Какие бывают треугольники?
Треугольники чаще всего распознаются нами как имеющие три стороны. Но какие конкретные типы может принимать треугольник и как мы можем их различать? По-видимому, треугольники можно описать либо по характеристикам их сторон, либо по их внутренним углам.
По длине стороныТреугольники можно классифицировать по длине стороны. Это может быть равносторонний треугольник, равнобедренный треугольник или разносторонний треугольник.
Равносторонний треугольник — это треугольник, в котором все стороны имеют одинаковую длину .
С другой стороны, равнобедренный треугольник является треугольником с двумя сторонами равной длины .
Если треугольник имеет всех сторон разной длины , говорят, что это разносторонний треугольник .
На основе внутренних углов Треугольники также можно классифицировать на основе величины их внутренних углов. В зависимости от внутренних углов треугольника они бывают трех типов: остроугольные, косоугольные и прямоугольные.
В зависимости от внутренних углов треугольника они бывают трех типов: остроугольные, косоугольные и прямоугольные.
Остроугольный треугольник — это треугольник, у которого два внутренних угла меньше 90°.
С другой стороны, косой треугольник — это треугольник, у которого один внутренний угол меньше 90°.
Тогда прямоугольный треугольник — это треугольник с одним внутренним углом, равным 90°.
Что такое периметр?
Мы определяем периметр двумерной формы как меру границы, окружающей его .
При интуитивном подходе мы можем связать идею периметра с тем, как далеко мы пробегаем круг в парке. Если мы начнем измерять расстояние от начала круга, а затем проследим замкнутый путь, пока не вернемся к начальной точке, мы сможем измерить периметр парка через круг, который мы пробежали:
Таким образом, для любой замкнутой формы мы можем получить ее периметр, взяв длину ребер, охватывающих фигуру.
Что такое площадь?
С другой стороны, мы можем определить площадь двумерной формы как меру пространства, которое она занимает в двумерной плоскости .
Интуитивно мы можем думать о формах на плоскости как об объектах в комнате. Каждый объект занимает определенное место в комнате, в зависимости от типа объекта и его размера. В этом смысле мы можем измерить площадь фигуры через ее размеры.
Периметр треугольника
Из определений, данных ранее, мы можем теперь подробно обсудить формулу для вычисления периметра треугольника. Сначала мы выведем базовую формулу, обеспечим интуитивное понимание, а затем покажем, как мы применяем эту формулу на нескольких примерах.
Вывод формулы периметра треугольника
Мы знаем, что периметр можно определить как сумму длин всех ребер, покрывающих фигуру. В треугольнике у нас три ребра. Следовательно, мы можем сказать, что периметр треугольника можно выразить как сумму длин каждой стороны треугольника:
Периметр=Длина 1 Сторона+Длина 2 nd Сторона+Длина 3 rd Сторона
Если мы обозначим каждую сторону как a, b и c, мы можем сократить эту формулу до более короткого Форма:
Периметр=a+b+c
Какова формула периметра треугольника?
Из предыдущего вывода периметр P треугольника, стороны которого a, b, c известны, определяется как:
P=a+b+c
Заметим, что единиц периметра выражается через тех же единиц , что и с данными сторонами.
Как это используется?
Чтобы попрактиковаться в применении формулы, давайте вместе поработаем над нахождением периметра треугольника, показанного ниже:
Исходя из данного рисунка, мы произвольно устанавливаем порядок сторон и присваиваем заданные значения каждой стороне. Следовательно, мы можем сказать, что:
a=4 единицы
b=3 единицы
c=5 единиц
Кроме того, поскольку длины всех сторон известны, мы можем использовать формулу периметра для треугольника:
P=a+b+c
Затем мы подставляем данные длины в формулу, чтобы получить:
P=4 единицы+3 единицы+5 единиц
После этого мы складываем числа, чтобы получить значение периметра :
P=12 единиц
Тогда мы заключаем, что периметр треугольника равен 12 единицам. Эта величина выражается в тех же единицах, что и радиус.
Площадь треугольника
Узнав о формуле периметра треугольника, мы можем, кроме того, измерить площадь треугольника на основе размеров указанной формы.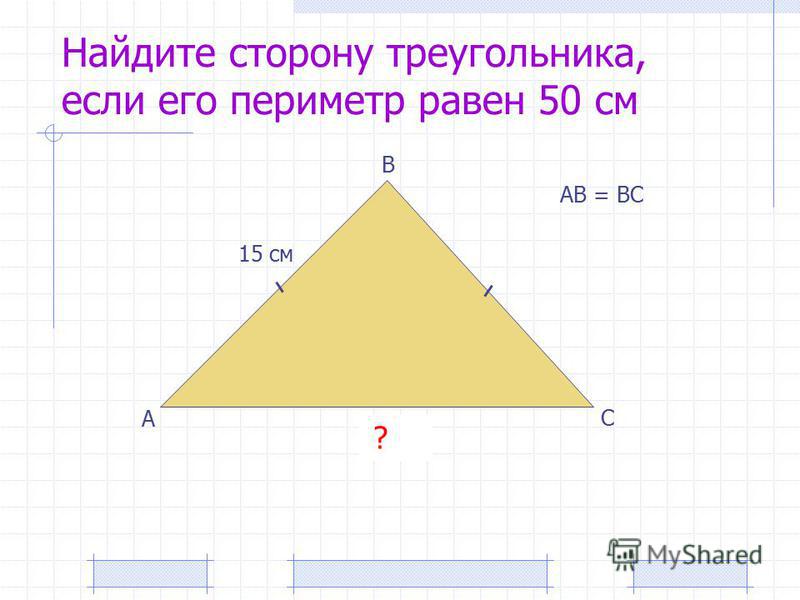
Вывод формулы площади треугольника
Сначала рассмотрим одну сторону треугольника, предпочтительно самую длинную сторону. Назовем эту сторону основанием треугольника:
Затем проведем прямую, перпендикулярную этой стороне и проходящую через одну из вершин треугольника. Это называется высотой треугольника:
Если мы представим треугольник как прямоугольный, стороны которого заданы основанием и высотой, мы получим следующую цифру:
Теперь предположим, что мы наложили прямоугольник, длина которого равна основанию треугольника, а высота равна высоте треугольника:
Из формулы площади прямоугольника мы знаем, что площадь этого прямоугольника определяется как:
A прямоугольник = основание × высота
При наблюдении мы видим, что площадь переосмысленного треугольника составляет половину площади наложенного прямоугольника. Следовательно, мы можем сказать, что:
Площадь = ½ x A прямоугольник
Если мы подставим формулу площади для прямоугольника, мы получим формулу площади для треугольника:
Площадь = ½ x основание x высота
Что такое формула площади треугольника?
С помощью ранее сделанного вывода площадь A треугольника, основание которого b и высота h известны, может быть выражена по формуле:
A=½bh площадь выражается через квадратные единицы заданного радиуса/диаметра.
Как это используется?
Опять же, мы практикуем то, что мы узнали до сих пор, работая над управляемым примером для нахождения площади треугольника:
Из данного рисунка нам дано, что основание треугольника равно 6 единицам, а его высота равна быть 2 ед. Следовательно, мы можем сказать, что:
b=6 единиц
h=2 единицы
Кроме того, поскольку известны основание и высота, мы можем использовать Формулу площади треугольника:
A=½ bh
Затем мы подставляем данные основания и высоты в формулу, и получаем:
A=½ x 6 единиц × 2 единицы
После этого мы перемножаем числа вместе, чтобы получить площадь треугольника :
A=6 единиц 2
Тогда мы заключаем, что площадь треугольника равна 6 единицам 2 . Эта величина выражается в квадратах единиц радиуса.
Примеры решения задач
Теперь мы можем приступить к решению примеров задач, чтобы применить то, что мы уже узнали. Каждая проблема решает различные обсуждаемые формулы и ставит перед нами задачу решить ее с помощью предоставленной нам информации.
Периметр треугольника
Пример задачи 1:
Каков периметр равнобедренного треугольного стекла, стороны которого равны 4 см 4 см и 3 см?
Решение:
Напомним, что периметр P треугольника находится по формуле:
P=a+b+c
При данных длинах сторон a=b=4 см и c=3 см , подставляем эти значения в формулу:
P=4 см+4 см+3 см
Наконец, сложив длины, мы получим значение периметра:
P=11 см
Следовательно, мы заключаем, что периметр треугольного стекла равен 11 см.
Пример задачи 2:
Спортсменка готовится к триатлону. На треугольном круге она пробегает двенадцать километров, проплывает пять километров, а затем проезжает тринадцать километров на велосипеде. Какое расстояние она преодолевает за один круг?
Решение:
Сначала мы можем соотнести стороны треугольного колена с каждой частью триатлона. Для этой задачи мы используем следующие значения:
a=12 км
b=5 км
c=13 км
Тогда периметр треугольника P находится по формуле:
P=a+b+c
Следовательно, мы можем заменить данное значения, которые нужно получить:
P=12 км+5 км+13 км
Наконец, мы берем сумму сторон, чтобы определить периметр круга:
P=30 км
Таким образом, мы заключаем, что спортсмен поезда для составляет 30 километров.
Пример задачи 3:
Предположим, у нас есть треугольник, третья сторона которого неизвестна. Длины двух сторон равны a=10 дюймов и b=15 дюймов. Затем нас спрашивают следующее: 92}$
Наконец, извлекаем квадратный корень из числа внутри корня, чтобы получить длину неизвестной стороны, затем округляем до ближайшего целого числа:
c=18 in
Следовательно, длина третья сторона 18 дюймов.
- Поскольку каждая сторона имеет разную длину, мы заключаем, что треугольник, образованный этими сторонами, является разносторонним треугольником .
- Напомним, что формула периметра треугольника задается как:
P=a+b+c
Используя данные длины сторон a=10 дюймов и b=15 дюймов вместе с вычисленной длиной третьей стороны c=18 дюймов, мы подставляем эти значения в уравнение, чтобы получить :
P=10 дюймов+15 дюймов+18 дюймов
Сложив эти числа, мы получим значение периметра:
P=43 дюйма
Следовательно, мы заключаем, что периметр треугольника равен 43 дюймам .
Площадь треугольника
Пример задачи 4:
Какова площадь прямоугольного треугольника, основание которого равно 10 единицам, а высота — 18 единицам?
Решение:
Напомним, что площадь треугольника A определяется формулой:
A=½bh
При данном основании b=10 u и высоте h=18 u подставляем в формулу, чтобы получить:
A=½ x 10 единиц x 18 единиц
Наконец, путем умножения трех чисел мы можем вычислить значение площади:
A=90 единиц 2
Следовательно, площадь прямоугольного треугольника равна 90 квадратных единиц.
Пример задачи 5:
На рисунке ниже дан равнобедренный треугольник, стороны которого показаны:
- Какова длина основания треугольника?
- Какова длина высоты треугольника?
- Какова площадь треугольника?
Решение:
- Сначала заметим, что на данном рисунке основание треугольника может быть выражено как сумма длин x и y:
b=x+y
Подставив заданные длины сторон x=y=7 см, получим значение b:
b=7 см+7 см=14 см
Следовательно, длина основания составляет 14 см.
- Заметим, что высота образует два прямоугольных треугольника. Чтобы определить длину высоты, мы применяем теорему Пифагора, используя стороны a, x и высоту h: уравнение относительно высоты, мы имеем: 92}$
Таким образом, значение неизвестного h можно получить, извлекая квадратный корень из полученной ранее разности:
h=24 см
Следовательно, длина высоты треугольника равна 24 см.
- Напомним, что формула площади треугольника задается следующим образом:
A=½bh
Используя значения, полученные из частей A и B, мы знаем, что основание и высота треугольника равны:
b=14 см
h=24 смПодставляя эти значения в формулу, получаем:
A=½×14 см×24 см
Наконец, перемножая числа между собой, получаем значение площади:
A=168 см 2
Следовательно, делаем вывод, что площадь равнобедренного треугольника равна 168 см 2 .
Пример задачи 6:
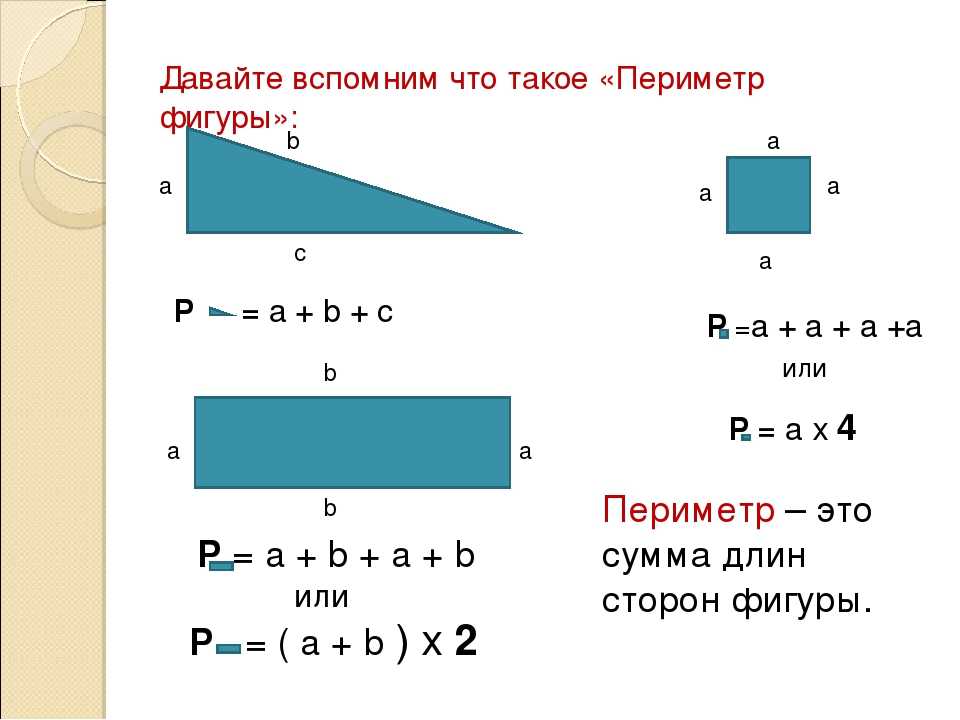
Предположим, художник хочет нарисовать сплошной красный треугольник, покрывающий половину квадратной стены размером 15 футов × 15 футов.
 На каждый литр краски можно окрасить площадь 100 квадратных футов. Сколько красной краски нужно художнику, чтобы закончить закрашивание треугольника?
На каждый литр краски можно окрасить площадь 100 квадратных футов. Сколько красной краски нужно художнику, чтобы закончить закрашивание треугольника?Решение:
Прежде всего заметим, что маляру поручили нарисовать прямоугольный равнобедренный треугольник красной краской. Следовательно, мы знаем, что основание и высота треугольника равны длине стороны квадратной стены:
b=h=15 футов
Затем мы находим площадь треугольника, которую нужно закрасить. . Используя Формулу площади треугольника, имеем:
A=½bh
Подставляя значения, полученные ранее, получаем произведение трех чисел: 92}$)=1,125 литра
Следовательно, маляру нужно 1,125 литра красной краски, чтобы закончить закрашивание красного треугольника.
Резюме
Треугольник — это фигура, у которой три стороны . Он также образован набором из трех внутренних углов , образованных между сторонами треугольника, и трех вершин , или пересечений сторон треугольника.

Треугольник можно классифицировать по следующим признакам:
На основе длины стороны : у равностороннего треугольника все стороны равны, у равнобедренного треугольника две равные стороны, а у разностороннего треугольника нет равных сторон,
На основе меры внутреннего угла : в остроугольном треугольнике два внутренних угла меньше 90°, в косоугольном треугольнике один внутренний угол меньше 90°, а в прямоугольном треугольнике один угол равен 9°.0°.
Периметр является мерой границы, охватывающей фигуру . Его можно получить, взяв длину ребер, охватывающих форму.
С другой стороны, площадь является мерой пространства, которое фигура занимает в двумерной плоскости . Это количество зависит от размеров формы.
Периметр P треугольника с известными сторонами a, b, c определяется по следующей формуле:
P=a+b+c
Площадь A треугольника, основание b и высота h которого известны, может быть определена по формуле: Площадь треугольников (на тему мороженого) Рабочие листы
Мы тратим много времени на изучение и сбор информации на этом сайте.
 Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!Как найти периметр треугольника (3 вещи, которые нужно знать) — JDM Educational
Нахождение периметра треугольника может помочь вам выяснить, сколько материала вам нужно для строительства конструкции. Вы также можете сравнить расстояние, которое вам потребуется, чтобы обойти два разных треугольника, чтобы увидеть, какой из них больше.
Итак, как найти периметр треугольника? Чтобы найти периметр треугольника, возьмите сумму длин трех сторон. Если длины одной или двух сторон отсутствуют (неизвестно), используйте закон косинусов, закон синусов, теорему Пифагора, специальные треугольники или координаты вершин, чтобы найти недостающие длины сторон.
Конечно, методы, которые вы можете использовать для нахождения отсутствующих длин сторон, будут зависеть от типа треугольника (например, прямоугольный треугольник или нет), а также от предоставленной вам информации.

В этой статье мы поговорим о том, как найти периметр треугольника при отсутствии различных фрагментов информации. Мы также рассмотрим несколько примеров, чтобы прояснить концепцию.
Начнем.
Как найти периметр треугольника
Чтобы найти периметр треугольника, мы складываем длины трех сторон. Формула:
- P = a + b + c
где P — периметр треугольника, а a, b, c — длины сторон треугольника.
Здесь мы видим треугольник со сторонами a, b, c. Периметр P = a + b + c.Вот пример.
Система счисления
Пожалуйста, включите JavaScript
Система счисления
Пример. Как найти периметр треугольника
Допустим, у нас есть треугольник, изображенный ниже.
У этого треугольника длины сторон 2, 3 и 4, а периметр равен 9..Длины сторон равны a = 2, b = 3 и c = 4. Формула периметра говорит нам, что:
- P = a + b + c
- P = 2 + 3 + 4 P = 9
Итак, периметр треугольника равен 9 единицам.

Формулу периметра треугольника легко применить, когда у нас есть длины всех трех сторон, как в приведенном выше примере.
Однако нам часто нужно найти длину одной или нескольких сторон с помощью полученной информации. Давайте теперь рассмотрим некоторые из этих сценариев.
Как найти периметр треугольника с координатами
Если нам известны координаты трех вершин («углов») треугольника, мы все равно можем найти площадь. Нам просто нужно использовать вершины, чтобы найти три длины сторон, а затем применить ту же формулу периметра, что и выше.
Помните, что расстояние D между двумя точками (x 1 , y 1 ) и (x 2 , y 2 ) определяется по формуле расстояния:
- d = √ ((x 2 — x 1 ) 2 + (Y 2 — Y 1 ) 2 )
(эта формала.
Формула расстояния между двумя точками взята из теоремы Пифагора.
Длины трех сторон треугольника, изображенного выше, можно определить по формулам:
- a = √((x 2 – x 1 ) 2 + (y 2 07 – 1 y 90 90 ) 2 )
- b = √((x 3 – x 1 ) 2 + (y 3 – y 1 ) 2 )
- c = √( (x 3 – x 2 ) 2 + (y 3 – y 2 ) 2 )
Вот пример.
Пример: как найти периметр треугольника с координатами
Допустим, у вас есть треугольник со следующими координатами: (3, 2), (3, 5) и (7, 2), как показано ниже.
Этот треугольник имеет вершины в точках (3, 2), (3, 5) и (7, 2).Мы назначим:
- (x 1 , Y 1 ) = (3, 2)
- (x 2 , Y 2 ) = (3, 5) , Y 2 ) = (3, 5) , Y 2 ) = (3, 5) , Y 2 ) = (3, 5) , Y 2 ) = (3, 5) , Y 2 ) = (3, 5) , Y 2 ) = (3, 5) , Y 2 ) (x 3 , y 3 ) = (7, 2)
Используя приведенную выше формулу для длины стороны a, мы получаем:
- a = √((x 2 4 – х 1 ) 2 + (у 2 – у 1 ) 2 )
- a = √ ((3 — 3) 2 + (5 — 2) 2 )
- A = √ (0) 2 9063 + (0).
 3) 2 )
3) 2 ) - a = √ (0 + 9)
- A = √9
- A = 3
Alamely, для BE GET:
996996999999999999999999999999999999999999999999969 9069 9000 29 2
29699 9069 9000 2
- B = √ ((7 — 3) 2 + (2 — 2) 2 )
- B = √ (4) 2 + (0) 2 )
- 999 2 )
- 999999999 2 ) b = √ (16 + 0)
- B = √ (16)
- B = 4
- C = √ (x 3
- C = √ (x 3
- C = – х 2 ) 2 + (у 3 – у 2 ) 2 )
- с = √((7 – 6 3) 2 0105 2 )
- C = √ ((4) 2 + (-3) 2 )
- C = √ (16 +
- C = √ (25)
- C = √ (25)
- C = √ (x 3
- C = √ (25)
- C = √ (25)
- C = √ (16 +
- C = √ (16 +
- C = √ (16 +
- C = √ (16 + 9)
- c = 5
- P = a + b + c
- P = 3 + 4 + 5
- P = 12
- a 2 + b 2 – 2abcos(C) = c 2
- b 2 + c 2 – 2bccos(A) = a 2
- a 2 + c 2 – 2accos(B) = b 2
- 5 2 + 10 2 — 2 (5) (10) COS (60) = B 2
- 25 + 100 — 100 (0,5) = B 2
- 125 — 50 = B 2 2 999 = B 2 2 99999999999 = B 2 2999 = B 2 9 99 75 = б 2
- √75 = б
- 5√3 = б
- P = a + b + c
- P = 5 + 5√3 + 10
- 90 3
- P = 5(3 + √3)
- sin(A)/a = sin(B)/b = sin(C)/c
- sin(A)/a = sin(C)/c
- sin(30)/5 = sin(C)/10
- 0,5/5 = sin(C)/10
- 0,5 (10) = 5sin (c) [по кросс -умножению]
- 5 = 5sin (c)
- 1 = SIN (C)
- 90 = C
- A + B + C = 180
- 30 + B + 90 = 180
- B + 120 = 180
- B = 60
- P = A + B + C
- P = 5 + 5√3 + 10
- P = 15 + 5√3
- P = 5 (3 + 5√3
- P = 5 (3 + √3)
- У равностороннего треугольника длины всех сторон одинаковы. Итак, если дана длина одной стороны, мы просто умножаем ее на 3, чтобы найти периметр треугольника.
- Для особого треугольника мы можем использовать отношения длин сторон, чтобы найти недостающие стороны.
 Например, треугольник 30-60-90 имеет длины сторон в соотношении 1:√3:2. Итак, если самая короткая сторона имеет длину 7, то две другие стороны имеют длины 7√3 и 14,9.0293
Например, треугольник 30-60-90 имеет длины сторон в соотношении 1:√3:2. Итак, если самая короткая сторона имеет длину 7, то две другие стороны имеют длины 7√3 и 14,9.0293 - Для треугольника, в котором даны одна сторона и два угла, мы можем найти третий угол (сумма трех углов равна 180 градусам), а затем использовать закон синусов, чтобы найти две недостающие стороны.
- A + B + C = 180
- A + 55 + 85 = 180
- A + 9104
- A = 40
- sin(A)/a = sin(B)/b
- sin(40)/5 = sin(55)/b
- bsin(40) = 5sin(55) [перекрестным умножением ]
- B = 5SIN (55)/SIN (40)
- B = 5 (0,8191) /0,6428
- B = 6,3719
- sin(A)/a = sin(C)/c
- sin(40)/5 = sin(85)/c
- csin(40) = 5sin(85) [by cross multiplication]
- c = 5sin(85)/sin(40)
- c = 5(0.9962)/0.6428
- c = 7.7490
- P = A + B + C
- P = 5 + 6,3719 + 7,7490
- P = 19,120
- P = 19,120
- P = 19,120
- P = 19,120
- P = 19,120
- .

- P = a + b + c
- 16 = 4 + 5 + c
- 16 = 9 + c
- 7 = c
- Если известны любые две стороны прямоугольного треугольника, третью можно найти по теореме Пифагора: a 2 + б 2 = с 2 .
- Если вы знаете одну сторону и один угол (помимо угла 90 градусов) в прямоугольном треугольнике, то вы можете найти третий угол, а затем использовать закон синусов, чтобы найти длины других сторон.
- A 2 + B 2 = C 2
- 5 2 + 12 2
- 5 2 + 12 211101110111011101110111011106 211106 2 2
2 2- .

- 25 + 144 = C 2
- 169 = C 2
- 13 = C
- P = 5 + 12 + 13
- P = 30
- A + B + C = 180
- A + 40 + 90 = 180
- A + 130 = 180
- A = 50
3
- A = 50
3
- A = 50
3
- A = 50
3
- 9000110
- 900010
- 0
- 9.
 что у нас есть угол A, мы можем использовать закон синусов, чтобы найти длины сторон b и c.
что у нас есть угол A, мы можем использовать закон синусов, чтобы найти длины сторон b и c.Чтобы найти b:
- sin(A)/a = sin(B)/b
- sin(50)/5 = sin(40)/b
- bsin(50) = 5sin(50) (40) [перекрестным умножением]
- b = 5sin(40)/sin(50)
- b = 5(0,6428)/0,7660
- b = 4,1950
- Теорема Пифагора. Мы будем использовать закон синусов:
- sin(A)/a = sin(C)/c
- sin(50)/5 = sin(90)/c
- sin(50) /5 = 1/c [sin(90) = 1]
- 5/sin(50) = c [возьмите обратные значения обеих сторон]
- 5/0,7660 = c
- 6.5270 = c
- P = a + b + c
- P = 5 + 4.195 + 6.

Now we can find the perimeter:
. √((х 3 – х 1 ) 2 + (у 3 – у 1 ) 2 )
Наконец, для C, мы получаем:
Теперь, когда у нас есть длины трех сторон a = 3, b = 4 и c = 5, мы можем найти периметр по формуле, приведенной выше:
Как найти периметр треугольника без одной стороны
Если у треугольника есть две стороны, но одна из них отсутствует, мы все равно можем найти периметр, если знаем угол между отсутствующей стороной.
В данном случае используется закон косинусов.
Этот треугольник имеет длины сторон a, b и c с соответствующими размерами углов A, B и C.Для треугольника с длинами сторон и углами на изображении выше закон косинусов гласит:
Конечно, мы также можем поменять местами стороны и углы, используемые в формуле, чтобы получить две другие формулы: 2
используйте закон синусов, чтобы найти угол напротив отсутствующей стороны, затем используйте закон косинусов.
Давайте попробуем несколько примеров.
Пример 1. Как найти периметр треугольника с отсутствующей стороной (закон косинусов)
Предположим, что у нас есть треугольник, изображенный ниже, с двумя известными длинами сторон и известным углом между ними (включенный угол):
Стороны этого треугольника равны a = 5, c = 10 и b неизвестны, а угол B = 60 градусов перпендикулярен неизвестной стороне b.
Тогда мы имеем a = 5, c = 10, B = 60 градусов, а b неизвестно.
Использование 2 nd formulation for the Law Of Cosines above, we get:
Теперь, когда у нас есть b, мы можем найти периметр:
Теперь мы попробуем аналогичный пример, но с изюминкой: нам также нужно будет использовать закон синусов.
Помните, что закон синусов гласит:
Итак, если у нас есть пара сторон и соответствующую пару углов, нам нужны только три из четырех, а четвертый мы можем найти с помощью закона синусов.
Пример 2. Как найти периметр треугольника с отсутствующей стороной (закон синусов и закон косинусов)
Предположим, что у нас есть треугольник, изображенный ниже, с двумя известными длинами сторон и углом между наименьшими сторонами. известная сторона:
Длина сторон этого треугольника равна a = 5, c = 10 и b неизвестна, а угол A = 30 градусов перпендикулярен известной стороне a.Тогда мы имеем a = 5, c = 10, A = 30 градусов.
Используя закон синусов, мы имеем:
. Замно из трех углов в треугольнике 180 градусов, поэтому:
Замно из трех углов в треугольнике 180 градусов, поэтому:
Теперь, когда у нас есть угол B, мы можем использовать тот же закон косинусов из предыдущего примера, чтобы найти b = 5√3.
Как выше:
Как найти периметр треугольника без двух сторон
В некоторых случаях мы можем найти периметр треугольника, у которого отсутствуют две стороны. Например:
Давайте рассмотрим пример последнего случая.
Пример: Как найти периметр треугольника с двумя отсутствующими сторонами (закон синусов)
Предположим, что у нас есть треугольник, изображенный ниже, с одной известной длиной стороны и двумя известными углами:
У этого треугольника есть известная сторона длина a = 5, с известными углами B = 55 градусов и C = 85 градусов. Длины сторон b и c неизвестны.Тогда у нас есть a = 5, B = 55 градусов и C = 85 градусов.
Помните, что сумма трех углов в треугольнике равна 180 градусам, поэтому:
Теперь, когда у нас есть угол A, мы можем использовать закон синусов, чтобы найти B и C.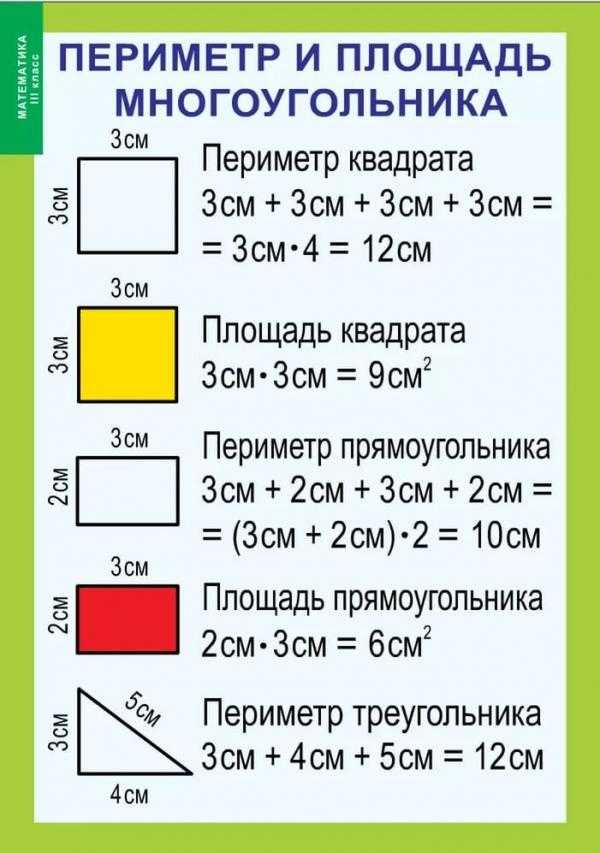
Используя закон синусов, мы можем найти длину стороны b:
. длина стороны c:
Теперь, когда у нас есть B и C, мы можем найти периметр треугольника:
Как найти третью сторону треугольника, если известен периметр
Чтобы найти третью сторону треугольника, когда известен периметр, мы просто используем исходную формулу и подставляем известные нам значения, а затем находим то, чего не знаем.
Пример. Как найти третью сторону треугольника, если известен периметр
Допустим, у нас есть треугольник с длинами сторон a = 4, b = 5 и периметром P = 16.
У этого треугольника известны длины сторон a = 4 и b = 5, с периметром 16. Длина стороны c неизвестна.Чтобы найти длину третьей стороны c, воспользуемся формулой периметра:
How To Find The Perimeter Of A Right Треугольник
При нахождении периметра прямоугольного треугольника мы можем использовать закон синусов, но мы также можем использовать теорему Пифагора (это частный случай закона косинусов, когда один из углов равен 90 градусов).
Пример 1. Как найти периметр прямоугольного треугольника с отсутствующей стороной (при длинах двух сторон)
Допустим, у нас есть прямоугольный треугольник с длинами сторон a = 5 и b = 12, изображенный ниже.
В этом прямоугольном треугольнике число 9Угол 0 градусов и две известные длины сторон a = 5 и b = 12. Длина третьей стороны c неизвестна.по теореме Пифагора, мы можем найти третью сторону длины C:
Теперь, We Ope Perseletemer:
.0005
скажем, у нас есть прямоугольный треугольник со стороной a = 5 и углом B = 40, изображенный ниже.
Этот прямоугольный треугольник имеет угол 90 градусов, угол B = 40 градусов и длину стороны a = 5. Длины сторон b и c неизвестны.Помните, что сумма трех углов прямоугольного треугольника равна 180, а один из углов равен 90 градусов по определению, так:

 На каждый литр краски можно окрасить площадь 100 квадратных футов. Сколько красной краски нужно художнику, чтобы закончить закрашивание треугольника?
На каждый литр краски можно окрасить площадь 100 квадратных футов. Сколько красной краски нужно художнику, чтобы закончить закрашивание треугольника?
 Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!


 3) 2 )
3) 2 )  Например, треугольник 30-60-90 имеет длины сторон в соотношении 1:√3:2. Итак, если самая короткая сторона имеет длину 7, то две другие стороны имеют длины 7√3 и 14,9.0293
Например, треугольник 30-60-90 имеет длины сторон в соотношении 1:√3:2. Итак, если самая короткая сторона имеет длину 7, то две другие стороны имеют длины 7√3 и 14,9.0293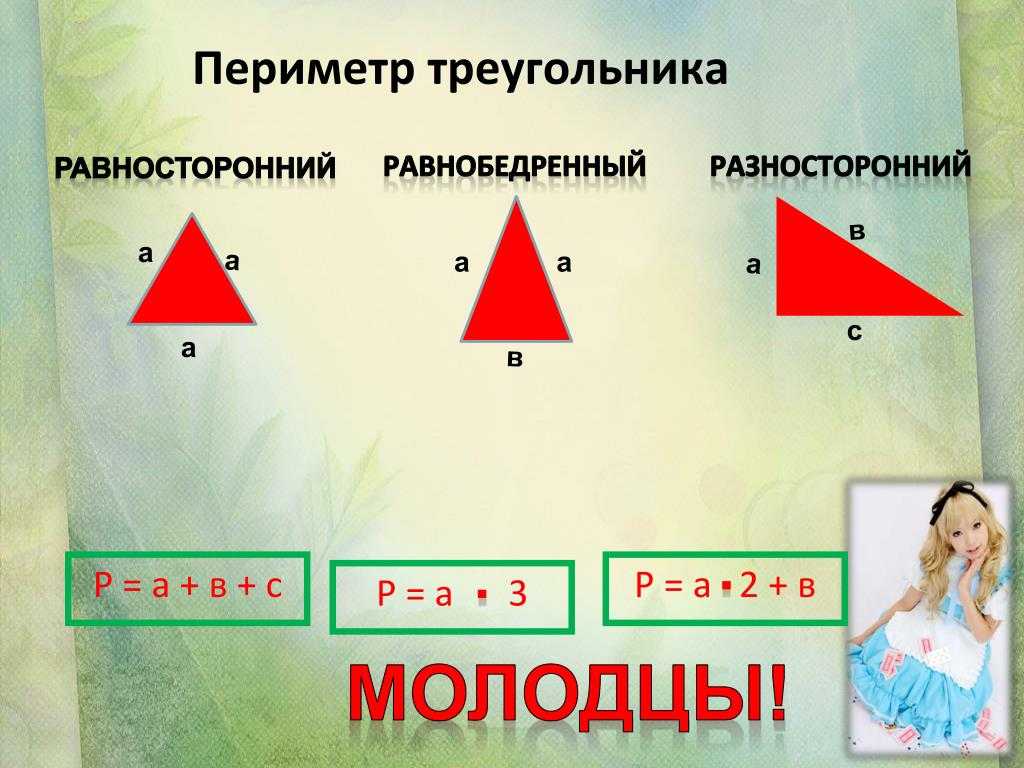
 что у нас есть угол A, мы можем использовать закон синусов, чтобы найти длины сторон b и c.
что у нас есть угол A, мы можем использовать закон синусов, чтобы найти длины сторон b и c.