Табличка косинусов и синусов: Таблица синусов и косинусов

Таблица синусов и косинусов — онлайн справочник для студентов

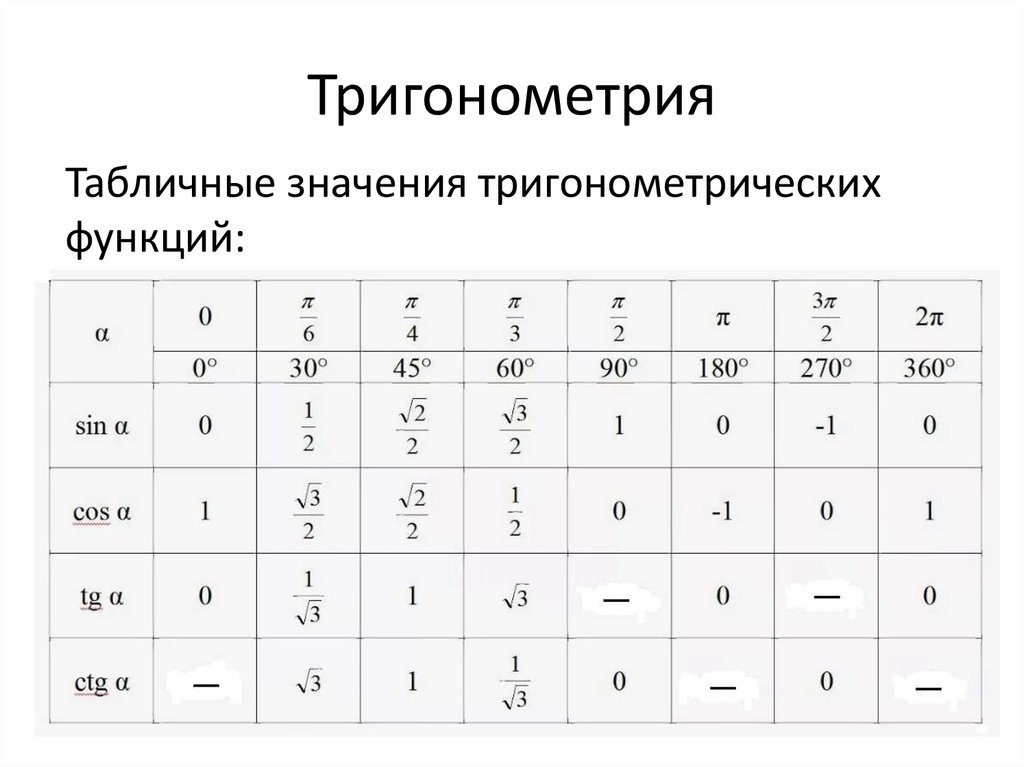
Таблица синусов и косинусов

Таблица 1

Используя эту таблицу, вы можете найти стандартное значение синуса или косинуса. Желаемое значение будет находиться на пересечении столбца, соответствующего данному аргументу (в радианах или градусах), и строке, соответствующей заданной функции.

Примеры решения проблем

ПРИМЕР 1

Задача

Использование таблицы значений синуса и косинуса для поиска: и

Решение

Найдите значение . В таблице значений синуса и косинуса (таблица 1) во второй строке (где углы находятся в градусах) мы находим значение . Тогда на пересечении столбца, соответствующего , и линия соответствующей синусоиды (рис.1) является искомым значением

Рис. 1

Найдем значение . В таблице 1 в первой строке (где углы указаны в радианах) находим значение . Искомое значение лежит на пересечении столбца соответствующего и строки соответствующей функции косинус (рис. 2), таким образом

Рис. 2.

Ответ

ПРИМЕР 2

Задание

Найти значение выражения:

Решение

Используя таблицу значений синусов и косинусов, найдем значения и (рис. 3).

Рис. 3

Подставляя найденные значения в исходное выражение, получим

Ответ

Физика

166

Реклама и PR

31

Педагогика

80

Психология

72

Социология

7

Астрономия

9

Биология

30

Культурология

86

Экология

8

Право и юриспруденция

36

Политология

13

Экономика

49

Финансы

9

История

16

Философия

8

Информатика

20

Право

35

Информационные технологии

6

Экономическая теория

7

Менеджент

719

Математика

338

Химия

20

Микро- и макроэкономика

1

Медицина

5

Государственное и муниципальное управление

2

География

542

Информационная безопасность

2

Аудит

11

Безопасность жизнедеятельности

3

Архитектура и строительство

1

Банковское дело

1

Рынок ценных бумаг

6

Менеджмент организации

2

Маркетинг

238

Кредит

3

Инвестиции

2

Журналистика

1

Конфликтология

15

Этика

9

Формулы дифференцирования Свойства тригонометрических функций Графики тригонометрических функций Тригонометрические неравенства и их решения Тригонометрические формулы понижения степени

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю  Политику  конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Как пользоваться таблицами синусов, косинусов, тангенсов.

(8 класс)

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

tgх = 0,8574
Единицы измерения углов:
градус – «°»,
минута – «´»,
секунда – «˝»
36 градусов 28 минут 47 секунд
36°28´47˝
© Кузьмина Е.А., Колобовская МСОШ, 2010
Брадис
Владимир
Модестович
1890 — 1975
Брадис Владимир Модестович – знаменитый
математик-педагог, член-корреспондент АПН СССР.
Заслуженный деятель науки РСФСР.
Основные труды Брадиса посвящены теоретической
и методической разработке вопросов повышения
вычислительной культуры учащихся средней школы.
Его «Методика преподавания математики в средней
школе» переиздавалась много раз и переведена на

другие языки. В 1921 году впервые вышли его
«Таблицы четырёхзначных логарифмов и
натуральных тригонометрических величин», позднее
издававшиеся под названием «Четырёхзначные
математические таблицы».
© Кузьмина Е.А., Колобовская МСОШ, 2010
Алгоритм нахождения синуса угла заданной величины по таблице Брадиса:
1. Находим в столбце А величину угла в градусах.
2. Находим в строке А ближайшее значение в минутах.
3. На пересечении строки «36°» и столбца «24´» находим значение синуса
4. Прибавляем к найденному значению поправку (или вычитаем).
sin36°26´= 0,5939 sin38°41´= 0,6250
© Кузьмина Е.А., Колобовская МСОШ, 2010
Алгоритм нахождения косинуса угла заданной величины по таблице Брадиса:
1. Находим в столбце А величину угла в градусах.
2. Находим в строке А ближайшее значение в минутах.
3. На пересечении строки «26°» и столбца «48´» находим значение косинуса
4. Прибавляем к найденному значению поправку (или вычитаем).
cos26°46´= 0,8929 cos28°13´= 0,8812
© Кузьмина Е.А., Колобовская МСОШ, 2010
Задание 1
Используя таблицы Брадиса, найдите:
sin 22° = 0,3749
sin 22°36´ = 0,3843
cos 68°18´ = 0,3697
tg 40°40´ = 0,8591
© Кузьмина Е.А., Колобовская МСОШ, 2010
Задание 2
Используя таблицы Брадиса, найдите:
1) sin16° = 0,2756 2) sin24°36´= 0,4163
cos16° = 0,9613
cos24°36´= 0,9092
3) sin70°32´= 0,9428 4) sin88°49´= 0,9998
cos70°32´= 0,3333 cos88°49´= 0,0206
© Кузьмина Е.А., Колобовская МСОШ, 2010
Задание 3
Используя таблицы Брадиса, найдите
величину угла:
1) sinх =0,0175
х = 1°
3) cosх =0,6814
х = 47°3´
2) sinх =0,5015
х = 30°6´
4) cosх =0,0670
х = 86°9´
© Кузьмина Е. А., Колобовская МСОШ, 2010
Используемая литература и Интернет-ресурсы:
1. Погорелов А.В. Геометрия: 7–9 классы – М.: Просвещение, 2004
2. Геометрия. 8 класс. Поурочные планы по учебнику А.В. Погорелова /
Авт.-сост. Н.В. Грицаева – Волгоград: Учитель, 2006
3. Википедия – свободная энциклопедия – http://ru.wikipedia.org/
Презентацию подготовила:
Кузьмина Елена Александровна
учитель математики и информатики
Колобовская МСОШ
Шуйский район
Ивановская область
2010 год

English     Русский Правила

Прямоугольные треугольники и тригонометрия Содержание

• Главная /
• Геометрия /
• Прямоугольные треугольники и тригонометрия /
• Содержание

• Прямоугольные треугольники и тригонометрия /
• Содержание
  
• • Введение
  • Темы
  • Примеры
  • Упражнения
  • Задачи Math Shack
  • Викторины
  • Условия
  • Раздаточный материал
  • Лучшее из Интернета
  • Содержание

  Прямоугольные треугольники и тригонометрия
  Темы
  Примеры прямоугольных треугольников и тригонометрии
  

  Прямоугольные треугольники и упражнения по тригонометрии
  Высоты и длины сторон
  Высоты и длины сторон Справка
  Среднее геометрическое
  Справка по среднему геометрическому
  Примеры среднего геометрического
  Справка по среднему геометрическому
  Теорема Пифагора 9005 Теорема Пифагора5 9005 Теорема Пифагора5 Теорема Пифагора Примеры
  Теорема Пифагора Упражнения
  Особые прямоугольные треугольники
  Особые прямоугольные треугольники Справка
  Особые прямоугольные треугольники Примеры
  Специальные упражнения на прямоугольные треугольники
  45-45-90 Треугольники
  45-45-90 Треугольники Помощь
  30-60-90 Треугольники
  30-60-90 Треугольники Помощь
  Тригонометрия
  Тригонометрия Помощь
  Тригонометрия Примеры
  Тригонометрия 005s Тригонометрия
  Trig Ratios Help
  Обратные Trig Ratios
  

  Trig Ratios Help0055 Примеры закона синусов
  Упражнения по закону синусов
  

  Закон косинусов
  Справка по закону косинусов
  Примеры закона косинусов
  Упражнения по закону косинусов
  Термины
  Лучшее из Интернета Хорошее, а не среднее геометрическое Правда или Ложь
  Чувство всех правильных треугольников
  Чувство всех правильных треугольников Правда или ложь
  Закон и порядок: Специальный блок тригонометрии
  Закон и порядок: Специальный блок тригонометрии Верно или неверно
  Раздаточный материал
  

  ---

  Выход из системы…

  Почему это смешно?

  ЗАКРЫТЬ

  Приложение V.

  Спецификация таблицы принудительного обнаружения Приложение V. Спецификация таблицы принудительного обнаружения

  Отдел ядерной медицины SimSETПриложение V: Спецификация таблицы принудительного обнаружения

  [Новости] [Руководство по установке] [Руководство пользователя] [ Информация для программистов ] [Ресурсы] [Контакты]

  ---

  Содержимое:

  1. Введение
  2. Почему таблицы принудительного обнаружения?
  3. Формат таблицы принудительного обнаружения
  4. Как используются таблицы принудительного обнаружения
  5. Как организованы таблицы принудительного обнаружения

   

  Введение:

  В этом документе описывается реализация таблиц принудительного обнаружения в модуле SimSET PHG. Он предназначен в качестве справочной информации для программиста, заинтересованного в понимании и/или модификации PHG. Он содержит схемы и описания структур данных, используемых для манипулирования данными принудительного обнаружения, а также алгоритмы использования содержащейся в них информации.

  [начало страницы]

   

  Почему таблицы принудительного обнаружения?

  Таблицы Forced Detection содержат предварительно вычисленные вероятности того, что фотон с определенным направлением и углом рассеется в выбранном диапазоне исходящих углов. Другими словами, таблицы отвечают на вопрос: Какова вероятность того, что фотон рассеется в заданном диапазоне при данном входящем направлении и энергии? Определенный диапазон вычисляется, чтобы гарантировать, что фотон войдет в детектор под приемлемым углом.

  В частности, таблицы принудительного обнаружения преобразуют координаты, используемые формулой Клейна-Нишины, входящую энергию и угол рассеяния в координаты, необходимые для реализации принудительного обнаружения (входящая энергия, исходящий косинус направления z и синус исходящего азимутального угла ).

  Использование предварительно вычисленных таблиц устраняет дорогостоящие вычисления, связанные с процессом.

  [начало страницы]

   

  Формат таблицы принудительного обнаружения

  Существует три таблицы принудительного обнаружения, каждая из которых обеспечивает различное представление распределения Клейна-Нишины:

  1. Таблица плотности Кляйна-Нишина : Это четырехмерная таблица, в которой представлены вероятности относительного рассеяния фотона с заданной энергией и направлением косинуса z (вероятности точны только до постоянного множителя, т.е. не сумма к 1.) . Вероятности определяются для заданных исходящих направлений z-косинуса и изменения азимутального угла. На приведенной ниже диаграмме показано:

  2. Совокупная таблица плотности Клейна-Нишины: Это четырехмерная таблица, которая дает кумулятивную сумму таблицы плотности Клейна-Нишины по двум последним переменным (исходящий косинус z и исходящий азимутальный угол) : 89
  3. Плотность Клейна-Нишины Совокупная общая таблица: Это трехмерная таблица, которая дает кумулятивную сумму значений плотности Клейна-Нишины для всех азимутальных углов для всех исходящих z-косинусов, меньших или равных z -позиция косинуса в таблице для каждого исходящего z-косинуса:

     [начало страницы]

  Как используются таблицы принудительного обнаружения

  После выбора точки взаимодействия вдоль линии прохождения через критическую зону необходимо выбрать угол рассеяния, чтобы гарантировать обнаружение. Алгоритм продолжения приведен ниже:

  Вычислите относительную вероятность того, что угол рассеяния окажется в пределах вычисленного допустимого диапазона.

  Сначала необходимо рассчитать «индекс бина таблицы KNDensity» для входящей энергии, входящего косинуса z, синуса минимального угла приема и синуса максимального угла приема. Они будут одинаковыми для всех таблиц и называются incomingEnergyIndex, incomingZCosineIndex, minAcceptanceAngleIndex и maxAcceptanceAngleIndex.

  probScatterInRange = KNDensCumTotal[incomingEnergyIndex]
  [incomingZCosineIndex][maxAcceptanceAngleIndex] —
  KNDensCum[incomingEnergyIndex][incomingZCosineBin]
  [minAcceptanceAngleIndex ][0]
  

  Выберите целевую вероятность из допустимого диапазона.

  targetScatterProbability = KNDensCum[входящая энергия]
  [incomingZCosineBin][minAcceptanceAngleIndex][0] +
  (случайное число * probScatterInRange).

  Теперь найдите ячейку в таблице KNDensityCumulative, которая содержит выбранную targetScatterProbability.

  Для этого требуется операция поиска в таблице. Вы знаете поступающую энергию и incomingZCosineIndex ; для тех значений, которые вы ищете в таблице от outgoingZCosineIndex = minAcceptanceAngleIndex до maxAcceptanceAngleIndex для каждого AzimuthalIndex, пока не найдете исходящие ZCosineIndex и AzimuthalChangeIndex такие, что

  KNDensCum[incomingEnergyIndex][incomingZCosineIndex]
  [outgoingZCosineIndex][AzimuthalChangeIndex] < targetScatterProbability < KNDensCum[incomingEnergyIndex][incomingZCosineIndex]
  [outgoingZCosineIndex][AzimuthalChangeIndex + 1]

  или, если AzimuthalIndex + 1 выходит за пределы диапазона для азимутальных индексов,

  KNDensCum[incomingEnergyIndex][incomingZCosineIndex]
  [outgoingZCosineIndex][AzimuthalChangeIndex] < targetScatterProbability < KNDensCumTotal[incomingEnergyIndex][incomingZCosineIndex]
  [исходящийZCosineIndex]

  Этот поиск дает нам два значения: outgoingZCosineIndex и AzimuthalChangeIndex.

  Выберите исходящий косинус z.

  Исходящий ZCosineIndex , вычисленный выше, определяет диапазон для исходящего косинуса z. Исходящий косинус z «zCosineOut» должен равняться начальной точке исходящего ZCosineBin плюс размер исходящего ZCosineIndex бин * случайное число.

  Выберите исходящий азимутальный угол.
  

  AzimuthalChangeIndex , вычисленный выше, определяет диапазон изменения азимутального угла. Исходящий азимутальный угол «azimuthOut» должен равняться входящему азимутальному углу + (начало AzimuthalChangeIndex + диапазон AzimuthalChangeIndex* случайное число).

  Определение xCosineOut и yCosineOut из azimuthOut

  Вычисление косинуса угла рассеяния

  CosScatteringAngle = (xCosIn * xCosOut) + (yCosIn * yCosOut) + (zCosIn * zCosOut)

  Расчет исходящей энергии

  Вычисление исходящего веса фотона

  WtOut = WtIn * (KN(CosScatterAngle, incomingEnergy, outgoingEnergy) / KNDensity[incomingEnergyIndex][incomingZCosineIndex]
  [outgoingZCosineIndex][AzimuthalChangeIndex] )

  где KN — функция плотности Клейна-Нишины, как указано в уравнении 11 Зерби (6) .

   [начало страницы]

   

  Как организованы таблицы принудительного обнаружения:

  На приведенных выше диаграммах представлено логическое представление таблиц принудительного обнаружения. Диаграмма ниже повторяет это представление в слегка измененном виде:

   

  Поскольку в C трудно работать с массивами с динамическим размером и выделением памяти, мы решили реорганизовать данные. Из обсуждения выше следует, что каждый фотон приходит с входящей энергией и косинусом направления z. С этими двумя переменными связаны три значения относительной вероятности (исходящий косинус z, исходящее азимутальное изменение, кумулятивное исходящее азимутальное изменение). Используя эту информацию, чтобы по-новому взглянуть на наши данные, мы реорганизовали данные, как показано на диаграмме ниже:

   

   

  Теперь у нас есть двумерная таблица, в которой каждый элемент содержит три массива.

  No related posts.