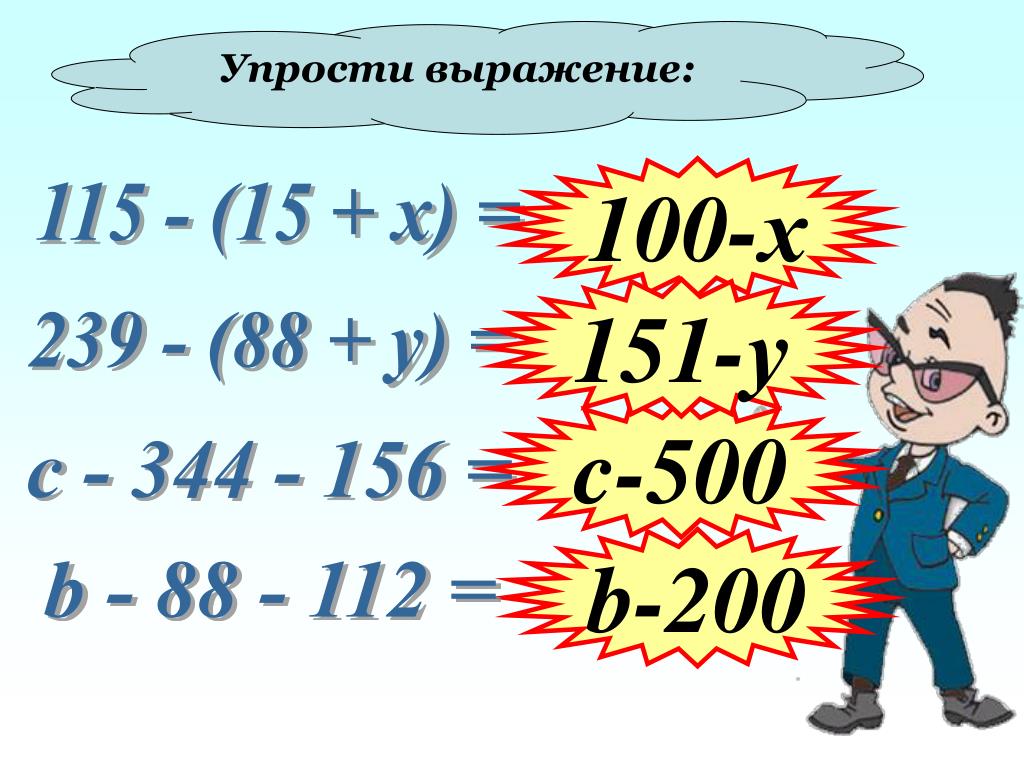
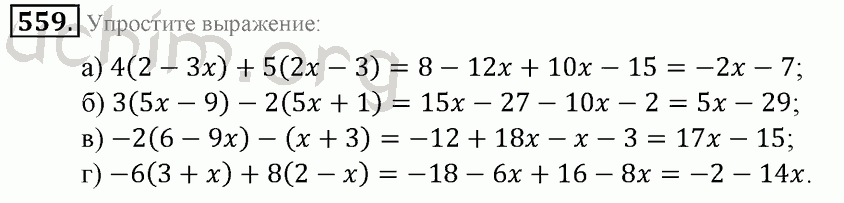Математика 5 класс упростите выражение: Упрощение выражений — урок. Математика, 5 класс.

Содержание

Упрощение выражений 5 класс с ответами

Тестовые задания для 5 класса по теме: Упрощение выражений.

Правильный вариант ответа отмечен знаком +

1. Как упростить выражение 2x+7x+11 + 7?

a. 5x+4 -

b. 9x+18 +

c. 9x+14 -

d. 5x+18 -

2. Чему равен x в примере 5x+6+8x+33?

a. 4 -

b. 1 -

c. 5 -

d. 3 +

3. Как упростить выражение 2a+4c+6a-2c?

a. 4a+6c -

b. 6a2+6c2 —

c. 8a+2c +

d. 6a-4c -

4. Какое равенство верное, где x-целое число?

a. 3x+6=4+4x +

b. x-9=15-2x -

c. 5x+4=10+2x -

d. 11-6x=21+3x -

5. Как записать сокращенно выражение 5×e+7d-3d?

a. 15ed -

b. 5e+10d -

c. 9ed -

d. 5e+4d +

Если перед скобками стоит знак минус, то знаки в скобках…

a. не меняются -

b. меняются +

c. отпадают -

d. прибавляется еще один знак -

7. В каком выражении x равен 5?

a. 5x+8+7+6x -

b. 12+x-10+3x -

c. 2x+14+4x+16 +

d. 9+7x+18+2x -

8. Как будет выглядеть пример 6x×3×2x×8 в упрощенном виде?

a. 18x×16x -

b. 12×2×24 +

c. 48x×6x -

d. 9x×10x -

9. 15z-10y-7z+3y= …

a. 5z-4y -

b. 5zy-4zy -

c. 8z-7y +

d. 12z-3y -

тест 10. В одной коробке x шоколадных конфет, во второй — в 4 раза больше, чем в первой, в третьей — в 2 раза конфет меньше, чем во второй. Как будет выглядеть общее количество конфет при решении в упрощенном виде?

a. 7x +

b. 10x -

c. 9x -

d. 12x -

11. Как называют числовой множитель по-другому?

a. логарифм -

b. коэффициент +

c. буквенный множитель -

d. гипербола -

12. Какого закона умножения для упрощения выражений не бывает?

a. распределительный -

b. сочетательный -

c. переместительный -

d. сложенный +

13. Как упростить выражение с буквенно-числовыми показателями 20d+7d?

a. (20+7)d=27d +

b. 27d2 -

c. не упрощается -

d. 13d -

14. Чему равен результат в 24x-10x при x=2?

a. 34x -

b. 14x=14×2=28 +

c. 14×2 -

d. 34×2 -

15. Как записать выражение со сложением в упрощенном виде, если известны слагаемые: 8e, 15e, 7n, 10n?

a. 23e+17n +

b. 15en+25en -

c. 23e2+17n2 -

d.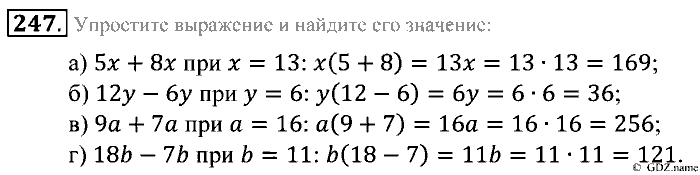 9e+3n -

16. 5y+6(y+x)-4x= …

a. 11y2–2×2 -

b. y-4x -

c. 11y+2x +

d. 11y-8x -

17. Какое правило свойственно для переместительного закона сложения?

a. от перестановки слагаемых сумма не меняется +

b. для того, чтобы к сумме двух чисел прибавить третье число, можно к первому числу прибавить сумму второго и третьего чисел -

c. для того, чтобы вычесть сумму из числа, можно отнимать каждое слагаемое по отдельности -

d. для того, чтобы определенное число умножить на сумму, нужно его умножить на каждое слагаемое по отдельности -

18. Какое неравенство составлено верно при m=4?

a. 5m-3m>4m+8m -

b. 3m+7m<6m+5m +

c. 9m-2m<3m+m -

d. 14m-12m>7m+9m -

19. Как представить в развернутом виде 74b?

a. 25b+39b -

b. 44b+31b -

c. 54b+30b +

d. 17b+47b -

тест-20. Чему равен y в примере 8y-4y+2y=18

a. 3 +

b. 7 -

c. 10 -

d. 5 -

21. Можно ли сократить выражение 7e+3f?

a. только числовые показатели -

b. только буквенные показатели -

c. нет +

d. да -

22. Как будет выглядеть пример 4(5+3-2) после раскрытия скобок?

a. 24 -

b. 20+12-8 +

c. 20 -

d. 20+3-2 -

23. 7x-5y+3y+2x= …

a. 2xy+5xy -

b. 4y+3y -

c. 12y+5x -

d. 9x-2y +

24. Расстояние от дома до автобусной остановки равно 2,5d, а расстояние от автобусной остановки до школы 1,5d. Чему равно расстояние от дома до школы?

a. 2,5d-1,5d=d -

b. 2,5d+1,5d=4d +

c. 2,5d×1,5d=3,75d2 -

d. 2,5d+1,5d=4d2 -

25. Как записать пример 63×8 помощью распределительного свойства умножения?

a. (60+3)×8 +

b. 6×8+3×8 -

c. 68×3 -

d. 6×83 -

26. Что является в примере 9y+y+(6-2):4 числовым множителем?

a. 18 -

b. 6 -

c. 10 -

d. 9 +

27. 56x-40x+17x= …

a. 18x -

b. 33x +

c. 40x -

d. 20x -

28. Как видоизменить пример 10b+2e, используя скобки?

a. 2(5b+e) +

b. (10b+2e) -

c. (10b)+(2e) -

d. (10×2)+(b×e) -

29. 21m×…=84mb

a. 6b -

b. 8b -

c. 4b +

d. 2b -

тест_30. Как упростить выражение на картинке?

a. a(3+7) +

b. 10a2 -

c. a(7-3) -

d. 4a —

Упрощение выражений — Математика — Презентации

Задания для домашней работы:

Запишите, какие остатки могут получиться при делении на 7.

1, 2, 3, 4, 5, 6

2. Проверьте, правильно ли выполнены вычисления:

а) 312 : 6 = 52 ; Верно

б) 319 : 6 = 52 (ост.7). Неверно, т.к. 319:6=53(ост. 1)

Число m разделили на 8. В частном получили 13, а в остатке 6. Найдите делимое m .

m= 13*8+6=110

Упрощение выражений

5 класс

Найдите значения выражений удобным способом

15*83+15*17 =

79*21-69*21=

А я знаю, нужно использовать распределительный закон умножения.

аb + ac = а(в + с)

аb — ac = а(в — с)

15(83+17)=

15*83+15*17 =

15*100 =

1500

79*21-69*21=

21(79-69)=

21*10 =

210

А как проще записать выражение?

2x + 3x =

8y – 5y =

Используем

распределительный закон

ab + аc = а(b + c)

ab — аc = а(b — c)

5*x =

(2 + 3)*x =

2x + 3x =

3*y =

8y – 5y =

(8 – 5)*y =

2x + 3x =

8y – 5y =

Тренируемся…

Упростите выражения:

12а + 7а =

19а

24т + m =

25т

16b -5b =

11b

18n — n =

17n

13а + 2b =

14а — 4b =

13а + 2b

15ab

14x – 2y

10xy

Эти выражения не упрощаются, так как буквенная часть не одинакова.

Слагаемые, у которых буквенная часть одинаковая, называются подобными .

Тренируемся…

Подчеркните подобные слагаемые:

2a + 3a + 7b

= 5а +7b

7c + 3d + 5c

= 12с +3d

15x — 6x + 23

= 9x +23

= 25y +8

17y +8y + 8

Упростите выражения.

А как преобразовать выражение?

Обратное преобразование называется вынесением общего множителя за скобки.

ab + аc = а(b + c)

9а

а(4 + 5) =

4а + 5а =

3а + 9 =

3(а + 3)

Какие выражения можно упростить?

6m + 6n

15x + 4y ,

8a – 4b,

Слагаемые в первом выражении не имеют одинаковых множителей, использовать распределительный закон невозможно. Второе выражение преобразуем и вынесем за скобки общий множитель .

В третьем выражении можно

вынести за скобки число 6 .

4 (2a – b)

8a – 4b =

4 *2a – 4

*b =

6(m + n)

6m + 6n =

Тренируемся.

Вынесите общий множитель за скобки.

2а + 2b =

2(а + b)

4а — 4c =

4(а — c)

а(2 + 3) = 5a

2а + 3a =

m(8 — 5) = 3m

8m — 5m =

x(3 + 1) = 4x

3x + x =

Определите, что пропущено в данных выражениях:

6а

9а — . .. = 3а

6х + … +13х = 19х + 9

22x

3х + … +15х + 1 + 4х = … +10

Определите, что пропущено в данных выражениях.

5(а — … ) = 5а — 5b

5(а — … ) = 5а — 10

4( … + 2) = 4а + …

Задача.

В столовую привезли картофеля в 2 раза больше мешка, чем капусты.

Всего привезли 9 мешков картофеля и капусты. Сколько привезли мешков картофеля и сколько капусты?

? мешков

Пусть капусты привезли х мешков.

Тогда картофеля 2х мешков.

Всего привезли 9 мешков.

x + 2x = 9

3x = 9

x = 9 : 3

x = 3 (мешка) капусты

2 * 3 = 6 ( мешков)картофеля

Составить и решить уравнение на доске.

Ответ: 3 мешка капусты

и 6 мешков картофеля.

6 мешков

3 мешка

Решение уравнений:

14y – 9y = 100

5x + 3x = 16

5y = 100

8x = 16

y = 100:5

8x = 16:8

y = 20

х = 2

13a – 8a + a = 36

7b + 3b — 10b = 3

6a = 36

0*b = 3

a = 36:6

Нет решений

a = 6

Самостоятельная работа

с последующей проверкой учителем.

Упростить выражение

и найти значение :

18x + 23 x — x при х = 37

2. Решить уравнение:

5y + 12y = 3553

3.Вынести общий множитель за скобки :

8x – 16 y + 80

20a — 28b

Контрольная работа № 3 (математика, 5 класс, по учебнику Виленкина)

K-3

Вариант 1

1. Найдите значение выражения (205 — m) + (176 — n), если m = 102 и n = 84.

2. Решите уравнение: а) 71 — x = 40; б) z + 37 = 48; в) (46 + y) — 13 = 54.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 21 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 27 и при m = 42.

4. Упростите выражение: а) m + 123 + 246; б) 1085 — (702 + m).

5. На отрезке AM = 38 см отметили точку K, такую, что AK = 18 см, и точку P, такую, что PM = 15 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 2

1. Найдите значение выражения (m — 156) — (95 + n), если m = 317 и n = 40.

2. Решите уравнение: а) y — 17 = 48; б) 24 + x = 45; в) (45 + y) — 30 = 47.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 74 см, AC = 31 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 23 и при n = 30.

4. Упростите выражение: а) 107 + n + 361; б) 459 — (k + 210).

5. На отрезке AM = 44 см отметили точку K, такую, что AK = 19 см, и точку P, такую, что PM = 12 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 3

1. Найдите значение выражения (m + 241) — (106 — n), если m = 123 и n = 58.

2. Решите уравнение: а) 43 — x = 27; б) z + 42 = 55; в) (57 + y) — 29 = 46.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 38 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 21 и при m = 48.

4. Упростите выражение: а) m + 213 + 372; б) 870 — (189 + m).

5. На отрезке AM = 19 см отметили точку K, такую, что AK = 14 см, и точку P, такую, что PM = 13 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 4

1. Найдите значение выражения (170 + n) — (m — 177), если m = 321 и n = 85.

2. Решите уравнение: а) y — 26 = 51; б) 57 + x = 78; в) (39 + y) — 24 = 30.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 101 см, AC = 30 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 15 и при n = 23.

4. Упростите выражение: а) 249 + n + 331; б) 606 — (k + 252).

5.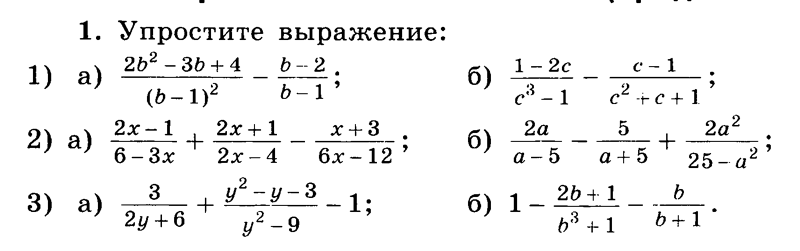 На отрезке AM = 42 см отметили точку K, такую, что AK = 10 см, и точку P, такую, что PM = 14 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 5

1. Найдите значение выражения (226 — m) + (43 — n), если m = 116 и n = 27.

2. Решите уравнение: а) 40 — x = 23; б) z + 27 = 57; в) (46 + y) — 11 = 47.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 23 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 30 и при m = 40.

4. Упростите выражение: а) m + 189 + 324; б) 986 — (555 + m).

5. На отрезке AM = 30 см отметили точку K, такую, что AK = 11 см, и точку P, такую, что PM = 10 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 6

1. Найдите значение выражения (m — 152) — (77 + n), если m = 261 и n = 30.

2. Решите уравнение: а) y — 31 = 24; б) 48 + x = 75; в) (46 + y) — 16 = 46.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 99 см, AC = 20 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 14 и при n = 19.

4. Упростите выражение: а) 139 + n + 274; б) 562 — (k + 450).

5. На отрезке AM = 21 см отметили точку K, такую, что AK = 12 см, и точку P, такую, что PM = 11 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 7

1. Найдите значение выражения (m + 345) — (118 — n), если m = 168 и n = 19.

2. Решите уравнение: а) 71 — x = 54; б) z + 45 = 58; в) (52 + y) — 15 = 54.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 41 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 26 и при m = 41.

4. Упростите выражение: а) m + 205 + 388; б) 851 — (490 + m).

5. На отрезке AM = 16 см отметили точку K, такую, что AK = 13 см, и точку P, такую, что PM = 15 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 8

1. Найдите значение выражения (107 + n) — (m — 141), если m = 283 и n = 64.

2. Решите уравнение: а) y — 17 = 60; б) 38 + x = 56; в) (27 + y) — 25 = 16.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 89 см, AC = 13 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 20 и при n = 31.

4. Упростите выражение: а) 261 + n + 230; б) 1013 — (k + 573).

5. На отрезке AM = 31 см отметили точку K, такую, что AK = 16 см, и точку P, такую, что PM = 14 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 9

1. Найдите значение выражения (385 — m) + (119 — n), если m = 195 и n = 72.

2. Решите уравнение: а) 59 — x = 26; б) z + 38 = 66; в) (33 + y) — 14 = 52.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 44 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 13 и при m = 43.

4. Упростите выражение: а) m + 138 + 282; б) 1141 — (487 + m).

5. На отрезке AM = 28 см отметили точку K, такую, что AK = 15 см, и точку P, такую, что PM = 20 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 10

1. Найдите значение выражения (m — 184) — (74 + n), если m = 337 и n = 27.

2. Решите уравнение: а) y — 24 = 54; б) 30 + x = 56; в) (49 + y) — 20 = 50.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 79 см, AC = 29 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 18 и при n = 25.

4. Упростите выражение: а) 211 + n + 344; б) 1095 — (k + 316).

5. На отрезке AM = 22 см отметили точку K, такую, что AK = 17 см, и точку P, такую, что PM = 12 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 11

1. Найдите значение выражения (m + 278) — (255 — n), если m = 108 и n = 83.

2. Решите уравнение: а) 55 — x = 36; б) z + 40 = 56; в) (34 + y) — 18 = 42.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 36 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 25 и при m = 48.

4. Упростите выражение: а) m + 265 + 299; б) 560 — (319 + m).

5. На отрезке AM = 39 см отметили точку K, такую, что AK = 10 см, и точку P, такую, что PM = 20 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 12

1. Найдите значение выражения (256 + n) — (m — 141), если m = 248 и n = 98.

2. Решите уравнение: а) y — 23 = 41; б) 58 + x = 85; в) (26 + y) — 30 = 13.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 102 см, AC = 13 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 11 и при n = 29.

4. Упростите выражение: а) 194 + n + 285; б) 1055 — (k + 416).

5. На отрезке AM = 25 см отметили точку K, такую, что AK = 18 см, и точку P, такую, что PM = 13 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 13

1. Найдите значение выражения (266 — m) + (60 — n), если m = 147 и n = 23.

2. Решите уравнение: а) 76 — x = 54; б) z + 57 = 90; в) (39 + y) — 29 = 38.

4. Упростите выражение: а) m + 162 + 394; б) 711 — (503 + m).

5. На отрезке AM = 28 см отметили точку K, такую, что AK = 16 см, и точку P, такую, что PM = 17 см. Найдите длину отрезка KP.

© А.П. Шестаков, 1996

K-3

Вариант 14

1. Найдите значение выражения (m — 156) — (47 + n), если m = 268 и n = 13.

2. Решите уравнение: а) y — 31 = 32; б) 30 + x = 55; в) (43 + y) — 27 = 49.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 82 см, AC = 30 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 13 и при n = 31.

4. Упростите выражение: а) 173 + n + 321; б) 872 — (k + 724).

5. На отрезке AM = 42 см отметили точку K, такую, что AK = 18 см, и точку P, такую, что PM = 20 см. Найдите длину отрезка KP.

K-3

Вариант 15

1. Найдите значение выражения (m + 276) — (134 — n), если m = 138 и n = 24.

2. Решите уравнение: а) 53 — x = 29; б) z + 34 = 45; в) (51 + y) — 25 = 43.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 28 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 30 и при m = 41.

4. Упростите выражение: а) m + 165 + 285; б) 303 — (274 + m).

5. На отрезке AM = 25 см отметили точку K, такую, что AK = 13 см, и точку P, такую, что PM = 16 см. Найдите длину отрезка KP.

K-3

Вариант 16

1. Найдите значение выражения (212 + n) — (m — 103), если m = 240 и n = 98.

2. Решите уравнение: а) y — 28 = 40; б) 44 + x = 66; в) (53 + y) — 27 = 48.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 80 см, AC = 31 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 23 и при n = 33.

4. Упростите выражение: а) 236 + n + 309; б) 644 — (k + 361).

5. На отрезке AM = 27 см отметили точку K, такую, что AK = 18 см, и точку P, такую, что PM = 20 см. Найдите длину отрезка KP.

K-3

Вариант 17

1. Найдите значение выражения (280 — m) + (118 — n), если m = 146 и n = 34.

2. Решите уравнение: а) 57 — x = 46; б) z + 38 = 62; в) (19 + y) — 26 = 25.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 14 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 32 и при m = 38.

4. Упростите выражение: а) m + 191 + 365; б) 950 — (377 + m).

5. На отрезке AM = 34 см отметили точку K, такую, что AK = 13 см, и точку P, такую, что PM = 19 см. Найдите длину отрезка KP.

K-3

Вариант 18

1. Найдите значение выражения (m — 193) — (74 + n), если m = 355 и n = 60.

2. Решите уравнение: а) y — 11 = 47; б) 37 + x = 56; в) (54 + y) — 18 = 58.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 90 см, AC = 17 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 25 и при n = 27.

4. Упростите выражение: а) 199 + n + 327; б) 939 — (k + 576).

5. На отрезке AM = 20 см отметили точку K, такую, что AK = 15 см, и точку P, такую, что PM = 12 см. Найдите длину отрезка KP.

K-3

Вариант 19

1. Найдите значение выражения (m + 303) — (235 — n), если m = 137 и n = 55.

2. Решите уравнение: а) 73 — x = 49; б) z + 26 = 42; в) (33 + y) — 17 = 28.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 48 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 22 и при m = 45.

4. Упростите выражение: а) m + 257 + 283; б) 622 — (336 + m).

5. На отрезке AM = 44 см отметили точку K, такую, что AK = 16 см, и точку P, такую, что PM = 18 см. Найдите длину отрезка KP.

K-3

Вариант 20

1. Найдите значение выражения (115 + n) — (m — 149), если m = 250 и n = 29.

2. Решите уравнение: а) y — 32 = 53; б) 50 + x = 68; в) (56 + y) — 29 = 46.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 89 см, AC = 11 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 18 и при n = 21.

4. Упростите выражение: а) 271 + n + 234; б) 975 — (k + 911).

5. На отрезке AM = 40 см отметили точку K, такую, что AK = 19 см, и точку P, такую, что PM = 21 см. Найдите длину отрезка KP.

K-3

Вариант 21

1. Найдите значение выражения (259 — m) + (148 — n), если m = 102 и n = 79.

2. Решите уравнение: а) 81 — x = 60; б) z + 28 = 60; в) (42 + y) — 17 = 49.

4. Упростите выражение: а) m + 238 + 289; б) 1033 — (858 + m).

5. На отрезке AM = 36 см отметили точку K, такую, что AK = 10 см, и точку P, такую, что PM = 11 см. Найдите длину отрезка KP.

K-3

Вариант 22

1. Найдите значение выражения (m — 170) — (96 + n), если m = 360 и n = 41.

2. Решите уравнение: а) y — 17 = 30; б) 47 + x = 62; в) (46 + y) — 13 = 58.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 85 см, AC = 20 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 16 и при n = 23.

4. Упростите выражение: а) 151 + n + 378; б) 880 — (k + 656).

5. На отрезке AM = 17 см отметили точку K, такую, что AK = 13 см, и точку P, такую, что PM = 12 см. Найдите длину отрезка KP.

K-3

Вариант 23

1. Найдите значение выражения (m + 293) — (123 — n), если m = 145 и n = 45.

2. Решите уравнение: а) 59 — x = 37; б) z + 20 = 36; в) (42 + y) — 23 = 33.

3. На отрезке AB отмечена точка M. Найдите длину отрезка AB, если отрезок AM равен 43 см, а отрезок MB длиннее отрезка AM на m см. Упростите получившееся выражение и найдите его значение при m = 34 и при m = 37.

4. Упростите выражение: а) m + 134 + 398; б) 1005 — (399 + m).

5. На отрезке AM = 20 см отметили точку K, такую, что AK = 13 см, и точку P, такую, что PM = 15 см. Найдите длину отрезка KP.

K-3

Вариант 24

1. Найдите значение выражения (205 + n) — (m — 169), если m = 358 и n = 16.

2. Решите уравнение: а) y — 16 = 52; б) 31 + x = 50; в) (57 + y) — 33 = 52.

3. На отрезке AB отмечены точки C и D так, что точка D лежит между точками C и B. Найдите длину отрезка DB, если AB = 82 см, AC = 27 см, CD = n см. Упростите получившееся выражение и найдите его значение при n = 13 и при n = 31.

4. Упростите выражение: а) 125 + n + 263; б) 1141 — (k + 349).

5. На отрезке AM = 22 см отметили точку K, такую, что AK = 12 см, и точку P, такую, что PM = 19 см. Найдите длину отрезка KP.

Сайт создан в системе uCoz

Упрощение выражений с помощью двух операций — Математические игры

Упрощение выражений с помощью двух операций — Математические игры — SplashLearn

Главная > Игры > Математические игры > Игра «Упрости выражения с помощью двух операций»

Попросите вашего малыша упростить выражения с помощью двух операций, чтобы играть в эту игру.

Играть в игру

Присвоить классу

ПРЕДМЕТЫ И ТЕМЫ

Узнайте больше об упрощении выражений с помощью двух операций. Игра

Проблемы с порядком операций можно легко преодолеть, если учащиеся будут практиковать эту концепцию весело и увлекательно! Игра включает в себя работу с набором задач на упрощение выражений, что помогает юным учащимся укрепить свое понимание концепции. В этом задании учащиеся будут использовать недавно изученную стратегию, то есть стратегию PEMDAS, для решения поставленных задач.

Исследуйте удивительные игры с числовыми выражениями

Просмотреть все 9 игр

Алгебра
Игра «Упрости выражения с помощью двух операций»
Попросите вашего малыша упростить выражения с помощью двух операций, чтобы сыграть в эту игру.
ПОДРОБНЕЕ
Алгебра
Вычисление выражений с помощью двух операций Игра
Дети учатся вычислять выражения с помощью двух операций.
ПОДРОБНЕЕ
Алгебра
Упростите выражения с помощью 2 или более операций Игра
Дети должны упростить выражения с помощью 2 или более операций.
ПОДРОБНЕЕ
Алгебра
Вычисление выражений с помощью 2 или более операций Игра
Наслаждайтесь чудом математики, научившись вычислять выражения с помощью 2 или более операций.
ПОДРОБНЕЕ
Алгебра
Форма алгебраических выражений Игра
Играйте, чтобы попрактиковаться в искусстве формирования алгебраических выражений.
ПОДРОБНЕЕ
Алгебра
Игра «Формирование числовых выражений»
Устройте собственную вечеринку на тему математики, научившись составлять числовые выражения.
ПОДРОБНЕЕ
Алгебра
Игра «Моделирование словесных задач»
Дети должны моделировать словесные задачи, чтобы практиковаться в алгебре.
ПОДРОБНЕЕ
Алгебра
Вычисление алгебраических выражений с помощью одной операции Игра
Посмотрите, как вычислять алгебраические выражения с помощью одной операции.
ПОСМОТРЕТЬ ДЕТАЛИ
Алгебра
Вычисление алгебраических выражений с помощью двух операций Игра
Используйте свои математические способности для вычисления алгебраических выражений с помощью двух операций.
ПОДРОБНЕЕ

Откройте для себя веселые игры по алгебре

Просмотреть все 35 игр

Алгебра
Введи правильное число, используя аддитивные шаблоны Игра
Введи правильное число, используя аддитивные шаблоны.
ПОСМОТРЕТЬ ДЕТАЛИ
Алгебра
Игра «Вставь правильное число, используя шаблоны вычитания»
Дети должны вписать правильное число, используя шаблоны вычитания.
ПОДРОБНЕЕ
Алгебра
Введи правильное число, используя мультипликативные шаблоны Игра
Введи правильное число, используя мультипликативные шаблоны, чтобы сделать обучение увлекательным.
ПОДРОБНЕЕ
Алгебра
Игра «Определи правильную закономерность»
Окунитесь в безумие математической мультивселенной, исследуя, как определить правильную закономерность.
ПОДРОБНЕЕ
Алгебра
Игра «Заполни числа по образцу чисел»
Используй свои навыки алгебры, чтобы заполнить числа по образцу чисел.
ПОДРОБНЕЕ
Алгебра
Определите правильное правило шаблона, используемого в игре
Погрузитесь глубоко в мир алгебры, научившись определять правильное правило используемого шаблона.
ПОДРОБНЕЕ
Алгебра
Игра «Определи закономерность и заполни правильное число»
Наслаждайся чудом математики, учась определять закономерность, чтобы заполнять правильное число.
ПОДРОБНЕЕ
Алгебра
Игра «Распознай закономерность в числовой последовательности»
Используй свои математические способности, чтобы распознать закономерность в числовой последовательности.
ПОСМОТРЕТЬ ДЕТАЛИ
Алгебра
Игра «Распознай правильный узор и закрась его»
Раскрой мудрость математики, научившись распознавать правильный узор и заполнять его соответствующим образом.
ПОДРОБНЕЕ
Алгебра
Игра «Выбери первые пять кратных различных чисел»
Устрой собственную математическую вечеринку, научившись выбирать первые пять кратных различных чисел.
ПОСМОТРЕТЬ ДЕТАЛИ
Алгебра
Игра «Вставь пропущенные кратные»
Отточи свои математические навыки, вписывая пропущенные кратные.
ПОДРОБНЕЕ
Алгебра
Игра «Выбери, правда или ложь»
Используйте свои навыки алгебры, чтобы выбрать между правдой и ложью.
ПОДРОБНЕЕ
Алгебра
Игра «Выбери правильную кратность»
Раскрой мудрость математики, научившись выбирать правильную кратность.
ПОСМОТРЕТЬ ДЕТАЛИ
Алгебра
Игра «Определить, правда или ложь»
Определить, является ли данное утверждение истинным или ложным.
ПОДРОБНЕЕ
Алгебра
Завершить пары множителей для числовой игры
Используйте свои навыки алгебры, чтобы составить пары множителей для числа.
ПОДРОБНЕЕ

Связанные рабочие листы

Просмотреть все 11 рабочих листов

Алгебра
Определить правило данного числового шаблона Рабочий лист
Закрепить математические понятия, практикуясь в определении правила заданного числового шаблона.
ПОДРОБНЕЕ
Алгебра
Рабочий лист «Создание числовых шаблонов»
Погрузитесь в этот увлекательный печатный рабочий лист, создав числовые шаблоны.
ПОДРОБНЕЕ
Алгебра
Определение упорядоченных пар на координатной сетке Рабочий лист
Превратите математику в увеселительную прогулку, идентифицируя упорядоченные пары на координатных сетках.
ПОДРОБНЕЕ
Алгебра
Отметка упорядоченных пар на координатной сетке Рабочий лист
Дети могут отмечать упорядоченные пары на координатной сетке, распечатав этот забавный рабочий лист.
ПОДРОБНЕЕ
Алгебра
Нанесение числовых закономерностей на рабочий лист графика
Будьте на пути к тому, чтобы стать математиком, нанося числовые закономерности на график.
ПОСМОТРЕТЬ ДЕТАЛИ
Алгебра
Лист определения выражений и уравнений
Совместите изучение математики с приключениями, решая, чтобы идентифицировать выражения и уравнения.
ПОДРОБНЕЕ
Алгебра
Запись и интерпретация числовых выражений Рабочий лист
В этом рабочем листе учащиеся получат возможность писать и интерпретировать числовые выражения.
ПОДРОБНЕЕ
Алгебра
Рабочий лист сравнения выражений без оценки
Раскройте секреты математического волшебства, потренировавшись сравнивать выражения без оценки.
ПОДРОБНЕЕ
Алгебра
Рабочий лист «Вычисление выражений, содержащих скобки»
Превратите математику в увлекательное занятие, решая задачи на вычисление выражений, содержащих круглые скобки.
ПОДРОБНЕЕ
Алгебра
Вычисление выражений с экспонентами Рабочий лист
Совместите изучение математики с приключениями, решив вычислить выражения, включающие показатели степени.
ПОДРОБНЕЕ
Алгебра
Расчет выражений с помощью рабочего листа PEMDAS
Распечатайте этот рабочий лист, чтобы вычислять выражения с помощью PEMDAS, как математическую легенду!
ПОДРОБНЕЕ
Алгебра
Определить правило данного числового шаблона Рабочий лист
Закрепить математические понятия, практикуясь в определении правила заданного числового шаблона.
ПОСМОТРЕТЬ ДЕТАЛИ
Алгебра
Рабочий лист «Создание числовых шаблонов»
Погрузитесь в этот увлекательный печатный рабочий лист, создав числовые шаблоны.
ПОДРОБНЕЕ
Алгебра
Определение упорядоченных пар на координатной сетке Рабочий лист
Превратите математику в увлекательное занятие, определяя упорядоченные пары на координатной сетке.
ПОДРОБНЕЕ
Алгебра
Отметка упорядоченных пар на координатной сетке. Рабочий лист
Дети могут отмечать упорядоченные пары на координатной сетке, распечатав этот забавный рабочий лист.
ПОДРОБНЕЕ

Универсальное решение для всех потребностей обучения в классе.

Дайте вашему ребенку страсть и уверенность, чтобы безбоязненно учиться чему-либо самостоятельно

Родители, зарегистрируйтесь бесплатно

Учителя, используйте бесплатно

4413+

4417+

ПОХОЖИЕ ТЕМЫ

Texas Go Math 5 класс, урок 7.4 Ответы на вопросы Упростите числовые выражения – Go Math Ответы

Обратитесь к нашему PDF-файлу ответов Texas Go Math на 5 класс, чтобы получить хорошие оценки на экзаменах. Проверьте себя, решая задачи из Texas Go Math Grade 5 Lesson 7. 4 Ключ к ответу Simplify Numerical Expressions.

Разблокировать проблему

Рецепт торта требует 4 стакана муки и 2 стакана сахара. Чтобы утроить рецепт, сколько всего стаканов муки и сахара нужно?

Упростите 3 × 4 + 3 × 2, чтобы найти общее количество чашек.
A. Хизер неправильно выполнила порядок операций.

Объясните, почему ответ Хизер неверен.
Ответ:
Ответ Хизер неверен. Поскольку он сначала сложил 4 и 3, а затем умножил 3 на 7 и 2, то произведение равно 42. Он не следует порядку операций, сначала умножая, а затем добавляя.

B. Следуйте порядку операций, сначала умножая, а затем добавляя.

Итак, необходимо ________ стаканов муки и сахара.
Ответ:

Итак, нужно 18 стаканов муки и сахара.
Пояснение:
Рецепт торта требует 4 стакана муки и 2 стакана сахара. Рецепт увеличился втрое. Выражение равно 3 x 4 + 3 x 2. Итак, сначала я умножил 3 на 4 и 3 на 2, произведение равно 12 и 6. Затем я добавил 12 к 6, и сумма составила 18.

Пример

Каждая партия кексы Лена делает использует 3 стакана муки, 1 стакан молока и 2 стакана сахара. Лена хочет испечь 5 порций кексов. Сколько всего чашек муки, молока и сахара ей понадобится?
Запишите выражение. 5 × (3 + 1 + 2)
I Сначала выполните операции в скобках. 5 × (_________)
Затем умножьте. _________
Итак, всего у Лены будет _________ стаканов муки, молока и сахара.
Ответ:
Выражение 5 х (3 + 1 + 2).
I Сначала выполните операции в скобках.
5 × (3 + 1 + 2)
5 × (6)
Затем умножьте.
5 x 6
30
Итак, всего у Лены будет 30 стаканов муки, молока и сахара.
Объяснение:
На каждую партию кексов Лены уходит 3 стакана муки, 1 стакан молока и 2 стакана сахара. Лена хочет испечь 5 порций кексов. Выражение 5 × (3 + 1 + 2). Сначала выполните операции в скобках. Прибавьте 3 к 1 и 2, сумма будет 6. Затем умножьте 5 на 6, и получится 30. Таким образом, всего у Лены будет 30 стаканов муки, молока и сахара.

Поделись и покажи

Упростите числовое выражение.

Вопрос 1.
10 + 36 ÷ 9 904:55 Подумай: сначала нужно разделить.
Ответ:
10 + 36 ÷ 9
10 + 4
14
Объяснение:
Числовое выражение 10 + 36 ÷ 9. Сначала я разделил 36 на 9, результат 4. Затем я добавил 10 к 4 сумме. равно 14. Упрощенная форма данного числового выражения: 14.

Вопрос 2.
10 + (25 – 10) ÷ 5
Ответ:
10 + (25 – 10) ÷ 5
10 + 15 ÷ 5
10 + 3
13
Объяснение:
Числовое выражение: 10 + (25 – 10) ÷ 5. Сначала я вычел 10 из 25, тогда разница составила 15. Затем я разделил 15 на 5, результат равен 3. Затем я прибавил 10. с 3 сумма равна 13. Упрощенная форма данного числового выражения 13.

Вопрос 3.
9 – (3 × 2) + 8
Ответ:
9 – (3 × 2) + 8
9 – (6) + 8
3 + 8
11
Объяснение:
Числовое значение выражение 9 — (3 × 2) + 8. Сначала я умножил 3 на 2, произведение равно 6. Затем я вычел 6 из 9, разница равна 3. Затем я добавил 3 к 8, сумма равна 11. Упрощенная форма данного числовое выражение равно 11.

Math Talk
Mathematical Processes

Райна упростил выражение 5 × 2 + 2, сначала сложив, а затем умножив. Будет ли ее ответ правильным? Объяснять.
Ответ:
5 × 2 + 2
5 x 4
20
Нет, ее ответ 20, это неправильно. Правильный ответ: 12.
Пояснение:
Райна упростил выражение 5 × 2 + 2, сначала сложив, а затем умножив. Ее ответ будет неверным. Потому что Райна должна сначала выполнить умножение, а затем сложение.

Решение проблем

Вопрос 4.
H.O.T. Использование символов Запишите 12 + 17 – 3 × 2 со скобками, чтобы получить значение 23.
Ответ:
Один тип:
12 + 17 – (3 x 2)
12 + 17 – 6
29 – 6
23
Другой тип:
(12 + 17) – 3 x 2 9045 5 905 – 5 23
Объяснение:
Скобки для выражения 12 + 17 – 3 × 2 равны 12 + 17 – (3 x 2) или (12 + 17) – 3 x 2. Решая это числовое выражение со скобками, получаем значение 23.

Вопрос 5.
Многошаговый Значение 100 – 30 ÷ 5 со скобками может иметь значение 14 или 94. Объясните.
Ответ:
Один тип:
100 – (30 ÷ 5)
100 – 6
94
Значение данного выражения с указанными скобками равно 94.
100 – (30 ÷ 5)
70 4 ÷ 5 5 14
Значение данного выражения с указанными выше скобками равно 14.
Объяснение:
Два возможных варианта данного выражения с круглыми скобками: 100 – (30 ÷ 5), 100 – (30 ÷ 5). Решая эти два выражения, получаем значения 94 и 14.

Разгадка проблемы

Вопрос 6.
Многоступенчатый Кинотеатр имеет 4 группы мест. Самая большая группа сидений в середине состоит из 20 рядов, по 20 мест в каждом ряду. По бокам есть 2 меньшие группы сидений, каждая по 20 рядов и по 6 сидений в каждом ряду. Группа сидений сзади имеет 5 рядов, по 30 мест в каждом ряду. Сколько мест в кинотеатре?

а. Что вы должны знать?
Ответ:
Нам нужно знать общее количество мест в кинотеатре.

б. С помощью какой операции можно найти количество мест в задней группе сидений? Напишите выражение.
Ответ:
Выражение 5 x 30 .
150
Объяснение:
Операция умножения используется для определения количества мест в задней группе сидений. Группа сидений сзади имеет 5 рядов, по 30 мест в каждом ряду. Выражение 5 х 30. В задней группе сидений 150 мест.

в. С помощью какой операции можно найти количество мест в обеих группах боковых сидений? Напишите выражение.
Ответ:
Выражение 2 x (20 x 6) .
2 x 120
240
Пояснение:
Операция умножения используется для определения количества мест в обеих группах боковых мест. По бокам есть 2 меньшие группы сидений, каждая по 20 рядов и по 6 сидений в каждом ряду. Выражение 2 х (20 х 6). В обеих группах боковых сидений по 240 мест.

д. С помощью какой операции можно найти количество мест в средней группе? Напишите выражение.
Ответ:
Выражение 20 x 20 .
400
Объяснение:
Операция умножения используется для определения количества мест в средней группе. Самая большая группа сидений в середине состоит из 20 рядов, по 20 мест в каждом ряду. Выражение 20 х 20. В средней группе 400 мест.

эл. Напишите выражение, обозначающее общее количество мест в театре.
Ответ:
Выражение для представления общего количества мест в театре: (20 х 20) + 2 х (20 х 6) + (5 х 30).

ф. Сколько мест в театре? Покажите шаги, которые вы используете для решения проблемы.
Ответ:
(20 x 20) + 2 x (20 x 6) + (5 x 30)
400 + 2 x 120 + 150
400 + 240 + 150
790
Общее количество посадочных мест театр 790.

Вопрос 7.
Многошаговый В дикой природе взрослая гигантская панда съедает около 30 фунтов пищи каждый день. Напишите и упростите числовое выражение, показывающее, сколько фунтов еды съедают 6 панд за 3 дня.
Ответ:
3 x (6 x 30)
3 x 180
540
За 3 дня 6 панд съедают 540 фунтов пищи.
Пояснение:
В дикой природе взрослая гигантская панда съедает около 30 фунтов пищи каждый день. Числовое выражение для 6 панд, съедающих пищу за 3 дня, равно 3 x (6 x 30). За 3 дня 6 панд съедают 540 фунтов еды.

Вопрос 8.
Г.О.Т. Соедините Напишите и упростите два эквивалентных числовых выражения, которые показывают распределительное свойство умножения.

Ответ:

Ежедневная оценочная задача

Полностью заполните кружок, чтобы показать свой ответ.

Вопрос 9.
Книги в необычной библиотеке помечены числовыми выражениями. Катрине нужно найти книгу с числовым выражением, которое имеет значение 12. Что ей выбрать?
(А) (6 + 26) – (4 × 5)
(Б) 2 × (15 – 7)
(В) 10 + 8 – 36 ÷ 9
(Г) (25 – 4) ÷ 7
Ответ :

(6 + 26) – (4 × 5)
32 – 20
12
Книга с числовым выражением, которое имеет значение 12, равно (6 + 26) – (4 × 5).
Итак, вариант А правильный.
Пояснение:
Книги в необычной библиотеке помечены числовыми выражениями. Катрине нужно найти книгу с числовым выражением, которое имеет значение 12. Книга с числовым выражением (6 + 26) – (4 × 5). Сначала мы должны добавить 6 к 26, чтобы получить сумму 32. Затем умножить 4 на 5, чтобы получить результат 20. Затем, вычитая 20 из 32, разница составит 12. Итак, вариант А правильный.

Вопрос 10.
Франко нужно упростить 3 × (8 – 4) + 7. Каким должен быть его первый шаг?
(A) Прибавьте 7 к 4.
(B) Из 8 вычтите 4.
(C) Умножьте 3 на 7.
(D) Прибавьте 3 к 7.
Ответ:

3 × (8 – 4) + 7
3 x 4 + 7
12 + 7
19
Первый шаг – решить (8 – 4).
Итак, вариант Б правильный.
Объяснение:
Данное числовое выражение равно 3 × (8 – 4) + 7. Сначала мы должны найти значения в скобках. Вычтите 4 из 8, разница будет 4. Далее нам нужно выполнить операцию умножения. Умножьте 3 на 4, получится 12. Затем прибавьте 12 к 7, сумма будет 19..

Вопрос 11.
Многошаговый Сара упростила каждое из показанных выражений. В чем разница между значениями двух выражений?
3 × 12 – 9 + 10
3 × (12 – 9) + 10
(А) 9
(Б) 18
(В) 12
(Г) 22
Ответ:

3 × 12 – 9 + 10
36 — 9 + 10
27 + 10
37
3 × (12 — 9) + 10
3 x 3 + 10
9 + 10
19
37 — 19 =
50
37 — 19 =
59 37 — 19 =
59 37 — 19 =
59 37 — 19 =
9 значения двух выражений равны 18,
Итак, вариант Б правильный.
Объяснение:
Сара упростила каждое из заданных выражений. Первое выражение 3 × 12 – 9 + 10. Сначала Сара умножила 3 на 12, произведение равно 36. Затем она вычла 9 из 36, разница составила 27. Затем она прибавила 27 к 10, сумма составила 37. Второе выражение равно 3. × (12 – 9) + 10. Сначала Сара вычла 9 из 12, разница равна 3. Затем она умножила 3 на 3, произведение равно 9. Она прибавила 9 к 10, сумма будет 18. Вычтем 18 из 37, разница будет 18. Разница между значениями двух выражений равна 18. Значит, вариант Б правильный.

Техасская подготовка к экзаменам

Вопрос 12.
Какое выражение имеет значение 6?
(А) (6 ÷ 3) × 4 + 8
(Б) 27 – 9 ÷ 3 × (4 + 1)
(В) (18 + 12) × 6 – 4
(Г) 71 – 5 × ( 9 + 4)
Ответ:

71 – 5 × (9 + 4)
71 – 5 x (13)
71 – 65
6
Выражение, имеющее значение 6, равно 71 – 5 × (9 + 4).
Итак, вариант D правильный.
Объяснение:
Выражение, имеющее значение 6, равно 71 – 5 × (9+ 4). Сначала добавьте значения в скобках. Прибавьте 9 к 4, и сумма будет 13. Затем умножьте 5 на 13, чтобы получить 65. Затем вычтите 65 из 71, и разница составит 6. .

Вопрос 1.
10 – (2 × 4) + 12
Ответ:
Данное выражение равно 10 – (2 × 4) + 12.
10 – 8 + 12
2 + 12
14
:
Данное выражение равно 10 – (2 × 4) + 12. Сначала упростите значения в скобках. Умножьте 2 на 4, произведение равно 8. Затем вычтите 8 из 10, тогда разница будет 2. Затем добавьте 2 к 12, и сумма будет 14. Упрощенная форма данного числового выражения: 14.

Вопрос 2.
14 + 35 ÷ 7
Ответ:
Данное выражение равно 14 + 35 ÷ 7.
14 + 5
19
Объяснение:
Первое выражение равно 14 + 35 3 ÷ 5. на 7 получается 5. Затем прибавляем 5 к 14, получается 19. Упрощенная форма данного числового выражения: 19.

Вопрос 3.
11 + (31 – 4) ÷ 9
Ответ:
Данное выражение 11 + (31 – 4) ÷ 9.
11 + 27 ÷ 9
11 + 3
14
Объяснение:
Данное выражение равно 11 + (31 – 4) ÷ 9. Сначала упростите значения в скобках. Вычтите 4 из 31, разница будет 27. Затем разделите 27 на 9, результат будет 3. Затем добавьте 11 к 3, и сумма будет 14. Упрощенная форма данного числового выражения: 14.

Вопрос 4.
25 – 4 × 5
Ответ:
Данное выражение равно 25 – 4 × 5.
25 – 20
5
Объяснение:
Данное выражение равно 25 – 4 × 5. Сначала умножьте 4 на 5, произведение равно 20. Затем вычтите 20 из 25 разница равна 5. Упрощенная форма данного числового выражения равна 5.

Вопрос 5.
3 × (6 + 3) – 15
Ответ:
Данное выражение равно 3 × (6 + 3) – 15.
3 x 9 – 15
27 – 15
12
Объяснение:
Данное выражение равно 3 × (6 + 3) – 15. Сначала упростите значения в скобках. Прибавьте 6 к 3, и сумма будет 9. Затем умножьте 3 на 9, и получится 27. Вычтите 15 из 27, и разница составит 12. Упрощенная форма данного числового выражения: 12.

Вопрос 6.
30 – 14 ÷ 2
Ответ:
Данное выражение равно 30 – 14 ÷ 2.
30 – 7
23
Объяснение:
Данное выражение равно 30 – 14 ÷ 2. Сначала разделите 14 на 2, результат будет 7. Затем вычтите 7 из 30 разницы равно 23. Упрощенная форма данного числового выражения: 23.

Перепишите выражение со скобками так, чтобы оно равнялось заданному значению.

Вопрос 7.
12 + 6 ÷ 2 + 4; значение: 13
Ответ:
Данное выражение равно 12 + 6 ÷ 2 + 4.
Перепишите выражение со скобками.
12 + 6 ÷ (2 + 4)
12 + 6 ÷ 6
12 + 1
13
Объяснение:
Данное выражение 12 + 6 ÷ 2 + 4 было переписано со скобками (( + 4) равным заданному значению. Данное выражение со скобками равно заданному значению 17.

Вопрос 8.
42 – 24 ÷ 6; значение: 3
Ответ:
Данное выражение равно 42 – 24 ÷ 6.
Перепишите выражение со скобками.
(42 – 24) ÷ 6
18 ÷ 6
3
Объяснение:
Данное выражение 42 – 24 ÷ 6 было переписано со скобками (42 – 24 )÷ 6, чтобы оно равнялось заданному значению. Данное выражение со скобками равно заданному значению 17.

Вопрос 9.
9 + 16 – 2 × 4; значение: 17
Ответ:
Данное выражение равно 9 + 16 – 2 × 4.
Перепишите выражение со скобками.
9 + 16 – (2 × 4)
9 + 16 – 8
9 + 8
17
Объяснение:
Данное выражение 9+ 16 – 2 × 4 пришлось переписать со скобками 9 + 16 – (2 × 4), чтобы оно равнялось заданному значению. Данное выражение со скобками равно заданному значению 17.

Вопрос 10.
60 – 3 + 2 × 5; значение: 35
Ответ:
Данное выражение равно 60 – 3 + 2 × 5.
Перепишите выражение со скобками.
60 – (3 + 2) × 5
60 – 5 x 5
60 – 25
35
Объяснение:
Данное выражение 60 – 3 + 2 × 5 было переписано со скобками 60 – (3 + 2 ) × 5, чтобы равняться заданному значению. Данное выражение со скобками равно заданному значению 35.

Вопрос 11.
18 + 9 ÷ 3; значение: 21
Ответ:
Данное выражение равно 18 + 9 ÷ 3.
Перепишите выражение со скобками.
18 + (9 ÷ 3)
18 + 3
21
Объяснение:
Данное выражение 18 + 9 ÷ 3 пришлось переписать со скобками 18 + (9 ÷ 3), чтобы оно равнялось заданному значению. Данное выражение со скобками равно заданному значению 21.

Вопрос 12.
5 × 2 + 4 + 3; значение: 45
Ответ:
Данное выражение равно 5 × 2 + 4 + 3.
Перепишите выражение со скобками.
5 × (2 + 4 + 3)
5 x 9
45
Объяснение:
Данное выражение 5 × 2 + 4 + 3 пришлось переписать со скобками 5 × (2 + 4 + 3) так, чтобы оно равнялось данное значение. Данное выражение со скобками равно заданному значению 45.

Решение задач

Вопрос 13.
Джулиан заплатил штрафы за свою библиотеку. Он заплатил по 2 доллара за каждую просроченную книгу и 16 долларов за потерянную книгу. Напишите и упростите числовое выражение, показывающее, сколько Джулиан заплатил штрафов в библиотеке.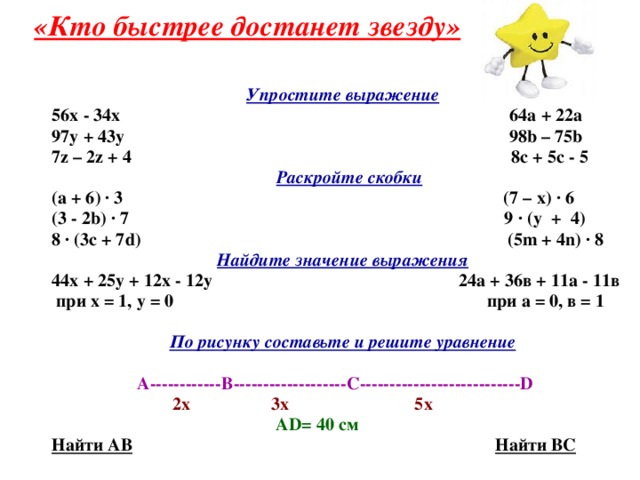
Ответ:
Ниже приведено числовое выражение.
2 x 4 + 16 долларов
8 долларов + 16 долларов
24 доллара
Джулиан заплатил 24 доллара в виде библиотечных штрафов.
Пояснение:
Джулиан заплатил штраф за свою библиотеку. Он заплатил по 2 доллара за каждую просроченную книгу и 16 долларов за потерянную книгу. Числовое выражение: $2 x 4 + $16. Упрощенная форма значения числового выражения составляет $24. Джулиан заплатил 24 доллара штрафа библиотеке.

Вопрос 14.
В течение 5 дней подряд на прошлой неделе Эддисон прочитала 9 страниц сборника стихов и 16 страниц своего любимого романа. Напишите и упростите числовое выражение, показывающее, сколько страниц прочитал Эддисон на прошлой неделе.
Ответ:
5 x (9 + 16)
5 x 25
125
На прошлой неделе Эддисон прочитал 125 страниц.
Пояснение:
В течение 5 дней подряд на прошлой неделе Эддисон прочитала 9 страниц сборника стихов и 16 страниц своего любимого романа. Числовое выражение 5 х (9 + 16). Упрощенная форма значения числового выражения — 125. На прошлой неделе Эддисон прочитал 125 страниц.

Проверка урока

Полностью заполните кружок, чтобы показать свой ответ.

Вопрос 15.
Миссис Харрисон записывает на доске числовое выражение, значение которого равно 16. Какое выражение пишет миссис Харрисон?
(А) (15 + 3) – 14 ÷ 2
(Б) 20 – 4 ÷ 2
(В) 3 × (5 + 1)
(Г) 18 + 13 – (5 × 3)
Ответ:

18 + 13 – (5 × 3)
18 + 13 – 15
31 – 15
16
Итак, вариант D правильный.
Пояснение:
Миссис Харрисон записывает на доске числовое выражение, имеющее значение 16. Миссис Харрисон записывает на доске 18 + 13 – (5 × 3) выражение. Значение этого выражения равно 16,9.0003

Вопрос 16.
Омар хочет упростить приведенное ниже выражение. Каким должен быть его первый шаг?
6 × (3 + 9) – 5
(A) Умножьте 6 на 3.
(B) Вычтите 5 из 9.
(C) Прибавьте 9 к 3.
(D) Вычтите 5 из 6.
Ответ:

6 × (3 + 9) – 5
6 x 12 – 5
72 – 5
67
Омар первый шаг – добавить 9 к 3.
Объяснение:
Омар хочет упростить выражение 6 × (3 + 9 ) – 5. Сначала Омар должен решить значения в скобках. Итак, первый шаг Омара — добавить 9к 3. Значит, вариант С правильный.

Вопрос 17.
Каково значение приведенного ниже числового выражения?
30 ÷ (3 + 2) × 8
(А) 96
(Б) 48
(В) 26
(Г) 40
Ответ:

30 ÷ (3 + 2) × 8
30 ÷ 5 х 8
6 х 8
48
Итак, вариант Б правильный.
Объяснение:
Данным числовым выражением является 30 ÷ (3 + 2) × 8. Сначала прибавьте 3 к 2, сумма будет 5. Затем разделите 30 на 5, и получится 6. Затем, после умножения 6 на 8, получится 48. Значит, вариант Б правильный.

Вопрос 18.
Бекка говорит, что когда она упрощает приведенное ниже выражение, значение на 6 меньше ее возраста. Сколько лет Бекке?
(7 + 11) – 8 ÷ 2
(А) 20
(Б) 14
(В) 26
(Г) 11
Ответ:

(7 + 11) – 8 ÷ 2
18 – 8 ÷ 2
18 – 4
14
20 – 6 = 14
Возраст Бекки 20 лет.
Итак, вариант А правильный.
Пояснение:
Бекка сказала, что когда она упрощает данное выражение (7 + 11) – 8 ÷ 2, значение на 6 меньше ее возраста. Упрощенная форма данного выражения — 14 лет. Возраст Бекки — 20 лет. Значит, вариант А верен.

Вопрос 19.
Многошаговый Калани и Портер упростили одно из приведенных ниже выражений. Если они сложит свои результаты вместе, какова будет их сумма?
Калани: 4 × 11 -5 + 12
Портер: 4 × 11 – (5 + 12)
(А) 78
(Б) 44
(В) 102
(Г) 54
Ответ:

Калани: 4 × 11 -5 + 12
44 – 5 + 12
39 + 12
51
Портер: 4 × 11 – (5 + 12)
44 – 17
27 9 9 7 7
5040455 Итак, вариант А правильный.
Объяснение:
Калани упростил данное выражение 4 × 11 -5 + 12. Значение выражения Калани равно 51. Портер упростил данное выражение 4 × 11 – (5 + 12). Значение выражения Портера равно 27. Они сложили свои результаты вместе. Прибавьте 51 к 27, и в сумме получится 78. Итак, вариант А правильный.

Вопрос 20.
Многошаговый Николь упростила приведенное ниже выражение. Затем она умножила значение выражения на 5. Чему равно произведение Николь?
36 + 6 ÷ 3 + 2
(А) 16
(Б) 80
(В) 40
(Г) 200
Ответ:

36 + 6 ÷ 3 + 2
36 + 2 + 2

5 40 90 Николь умножил значение выражения на 5.
40 x 5 = 200
Произведение Николь равно 200.
Итак, вариант D верен.
Объяснение:
Николь упростила выражение 36 + 6 ÷ 3 + 2. Значение упрощенного данного выражения равно 40. Затем она умножила значение выражения на 5. Произведение Николь равно 200. Значит, вариант D верен.

Что такое распределительная собственность: 5 эффективных примеров использования в классе

Что такое распределительная собственность ? Также известный как распределительный закон умножения, это одно из наиболее часто используемых свойств в математике.

Когда вы что-то распространяете, вы делите это на части. В математике свойство дистрибутивности помогает упростить сложные задачи, поскольку оно разбивает выражения на сумму или разность двух чисел.

В соответствии с этим принципом, умножение суммы двух слагаемых на число даст нам точно такой же результат, как и умножение каждого слагаемого по отдельности на число, а затем их сложение.

Понимание распределительного свойства
Для выражений в форме a(b+c) распределительное свойство показывает нам, как их решать:
внутри
Сложение продуктов вместе
Что насчет PEMDAS? Что случилось с первой оценкой того, что находится внутри скобок?
Если ваши ученики задаются вопросом, почему вы не следуете тому порядку операций, которому их учили в прошлом, они не ошибаются.
Однако, когда алгебраические выражения имеют круглые скобки, содержащие переменные — количество, которое может измениться в контексте математической задачи, обычно представленное одной буквой — выполнение этой операции невозможно.
Распределительное свойство умножения над сложением
Независимо от того, используете ли вы распределительное свойство или следуете порядку операций, вы получите один и тот же ответ. В первом примере ниже мы просто оцениваем выражение в соответствии с порядком операций, упрощая сначала то, что было в скобках.
Используя закон распределения, мы:
Умножаем или распределяем внешний член на внутренние члены.
Объедините похожие термины.
Решите уравнение.
Давайте используем сценарий из реальной жизни в качестве примера распределительного свойства.
Представьте, что у одной ученицы и двух ее друзей есть по семь ягод клубники и четыре клементина. Сколько всего фруктов у всех трех учеников?
В их пакетах для завтрака — или, в скобках — у каждого из них по 7 клубник и 4 клементина. Чтобы узнать общее количество кусочков фруктов, им нужно умножить все это на 3.
Разбивая его, вы умножаете 7 ягод клубники и 4 клементина на 3 учеников. Итак, у вас получится 21 клубника и 12 клементинов, всего 33 фрукта.
Распределительное свойство умножения над вычитанием
Подобно предыдущей операции, выполнение распределительного свойства с вычитанием следует тем же правилам, за исключением того, что вы находите разность вместо суммы.
Примечание : не имеет значения, плюсовая операция или минусовая. Оставьте то, что в скобках.
Распределительное свойство с переменными
Помните, что мы говорили об алгебраических выражениях и переменных? Распределительное свойство позволяет нам упростить уравнения при работе с неизвестными величинами .
Используя закон распределения с задействованными переменными, мы можем изолировать x :
Умножить или распределить внешний член на внутренние члены.
Объедините похожие термины.
Расположите термины так, чтобы константы и переменные находились по разные стороны от знака равенства.
Решите уравнение и при необходимости упростите его.
Примечание : При изоляции переменных (см. третий шаг) то, что вы делаете с одной стороной, вы должны делать и с другой. Чтобы исключить 12 с левой стороны, вы должны добавить по двенадцать и к левой, и к правой стороне. То же самое касается умножения и деления: чтобы изолировать x , разделите каждую сторону на 4.
Распределительное свойство с показателями
Показатель степени — это сокращенная запись, показывающая, сколько раз число умножается само на себя. Когда скобки и степени, использование дистрибутивного свойства может значительно упростить выражение.
Расширьте уравнение.
Умножьте (распределите) первые числа каждого набора, внешние числа каждого набора, внутренние числа каждого набора и последние числа каждого набора.
Объедините похожие термины.
Решите уравнение и при необходимости упростите его.
Примечание . На втором этапе используйте метод FOIL (первое, внешнее, внутреннее, последнее) для распределения каждого выражения.
Распределительное свойство с дробями
Решение алгебраических выражений с дробями выглядит сложнее, чем есть на самом деле. Выполните шаги, описанные ниже, чтобы увидеть, как это делается.
Надеюсь, этот пошаговый процесс поможет вашим учащимся понять, как и почему свойство дистрибутивности может пригодиться при упрощении дробей и комплексных чисел.
Определите дроби. Используя свойство распределения, вы в конечном итоге превратите их в целые числа.
Для всех дробей найдите наименьшее общее кратное (НОК) — наименьшее число, в которое могут точно вписаться оба знаменателя. Это позволит вам добавлять дроби.
Умножьте каждый член уравнения на НОК.
Изолировать переменные, добавляющие или вычитающие одинаковые термины по обе стороны от знака равенства.
Объедините похожие термины.
Решите уравнение и при необходимости упростите его.
Примечание : На шагах два и три мы находим НОК и используем его для умножения дробей, чтобы упростить их и избавиться от них. Нужна быстрая переподготовка? См. статью в нашем блоге о том, как умножать дроби.
Разнообразные свойства
Помимо распределительного свойства, существуют и другие часто используемые свойства, такие как ассоциативное свойство и коммутативное свойство.
Давайте посмотрим на ассоциативное свойство:
Ассоциативное свойство относится к группированию элементов вместе. Это правило гласит, что то, как числа (или целые числа) сгруппированы в математической задаче, не изменит результат.
Дополнительный пример:
a + (b +c) = (a + b) + c или 2 + (3 + 4) = (2 + 3) + 4
Пример умножения:
5×4×2 = ( 5 x 4) x 2 = 20 x 2 = 40
Это свойство работает с умножением, сложением, вычитанием и делением.
Различные способы изучения дистрибутивной собственности
1. Prodigy
Prodigy — это адаптивная игровая обучающая математическая платформа, которую любят более миллиона учителей и 150 миллионов учащихся по всему миру! Он предлагает материалы, соответствующие учебной программе, по всем основным математическим темам в 1–8 классах, в том числе инструкции:
Используйте распределительное свойство для расширения и решения выражений
Заполните пропущенные числа в эквивалентных выражениях, используя распределительное свойство
Использование Prodigy Math Game может помочь учащимся изучать и практиковать математику, помимо беглости фактов, и перейти на второй и третий уровни DoK . Ответив на такие вопросы, как приведенный выше, учащиеся получат массу удовольствия, пока будут практиковать распределительное свойство.
Хотите дополнить уроки математики увлекательной игровой платформой для обучения и мощными инструментами для учителей?
Зарегистрируйтесь прямо сейчас, чтобы получить бесплатную учетную запись учителя
2. Словесные задачи
Распределяющее свойство может быть неприменимым в повседневной жизни, но давайте посмотрим на это в действии через некоторые словесные задачи!
У Лиама разнообразный музыкальный вкус. Просматривая музыку на своем телефоне, друзья Лиама находят песни трех разных жанров: поп, металл и кантри. Металлических песен в шесть раз больше, чем поп-песен, и кантри-песен в 11 раз больше, чем поп-песен. Если x представляет собой количество поп-песен, сколько всего песен у Лиама на телефоне? Напишите выражение. Упрощать.
Чтобы получить количество металлических песен, умножьте количество поп-песен на пять — 5x . Чтобы получить количество кантри-песен, умножьте количество поп-песен на 11 — 11x . Поскольку вы знаете, что x — это количество поп-песен, вы можете написать выражение как:
Школьный тренер по футболу снабжает свою команду новой формой: майкой, парой шорт и щитками для голеней. Одна футболка стоит 15 долларов, пара шорт — 11 долларов, а комплект щитков — 8 долларов.
Сколько стоит форма на одного товарища по команде? Напишите выражение и упростите.
Сколько всего будет стоить, если в команде 11 игроков? Напишите выражение и упростите.
3. Массивы
Визуальные или практические манипуляции помогают учащимся разобраться в математике и конкретизировать абстрактные понятия. Они особенно полезны для углубления понимания вашими учащимися свойства распределения.
Используйте предметы, картинки, цифры — что угодно! — в строках и столбцах как полезный способ представления математических выражений, таких как 4×5 и 5×9. Взгляните на приведенный ниже пример на Indulgy:
Разбивая выражения на маленькие кусочки, учащиеся могут решать более крупные и сложные математические задачи. Вот где распределительная собственность помогает.
Если ребенок не может ответить на 45, используйте массивы меньшего размера и перепишите выражение как 4(3+2) или 4(3)+4(2). Это четыре строки по три плюс четыре строки по два , что соответствует массиву из 9.
No related posts.