Образовательная платформа московских колледжей
Модуль
«ЕН.01 Математика»
Занятие
Операции над множествами: пересечение, объединение, разность, симметрическая разность
Материалы
Контроль знаний
Операции над множествами: пересечение, объединение, разность, симметрическая разность
|
Основные математические символы |
Нет |
Часто используемые математические символы, такие как > и < |
|
Греческие буквы |
Строчные буквы |
Строчные буквы греческого алфавита |
|
Прописные буквы |
Прописные буквы греческого алфавита |
|
|
Буквоподобные символы |
Нет |
Символы, которые напоминают буквы |
|
Операторы |
Обычные бинарные операторы |
Символы, обозначающие действия над двумя числами, например + и ÷ |
|
Обычные реляционные операторы |
Символы, обозначающие отношение между двумя выражениями, такие как = и ~ |
|
|
Основные N-арные операторы |
Операторы, осуществляющие действия над несколькими переменными |
|
|
Сложные бинарные операторы |
Дополнительные символы, обозначающие действия над двумя числами |
|
|
Сложные реляционные операторы |
Дополнительные символы, обозначающие отношение между двумя выражениями |
|
|
Стрелки |
Нет |
Символы, указывающие направление |
|
Отношения с отрицанием |
Нет |
Символы, обозначающие отрицание отношения |
|
Наборы знаков |
Наборы знаков |
Математический шрифт Script |
|
Готические |
Математический шрифт Fraktur |
|
|
В два прохода |
Математический шрифт с двойным зачеркиванием |
|
|
Геометрия |
Нет |
Часто используемые геометрические символы |
Урок «Пересечение и объединение множеств»
Цели урока
:- образовательные: формирование умений выделять множества, подмножества; формирование навыков находить на изображениях область пересечения и объединения множеств и называть элементы из этой области, решать задачи;
- развивающие: развитие познавательного интереса учащихся; развитие интеллектуальной сферы личности, развитие умений сравнивать и обобщать.

- воспитательные: воспитывать аккуратность и внимательность при решении.
1. Организационный момент.
2. Учитель сообщает тему урока, совместно с учащимися формулирует цели и задачи.
3. Учитель совместно с учащимися вспоминает материал, изученный по теме «Множества» в 7 классе, вводит новые понятия и определения, формулы для решения задач.
<Приложение1.ppt>
«Множество есть многое, мыслимое нами как единое» (основатель теории множеств – Георг Кантор). КАНТОР (Cantor) Георг (1845—1918) — немецкий математик, логик, теолог, создатель теории трансфинитных (бесконечных) множеств, оказавшей определяющее влияние на развитие математических наук на рубеже 19— 20 вв.
Множество — одно из основных понятий современной математики, используемое почти во всех её разделах.
К сожалению, основному понятию теории – понятию множества – нельзя дать строгого определения. Разумеется, можно сказать, что множество – это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. однако всё это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.
Разумеется, можно сказать, что множество – это «совокупность», «собрание», «ансамбль», «коллекция», «семейство», «система», «класс» и т. д. однако всё это было бы не математическим определением, а скорее злоупотреблением словарным богатством русского языка.
Для того чтобы определить какое – либо понятие, нужно, прежде всего, указать, частным случаем какого более общего понятия, оно является, для понятия множества сделать это невозможно, потому что более общего понятия, чем множество, в математике нет.
Часто приходится говорить о нескольких вещах, объединенных некоторым признаком. Так, можно говорить о множестве всех стульев в комнате, о множестве всех клеток человеческого тела, о множестве всех картофелин в данном мешке, о множестве всех рыб в океане, о множестве всех квадратов на плоскости, о множестве всех точек на данной окружности т. д.
Предметы, составляющие данное множество, называются его элементами.
Например, множество дней недели состоит из элементов: понедельник, вторник, среда, четверг, пятница, суббота, воскресенье.
Множество месяцев – из элементов: январь, февраль, март, апрель, май, июнь, июль, август, сентябрь, октябрь, ноябрь, декабрь.
Множество арифметических действий — из элементов: сложение, вычитание, умножение, деление.
Например, если А означает множество всех натуральных чисел, то 6 принадлежит к А, а 3 не принадлежит к А.
Если А — множество всех месяцев в году, то май принадлежит к А, а среда не принадлежит к А.
Если множество содержит конечное число элементов, то его называют конечным, а если в нем бесконечно много элементов, то бесконечным. Так множество деревьев в лесу конечно, а множество точек на окружности бесконечно.
Парадокс в логике — это противоречие, имеющее статус логически корректного вывода и, вместе с тем, представляющее собой рассуждение, приводящее к взаимно исключающим заключениям.
Как уже упоминалось, понятие множества лежит в основе математики. Используя простейшие множества и различные математические конструкции, можно построить практически любой математический объект.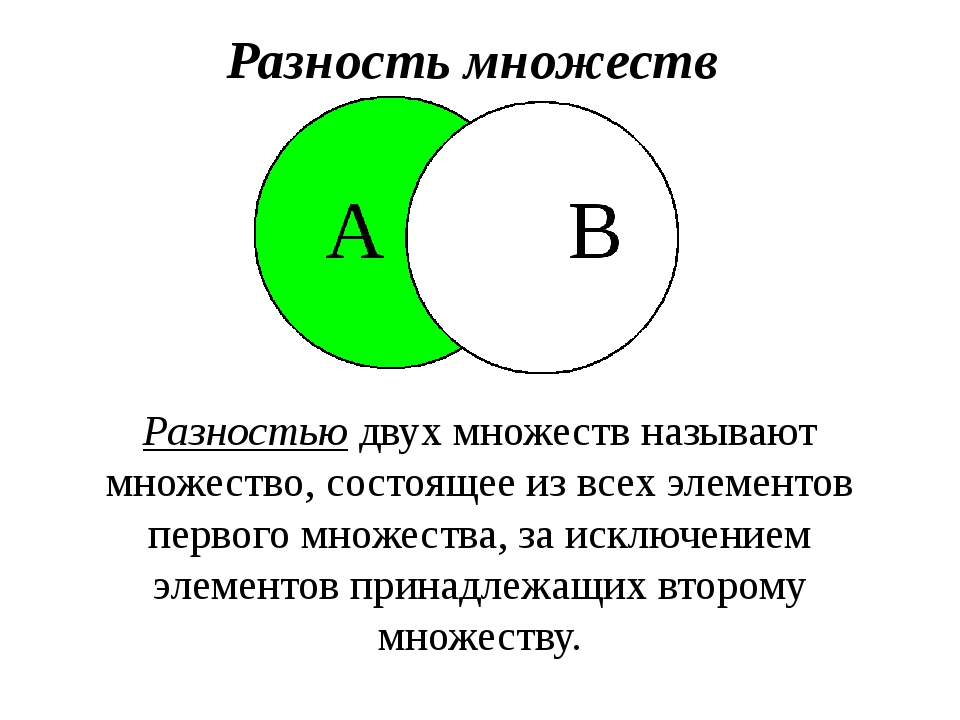 Идею построения всей математики на основе теории множеств активно пропагандировал Г.Кантор. Однако, при всей своей простоте, понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.
Идею построения всей математики на основе теории множеств активно пропагандировал Г.Кантор. Однако, при всей своей простоте, понятие множества таит в себе опасность появления противоречий или, как ещё говорят, парадоксов. Появление парадоксов связано с тем, что далеко не всякие конструкции и не всякие множества можно рассматривать.
Самый простой из парадоксов — это «парадокс брадобрея«.
Одному солдату было приказано брить тех и только тех солдат его взвода, которые сами себя не бреют. Неисполнение приказа в армии, как известно, тягчайшее преступление. Однако возник вопрос, брить ли этому солдату самого себя. Если он побреется, то его следует отнести к множеству солдат, которые сами себя бреют, а таких брить он не имеет права. Если же он себя брить не будет, то попадёт во множество солдат, которые сами себя не бреют, а таких солдат согласно приказу он обязан брить. Парадокс.
Над множествами, как и над многими другими математическими объектами, можно совершать различные операции, которые иногда называют теоретико-множественными операциями или сет-операциями.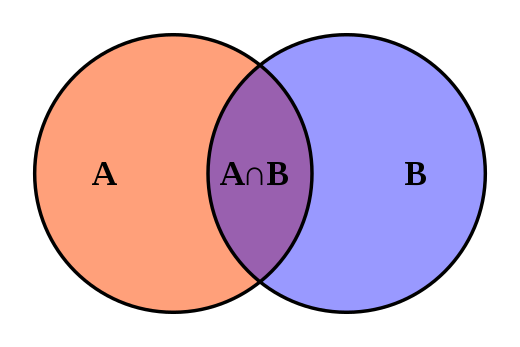
Два множества А и В называются равными ( А = В ), если они состоят из одних и тех же элементов, то есть каждый элемент множества А является элементом множества В и наоборот, каждый элемент множества В является элементом множества А .
Сравнение множеств.
Множество A содержится во множестве B (множество B включает множество A), если каждый элемент A есть элемент В:
Говорят, что множество А содержится в множестве В или множество Аявляется подмножеством множества В ( в этом случае пишут А В ), если каждый элемент множества А одновременно является элементом множества В . Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: ØА и А А
Эта зависимость между множествами называется включением. Для любого множества А имеют место включения: ØА и А А
В этом случае A называется подмножеством B, B — надмножеством A. Если , то A называется собственным подмножеством В. Заметим, что ,
По определению ,
Два множества называются равными, если они являются подмножествами друг друга
Операции над множествами
Пересечение.
Объединение.
Свойства.
1.Операция объединения множеств коммутативна
2.Операция объединения множеств транзитивна
3. Пустое множество X является нейтральным элементом операции объединения множеств
Примеры:
1. Пусть A = {1,2,3,4},B = {3,4,5,6,7}. Тогда
Пусть A = {1,2,3,4},B = {3,4,5,6,7}. Тогда
2. А={2,4,6,8,10}, В = {3,6,9,12}. Найдём объединение и пересечение этих множеств:
{2,4,6,8, 10,3,6,9,12}, = {6}.
3. Множество детей является подмножеством всего населения
4. Пересечением множества целых чисел с множеством положительных чисел является множество натуральных чисел.
5. Объединением множества рациональных чисел с множеством иррациональных чисел является множество положительных чисел.
6.Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Диаграммы Венна (Venn diagrams) — общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства; разновидностями диаграмм Венна служат: диаграммы Эйлера,
Диаграмма Венна четырёх множеств.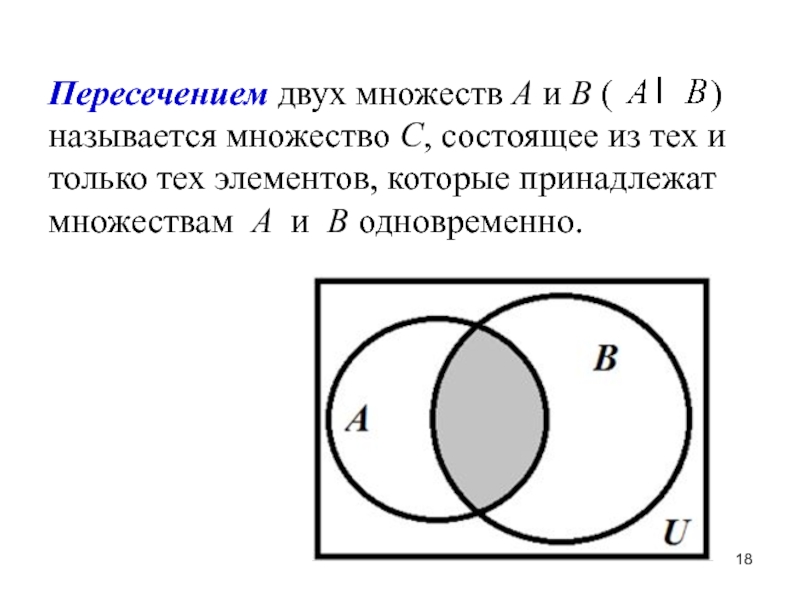
Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.
Диаграммы Эйлера
Диаграммы Эйлера аналогичны диаграммам Венна.Диаграммы Эйлера можно использовать, для того, чтобы оценивать правдоподобность теоретико-множественных тождеств.
Задача 1. В классе 30 человек, каждый из которых поёт или танцует. Известно, что поют 17 человек, а танцевать умеют 19 человек. Сколько человек поёт и танцует одновременно?
Решение: Сначала заметим, что из 30 человек не умеют петь 30 — 17 = 13 человек.
Все они умеют танцевать, т. к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.
к. по условию каждый ученик класса поёт или танцует. Всего умеют танцевать 19 человек, из них 13 не умеют петь, значит, танцевать и петь одновременно умеют 19-13 = 6 человек.
Задачи на пересечение и объединение множеств.
- Даны множества А = {3,5, 0, 11, 12, 19}, В = {2,4, 8, 12, 18,0}.
Найдите множества AU В, - Составьте не менее семи слов, буквы которых образуют подмножества множества
А -{к,а,р,у,с,е,л,ь}. - Пусть A — это множество натуральных чисел, делящихся на 2, а В — множество натуральных чисел, делящихся на 4. Какой вывод можно сделать относительно данных множеств?
- На фирме работают 67 человек. Из них 47 знают английский язык, 35 — немецкий язык, а 23 — оба языка. Сколько человек фирмы не знают ни английского, ни немецкого языков?
- Из 40 учащихся нашего класса 32 любят молоко, 21 — лимонад, а 15 — и молоко, и лимонад. Сколько ребят в нашем классе не любят ни молоко, ни лимонад?
- 12 моих одноклассников любят читать детективы, 18 -фантастику, трое с удовольствием читают и то, и другое, а один вообще ничего не читает.
 Сколько учеников в нашем классе?
Сколько учеников в нашем классе? - Из тех 18 моих одноклассников, которые любят смотреть триллеры, только 12 не прочь посмотреть и мультфильмы. Сколько моих одноклассников смотрят одни «мультики», если всего в нашем классе 25 учеников, каждый из которых любит смотреть или триллеры, или мультфильмы, или и то и другое?
- Из 29 мальчишек нашего двора только двое не занимаются спортом, а остальные посещают футбольную или теннисную секции, а то и обе. Футболом занимается 17 мальчишек, а теннисом — 19. Сколько футболистов играет в теннис? Сколько теннисистов играет в футбол?
- 65 % бабушкиных кроликов любят морковку, 10 % любят и морковку, и капусту. Сколько процентов кроликов не прочь полакомиться капустой?
- В одном классе 25 учеников. Из них 7 любят груши, 11 -черешню. Двое любят груши и черешню; 6 — груши и яблоки; 5 -яблоки и черешню. Но есть в классе два ученика, которые любят все и четверо таких, что не любят фруктов вообще.
 Сколько учеников этого класса любят яблоки?
Сколько учеников этого класса любят яблоки? - В конкурсе красоты участвовали 22 девушки. Из них 10 было красивых, 12 -умных и 9 -добрых. Только 2 девушки были и красивыми, и умными; 6 девушек были умными и одновременно добрыми. Определите, сколько было красивых и в то же время добрых девушек, если я скажу вам, что среди участниц не оказалось ни одной умной, доброй и вместе с тем красивой девушки?
- В нашем классе 35 учеников. За первую четверть пятерки по русскому языку имели 14 учеников; по математике — 12; по истории — 23. По русскому и математике — 4; по математике и истории — 9; по русскому языку и истории — 5. Сколько учеников имеют пятерки по всем трем предметам, если в классе нет ни одного ученика, не имеющего пятерки хотя бы по одному из этих предметов?
- Из 100 человек 85 знают английский язык, 80 — испанский, 75 — немецкий. Все владеют, по крайней мере, одним иностранным языком. Среди них нет таких, которые знают два иностранных языка, но есть владеющие тремя языками.
 Сколько человек из этих 100 знают три языка?
Сколько человек из этих 100 знают три языка? - Из сотрудников фирмы 16 побывали во Франции, 10 -в Италии, 6 — в Англии; в Англии и Италии — 5; в Англии и Франции — 6; во всех трех странах — 5 сотрудников. Сколько человек посетили и Италию, и Францию, если всего в фирме работают 19 человек, и каждый из них побывал хотя бы в одной из названных стран?
- Мне больше всего удалось…
- Для меня было открытием то, что …
- За что ты можешь себя похвалить?
- Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
- Мои достижения на уроке.
- Макарычев. Пункт 13. №263, №264, №265, №266, № 271, №272.
- Составить задачи на применение теории множеств.
- По группам подготовить презентации по теме « Множества».

Что такое пересечение, объединение и разность множеств?
☰
Пересечением двух множеств, называется третье множество, сформированное из элементов, которые входят в оба первых множества.
Например, если в одно множество входят числа от 1 до 10, а во второе — от 5 до 20, то пересечением этих множеств будут числа от 5 до 10, так как они входят в оба.
Пересечение множеств записывается так:
A ∩ B = {x | x ∈ A и x ∈ B}
На диаграмме Эйлера-Венна пересечение множеств обозначается общей частью кругов.
Множества могут не пересекаться вообще, одно может полностью включать другое.
Пересечение множеств может использоваться тогда, когда надо найти элементы, которые удовлетворяют нескольким условиям.
Объединением двух множеств, называется третье множество, сформированное из всех элементов обоих первых множеств. При этом если элемент входит в оба множества, то в объединенное он входит один раз. Это и понятно, так как множество по определению включает только разные элементы.
Это и понятно, так как множество по определению включает только разные элементы.
Например, объединением множества натуральных чисел от 1 до 10 и множества натуральных от 5 до 15 будет множество натуральных чисел от 1 до 15.
Объединение множеств описывается так:
A ∪ B = {x | x ∈ A или x ∈ B}
На диаграмме Эйлера-Венна объединение множеств обозначается всей областью кругов.
Разностью двух множеств, называют третье множество, в которое входят все элементы одного из двух множеств и не входят элементы принадлежащие обоим множествам.
Если результат пересечения и объединения двух множеств не меняется от перестановки множеств при выполнении операции, то результат разности зависит от того, какое множество из какого «вычитают».
Сравните. Даны множества A = {1,2,3,4,5} и B = {4,5,8,9}. Разность множеств обозначается знаком \.
A \ B = {1,2,3}, т. к. 4 и 5 входят в множество B.
В то время как B \ A = {8,9}.
Понятно, что если у множеств нет общих элементов, то их разность будет равна «уменьшаемому», т. е. первому множеству. Если же множества полностью совпадают, то их разностью будет пустое множество.
Если все элементы «вычитаемого» множества B входят в состав «уменьшаемого» A (A \ B), то B называют дополнением некого множества C до A.
Операции над множествами
Предварительные навыкиПересечение множеств
Рассмотрим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = { | Том, Фред, Макс, Джорж } |
| Друзья Майкла = { | Лео, Том, Фред, Эван } |
Видим, что Том и Фред одновременно являются друзьями Джона и Майкла.
Говоря на языке множеств, элементы Том и Фред принадлежат как множеству друзей Джона, так и множеству друзей Майкла.
Зададим новое множество с названием «Общие друзья Джона и Майкла» и в качестве элементов добавим в него Тома и Фреда:
| Общие друзья Джона и Майкла | = { Том, Фред } |
В данном случае множество «Общие друзья Джона и Майкла» является пересечением множеств друзей Джона и Майкла.
Пересечением двух (или нескольких) исходных множеств называется множество, которое состоит из элементов, принадлежащих каждому из исходных множеств.
В нашем случае элементы Том и Фред принадлежат каждому из исходных множеств, а именно: множеству друзей Джона и множеству друзей Майкла.
Обозначим множество друзей Джона через букву A, множество друзей Майкла — через букву B, а множество общих друзей Джона и Майкла обозначим через букву C:
A = { Том, Фред, Макс, Джордж }
B = { Лео, Том, Фред, Эван }
C = { Том, Фред }
Тогда пересечением множеств A и B будет множество C и записываться следующим образом:
A ∩ B = C
Символ ∩ означает пересечение.
Говоря о множестве, обычно подразумевают элементы, принадлежащие этому множеству. Символ пересечения ∩ читается, как союз И. Тогда выражение A ∩ B = C можно прочитать следующим образом:
«Элементы, принадлежащие множеству A И множеству B, есть элементы, принадлежащие множеству C».
Или еще проще:
«Друзья, одновременно принадлежащие Джону И Майклу, есть общие друзья Джона и Майкла».
Теперь представим, что у Джона и Майкла нет общих друзей. Для удобства, как и прежде обозначим множество друзей Джона через букву A, а множество друзей Майкла через букву B
A = { Макс, Джордж }
B = { Лео, Эван }
В этом случае говорят, что исходные множества не имеют общих элементов и пересечением таких множеств является пустое множество. Пустое множество обозначается символом ∅
A ∩ B = ∅
Пример 2. Рассмотрим два множества: множество A, состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
Рассмотрим два множества: множество A, состоящее из чисел 1, 2, 3, 5, 7 и множество B, состоящее из чисел 1, 2, 3, 4, 6, 12, 18
A = { 1, 2, 3, 5, 7 }
B = { 1, 2, 3, 4, 6, 12, 18 }
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
C = { 1, 2, 3 }
Множество С является пересечением множеств A и B, поскольку элементы множества C одновременно принадлежат множеству A и множеству B
Пример 3. Рассмотрим два множества: множество A, состоящее из чисел 1, 5, 7, 9 и множество B, состоящее из чисел 1, 4, 5, 7
A = { 1, 5, 7, 9 }
B = { 1, 4, 5, 7 }
Зададим новое множество C и добавим в него элементы, которые одновременно принадлежат множеству A и множеству B
C = { 1, 5, 7 }
Множество С является пересечением множеств A и B, поскольку элементы множества C одновременно принадлежат множеству A и множеству B.
Пример 4. Найти пересечение следующих множеств:
A = { 1, 2, 3, 7, 9 }
B = { 1, 3, 5, 7, 9}
С = { 3, 4, 5, 8, 9}
Пересечением множеств A, B и C будет множество, состоящее из элементов, принадлежащих каждому из множеств A, B и C. Этими элементами являются числа 3 и 9.
Зададим новое множество D и добавим в него элементы 3 и 9. Затем с помощью символа пересечения ∩ запишем, что пересечением множеств A, B и C является множество D
D = { 3, 9}
A ∩ B ∩ C = D
Чтобы найти пересечение, вовсе необязательно задавать множества с помощью букв. Если элементов мало, то множество можно задать прямым перечислением элементов.
К примеру, пусть первое множество состоит из элементов 1, 3, 5, а второе из элементов 2, 3, 5. Пересечением в данном случае является множество, состоящее из элементов 3 и 5.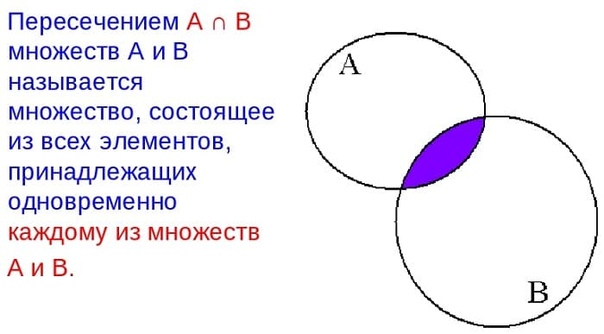 Чтобы записать пересечение, можно воспользоваться прямым перечислением:
Чтобы записать пересечение, можно воспользоваться прямым перечислением:
{ 1, 3, 5 } ∩ { 2, 3, 5 } = { 3, 5 }
Числовые промежутки, которые мы рассмотрели в предыдущих уроках, тоже являются множествами. Элементами таких множеств являются числа, входящие в числовой промежуток.
Например, отрезок [2; 6] можно понимать, как множество всех чисел от 2 до 6. Для наглядности можно перечислить все целые числа, принадлежащие данному отрезку:
2, 3, 4, 5, 6 ∈ [2; 6]
Следует иметь ввиду, что мы перечислили только целые числа. Отрезку [2; 6] также принадлежат и другие числа, не являющиеся целыми, например, десятичные дроби. Десятичные дроби располагаются между целыми числами, но их количество настолько велико, что перечислить их не представляется возможным.
Еще пример. Интервал (2; 6) можно понимать, как множество всех чисел от 2 до 6, кроме чисел 2 и 6. Ранее мы говорили, что интервал это такой числовой промежуток, границы которого не принадлежат ему. Для наглядности можно перечислить все целые числа, принадлежащие интервалу (2; 6):
3, 4, 5 ∈ (2; 6)
Поскольку числовые промежутки являются множествами, то мы можем находить пересечения между различными числовыми промежутками. Рассмотрим несколько примеров.
Рассмотрим несколько примеров.
Пример 5. Даны два числовых промежутка: [2; 6] и [4; 8]. Найти их пересечение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [2; 6] и [4; 8]:
2, 3, 4, 5, 6 ∈ [2; 6]
4, 5, 6, 7, 8 ∈ [4; 8]
Видно, что числа 4, 5, 6 принадлежат как первому промежутку [2; 6], так и второму [4; 8].
Тогда пересечением числовых промежутков [2; 6] и [4; 8] будет числовой промежуток [4; 6]
[2; 6] ∩ [4; 8] = [4; 6]
Изобразим промежутки [2; 6] и [4; 8] на координатной прямой. На верхней области отметим числовой промежуток [2; 6], на нижней — промежуток [4; 8]
Видно, что числа, принадлежащие промежутку [4; 6], принадлежат как промежутку [2; 6], так и промежутку [4; 8]. Можно также заметить, что штрихи, входящие в промежутки [2; 6] и [4; 8] пересекаются в промежутке [4; 6]. В такой ситуации, когда перед глазами есть координатная прямая, понятие пересечения множеств можно понимать в прямом смысле, что очень удобно.
Пример 6. Найти пересечение числовых промежутков [−2; 3] и [4; 7]
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие промежуткам [−2; 3] и [4; 7]:
−2, −1, 0, 1, 2, 3 ∈ [−2; 3]
4, 5, 6, 7 ∈ [4; 7]
Видно, что числовые промежутки [−2; 3] и [4; 7] не имеют общих чисел. Поэтому их пересечением будет пустое множество:
[−2; 3] ∩ [4; 7] = Ø
Если изобразить числовые промежутки [−2; 3] и [4; 7] на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Пример 7. Дано множество из одного элемента { 2 }. Найти его пересечение с промежутком (−3; 4)
Множество, состоящее из одного элемента { 2 }, на координатной прямой изображается в виде закрашенного кружка, а числовой промежуток (−3; 4) это интервал, границы которого не принадлежат ему. Значит границы −3 и 4 будут изображаться в виде пустых кружков:
Пересечением множества { 2 } и числового промежутка (−3; 4) будет множество, состоящее из одного элемента { 2 }, поскольку элемент 2 принадлежит как множеству { 2 }, так и числовому промежутку (−3; 4)
{ 2 } ∩ (−3; 4) = { 2 }
На самом деле мы уже занимались пересечением числовых промежутков, когда решали системы линейных неравенств. Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
Вспомните, как мы решали их. Сначала находили множество решений первого неравенства, затем множество решений второго. Затем находили множество решений, которые удовлетворяют обоим неравенствам.
По сути, множество решений, удовлетворяющих обоим неравенствам, является пересечением множеств решений первого и второго неравенства. Роль этих множеств берут на себя числовые промежутки.
Например, чтобы решить систему неравенств , мы должны сначала найти множества решений каждого неравенства, затем найти пересечение этих множеств.
В данном примере решением первого неравенства x ≥ 3 является множество всех чисел, которые больше 3 (включая само число 3). Иначе говоря, решением неравенства является числовой промежуток [3; +∞)
Решением второго неравенства x ≤ 6 является множество всех чисел, которые меньше 6 (включая само число 6). Иначе говоря, решением неравенства является числовой промежуток (−∞; 6]
А общим решением системы будет пересечение множеств решений первого и второго неравенства, то есть пересечение числовых промежутков [3; +∞) и (−∞; 6]
Если мы изобразим множество решений системы на координатной прямой, то увидим, что эти решения принадлежат промежутку [3; 6], который в свою очередь является пересечением промежутков [3; +∞) и (−∞; 6]
[3; +∞) ∩ (−∞; 6] = [3; 6]
Поэтому в качестве ответа мы указывали, что значения переменной x принадлежат числовому промежутку [3; 6], то есть пересечению множеств решений первого и второго неравенства
x ∈ [3; 6]
Пример 2. Решить неравенство
Решить неравенство
Все неравенства, входящие в систему уже решены. Нужно только указать те решения, которые являются общими для всех неравенств.
Решением первого неравенства является числовой промежуток (−∞; −1).
Решением второго неравенства является числовой промежуток (−∞; −5).
Решением третьего неравенства является числовой промежуток (−∞; 4).
Решением системы будет пересечение числовых промежутков (−∞; −1), (−∞; −5) и (−∞; 4). В данном случае этим пересечением является промежуток (−∞; −5).
(−∞; −1) ∩ (−∞; −5) ∩ (−∞; 4) = (−∞; −5)
На рисунке представлены числовые промежутки и неравенства, которыми эти числовые промежутки заданы. Видно, что числа, принадлежащие промежутку (−∞; −5), одновременно принадлежат всем исходным промежуткам.
Запишем ответ к системе с помощью числового промежутка:
x ∈ (−∞; −5)
Пример 3. Решить неравенство
Решением первого неравенства y > 7 является числовой промежуток (7; +∞).
Решением второго неравенства y < 4 является числовой промежуток (−∞; 4).
Решением системы будет пересечение числовых промежутков (7; +∞) и (−∞; 4).
В данном случае пересечением числовых промежутков (7; +∞) и (−∞; 4) является пустое множество, поскольку эти числовые промежутки не имеют общих элементов:
(7; +∞) ∩ (−∞; 4) = ∅
Если изобразить числовые промежутки (7; +∞) и (−∞; 4) на координатной прямой, то можно увидеть, что они нигде не пересекаются:
Объединение множеств
Объединением двух (или нескольких) исходных множеств называют множество, которое состоит из элементов, принадлежащих хотя бы одному из исходных множеств.
На практике объединение множеств состоит из всех элементов, принадлежащих исходным множествам. Поэтому и говорят, что элементы такого множества принадлежат хотя бы одному из исходных множеств.
Рассмотрим множество A с элементами 1, 2, 3 и множество B с элементами 4, 5, 6.
A = { 1, 2, 3 }
B = { 4, 5, 6 }
Зададим новое множество C и добавим в него все элементы множества A и все элементы множества B
C = { 1, 2, 3, 4, 5, 6 }
В данном случае объединением множеств A и B является множество C и обозначается следующим образом:
A ∪ B = C
Символ ∪ означает объединение и заменяет собой союз ИЛИ. Тогда выражение A ∪ B = C можно прочитать так:
Элементы, принадлежащие множеству A ИЛИ множеству B, есть элементы, принадлежащие множеству C.
В определении объединения сказано, что элементы такого множества принадлежат хотя бы одному из исходных множеств. Данную фразу можно понимать в прямом смысле.
Вернёмся к созданному нами множеству C, куда входят все элементы множеств A и B. Возьмём для примера из этого множества элемент 5. Что можно про него сказать?
Если 5 является элементом множества C, а множество С является объединением множеств A и B, то можно с уверенностью заявить, что элемент 5 принадлежит хотя бы одному из множеств A и B. Так оно и есть:
A = { 1, 2, 3 }
B = { 4, 5, 6 }
C = { 1, 2, 3, 4, 5, 6 }
Возьмем ещё один элемент из множества С, например, элемент 2. Что можно про него сказать?
Если 2 является элементом множества C, а множество С является объединением множеств A и B, то можно с уверенностью заявить, что элемент 2 принадлежит хотя бы одному из множеств A и B. Так оно и есть:
A = {1, 2, 3}
B = {4, 5, 6}
C = { 1, 2, 3, 4, 5, 6 }
Если мы захотим объединить два или более множества и вдруг обнаружим, что один или несколько элементов принадлежат каждому из этих множеств, то в объединение повторяющиеся элементы будут входить только один раз.
Например, рассмотрим множество A с элементами 1, 2, 3, 4 и множество B с элементами 2, 4, 5, 6.
A = {1, 2, 3, 4}
B = {2, 4, 5, 6}
Видим, что элементы 2 и 4 одновременно принадлежат и множеству A, и множеству B. Если мы захотим объединить множества A и B, то новое множество C будет содержать элементы 2 и 4 только один раз. Выглядеть это будет так:
C = { 1, 2, 3, 4, 5, 6 }
Чтобы при объединении не допустить ошибок, обычно поступают так: сначала в новое множество добавляют все элементы первого множества, затем добавляют элементы второго множества, которые не принадлежат первому множеству. Попробуем сделать такое объединение с множествами A и B.
Итак, у нас имеются следующие исходные множества:
A = { 1, 2, 3, 4 }
B = { 2, 4, 5, 6 }
Зададим новое множество С и добавим в него все элементы множества A
C = { 1, 2, 3, 4,
Теперь добавим элементы из множества B, которые не принадлежат множеству A. Множеству A не принадлежат элементы 5 и 6. Их и добавим во множество C
C = { 1, 2, 3, 4, 5, 6 }
Пример 2. Друзьями Джона являются Том, Фред, Макс и Джордж. А друзьями Майкла являются Лео, Том, Фред и Эван. Найти объединение множеств друзей Джона и Майкла.
Для начала зададим два множества: множество друзей Джона и множество друзей Майкла.
| Друзья Джона = { | Том, Фред, Макс, Джорж } |
| Друзья Майкла = { | Лео, Том, Фред, Эван } |
Зададим новое множество с названием «Все друзья Джона и Майкла» и добавим в него всех друзей Джона и Майкла.
Заметим, что Том и Фред одновременно являются друзьями Джона и Майкла, поэтому мы добавим их в новое множество только один раз, поскольку сразу двух Томов и двух Фредов не бывает.
| Все друзья Джона и Майкла | = { Том, Фред, Макс, Джордж, Лео, Эван } |
В данном случае множество всех друзей Джона и Майкла является объединением множеств друзей Джона и Майкла.
Друзья Джона ∪ Друзья Майкла = Все друзья Джона и Майкла
Пример 3. Даны два числовых промежутка: [−7; 0] и [−3; 5]. Найти их объединение.
Оба промежутка обрамлены квадратными скобками, значит их границы принадлежат им.
Для наглядности перечислим все целые числа, принадлежащие этим промежуткам:
−7, −6, −5, −4, −3,−2, −1, 0 ∈ [−7; 0]
−3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−3; 5]
Объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5], который содержит все числа промежутка [−7; 0] и [−3; 5] без повторов некоторых из чисел
−7, −6, −5, −4, −3,−2, −1, 0, 1, 2, 3, 4, 5 ∈ [−7; 5]
Обратите внимание, что числа −3,−2, −1 принадлежали и первому промежутку и второму. Но поскольку в объединение допускается включать такие элементы только один раз, мы включили их единоразово.
Значит объединением числовых промежутков [−7; 0] и [−3; 5] будет числовой промежуток [−7; 5]
[−7; 0] ∪ [−3; 5] = [−7; 5]
Изобразим на координатной прямой промежутки [−7; 0] и [−3; 5]. На верхней области отметим числовой промежуток [−7; 0], на нижней — промежуток [−3; 5]
Ранее мы выяснили, что промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5]. Здесь полезно вспомнить про определение объединения множеств, которое было приведено в самом начале. Объединение трактуется, как множество, состоящее из всех элементов, принадлежащих хотя бы одному из исходных множеств.
Действительно, если взять любое число из промежутка [−7; 5], то окажется, что оно принадлежит хотя бы одному из промежутков: либо промежутку [−7; 0] либо промежутку [−3; 5].
Возьмём из промежутка [−7; 5] любое число, например число 2. Поскольку промежуток [−7; 5] является объединением промежутков [−7; 0] и [−3; 5], то число 2 будет принадлежать хотя бы одному из этих промежутков. В данном случае число 2 принадлежит промежутку [−3; 5]
Возьмём ещё какое-нибудь число. Например, число −4. Это число будет принадлежать хотя бы одному из промежутков: [−7; 0] или [−3; 5]. В данном случае оно принадлежит промежутку [−7; 0]
Возьмём ещё какое-нибудь число. Например, число −2. Оно принадлежит как промежутку [−7; 0], так и промежутку [−3; 5]. Но на координатной прямой оно указывается только один раз, поскольку в одной точке сразу два числа −2 не бывает.
Не каждое объединение числовых промежутков является числовым промежутком. Например, попробуем найти объединение числовых промежутков [−2; −1] и [4; 7].
Идея остаётся та же самая — объединением числовых промежутков [−2;−1] и [4; 7] будет множество, состоящее из элементов, принадлежащих хотя бы одному из промежутков: [−2; −1] или [4; 7]. Но это множество не будет являться числовым промежутком. Для наглядности перечислим все целые числа, принадлежащие этому объединению:
[−2; −1] ∪ [4; 7] = { −2, −1, 4, 5, 6, 7 }
Получили множество { −2, −1, 4, 5, 6, 7 }. Это множество не является числовым промежутком по причине того, что числа, располагающиеся между −1 и 4, не вошли в полученное множество
Числовой промежуток должен содержать все числа от левой границы до правой. Если одно из чисел отсутствует, то числовой промежуток теряет смысл. Допустим, имеется линейка длиной 15 см
Эта линейка является числовым промежутком [0; 15], поскольку содержит все числа в промежутке от 0 до 15 включительно. Теперь представим, что на линейке после числа 9 сразу следует число 12.
Эта линейка не является линейкой в 15 см, и её нежелательно использовать для измерения. Также, её нельзя назвать числовым промежутком [0; 15], поскольку она не содержит все числа, которые должна была содержать.
Решение неравенств, содержащих знак ≠
Некоторые неравенства содержат знак ≠ (не равно). Например, 2x ≠ 8. Чтобы решить такое неравенство, нужно найти множество значений переменной x, при которых левая часть не равна правой части.
Решим неравенство 2x ≠ 8. Разделим обе части данного неравенства на 2, тогда получим:
Получили равносильное неравенство x ≠ 4. Решением этого неравенства является множество всех чисел, не равных 4. То есть если мы подставим в неравенство x ≠ 4 любое число, которое не равно 4, то получим верное неравенство.
Подставим, например, число 5
5 ≠ 4 — верное неравенство, поскольку 5 не равно 4
Подставим 7
7 ≠ 4 — верное неравенство, поскольку 7 не равно 4
И поскольку неравенство x ≠ 4 равносильно исходному неравенству 2x ≠ 8, то решения неравенства x ≠ 4 будут подходить и к неравенству 2x ≠ 8. Подставим те же тестовые значения 5 и 7 в неравенство 2x ≠ 8.
2 × 5 ≠ 8
2 × 7 ≠ 8
Изобразим множество решений неравенства x ≠ 4 на координатной прямой. Для этого выколем точку 4 на координатной прямой, а всю оставшуюся область с обеих сторон выделим штрихами:
Теперь запишем ответ в виде числового промежутка. Для этого воспользуемся объединением множеств. Любое число, являющееся решением неравенства 2x ≠ 8 будет принадлежать либо промежутку (−∞; 4) либо промежутку (4; +∞). Так и записываем, что значения переменной x принадлежат (−∞; 4) или (4; +∞). Напомним, что для слова «или» используется символ ∪
x ∈ (−∞; 4) ∪ (4; +∞)
В этом выражении говорится, что значения, принимаемые переменной x, принадлежат промежутку (−∞; 4) или промежутку (4; +∞).
Неравенства, содержащие знак ≠, также можно решать, как обычные уравнения. Для этого знак ≠ заменяют на знак =. Тогда получится обычное уравнение. В конце решения найденное значение переменной x нужно исключить из множества решений.
Решим предыдущее неравенство 2x ≠ 8, как обычное уравнение. Заменим знак ≠ на знак равенства =, получим уравнение 2x = 8. Разделим обе части данного уравнения на 2, получим x = 4.
Видим, что при x, равном 4, уравнение обращается в верное числовое равенство. При других значениях равенства соблюдаться не будет. Эти другие значения нас и интересуют. А для этого достаточно исключить найденную четвёрку из множества решений.
Пример 2. Решить неравенство 3x − 5 ≠ 1 − 2x
Перенесем −2x из правой части в левую часть, изменив знак, а −5 из левой части перенесём в правую часть, опять же изменив знак:
Приведем подобные слагаемые в обеих частях:
Разделим обе части получившегося неравенства на 5
Решением неравенства x ≠ 1,2 является множество всех чисел, не равных 1,2.
Изобразим множество решений неравенства x ≠ 1,2 на координатной прямой и запишем ответ в виде числового промежутка:
x ∈ (−∞; 1,2) ∪ (1,2; +∞)
В этом выражении говорится, что значения, принимаемые переменной x принадлежат промежутку (−∞; 1,2) или промежутку (1,2; +∞)
Решение совокупностей неравенств
Рассмотрим ещё один вид неравенств, который называется совокупностью неравенств. Такой тип неравенств, возможно, вы будете решать редко, но для общего развития полезно изучить и их.
Совокупность неравенств очень похожа на систему неравенств. Различие в том, что в системе неравенств нужно найти множество решений, удовлетворяющих каждому неравенству, образующему эту систему.
А в случае с совокупностью неравенств, нужно найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность.
Совокупность неравенств обозначается квадратной скобкой. Например, следующая запись из двух неравенств является совокупностью:
Решим данную совокупность. Сначала нужно решить каждое неравенство по отдельности.
Решением первого неравенства x ≥ 3 является числовой промежуток [3; +∞). Решением второго неравенства x ≤ 6 является числовой промежуток (−∞; 6].
Множество значений x, при которых верно хотя бы одно из неравенств, будет принадлежать промежутку [3; +∞) или промежутку (−∞; 6]. Так и записываем:
x ∈ [3; +∞) ∪ (−∞; 6]
В этом выражении говорится, что переменная x, входящая в
совокупность принимает все значения, принадлежащие промежутку [3; +∞) или промежутку (−∞; 6]. А это то, что нам нужно. Ведь решить совокупность означает найти множество решений, удовлетворяющих хотя бы одному неравенству, образующему эту совокупность. А любое число из промежутка [3; +∞) или промежутка (−∞; 6] будет удовлетворять хотя бы одному неравенству.
Например, число 9 из промежутка [3; +∞) удовлетворяет первому неравенству x ≥ 3. А число −7 из промежутка (−∞; 6] удовлетворяет второму неравенству x ≤ 6.
Посмотрите внимательно на выражение x ∈ [3; +∞) ∪ (−∞; 6], а именно на его правую часть. Ведь выражение [3; +∞) ∪ (−∞; 6] представляет собой объединение числовых промежутков [3; +∞) и (−∞; 6]. Точнее, объединение множеств решений первого и второго неравенства.
Стало быть, решением совокупности неравенств является объединение множеств решений первого и второго неравенства.
Иначе говоря, решением совокупности будет объединение числовых промежутков [3; +∞) и (−∞; 6]
Объединением числовых промежутков [3; +∞) и (−∞; 6] является промежуток (−∞; +∞). Точнее, объединением числовых промежутков [3; +∞) и (−∞; 6] является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
[3; +∞) ∪ (−∞; 6] = (−∞; +∞)
Ответ можно оставить таким, каким мы его записали ранее:
x ∈ [3; +∞) ∪ (−∞; 6]
либо заменить на более короткий:
x ∈ (−∞; +∞)
Возьмём любое число из полученного объединения, и проверим удовлетворяет ли оно хотя бы одному неравенству.
Возьмем для примера число 8. Оно удовлетворяет первому неравенству x ≥ 3.
8 ≥ 3
Возьмем еще какое-нибудь число, например, число 1. Оно удовлетворяет второму неравенству x ≤ 6
1 ≤ 6
Возьмем еще какое-нибудь число, например, число 5. Оно удовлетворяет и первому неравенству x ≥ 3 и второму x ≤ 6
Пример 2. Решить совокупность неравенств
Чтобы решить эту совокупность, нужно найти множество решений, которые удовлетворяют хотя бы одному неравенству, образующему эту совокупность.
Для начала найдём множество решений первого неравенства x < −0,25. Этим множеством является числовой промежуток (−∞; −0,25).
Множеством решений второго неравенства x ≥ −7 является числовой промежуток [−7; +∞).
Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.
x ∈ (−∞; −0,25) ∪ [−7; +∞)
Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −0,25) и [−7; +∞)
Объединением числовых промежутков (−∞; −0,25) и [−7; +∞) является является вся координатная прямая. А вся координатная прямая это все числа, которые только могут быть
(−∞; −0,25) ∪ [−7; +∞) = (−∞; +∞)
Ответ можно оставить таким, каким мы его записали ранее:
x ∈ (−∞; −0,25) ∪ [−7; +∞)
либо заменить на более короткий:
x ∈ (−∞; +∞)
Пример 3. Решить совокупность неравенств
Решим каждое неравенство по отдельности:
Множеством решений первого неравенства x < −3 является числовой промежуток (−∞; −3).
Множеством решений второго неравенства x ≤ 0 является числовой промежуток (−∞; 0].
Решением совокупности неравенств будет объединение множеств решений первого и второго неравенства.
x ∈ (−∞; −3) ∪ (−∞; 0]
Иначе говоря, решением совокупности будет объединение числовых промежутков (−∞; −3) и (−∞; 0]
Объединением числовых промежутков (−∞; −3) и (−∞; 0] является числовой промежуток (−∞; 0]
(−∞; −3) ∪ (−∞; 0] = (−∞; 0]
Ответ можно оставить таким, каким мы его записали ранее:
x ∈ (−∞; −3) ∪ (−∞; 0]
либо заменить на более короткий:
x ∈ (−∞; 0]
Задания для самостоятельного решения
Задание 1. Найдите пересечение и объединение следующих множеств:
А = { 1, 2, 5 }
B = { 3, 4, 5 }
Решение:
A ∩ B = { 5 }
A ∪ B = { 1, 2, 3, 4, 5 }
Задание 2. Найдите пересечение и объединение следующих множеств:
А = { −3, −2, −1, 0, 1, 2 }
B = { 1, 2, 3, 4, 5 }
Решение:
A ∩ B = { 1, 2 }
A ∪ B = { −3, −2, −1, 0, 1, 2, 3, 4, 5 }
Задание 3. Найдите пересечение и объединение следующих множеств:
А = { 1, 2, 3 }
B = { 3, 4 }
Решение:
A ∩ B = { 3 }
A ∪ B = { 1, 2, 3, 4 }
Задание 4. Найдите пересечение и объединение следующих числовых промежутков:
[−2; 7) и (0; 10]
Решение:
[−2; 7) ∩ (0; 10] = (0; 7)
[−2; 7) ∪ (0; 10] = [−2; 10]
Задание 5. Найдите пересечение и объединение следующих числовых промежутков:
(−∞; 3] и [−2; 1)
Решение:
(−∞; 3] ∩ [−2; 1) = [−2; 1)
(−∞; 3] ∪ [−2; 1) = (−∞; 3]
Задание 6. Найдите пересечение и объединение следующих числовых промежутков:
(3; +∞) и [2; +∞)
Решение:
(3; +∞) ∩ [2; +∞) = (3; +∞)
(3; +∞) ∪ [2; +∞) = [2; +∞)
Задание 7. Найдите пересечение и объединение следующих числовых промежутков:
[−3; −1] и (−2; 4]
Решение:
[−3; −1] ∩ (−2; 4] = (−2; −1]
[−3; −1] ∪ (−2; 4] = [−3; 4]
Задание 8. Решите неравенство:
Задание 9. Решите неравенство:
Задание 10. Решите совокупность неравенств:
Задание 11. Решите совокупность неравенств:
Задание 12. Решите совокупность неравенств:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Дискретная математика. Множества. Теория графов. Виды, типы, свойства, отношения, операции. / / Множества. Свойства и операции над ними. Объединение, пересечение, разность, симметричная разность и дополнение множеств. Свойства множеств относительное операций. Закон де Моргана. Законы поглощения, операции с множествами. Поделиться:
| |||||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator | |||||||
ЛШСМ-2019: В.А.Клепцын
ЛШСМ-2019: В.А.КлепцынСуммы и пересечения динамически определённых канторовых множеств
В. А. Клепцын планирует провести 4 занятия.
Доступны 4 видеозаписи курса.
Простейшее канторово множество K строится так: берём отрезок [0,1], выкидываем из него (открытую) среднюю треть, из каждого из двух получившихся отрезков по средней трети, и так далее. Получается множество очень «дырявое», но тем не менее равномощное [0,1]. А вот сумма такого множества с самим собой оказывается уже опять «толстой» — это отрезок [0,2] (докажите!). Поэтому пересечение K со сдвигами (a-K) непусто при всех a∈[0,2]; а это весьма удивительно: два дырявых множества пересекаются так, что малым шевелением «расцепить» их не получается.
А что будет, если взять чуть-чуть другие канторовы множества: как будет вести себя их сумма? Легко ли разрушить их пересечение?
Такие вопросы возникают в теории динамических систем, где канторовы множества возникают из множества «скатывающихся» или «набегающих» на инвариантное множество траекторий, а неразрушимость их пересечения нужна для некоторых важных примеров. Возникают они и на границе теории операторов и математической физики. В довольно естественном классе задач с разделяющимся потенциалом, спектр оказывается суммой «одномерных» спектров — и зачастую это именно сумма канторовых множеств. Можно вспомнить и теорию чисел — где такие вопросы оказываются связанными с описанием возможных приближений действительных чисел рациональными (более точно, со спектрами Лагранжа и Маркова). Наконец, часть вопросов формулируется настролько просто и естественно, что интересна сама по себе.
Оказывается, эффекты при сложении канторовых множеств бывают разные — и далеко не все из естественных гипотез, описывающих поведение таких сумм, уже доказаны.
Предварительных знаний не требуется — курс предполагается доступным школьникам.
План курса
- Динамически определённые канторовы множества на прямой. Их характеристики: хаусдорфова размерность и густота (тау-параметр).
- Суммы и устойчивые пересечения в простейшем случае: лемма Ньюхауса.
- Связь с теорией чисел: цепные дроби, F(4)+F(4) и спектры Лагранжа и Маркова.
- Обзор известного и неизвестного: гипотезы и теоремы.
- Применение в динамических системах: подкова Смейла и область Ньюхауса.
- Метрическая и топологическая типичность, гипотеза Палиса и теорема Пьера Берже.
пересечение | Math Goodies
В предыдущих уроках мы использовали диаграммы Венна для представления отношений между множествами. Давайте посмотрим на взаимосвязь наборов, описанных в примере 1 ниже.
Пример 1: Пусть X = {1, 2, 3} и пусть Y = {3, 4, 5}. Что общего у X и Y ?
Анализ: Нарисуем диаграмму Венна из двух перекрывающихся кругов. Элементы, общие для обоих наборов, будут размещены в средней части, где круги перекрываются.
Решение:
Пояснение: Круг слева представляет набор X , а круг справа представляет набор Y . Заштрихованная область посередине — это то, что у них общего. Это их пересечение. Пересечение наборов X и Y равно 3.
Диаграмма Венна в примере 1 позволяет легко увидеть, что число 3 является общим для обоих наборов. Таким образом, пересечение X и Y равно 3, и это записывается как:
X ∩ Y = {3}
| Определение: | Пересечение двух наборов, X и Y, — это набор элементов, общих для X и Y .Он обозначается как X ∩ Y, и читается как « X пересекает Y ». |
Таким образом, пересечение двух наборов — это набор элементов, общих для обоих наборов. Давайте рассмотрим еще несколько примеров пересечения.
Пример 2: Пусть = {подсчет чисел}, P = {число, кратное 3 меньше 20} и Q = {четные числа меньше 20}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать пересечение P и Q .
Анализ: Начните с заполнения элементов на пересечении. Поскольку P = {3, 6, 9, 12, 15, 18} и Q = {2, 4, 6, 8, 10, 12, 14, 16, 18}, мы знаем, что 6, 12 и 18 будут заполнены первыми.
Решение:
Обозначение: P ∩ Q = {6, 12, 18}
Другой способ определить пересечение двух множеств:
A ∩ B = {x | x A и x B }
Процедура построения пересечения двух множеств показана ниже.
Процедура построения пересечения двух наборов перекрывающихся наборов
Шаг 1:
Шаг 2:
Шаг 3:
Давайте посмотрим на пересечение других типов множеств. В примере 3 ниже, данные наборы не перекрываются.
Пример 3: Пусть = {животные}, A = {собаки} и B = {кошки}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать пересечение A и B .
Анализ: наборы A и B не перекрываются. Эти множества не пересекаются и не имеют общих элементов.
Решение:
Обозначение: A ∩ B = Ø
Два набора A и B не пересекаются, если их пересечение равно нулю. Это обозначается как A ∩ B = Ø , , где Ø — это нулевой или пустой набор .
Напомним, что универсальный набор — это набор всех рассматриваемых элементов, обозначенных заглавной буквой.Все остальные множества являются подмножествами универсального множества. Итак, в каждом приведенном выше примере кружки являются подмножествами универсального набора. Мы исследовали пересечение перекрывающихся множеств и непересекающихся множеств. Давайте посмотрим на пересечение одного набора, содержащегося в другом.
Пример 4: Пусть C = {a, r, e} и D = {f, a, i, r, e, s, t}. Нарисуйте и обозначьте диаграмму Венна, чтобы показать пересечение множеств C и D.
Анализ: C — это подмножество D. Напомним, что это обозначается C D.
Решение:
Пояснение: Оказывается, C ∩ D = {a, r, e}, что равно множеству C.
В примере 4, поскольку C D , получаем, что C ∩ 902 925 Эти отношения определены ниже.
Процедура рисования пересечения одного набора, содержащегося в другом, показана ниже.
| Процедура построения пересечения одного набора, содержащегося в другом | |
| Шаг 1: | Нарисуйте один круг внутри другого. |
| Шаг 2: | Запишите элементы внутреннего круга. |
| Шаг 3: | Запишите оставшиеся элементы внешнего круга. |
Давайте посмотрим, сможете ли вы выполнить задачу, представленную в примере 5.
Пример 5: Учитывая приведенную ниже диаграмму Венна, назовите участника Band, который не входит в Band и Chorus одновременно.
Анализ: Эта проблема просит нас найти участника Band, который не находится на пересечении Band и Chorus.
Решение:
Пояснение: Сэм, Лорри и Рауль являются членами только группы. Кроме того, эти студенты не участвуют в оркестре и хоре.
Резюме: Пересечение двух множеств A и B, обозначенное A ∩ B, является набором элементов, общих как для A, так и для B.Формальное определение пересечения показано ниже.
A ∩ B = { x | x A и x B }
Упражнения
Указания: нарисуйте и обозначьте диаграмму Венна, чтобы помочь вам ответить на каждый из приведенных ниже вопросов. Выберите свой ответ, нажав соответствующую кнопку. Отзыв на ваш ответ представлен в БЛОКЕ РЕЗУЛЬТАТОВ. Если вы допустили ошибку, переосмыслите свой ответ, а затем выберите другую кнопку.
| 1. | Учитывая = {яблоки, апельсины, бананы, груши} и = {апельсины, груши, виноград}, что будет ∩ ? |
| 2. | Учитывая = {четные целые числа} и = {простые числа}, что будет ∩ ? |
| 3. | Учитывая = {13, 21, 34, 55, 89} и = {однозначные цифры}, что будет ∩ ? |
| 4. | Учитывая = {суббота, воскресенье} и = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}, что такое ? |
| C ∩ D = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье} C ∩ D = {понедельник, вторник, среда, четверг, пятница} C ∩ D = {суббота, воскресенье} Все выше. БЛОК РЕЗУЛЬТАТОВ: |
| 5. | Учитывая приведенную ниже диаграмму Венна, что из следующего является элементом , а не элементом ( ∩ )? |
| | |
Пересечение наборов
Литература к занятию 5 — (продолжение)
Пересечение наборов
Перед продолжая читать эту сессию, вы можете просмотреть математические определения слов и и или , которые будут рассмотрены позже в этом сеансе.
Перекресток : Установленная операция перекресток принимает только элементы, которые есть в обоих наборах. Пересечение содержит элементы, которые два набора есть общее. В пересечение — это место, где два набора пересекаются.
В обозначении конструктора наборов: A ∩ B = { x ∈ U : х ∈ A и х ∈ B }.
Диаграмма Венна для A ∩ B показан справа где заштрихованная область представляет набор A ∩ Б. |
Пример: Позволять A = { a,
b, c, d } и B = { b,
д, д} .потом А ∩ В = { b,
d }.
Элементы b и d — единственные
элементы, которые есть в обоих наборах A и Б .
Пример: Позволять G = { т, a, n } и H = { n, a, t }.потом G ∩ H = { a, n, т }. Обратите внимание, что здесь G = H = G ∩ H .
Пример: Позволять C = {2, 6, 10, 14,…} и D = {2, 4, 6, 8, …}. Тогда C ∩ D = {2, 6, 10, 14,…} = С .
Пример: Почему место, где улица и перекресток проспекта, называемый перекресток ? Местоположение содержится как в улице, так и в проспект.
Пример: Позволять E = { d, a, y } и F = { n, i, g, h, t }. Тогда E ∩ F = ∅.
Примечание: Во всех примерах пересечение — это подмножество каждого множества, образующего пересечение, то есть A ∩ В ⊆ A и А ∩ В ⊆ Б.
Непересекающиеся множества: Два набора, чьи пересечение пустое множество называются непересекающихся множеств .
Пример: Позволять E = { d, a, y } и F = { n, i, g, h, t }. С E ∩ F = ∅ множества E и F — непересекающиеся множества.
Возврат
на домашнюю страницу Пейля | Миннесота
Государственный университет Мурхед | Математика
Отдел
4.3: Объединения и пересечения — Математика LibreTexts
Мы можем сформировать новый набор из существующих наборов, выполнив операцию над наборами.
Мы хотели бы напомнить читателям, что авторы нередко принимают разные обозначения для одного и того же математического понятия.Точно так же одни и те же обозначения могут означать что-то другое в другом учебнике или даже в другом разделе математики. Когда вы начинаете читать математическое изложение, важно выработать привычку изучать контекст и убедиться, что вы понимаете значение обозначений.
практическое упражнение \ (\ PageIndex {1} \ label {he: unionint-01} \)
Пусть \ ({\ cal U} = \ {\ mbox {Джон}, \ mbox {Мэри}, \ mbox {Дэйв}, \ mbox {Люси}, \ mbox {Питер}, \ mbox {Ларри} \} \ ), \ [A = \ {\ mbox {John}, \ mbox {Mary}, \ mbox {Dave} \}, \ qquad \ mbox {и} \ qquad B = \ {\ mbox {John}, \ mbox { Ларри}, \ mbox {Люси} \}.\] Найдите \ (A \ cap B \), \ (A \ cup B \), \ (AB \), \ (BA \), \ (\ overline {A} \) и \ (\ overline {B } \).
Пример \ (\ PageIndex {5} \ label {например: unionint-05} \)
Теперь мы можем описать следующий набор \ [\ {x \ in \ mathbb {R} \ mid (x <5) \ vee (x> 7) \} \] в обозначении интервалов. Его можно записать как \ ((- \ infty, 5) \ cup (7, \ infty) \) или, используя дополнение, \ (\ mathbb {R} — [5,7 \,] \). Следовательно, сказать \ (x \ notin [5,7 \,] \) — это то же самое, что сказать \ (x \ in (- \ infty, 5) \ cup (7, \ infty) \) или, что то же самое, \ ( х \ в \ mathbb {R} — [5,7 \,] \).- \)
(е) \ ((4,5) \ cap \ mathbb {Z} \)
- Ответ
(а) \ (\ {- 4, -3, -2, -1,0,1,2,3,4 \} \)
(б) \ (\ {- 3, -2, -1,0,1,2,3,4 \} \)
(с) \ (\ {- 3, -2, -1,0,1,2,3, \ ldots \} \)
Упражнение \ (\ PageIndex {2} \ label {ex: unionint-02} \)
Предположим, \ ({\ cal U} = \ mathbb {Z} \), и пусть
\ (A = \ {\ ldots, -6, -4, -2,0,2,4,6, \ ldots \} = 2 \ mathbb {Z}, \)
\ (B = \ {\ ldots, -9, -6, -3,0,3,6,9, \ ldots \} = 3 \ mathbb {Z}, \)
\ (C = \ {\ ldots, -12, -8, -4,0,4,8,12, \ ldots \} = 4 \ mathbb {Z}.\)
Опишите следующие наборы, явно перечислив их элементы.
(a) \ (A \ cap B \)
(б) \ (C-A \)
(в) \ (A-B \)
(г) \ (A \ cap \ overline {B} \)
(e) \ (B-A \)
(ж) \ (В \ чашка С \)
(г) \ ((A \ чашка B) \ крышка C \)
(h) \ ((A \ чашка B) -C \)
Упражнение \ (\ PageIndex {3} \ label {ex: unionint-03} \)
Верны эти утверждения или нет?
(а) \ ([1,2] \ cap [2,3] = \ emptyset \)
(б) \ ([1,2) \ чашка (2,3] = [2,3] \)
- Ответ
(а) ложь (б) ложь
Упражнение \ (\ PageIndex {4} \ label {ex: unionint-04} \)
Пусть универсальный набор \ ({\ cal U} \) будет набором людей, проголосовавших в U 2012.С. Президентские выборы. Определите подмножества \ (D \), \ (B \) и \ (W \) из \ ({\ cal U} \) следующим образом: \ [\ begin {align} D & = & \ {x \ in {\ cal U} \ mid x \ mbox {зарегистрирован как демократ} \}, \\ B & = & \ {x \ in {\ cal U} \ mid x \ mbox {проголосовал за Барака Обаму} \}, \ \ W & = & \ {x \ in {\ cal U} \ mid x \ mbox {принадлежал к объединению} \}. \ end {align} \] Выразите следующие подмножества \ ({\ cal U} \) через \ (D \), \ (B \) и \ (W \).
(а) Люди, которые не голосовали за Барака Обаму.
(б) Члены Союза, проголосовавшие за Барака Обаму.
(c) Зарегистрированные демократы, голосовавшие за Барака Обаму, но не принадлежавшие ни к какому союзу.
(d) Члены профсоюзов, которые либо не были зарегистрированы как демократы, либо голосовали за Барака Обаму.
(e) Люди, которые голосовали за Барака Обаму, но не были зарегистрированы как демократы и не были членами профсоюзов.
(е) Люди, которые либо были зарегистрированы как демократы и были членами профсоюзов, либо не голосовали за Барака Обаму.
Упражнение \ (\ PageIndex {5} \ label {ex: unionint-05} \)
Страховая компания классифицирует свою группу \ ({\ cal U} \) держателей полисов по следующим группам: \ [\ begin {align} A & = & \ {x \ mid x \ mbox {управляет малолитражным автомобилем} \ }, \\ B & = & \ {x \ mid x \ mbox {водит машину старше 5 лет} \}, \\ C & = & \ {x \ mid x \ mbox {женат} \}, \ \ D & = & \ {x \ mid x \ mbox {старше 21 года} \}, \\ E & = & \ {x \ mid x \ mbox {- мужчина} \}.\ end {align} \] Опишите каждое из следующих подмножеств \ ({\ cal U} \) в терминах \ (A \), \ (B \), \ (C \), \ (D \), и \ (E \).
(a) Страхователи-мужчины старше 21 года.
(b) Страхователи, являющиеся женщинами или водителями автомобилей старше 5 лет.
(c) Женщины-полисы старше 21 года, которые водят малолитражные автомобили.
(d) Страхователи-мужчины, состоящие в браке или старше 21 года, не водящие малолитражные автомобили.
- Ответ
(а) \ (E \ cap D \) (b) \ (\ overline {E} \ cup B \)
Упражнение \ (\ PageIndex {6} \ label {ex: unionint-06} \)
Пусть \ (A \) и \ (B \) — произвольные множества.Выполните следующие утверждения.
(a) \ (A \ substeq B \ Leftrightarrow A \ cap B = \) ___________________
(b) \ (A \ substeq B \ Leftrightarrow A \ cup B = \) ___________________
(c) \ (A \ substeq B \ Leftrightarrow A — B = \) ___________________
(d) \ (A \ subset B \ Leftrightarrow (A-B = \) ___________________ \ (\ wedge \, B-A \ neq \) ___________________ \ () \)
(e) \ (A \ subset B \ Leftrightarrow (A \ cap B = \) ___________________ \ (\ wedge \, A \ cap B \ neq \) ___________________ \ () \)
(f) \ (A — B = B — A \ Leftrightarrow \) ___________________
Упражнение \ (\ PageIndex {7} \ label {ex: unionint-07} \)
Приведите примеры множеств \ (A \) и \ (B \) таких, что \ (A \ in B \) и \ (A \ subset B \).
- Ответ
Например, возьмите \ (A = \ {x \} \) и \ (B = \ {\ {x \}, x \} \).
Упражнение \ (\ PageIndex {8} \ label {ex: unionint-08} \)
(а) Докажите закон Де Моргана, (а).
(b) Докажите закон Де Моргана, (b).
Упражнение \ (\ PageIndex {9} \ label {ex: unionint-09} \)
Пусть \ (A \), \ (B \) и \ (C \) — любые три множества. Докажите, что если \ (A \ substeq C \) и \ (B \ substeq C \), то \ (A \ cup B \ substeq C \).
- Ответ
Предположим, \ (A \ substeq C \) и \ (B \ substeq C \), мы хотим показать, что \ (A \ cup B \ substeq C \).
Пусть \ (x \ in A \ cup B \). мы также хотим показать, что \ (x \ in C \).
Поскольку \ (x \ in A \ cup B \), то либо \ (x \ in A \), либо \ (x \ in B \) по определению объединения.
Случай 1: Если \ (x \ in A \), то \ (A \ substeq C \) влечет, что \ (x \ in C \) по определению подмножества.
Случай 2: Если \ (x \ in B \), то \ (B \ substeq C \) влечет, что \ (x \ in C \) по определению подмножества.
В обоих случаях находим \ (x \ in C \). Итак, если \ (x \ in A \ cup B \), то \ (x \ in C \).
Это доказывает, что \ (A \ cup B \ substeq C \) по определению подмножества.
\ (\ следовательно \) Для любых множеств \ (A \), \ (B \) и \ (C \), если \ (A \ substeq C \) и \ (B \ substeq C \), то \ ( A \ чашка B \ substeq C \).
Упражнение \ (\ PageIndex {10} \ label {ex: unionint-10} \)
Докажите теорему 4.3.1
Упражнение \ (\ PageIndex {11} \ label {ex: unionint-11} \)
(a) Докажите теорему 4.3.2 часть (а)
(b) Докажите теорему 4.3.2 часть (b)
Упражнение \ (\ PageIndex {12} \ label {ex: unionint-12} \)
Пусть \ (A \), \ (B \) и \ (C \) — любые три множества. Докажите, что
(a) \ (A-B = A \ cap \ overline {B} \)
(b) \ (A = (A-B) \ чашка (A \ cap B) \)
(c) \ (A- (B-C) = A \ cap (\ overline {B} \ cup C) \)
(г) \ ((A-B) -C = A- (B \ чашка C) \)
Упражнение \ (\ PageIndex {13} \ label {ex: unionint-13} \)
Прокомментируйте следующие утверждения.Правильны ли они синтаксически?
(a) \ (x \ in A \ cap x \ in B \ Equiv x \ in A \ cap B \)
(b) \ (x \ in A \ клин B \ Rightarrow x \ in A \ cap B \)
- Ответ
(a) Обозначение \ (\ cap \) используется для соединения двух наборов, но «\ (x \ in A \)» и «\ (x \ in B \)» являются логическими утверждениями. Мы также должны использовать \ (\ Leftrightarrow \) вместо \ (\ Equiv \). Заявление должно было быть записано как «\ (x \ in A \, \ wedge \, x \ in B \ Leftrightarrow x \ in A \ cap B \).”
(b) Если мы прочитаем это вслух, это звучит идеально: \ [\ mbox {Если $ x $ принадлежит $ A $ и $ B $, то $ x $ принадлежит $ A \ cap B $}. \] Проблема в том, что каждое обозначение имеет собственное значение и конкретное использование. В этом случае \ (\ wedge \) не совсем замена английского слова «и». Вместо этого это обозначение соединения двух логических утверждений для образования соединения. Перед \ (\ wedge \) у нас есть «\ (x \ in A \)», что является логическим утверждением. Но после \ (\ wedge \) у нас есть «\ (B \)», который является набором, а не логическим утверждением.Он должен быть записан как «\ (x \ in A \, \ wedge \, x \ in B \ Rightarrow x \ in A \ cap B \)».
Упражнение \ (\ PageIndex {14} \ label {ex: unionint-14} \)
Докажите или опровергните каждое из следующих утверждений о произвольных наборах \ (A \) и \ (B \). Если вы думаете, что утверждение верно, докажите его; если вы считаете, что это ложь, приведите контрпример.
(а) \ (\ mathscr {P} (A \ cap B) = \ mathscr {P} (A) \ cap \ mathscr {P} (B) \)
(б) \ (\ mathscr {P} (A \ cup B) = \ mathscr {P} (A) \ cup \ mathscr {P} (B) \)
(c) \ (\ mathscr {P} (A — B) = \ mathscr {P} (A) — \ mathscr {P} (B) \)
- Замечание
Чтобы показать, что два множества \ (U \) и \ (V \) равны, мы обычно хотим доказать, что \ (U \ substeq V \) и \ (V \ substeq U \).Для отношения подмножества мы начинаем с let \ (x \ in U \). В этой задаче элемент \ (x \) на самом деле является множеством. Поскольку мы обычно используем прописные буквы для обозначения множеств, для (а) мы должны начать доказательство отношения подмножеств «Пусть \ (S \ in \ mathscr {P} (A \ cap B) \)», используя заглавную букву для подчеркните, что элементы \ (\ mathscr {P} (A \ cap B) \) являются наборами. Эти замечания также относятся к (b) и (c).
Упражнение \ (\ PageIndex {15} \)
Пусть \ ({\ cal U} = \ {1,2,3,4,5,6,7,8 \} \), \ (A = \ {2,4,6,8 \} \), \ (B = \ {3,5 \} \), \ (C = \ {1,2,3,4 \} \) и \ (D = \ {6,8 \} \).Найдите
(a) \ (A \ cap C \) (b) \ (A \ cap B \) (c) \ (\ emptyset \ cup B \)
(d) \ (\ emptyset \ cap B \) (e) \ (A- (B \ cup C) \) (f) \ (C-B \)
(g) \ (A \ bigtriangleup C \) (h) \ (A \ cup {\ cal U} \) (i) \ (A \ cap D \)
(j) \ (A \ чашка D \) (k) \ (B \ cap D \) (l) \ (B \ bigtriangleup C \)
(м) \ (A \ cap {\ cal U} \) (n) \ (\ overline {A} \) (o) \ (\ overline {B} \).
(p) \ (D \ cup (B \ cap C) \) (q) \ (\ overline {A \ cup C} \) (r) \ (\ overline {A} \ cup \ overline {C} \ )
(s) Какие пары множеств не пересекаются?
- Ответ
(a) \ (\ {2,4 \} \) (b) \ (\ emptyset \) (c) \ (B \) (d) \ (\ emptyset \)
Упражнение \ (\ PageIndex {16} \)
Доказательство:
Если \ (A \ substeq B \), то \ (A-B = \ emptyset.\)
Союз, пересечение и дополнение | Математика для гуманитарных наук
Обычно наборы взаимодействуют. Например, вы и ваш новый сосед по комнате решили устроить домашнюю вечеринку, и вы оба приглашаете свой круг друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Союз, пересечение и дополнение
Объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах).
Штуцер обозначен A ⋃ B.
Более формально, x ∊ A ⋃ B , если x ∊ A или x ∊ B (или оба)
Пересечение двух наборов содержит только элементы, которые есть в обоих наборах.
Перекресток обозначен A ⋂ B.
Более формально, x ∊ A ⋂ B , если x ∊ A и x ∊ B
Дополнение набора A содержит все, что равно , а не в наборе A .
Дополнение обозначается как A ’, или Ac , или иногда ~ A .
Пример 5
Рассмотрим наборы: A = {красный, зеленый, синий} B = {красный, желтый, оранжевый}
C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый}
a) Найдите A ⋃ B
Объединение содержит все элементы в любом наборе: A ⋃ B = {красный, зеленый, синий, желтый, оранжевый}
Обратите внимание, мы указываем красный только один раз.
б) Найдите A ⋂ B
Пересечение содержит все элементы в обоих наборах: A ⋂ B = {красный}
c) Найдите Ac ⋂ C
Здесь мы ищем все элементы, которые являются , а не в наборе A , а также находятся в C .
Ac ⋂ C = {оранжевый, желтый, фиолетовый}
Попробовать 2
Используя наборы из предыдущего примера, найдите A ⋃ C и Bc ⋂ A
Обратите внимание, что в приведенном выше примере было бы сложно просто попросить Ac , поскольку все, от цвета фуксии до щенков и арахисового масла, включено в комплект.По этой причине дополнения обычно используются только на перекрестках или когда у нас есть универсальный набор.
Универсальный набор
Универсальный набор — это набор, который содержит все интересующие нас элементы. Это должно быть определено контекстом.
Дополнение относится к универсальному набору, поэтому Ac содержит все элементы универсального набора, которых нет в A .
Пример 6
а) Если бы мы обсуждали поиск книг, универсальный набор мог бы включать все книги в библиотеке.
b) Если бы мы группировали ваших друзей на Facebook, универсальный набор был бы всеми вашими друзьями на Facebook.
c) Если вы работали с наборами чисел, универсальный набор мог бы состоять из целых чисел, всех целых чисел или всех действительных чисел
Пример 7
Предположим, что универсальным набором является U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то
Ac = {3, 5, 6, 7, 8, 9}.
Как мы видели ранее с выражением Ac ⋂ C , операции над множествами могут быть сгруппированы вместе.Символы группировки можно использовать так же, как и в арифметике, — для задания порядка операций.
Пример 8
Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик}
W = {утка, кролик, олень, лягушка, мышь}
a) Найдите ( H ⋂ F ) ⋃ W
Начинаем с пересечения: H ⋂ F = {собака, кролик}
Теперь мы объединяем этот результат с W : ( H ⋂ F ) ⋃ W = {собака, утка, кролик, олень, лягушка, мышь}
b) Найдите H ⋂ ( F ⋃ W )
Начинаем с союза: F ⋃ W = {собака, корова, кролик, утка, свинья, олень, лягушка, мышь}
Теперь мы пересекаем этот результат с H : H ⋂ ( F ⋃ W ) = {собака, кролик, мышь}
c) Найти ( H ⋂ F ) c ⋂ W
Начинаем с пересечения: H ⋂ F = {собака, кролик}
Теперь мы хотим найти элементы W , которые равны , а не в H ⋂ F
( H ⋂ F ) c ⋂ W = {утка, олень, лягушка, мышь}
Установить операции | Союз | Пересечение | Дополнение | Разница | Взаимоисключающие | Перегородки | Закон Де Моргана | Распределительный закон
1.2.2 Настройка операций
Объединение двух наборов — это набор, содержащий все элементы, которые находятся в $ A $ или в $ B $ (возможно, оба). Например, $ \ {1,2 \} \ cup \ {2,3 \} = \ {1,2,3 \} $. Таким образом, мы можем написать $ x \ in (A \ cup B) $ тогда и только тогда, когда $ (x \ in A) $ или $ (x \ in B) $. Обратите внимание, что $ A \ cup B = B \ cup A $. На рисунке 1.4, объединение множеств $ A $ и $ B $ показано заштрихованной областью на диаграмме Венна.
Рис.1.4 — Заштрихованная область показывает набор $ B \ cup A $.{n} A_i. $$ Например, если $ A_1 = \ {a, b, c \}, A_2 = \ {c, h \}, A_3 = \ {a, d \} $, то $ \ bigcup_ {i} A_i = A_1 \ cup A_2 \ cup A_3 = \ {a, b, c, h, d \} $. Аналогичным образом мы можем определить объединение бесконечного множества множеств $ A_1 \ чашка A_2 \ чашка A_3 \ чашка \ cdots $.Пересечение двух множеств $ A $ и $ B $, обозначенное $ A \ cap B $, состоит из всех элементов которые оба находятся в $ A $ $ \ underline {\ textrm {и}} $ $ B $. Например, $ \ {1,2 \} \ cap \ {2,3 \} = \ {2 \} $. На рисунке 1.5 пересечение множеств $ A $ и $ B $ показано заштрихованной областью с использованием диаграммы Венна.c $.
Рис.1.8 — Заштрихованная область показывает набор $ A-B $.Два набора $ A $ и $ B $ являются взаимоисключающими или непересекающимися , если у них нет общего элементы; т.е. их пересечение — это пустое множество, $ A \ cap B = \ emptyset $. В общем, несколько наборов называются непересекающимися, если они попарно не пересекаются, т. е. никакие два из них не имеют общих элементов. На рис. 1.9 показаны три непересекающихся множества.
Рис.1.9 — Множества $ A, B, $ и $ C $ не пересекаются.Если нашим образцом является земная поверхность, мы могли бы разделить ее на разные континенты. Точно так же страна может быть разделена на разные провинции. В общем, набор непустых множества $ A_1, A_2, \ cdots $ — это разбиение множества $ A $, если они не пересекаются и их объединение равно $ A $. c = \ {3,4,5,6 \} \ cap \ {1,3,6 \} = \ {3,6 \}.$
A Декартово произведение двух наборов $ A $ и $ B $, записанное как $ A \ times B $, представляет собой набор, содержащий упорядоченных пары из $ A $ и $ B $. То есть, если $ C = A \ times B $, то каждый элемент $ C $ имеет форму $ (x, y) $, где $ x \ in A $ и $ y \ in B $: $$ A \ times B = \ {(x, y) | x \ in A \ textrm {и} y \ in B \}.$$ Например, если $ A = \ {1,2,3 \} $ и $ B = \ {H, T \} $, то $$ A \ times B = \ {(1, H), (1, T), (2, H), (2, T), (3, H), (3, T) \}. $$ Обратите внимание, что здесь пары упорядочены, например, $ (1, H) \ neq (H, 1) $. Таким образом, $ A \ times B $ — это , а не . то же, что и $ B \ times A $.
Если у вас есть два конечных множества $ A $ и $ B $, где $ A $ содержит $ M $ элементов, а $ B $ — $ N $ элементов, то $ A \ times B $ имеет $ M \ times N $ элементов. Это правило называется принципом умножения и очень полезно при подсчете количество элементов в наборах.Количество элементов в наборе обозначается $ | A | $, поэтому здесь мы пишем $ | A | = M, | B | = N $ и $ | A \ times B | = MN $. В приведенном выше примере $ | A | = 3, | B | = 2 $, поэтому $ | A \ times B | = 3 \ times 2 = 6 $. Аналогичным образом мы можем определить декартово произведение $ n $ множеств $ A_1, A_2, \ cdots, A_n $ как $$ A_1 \ times A_2 \ times A_3 \ times \ cdots \ times A_n = \ {(x_1, x_2, \ cdots, x_n) | x_1 \ в A_1 \ textrm {и} x_2 \ in A_2 \ textrm {и} \ cdots x_n \ in A_n \}. $$ Принцип умножения утверждает, что для конечных множеств $ A_1, A_2, \ cdots, A_n $, если $$ | A_1 | = M_1, | A_2 | = M_2, \ cdots, | A_n | = M_n, $$ затем $$ \ mid A_1 \ times A_2 \ times A_3 \ times \ cdots \ times A_n \ mid = M_1 \ times M_2 \ раз M_3 \ раз \ cdots \ times M_n.3 = \ mathbb {R} \ times \ mathbb {R} \ times \ mathbb {R} $ и так далее.
Пересечение в математике: определение и символ
Пересечение линий
Давайте посмотрим, как это работает с линиями. Когда у вас есть две линии в математике, которые пересекаются друг с другом, у вас будет точка или точки, в которых они встречаются.
Эта встреча линий — это то, что мы называем пересечением двух линий.У нас может быть несколько разных сценариев пересечения линий. Давайте рассмотрим их один за другим.
1. Две разные прямые, которые не параллельны друг другу, будут иметь только одну точку пересечения. Если линии разные и не параллельны, они в конечном итоге пересекут друг друга. Они пересекутся друг с другом только один раз, ровно в одной точке. Когда линии нанесены на координатную плоскость, вы можете указать точку, задав координату точки пересечения.
2. Две параллельные линии никогда не пересекаются и не имеют точки пересечения. Подумай об этом. Что значит быть параллельным? Это значит, что две линии никогда не встретятся, верно? Да, и если это так, они никогда не пересекутся.
3. Две одинаковые прямые параллельны друг другу и пересекаются во всех точках на прямой.Две одинаковые линии лежат друг на друге и имеют одинаковые точки. Можно сказать, что их пересечение — это сама линия. В этом случае существует более одной точки пересечения. Две линии на самом деле имеют бесконечное количество точек пересечения, потому что линии продолжаются бесконечно.
Пересечение множеств
В математике есть еще одна область, где есть пересечение, и это когда мы имеем дело с наборами или группами элементов. Набор в математике — это группа предметов.Это может быть группа чисел, переменных или что-нибудь еще, о чем вы можете подумать. Когда две или более группы имеют общий элемент или элементы, то подмножество общих элементов является тем, что мы называем пересечением множеств.
Например, у нас есть два разных набора чисел. Набор A имеет номера {2, 4, 6, 8}, а набор B — {6, 8, 10, 12}. Есть ли у этих двух наборов что-нибудь общее? Да, это так. Оба набора имеют 6 и 8. Итак, набор A и набор B пересекаются {6, 8}, потому что эти элементы — то, что у них общего.
Символ пересечения для множеств
Для пересечения множеств у нас есть специальный символ. Этот символ выглядит как перевернутая буква U, как показано в этом примере задачи.
Этот уникальный символ используется с наборами, но не с линиями. Для пересекающихся линий не используется никакого символа.
Краткое содержание урока
Точка или точки, в которых встречаются два объекта, называются их пересечением.Две прямые могут иметь одну точку пересечения, отсутствие пересечения или бесконечное количество точек пересечения. Пересечение наборов включает в себя поиск общих элементов. Если у наборов нет ничего общего, значит, у них нет пересечения. Если все наборы имеют общий элемент или элементы, то набор этих общих элементов является пересечением этих наборов.
Пересечение в математике Обзор
| Термины | Пояснения |
|---|---|
| Перекресток | место встречи двух вещей |
| 2 линии не параллельны | имеют один перекресток |
| 2 параллельные линии | никогда не будет перекрестка |
| Наборы | группа элементов, таких как числа, переменные или что-нибудь еще, что вы можете придумать; общее подмножество элементов — это то, что мы называем пересечением наборов |
Результаты обучения
Оцените свою способность выполнять следующие действия после завершения урока, приведенного выше:
- Распознавать пересечение по математике
- Определите пересечение линий и пересечение множеств
- Нарисуйте символ пересечения множеств
Союз, пересечение и дополнение | Математика для гуманитарных наук
Результаты обучения
- Опишите членство наборов, включая пустой набор, используя правильную нотацию, и решите, являются ли данные элементы членами, и определите количество элементов данного набора.
- Опишите отношения между множествами относительно членства, равенства, подмножества и надлежащего подмножества, используя правильную нотацию.
- Выполнять операции объединения, пересечения, дополнения и разности на множествах, используя правильную нотацию.
- Уметь рисовать и интерпретировать диаграммы Венна отношений и операций множества и использовать диаграммы Венна для решения проблем.
- Узнавать, когда теория множеств применима к ситуациям реальной жизни, решать реальные проблемы и сообщать другим о реальных проблемах и решениях.
Обычно наборы взаимодействуют друг с другом. Например, вы и ваш новый сосед по комнате решили устроить домашнюю вечеринку, и вы оба приглашаете свой круг друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Союз, пересечение и дополнение
Объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах). Объединение имеет обозначение A ⋃ B. Более формально x ∊ A ⋃ B , если x ∈ A или x ∈ B (или оба)
Пересечение двух наборов содержит только элементы, которые есть в обоих наборах.Пересечение обозначено как A ⋂ B. Более формально x ∈ A ⋂ B , если x ∈ A и x ∈ B.
Дополнение набора A содержит все, что равно , а не в наборе A . Дополнение обозначается как A ’, или A, c , или иногда ~ A .
Универсальный набор — это набор, в который входят все интересующие нас элементы.Это должно определяться контекстом.
Дополнение относительно универсального набора, поэтому A c содержит все элементы универсального набора, которых нет в A .
Пример
- Если бы мы обсуждали поиск книг, универсальный набор мог бы включать все книги в библиотеке.
- Если бы мы группировали ваших друзей на Facebook, универсальный набор состоял бы из всех ваших друзей на Facebook.
- Если вы работали с наборами чисел, универсальный набор мог бы состоять из целых чисел, всех целых чисел или всех действительных чисел
Пример
Предположим, что универсальным набором является U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то A c = {3, 5, 6, 7, 8, 9}.
Пример
Рассмотрим комплектов:
A = {красный, зеленый, синий}
B = {красный, желтый, оранжевый}
C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый}
Найдите следующее:
- Найти A ⋃ B
- Найти A ⋂ B
- Найти A c ⋂ C
- Объединение содержит все элементы в любом наборе: A ⋃ B = {красный, зеленый, синий, желтый, оранжевый} Обратите внимание, что мы перечисляем красный только один раз.
- Пересечение содержит все элементы в обоих наборах: A ⋂ B = {красный}
- Здесь мы ищем все элементы, которые являются , а не в наборе A , а также находятся в C . A c ⋂ C = {оранжевый, желтый, фиолетовый}
Обратите внимание, что в приведенном выше примере было бы сложно просто попросить A c , так как все, от цвета фуксии до щенков и арахисового масла, входит в комплект.По этой причине дополнения обычно используются только на перекрестках или когда у нас есть универсальный набор.
Как мы видели ранее с выражением A c ⋂ C , операции над множествами могут быть сгруппированы вместе. Символы группировки можно использовать так же, как и в арифметике, — для задания порядка операций.
Пример
Предположим, что H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик} и W = {утка, кролик, олень, лягушка, мышь}
- Найти ( H ⋂ F ) ⋃ W
- Найдите H ⋂ ( F ⋃ W )
- Найти ( H ⋂ F ) c ⋂ W
- Начнем с перекрестка: H ⋂ F = {собака, кролик}.Теперь объединим полученный результат с W : ( H ⋂ F ) ⋃ W = {собака, утка, кролик, олень, лягушка, мышь}
- Начнем с объединения: F ⋃ W = {собака, корова, кролик, утка, свинья, олень, лягушка, мышь}. Теперь мы пересекаем этот результат с H : H ⋂ ( F ⋃ W ) = {собака, кролик, мышь}
- Начинаем с пересечения: H ⋂ F = {собака, кролик}. Теперь мы хотим найти элементы W , которые равны , а не в H ⋂ F. ( H, ⋂ F) c ⋂ W = {утка, олень, лягушка, мышь}
Диаграммы Венна
Чтобы визуализировать взаимодействие множеств, Джон Венн в 1880 году подумал об использовании перекрывающихся кругов, опираясь на аналогичную идею, которую использовал Леонард Эйлер в 18 веке. Эти иллюстрации теперь называются Диаграммы Венна .
Диаграмма Венна
Диаграмма Венна представляет каждый набор в виде круга, обычно рисуемого внутри контейнера, представляющего универсальный набор.Перекрывающиеся области указывают на элементы, общие для обоих наборов.
Базовые диаграммы Венна могут иллюстрировать взаимодействие двух или трех наборов.
Пример
Создайте диаграммы Венна для иллюстрации A ⋃ B , A ⋂ B и Ac ⋂ B
A ⋃ B содержит все элементы из набора или .
Показать решениеA ⋂ B содержит только те элементы в обоих наборах — в перекрытии кругов.
Ac будет содержать все элементы , а не в наборе A. A c ⋂ B будет содержать элементы в наборе B , которых нет в наборе A .
Пример
Используйте диаграмму Венна для иллюстрации ( H ⋂ F ) c ⋂ W
Начнем с идентификации всего в наборе H ⋂ F
Теперь ( H ⋂ F ) c ⋂ W будет содержать все , а не в указанном выше наборе, который также находится в наборе W .

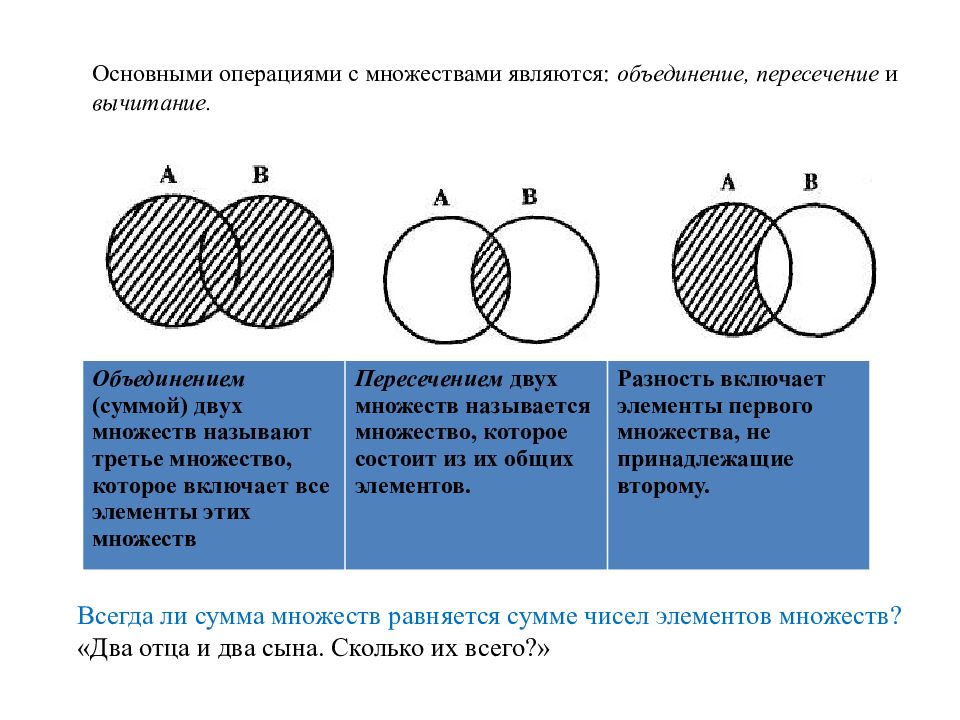
 Сколько учеников в нашем классе?
Сколько учеников в нашем классе? Сколько учеников этого класса любят яблоки?
Сколько учеников этого класса любят яблоки?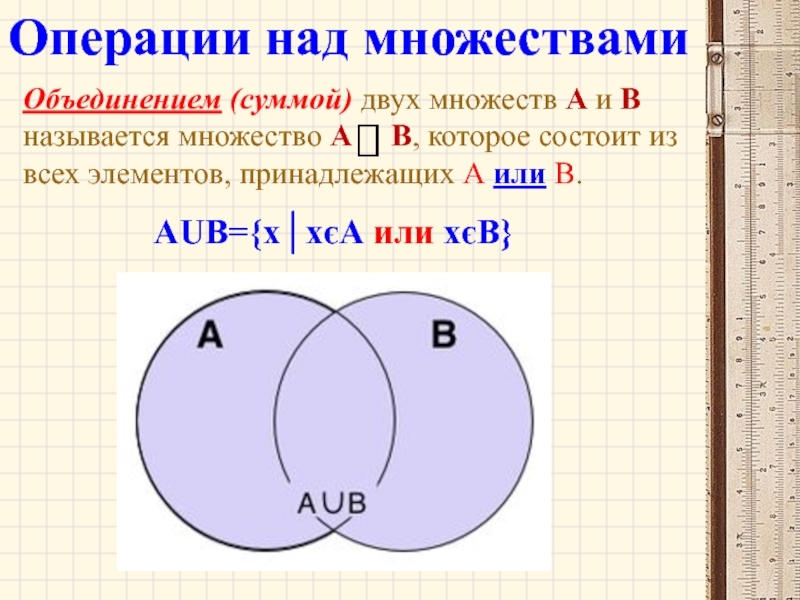 Сколько человек из этих 100 знают три языка?
Сколько человек из этих 100 знают три языка?