Сочетания.
1) Сочетания без повторений.
Определение
3: Сочетания
из 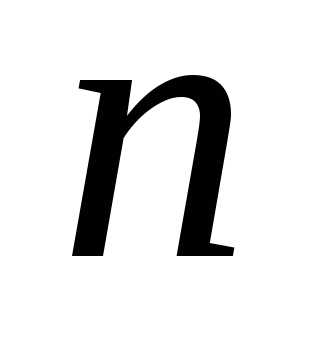 элементов по
элементов по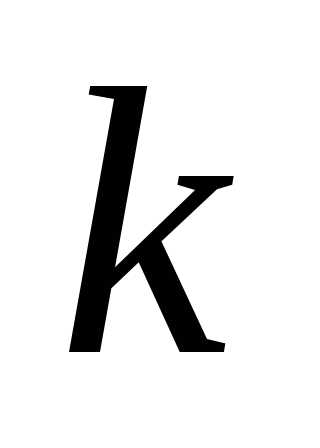 элементов (
элементов (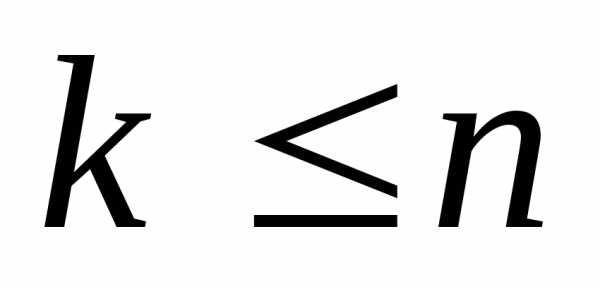 )
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают:
)
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают: 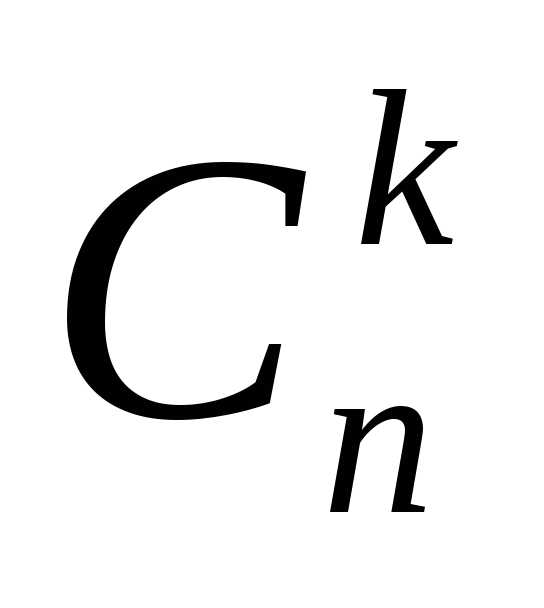 .
.
Теорема 4: Число сочетаний находится по следующей формуле:
.
Доказательство:  .
.
Следствие:
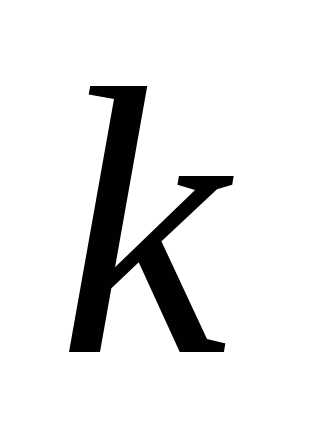 элементов одного типа и
элементов одного типа и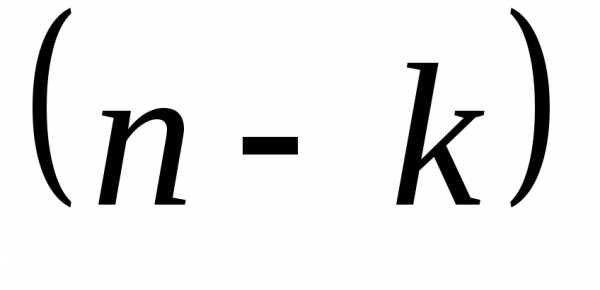 элементов второго типа:
элементов второго типа:.
Иными словами справедливо равенство: .
Примеры: Выбор делегации, число призеров в соревновании и т. д.
Замечание: 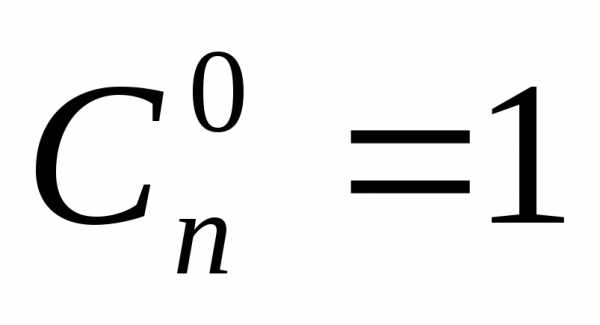 ,
, 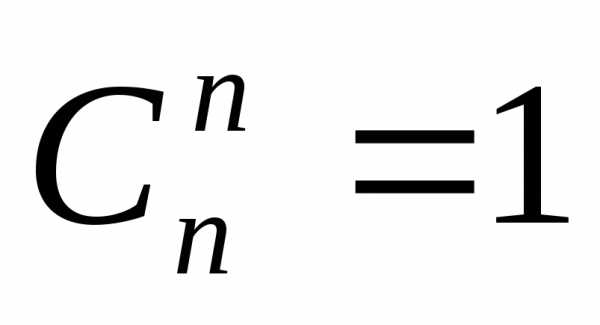 .
.
Существенное отличие числа сочетаний от числа соответствующих размещений состоит в том, что для размещений важен состав и порядок элементов в подмножествах, а для сочетаний важен только состав.
2) Сочетания с повторениями.
Пусть
имеется предметы 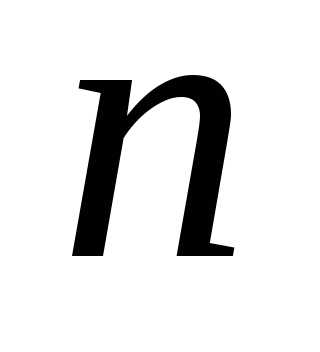
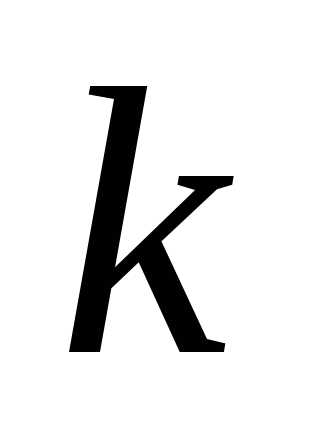 комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.
комбинаций можно сделать из них, если
не принимать во внимание порядок
элементов? Эту задачу в общем виде можно
решать точно так же, как задачу с
пирожными.Задача: В кондитерском магазине продаются пирожные 4 сортов: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Зашифруем каждую покупку с помощью нулей и единиц. Напишем столько единиц, сколько куплено наполеонов, затем пишем 0, чтобы отделить пирожные одного типа от другого и т.д. Тогда каждой покупке будет соответствовать последовательность из семи единиц и трех нулей в различном порядке. Число всех таких покупок тогда будет равно:
.
Для числа сочетаний с повторениями существует формула:
.
§2. Свойства сочетаний. Бином Ньютона.
1. 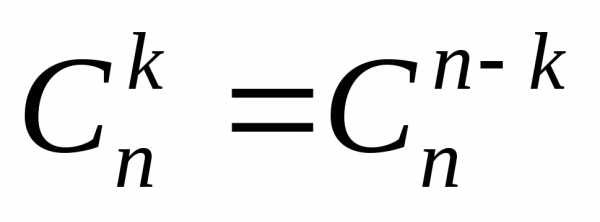 .
.
2. .
Доказательство:
1) .
2) .
Сочетания можно встретить и в школьном курсе математики. Например, в качестве коэффициентов бинома Ньютона выступают именно сочетания. Формула бинома Ньютона в общем виде и её доказательство приводятся в следующей теореме.
Теорема 1: .
Доказательство: Применим индукцию по 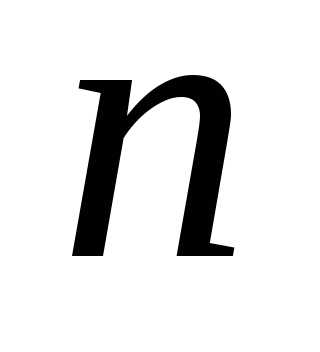 .
.
При 
Пусть формула верна, для случая, когда . В этом случае следующее равенство будем считать выполненным:
.
Покажем,
что формула выполняется для 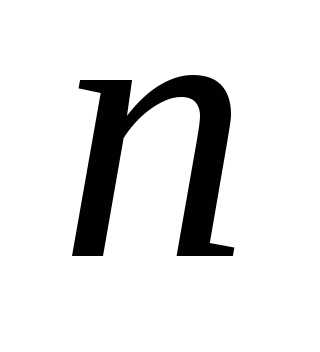 —
й степени:
—
й степени:
.
В доказательстве можно также использовать свойство: .
Следствие: Рассмотрим некоторые частные случаи формулы бинома Ньютона:
1) если , то.
2) если , то.
Определение
1: Коэффициенты 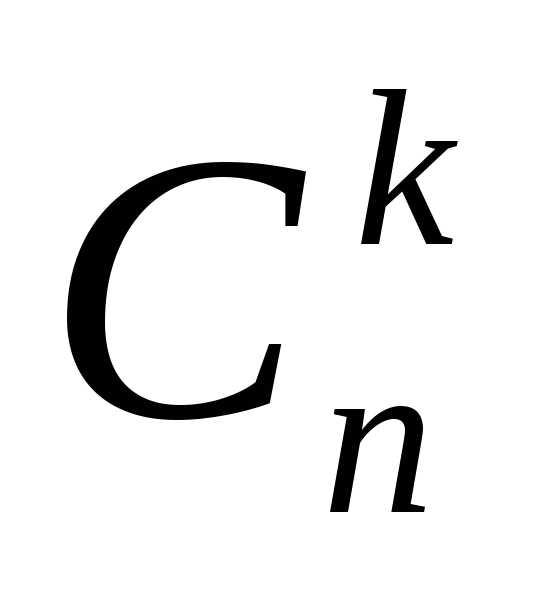 бинома Ньютонаназываются
биномиальными коэффициентами.
бинома Ньютонаназываются
биномиальными коэффициентами.
Числовые
значения биномиальных коэффициентов
вычисляются по формуле числа сочетаний: 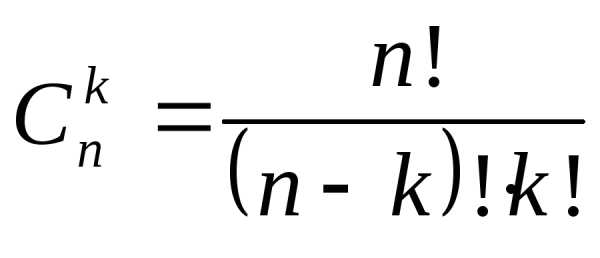
1 n = 0
1 1 n = 1
1 2 1 n = 2
1 3 3 1 n = 3
1 4 6 4 1 n = 4
1 5 10 10 5 1 n = 5
. . . . . . . . . . . . . . . . . . . . . . . . .
Треугольник
Паскаля строится следующим образом.
Боковые стороны состоят из единиц.
Числа, находящиеся внутри, являются
суммой вышестоящих чисел. Каждая строка
треугольника соответствует некоторой
степени для суммы 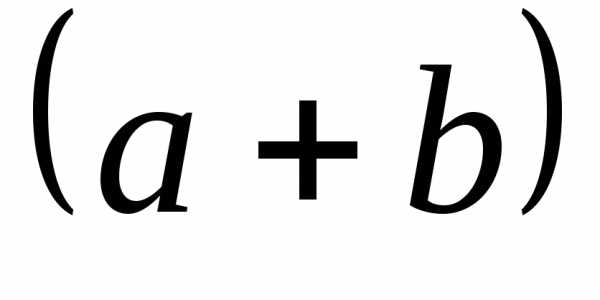 и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы
и содержит соответствующие биномиальные
коэффициенты. Таким образом, для того,
чтобы раскрыть степень суммы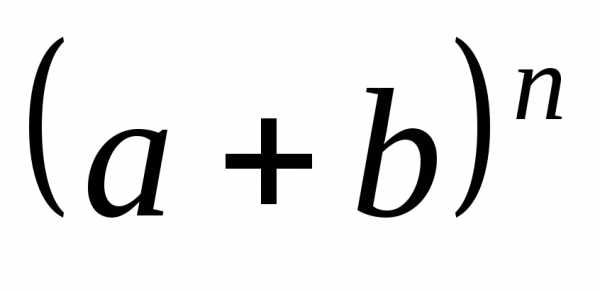
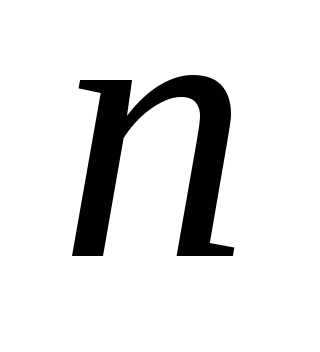 .
Эта строка будет содержать нужные
коэффициенты
.
Эта строка будет содержать нужные
коэффициенты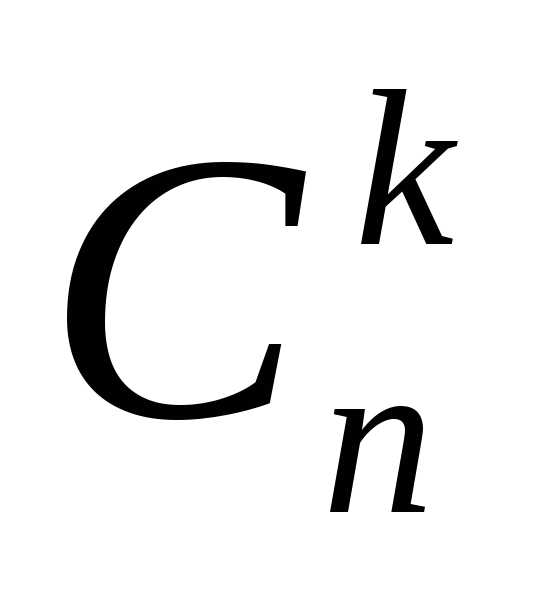 ,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент.
,
к которым приписываются соответствующие
буквенные выражения. Можно заметить,
что строки треугольника Паскаля
симметричны, поэтому достаточно взять
только половину биномиальных коэффициентов
и, если нужно, средний элемент.Формула бинома Ньютона применяется, когда нужно возвести в целую степень сумму двух слагаемых. Если же это требуется произвести для суммы трёх и более слагаемых, тогда применяют полиномиальную формулу:
Сумма
в правой части формулы строится по
аналогии с формулой бинома. Она
представляет собой сумму слагаемых,
состоящих из коэффициента
и буквенной части.
Сумма этих слагаемых берется по
всевозможным разбиениям числа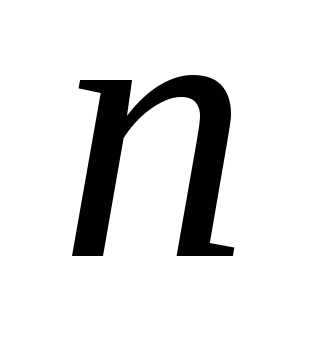
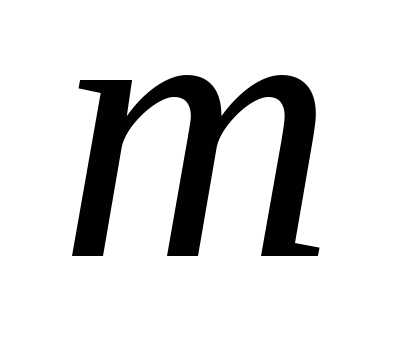 целых неотрицательных слагаемых,
при этом коэффициент находится по
формуле числа перестановок с повторениями:
целых неотрицательных слагаемых,
при этом коэффициент находится по
формуле числа перестановок с повторениями:.
Если
числа 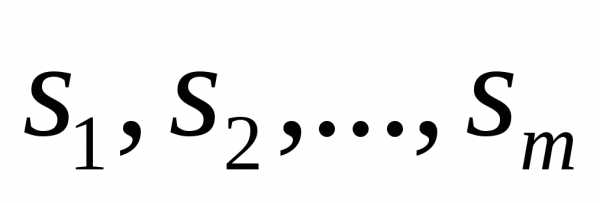 получаются перестановкой из чисел,
то считается, что
получаются перестановкой из чисел,
то считается, что
.
Пример: Возвести в пятую степень сумму трёх слагаемых.
Здесь учитывается, что 5 можно разбить на 3 слагаемых пятью способами:
;;;;.
Тогда
для каждого такого разбиения известны
числа 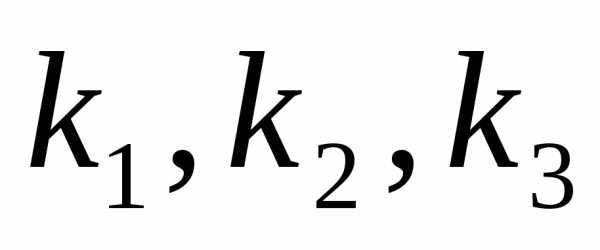 ,
,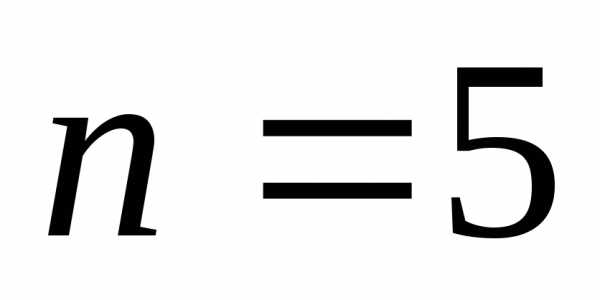 .
Значит, все коэффициенты можно для
каждого случая найти по формуле:
.
Значит, все коэффициенты можно для
каждого случая найти по формуле:
.
Полученные
коэффициенты: 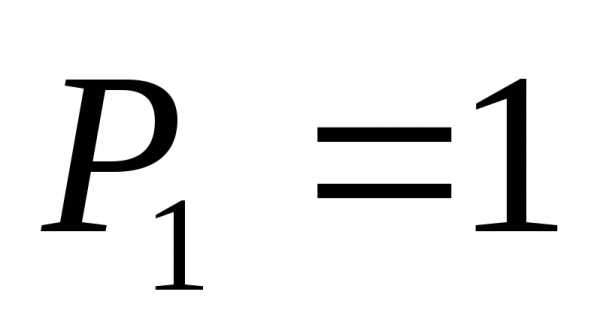 ,
,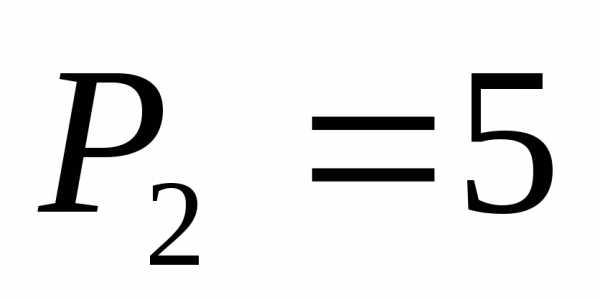 ,
,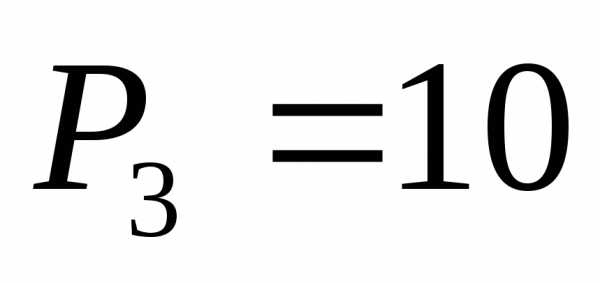 ,
,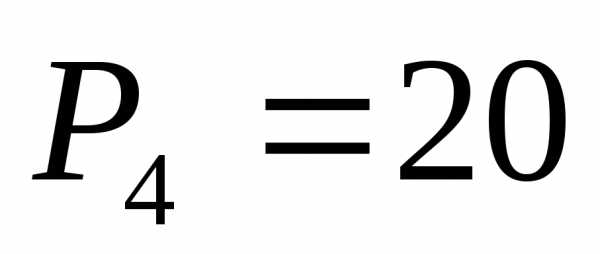 ,
,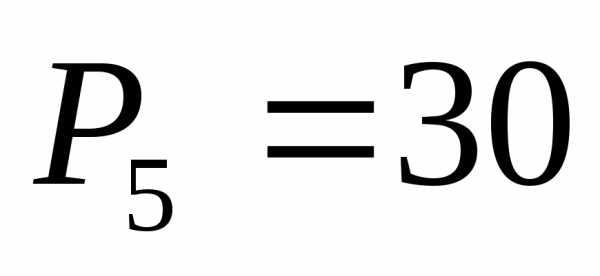 .
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше.
.
Буквенная часть также формируется в
связи с разложениями числа 5 на 3 слагаемых.
Таким образом, получается разложение,
приведённое выше.
Замечание: Сумма полиномиальных коэффициентов может быть найдена по формуле:
.
Для коэффициентов из рассмотренного примера можно проверить:
,
.
Рассмотрим 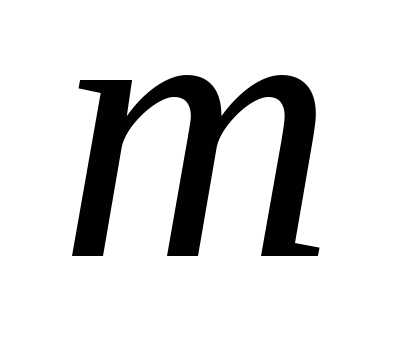
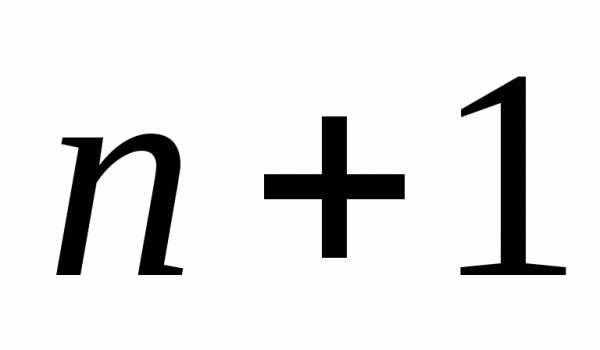 типа, например из
типа, например из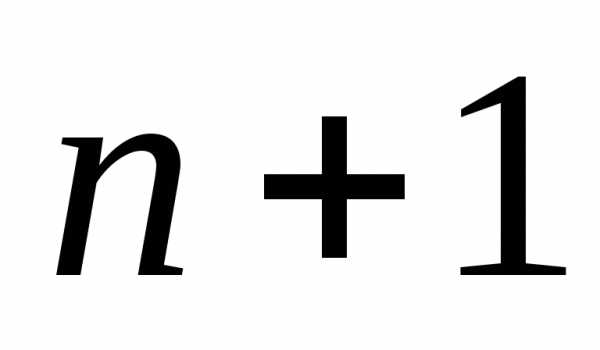 буквы.
Число таких сочетаний равно:
буквы.
Число таких сочетаний равно: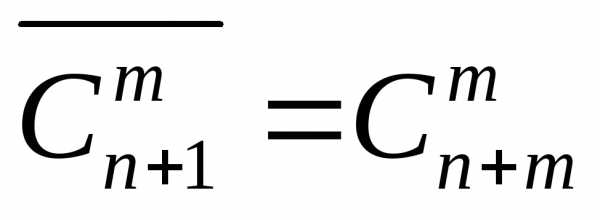 .
Разобьём все эти сочетания на классы,
отнеся к
.
Разобьём все эти сочетания на классы,
отнеся к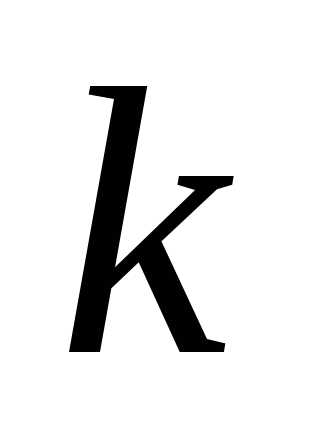 ‑
му классу сочетания, в которых
‑
му классу сочетания, в которых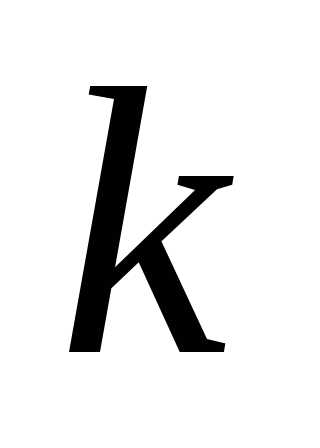 раз входит буква
раз входит буква .
Остальные
.
Остальные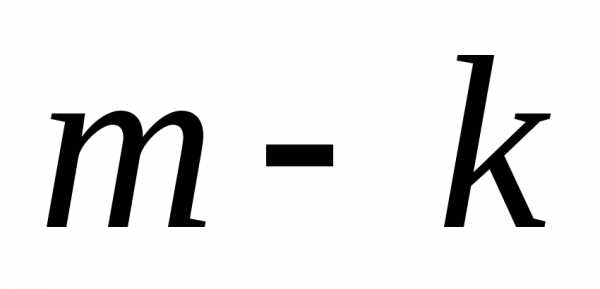 мест могут быть заняты оставшимися
буквами
мест могут быть заняты оставшимися
буквами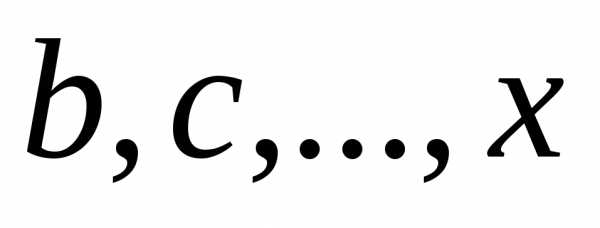 ,
число которых равно
,
число которых равно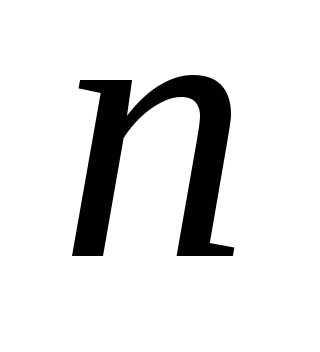 .
Поэтому в
.
Поэтому в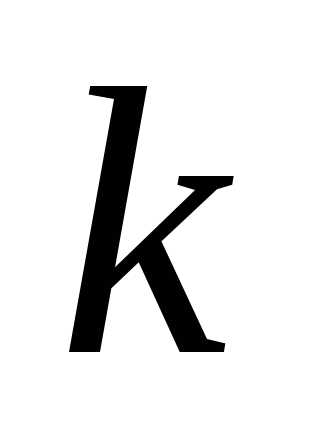 —
й класс входит столько сочетаний, сколько
можно составить
—
й класс входит столько сочетаний, сколько
можно составить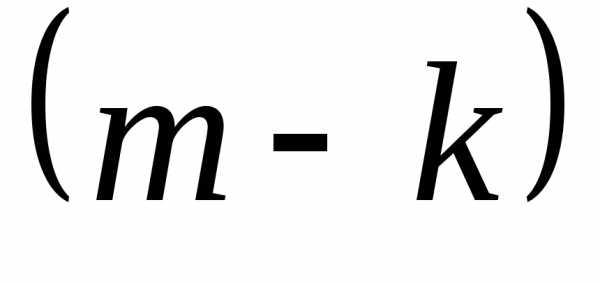 сочетаний с повторениями из элементов
сочетаний с повторениями из элементов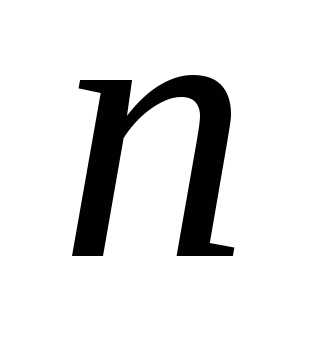 типов, т.е.
типов, т.е.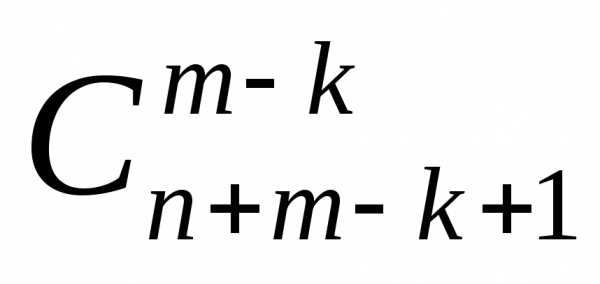 .
.Значит общее число всех таких сочетаний равно:
, т.е.
.
Меняя
теперь 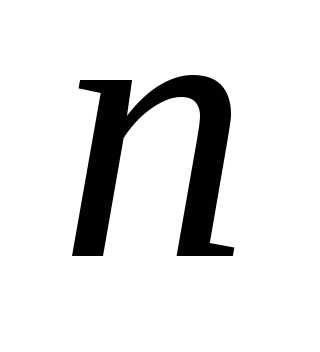 на
на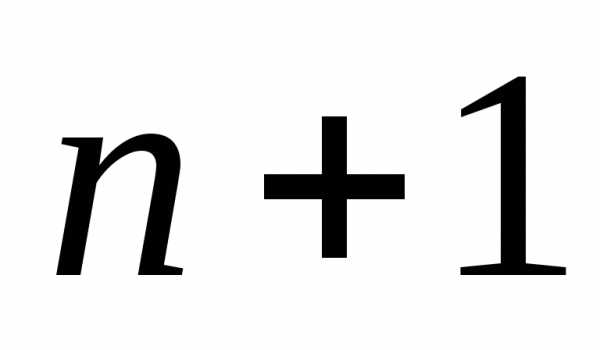 и
и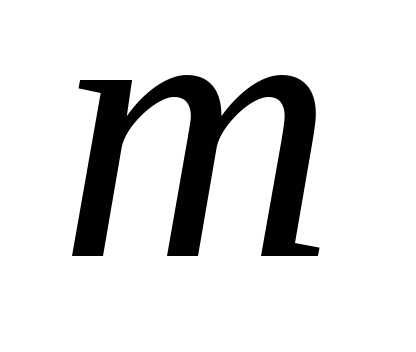 на
на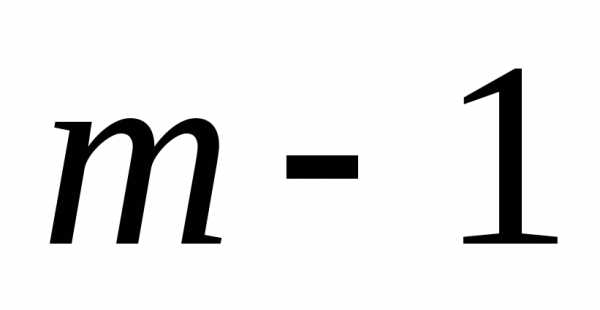 и используя равенство
и используя равенство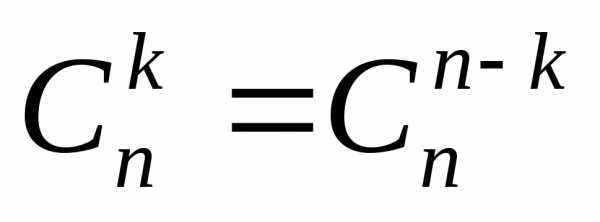 ,
получаем зависимость между биномиальными
коэффициентами:
,
получаем зависимость между биномиальными
коэффициентами:
.
Доказать
эту формулу можно методом математической
индукции по числу слагаемых в правой
части. Используя эту зависимость, можно
получить формулы для подсчёта суммы
чисел натурального ряда от 1 до 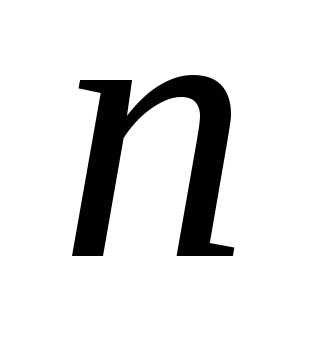 (при
(при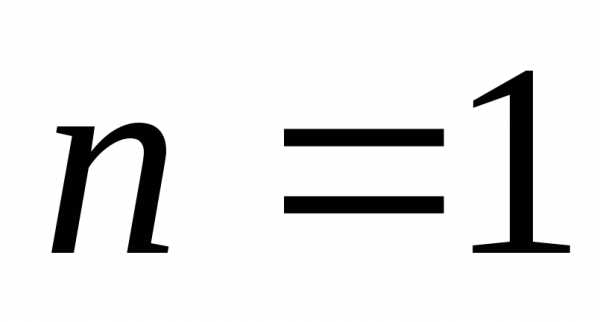 ),
суммы квадратов натуральных чисел (при
),
суммы квадратов натуральных чисел (при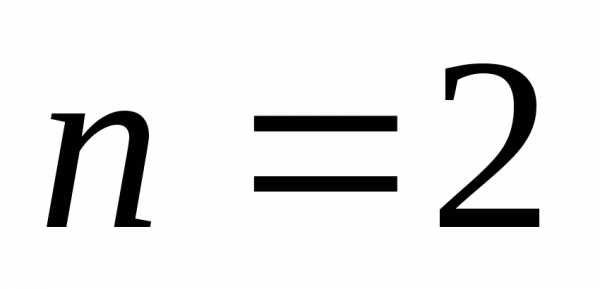 ),
сумму кубов (при
),
сумму кубов (при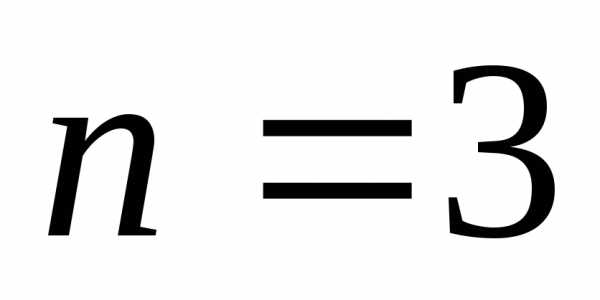 ).
).
Если 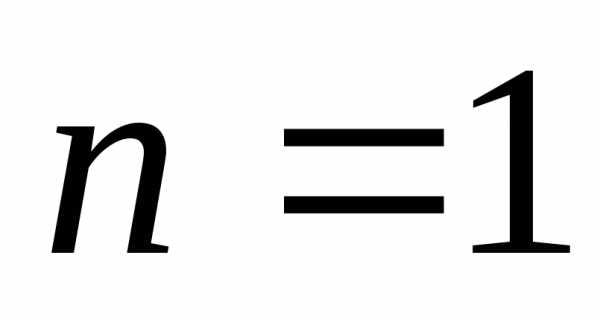 ,
то искомая зависимость имеет вид:
,
то искомая зависимость имеет вид:
.
Для 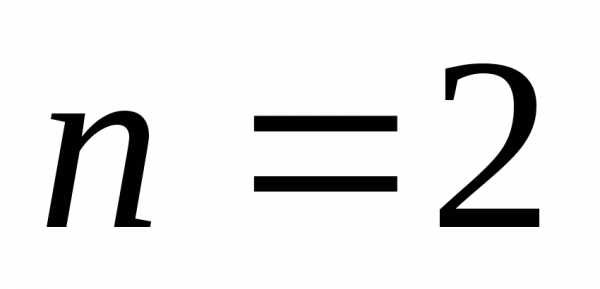 имеем:
имеем:
,
или окончательно:
.
Для 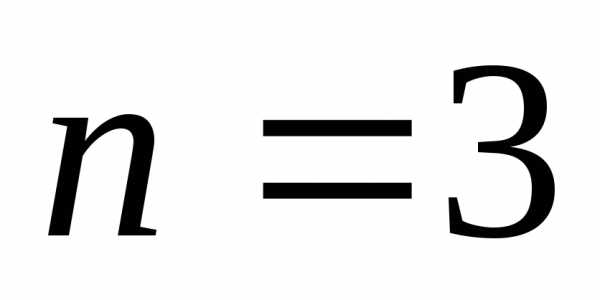 получаем:
получаем:
,
или после преобразований:
.
Таким образом, можно получить формулы для сумм более высоких степеней натуральных чисел.
studfiles.net
1.7. Основные формулы комбинаторики
При нахождении вероятностей в схеме классического определения широко используется комбинаторика, поэтому напомним наиболее употребительные определения и формулы для вычисления.
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества.
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
Рn = n!
Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.
Пример. Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз?
Решение. Искомое число трехзначных чисел Р3 = 3! = 123 = 6.
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений
.
Пример. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2?
Решение. Искомое число сигналов .
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний
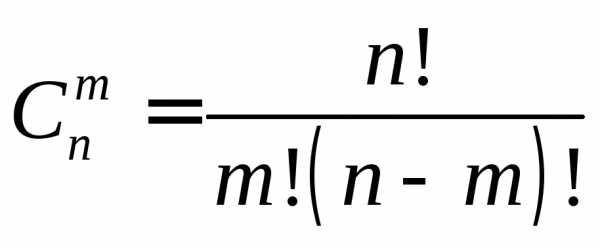 .
.
Пример. Сколькими способами можно выбрать две детали из ящика, содержащего 10 деталей?
Решение.
Искомое число способов 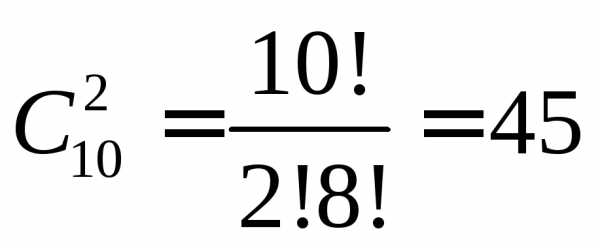 .
.
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
Замечание. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т. д., то число перестановок с повторениями
,
где n1 + n2 + … = n.
При решении задач комбинаторики используют следующие правила:
1. Правило суммы. Если некоторый объект A может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
2. Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Приведем несколько примеров непосредственного вычисления вероятностей.
Пример 1. Набирая номер телефона, абонент забыл одну цифру и набрал ее наудачу. Найти вероятность того, что набрана нужная цифра.
Решение. Обозначим через А событие – набрана нужная цифра. Абонент мог набрать любую из 10 цифр, поэтому общее число возможных элементарных исходов равно 10. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию А лишь один исход (нужная цифра лишь одна). Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
Р(А)=1/10.
Пример 2. Набирая номер телефона, абонент забыл последние две цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Найти вероятность того, что набраны нужные цифры.
Решение. Обозначим через В событие – набраны две нужные цифры. Всего можно набрать столько различных цифр, сколько может быть составлено размещений из десяти цифр по две, т.е. . Таким образом, общее число возможных элементарных исходов равно 90. Эти исходы несовместны, равновозможны и образуют полную группу. Благоприятствует событию В лишь один исход. Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
Р(В)=1/90.
Пример 3. Указать ошибку «решения» задачи: «Брошены две игральные кости. Найти вероятность того, что сумма выпавших очков равна 4 (событие А)».
Решение. Всего возможны 2 исхода испытания: сумма выпавших очков равна 4, сумма выпавших очков не равна 4. Событию А благоприятствует один исход; общее число исходов равно двум. Следовательно, искомая вероятность
Р(А) = 1/2.
Ошибка этого решения состоит в том, что рассматриваемые исходы не являются равновозможными.
Правильное решение. Общее число равновозможных исходов испытания равно 66 = 36 (каждое число выпавших очков на одной кости может сочетаться со всеми числами очков другой кости). Среди этих исходов благоприятствуют событию А только 3 исхода: (1; 3), (3; 1), (2; 2) (в скобках указаны числа выпавших очков). Следовательно, искомая вероятность
Р(А) = 3/36 = 1/12.
Пример 4. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди шести взятых наудачу деталей 4 стандартных.
Решение. Общее число возможных элементарных
исходов испытания равно числу способов,
которыми можно извлечь 6 деталей из 10,
т. е. числу сочетаний из 10 элементов но
6 элементов (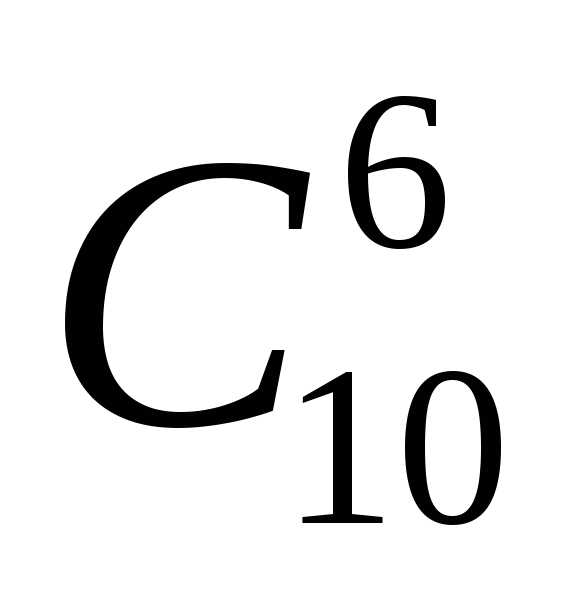 ).
).
Определим
число исходов, благоприятствующих
интересующему нас событию А (среди шести взятых деталей 4 стандартных).
Четыре стандартные детали можно взять
на семи стандартных деталей  способами; при этом остальные 6 – 4 = 2
детали должны быть нестандартными;
взять же 2 нестандартные детали из 10 –
7 = 3 нестандартных деталей можно
способами; при этом остальные 6 – 4 = 2
детали должны быть нестандартными;
взять же 2 нестандартные детали из 10 –
7 = 3 нестандартных деталей можно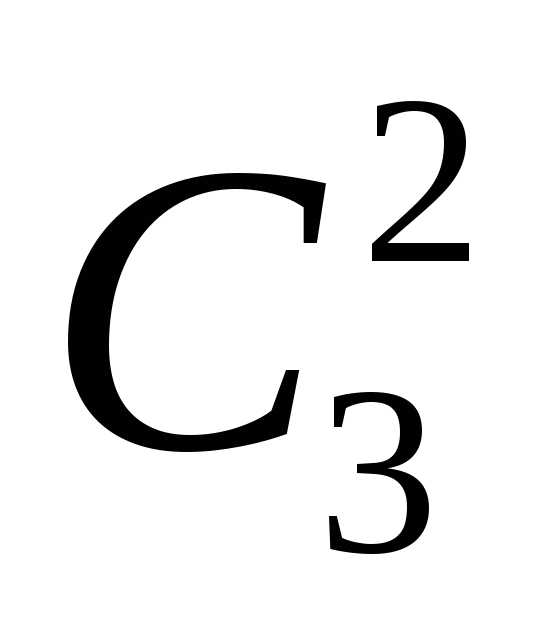 способами. Следовательно, число
благоприятствующих исходов равно
способами. Следовательно, число
благоприятствующих исходов равно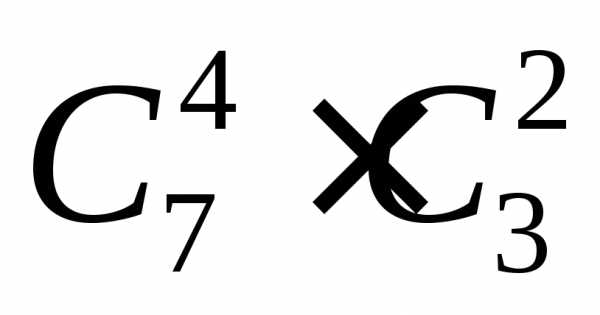 .
.
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
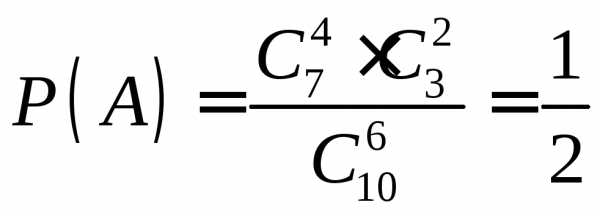
studfiles.net
Важнейшие формулы комбинаторики / Теория вероятности [Калинин В.М., Тихомиров С.Р.] / 3dstroyproekt.ru
Рассмотрим пару множеств $ { \rm A } =\left\{ { a_1 ,a_2 \ldots a_n }\right\} , { \rm B } =\left\{ { b_1 ,b_2 \ldots b_m }\right\} $ размерности $n\left({\rm A }\right)=n$ и $n\left({\rm B }\right)=m$
Следуя терминологии, принятой в Т.В. каждое из множеств будем называть генеральной совокупностью { Г.С. } объема $n$ и $m$.
Определение Упорядоченное подмножество из $k$ элементов $\left\{ { a_1 \ldots a_k }\right\} $, входящих в Г.С. $ { \rm A } =\left\{ { a_1 \ldots a_n }\right\} $ объема $n$, называется выборкой объема $k$ из этой Г.С.
Выбор с возвращением. Выбор производится каждый раз из всей Г.С., то есть перед следующим выбором предыдущий элемент возвращается.
Выбор без возвращения Выбранный элемент удаляется из Г.С., выборка не содержит повторений.
Определение
Выборка без возвращения называется размещением $ { \rm A } _n^k $
Замечание Две выборки одного объема будут отличаться друг от друга, если они содержат хотя бы по одному различному элементу.
Теорема Число размещений $ { \rm A } _n^k $, { для выборки без возвращения } равно
$ { \rm A } _n^k =\prod\limits_ { i=0 } ^ { k-1 } { \left( { n-i }\right) } =n\left( { n-1 }\right)\ldots \left( { n-k+1 }\right)=\frac { n! } { \left( { n-k }\right)! } $ { 1 } .
Число различных выборок { для выборки с возвращением } будет равно $\begin{equation} \label { eq1 } { \rm N } _n^k =n^k \qquad (1) \end{equation} $
Определение Выборка без повторений объема $n$ из Г.С. объема $n$ называются перестановкой $ { \rm P } _n $, { предполагается, что в Г.С. нет повторяющих элементов } .
Теорема Число всех различных перестановок из n элементов может быть подсчитано по формуле
$\begin{equation} \label { eq2 } { \rm P } _n =n! \qquad (2) \end{equation} $
легко показать, что $ { \rm P } _n = { \rm A } _n^n =\frac { n! } { 0! } =n!$
Пусть имеется $m$ Г.С. объема $n_1 \ldots n_m $. Составим различные комбинации так, что из каждой Г.С. в комбинацию входит по одному элементу $\left.{ { \begin{array} { c } { a_1 \ldots a_ { n1 } } \\ { b_1 \ldots b_ { n2 } } \\ { { \begin{array} { c } \cdots \\ { c_1 \ldots c_ { nm } } \\ \end{array} } } \\ \end{array} } }\right\} $ m Г.С.
$\left({ a_i ,b_j ,\ldots c_k }\right)$, где $\begin{array} { c } { i=1\ldots n_1 } \\ { j=1\ldots n_2 } \\ { k=1\ldots n_m } \\ \end{array} $ тогда число комбинаций $\begin{equation} \label { eq3 } { \rm N } =n_1 \cdot n_2 \ldots n_m \qquad (3) \end{equation} $
Определение Различные подмножества элементов, отличающих как составом так и порядком называются соединениями.
Определение Соединения, которые отличаются друг от друга только составом называются сочетаниями и обозначаются $C_n^m $.
Число сочетаний может быть вычислено по формуле $ \begin{equation} \label { eq4 } C_n^m =\frac { { \rm A } _n^m } { { \rm P } _m } =\frac { n! } { m!\left( { n-m }\right)! } \qquad (4) \end{equation} $
Определение Перестановки с повторениями. { элементы могут повторяться, но отличаются порядком расположения }
$ { \rm P } _ { n\,k_1 \ldots k_i } =\frac { n! } { k_1 !\ldots k_n ! } $(6) $ { \begin{array} { c } { a_1 -повтор\,k_1 } \\ { a_2 -повтор\,k_2 } \\ { { \begin{array} { c } \cdots \\ { a_n \ldots k_n } \\ \end{array} } } \\ \end{array} } $
Определение Сочетания с повторениями. { один элемент входит в различные сочетания разное число раз } $\begin{equation} \label { eq5 } f_n^m =C\cdot C_n^m =C_ { n+m-1 } ^m =\frac { \left( { n+m-1 }\right)\,! } { m\,!\left( { n-1 }\right)\,! } \qquad (5) \end{equation} $
Замечание при вычислении факториалов больших чисел пользуются формулой Стирлинга.
$\begin{equation} \label { eq6 } n!\approx \sqrt { 2\cdot \pi \cdot n } \cdot n^n\cdot e^ { -n } \qquad (6) \end{equation} $
Сводка основных формул
- Размещения $ { \rm A } _n^k =\frac { n! } { \left( { n-k }\right)\,! } $ { состав и порядок }
- Перестановки $ { \rm P } _n =n!$ { порядок }
- Сочетания $C_n^k =\frac { n\,! } { k\,!\left( { n-k }\right)\,! } $ { только состав }
- Перестановки с повторениями $ { \rm P } _ { n,k_1 \ldots k_m } =\frac { n! } { k_1 !\ldots k_m ! } $
- Сочетание с повторениями $C\cdot C_n^k =C_ { n+k-1 } ^k =\frac { \left( { n+k-1 }\right)\,! } { k\,!\left( { n-1 }\right)\,! } $
- Комбинации $ { \rm N } =n_1 \cdot n_2 \cdot n_3 \cdot \ldots \cdot n_k $
- Выбор с возвращением $ { \rm N } _n^k =n^k$
Примеры:
Задача 1. Сколькими способами можно выбрать из студенческой группы в 25 человек троих на профсоюзную конференцию?
Решение. Студенческая группа — генеральная совокупность — ее объем $n(A)=25$ из нее извлекают выборку объема $k=3$. Из условия задачи ясно, что важен только состав } { три студента выбирают } , следовательно, число способов равно числу сочетаний из 25 по 3 { формула 5 } . $ C_ { 25 } ^3 =\frac { 25! } { ( { 25-3 } )!\cdot 3! } =\frac { 25! } { 22!\cdot 3! } =2300. $
Задача 2. Сколькими способами можно избрать треугольник студенческой группы { старосту, физорга, профорга } в 25 человек?
Решение. Студенческая группа — генеральная совокупность — ее объем $n(A)=25$ из нее извлекают выборку объема $k=3$. Из условия задачи ясно, что важен не только состав, но и порядок } { распределение обязанностей } , следовательно, число способов равно числу размещений из 25 по 3 { формула 1 } .
$ A_ { 25 } ^3 =\frac { 25! } { ( { 25-3 } )! } =\frac { 25! } { 22! } =13800. $
Задача 3. Сколько различных «слов» можно составить, переставляя буквы слова «математика»?
Решение. Генеральная совокупность — количество букв, содержащихся в слове математика — ее объем $n(A)=10$. Из условия задачи ясно, что при составлении различных «слов» объем генеральной совокупности не меняется, а важен только порядок } расположения букв, поэтому количество «слов» равно числу перестановок из 10-и букв { формула 3 } .
$ P_ { 10 } ^ =10!=151200. $
Задача 4. Сколько существует шестизначных чисел без нуля в записи?
Решение. Генеральная совокупность — количество цифр без нуля $1,2,3, { \ldots } 9$ — ее объем $n(A)=9$. Из нее извлекают выборку объема $k=6$. Из условия задачи ясно, что цифры могут повторяться { поскольку не сказано, что цифры различны } . При составлении различных выборок важен не только состав, но и порядок расположения цифр, поэтому количество шестизначных чисел равно числу размещений с повторениями { выбор с возвращением } { формула 2 } .
$ N_9^6 =9^6=531441. $
Задача 5. Сколько разных буквосочетаний можно сделать из букв слова «математика»?
Решение. Генеральная совокупность — количество букв, содержащихся в слове математика — ее объем $n(A)=10$. Из условия задачи ясно, что при составлении разных буквосочетаний объем генеральной совокупности не меняется. Здесь — 1 буква «е», 2 буквы «м», 3 буквы «а», 2 буквы «т», 1 буква «и», 1 буква «к». Среди выбираемых элементов есть одинаковые { выборка с возвращением } , чтобы получить разные буквосочетания, важен порядок расположения букв, поэтому количество таких буквосочетаний равно числу перестановок с повторениями из 9-и букв { формула 6 } .
$ P_ { 9,k_1 \ldots k_m } =\frac { n! } { k_1 !\ldots k_m ! } = P_ { 9,1,2,3,2,1,1 } =\frac { 9! } { 1!\cdot 2!\cdot 3!\cdot 2!\cdot 1!\cdot 1! } =15120. $
Задача 6. В кафе имеются торты четырех разных сортов: «Анастасия», «Тайна», «Астория» и «Фантазия». Сколькими способами можно купить 8 тортов?
Решение. Очевидно, что порядок, в котором выбираются торты, значения не имеет, важен только состав { 8 тортов } . В выбранную комбинацию могут входить повторяющиеся элементы { например, можно купить все тортики одного сорта } . Следовательно, число способов покупки 8 тортов определяется числом сочетаний с повторениями из 4 элементов по 8 { формула 7 } .
$ C\cdot C_n^k =C_ { n+k-1 } ^k =\frac { ( { n+k-1 } )\,! } { k\,!( { n-1 } )\,! } $ $ C\cdot C_4^8 =C_ { 4+8-1 } ^8 =\frac { ( { 4+8-1 } )\,! } { 8\,!( { 4-1 } )\,! } =\frac { 11! } { 8\,!\cdot 3\,! } =165 $
Задача 7. Из Москвы до Новосибирска можно добраться поездом и самолетом. Из Новосибирска в Томск — поездом, самолетом, автобусом, пароходом. Сколькими способами можно осуществить путешествие по маршруту Москва — Новосибирск — Томск?
Решение. Пусть первую генеральную совокупность образуют поезд и самолет, которыми можно добраться из Москвы до Новосибирска, ее объем $n(A)=2$. Вторую генеральную совокупность образуют поезд, самолет, автобус и пароход, которыми можно добраться из Новосибирска в Томск, ее объем $n { B } =4$. Очевидно, что путешествие по маршруту Москва — Новосибирск — Томск обязательно должно производится двумя видами транспорта, причем по одному из каждой генеральной совокупности. Следовательно, число способов будет равно числу комбинаций, образованных двумя элементами, взятыми по одному из каждой генеральной совокупности { формула 4 } .
$ { \rm N } =n_A \cdot n_B $
$ { \rm N } =2\cdot 4=8 $
3dstroyproekt.ru
размещения, сочетания, перестановки. — КиберПедия
Формулы комбинаторики
Рассмотрим задачу подсчета числа выборок из данного множества в общем виде. Пусть имеется некоторое множество N, состоящее из n элементов. Любое подмножество, состоящее из m элементов можно рассматривать без учета их порядка, так и с его учетом, т.е. при изменении порядка переходим к другой m – выборке.
Сформулируем следующие определения:
Размещения без повторения
Размещением без повторения из n элементов по m называется всякое упорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два размещения отличаются друг от друга, как элементами, так и их порядком, даже если элементы одинаковы.
Теорема 3. Число размещений без повторения равно произведению m сомножителей, наибольшим из которых является число n. Записывают:
Перестановки без повторений
Перестановками из n элементов называются различные упорядочения множества N.
Из этого определения следует, что две перестановки отличаются только порядком элементов и их можно рассматривать как частный случай размещений.
Теорема 4. Число различных перестановок без повторений вычисляется по формуле
Сочетания без повторений
Сочетанием без повторения из n элементов по m называется любое неупорядоченное подмножество множества N, содержащее m различных элементов.
Из определения следует, что два сочетания различаются только элементами, порядок не важен.
Теорема 5. Число сочетаний без повторений вычисляют по одной из следующих формул:
Пример 1. В комнате 5 стульев. Сколькими способами можно разместить на них
а) 7 человек; б) 5 человек; в) 3 человека?
Решение: а) Прежде всего надо выбрать 5 человек из 7 для посадки на стулья. Это можно сделать способом. С каждым выбором конкретной пятерки можно произвести перестановок местами. Согласно теореме умножения искомое число способов посадки равно .
Замечание: Задачу можно решать, используя только теорему произведения, рассуждая следующим образом: для посадки на 1-й стул имеется 7 вариантов, на 2-й стул-6 вариантов, на 3-й -5, на 4-й -4 и на 5-й -3. Тогда число способов посадки 7 человек на 5 стульев равно . Решения обоими способами согласуются, так как
б) Решение очевидно —
в) — число выборов занимаемых стульев.
— число размещений трех человек на трех выбранных стульях.
Общее число выборов равно .
Не трудно проверить формулы ;
;
— число всех подмножеств множества, состоящего из n элементов.
Вероятность суммы событий.
Пусть А и В – два несовместных события. Тогда в соответствии с третьей аксиомой для вероятности имеем
P(A+B) = P(A) + P(B). (3.6)
Это равенство известно как теорема сложения вероятностей несовместных событий. Для классической схемы это свойство не нужно постулировать, т.к. легко выводится из классического определения вероятности (доказать самостоятельно).
Пример 3.5. Из колоды в 36 карт наугад вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.
Решение. Введем следующие события: B={появление хотя одного туза}, A1={появление одного туза}, A2={появление двух тузов}, A3={появление трех тузов}. Очевидно, что B=A1+A2+A3. Поскольку события A1, A2 и A3.несовместны, то
P(B) = P(A1)+P(A2)+P(A3) =
Эту задачу можно решить иначе. Событие , противоположное событию В, состоит в том, что среди вынутых из колоды трех карт нет ни одного туза. ПосколькуP(B)+P( )=1, то
P(B) = 1 – P( ) =
Пусть А и В – два произвольных события, т.е. они, в общем случае, совместны. Запишем события А+В и В в виде
A+B = A+B и B = B +BA.
(объясните эти равенства, используя диаграммы Вьенна). Поскольку событие, стоящие в правых частях этих равенств, несовместны, то
P(A+B) = P(A) + P(B ), P(B) = P(B )+P(BA).
Исключая P(B ),получим
P(A+B) = P(A)+P(B)–P(AB). (3.7)
Это равенство известно как теорема сложения вероятностей совместных событий.
Полученная формула сложения вероятностей хорошо иллюстрируется при помощи диаграмм Вьенна. Здесь следует помнить, что вероятность события пропорциональна площади фигуры, которая соответствует данному событию. Событию А+В на рисунке соответствует вся заштрихованная фигура, площадь которой можно представить в виде суммы трех слагаемых SA+B=S1+S2+SAB, где S1 соответствует событию А–АВ, а S2 – событию В–АВ. Тогда, событию А будет соответствовать фигура с площадью SА= S1+SАВ, а событию В – SВ= S2+SАВ. В результате получим, что SА+В= SА+SВ–SАВ. Полученное равенство соответствует теореме сложения вероятностей.
Теорему сложения вероятностей можно обобщить на случай произвольного числа слагаемых. Вчастности,
P(A+B+C) = P(A)+P(B)+P(C)–(AB)–P(AC)–P(BC)+P(ABC). (3.8)
Докажите данную формулу самостоятельно.
Пример 3.6. Два стрелка делают по одному выстрелу по мишени. Вероятность попадания для первого стрелка равна 0,8, для второго – 0,7. Какова вероятность поражения цели?
Решение. Пусть A1={первый стрелок попал по цели}, A2={второй стрелок попал по цели}. Мишень будет поражена (событие В), если произойдет событие А1+А2. Поскольку события А1 и А2 совместны, но независимы, то
P(А1+А2) = P(А1)+P(А2)–P(А1)P(А2) = 0,7+0,8–0,7×0,8 = 0,94.
Отметим, что событие В можно записать также в виде A1 + A2+A1A2. Тогдаполучим
P(B) = P(A1)P( )+P( )P(A2)+P(A1)P(A2) = = 0,8×0,3+0,2×0,7+0,7×0,8 = 0,94.
Однако такой путь слишком длинный.
cyberpedia.su
Основные формулы и правила комбинаторики — Мегаобучалка
Комбинаторика – раздел элементарной математики, в котором изучают количества комбинаций, подчиненных определенным условиям и составляемых из конечного набора элементов (множества) безразлично какой природы.
Формулы и правила комбинаторики используют при непосредственном вычислении вероятностей (по формуле (1.1)).
Формулы комбинаторики
Перестановки – комбинации, состоящие из одних и тех же различных элементов и отличающиеся только их порядком.
Количество перестановок без повторений
(1.2)
Пример:
1. Сколько трехзначных чисел можно образовать из цифр 1, 2, 3, если каждая цифра в числе содержится один раз?
Решение
— количество цифр
123, 132, 213, 231, 321, 312.
2. Сколько четырехзначных чисел можно образовать из цифр 0, 1, 2, 3 не повторяя их?
Решение.
(1,2,3,0)
Учитывая, что число с нулем на первом месте является трехзначным, подсчитаем количество таких чисел:
(1,2,3)
Тогда .
Размещения – комбинации, составленные из различных элементов, взятых по элементов, которые отличаются либо составом элементов, либо их порядком.
Число размещений без повторений:
(1.3)
Формулы (1.3) и (1.2) связаны между собой формулой при
Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе не повторяются?
Решение:
12, 13, 21, 23, 31, 32
Число размещений с повторениями
(1.4)
Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе могут повторяться?
Решение:
11, 12, 13, 21, 22, 23, 31, 32, 33.
Сочетания – комбинации, составленные из различных элементов, взятых по элементов, которые отличаются хотя бы одним элементом.
Числовозможных сочетаний безповторений
(1.5)
Пример. Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, если цифры в числе не повторяются?
Решение:
12, 13, 23.
Формулы (1.2), (1.3) и (1.5) связаны между собой следующей формулой
(1.6)
Правила комбинаторики
Правило суммы – если объект может быть выбран из совокупности объектов способами, а объект — способами, то выбрать либо , либо можно способами.
Пример. В корзине белых шаров и черных шаров. Из корзины вынимают два шара. Найти вероятность того, что оба шара будут белыми или черными.
Решение:
— событие «вытащили оба шара белые»
— событие «вытащили оба шара черные»
— событие «вытащили оба шара белые или оба шара черные»
Правило произведения – если объект можно выбрать из совокупности объектов способами и после каждого такого выбора объект можно выбрать способами, то пара объектов и в указанном порядке может быть выбрана способами.
Пример. В партии из изделий бракованных. Из партии выбирают наугад изделий. Определить вероятность того, что среди этих изделий будет ровно бракованных.
Решение.
Общее число случаев равно , число благоприятных случаев , откуда вероятность интересующего нас события по (1.1)
(1.7)
Формула (1.7) получила название гипергеометрической формулы для расчета вероятностей.
megaobuchalka.ru
Основные формулы комбинаторики. Комбинаторика: формула перестановки, размещения
В данной статье речь пойдет об особом разделе математики под названием комбинаторика. Формулы, правила, примеры решения задач – все это вы сможете найти здесь, прочитав статью до самого конца.
Итак, что же это за раздел? Комбинаторика занимается вопросом подсчета каких-либо объектов. Но в данном случае объектами выступают не сливы, груши или яблоки, а нечто иное. Комбинаторика помогает нам находить вероятность какого-либо события. Например, при игре в карты – какова вероятность того, что у противника есть козырная карта? Или такой пример – какова вероятность того, что из мешка с двадцатью шариками вы достанете именно белый? Именно для подобного рода задач нам и нужно знать хотя бы основы данного раздела математики.
Комбинаторные конфигурации
Рассматривая вопрос основных понятий и формул комбинаторики, мы не можем не уделить внимание комбинаторным конфигурациям. Они используются не только для формулировки, но и для решения различных комбинаторных задач. Примерами таких моделей служат:
- размещение;
- перестановка;
- сочетание;
- композиция числа;
- разбиение числа.
О первых трех мы поговорим более подробно далее, а вот композиции и разбиению мы уделим внимание в данном разделе. Когда говорят о композиции некого числа (допустим, а), то подразумевают представление числа а в виде упорядоченной суммы неких положительных чисел. А разбиение – это неупорядоченная сумма.
Разделы

Прежде чем мы перейдем непосредственно к формулам комбинаторики и рассмотрению задач, стоит обратить внимание на то, что комбинаторика, как и другие разделы математики, имеет свои подразделы. К ним относятся:
- перечислительная;
- структурная;
- экстремальная;
- теория Рамсея;
- вероятностная;
- топологическая;
- инфинитарная.
В первом случае речь идет об исчисляющей комбинаторике, задачи рассматривают перечисление или подсчет разных конфигураций, которые образованы элементами множеств. На данные множества, как правило, накладываются какие-либо ограничения (различимость, неразличимость, возможность повтора и так далее). А количество этих конфигураций подсчитывается при помощи правила сложения или умножения, о которых мы поговорим немного позже. К структурной комбинаторике относятся теории графов и матроидов. Пример задачи экстремальной комбинаторики – какова наибольшая размерность графа, который удовлетворяет следующим свойствам… В четвертом пункте мы упомянули теорию Рамсея, которая изучает в случайных конфигурациях наличие регулярных структур. Вероятностная комбинаторика способна нам ответить на вопрос – какова вероятность того, что у заданного множества присутствует определенное свойство. Как нетрудно догадаться, топологическая комбинаторика применяет методы в топологии. И, наконец, седьмой пункт – инфинитарная комбинаторика изучает применение методов комбинаторики к бесконечным множествам.
Правило сложения
Среди формул комбинаторики можно найти и довольно простые, с которыми мы достаточно давно знакомы. Примером является правило суммы. Предположим, что нам даны два действия (С и Е), если они взаимоисключаемы, действие С выполнимо несколькими способами (например а), а действие Е выполнимо b-способами, то выполнить любое из них (С или Е) можно а+b способами.

В теории это понять достаточно трудно, постараемся донести всю суть на простом примере. Возьмем среднюю численность учеников одного класса — допустим, это двадцать пять. Среди них пятнадцать девочек и десять мальчиков. Ежедневно в классе назначается один дежурный. Сколько есть способов назначить дежурного по классу сегодня? Решение задачи достаточно простое, мы прибегнем к правилу сложения. В тексте задачи не сказано, что дежурными могут быть только мальчики или только девочки. Следовательно, им может оказаться любая из пятнадцати девочек или любой из десяти мальчиков. Применяя правило суммы, мы получаем достаточно простой пример, с которым без труда справится школьник начальных классов: 15 + 10. Подсчитав, получаем ответ: двадцать пять. То есть существует всего двадцать пять способов назначить на сегодня дежурного класса.
Правило умножения
К основным формулам комбинаторики относится и правило умножения. Начнем с теории. Допустим, нам необходимо выполнить несколько действий (а): первое действие выполняется с1 способами, второе – с2 способами, третье – с3 способами и так далее до последнего а-действия, выполняемого са способами. Тогда все эти действия (которых всего у нас а) могут быть выполнены N способами. Как высчитать неизвестную N? В этом нам поможет формула: N = с1 * с2 * с3 *…* са.

Опять же, в теории ничего не понятно, переходим к рассмотрению простого примера на применение правила умножения. Возьмем все тот же класс из двадцати пяти человек, в котором учится пятнадцать девочек и десять мальчиков. Только на этот раз нам необходимо выбрать двух дежурных. Ими могут быть как только мальчики или девочки, так и мальчик с девочкой. Переходим к элементарному решению задачи. Выбираем первого дежурного, как мы решили в прошлом пункте, у нас получается двадцать пять возможных вариантов. Вторым дежурным может быть любой из оставшихся человек. У нас было двадцать пять учеников, одного мы выбрали, значит вторым дежурным может быть любой из оставшихся двадцати четырех человек. Наконец, применяем правило умножения и получаем, что двоих дежурных можно избрать шестью сотнями способов. Мы данное число получили умножением двадцати пяти и двадцати четырех.
Перестановка
Сейчас мы рассмотрим еще одну формулу комбинаторики. В данном разделе статьи мы поговорим о перестановках. Рассмотреть проблему предлагаем сразу же на примере. Возьмем бильярдные шары у нас их n-ое количество. Нам нужно подсчитать: сколько есть вариантов расставить их в ряд, то есть составить упорядоченный набор.
Начнем, если у нас нет шаров, то и вариантов расстановки у нас так же ноль. А если у нас шар один, то и расстановка тоже одна (математически это можно записать следующим образом: Р1 = 1). Два шара можно расставить двумя разными способами: 1,2 и 2,1. Следовательно, Р2 = 2. Три шара можно расставить уже шестью способами (Р3=6): 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,2,1; 3,1,2. А если таких шаров не три, а десять или пятнадцать? Перечислять все возможные варианты очень долго, тогда нам на помощь приходит комбинаторика. Формула перестановки поможет нам найти ответ на интересующий нас вопрос. Pn = n *P (n-1). Если попытаться упростить формулу, то получаем: Pn = n* (n — 1) *…* 2 * 1. А это и есть произведение первых натуральных чисел. Такое число называется факториалом, а обозначается как n!

Рассмотрим задачу. Вожатый каждое утро выстраивает свой отряд в шеренгу (двадцать человек). В отряде есть три лучших друга – Костя, Саша и Леша. Какова вероятность того, что они будут стоять рядом? Чтобы найти ответ на вопрос, нужно вероятность «хорошего» исхода поделить на общее количество исходов. Общее число перестановок составляет 20! = 2,5 квинтиллиона. Как посчитать количество «хороших» исходов? Предположим, что Костя, Саши и Леша – это один сверхчеловек. Тогда мы имеем всего восемнадцать субъектов. Число перестановок в данном случае равняется 18 = 6,5 квадриллионов. При всем этом, Костя, Саша и Леша могут произвольно перемещаться между собой в своей неделимой тройке, а это еще 3! = 6 вариантов. Значит всего «хороших» расстановок у нас 18! * 3! Нам остается только найти искомую вероятность: (18! * 3!) / 20! Что равняется примерно 0,016. Если перевести в проценты, то это получается всего 1,6%.
Размещение
Сейчас мы рассмотрим еще одну очень важную и необходимую формулу комбинаторики. Размещение – это наш следующий вопрос, который предлагаем вам рассмотреть в данном разделе статьи. Мы идем на усложнение. Предположим, что мы хотим рассмотреть возможные перестановки, только не из всего множества (n), а из меньшего (m). То есть мы рассматриваем перестановки из n предметов по m.
Основные формулы комбинаторики стоит не просто заучивать, а понимать их. Даже несмотря на то, что они усложняются, так как у нас не один параметр, а два. Предположим, что m = 1, то и А = 1, m = 2, то А = n * (n — 1). Если далее упрощать формулу и перейти на запись при помощи факториалов, то получится вполне лаконичная формула: А = n! / (n — m)!
Сочетание
Мы рассмотрели практически все основные формулы комбинаторики с примерами. Теперь перейдем к заключительному этапу рассмотрения базового курса комбинаторики – знакомство с сочетанием. Сейчас мы будем выбирать m предметов из имеющихся у нас n, при этом всем мы будем выбирать всеми возможными способами. Чем же тогда это отличается от размещения? Мы не будем учитывать порядок. Этот неупорядоченный набор и будет являться сочетанием.

Сразу введем обозначение: С. Берем размещения m шариков из n. Мы перестаем обращать внимание на порядок и получаем повторяющиеся сочетания. Чтобы получить число сочетаний нам надо поделить число размещений на m! (m факториал). То есть С = А / m! Таким образом, способов выбрать из n шаров немножко, равняется примерно столько, сколько выбрать почти все. Этому есть логическое выражение: выбрать немножко все равно, что выкинуть почти все. Еще в данном пункте важно упомянуть и то, что максимальное число сочетаний можно достигнуть при попытке выбрать половину предметов.
Как выбрать формулу для решения задачи?
Мы подробно рассмотрели основные формулы комбинаторики: размещение, перестановка и сочетание. Теперь наша задача – облегчить выбор необходимой формулы для решения задачи по комбинаторике. Можно воспользоваться следующей довольно простой схемой:
- Задайте себе вопрос: порядок размещения элементов учитывается в тексте задачи?
- Если ответ нет, то воспользуйтесь формулой сочетания (С = n! / (m! * (n — m)!)).
- Если ответ нет, то необходимо ответить на еще один вопрос: все ли элементы входят в комбинацию?
- Если ответ да, то воспользуйтесь формулой перестановки (Р = n!).
- Если ответ нет, то воспользуйтесь формулой размещения (А = n! / (n — m)!).
Пример
Мы рассмотрели элементы комбинаторики, формулы и некоторые другие вопросы. Теперь перейдем к рассмотрению реальной задачи. Представьте, что перед вами лежат киви, апельсин и банан.

Вопрос первый: сколькими способами их можно переставить? Для этого воспользуемся формулой перестановок: Р = 3! = 6 способов.
Вопрос второй: сколькими способами можно выбрать один фрукт? Это очевидно, у нас всего три варианта – выбрать киви, апельсин или банан, но применим формулу сочетаний: С = 3! / (2! * 1!) = 3.
Вопрос третий: сколькими способами можно выбрать два фрукта? Какие есть у нас вообще варианты? Киви и апельсин; киви и банан; апельсин и банан. То есть три варианта, но это легко проверить при помощи формулы сочетания: С = 3! / (1! * 2!) = 3
Вопрос четвертый: сколькими способами можно выбрать три фрукта? Как видно, выбрать три фрукта можно одним-единственным способом: взять киви, апельсин и банан. С = 3! / (0! * 3!) = 1.
Вопрос пятый: сколькими способами можно выбрать хотя бы один фрукт? Это условие подразумевает, что мы можем взять один, два или все три фрукта. Следовательно, мы складываем С1 + С2 + С3 =3 + 3 + 1 = 7. То есть у нас есть семь способов взять со стола хотя бы один фрукт.
fb.ru
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Комбинаторика. Факториал. Перестановки. Размещения. Сочетания. Биноминальные коэффициенты. Треугольник Паскаля. Свойства биноминальных коэффициентов. Формула бинома
|
dpva.ru

