Сочетания 9 класс онлайн-подготовка на Ростелеком Лицей
Тема 20.
Сочетания.
В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов во множестве. Важно лишь то, какие именно элементы составляют множество.
К примеру, имеются пять гвоздик разного цвета. Обозначим их буквами a,b,c,d,e. Требуется составить букет из трёх гвоздик. Выясним, какие букеты могут быть составлены.
Если в букет входит гвоздика a, то можно составить такие букеты:
abc, abd, abe, acd, ace, ade.
Если в букет не входит гвоздика а, но входит гвоздика b, то можно получить такие букеты:
bcd, bce, bde.
Если в букет не входит ни гвоздика а, ни гвоздика b, то возможен только один вариант составления букета:
сde.
Определение. Сочетаниям из n элементов по k называется любое множество, составленное из k, элементов, выбранных из данных n элементов.
Число сочетаний из n элементов по k, обозначают (читается «С из n по k»).
В рассмотренном примере, составив все сочетания из 5 элементов по 3, мы нашли, что
С53=10
Выведем формулу числа сочетаний из n элементов по k, где k≤n.
Выясним сначала, как С53 выражается через А53 и Р3. Мы нашли, что из 5 элементов можно составить следующие сочетания по 3 элемента:
abc, abd, abe, acd, ace, ade, bcd, bce, bde, сde.
В каждом сочетании выполним все перестановки. Число перестановок из 3 элементов равно Р3. В результате получим все возможные комбинации из 5 элементов по 3, которые различаются либо самими элементами, либо порядком элементов, т.
Значит,
С53∙Р3=А53
Отсюда, С53=А53Р3
Аналогично будем рассуждать в общем случае. Допустим, что имеется множество, содержащее n элементов, и из его элементов составлены все возможные сочетания по k элементов. Число таких сочетаний равно Сnk. В каждом сочетании можно выполнить Рk перестановок. В результате мы получим все размещения, которые можно составить из n элементов по k. Их число равно Аnk. Значит, Ank=Cnk∙Pk
Отсюда, Сnk=АnkРk, пользуясь тем, что Аnk=n!n-k!, где k≤n, находим, что
Сnk=n!k!n-k!.
Мы получили формулу для вычисления числа сочетаний из n элементов по k при любом k≤n.
Рассмотрим примеры:
Задача 1. Сколько различных стартовых шестерок можно образовать из числа 10 волейболистов?
Решение:
Так как при игре в волейбол функции игроков практически равны, то значение имеет только состав шестерки.
Тогда
Ответ: 210 стартовых шестерок.
В шахматном кружке занимаются 2 девочки и 7 мальчиков. Для участия в соревновании необходимо составить команду из четырёх человек, в которую обязательно должна входить хотя бы одна девочка. Сколькими способами это можно сделать?
В команду входит либо одна девочка, либо две. Разберём оба случая. Если в команде две девочки, то двух мальчиков к ним можно добавить С72 способами. Если же в команду входит только одна девочка (её можно выбрать двумя способами), то команду можно дополнить тремя мальчиками С73 различными способами. Таким образом, общее число возможных команд равно.
С72+2С73=91
Размещения | Сочетания | |
n элементов n клеток | n элементов k клеток | n элементов k клеток |
Порядок имеет значение | Порядок имеет значение | Порядок не имеет значения |
(Тем самым он учится быть и руководителем, и секретарем и т.д). Переходя от каждого нового задания, обучающиеся меняются поручениями.
У нас имеется 5 книг, что у нас всего одна полка, и что на ней вмещается лишь 3 книги . Сколькими способами можно расставить на полке 3 книги?
Сколькими способами можно расставить 3 тома на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 5 книг?
Сколькими способами из 8 учебных предметов можно составить расписание учебного дня из 4 различных уроков.
по скоростной сборке кубика Рубика, составило всего 22,95 секунды.
Алгебра: учеб. для 7 класса общеобразоват. учреждений (Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева) под ред. Г.В. Дорофеева. – 2-е изд. – М. : Просвещение, 2006.Комбинированная математика — Статья и задачи
В прошлый раз мы рассмотрели следующую практическую задачу GMAT по комбинаторике, которая выдает себя за задачу ПЕРЕСТАНОВКИ, потому что связана с «порядком», и поэтому нас интересует порядок, в котором появляются элементы:
На дегустации сыра шеф-повар должен представить главному судье несколько своих лучших творений. Из-за очень странных ограничений мероприятия он должен представить ровно три или четыре сыра. Он принес свой лучший чеддер, бри, гауда, рокфор, грюйер и камамбер.
Сколько потенциальных заказов сыров может составить шеф-повар, чтобы представить их судье?
A) 120
B) 240
C) 360
D) 480
E) 600
(обзор предыдущий пост, как вы, как вы, вроде объяснения. ответ.)
Теперь давайте посмотрим, как небольшое изменение кадра переключает это на КОМБИНИРОВАННУЮ задачу:
На фермерском рынке шеф-повар должен продать некоторые из своих лучших сыров. Из-за очень странных ограничений рынка он может продать ровно два или три сыра. Он принес свой лучший чеддер, бри, гауда, рокфор, грюйер и камамбер. Сколько потенциальных групп сыров он может создать для показа покупателям?
A) 6
B) 15
C) 20
D) 35
E) 120
Doft You Awe Why At Ascompate Complecation Asgive Asgive. проблемы ПЕРЕСТАНОВКИ? В задаче говорилось о «группировках». Это означает, что нас интересуют только задействованные элементы, а не последовательность их появления.
Чеддер, за которым следует бри, за которым следует гауда не считается отличным от бри, за которым следует гауда, а затем чеддер , потому что задействованы одни и те же три сыра, что дает одну и ту же группу.
Итак, как работает математика? Что ж, оказывается, есть быстрая комбинаторная формула, которую вы можете использовать, и она выглядит так:
Давайте демистифицируем ее. Левая сторона просто обозначена, где «C» означает «комбинация». «n» и «k» обозначают большую и меньшую группы соответственно. Итак, если у меня есть группа из 10 картин, и я хочу знать, сколько групп из 4 я могу создать, это будет означать n=10 и k=4. Условно это будет выглядеть так:
Теперь помните, восклицательный знак указывает на факториал . Простой пример: 4! = 4*3*2*1. Вы просто умножаете каждое положительное целое число, полученное с помощью факториала, на единицу.
Итак, как это работает для нашей задачи? Давайте посмотрим:
На фермерском рынке шеф-повар должен продать несколько своих лучших сыров.
Из-за очень странных ограничений рынка он может продать ровно два или три сыра. Он принес свой лучший чеддер, бри, гауда, рокфор, грюйер и камамбер. Сколько потенциальных групп сыров он может создать для показа покупателям?
A) 6
B) 15
C) 20
D) 35
E) 120
Процесс рассмотрения двух чехлов останется такой же. Не может быть одновременно двух и трех сыров. Итак, давайте сначала рассмотрим случай с двумя сырами. На выбор шесть сыров, и мы выбираем подгруппу из двух. Это означает, что n=6 и k=2:
Теперь давайте углубимся и посчитаем:
Отсюда вы заметите, что 4*3*2*1 сокращается сверху и снизу, в результате чего получается 6*5 = 30 в числителе и 2*1 в знаменателе:
Остается мы с:
6C2 = 15 комбинаций двух сыров
А как насчет случая с тремя сырами? Точно так же есть шесть сыров на выбор, но теперь мы выбираем подгруппу из трех.
Это означает, что n=6 и k=3:
Отсюда вы заметите, что 3*2*1 внизу сокращается с 6 вверху, оставляя 5*4 = 20 в числителе. :
Остается:
6C3 = 20 комбинаций трех сыров
С учетом 15 случаев в первой ситуации и 20 во второй, всего 35 случаев, и наш окончательный ответ D.
В следующий раз , мы поговорим о том, что происходит, когда у нас есть перестановки с повторяющимися элементами.
А пока, в качестве упражнения, прокрутите назад и вернитесь к задаче на 10 рисунков, которую я представил ранее, и посмотрите, сможете ли вы найти ответ. Бонусный вопрос: переделайте задачу с подгруппой из 6 картин вместо 4 картин. Попробуйте предугадать: как вы думаете, у нас будет больше комбинаций в этом новом случае или меньше?
Перестановки и комбинации. Введение. Одна проблема, два подхода
Автор: Рич Звеллинг, инструктор Apex GMAT
Дата: 23 февраля 2021 г.
1.3: Комбинации и перестановки — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14748
- Оскар Левин
- Университет Северного Колорадо
Расследуй!
У вас есть набор фишек пяти разных цветов: красный, синий, зеленый, фиолетовый и желтый.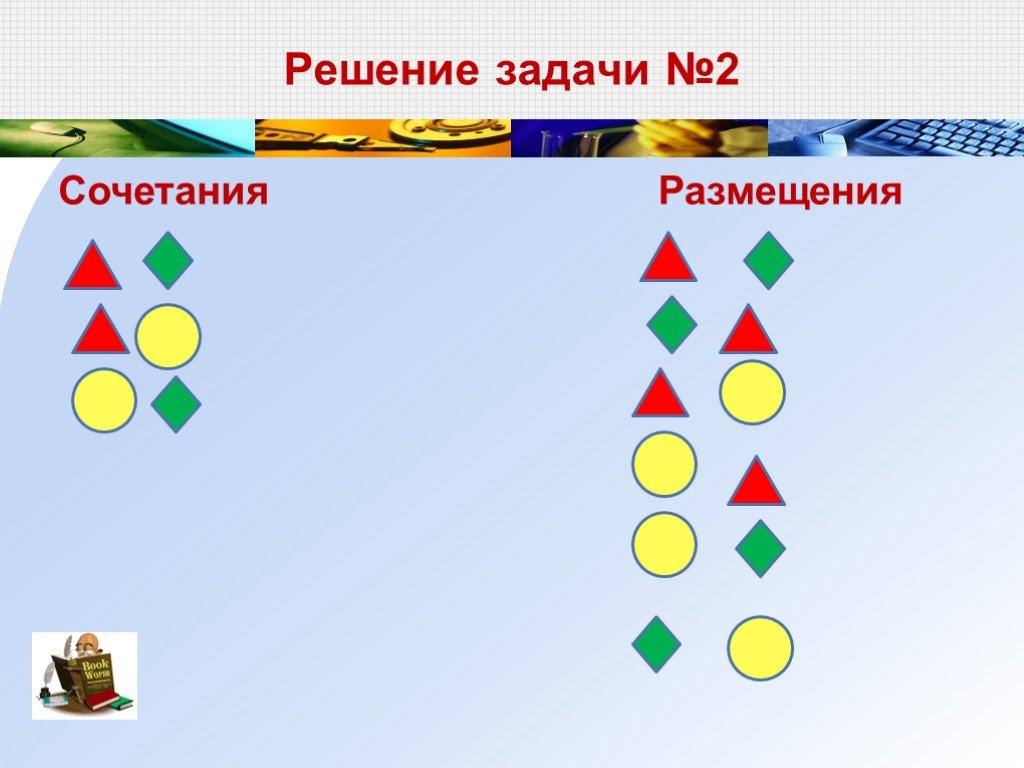
- Сколько различных стопок по две фишки можно составить, если нижняя фишка должна быть красной или синей? Объясните свой ответ, используя как аддитивный, так и мультипликативный принцип.
- Сколько различных стопок по три фишки можно составить, если нижняя фишка должна быть красной или синей, а верхняя — зеленой, фиолетовой или желтой? Как эта проблема связана с предыдущей?
- Сколько существует различных стопок по три фишки, в которых ни один цвет не повторяется? Как насчет стеков из четырех фишек?
- Предположим, вы хотите взять три фишки разного цвета и положить их в карман. Сколько различных вариантов у вас есть? Что, если вы хотите четыре фишки разного цвета? Как эти проблемы связаны с предыдущими?
Перестановка — это (возможная) перестановка объектов. Например, есть 6 перестановок букв 9.0199 а, б, в :
\begin{equation*} abc, ~~ acb, ~~ bac, ~~bca, ~~ cab, ~~ cba. \end{уравнение*} Мы знаем, что у нас есть все перечисленные выше — есть 3 варианта, какую букву поставить первой, затем 2 варианта, какая буква будет следующей, что оставляет только 1 вариант для последней буквы.
Пример \(\PageIndex{1}\)
Сколько существует перестановок букв a, b, c, d, e, f ?
- Ответить
Мы НЕ хотим пытаться перечислить все это. Однако, если бы мы это сделали, нам нужно было бы выбрать букву для записи в первую очередь. Есть 6 вариантов этой буквы. Для каждого выбора первой буквы есть 5 вариантов второй буквы (мы не можем повторить первую букву, мы переставляем буквы и имеем только по одной каждой), и для каждой из них есть 4 варианта третьей, 3 варианты для четвертого, 2 варианта для пятого и, наконец, только 1 вариант для последней буквы. Итак, есть \(6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\) перестановки 6 букв.
Здесь будет полезна небольшая запись: \(n!\text{,}\) читается как «\(n\) факториал», является произведением всех положительных целых чисел, меньших или равных \(n\) (по причинам для удобства мы также определяем 0! как 1).
Таким образом, количество перестановок 6 букв, как видно из предыдущего примера, равно \(6! = 6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\text{.}\) Это обобщает:
Перестановки \(n\) элементов
Существуют \(n! = n\cdot (n-1)\cdot (n-2)\cdot \cdots \cdot 2\cdot 1\) перестановки \(n \) (различные) элементы.
Подсчет биективных функций
Сколько функций \(f:\{1,2,\ldots,8\} \to \{1,2,\ldots, 8\}\) являются биективными ?
- Раствор
Вспомните, что означает биективность функции: каждый элемент в области кодов должен быть образом ровно одного элемента области. Используя двухстрочную запись, мы могли бы записать одну из этих биекций как
. \begin{equation*} f = \twoline{1 \amp 2 \amp 3 \amp 4 \amp 5 \amp 6 \amp 7 \amp 8} {3 \amp 1 \amp 5 \amp 8 \amp 7 \amp 6 \amp 2 \amp 4} \end{уравнение*}На самом деле мы просто переставляем элементы кодового домена, поэтому мы создаем перестановку из 8 элементов.
На самом деле «перестановка» — это еще один термин, используемый для описания биективных функций из конечного множества в себя.Если вы в это верите, то вы видите, что ответ должен быть \(8! = 8 \cdot 7 \cdot\cdots\cdot 1 = 40320\text{.}\) Это можно увидеть и непосредственно: для каждого элемента домен, мы должны выбрать отдельный элемент кодового домена для сопоставления. Есть 8 вариантов, куда отправить 1, затем 7 вариантов, куда отправить 2, и так далее. Умножаем по принципу мультипликативности.
На самом деле «перестановка» — это еще один термин, используемый для описания биективных функций из конечного множества в себя.Иногда мы не хотим переставлять все буквы/цифры/элементы, которые нам даны.
Пример \(\PageIndex{3}\)
Сколько четырехбуквенных «слов» можно составить из букв от a до f без повторяющихся букв?
- Раствор
Это похоже на задачу перестановки 4 букв, только теперь у нас больше вариантов для каждой буквы. Для первой буквы есть 6 вариантов. Для каждого из них есть 5 вариантов второй буквы.
Затем есть 4 варианта для третьей буквы и 3 варианта для последней буквы. Общее количество слов равно \(6\cdot 5\cdot 4 \cdot 3 = 360\text{.}\). Это не \(6!\), потому что мы никогда не умножали на 2 и 1. Мы могли бы начать с \ (6!\), а затем сократите 2 и 1 и, таким образом, напишите \(\frac{6!}{2!}\text{.}\)В общем, мы можем спросить, сколько существует перестановок \(k\) объектов, выбирающих эти объекты из большего набора \(n\) объектов. (В приведенном выше примере \(k = 4\text{,}\) и \(n = 6\text{.}\)) Мы пишем это число \(P(n,k)\) и иногда называем его \(k\)-перестановка \(n\) элементов . Из приведенного выше примера мы видим, что для вычисления \(P(n,k)\) мы должны применить принцип умножения к \(k\) числам, начиная с \(n\) и считая в обратном порядке. Например
\begin{уравнение*} P(10, 4) = 10\cdot 9\cdot 8 \cdot 7. \end{уравнение*}Еще раз обратите внимание, что \(P(10,4)\) начинается с вида \(10!\text{,}\), но мы останавливаемся после 7.
\begin{equation*} P(10,4) = \frac{10\cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = \frac{10!}{6!}. \end{уравнение*} Мы можем формально объяснить эту «остановку», отделив часть факториал нам не нужен:
Затем есть 4 варианта для третьей буквы и 3 варианта для последней буквы. Общее количество слов равно \(6\cdot 5\cdot 4 \cdot 3 = 360\text{.}\). Это не \(6!\), потому что мы никогда не умножали на 2 и 1. Мы могли бы начать с \ (6!\), а затем сократите 2 и 1 и, таким образом, напишите \(\frac{6!}{2!}\text{.}\)
Мы можем формально объяснить эту «остановку», отделив часть факториал нам не нужен:\(k\)-перестановок \(n\) элементов
\(P(n,k)\) количество \(k\)-перестановок \(n\) элементов, число способов упорядочить \(k\) объектов, выбранных из \(n\) различных объектов.
\begin{equation*} P(n,k) = \frac{n!}{(n-k)!}. \end{уравнение*}
Обратите внимание, что когда \(n = k\text{,}\) мы имеем \(P(n,n) = \frac{n!}{(n-n)!} = n!\) (поскольку мы определили \( 0!\) на 1). Это имеет смысл — мы уже знаем, что \(n!\) дает количество перестановок всех \(n\) объектов.
Счетные инъективные функции
Сколько функций \(f:\{1,2,3\} \to \{1,2,3,4,5,6,7,8\}\) являются инъективными ?
- Раствор
Обратите внимание, что здесь не имеет смысла запрашивать число биекций , поскольку их нет (поскольку кодовый домен больше домена, сюръекций нет).
Но чтобы функция была инъективной, мы просто не можем использовать элемент кодового домена более одного раза.Нам нужно выбрать элемент из кодового домена, который будет изображением 1. Есть 8 вариантов. Затем нам нужно выбрать один из оставшихся 7 элементов, чтобы он был образом 2. Наконец, один из оставшихся 6 элементов должен быть образом 3. Таким образом, общее количество функций равно \(8\cdot 7 \cdot 6 = Р(8,3)\текст{.}\)
В целом это демонстрирует, что число инъекций \(f:A \to B\text{,}\), где \(\card{A} = k\) и \(\card{B} = n\ текст{,}\) равен \(P(n,k)\text{.}\)
Но чтобы функция была инъективной, мы просто не можем использовать элемент кодового домена более одного раза. Вот еще один способ найти количество \(k\)-перестановок \(n\) элементов: сначала выбрать, какие \(k\) элементы будут в перестановке, затем подсчитать, сколько существует способов их расположить . После того, как вы выбрали \(k\) объектов, мы знаем, что есть \(k!\) способов упорядочить (переставить) их. Но как выбрать \(k\) объектов из \(n\text{?}\) У вас есть \(n\) объектов, и вам нужно выбрать \(k\) из них.
Вы можете сделать это \({n \выбрать k}\) способами. Тогда для каждого выбора из этих \(k\) элементов мы можем переставить их \(k!\) способов. Используя мультипликативный принцип, мы получаем другую формулу для \(P(n,k)\text{:}\)
Теперь, поскольку у нас уже есть замкнутая формула для \(P(n,k)\), мы можем подставить ее в:
\begin{equation*} \frac{n!}{(n-k)!} = {n \выберите k} \cdot k!. \end{уравнение*}Если мы разделим обе части на \(k!\), мы получим замкнутую формулу для \({n \choose k}\text{.}\)
Замкнутая формула для \({n \выбрать k}\)
\begin{equation*} {n \choose k} = \frac{n!}{(n-k)!k!} \end{equation*}
Мы говорим, что \(P(n,k)\) считает перестановок , а \({n \choose k}\) считает комбинаций . Формулы для каждого из них очень похожи, просто в знаменателе \({n \choose k}\text{.}\) есть лишний \(k!\) что \({n \choose k}\) не различает различные порядки, в которых могут появляться \(k\) объекты.
Мы просто выбираем (или выбираем) \(k\) объекты, а не упорядочиваем их. Возможно, «комбинация» — обманчивый ярлык. Мы не имеем в виду кодовый замок (где порядок определенно имеет значение). Возможно, лучшая метафора — это сочетание вкусов — вам просто нужно решить, какие вкусы сочетать, а не в каком порядке их комбинировать.
Чтобы еще больше проиллюстрировать связь между комбинациями и перестановками, мы закончим пример.
Пример \(\PageIndex{5}\)
Вы решили устроить званый ужин. Несмотря на то, что вы невероятно популярны и у вас 14 разных друзей, у вас достаточно стульев, чтобы пригласить только 6 из них.
- Сколько у вас есть вариантов, кого из 6 друзей пригласить?
- Что, если вам нужно решить не только, кого из друзей пригласить, но и где их рассадить за длинным столом? Сколько вариантов у вас есть тогда?
- Раствор
- Вы должны просто выбрать 6 друзей из 14. Это можно сделать \({14 \выбрать 6}\) способами. Мы можем найти это число, используя треугольник Паскаля или замкнутую формулу: \(\frac{14!}{8!\cdot 6!} = 3003\text{.}\)
- Здесь вы должны подсчитать все способы, которыми вы можете переставить 6 друзей, выбранных из группы из 14. Таким образом, ответ равен \(P(14, 6)\text{,}\), который можно рассчитать как \(\frac{14 !}{8!} = 2192190\текст{.}\)
Обратите внимание, что мы можем думать об этой задаче на подсчет как о вопросе о счетных функциях: сколько инъективных функций есть в вашем наборе из 6 стульев и в вашем наборе из 14 друзей (функции инъективны, потому что у вас не может быть ни одного стула). иди к двум своим друзьям).
Как связаны эти числа? Обратите внимание, что \(P(14,6)\) намного больше, чем \({14 \choose 6}\text{.}\). Это имеет смысл. \({14 \выбрать 6}\) выбирает 6 друзей, но \(P(14,6)\) упорядочивает 6 друзей, а также выбирает их. На самом деле, мы можем точно сказать, насколько больше \(P(14,6)\). В обеих задачах на подсчет мы выбираем 6 из 14 друзей.
Для первого мы останавливаемся там, на 3003 способах. Но во второй задаче на подсчет каждый из этих 3003 вариантов выбора из 6 друзей можно упорядочить ровно \(6!\) способами. Итак, теперь у нас есть \(3003\cdot 6!\) вариантов, и это ровно \(2192190\текст{.}\)Как вариант, посмотрите на первую проблему иначе. Мы хотим выбрать 6 из 14 друзей, но нас не волнует порядок, в котором они выбираются. Чтобы выбрать 6 из 14 друзей, мы можем попробовать это:
\begin{equation*} 14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9. \end{equation*}
Это разумное предположение, так как у нас есть 14 вариантов для первого гостя, затем 13 для второго и так далее. Но догадка неверна (на самом деле это произведение равно \(2192190 = Р(14,6)\)). Он различает разные порядки, в которых мы могли бы пригласить гостей. Чтобы исправить это, мы могли бы разделить на количество различных расстановок 6 гостей (чтобы все они считались одним исходом). Существует ровно \(6!\) способов разместить 6 гостей, поэтому правильный ответ на первый вопрос —
.- Вы должны просто выбрать 6 друзей из 14. Это можно сделать \({14 \выбрать 6}\) способами.
Мы можем найти это число, используя треугольник Паскаля или замкнутую формулу: \(\frac{14!}{8!\cdot 6!} = 3003\text{.}\)
Для первого мы останавливаемся там, на 3003 способах. Но во второй задаче на подсчет каждый из этих 3003 вариантов выбора из 6 друзей можно упорядочить ровно \(6!\) способами. Итак, теперь у нас есть \(3003\cdot 6!\) вариантов, и это ровно \(2192190\текст{.}\)