Вертикальный угол — это… Что такое Вертикальный угол?
«∠», обозначение угла в математике
Плоский у́гол — неограниченная геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла).
Углом также называют фигуру образованную всеми точками плоскости, заключёнными между этими лучами (Вообще говоря, двум таким лучам соответствуют два угла, так как они делят плоскость на две части. Один из этих углов условно называют внутренним, а другой — внешним.
Иногда, для краткости, углом называют угловую меру.
Угловая мера
Угол в измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется.
1 оборот = 2π радианам = 360° = 400 градам.
В системе СИ принято использовать радианы.
В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружности
В математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
В географии в качестве начала отсчёта углов принято направление оси ординат (то есть для наблюдателя, расположенного в начале координат, — относительно направления север (вперёд)), и отсчитывается по часовой стрелке.
Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°.
Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
Центральные и вписанные углы окружности.
В зависимости от величины углы разделяются на:
Невыпуклый угол
Прямой угол
Вариации и обобщения
Величиной ориентированного угла между прямыми AB и CD (обозначение: ) называбт величину угла, на который нужно повернуть против часовой стрелки прямую AB так, чтобы она стала параллельна прямой CD. При этом углы, отличающиеся на , считаются равными. Следует отметить, что ориентированный угол между прямыми CD и AB не равен ориентированному углу между прямыми AB и CD (они составляют в сумме или, что по нашему соглашению то же самое, ). Ориентированные углы обладает следующими свойствами: а) ; б) ; в) точки A,B,C,D, не лежащие на одной прямой, принадлежат одной окружности тогда и только тогда, когда .
Ряд практических задач приводит к целесообразности рассматривать угол как фигуру, получающуюся при вращении фиксированного луча вокруг точки О (из которой исходит луч) до заданного положения. В этом случае угол является мерой поворота луча. Такое определение позволяет обобщить понятие угла: в зависимости от направления вращения различают положительные и отрицательные углы, рассматривают углы, большие 360°, углы, равные 0°, и т. д. В тригонометрии такое рассмотрение позволяет изучать тригонометрические функции для любых значений аргумента.
Понятие угла обобщается также на различные объекты, рассматриваемые в стереометрии (двугранный угол, многогранный угол, телесный угол).
Кроме этого, рассматривается угол между гладкими кривыми в точке касания: по определению, его величина равна величине угла между касательными к кривым.
Wikimedia Foundation. 2010.
dic.academic.ru
ВЕРТИКАЛЬНЫЕ УГЛЫ — это… Что такое ВЕРТИКАЛЬНЫЕ УГЛЫ?
- ВЕРТИКАЛЬНЫЕ УГЛЫ
- ВЕРТИКАЛЬНЫЕ УГЛЫ — см. Угол.
Большой Энциклопедический словарь. 2000.
- ВЕРТИКАЛЬНАЯ КОНЦЕНТРАЦИЯ
- ВЕРТИНСКАЯ Анастасия Александровна
Смотреть что такое «ВЕРТИКАЛЬНЫЕ УГЛЫ» в других словарях:
Вертикальные углы — пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого. На рис. две пары В. у. Рис. к ст. Вертикальные углы … Большая советская энциклопедия
вертикальные углы — см. Угол. * * * ВЕРТИКАЛЬНЫЕ УГЛЫ ВЕРТИКАЛЬНЫЕ УГЛЫ, см. Угол (см. УГОЛ) … Энциклопедический словарь
Вертикальные углы — Две прямые пересекаются, создавая пару вертикальных углов. Одна пара состоит из углов A и B, другая из C и D. В геометрии, два угла называются вертикальными, если они созданы пересечением двух … Википедия
ВЕРТИКАЛЬНЫЕ УГЛЫ — см. Угол … Естествознание. Энциклопедический словарь
углы геометрической видимости — Углы, определяющие зону минимального телесного угла, в которой должна быть видна видимая поверхность огня. Эта зона определяется сегментами сферы, центр которой совпадает с исходным центром огня, а экватор параллелен грунту. Эти сегменты… … Справочник технического переводчика
углы геометрической видимости — 2.12 углы геометрической видимости: Углы, определяющие зону минимального телесного угла, в которой должна быть видна видимая поверхность огня. Эта зона определяется сегментами сферы, центр которой совпадает с исходным центром огня, а экватор… … Словарь-справочник терминов нормативно-технической документации
Инсоляционные углы светопроема — горизонтальные и вертикальные углы, в пределах которых на плоскости светопроема возможно поступление прямых солнечных лучей. При расчете инсоляционных углов глубина световых проемов принимается равной расстоянию от наружной плоскости стены до… … Официальная терминология
ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера
Угол — У этого термина существуют и другие значения, см. Угол (значения). Угол ∠ Размерность ° Единицы измерения СИ Радиан … Википедия
ГОСТ Р ИСО 12509-2010: Машины землеройные. Осветительные, сигнальные и габаритные огни и светоотражатели — Терминология ГОСТ Р ИСО 12509 2010: Машины землеройные. Осветительные, сигнальные и габаритные огни и светоотражатели оригинал документа: 3.1.5 габаритная ширина (overall width): Расстояние между двумя вертикальными плоскостями объемного… … Словарь-справочник терминов нормативно-технической документации
Книги
- Геометрия. 7 класс. Комплексная тетрадь для контроля знаний, И. С. Маркова, С. П. Бабенко, В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия… Издатель: Наша школа, АРКТИ, Подробнее Купить за 164 руб
- Геометрия. 8 класс. Комплексная тетрадь для контроля знаний, И. С. Маркова, С. П. Бабенко, В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 8 класса. Содержание пособия… Издатель: АРКТИ, Наша школа, Подробнее Купить за 157 руб
- Комплексная тетрадь для контроля знаний. Геометрия. 7 класс. ФГОС, Бабенко Светлана Павловна, Маркова Ирина Сергеевна, В пособии представлены контрольно-измерительные материалы (КИМы) по геометрии для проведения текущего, тематического и итогового контроля качества знаний учащихся 7 класса. Содержание пособия… Серия: Комплексная тетрадь для контроля знаний Издатель: Наша школа, Производитель: Наша школа, Подробнее Купить за 144 грн (только Украина)
dic.academic.ru
Вертикальные углы
Вертикальный угол — это плоский угол, лежащий в вертикальной плоскости. К вертикальным углам относятся угол наклона и зенитное расстояние. Угол между горизонтальной плоскостью и направлением линии местности называется углом наклона и обозначается буквой ν. Углы наклона бывают положительные и отрицательные.
Вертикальный круг теодолита. Вертикальный круг теодолита предназначен для измерения вертикальных углов, то есть, углов наклона или зенитных расстояний.
Вертикальный круг большинства теодолитов устроен следующим образом: лимб вертикального круга жестко соединен с трубой (насажен на один из концов оси трубы), центр лимба совмещен с геометрической осью вращения трубы, а его плоскость перпендикулярна этой оси. Деления на лимбе наносят по разному: либо от 0o до 360o, либо от 0o до 180o в обе стороны со знаками «плюс» и «минус» или без знаков и т.д. Для отсчета по лимбу имеется алидада. Основные части алидады: отсчетное приспособление, цилиндрический уровень (или компенсатор) и микрометренный винт.
Пузырек уровня в момент отсчета приводится в нуль-пункт, то есть, ось уровня служит указателем горизонтального направления. Отсчетным индексом является нулевой штрих отсчетного приспособления. Ось уровня и линия отсчетного индекса (линия, соединяющая отсчетный индекс с центром лимба) должны быть параллельны; при выполнении этого условия линия отсчетного индекса будет горизонтальна в момент взятия отсчета по вертикальному кругу.
Взаимное положение лимба и зрительной трубы должно удовлетворять условию: визирная линия трубы и нулевой диаметр лимба должны быть параллельны.
Оба условия вместе составляют так называемое главное условие вертикального круга теодолита; оно читается так: визирная линия трубы должна занимать горизонтальное положение, когда отсчет по лимбу равен нулю и пузырек уровня находится в нуль пункте. На практике оба эти условия могут не выполняться и имеет место случай, изображенный на рис. 4.21-а.
Во-первых, при насаживании лимба на ось трубы между нулевым диаметром лимба и визирной линией трубы остается малый угол x. Во-вторых, линия отсчетного индекса может быть не параллельна оси уровня и между ними существует малый угол y. Таким образом, хотя отсчет по лимбу равен нулю, визирная линия трубы занимает наклонное положение, и угол наклона ее равен:
ν = x + y.
Рис. 4.21 (a) Рис. 4.21 (б)
Если установить визирную линию горизонтально (рис.4.21-б), то отсчет по лимбу станет равным:
N = 360o — (x + y).
Этот отсчет называется местом нуля вертикального круга и обозначается М0.
Таким образом, место нуля вертикального круга теодолита — это отсчет по лимбу вертикального круга при горизонтальном положении визирной линии трубы и оси уровня вертикального круга.
Для конкретного теодолита формулы для вычисления угла наклона и места нуля приводятся в паспорте. Например, для теодолитов 2Т30 и Т15 эти формулы имеют вид:
М0 = 0.5 . (NL + NR),
ν = 0.5 . (NL — NR),
ν = NL — M0,
ν = M0 — NR.
Положение вертикального круга, при котором отсчет по лимбу вертикального круга равен (с точностью до M0) углу наклона, считается основным; у большинства современных теодолитов основным положением является КЛ.
Для измерения углов наклона удобно иметь М0 близким к нулю, поэтому нужно регулярно выполнять поверку места нуля, которая предусматривает следующие действия:
наведение трубы на точку при КЛ, приведение пузырька уровня в нуль-пункт и взятие отсчета по вертикальному кругу,
перевод трубы через зенит, наведение трубы на точку при КП, приведение пузырька уровня в нуль-пункт и взятие отсчета по вертикальному кругу,
вычисление по соответствующим формулам места нуля М0 и угла наклона ν.
Если М0 получается большим, то при основном положении круга нужно навести трубу на точку и микрометренным винтом алидады установить отсчет, равный углу наклона; при этом пузырек уровня отклонится от нуль-пункта. Исправительными винтами уровня привести пузырек в нуль-пункт.
studfiles.net
Привет. какие углы называются смежными, а какие вертикальные?
Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая) . Сумма смежных углов равна 180°. Вертикальные углы — два угла, которые образуются при пересечении двух прямых и не имеют общих сторон. Два вертикальных угла равны.
смежные: это у которых угол равен 180° а вертикальный не знаю
помню только что смежные-это те, сумма которых равна 180 градусов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)<img src=»//otvet.imgsmail.ru/download/1afdabd87bce427e79c58192cc476cb2_i-188.jpg» > Углы 1 и 3, 2 и 4 – вертикальные. <img src=»//otvet.imgsmail.ru/download/1afdabd87bce427e79c58192cc476cb2_i-189.jpg» >
touch.otvet.mail.ru
Ответы@Mail.Ru: докажите свойство вертикальных углов
Два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Теперь доказательство теоремы: Вертикальные углы равны! Представь углы 1, 3 и 2, 4. Угол 2 является смежным как с углом 1 так и с углом 3. Два угла, у которых одна сторона общая а две другие являются продолжениями одна другой, называються смежными. По свойству смежных углов < 1+<2=180градусов. <3+<2=180градусов Отсюда получаем <1=180-<2. <3=180-<2 таким образом, градусные меры углов 1 и 3 равны. Значит и сами углы равны. Теорема доказана
Два угла называются вертикальными, если стороны одного составляют продолжение сторон другого. Так, при пересечении двух прямых AB и СD образуются две пары вертикальных углов: AOD и СOB; AOС и DOB . Теорема. Два вертикальных угла равны. Свойства смежных и вертикальных углов. Пусть даны два вертикальных угла: AOD и СOB т. е. OB есть продолжение OA, а OС продолжение OD. Требуется доказать, что AOD = СOB. По свойству смежных углов можем написать: AOD + DOB = 2d DOB + BOС = 2d Значит: AOD + DOB = DOB + BOС. Если вычесть из обеих частей этого равенства по углу DOB, получим: AOD = BOС, что и требовалось доказать. Аналогично докажем, что AOС = DOB. на рисунке поменяйте В и С местами <img src=»//otvet.imgsmail.ru/download/247168206_c6d3bac30a6cd1eccaf90906d4c1ec73_800.jpg» data-lsrc=»//otvet.imgsmail.ru/download/247168206_c6d3bac30a6cd1eccaf90906d4c1ec73_120x120.jpg» data-big=»1″>
touch.otvet.mail.ru
| Этап урок | Деятельность учителя | Деятельность учащихся | Планируемый результат |
| 1.Организационный этап Цель: вовлечение учащихся в учебный процесс |
Организует положительный настрой на
урок, вспоминает с учащимися способы
деятельности Добрый день. Начинаем наш урок. С каким настроением вы приступаете к работе? — Прежде чем выяснить, чего мы не знаем, что необходимо сделать? |
Воспринимают информацию, реагируют на
вопросы учителя. Учащиеся дают ответ с помощью сигнальных карточек-смайликов -Надо выяснить, чего мы не знаем и самостоятельно найти выход из затруднения. -Выяснить, что нам известно. |
Включение учащихся в учебную деятельность, формирование познавательных УУД |
| 2.Актуализаци опорных знаний. Мотивация
учебной деятельности учащихся Цель: активизация мотивационной деятельности |
Информирует о новых знаниях, мотивирует
учебную деятельность: — В какой большой теме мы с вами сейчас работаем? — Вспомните план, по которому идет изучение любой темы?
— Что из перечисленного мы уже изучили? Сформулируйте свойство смежных углов. |
Воспринимают информацию,
обнаруживают первичное понимание: — Углы 1. Определение 2. Свойства, 3. Сравнение 4. Действия. Определение угла, смежные углы, дают определения, вспоминают свойство смежных углов. |
Развитие коммуникативных компетенций, коммуникативных УУД |
| 3.Актуализация знаний Цель: подготовка к усвоению новых знаний |
Слайд 1
Слайд 2 Ребята, а что можно сказать об углах 4 и 2, 1 и 3, 5 и 7? |
Учащиеся на основании определения
смежных углов находят пары смежных углов
Учащиеся предполагают, что они равны, что стороны одного являются дополнительными полупрямыми к сторонам другого, возможно среди предполагаемых названий пар возникнет название “вертикальные” |
Осознание потребности к построению нового способа действий. |
| 4.Первичное усвоение новых знаний Цель: восприятие учащимися и первичное осознание нового учебного материала |
Организует первичное усвоение знаний
учащимися Как они выглядят, какое название им можно дать? Тема сегодняшнего урока: Слайд 3 Цель нашего урока: познакомиться с понятием вертикальных углов, их свойством и научиться решать задачи с применением этих свойств. Два угла называются вертикальными, если стороны одного являются дополнительными полупрямыми сторон другого Слайд 4 Что можно сказать о вертикальных углах, каким свойством они обладают? Верно! Давайте докажем это. Итак, теорема: Вертикальные углы равны. Доказательство: Пусть 1 и 2 – данные вертикальные углы, СОD и DOA. Отсюда, по теореме о сумме смежных углов заключаем, что каждый из углов DOC и AOB дополняет угол AOD до 180 градусов, т.е. 1 = 2. Что и требовалось доказать. Давайте найдем, где в учебнике рассказано о вертикальных углах и их свойствах, откройте стр. 22 учебника, п.15. Найдите определение вертикальных углов. Прочитайте. Найдите Теорему о вертикальных углах, прочитайте. |
Осмысливают, углубляют понимание
нового материала Вертикальные углы
Учащиеся записывают дату, тему урока в тетрадь
Учащиеся переносят рисунок в тетрадь, наносят обозначения Учащиеся выдвигают гипотезу, что вертикальные углы равны Учащиеся записывают краткую запись теоремы: если 1 и 2 вертикальные, то 1 = 2 Учащиеся записывают доказательство. Учащиеся работают с учебником, читают вслух определение вертикальных углов и теорему о вертикальных углах. |
Усвоение нового понятия “вертикальные углы”, и новых способов деятельности, развитие регулятивной компетенции |
| 5. Первичная проверка понимания Цель: становление правильности и осознанности усвоения нового учебного материала; выявление пробелов и неверных представлений и их коррекция |
Организует проверку понимания на
примере нестандартной ситуации А теперь, ребята, найдем вертикальные углы в нестандартных ситуациях, внимание на интерактивную доску: Слайд 6 На основании чего можно сделать такой вывод? |
Демонстрируют первичное понимание
полученных знаний: Учащиеся определяют пары вертикальных углов: 6 и 4, 3 и 5 и объясняют почему они вертикальные.
DFM и BFA, DFB и MFA, |
Усвоение понятия вертикальных углов и их свойств, формирование критического мышления |
| 6.Первичное закрепление Цель: выявление пробелов, неверных представлений и их коррекция |
Организует решением задач А теперь рассмотрим следующую задачу: — Какие углы изображены на чертеже? — Сколько пар вертикальных углов вы видите? — Чтобы найти углы 1 и 2 какие свойства нужно применить? Приступим к решению: DOA и AOB являются смежными, т.к. АО – общая, а DO и OB – дополнительные полупрямые. Значит, по свойству смежных углов: DOA + AOB=1800, следовательно, ? AOB=1800— DOA; AOB= 1800— 1200 AOB = 600. Мы нашли величину угла 1. 1 и 2 – вертикальные, т.к. стороны угла 1 ОС и OD являются дополнительными полупрямыми к сторонам угла 2 АО и ОВ. По свойству вертикальных углов ? = 2 = 600. Ответ: 600; 600 Решим ещё одну задачу. Откройте учебник, стр.26, задача №7. Что дано в задаче? Учитель делает чертеж на доске: Какие углы при этом образуются? Повторим свойства смежных и вертикальных углов. Решение задачи: AOB= СOD, как вертикальные, значит, СOD=300. AOB и ВОС – смежные углы. Сумма смежных углов равна 180о, значит, ВОС= 180 — AOB. ВОС = 150о. ВОС и АОD – вертикальные, значит они равны. АОD = 150о. Ответ: 300; 150о; 150о. |
Закрепляют полученные знания: Учащиеся записывают условие задачи, делают чертёж, наносят обозначения. Учащиеся отвечают: — вертикальные; — 2 пары; — свойства смежных углов, свойства вертикальных углов, формулируют эти свойства; К доске выходит 1 ученик и решает задачу совместно с классом под руководством учителя. Учащиеся записывают решение в тетрадь.
Учащиеся работают с учебником. Читают задачу вслух: Один из углов, которые получаются при пересечении двух прямых, равен 30 градусов. Чему равны остальные углы? Две пересекающиеся прямые.
Острые, тупые, вертикальные, смежные. Учащиеся озвучивают свойства смежных и вертикальных углов. Один из учащихся идет к доске для решения задачи. |
Применение свойств вертикальных углов при решении задач, формирование способности к обобщению, развитие умения работать с текстом |
| 7.Информация о домашнем задании,
инструктаж по его выполнению Цель: обеспечение понимания цели, содержания и способов выполнения домашнего задания |
Закройте тетради, откройте дневники,
запишите домашнее задание: Слайд 8 |
xn--i1abbnckbmcl9fb.xn--p1ai
Измерение вертикальных углов —
Вертикальные углы – это углы в вертикальной плоскости, проходящей через ось вращения теодолита и визирную ось зрительной трубы (коллимационная плоскость).
Вертикальный угол между отвесной линией и линией визирования называется зенитным расстоянием Z (рис.20).
Вертикальный угол между горизонтальной линией и линией визирования называется углом наклона () (см. рис.20).
Z + = 90°.
С помощью теодолитов ТЗО, 2ТЗО которые используются при выполнении этой лабораторной работы, измеряются углы наклона,
поэтому в дальнейшем будем говорить об измерении углов наклона. Полный приём измерения угла наклона состоит из измерений в положениях «круг лево» и «круг право».
Теодолит устанавливается над заданной точкой и приводится в рабочее положение. Ослабив закрепительные винты алидады горизонтального круга и вертикального круга, выполняется наведение на визирную цель. При выполнении работы в лаборатории визирной целью является учебная марка. На рис. 21 показаны варианты наведения на различные виды марок при измерении вертикальных углов.
Наведение выполняется сначала грубо «вручную», а затем, закрутив закрепительные винты и добившись чёткого изображения визирной цели, выполняется точное наведение с помощью наводящих винтов. После этого берётся отсчёт по шкале отсчётного устройства вертикального круга теодолита.
При работе с теодолитами ТЗО, 2ТЗО перед взятием отсчёта с помощью подъёмных винтов приводится в нуль-пункт пузырёк уровня алидады горизонтального круга. Такие измерения выполняются в пол жениях «круг лево» и «круг право».
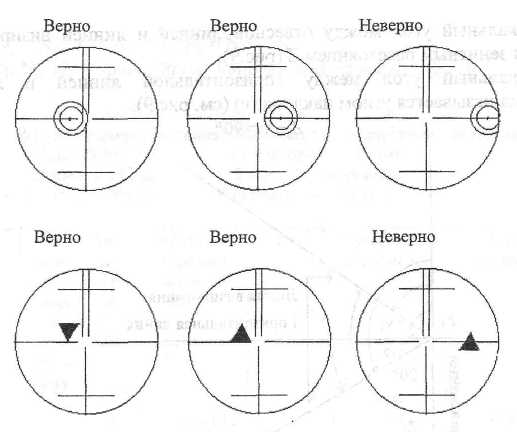
Рис. 21. Схема наведения на марки
Углы вычисляются по формулам:
для теодолита ТЗО
= (КЛ – КП -180) / 2;
= КЛ-МО; МО = (КЛ + КП +180) / 2; (11)
= МО – КП -180;
для теодолитов 2ТЗО
= (КЛ – КП) / 2;
= КЛ – МО; МО = (КЛ + КП) / 2; (12)
= МО – КП,
где КЛ – отсчёт по шкале вертикального круга, взятый в положении теодолита «круг лево»; КП – отсчет по шкале вертикального круга, взятый в положении теодолита «круг право»; МО – место нуля.
Место нуля — это отсчёт по шкале вертикального круга,
соответствующий горизонтальному положению визирной оси зрительной трубы и оси уровня вертикального круга. Для записи
результатов измерений углов наклона может использоваться журнал
измерений, приведённый в табл. 13.
Таблица 13
Журнал измерения углов наклона
Дата: 7.07.2010 Погода: облачно, тихо
Время: 8 ч 48 мин Видимость: хорошая
Теодолит:2ТЗОП № 848 Наблюдал: Иванов В.И.
| Назва-ние или номер станции | Назва- ние или номер точки визиро-вания | Положение КЛ КП | Отсчёты по вертикальному кругу | Место нуля МО | Угол наклона |
| о / | о / | ||||
| А | 1 | кл кп | +2 17,5 (1) -2 19,0 (2) | -0,8(3) | +2 18,2(4) |
| 2 | кл кп | -1 02,0 (5) + 1 01,0 (6) | -0,5(7) | -1 01,5(8) |
Примечание. Цифры в скобках указывают последовательность измерений и записей.
Контролируется качество измерения углов наклона по постоянству места нуля, Колебание места нуля не должно превышать 1′ для теодолита 2ТЗОП.
* – все приведённые в методических указаниях допуски при выполнении лабораторной работы могут быть увеличены в два раза.
einsteins.ru
