Способы решения уравнения y(x)=0
Решение уравнений в пакете Excel
Решить уравнение, это значит найти те значения аргумента, при которыхфункция равна нулю. Или говорят: найти нули функции.
1.Табличный
2.Графический
3.Аналитический
4.Численный
Рассмотрим пример нахождения корней уравнения:
5 sin( 3 x + 2 )- 2 .5x 2 + e x = 0
1.Табличный способ: в общем случае корни заранее не известны,
поэтому | необходимо сначала | функцию протабулировать | на некотором | ||||
интервале значений аргумента, проанализировать где функция меняет знак с+ |
| ||||||
на – или с – на +, там она и будет иметь корни. |
|
|
|
| |||
2. | Графический способ: если полученную таблицу значений функции |
| |||||
обратить в график, т.е. наглядно представим числовые значения в виде графика, |
| ||||||
то увидим примерно точки пересечения графика с осью аргумента. Абсциссы |
| ||||||
этих точек и будут корнями уравнения. |
|
|
|
| |||
3. | Аналитический | способ: | это | точное | нахождение | корней | по |
формулам. |
|
|
|
|
|
|
|
4. | Численный способ: известны методы секущих, дихотомии и др. В |
| |||||
различных пакетах компьютер в основном использует численные методы при решении уравнений. В Excel рассмотрим две команды позволяющие найти корни: подбор параметра ипоиск решения. Ищем корни уравнения, задавая соответствующим образом начальные значения аргумента при поиске корня одной из команд системы Excel.
Построение таблицы значений функции
Создайте список значений аргумента в диапазоне [–1;2],с шагом 0,2.
1. В окне открытого листа введите начальные значения создаваемого ряда прогрессии в первую ячейку и вторую ячейку диапазона.
Для этого введите в ячейку A2 значение –1,в ячейку А3 значение–0,8.
2. Выделяем эти две ячейки А2 и А3. Наведите курсор мыши на правый нижний угол выделенных ячеек и, когда курсор станет тонким черным крестом,
при нажатой ЛЕВОЙ кнопке мыши протащите маркер заполнения вверх или вниз по столбцу либо вправо, либо влево по строке.
Рис. 7
3.В конце нужного диапазона отпустите левую кнопку мыши. Столбец будет заполнен значениями аргумента.
4.Для создания значений функции заполните следующий столбец.
Щелкните в ячейке B2. Введите в строку формул символы=, затем по виду функции вводим =5*SIN(3*А2+2)-2,5*А2^2+EXP(А2)и нажмите клавишу
Enter.
5. Выделите диапазон B2…B17 (этот диапазон включает в себя столько же
строк, сколько и диапазон аргументов | в столбце). | ВыберитеА | команду |
Главная\Редактирование\Заполнить\Вниз, и | столбец B | будет | заполнен |
значениями функции. Или заполнение можно было сделать и проще: взять ячейку В2 за маркер заполнения и протащить левой кнопкой по нужному диапазону.
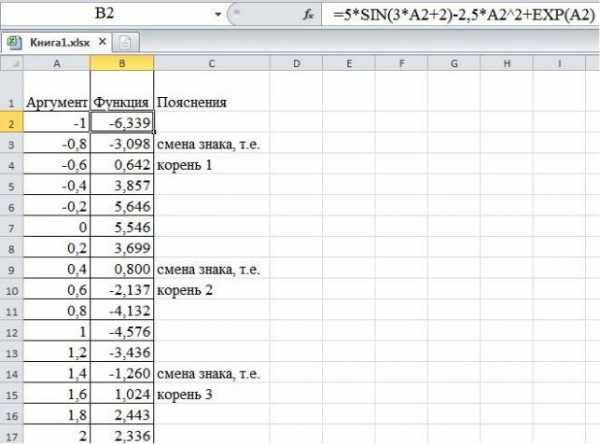
Рис. 8 6. Анализируя столбец В, видим, что первый корень находится между
–0,8и–0,6;второй корень – между 0,4 и 0,6; третий корень – между 1,4 и 1,6
(Рис. 8).
Построение графика функции
Выделите мышью все значения в столбцах А иB (в том числе и ячейки А1 и В1 где слова, они будут в легенде). Выполните команду Вставка\
Диаграммы \ Точечная \ Точечная с гладкими кривыми. В лист будет вставлена диаграмма с изображением нашего графика (Рис. 9).
23
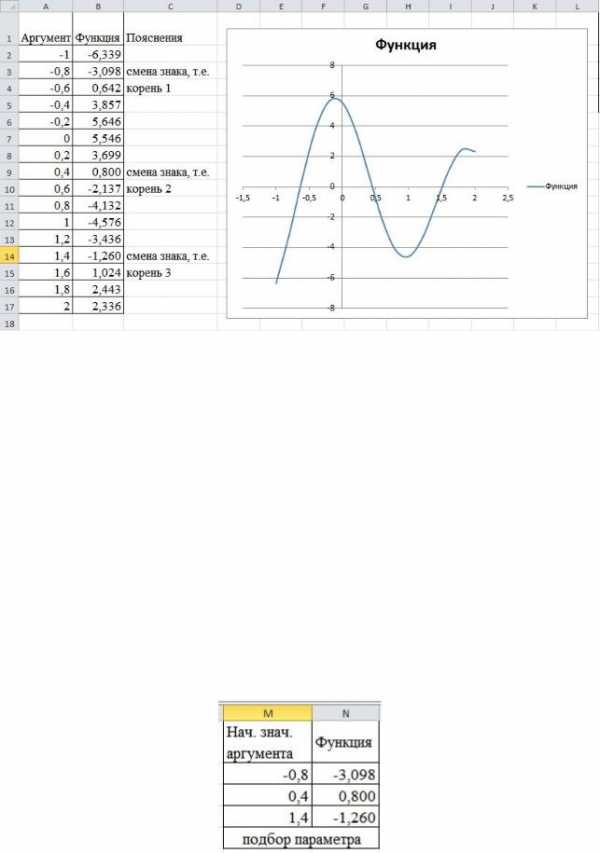
Рис. 9
Глядя на график, делаем вывод о существовании трёх корней, т.к. три
точки пересечения с осью аргумента.
Два способа решения уравненияy(x)=0 в системе Excel, реализующие численные методы решения.
Первый способ
Корни уравнения найдём с помощью командыПодбор параметра.
Исходную информацию занесём в ячейки вспомогательной таблицы:
1. Скопируем из таблицы ячейки из столбцов A и B, где функция меняет
знак и вставим их во вспомогательной таблице в качестве начальны приближенных значений корней (Рис. 10).
Рис. 10
24
2. Скопируйте таблицу и вставьте рядом для второго способа, т.к.
начальные приближенные значения корней будут такие же.
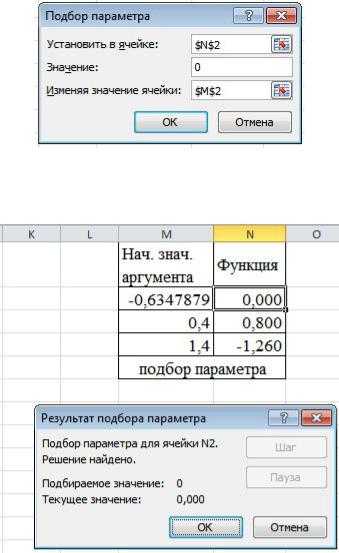
3.После этого выполним командуПодбор параметра. Для этого Выберите команду:Данные\Работа с данными \Анализ «Что-если» \Подбор параметра. На экран будет выведено диалоговое окно с названиемПодбор
параметра.
4.В поле Установить в ячейке введите ссылку на ячейку, в которой содержится формула уравнения (Рис. 11). В полеЗначение введите значение,
которое находится по другую сторону знака равенства в уравнении( нашем случае 0). В поле Изменяя значение ячейки введите ссылку на ячейку,
в которой содержится значение аргумента уравнения. Щелкните на кнопке OK.
Рис. 11
Вы получите результат в диалоговом окне (Рис. 12).
Рис. 12
studfiles.net
Решите уравнение x^2+y=0 (х в квадрате плюс у равно 0)
Найду корень уравнения: x^2+y=0
Виды выражений
Решение
Подробное решение[LaTeX]
Это уравнение видаa*x^2 + b*x + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$x_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$x_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = y$$
, то
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (y) = -4*y
Уравнение имеет два корня.
x1 = (-b + sqrt(D)) / (2*a)
x2 = (-b - sqrt(D)) / (2*a)
или
$$x_{1} = \sqrt{- y}$$
$$x_{2} = — \sqrt{- y}$$ Быстрый ответ
[LaTeX]
_________________ _________________
4 / 2 2 /atan2(-im(y), -re(y))\ 4 / 2 2 /atan2(-im(y), -re(y))\
x1 = - \/ im (y) + re (y) *cos|---------------------| - I*\/ im (y) + re (y) *sin|---------------------|
\ 2 / \ 2 /$$x_{1} = — i \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \sin{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )} — \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \cos{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )}$$
_________________ _________________
4 / 2 2 /atan2(-im(y), -re(y))\ 4 / 2 2 /atan2(-im(y), -re(y))\
x2 = \/ im (y) + re (y) *cos|---------------------| + I*\/ im (y) + re (y) *sin|---------------------|
\ 2 / \ 2 /$$x_{2} = i \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \sin{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )} + \sqrt[4]{\left(\Re{y}\right)^{2} + \left(\Im{y}\right)^{2}} \cos{\left (\frac{1}{2} \operatorname{atan_{2}}{\left (- \Im{y},- \Re{y} \right )} \right )}$$
www.kontrolnaya-rabota.ru
Как решать уравнения типа x+y=xy? Подскажите общий алгоритм. Не уравнение x+y=xy, а уравнения типа x+y=xy!! 🙂
Там в конечном уже факториалы всплыли?
Откинь явное решение: x = y = 0, подели обе части на xy и подставляя в полученное, например, x = 3, вычисли y. Понятно, что решений будет — невообразимое количество.
y+x=y x. y= yx-x. y-yx=-x. y (1-x)=-x. y=-x/(1-x).
ОДНО уравнение с ДВУМЯ переменными НЕ РЕШАЕТСЯ. Иногда бывают диофантовы уравнения, но всё равно нужно ещё хотя бы одно данное. А вы хотите из одного данного получить два. Так не бывает. И это проходят и доказывают ещё на 1ом курсе.
А может, автор вопроса имеет в виду ху факориал-факториал? Тогда все математики будут в шоке)
touch.otvet.mail.ru
