Предел функции. Повторные пределы функции. Предел функции нескольких переменных
Функция f(M) =f(x1,x2, …,xn) имеет предел АRmпри стремлении переменных M (x1,x2, …,xn)Rnк величинам M0 (a1,a2, …,an)Rn, если для любого как угодно малого положительного числа ε > 0 существует положительное и зависящее от этого ε число δ, что для всех точек М (x1,x2, …,xn)Rnпопадающих в δ окрестность точки М0значения функции попадают в ε окрестность точки А:
( ε > 0) (δ = δ(ε) > 0) (MOδ( M0 ) \ {M0}):f
Точка М может и не совпадать с М0. Следует отметить, что этот предел должен существовать и не зависеть от способа стремления переменных (x1,x2, …,xn) к величинам (a1,a2, … ,an). Это свойство можно записать так.
На основании леммы п. 1можно утверждать, что стремление к точке означает координатную сходимость | . |
Независимость стремления переменной точки к точке сгущения означает, что
.
Рассмотрим примеры, которые иллюстрируют зависимость значения предела от характера стремления текущей точки к точке сгущения, что означает отсутствие предела.
Теорема 1.Если
1) существует двойной предел
2) при любом yсуществует простой предел по переменной х:
то существует повторный предел
и он равен значению двойного предела А.
Доказательство.Соотношение (1.1) означает, что
(ε > 0) (δ = δ (ε, M0) > 0) (0 < |x – a| < δ, 0 < |y — b | < δ)): |f(x,y) – A| < ε
Зафиксируем переменную у в интервале 0 < |у — b| < δ и перейдём к пределу в неравенстве | f(x,y) — А | < δ прих→а. Получим | φ(y) — А| < ε, где 0 < | у — b | < δ, что означает
.
Для функции нескольких переменных можно определить понятие предела по одной из переменныхпри фиксированных значениях остальных переменных. В связи с этим возникает понятиеповторного предела.
Определение
Рассмотрим функцию двух переменных , определенную в некоторой выколотой окрестности точки. Выберем и зафиксируем переменную. Получим функцию как бы одной переменной. Рассмотрим предел:
Будем считать, что существует. Теперь снимем фиксацию с переменнойи рассмотрим следующий предел:
Если этот предел существует, то говорят, что есть повторный предел функциив точке.
Аналогично мы можем фиксировать сначала переменную . В этом случае мы также получим повторный предел, но, вообще говоря, другой:
Это определение можно распространить и на функции нескольких переменных .
Равенство повторных пределов
Пусть функция , определена в выколотой окрестности точкии имеет в этой точке предел (обычный). Тогда любой повторный предел в точкесуществует и равен обычному пределу этой функции в этой же точке.
В обратную сторону утверждение, вообще говоря, неверно.
Критерий Коши существования предела функции.
Для того чтобы функция имела в точке x0 конечный предел, необходимо и достаточно, чтобы для любого> 0 существовало такое>0, что для любых x1X и x2X, удовлетворяющих условиям, выполнялось неравенство.
Если же x0=, то критерий Коши имеет следующий вид:
для любого > 0 существует такое> 0, что для любых x1X и x2X, удовлетворяющих условиям, выполняется неравенство.
Доказательство. Необходимость. Пусть и. Это означает, что для любого> 0 существует такое> 0, что для всех точексправедливо неравенство.
Выберем x1X и x2X так, чтобы выполнялись условия. Тогда имеем
Достаточность. Пусть функция такова, что для любого> 0 существует такая окрестность точки x0, что для всех точекиз этой окрестности справедливо неравенство.
Покажем, что отсюда следует существование у функции f конечного предела в точке x0. Возьмём какую-либо последовательность и произвольно зададим>0. Для этого, согласно сделанному предположению, существует такая окрестность точки x0, для всех точекиз которой справедливо неравенство.
Поскольку последовательность xn сходится к x0, существует такое N, что все xn при n > N попадают в указанную окрестность точки x0. Поэтому для всех n > N, m > N
т. е. числовая последовательность удовлетворяет условиям критерия Больцано–Коши для числовых последовательностей и, следовательно, сходится. Таким образом, для каждой последовательности, последовательностьсходится. Отсюда, как известно, следует существование конечного предела. □
studfiles.net
2 предел и непр-ть
7. Предел функции нескольких переменных
Говорят,
что последовательность
точек  с координатами
стремится к точке
сгущения некоторого множества
с координатами
стремится к точке
сгущения некоторого множества  ,
если
,
если
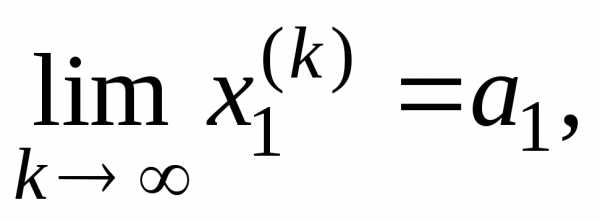
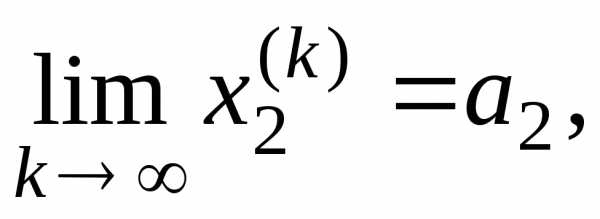
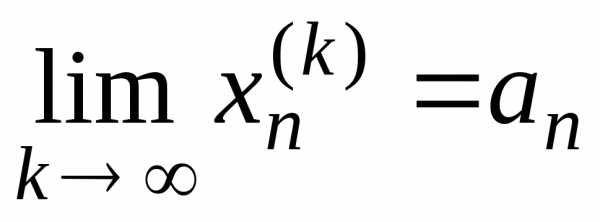 .
. При
этом расстояние 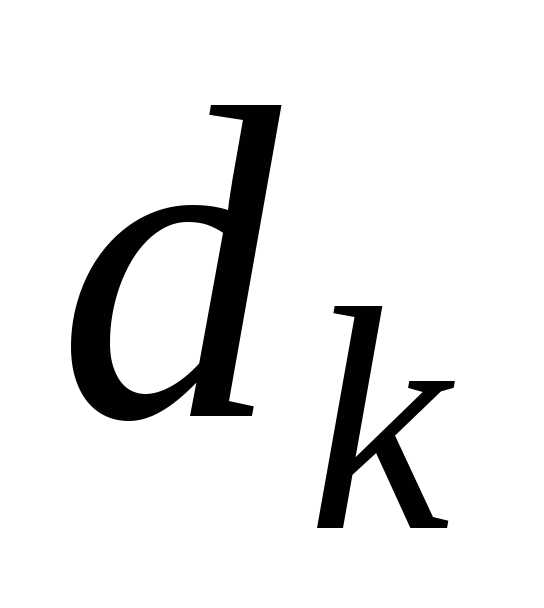 между точкамипоследовательности
и точкой
,
когданеограниченно возрастает, стремится
к нулю, т.е.
между точкамипоследовательности
и точкой
,
когданеограниченно возрастает, стремится
к нулю, т.е.
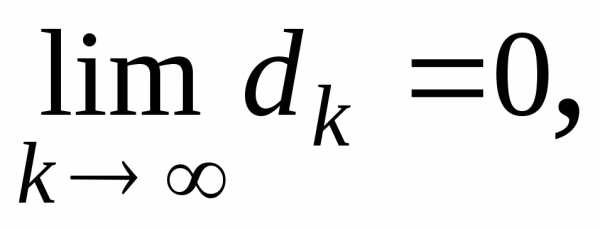
так как
 =
= 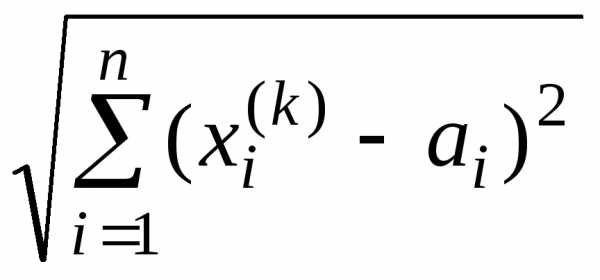 =
.
=
.
Верно и обратное: если 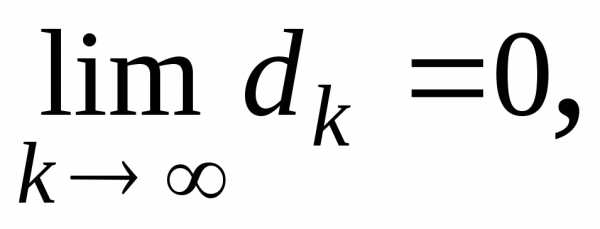 то последовательность точекстремится к точке.
то последовательность точекстремится к точке.
Пусть
функция определена в
некоторой окрестности D точки  ,
за исключением, быть может, самой точки
,
за исключением, быть может, самой точки 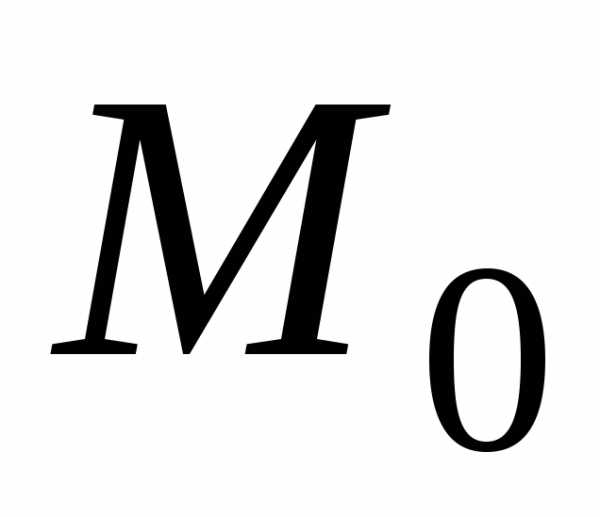 .
.
По
аналогии с определением предела функции
одной переменной, говорят, что функция  при стремлении
переменных
,соответственно,
к
,если для каждого
сколь угодно малого наперед заданного
положительного числа
при стремлении
переменных
,соответственно,
к
,если для каждого
сколь угодно малого наперед заданного
положительного числа  (эпсилон) существует такое число
(эпсилон) существует такое число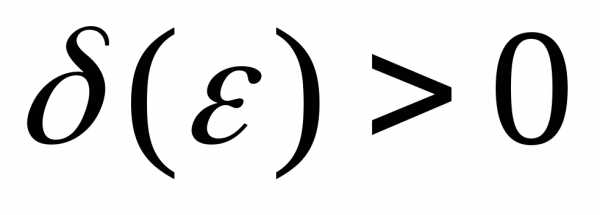 ,
что
,
что
(2)
как только
, …,.
При этом точка предполагается взятой изD и отличной от . Итак, неравенство (2) для функции должно выполняться во всех точках множества D, лежащих в достаточно малой окрестности
точки , но исключая саму эту точку (если она принадлежитD). В этом случае обозначают предел функции так:
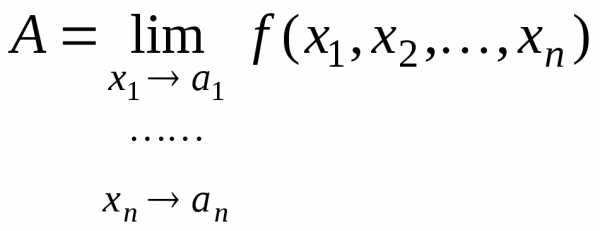 .
.
В геометрических терминах можно перефразировать данное определение следующим образом.
Говорят,
что число  являетсяпределом
функции
являетсяпределом
функции 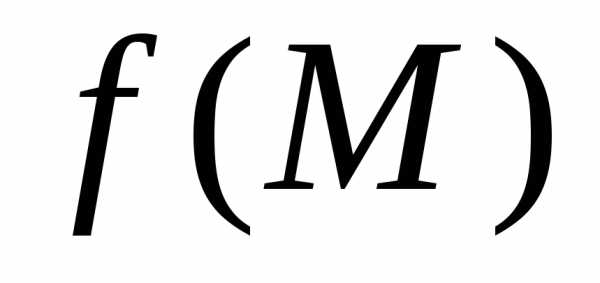 при стремлении
точки
при стремлении
точки  к точке
к точке (или – пределом функции
(или – пределом функции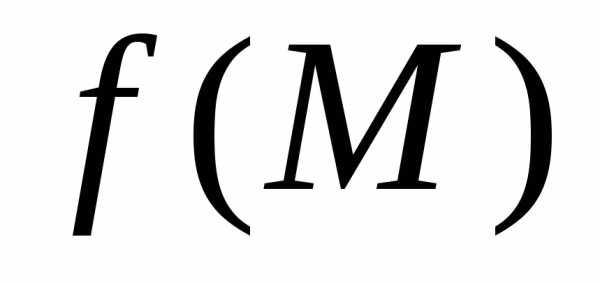 в точке
в точке 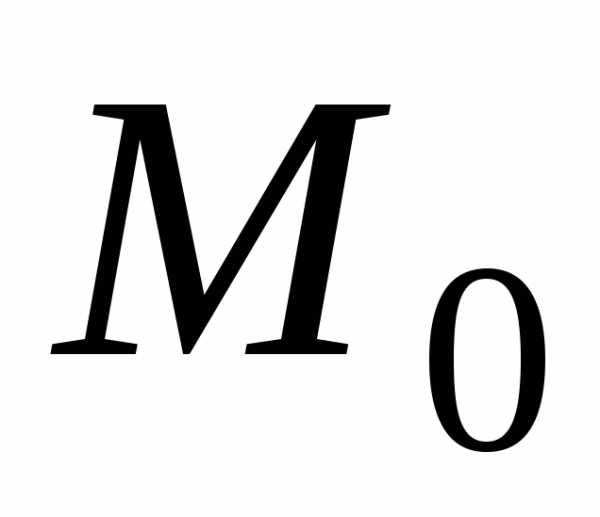 ),
если для каждого сколь угодно малого
наперед заданного положительного числа
),
если для каждого сколь угодно малого
наперед заданного положительного числа  существует такое число
существует такое число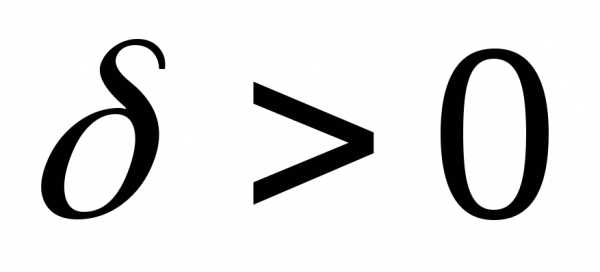 ,
что
,
что
( )
)
как только расстояние между точками .
 предполагается взятой изD и отличной
от
предполагается взятой изD и отличной
от  ,
а неравенство для функции должно
выполняться во всех точках множества D,
лежащих в достаточно малой сферической окрестности точки
,
а неравенство для функции должно
выполняться во всех точках множества D,
лежащих в достаточно малой сферической окрестности точки 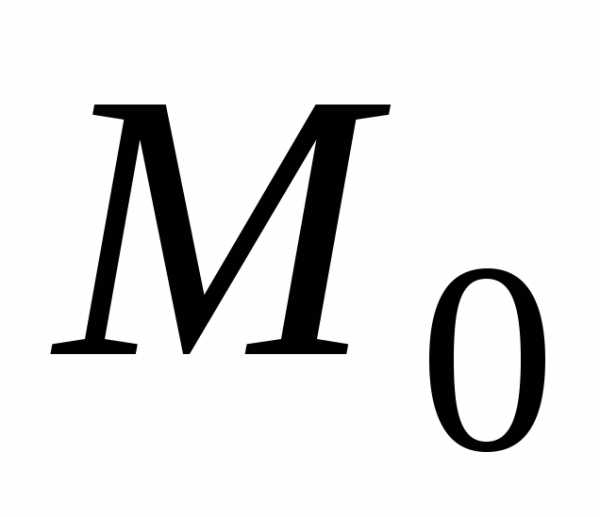 ,
за исключением самой этой точки.
,
за исключением самой этой точки.Обозначение предела функции, соответствующее данному определению:
.
Два приведенных выше определения предела функции многих переменных являются равносильными.
Аналогично устанавливается понятие о бесконечном пределе функции: неравенство (2) заменяется на
,
если ,
и
,
и
, если,
где  – произвольное наперед заданное сколь
угодно большое положительное число.
– произвольное наперед заданное сколь
угодно большое положительное число.
Точка является для областиDточкой сгущения, если в этой области найдутся точки со сколь угодно большими (положительными) координатами.
Тогда
говорят, что функция имеет пределом
число  при стремлении
переменных к
при стремлении
переменных к 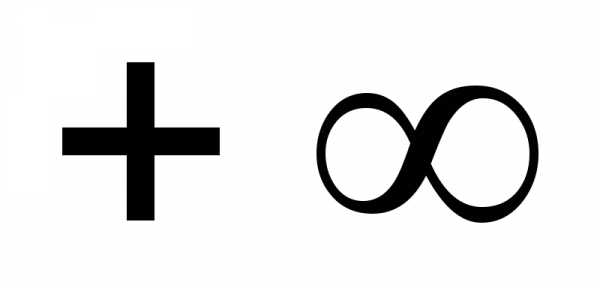 ,
если для каждого сколь угодно малого
наперед заданного положительного числа
,
если для каждого сколь угодно малого
наперед заданного положительного числа существует такое число
существует такое число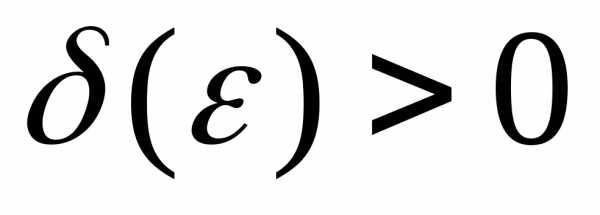 ,
что
,
что
как только
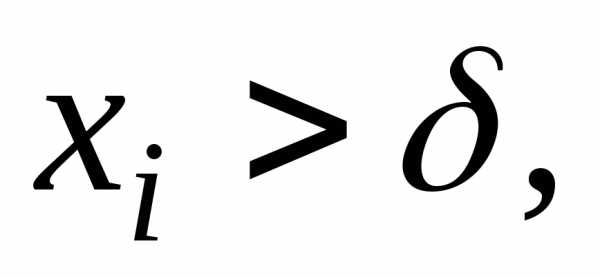
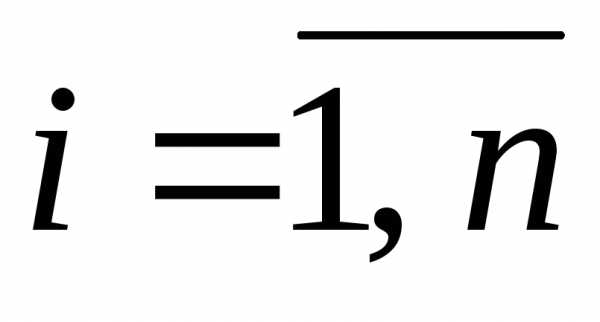 .
.
Обозначаем это следующим образом:
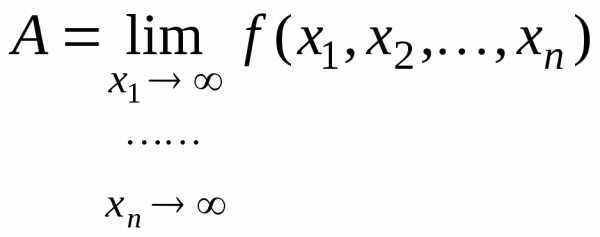
Условие, необходимое и достаточноедля
существования предела функции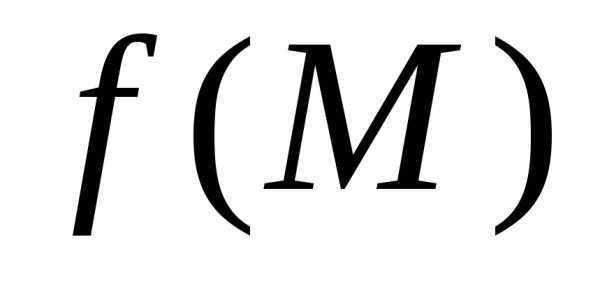 в точке
в точке формулирует следующая теорема.
формулирует следующая теорема.
Теорема. Если
из множестваD извлечь последовательность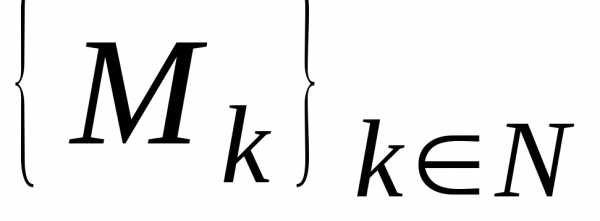 отличных от
отличных от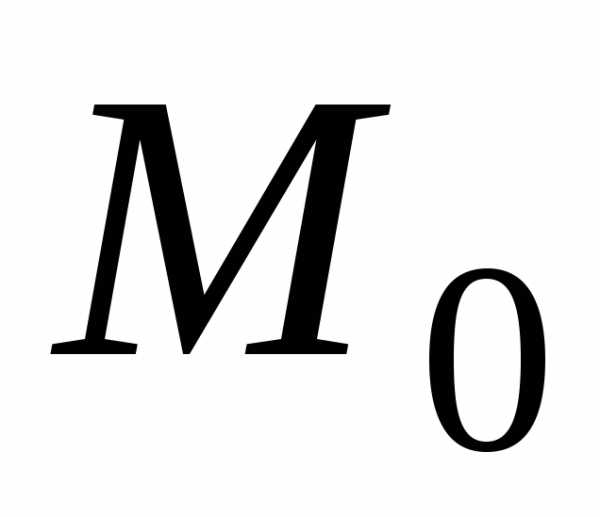 точек, сходящуюся к
точек, сходящуюся к ,
то числовая последовательность,
состоящая из соответствующих значений
функции, всегда сходится к.
,
то числовая последовательность,
состоящая из соответствующих значений
функции, всегда сходится к.
8. Повторные пределы
Наряду с
рассмотренным пределом функции
приодновременном стремлении всех
ее аргументовк их пределам, определим
несколько иной предел для функции многих
переменных, который получается в
результатеряда последовательных
предельных переходов по каждому
ее аргументу в том или ином порядке.
Будем называть такой пределповторным,
тогда как рассмотренный ранее — 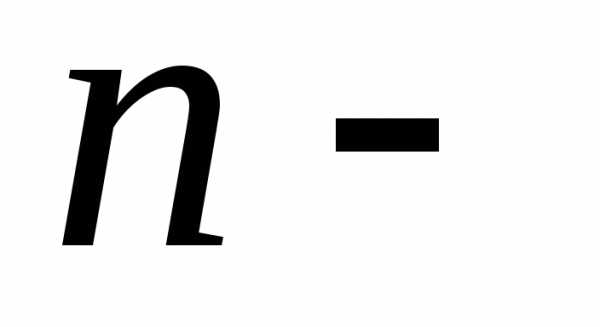 кратным(илидвойным, тройным и т.д. –
при,
соответственно).
кратным(илидвойным, тройным и т.д. –
при,
соответственно).
Для простоты
ограничимся случаем функции двух
переменных 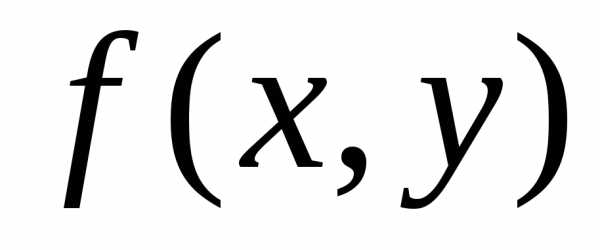 .
Пусть областьDизменения переменных
.
Пусть областьDизменения переменных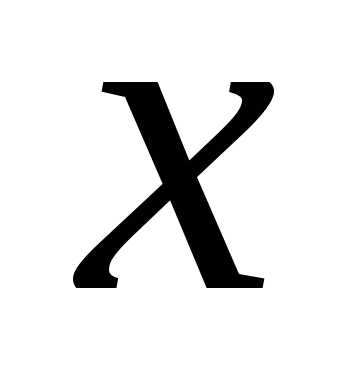 и
и такова, что
такова, что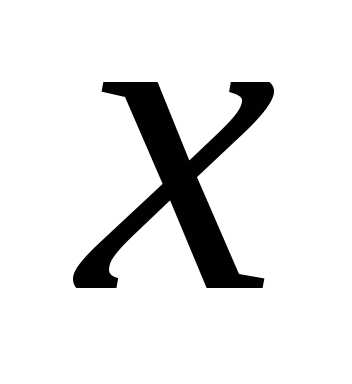 независимо от
независимо от  может принимать любое значение из
некоторого множества
может принимать любое значение из
некоторого множества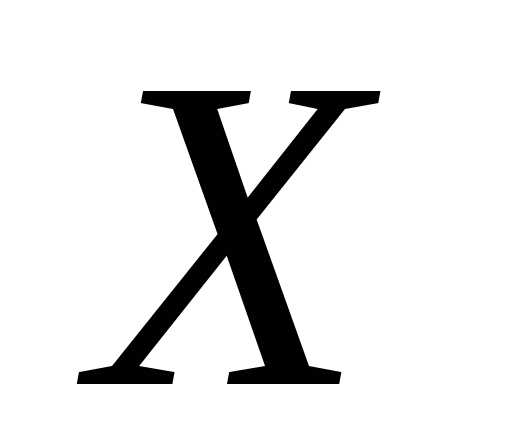 ,
для которого
,
для которого служит точкой сгущения, но не принадлежит
ему, а переменная
служит точкой сгущения, но не принадлежит
ему, а переменная ,
тоженезависимо от
,
тоженезависимо от  ,
– любое значение из множества
,
– любое значение из множества с не принадлежащей ему точкой сгущения
с не принадлежащей ему точкой сгущения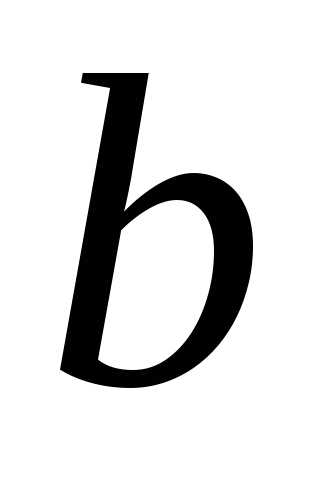 .
Тогда областьD.
.
Тогда областьD.
Если при любом фиксированном 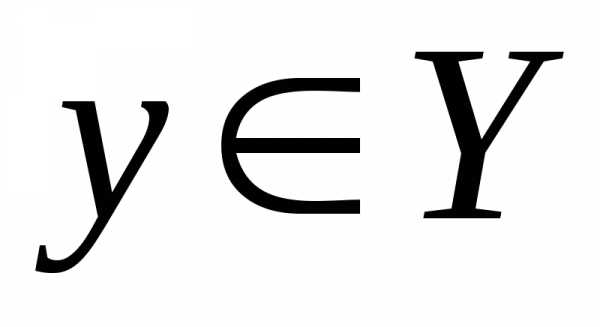 для функции
для функции (которая при фиксированном
(которая при фиксированном будет функцией одной переменной
будет функцией одной переменной )
существует предел при,
то он, этот предел, вообще говоря, будет
зависеть от зафиксированного
)
существует предел при,
то он, этот предел, вообще говоря, будет
зависеть от зафиксированного :
:
.
Если теперь существует предел функции 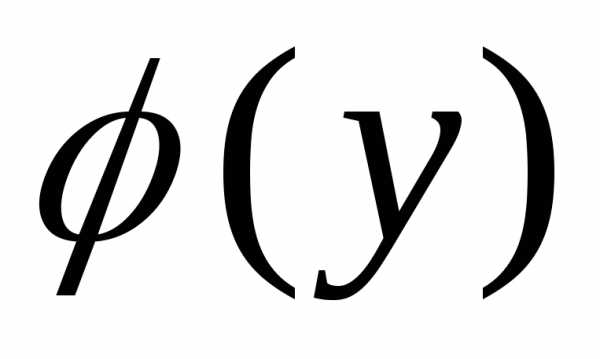 при
при ,
,
,
то он и будет являться одним из повторных
пределов функции 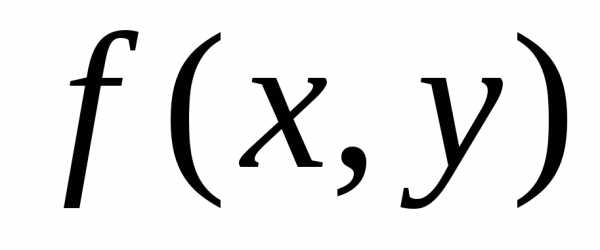 .
.
Если предельные переходы произвести в другом порядке, то получим другой повторный предел этой же функции:
.
Вообще говоря, повторные пределы не обязательно равны между собой. Может случиться и так, что один из повторных пределов существует, а другой – нет.
Для иллюстрации этого рассмотрим несколько примеров. Пусть в области заданы функции:
1. и. Тогда
,
,
а ,
.
2.  3.
3. .
.
Здесь в обоих
случаях существует повторный предел
,
но нет повторного предела.
А в последнем примере нет и простого
предела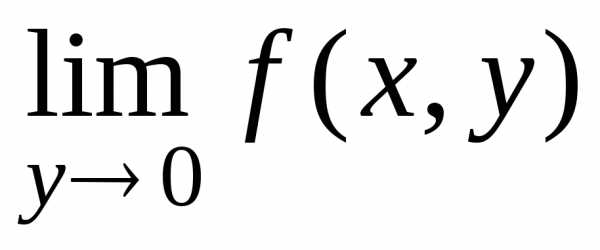 .Проверьте!
.Проверьте!
Связь между двойными и повторными пределами устанавливает следующая теорема.
Теорема.Если
существует двойной предел (конечный или нет)
 и
и
при любом
 существуетконечный простой предел
по
существуетконечный простой предел
по 
,
то существует повторный предел
и равен двойному:
= .
.
Если, наряду с
условиями 1 и 2 теоремы, при любом 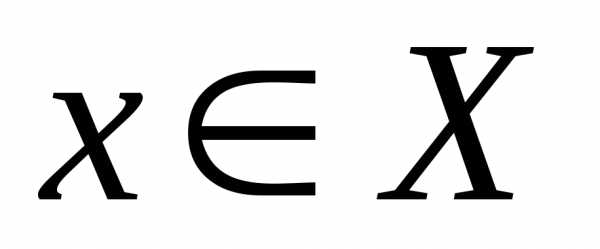 существуетконечный простой предел
по
существуетконечный простой предел
по 
,
то существует и второй повторный предел, который тоже равен двойному, т.е.
,
тем самым мы определили условия, при которых оба повторных предела равны.
Из этой теоремы становится ясно, что в примерах 1 и 2 двойной предел не существует, а в примере 3 он существует и равен 0, откуда следует, что выполнение условия 1) теоремы не влечет за собой выполнения условия 2).
Замечание. Существование двойного предела не является необходимым условием для равенства повторных пределов.
Рассмотрим еще
один пример. Функция  определена на всей плоскости
определена на всей плоскости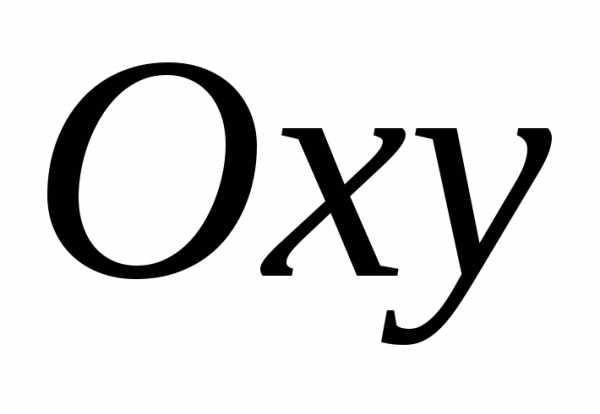 за исключением точки
за исключением точки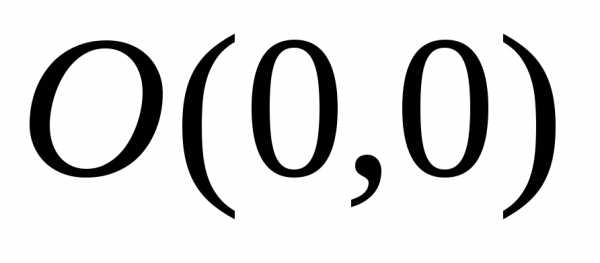 .
.
Возьмем две
сходящиеся к 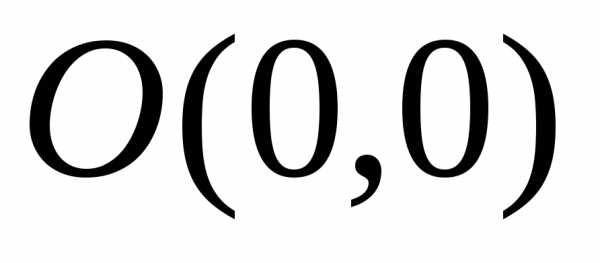 последовательности точек из области
последовательности точек из области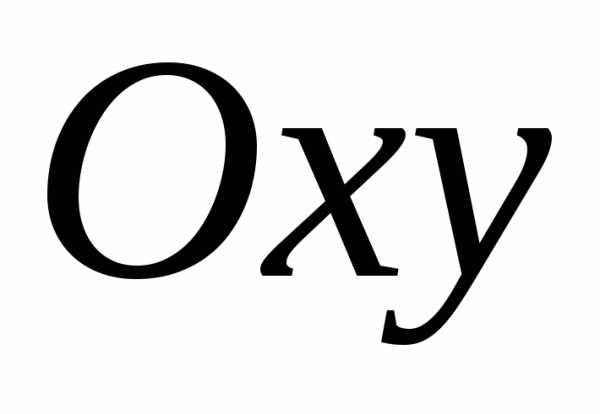 :
:
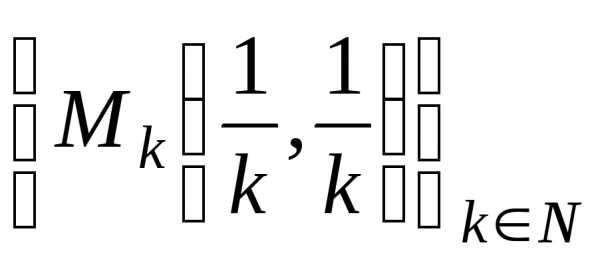 и
и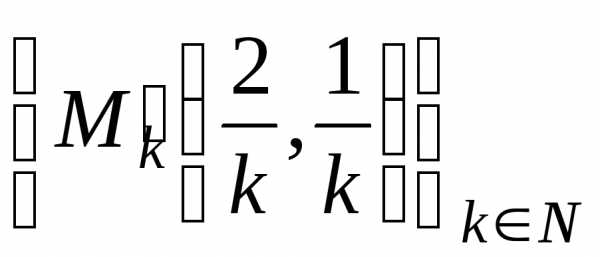 .
.
Построим две соответствующие последовательности значений функции:
и.
Очевидно, что
эти последовательности «сходятся» к
разным значениям. Отсюда следует, что
у данной функции двойного предела в
точке  не существует.
не существует.
Рассмотрим повторные пределы этой функции:
и.
, ,
,.
Мы видим, что
оба повторных предела функции в точке 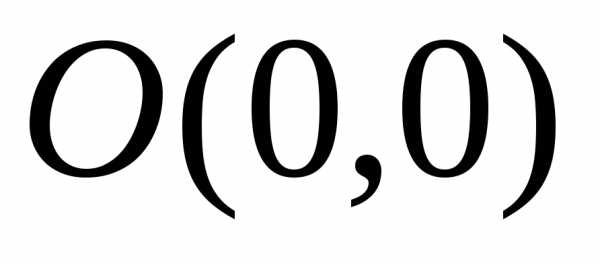 существуют и оба равны 0, хотя двойного
предела данная функция в данной точке
не имеет.
существуют и оба равны 0, хотя двойного
предела данная функция в данной точке
не имеет.
Примеры.
 ,.
,. ,.
,. ,.
,. .
.
9. Непрерывность
Пусть функция
определена в некотором множествеD точек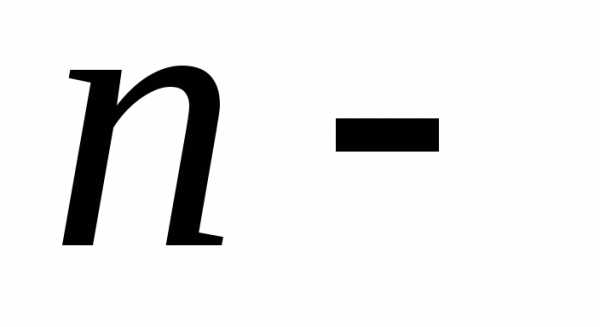 мерного пространства, и– точка сгущения этого множества,принадлежащая самому множеству,
т.е.
мерного пространства, и– точка сгущения этого множества,принадлежащая самому множеству,
т.е.  D.
D.
Говорят, что функция непрерывна в точке, если имеет место равенство
, (3)
в противном случае говорят, что функция в данной точке терпит разрыв.
На
языке «ε – δ» (эпсилон – дельта)
определение непрерывности функции в
точке будет звучать так: функция
непрерывна в точке,
если для каждого сколь угодно малого
наперед заданного положительного числа  найдется такое число
найдется такое число ,
что
,
что
(4)
как только расстояние между точками будет удовлетворять неравенству
 ,
или
,
или
, …,. (5)
При
этом точка
предполагается взятой изD и, в частности,
может совпадать с точкой .
По причине того, что предел функции в
точке должен быть равен значению функции
в этой точке, требование, чтобы 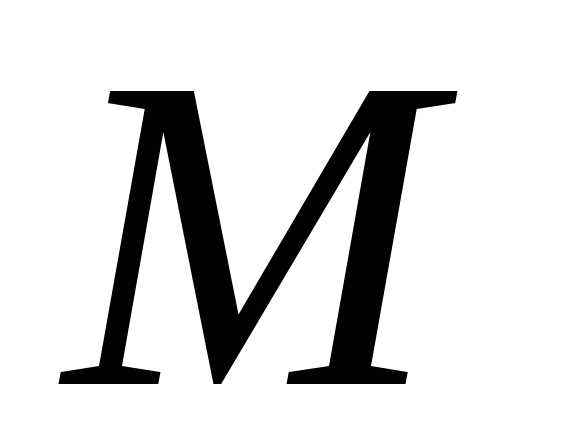 не совпадалаc
не совпадалаc  становится лишним.
становится лишним.
Рассматривая разности в (5) как приращения независимых переменных, а разность в (4) – как приращение функции, можно данное определение перефразировать следующим образом:
Функция непрерывна, если бесконечно малым приращениям независимых переменных соответствует бесконечно малое приращение функции.
Если функция непрерывна в каждой точке множества D, то говорят, что она непрерывна в D.
Все основные теоремы о непрерывных функциях, приводимые для функций одной переменной, распространяются и на случай функций нескольких переменных.
Теорема.Сумма,
разность, произведение и частное
непрерывных в точке функций есть непрерывная в этой точке
функция, если, конечно, в случае частного,
функция, стоящая в знаменателе, в точке
функций есть непрерывная в этой точке
функция, если, конечно, в случае частного,
функция, стоящая в знаменателе, в точке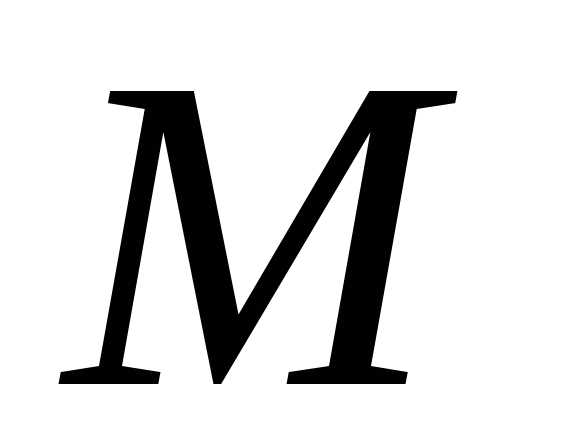 не обращается в ноль.
не обращается в ноль.
Функцию
будем называтьэлементарной функцией переменных, если она может быть получена
из этих переменных и констант при помощи
конечного числа алгебраических операций.
переменных, если она может быть получена
из этих переменных и констант при помощи
конечного числа алгебраических операций.
Как и в случае одной переменной, элементарные функции непрерывны внутри своих естественных областей определения. Суперпозиция (сложная функция) непрерывных функций является непрерывной функцией в своей области определения.
Примерами элементарных функций, непрерывных на всей плоскости, могут служить функции
,
 .
.
Функция
,
являясь суперпозицией элементарных
функций, тоже непрерывна на всей
плоскости. А функция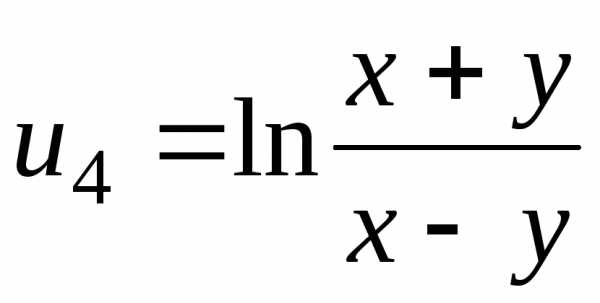 определена и непрерывна только в тех
точках, в которых дробь
определена и непрерывна только в тех
точках, в которых дробь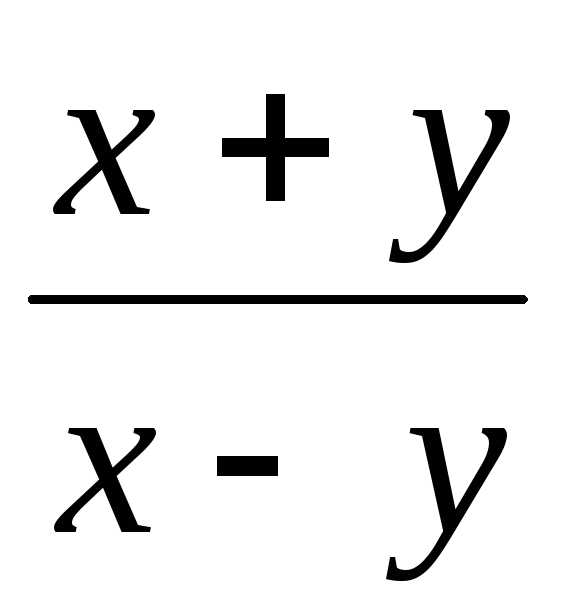 неотрицательна, а знаменатель этой
дроби не равен нулю.
неотрицательна, а знаменатель этой
дроби не равен нулю.
18
studfiles.net
Решение кратных интегралов. Примеры из Кузнецова · Как пользоваться Контрольная Работа РУ
Вот вы поступили в ВУЗ и дали Вам задачи на решение кратных интегралов из сборника задач Кузнецова.
Что же мы можем рассказать про кратные интегралы: Кратный интеграл обычно задан какой-то областью, вот, но чтобы решить кратный интеграл с помощью нашего калькулятора, нужно сначала найти границы этой области интегрирования. Ниже будет приведен пример, как все же это решать.
Как решать
решение кратных интегралов позволяет получить сервис по решению двойных и тройных интегралов здесь.Как же все таки решать, чтобы не быть голословным, покажем на примере из сборника Кузнецова.
Примеры
примеры кратных интегралов. Вот, например, перед нами сборник задач (Кузнецов). Нужно решить задачку:Для каждой такой задачки надо выполнить два простых действия:
- Найти границы интегрирования из области D
- Подставить подинтегральную функцию в представленный нами и сервис и получить ответ! Кстати по указанной ссылке есть еще видео пример
Найдем пределы интегрирования
Пределы интегрирования найдем с помощью рисунка (построим графики функций: y=x2 и y=-корень из x; ну еще начертим линию x=1)Посмотреть, как выглядят графики функции и построить их можно здесь.
Вот, из графика можно увидеть область пересечения линий и найти ее границы, а значит пределы интегрирования.
Смотрю я и нахожу: x от 0 до 1, y от линии -√x до x2.
Что подставлять в калькулятор
Теперь подставим полученные пределы интегрирования и подинтегральную функцию в калькулятор тут.Пределы x от 0 до 1, y от -sqrt(x) до x^2, функция 24*x*y-48*x^3*y^3 как на картинке ниже
и получаем ответ
Задачи
кратные интегралы задачи и другие подобные из решебника Кузнецова приведены тут и вы сможете подобным же образом решать другие кратные двойные интегралыУже появился сервис по решению тройных интегралов.
www.kontrolnaya-rabota.ru
Предел функции. Основные понятия: ограниченность функции, замечательные пределы, односторонние и бесконечные пределы, необходимые и достаточные условия существования предела функции в точке.
Предел функции. Основные понятия: ограниченность функции, замечательные пределы, односторонние и бесконечные пределы, необходимые и достаточные условия существования предела функции в точке.
1.Ограниченность функции.
Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что
m ≤ f(x) ≤ M
при хє(a,b).
Число mo= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции ,
а число Mo= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).
Разность Mo— mo называется колебанием функции на промежутке (a,b).
2. Предел функции в точке.
Пусть функция f(x)определена на множестве X = {x}, имеющем точку сгущения (предельную точку) a. Запись
обозначает, что для любого числа ε > 0 cуществует число δ = δ (ε) > 0 такое, что для всех x, для которых f(x) имеет смысл и которые удовлетворяют условию 0 < |x — a| < δ, справедливо неравенство:
|f(x )- A |< ε.
Имеют место два замечательных предела:
1)
2)
Критерий Коши:
Предел функции f(x) в точке a существует тогда и только тогда, если для каждого ε > 0 найдется такое δ = δ (ε) >0, что
|f(x’ ) — f(x» )| < ε,
как только 0 < |x’ — a| < δ и 0 < |x’ — a| < δ, где x’ и x» — любые точки из области определения функции f(x).
3. Односторонние пределы.
Число A’ называется пределом слева функции f(x) в точке a:
если
|A’ — f(x)| < ε при 0 < a — x < δ (ε).
Аналогично, число A» называется пределом справа функции f(x) в точке a:
если
Для существования предела функции в точке необходимо и достаточно, чтобы|A» — f(x) |< ε при 0 < x — a < δ (ε).
f (a — 0) = f(a + 0).
4. Бесконечный предел.
Условная запись
обозначает, что для любого E > 0 справедливо неравенство:
|f(x)| > E, если только 0 < |x — a| < δ (E) .
tehtab.ru
Предел функции. Основные понятия: ограниченность функции, замечательные пределы, односторонние и бесконечные пределы, необходимые и достаточные условия существования предела функции в точке.
Предел функции. Основные понятия: ограниченность функции, замечательные пределы, односторонние и бесконечные пределы, необходимые и достаточные условия существования предела функции в точке.
1.Ограниченность функции.
Функция f(x) называется ограниченной на данном промежутке (a,b), если существуют некоторые числа m и M такие, что
m ≤ f(x) ≤ M
при хє(a,b).
Число mo= inf {f(x)} [x є (a,b)] = max m называется нижней гранью функции ,
а число Mo= sup {f(x)} [x є (a,b)]=min M называется верхней гранью функции на данном промежутке (a,b).
Разность Mo— mo называется колебанием функции на промежутке (a,b).
2. Предел функции в точке.
Пусть функция f(x)определена на множестве X = {x}, имеющем точку сгущения (предельную точку) a. Запись
обозначает, что для любого числа ε > 0 cуществует число δ = δ (ε) > 0 такое, что для всех x, для которых f(x) имеет смысл и которые удовлетворяют условию 0 < |x — a| < δ, справедливо неравенство:
|f(x )- A |< ε.
Имеют место два замечательных предела:
1)
2)
Критерий Коши:
Предел функции f(x) в точке a существует тогда и только тогда, если для каждого ε > 0 найдется такое δ = δ (ε) >0, что
|f(x’ ) — f(x» )| < ε,
как только 0 < |x’ — a| < δ и 0 < |x’ — a| < δ, где x’ и x» — любые точки из области определения функции f(x).
3. Односторонние пределы.
Число A’ называется пределом слева функции f(x) в точке a:
если
|A’ — f(x)| < ε при 0 < a — x < δ (ε).
Аналогично, число A» называется пределом справа функции f(x) в точке a:
если
Для существования предела функции в точке необходимо и достаточно, чтобы|A» — f(x) |< ε при 0 < x — a < δ (ε).
f (a — 0) = f(a + 0).
4. Бесконечный предел.
Условная запись
обозначает, что для любого E > 0 справедливо неравенство:
|f(x)| > E, если только 0 < |x — a| < δ (E) .
tehtab.ru

 существуетконечный простой предел
по
существуетконечный простой предел
по 
 ,.
,.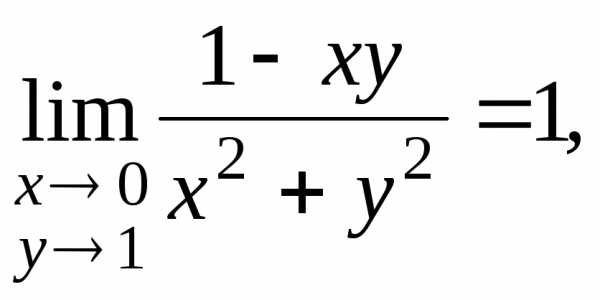 ,.
,.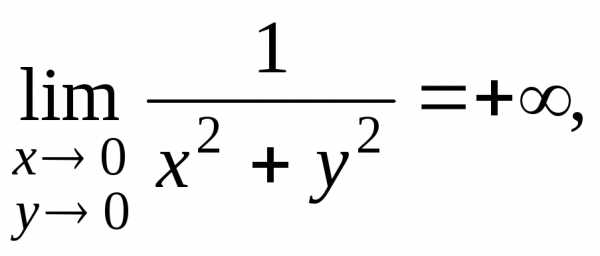 ,.
,.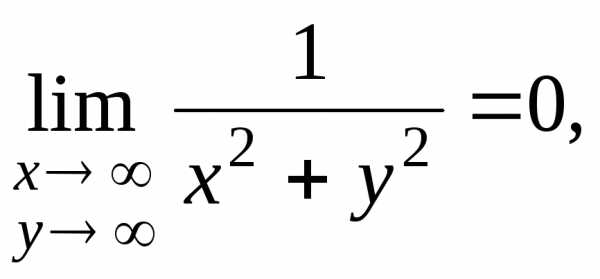 .
.