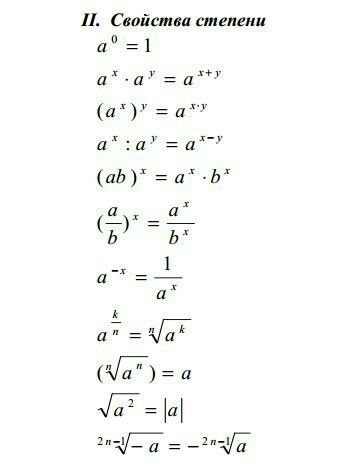Математика степени: Свойства степеней, действия со степенями

Степени.Корни. — Математика

Степени.Корни. Степенью числа a с натуральным показателем n называется произведение nмножителей, каждый из которых равен a. Записывается an. Определим: Также заметим, что , где m  Z, n  N, n > 1, a > 0; a0 = 1, где a ≠ 0. Свойства степени с рациональным показателем: Если a > 0, b > 0, p, q  Q, то справедливы следующие свойства утверждения: Корнем n-ой степени (n  N, n > 1) из числа a называется такое число b, n-ая степень которого равна a, т.е. bn = a. Арифметическим корнем n-ой степени (n  N, n > 1) из числа a называется неотрицательное число b, n-ая степень которого равна а. Обозначение: . Свойства корней: Упростить выражение a5a-3a2 / a3a-4a-1. _________________________________ Пользуемся свойствами степеней. В числителе получаем a5a-3a2 = a5-3+2 = a4. В знаменателе — a3a-4a-1 = a3-4-1 = a-2. В итоге a4 / a-2 = a6. Ответ: a6   Упростить выражение z (p — 3) / (p2 + 3 p) : z 12 / (9 — p2) · z 3 / (3p — p2) . _________________________________________________ Пользуемся свойствами степеней и делаем преобразования: z (p — 3) / (p2 + 3p) : z 12 / (9 — p2) · z 3 / (3p — p2) = z (p — 3) / p · (p + 3) — 12 / (3 — p) · (3 + p) + 3 / p · (3 — p) . Далее упрощаем значение степени z. Сводим к общему знаменателю: (p — 3) / [p(p + 3)] — 12 / [(3 — p)(3 + p)] + 3 / [p(3 — p)] = [(p — 3)2 + 12p — 3(p + 3)] / [p(p + 3)(p — 3)] = [p2 — 6p + 9 + 12 p — 3p — 9] / [p(p + 3)(p — 3)] = [p2 + 3p] / [(p2 + 3p)(p — 3)] = 1/(p — 3) Потому исходное выражение будет иметь вид z 1 / (p — 3) Ответ: z 1 / (p — 3)   Упростить выражение . ______________________________________ Пользуясь свойствами степеней и формулами сокращенного умножения делаем следующие преобразования:  =  =  =  =  = . Ответ: .   Упростить выражение √7 — 2√12. ____________________________ Чтобы упростить данное выражение попробуем выделить под корнем полный квадрат: √7 — 2√12 = √7 — 4√3 = √4 — 4√3 + 3 = √(2 — √3)2 = |2 — √3| = 2 — √3 Ответ: 2 — √3

Открытая Математика. Алгебра. Степень с произвольным показателем

Степень с произвольным показателем

Пусть теперь a≥0, m, n∈ℕ, n≥2. По определению полагают, что amn=amn. Если же a > 0, то по определению полагают, что a-mn=1amn.

Понятие нецелой степени отрицательного числа не имеет смысла.

Вычислить 1) 2713; 2) 81-34; 3) 116-12.

1) 2713=273=3;

2) 81-34=18134=18134=1(34)34=13124=133=127;

3) (116)-1/2=1(116)1/2=1116=1116=114=4.

Ответ. 1) 3; 2) 127; 3) 4.

Пусть a > 0, b > 0, r, s − любые рациональные числа. Тогда степень с любым рациональным показателем обладает следующими свойствами.

1. a^r ċ a^s = a^{r + s}.
2. a^r  : a^s = a^{r – s}.
3. (a^r)^s = a^rs.
4. a^r ċ b^r = (ab)^r.
5. arbr=(ab)r.

Упростите выражения 1) 8×56:4x-23; 2) x1/2-y1/2(x1/2+y1/2).

1) 8×56:4x-23=2×56-(-23)=2×56+23=2×96=2×32.

2) (x1/2-y1/2)(x1/2+y1/2)=(x1/2)2-(y1/2)2=x-y.

Ответ. 1) 2×32; 2) x – y.

 

Итак, для любого действительного числа мы определили операцию возведения в натуральную степень; для любого числа a≠0 мы определили возведения в нулевую и целую отрицательную степень; для любого a≥0 мы определили операцию возведения в положительную дробную степень; для любого a>0 мы определили операцию возведения в отрицательную дробную степень.

Возникает естественный вопрос: можно ли каким-либо образом определить операцию возведения в иррациональную степень, а, следовательно, определить смысл выражения

a^x и для любого действительного числа x? Оказывается, что для положительных чисел a можно придать смысл записи a^α , где α − иррациональное число. Для этого нужно рассмотреть три случая: a = 1, a > 1, 0 < a < 1.

1. Если a = 1, то по определению полагают, что 1^α = 1.
2. Если a > 1, то выберем любое рациональное число r₁ < α и любое рациональное число r₂ > α. Тогда, очевидно, r₁ < r₂ и, следовательно: ar1ar2====св-во 2ar1-r2=1ar2-r1.

   Но r2-r1>0 и потому (так как a > 1) ar2-ar1>1  и, наконец, ar1ar2<1⇒ar1<ar2.

   Под aα понимают такое число, которое лежит между ar1 и ar2 при любом выборе чисел r1 и r2, обладающих свойством r1<α<r2.
   Можно доказать, что число aα существует и единственно для любого a > 1 и любого иррационального α.
3. Если 0 < a < 1, то выберем любое рациональное число r1<α и любое рациональное число r2>α. Тогда, очевидно, r1<r2 и, следовательно, ar1>ar2 (это неравенство доказывается аналогично приведённому выше для a > 1). Под aα понимают такое число, которое лежит между ar1 и ar2 при любом выборе чисел r1 и r2, обладающих свойством r1<α<r2. Можно доказать, что число aα существует и единственно для любого 0 < a < 1 и любого иррационального α.

Итак, для a > 0 мы определили степень с любым действительным показателем.

Пусть a > 0, b > 0, x и y − любые действительные числа. Тогда справедливы следующие свойства степени с любым действительным показателем:

1. a^x ċ a^y = a^{x + y}.
2. a^x : a^y = a^{x – y}.
3. (a^x)^y = a^xy.
4. a^x ċ b^x = (ab)^x.
5. axbx=(ab)x.

Выше мы определили значение выражения a^b для всех вещественных a > 0 и всех вещественных b. Теперь мы можем определить степенную функцию.

Степенной функцией с вещественным показателем a называется функция y = x^a, x > 0.

Заметим, что для натуральных

a степенная функция определена на всей числовой оси, подробнее об этом см. курс «Открытая Математика 2.6. Функции и Графики», § 2.4.2. Для произвольных вещественных a это невозможно, поэтому степенная функция с вещественным показателем определена только для положительных x.

К основным свойствам степенной функции y = x^a при a > 0 относятся:

1. Область определения функции − промежуток (0; +∞).
2. Область значений функции − промежуток (0; +∞).
3. Для любых a график функции проходит через точку (1; 1).
4. Функция строго монотонно возрастает на всей числовой прямой, то есть, если x1<x2, то ax1<ax2.
5. График степенной функции при a > 0 изображён на рисунке.

Степенная функция

y = x^a при a > 0 Степенная функция y = x^a при a < 0

К основным свойствам степенной функции y = x^a при a < 0 относятся:

1. Область определения функции − промежуток (0; +∞).
2. Область значений функции − промежуток (0; +∞).
3. Для любых a график функции проходит через точку (1; 1).
4. Функция строго монотонно убывает на всей числовой прямой, то есть если x1<x2, то ax1>ax2.
5. График степенной функции при a < 0 изображён на рисунке.

Справедливы следующие свойства степенной функции:

1. xa1xa2=xa1+a2.
2. xa1:xa2=xa1-a2.
3. (xa1)a2=xa1a2, если n > k.
4. xa1>xa2 на участке x > 1, если a1>a2.
5. xa1<xa2 на участке 0 < x < 1, если a1>a2.





 

Смотрите также: Математика, Английский язык, Химия, Биология, Физика, География, Астрономия.
А также: библиотека ЭОРов и образовательный онлайн-сервис с тысячами интерактивных работ «Облако знаний».

Бакалавр математики (BA & BS) | КоАС

«Математика была моей платформой для входа в мир бизнеса — все признают ее ценность».

Ханна Кнарр

BA Mathematics ’18

Подробнее о Ханне

Бакалавр математики

Бакалавр гуманитарных наук в области математики обеспечивает сильный общий математический фон, но при этом позволяет учащимся создавать программу, адаптированную к их интересам. Это чрезвычайно полезно для студентов, стремящихся к карьере преподавателя или актуарной профессии. Поскольку степень бакалавра математики предлагает больше бесплатных факультативов, студенты, интересующиеся другой областью обучения, могут получить вторую специальность.

Студенты, работающие над получением степени бакалавра математики, должны пройти только две четверти естественных наук, а также дополнительные курсы в областях, связанных с математикой. Эти дополнительные курсы могут охватывать естествознание, экономику, финансы, информатику или инженерное дело и выбираются учащимися.

Узнайте больше о степени в каталоге курсов

бакалавриат по математике

Бакалавр наук в области математики позволяет учащимся изучить широкий спектр математических тем, приобретая при этом глубокие знания в определенных областях. В программе бакалавриата по математике особое внимание уделяется вычислениям и математическому моделированию, потому что эти две области дают нашим студентам конкурентное преимущество при начале своей карьеры.

Для получения степени бакалавра математики требуется серия курсов, посвященных вычислениям и знакомящих студентов с широко используемыми программными пакетами, такими как программное обеспечение для статистического анализа (SAS) и MATLAB. Студенты, изучающие математику, часто имеют второстепенное значение в областях, связанных с математикой, таких как информатика, экономика и финансы. Делая это, студенты становятся более сильными кандидатами на рынке труда или при подаче заявок на программы магистратуры.

Узнайте больше о степени в каталоге курсов

Вступительные тесты по математике

Существует два вступительных экзамена по математике: экзамен на готовность к математическим вычислениям для учащихся, изучающих естественные науки или технические специальности, и вступительный экзамен по математике для учащихся, не изучающих технические специальности.

Экзамены основаны на темах, изучаемых в школьных курсах; отсутствуют примеры вопросов. Важно, чтобы вы сдали эти экзамены самостоятельно, чтобы ваш консультант получил истинное представление о вашей академической подготовке.

Узнайте больше о вступительных экзаменах по математике

DREXEL CO-OP FOR MATH

Специалисты по математике в Drexel проходят до трех шестимесячных периодов работы, изучая варианты своей карьеры, улучшая свои резюме и создавая профессиональную сеть в процессе. Учебная программа Drexel по математике разработана с учетом отраслевых стандартов, что позволяет нашим учащимся оказывать влияние с первого дня совместной работы. Последние математические специальности занимали совместные должности, такие как:

• Производственно-инженерный кооператив, Tesla Inc.
• Макроаналитик США, TD Securities
• Co-op Finance & Diversity Analytics, FMC Corporation
• Кооператив судебно-бухгалтерских и финансовых расследований, Kroll Inc.
• Кооператив Data Science, Exelon Corporation
• Аналитик клинических данных, Детская больница Филадельфии

Узнайте больше о Drexel Co-op

КАРЬЕРА ДЛЯ СТУДЕНТОВ СО СТЕПЕНЬЮ БАКАЛАВРА ПО МАТЕМАТИКЕ

Специалисты по математике Drexel — это начинающие студенты, которые становятся желанными кандидатами для карьеры в различных отраслях. Наши недавние выпускники сделали успешную карьеру в:

• Анализ данных
• Актуарная наука
• Разработка программного обеспечения
• Анализ обеспечения качества
• Клинические исследования
• И многое другое!

Узнайте больше о карьере в области математики

ПОДАТЬ ЗАЯВКУ НА ПОЛУЧЕНИЕ СТЕПЕНИ ПО МАТЕМАТИКЕ

Подайте заявку на получение степени по математике или посетите кампус, чтобы получить информацию из первых рук об образовании Drexel. Свяжитесь с Департаментом математики по адресу [email protected] для получения дополнительной информации.

*Ссылка: из опроса выпускников за год до выпуска, выпускные классы 2015, 2016 и 2017 годов.

Математика | Университет Южной Каролины

Альберт Эйнштейн, который довольно много знал о таких вещах, сказал: «Чистая математика — это своего рода поэзия логических идей». Кафедра математики ставит это «поэзии» в действие с выдающейся программой обучения, исследований и служения.

Чего ожидать

Изучая математику, вы также разовьете востребованные навыки, такие как способность логически и критически оценивать ситуации, включая разработку и внедрение эффективных стратегии решения проблем, включающие широкий спектр идей и данных. Тебе понравится относительно небольшие классы с повышенным взаимодействием с вашими профессорами.

Мы рекомендуем вам воспользоваться Математической библиотекой и Hedberg Student Гостиная с холодильником, микроволновой печью, раковиной и классной доской — идеально подходит для обучение в группах.

Вы выберете специализацию: актуарную, образовательную, прикладную или общую. Кроме того, список стипендий Knowles Science для преподавателей математики получателей растет очень быстро. Эти национальные награды обеспечивают финансирование завершение обучения студента, а также первые несколько лет обучения.

 

Степень бакалавра

Б Б.С. по математике

Математический факультет Колледжа искусств и наук предлагает высококачественную подготовку для студентов предоставляя всестороннее образование в области математики с прочной основой в гуманитарные науки.

• Исчисление I и II
• Векторное исчисление
• Алгоритмический дизайн I
• Вероятность
• Математическая статистика
• Статистика для инженеров или статистические методы I
• Алгоритмический дизайн II или статистические методы II

Степень бакалавра наук с отличием по математике доступна любому математику специальностей, которые завершают 12 часов дополнительной курсовой работы по математике и готовят и публично представляет утвержденный исследовательский проект бакалавриата.

Подать заявку на поступление в бакалавриат

Наш отдел по приему в бакалавриат предоставляет самую последнюю информацию о процессе подачи заявления, чтобы вы могли проверить требования в зависимости от вашего текущего статуса и найти университетские стипендии.

 

Степень магистра

Математический факультет Колледжа искусств и наук предлагает три программы получения степени магистра: степень магистра искусств, магистр наук и магистр математики. доктор философии программа также доступный.

Также доступна степень магистра педагогических наук, которая ведет к первоначальной лицензии/сертификации учителя. в математике. Для получения дополнительной информации ознакомьтесь с информацией о программе среднего образования.

Узнайте больше о The Graduate School, вариантах получения степени и о том, как подать заявку на поступление на докторские, магистерские, сертификационные и комбинированные программы обучения в Южной Каролине.