Math abc: Math.abs() — JavaScript | MDN

Preschool Educational Classroom — Math,ABC,Number 4.0 Загрузить APK Android

Today’s smart Kids complete their Classroom Work With google. They Learn Math , ABC , Number , Alphabet , Animal Voice , Rhymes , vocabulary Etc By Educational Games.

Learn Language become so easy nowadays with the learning app.Kids learn Chinese Or Spanish Language with the google apps and the games. for maths kids not use calculator and they not remind to complete their tasks like arrange their books in bag .from the scratch with their preschool age they learn about religion with bible , Geeta Or Quran with the use of Educational Apps.

Kids search Words , Cartoon Animals , Cartoon Tv episodes,free games, Design their room and home.connect the words to make the complete sentences.

You Can also Like Our Other Game Like :-

Kitty Care Pet Salon — Cat Love Furry Grooming

Matching Object : Educational Pair Making Game

Kids Maze : Educational Maze Game for Kids

Music Piano Christmas Games

Crazy Babysitter — Newborn Baby Fun Care Game

Free Educational ABC Learning Games for Kids

Kids Computer — Preschool Learning Activity

cool math — cool math for kids — math games

Brain Memory Games

Free Educational ABC Learning Games for Kids

Wedding Chocolate Cake Factory

Snakes And Ladders — Classic

Royal Princess: Lips Makeup Salon Games for Girls

Features :

Preschool Theme

Toddler Activities

Learn By Fun Game

Educational Activities with cute Animals Alphabet and Numbers.

HD Graphics

Unlimited Gameplay.

Share With your Friends And Family.

if you like this game share it with friends or family with the gmail , WhatsApp , WeChat Etc.

If you have any suggestion Please feel Free to Write us on twitter . Follow us on instagram or gmail us.

Сегодня умные дети заканчивают работу в классе с помощью Google. Они Learn Math, ABC, номер, алфавит, животные голос, Rhymes, словарный запас Etc образовательных игр.

Подробнее Язык становится так легко в наше время с изучением app.Kids выучить китайский или испанский язык с приложениями Google и играми. для детей математика не использовать калькулятор и они не напоминают, чтобы завершить свои задачи, как организовать свои книги в сумке .from царапины с их дошкольным возрастом они узнают о религии с Библией, Гит Или Коран с использованием образовательных приложений.

Дети поиск слова, мультфильм животных, мультфильм телесериалы, бесплатные игры, дизайн их комната и home.connect слова, чтобы сделать полные предложения.

Вы можете также как и другие наши игры, как: —

Kitty Care Pet Salon — Cat Любовь Furry Уход

Соответствие объекта: Образовательная пара Создание игры

Дети Maze: Обучающие Maze игры для детей

Музыка Пианино Рождественские игры

Сумасшедшие Няни — Игра Новорожденного Fun Уход

Бесплатная образовательный ABC обучение игра для детей

Детский компьютер — Дошкольное обучение активность

крутая математика — крутая математика для детей — математические игры

Мозг Игры памяти

Бесплатная образовательный ABC обучение игра для детей

Свадебный Шоколадный торт фабрика

Змеи и лестницы — Классические

Royal Princess: Губы Макияж салон Игры для девочек

Особенности :

Дошкольный Theme

малыша Мероприятия

Подробнее веселье игра

Воспитательная работа с симпатичными животными алфавит и цифры.

HD Graphics

Неограниченный геймплей.

Поделитесь с друзьями и семьей.

если вам понравилась эта игра поделиться им с друзьями или семьей с Gmail, WhatsApp, WeChat Etc.

Если у вас есть какие-либо предложения, пожалуйста, не стесняйтесь писать нам на твиттере. Следуйте за нами на Instagram или GMAIL нас.

Модуль числа в Python 3 — Функция abs библиотеки math

Очень часто возникает необходимость вычисления модуля числа в Python. Рассмотрим, что такое модуль числа, какие есть способы его вычисления. Так же отдельно коснемся комплексных чисел.

Модуль числа

Часто в программировании требуется вычислить абсолютное значение числа. Иначе говоря, отбросить знак.

При вычислении модуля возможны 3 ситуации:

• Когда число больше 0. Если взять его по модулю — не изменится.
• Модуль нуля так же равен нулю.
• У отрицательного числа отбрасываем знак. То есть умножаем его на -1.

Но это все справедливо только для действительных чисел. Чему же тогда будет равен модуль комплексных?

Комплексное число состоит из действительной составляющей и мнимой. Геометрически это можно представить как 2 ортогональные оси: действительную и мнимую. Отмечаем на координатных осях требуемую точку. Модулем будет длина отрезка, проведенного из начала координат в эту точку.

Исходя из теоремы Пифагора получаем, что модуль комплексного числа это корень квадратный из суммы квадратов мнимой и действительной частей.

Вычисление

Вычислять модуль можно следующими способами:

• Используя стандартную функцию abs.
• С помощью функции fabs библиотеки math.
• При помощи самостоятельно написанной функции.

Все эти функции работают как в Python 2, так и в Python 3.

abs

Для вычисления в Python модуля числа используется функция abs. Результат функции того же типа, которого был аргумент.

a = -10
b = abs(a)
print(b)
print(type(b))

10
<class 'int'>

fabs

Можно так же воспользоваться функцией fabs из библиотеки math. Библиотеку можно подключить с помощью from math import fabs.

from math import fabs
a = -10
b = fabs(a)
print(b)
print(type(b))

10.
  0
<class 'float'>

Отличие abs от fabs заключается в том, что функция abs возвращает значение того же типа, что и аргумент. Функция же fabs вначале преобразует тип аргумента к вещественному числу.

Свое решение

Если по каким то причинам нет возможности или желания использовать стандартные функции, то можно написать свое решение.

Например, можно вычислить воспользоваться тернарным оператором.

a = -10
b = a if a > 0 else -a
print(b)

10

На основе такого условия сделаем свою функцию.

def my_abs(a):
    return a if a > 0 else -a
print(my_abs(-3))

3

Модуль комплексного числа

Мы разобрались как происходит вычисление с действительными числами. Теперь посмотрим, как в языке программирования Python можно получить модуль комплексного.

Функцией fabs мы не сможем воспользоваться. Если попытаемся это сделать, то получим ошибку приведения комплексного числа к действительному (TypeError).

from math import fabs
a = -10-2j
b = fabs(a)
print(b)

Traceback (most recent call last):
  File "main.py", line 3, in <module>
    b = fabs(a)
TypeError: can't convert complex to float

А вот с помощью abs преобразование удается.

a = -10-2j
b = abs(a)
print(b)

10.19803902718557

Или же напишем свою функцию:

from math import sqrt
def my_abs_complex(c):
    return sqrt(c.real**2 + c.imag**2)
a = -10-2j
b = my_abs_complex(a)
print(b)

10.198039027185569

Результаты получились одинаковыми. Но нам все равно пришлось подключить библиотеку math для вычисления квадратного корня.

Модуль math | Python 3 для начинающих и чайников

Модуль math – один из наиважнейших в Python. Этот модуль предоставляет обширный функционал для работы с числами.

math.ceil(X) – округление до ближайшего большего числа.

math.copysign(X, Y) — возвращает число, имеющее модуль такой же, как и у числа X, а знак — как у числа Y.

math.fabs(X) — модуль X.

math.factorial(X) — факториал числа X.

math.floor(X) — округление вниз.

math.fmod(X, Y) — остаток от деления X на Y.

math.frexp(X) — возвращает мантиссу и экспоненту числа.

math.ldexp(X, I) — X * 2ⁱ. Функция, обратная функции math.frexp().

math.fsum(последовательность) — сумма всех членов последовательности. Эквивалент встроенной функции sum(), но math.fsum() более точна для чисел с плавающей точкой.

math.isfinite(X) — является ли X числом.

math.isinf(X) — является ли X бесконечностью.

math.isnan(X) — является ли X NaN (Not a Number — не число).

math.modf(X) — возвращает дробную и целую часть числа X. Оба числа имеют тот же знак, что и X.

math.trunc(X) — усекает значение X до целого.

math.exp(X) — e^X.

math.expm1(X) — e^X — 1. При X → 0 точнее, чем math. exp(X)-1.

math.log(X, [base]) — логарифм X по основанию base. Если base не указан, вычисляется натуральный логарифм.

math.log1p(X) — натуральный логарифм (1 + X). При X → 0 точнее, чем math.log(1+X).

math.log10(X) — логарифм X по основанию 10.

math.log2(X) — логарифм X по основанию 2. Новое в Python 3.3.

math.pow(X, Y) — X^Y.

math.sqrt(X) — квадратный корень из X.

math.acos(X) — арккосинус X. В радианах.

math.asin(X) — арксинус X. В радианах.

math.atan(X) — арктангенс X. В радианах.

math.atan2(Y, X) — арктангенс Y/X. В радианах. С учетом четверти, в которой находится точка (X, Y).

math.cos(X) — косинус X (X указывается в радианах).

math.sin(X) — синус X (X указывается в радианах).

math.tan(X) — тангенс X (X указывается в радианах).

math.hypot(X, Y) — вычисляет гипотенузу треугольника с катетами X и Y (math. sqrt(x * x + y * y)).

math.degrees(X) — конвертирует радианы в градусы.

math.radians(X) — конвертирует градусы в радианы.

math.cosh(X) — вычисляет гиперболический косинус.

math.sinh(X) — вычисляет гиперболический синус.

math.tanh(X) — вычисляет гиперболический тангенс.

math.acosh(X) — вычисляет обратный гиперболический косинус.

math.asinh(X) — вычисляет обратный гиперболический синус.

math.atanh(X) — вычисляет обратный гиперболический тангенс.

math.erf(X) — функция ошибок.

math.erfc(X) — дополнительная функция ошибок (1 — math.erf(X)).

math.gamma(X) — гамма-функция X.

math.lgamma(X) — натуральный логарифм гамма-функции X.

math.pi — pi = 3,1415926…

math.e — e = 2,718281…

Обучающих игр, книг, головоломок и песен для детей и малышей

(изображение) Пошаговый путь обучения

10 уровней. Более 850 уроков. Более 10 000 индивидуальных учебных мероприятий.

Более 850 уроков на 10 уровнях

Пошаговая инструкция по обучению представляет собой полную ABCmouse.comcurriculum в тщательно разработанной программе из более чем 850 уроков на десяти уровнях. По мере того, как ваш ребенок завершает каждый урок, его направляют к следующему и мотивируют продолжить обучение системой билетов и вознаграждений ABCmouse.com.

(изображение)

«Любите прогрессивные занятия! Мне не нужно тратить время на поиск занятий для моей трехлетней девочки, а пятилетняя девочка просто следует за ней, когда играет одна… Так что я знаю, что каждый делает то, что нужно для своего возраста! »

—Кристал, мать трех- и пятилетних девочек

(изображение) (изображение) (изображение)

Доступно на компьютерах, планшетах и ​​смартфонах!

(изображение) Предметы

Чтение и языковые навыки

(изображение)

Программа чтения включает:

• Распознавание прописных и строчных букв
• Телефоника
• Рифмующие слова и семейства слов
• Более 450 книг и начинающих читателей
• Структура предложения
• Части речи

ABCmouse. Учебная программа чтения com охватывает весь диапазон раннего чтения, от изучения названий каждой буквы и звуков, которые они представляют, до умения читать книги, начиная с нескольких слов на странице и постепенно переходя к абзацам. Учебная программа для первого класса также включает навыки письма и языка, такие как структура предложения и пунктуация, части речи и практика написания жанров.

Математика

(изображение)

Учебная программа по математике включает:

• Распознавание и счет чисел 1–120
• Система десятичных оснований
• Значение места
• Сложение и вычитание
• Названия и атрибуты 2D и 3D фигур
• Измерение длины, времени и денег

ABCmouse. com учит числа, сложение и вычитание, формы, узоры, измерения и многое другое! Наши игры и творческие занятия делают математику увлекательной, давая юным ученикам возможность практиковаться, чтобы заложить прочный фундамент успеха.

Мир вокруг нас

(изображение)

Программа обучения естествознанию и обществознанию включает:

• Тело и здоровье
• Растения и животные
• Погода, климат и времена года
• Окружающая среда Земли
• Карты
• Регионы США
• Солнечная система
• Материя и ее свойства

(изображение)

Наука и социальные исследования ABCmouse. Учебная программа по естественным наукам и общественным наукам помогает детям понять мир, в котором они живут, и пробуждает любопытство.

Искусство и цвета

(изображение)

Учебная программа «Искусство и цвета» включает:

• Основные и второстепенные цвета
• Оттенки цвета
• Раскраска по номерам
• Цифры и буквы точка-точка

(изображение)

ABCmouse.Уникальная программа рисования и рисования дает детям всех возрастов возможность использовать линии, формы и цвета для создания оригинальных произведений искусства. Игры, книги, раскраски по номерам и головоломки учат детей называть и использовать различные цвета.

«Моя дочь любит этот сайт! Она узнала гораздо больше, чем я думал, она могла узнать в ее возрасте. Азбука — это ее любимое занятие, и с тех пор, как я запустил ее на этом веб-сайте, она научилась читать слова значительно старше своего возраста.”

—Моргин, мать двухлетней девочки

(изображение) Деятельность

Анимации

(изображение) (изображение) (изображение) (изображение)

Учебная программа ABCmouse.com включает сотни увлекательных анимационных мероприятий, каждое из которых посвящено определенной теме обучения.От геолога Пола, открывающего новые комбинации букв, до царя Грамма, объясняющего своим жителям имена собственные, — эти анимационные видеоролики увлекают детей, пока они учатся.

Игры

(изображение)

ABCmouse.com предлагает сотни забавных и интерактивных игр, каждая из которых разработана с учетом определенной образовательной концепции.Ваш ребенок может играть в игры, чтобы выучить алфавит, выучить новые слова, узнать числа и формы и даже узнать о планетах! Поскольку все игры на сайте содержат озвученные инструкции, их легко освоить и играть даже маленьким детям.

Книги

(изображение)

ABCmouse с более чем 450 традиционными и оригинальными рассказами и научно-популярными книгами.Библиотека com открывает двери в мир знаний, приключений и развлечений для детей. Каждая тема нашей учебной программы — будь то звук письма, счет от 1 до 100, четыре сезона в году или регионы США — объясняется на понятном для детей языке в одной из наших библиотечных книг.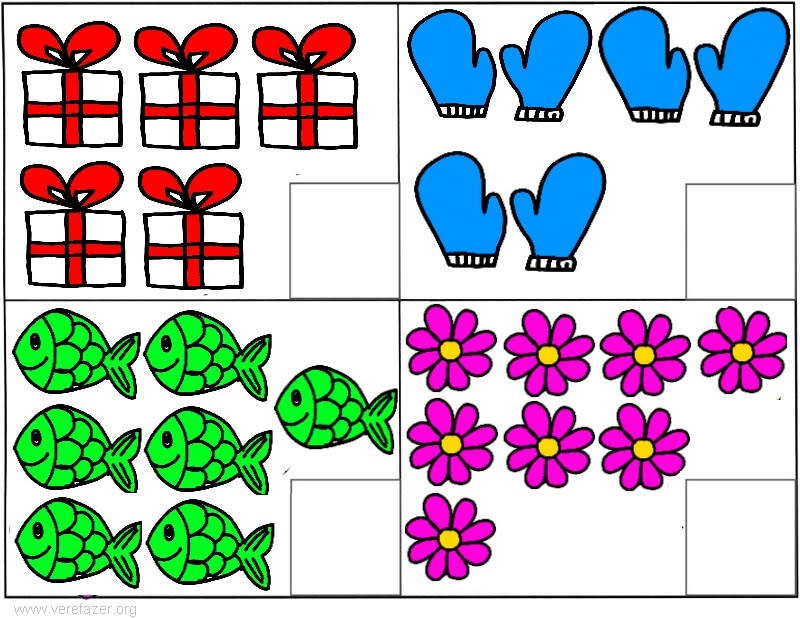

Песни

(изображение)

ABCmouse.В музыкальной коллекции com представлены оригинальные песни о каждой букве алфавита и многих других темах нашей учебной программы, а также недавно выпущенные и записанные детские классические произведения. Разнообразие музыки на нашем сайте не только усиливает другие предметы, но также знакомит детей с целым рядом музыкальных стилей и тем. Вашему ребенку понравится подпевать!

Пазлы

(изображение)

Найдите сотни головоломок и головоломок, которые помогут развить навыки решения проблем и критического мышления.Пазлы также помогают детям запомнить важные идеи и навыки чтения, математики, естественных наук, искусства, общественных наук и музыки. Есть головоломки для каждой буквы алфавита, ключевых слов, рассказов, чисел, фигур, животных, десятичной системы чисел, элементов художественной литературы и многих, многих других тем.

Арт

(изображение)

ABCmouse предлагает множество различных видов художественной деятельности, включая раскраски, точки-точки, раскраски по номерам, трассировки и печатные формы.com помогает детям изучать чтение, математику и другие предметы, пока они выражают себя художественно.

Распечатки

(изображение)

ABCmouse.com предлагает более 2000 видов печатных работ по чтению, математике, рисованию, цветам и многому другому. Мы призываем детей продолжать свое обучение в автономном режиме с помощью печатных заданий, которые включают отслеживание букв и номеров, раскрашивание, точечные рисунки, рисование по номерам, лабиринты и действия по распознаванию образов.

(изображение) Больше возможностей

Отслеживание прогресса

(изображение)

С помощью ABCmouse.comProgress Tracker легко увидеть, насколько успешен ваш ребенок. В дополнение к отображению общего количества учебных занятий, выполненных в каждой категории (книги, песни, головоломки, игры и искусство), есть удобные для чтения графики, которые показывают прогресс как по академическому уровню, так и по предметам учебной программы.

Билеты и награды

(изображение)

ABCmouse. com поощряет детей к завершению учебной деятельности, награждая их билетами. Билеты можно использовать для «покупки» виртуальных предметов на сайте, например, новой рыбы для класса.Система билетов и вознаграждений превращает обучение в игру, а также обучает важным математическим навыкам, поскольку дети отслеживают, сколько билетов было куплено и сколько потрачено.

Настраиваемый аватар

(изображение)

Аватар — это персонаж, которого ваш ребенок может выбрать, чтобы представлять себя или себя, находясь на ABCmouse.com. Существует широкий выбор персонажей и одежды, а также другие предметы, связанные с аватарами, которые можно приобрести с помощью билетов.

Интерактивный зоопарк

(изображение)

Зоопарк ABCmouse. com позволяет детям взаимодействовать с реалистичными животными зоопарка, включая слонов, львов, обезьян, зебр, пингвинов и многих других! Узнавайте факты о каждом животном, читайте книги, играйте в игры, решайте головоломки и занимайтесь рисованием для каждого из них.

Аквариум

(изображение)

Ваш ребенок может выбрать экзотических тропических рыбок и другие предметы для своего Классного аквариума и одновременно узнать много интересных фактов о рыбах.

Интерактивная ферма

(изображение)

ABCmouse. На интерактивной ферме com представлены лошади, куры, коровы и многое другое! Смотрите прекрасные анимации наших сельскохозяйственных животных, узнавайте забавные и интересные факты о каждом из них и занимайтесь деятельностью, связанной с фермерством.

«Моему ребенку очень нравится все на этом сайте, и я уже вижу улучшения в ее подсчете и цветовой ассоциации. Я считаю, что это фантастический сайт ».

— Отец 3-летней девочки

(изображение)

(изображение)

Получите первый месяц БЕСПЛАТНО!

ЦЕНА ПОДПИСКИ

$ 9 95 доллар США В МЕСЯЦ

Азбука математических понятий

В математике есть гораздо больше, чем просто сложение и вычитание, и по мере того, как ваш ребенок становится старше, математика усложняется. Чтобы помочь вашему ребенку в обучении математике, вот краткий обзор математических понятий и терминов от добавления до нуля.

Математические термины от А до Я

• A — это добавление : Добавление — это одно из чисел, которые будут добавлены в задаче сложения. В задаче 3 + 5 = 8, 3 и 5 — слагаемые.
• B для скобок : Скобки — это квадратные [], круглые (), фигурные {} или угловые <>, используемые в алгебре символы.Они используются для смещения частей сложных уравнений, чтобы ваш ребенок проделал правильный порядок действий для решения задачи.
• C соответствует кардинальным числам : Многие люди путают кардинальные и порядковые числа. Кардинальные числа — это числовые слова или цифры, которые используются для подсчета или определения количества. Например, «1, 2, 3» или «один, два, три».
• D для фактов двойников : Фактов двойников — важный способ для вашего ребенка запоминать факты сложения.Двойной факт — это когда число добавляется к самому себе, например, 1 + 1 = 2, 2 + 2 = 4, 4 + 4 = 8 и 8 + 8 = 16.
• E соответствует уравнению : Уравнение — это математическое предложение, в котором есть хотя бы один знак равенства. Уравнения могут быть простыми задачами сложения или сложными алгебраическими предложениями.
• F предназначен для семейств фактов : Семейства фактов — это набор чисел, которые связаны друг с другом посредством математической операции и уравнений, которые они могут создавать вместе.
• G предназначен для геометрии : Геометрия — это раздел математики, изучающий двухмерные и трехмерные фигуры. По мере того, как ваш ребенок изучает более сложную математику, геометрия будет играть большую роль в том, что он изучает.
• H соответствует гипотенузе : Гипотенуза — это самая длинная сторона прямоугольного треугольника, сторона, противоположная углу 90 градусов.
• I означает бесконечность : Бесконечность — это «число», представленное боковым восьмеркой: ∞ Оно больше любого действительного числа и имеет большее значение.Также существует отрицательная бесконечность, которая больше любого действительного отрицательного числа.
• J для обоснований : Хотя вы можете думать об оправданиях как о том, что ваш ребенок дает вам как оправдание, когда он сделал что-то неправильно, в математике оправдание — это утверждение, которое доказывает, что математический вывод верен. . Обоснования в основном используются при доказательстве геометрических теорем.
• K соответствует последовательности клавиш : Последовательность клавиш далеко не так интересна, как кажется.Это просто указания того, что вводить в калькулятор и в каком порядке. цифры и символы клавиш обычно рисуются внутри маленьких прямоугольников.
• L соответствует наименьшему общему знаменателю или кратному : Наименьший общий знаменатель (LCD) и наименьшее общее кратное (LCM) связаны. Наименьшее общее кратное — это наименьшее положительное целое число, на которое можно равномерно разделить два числа. Наименьший общий знаменатель — это наименьшее наименьшее общее кратное, которое разделяет нижнее число (знаменатель) двух данных дробей.
• M означает среднее значение, режим и медиана : По какой-то причине эти три концепции сбивают с толку многих детей, когда дело касается математики. Среднее значение — это среднее значение набора чисел. Режим — это номер, который чаще всего отображается в списке чисел. Медиана — это число в наборе чисел, ниже которого ровно половина остальных чисел, а выше — ровно половина остальных чисел. В основном это середина списка.
• N соответствует вложенным круглым скобкам : Вложенные круглые скобки представляют собой набор круглых скобок внутри других круглых скобок, как русские матрешки.Это способ сообщить вашему ребенку, какое уравнение нужно решить в первую очередь — самые сокровенные скобки.
• O соответствует упорядоченной паре : Упорядоченная пара — это набор координат графика, выраженный как (x, y). x всегда является первым числом, а y всегда вторым.
• P соответствует параллельному : У вас могут быть параллельные прямые и параллельные плоскости, у которых нет общих точек, то есть они никогда, никогда не пересекаются.
• Q соответствует частному : Частное — это ответ на проблему деления.
• R соответствует остатку : Остаток — это сумма, оставшаяся в задаче деления, если число не может быть разделено поровну.
• S предназначен для решения и решения : решение проблемы — это ответ, который заполняет пробел. В простой математике это число после знака равенства.В более сложной математике это значение неизвестной (ых) переменной (ей). Например, если ваш ребенок решает для x в этом уравнении, 2x + 5 = 15, решение равно 5 или значение x .
• T для членов : Термины — это числа или части уравнения, разделенные знаком сложения, вычитания или запятыми. Термины могут быть решением уравнения внутри вложенных круглых скобок.
• U соответствует неизвестно : Когда ваш ребенок работает над сложной математической задачей, иногда значения переменных неизвестны.
• V соответствует переменной : Переменная — это буква, используемая для замены неизвестного значения. Это потому, что значение может варьироваться в зависимости от решения остальной части уравнения.
• W для целых чисел : Целые числа — это целые числа (или числа), которые не являются отрицательными. Например, 0, 1, 2, 3 и т. Д.
• X соответствует оси x : Ось x — это горизонтальная (проходящая) линия числового графика.
• Y соответствует оси Y : Ось Y представляет собой вертикальную (восходящую) линию числового графика.
• Z соответствует нулю : Ноль (0) — это число без значения. Это не означает никакого количества, и это ни отрицательное, ни положительное значение.

Математическое доказательство того, что теория чисел потрясена, будет опубликована

Математик Шиничи Мотидзуки Фото: Университет Киото

После восьмилетней борьбы упавший в боевую готовность японский математик Шиничи Мочизуки, наконец, получил некоторое подтверждение.Его 600-страничное доказательство гипотезы abc , одной из самых больших открытых проблем в теории чисел, было принято к публикации.

Принятие работы в издании Исследовательского института математических наук (RIMS) — последнее достижение в долгой и яростной полемике по поводу доказательства математика. Журнал, главным редактором которого является Мотидзуки, издается Японским научно-исследовательским институтом математических наук (RIMS) при Киотском университете, где он работает.

Два других математика RIMS, Масаки Касивара и Акио Тамагава, говорящие по-японски, объявили об этой публикации на пресс-конференции в Киото 3 апреля. Газета «окажет большое влияние», — сказал Кашивара. На вопрос, как Мотидзуки отреагировал на известие о принятии газеты, Кашивара ответил: «Думаю, он почувствовал облегчение».

Мотидзуки, который на протяжении многих лет отказывал в просьбах об интервью, не появлялся на пресс-конференции и не предоставлялся репортерам.

Восемь лет назад Мотидзуки опубликовал в Интернете четыре огромных статьи, в которых утверждал, что он решил гипотезу abc .Эта работа сбила с толку математиков, которые годами пытались ее понять. Затем, в 2018 году, два уважаемых математика заявили, что уверены в том, что обнаружили изъян в доказательстве Мотидзуки, что многие сочли смертельным ударом по его утверждениям.

Последнее сообщение вряд ли переместит многих исследователей в лагерь Мотидзуки. «Я думаю, можно с уверенностью сказать, что с 2018 года мнение сообщества не сильно изменилось», — говорит Киран Кедлая, теоретик чисел из Калифорнийского университета в Сан-Диего, который был среди экспертов, которые приложили значительные усилия, пытаясь для проверки заявленных доказательств Мотидзуки. Другой математик, Эдвард Френкель из Калифорнийского университета в Беркли, говорит: «Я воздержусь от своего суждения о публикации этой работы, пока это не произойдет, поскольку может появиться новая информация».

Нерешенная проблема

Гипотеза abc выражает глубокую связь между сложением и умножением целых чисел. Любое целое число можно разложить на простые числа, его «делители»: например, 60 = 5 x 3 x 2 x 2. Гипотеза примерно утверждает, что если много маленьких простых чисел делят два числа a, и b, , то тогда лишь немногие, крупные делят свою сумму, c .

Доказательство, в случае его подтверждения, могло бы изменить облик теории чисел, например, предоставив новаторский подход к доказательству последней теоремы Ферма, легендарной проблемы, сформулированной Пьером де Ферма в 1637 году и решенной только в 1994 году.

Сага началась, когда Мотидзуки, уважаемый теоретик чисел, тихо разместил свои препринты 30 августа 2012 года — не на arXiv. org, предпочитаемом математиками хранилище, а на своей собственной веб-странице в RIMS. Написанные в непонятном, своеобразном стиле, статьи, казалось, были полностью построены на математических концепциях, которые были совершенно незнакомы остальной части сообщества — «как будто вы читаете статью из будущего или из космоса», — писал Джордан Элленберг. , теоретик чисел из Университета Висконсин-Мэдисон, в своем блоге вскоре после появления статей.

Мотидзуки отклонил все приглашения поехать за границу и читать лекции о своей работе. Хотя в то время некоторые из его близких соратников заявили, что они нашли доказательство правильным, эксперты по всему миру изо всех сил пытались, часто неохотно, тщательно его проанализировать, не говоря уже о проверке. В последующие годы проводились конференции по этой теме, и участники сообщили о частичном прогрессе, но сказали, что, вероятно, потребуется много лет, чтобы прийти к заключению. Многие, в том числе собственный доктор Мотидзуки, Герд Фалтингс, открыто критиковали Мотидзуки за то, что он не пытался более четко изложить свои идеи.

Затем, 16 декабря 2017 года, Asahi Shimbun , японская ежедневная газета, заявила, что доказательство Мотидзуки было близко к тому, чтобы быть официально подтвержденным, достижение, которое будет наравне с решением последней теоремы Ферма в 1994 году.

Между тем распространился слух, что публикаций RIMS приняли четыре статьи Мотидзуки, что в то время отрицали ее редакторы. Но спор разгорелся снова, и некоторые математики сетовали на плохое восприятие Мотидзуки, якобы публикуемого в журнале его института.

В декабре 2017 года Питер Войт, физик-математик из Колумбийского университета в Нью-Йорке, написал в своем блоге, что признание журнала создаст ситуацию, которая «исторически не имеет аналогов в математике: заявление уважаемого журнала о том, что они проверили доказательство чрезвычайно известной гипотезы, в то время как большинство экспертов в этой области, которые исследовали это, не смогли понять доказательство ».

Не забывайте о пробеле

Слух о скорой публикации оказался необоснованным. Затем, через несколько месяцев, положение Мотидзуки резко ухудшилось. Два немецких математика — Петер Шольце из Боннского университета и Якоб Стикс из Университета Гете во Франкфурте — в частном порядке распространили опровержение его доказательства abc , сосредоточившись на одном важном отрывке, который, по их мнению, был ошибочным. Шольце, в частности, считается авторитетом в теории чисел и в августе 2018 года получит медаль Филдса — высшую награду среди математиков. В сентябре того же года Шольце и Стикс стали публичными, когда они были процитированы в эксклюзивная статья в математическом и физическом журнале Quanta , в которой говорится, что они обнаружили «серьезную, неустранимую брешь», как выразился Стикс.«Я думаю, что гипотеза abc все еще открыта», — сказал Шольце Quanta . «У каждого есть шанс это доказать».

В комментариях, размещенных на его веб-сайте в то время, Мотидзуки отбросил критику, намекнув, что два автора просто не смогли понять его работу. Но несколько экспертов сказали Nature , что большая часть математического сообщества считает, что на этом вопрос решен.

Официальное принятие документов сейчас вряд ли изменит эту позицию.«Мое мнение никоим образом не изменилось с тех пор, как я написал эту рукопись вместе с Якобом Стиксом», — сказал Шольце Nature по электронной почте. (В отдельном электронном письме Stix отклонил запрос на комментарий.)

На пресс-конференции Тамагава сказал, что само решение не изменилось в ответ на критику Шольце и Stix. Некоторые комментарии по этому поводу будут опубликованы в рукописи, но принципиальных изменений не будет, — сказал Тамагава.

Если редакция журнала «отмахнется от этой критики» и опубликует статью без серьезных исправлений, это плохо отразится на них и на самом Мотидзуки, говорит Фолькер Мехрманн, президент Европейского математического общества (EMS), которое издает журнал от имени RIMS.(По словам Мерманна, EMS не контролирует содержание журнала, и он не знал, что объявление неизбежно, пока не связались с Nature . )

Но один математик, который предпочитает цитировать анонимно, говорит, что редакторы и рецензенты занимаются этим бумаги могли оказаться в почти безвыходной ситуации. «Если лучшие математики проводят время, пытаясь понять, что происходит, и терпят неудачу, как может один судья иметь хоть какой-то шанс?»

Долгий и извилистый путь к признанию

Математики часто публикуют статьи в журналах, редакторами которых они являются.Пока авторы отказываются от процесса рецензирования, «такой случай не является нарушением какого-либо правила и является обычным явлением», — говорит Хираку Накадзима, математик из Института физики и математики Вселенной им. Кавли. Токио, и ранее входил в состав редакционной коллегии журнала Publications RIMS . Мерманн подтверждает, что это не нарушит директив EMS.

Кашивара сказал, что Мотидзуки отказался от процесса рецензирования и не присутствовал ни на одном из собраний редакционной коллегии по поводу статьи.По его словам, ранее в журнале публиковались статьи других членов редакционной коллегии.

Статья Мотидзуки была принята 5 февраля, но дата публикации не определена. «Это очень длинная рукопись и будет специальным выпуском, поэтому мы не можем сказать, сколько времени это займет», — сказал Кашивара.

В мире математики одобрение журнала часто не является концом процесса рецензирования. Важный результат действительно становится принятой теоремой только после того, как сообщество достигнет консенсуса в том, что он верен, а достижение этого может занять годы после официальной публикации статьи.

«Несмотря на все трудности на протяжении многих лет, я все же думаю, что было бы здорово, если бы идеи Мочизуки оказались правильными», — говорит Минхён Ким, математик из Оксфордского университета, Великобритания.

A-B-C: Составлять книги по математике с помощью 1-2-3 легко

На этом уроке учащиеся пишут друг для друга книги по математическому алфавиту, чтобы повторить математическую терминологию. Они публикуют свои книги с помощью приложения Alphabet Organizer, а затем делятся своими новыми книгами со своими одноклассниками.

Приложение

Alphabet Organizer: учащиеся будут использовать это бесплатное приложение для создания книг с алфавитом, чтобы проиллюстрировать математические термины.

Ларсон, Дикс и Таунсенд считают, что предоставление студентам возможности практиковать академический словарный запас неоценимо.Они предсказывают, что такие упражнения со словарным запасом обеспечат студентам успехи в учебе. Они также предполагают, что изучение словарного запаса должно быть активным и увлекательным, чтобы учащиеся «понимали» важность изучения новых слов и понятий. Точно так же Коллиер утверждает, что учащиеся должны заниматься «осмысленными и разнообразными действиями, чтобы закрепить эти слова в долговременной памяти», а также устанавливать связи с тем, что они уже знают. Этот урок представляет собой уникальный метод обзора словарного запаса математического содержания и объединяет технологии, позволяющие учащимся овладеть технологическими инструментами, которые поддерживаются определением NCTE для грамотности 21 века.

Этот ресурс был приведен в соответствие со стандартами Common Core State Standards для штатов, в которых они были приняты. Если состояние не отображается в раскрывающемся списке, это означает, что предстоит согласование CCSS.

Этот урок соответствует стандартам в следующих штатах. Если состояние не отображается в раскрывающемся списке, стандартные выравнивания в настоящее время недоступны для этого состояния.

NCTE / IRA Национальные стандарты английского языка

• 1. Студенты читают широкий спектр печатных и непечатных текстов, чтобы лучше понять тексты, самих себя, а также культур США и мира; получать новую информацию; реагировать на нужды и запросы общества и рабочего места; и для личного самореализации. Среди этих текстов — художественная и документальная литература, классические и современные произведения.
• 3. Учащиеся применяют широкий спектр стратегий для понимания, интерпретации, оценки и оценки текстов. Они опираются на свой предыдущий опыт, свое взаимодействие с другими читателями и писателями, свое знание значения слов и других текстов, свои стратегии идентификации слов и свое понимание текстовых функций (например, соответствие между звуками и буквами, структуру предложения, контекст, графику). ).
• 4. Учащиеся корректируют использование устной, письменной и визуальной речи (напр.g., условности, стиль, словарный запас) для эффективного общения с различными аудиториями и для разных целей.
• 5. Студенты используют широкий спектр стратегий при написании и используют различные элементы процесса письма соответствующим образом для общения с разной аудиторией для различных целей.
• 6. Учащиеся применяют знания о структуре языка, языковых условных обозначениях (например, орфографии и пунктуации), медиа-техниках, образном языке и жанрах для создания, критики и обсуждения печатных и непечатных текстов.
• 8. Учащиеся используют различные технологические и информационные ресурсы (например, библиотеки, базы данных, компьютерные сети, видео) для сбора и синтеза информации, а также для создания и передачи знаний.
• 11. Учащиеся участвуют как знающие, размышляющие, творческие и критически настроенные члены различных сообществ грамотности.
• 12. Учащиеся используют устную, письменную и визуальную речь для достижения своих целей (e.g., для обучения, развлечения, убеждения и обмена информацией).

Студенты будут

• определяют самостоятельно выбранные математические термины.

• иллюстрируют математические термины изображениями.

• применяют определение математических терминов, как показано, предоставляя примеры их использования.

• Создайте алфавитную книгу с помощью мобильного приложения.

1. Разделите учащихся на группы по три или четыре человека. В своих группах попросите учащихся составить список всех математических терминов, которые они могут запомнить.
2. Когда у учащихся будет достаточно времени, чтобы вспомнить математические термины, снова соберите класс и спроецируйте лист планирования книги по математике. По мере того как учащиеся сообщают, какие термины они перечислили, напишите их в Таблице планирования математики соответствующей буквой.
3. После того, как все ответы будут записаны, объясните ученикам, что они будут создавать учебники по математическому алфавиту друг для друга, чтобы закрепить математические термины. Для каждой буквы алфавита они создадут страницу с математическим термином, его определением, примером его использования в мире и изображением.
4. Покажите ученикам созданный вами образец или образец математических терминов. Раздайте рубрику «Книги по математике» и попросите учащихся оценить образец по этой рубрике.
5. Раздайте лист планирования книги по математике.Дайте студентам время поработать над листом. Напомните учащимся, что, согласно рубрике, они должны писать полными предложениями. Кроме того, напомните учащимся, что эти книги читают друг друга, поэтому определения нужно писать их собственными словами, а не просто копировать из словаря или веб-сайта. Для букв, которым они не могут придумать математический термин, попросите учащихся использовать предлагаемые веб-сайты.
6. Поручите студентам заполнить распечатку листа планирования учебника математики перед следующим занятием.

1. Убедитесь, что все учащиеся заполнили распечатанные листы планирования учебника математики. Помогите тем, кому может понадобиться дополнительная помощь. При необходимости предоставьте учащимся дополнительное время для использования веб-сайтов для писем, в которых у них нет терминов.
2. Смоделируйте для студентов три варианта поиска изображений для их условий:
   • Покажите студентам, как делать фотографии с помощью планшетов.
   • Покажите студентам, как находить изображения в Интернете и сохранять на планшеты.
   • Скажите студентам, что они также могут рисовать картинки, а затем использовать планшеты для фотографирования своих иллюстраций.
3. Дайте студентам время поработать над поиском своих изображений. Обращайтесь по классу и отметьте время, затрачиваемое на задание, поскольку оно является частью рубрики. Помогите студентам освоить технологию. Спросите учащихся о том, почему они выбрали определенные изображения для своих условий.

1. Подключите один из планшетов к ЖК-проектору и покажите учащимся, как использовать приложение Alphabet Organizer.Включите в свою демонстрацию следующие моменты:
   • Попросите учащихся включить свои имена в название проекта, чтобы при отправке файлов по электронной почте было ясно, какая книга была написана каким учащимся.
   • Попросите их выбрать шаблон справа, в котором написано «одно слово и одно изображение на букву».
2. Дайте студентам время для создания своих книг с алфавитом. Пока студенты работают, помогайте тем, у кого проблемы с технологией. Убедитесь, что все ученики нашли свои фотографии.Помогите тем ученикам, которые могут стоять за поиском изображений. Убедитесь, что учащиеся пишут определения терминов своими словами и полными предложениями.
3. Наблюдайте за поведением учеников и временем выполнения задания, так как это является частью рубрики.
4. Покажите студентам ближе к концу третьего занятия, как сохранять свои проекты.
5. В конце четвертого занятия попросите студентов поделиться своим заключительным проектом, отправив книги по электронной почте.

1. Раздайте распечатку Листа для прослушивания математических терминов.Пока другие присутствуют, объясните классу, что они должны заполнить этот лист. Предложите классу, что им может понравиться, насколько хорошо ученик объяснил термин. Им может понравиться другой термин, потому что изображение очень хорошо соответствует определению.
2. Попросите учащихся поделиться своими книгами с алфавитом с классом, подключив мобильные устройства к ЖК-проектору с помощью адаптера.
3. После того, как каждый студент закончит, дайте ему время заполнить свои таблицы, а также прокомментировать примеры и изображения друг друга.
4. После того, как все представили, попросите студентов заполнить рефлексивные утверждения в разделе оценки:

   Из этого проекта я узнал ___________________________.

   Этот проект мог быть улучшен ___________________.

5. Соберите лист для заслушивания математических терминов и размышления учащихся.

• Если планшеты недоступны, учащиеся могут создавать бумажные копии своих книг по алфавиту или использовать интерактивный органайзер для учащихся, если есть компьютеры.

• Этот урок можно сократить, попросив учащихся охватить только одну букву алфавита и один математический термин. Затем страницы можно было распечатать и собрать в учебник.

• Поделитесь книгами с другими классами школы, распечатав готовые книги.

• Разместите книги на вики-странице класса или на веб-сайте для всеобщего обозрения.

• Попробуйте приложение Alphabet Organizer для другого словарного запаса, например, алфавита научных терминов.
  

Оценка учащихся / Размышления

Возможная оценка студентов включает

Из этого проекта я узнал ___________________________.

Этот проект мог быть улучшен ___________________.

Учите математику и азбуку в App Store

Agnitus — это адаптивная программа обучения для детей от 2 до 7 лет, основанная на руководящих принципах программы Common Core State Standard с подробным отслеживанием успеваемости.

Ваш ребенок будет изучать: математику, числа и счет, алфавиты и контрольные слова, науку, животных, формы, цвета, чтение и письмо, науку, музыку, искусство и многое другое.

Превратите экранное время во время обучения с помощью забавных интерактивных игр. и мероприятия, которые обучают основным навыкам дошкольного образования и детского сада. Разработано учителями в соответствии с общепринятыми стандартами учебной программы!

* УДОВОЛЬСТВИЕ и интерактивные обучающие навыки и мероприятия для детей от 2 до 7 лет

* Победитель TeachersWithApps Award и Parent Choice Award

* Преподает математику, чтение, письмо, детские стихи, развивающие игры, интерактивные книги и многое другое.

* Agnitus — одна из первых академий цифрового обучения. Будьте готовы восхищаться успехами и знаниями вашего ребенка!

* Отзыв учителя: «В рамках технологического внедрения в Объединенный школьный округ Милпитас — Центры развития детей рады заполнить наши классы iPad mini — и Agnitus подбадривает наших детей играть, чтобы учиться! … это многогранное обучающее приложение меняет наш взгляд на игры, развитие навыков и оценку в дошкольных учреждениях.Кэтлин Линкольн, директор программы Объединенного школьного округа Милпитас

* Parent’s Review: «Я думаю, что это лучшее приложение для малышей, которое я когда-либо видел. Моя дочь любит играть с ней, потому что игры всплывают случайным образом, и ей совсем не скучно. Табель успеваемости потрясающий, настолько полный, что трудно не понять. Нам это просто нравится! »Касла, мать 3-летней девочки

Другие отзывы родителей и учителей:
« Моей 3-летней дочери очень нравится это приложение.Она медленно продвигается по основной учебной программе. Я не могу дождаться, когда остальная часть будет добавлена ​​/ открыта, чтобы она могла поработать. Панель управления для родителей и табели успеваемости отлично подходят для меня, чтобы отслеживать ее успехи. Я очень рекомендую это приложение. «Мать трехлетнего ребенка.

» Это приложение, его учебная программа и аналитические возможности действительно выводят образовательный процесс на совершенно новый уровень. Я очень рекомендую это приложение всем родителям, которые хотят построить прекрасное будущее для своих детей. Доступ к таким данным может сыграть огромную роль в будущем детей.«Мама 6-летнего ребенка,

» Этим приложением пользуются мои 2-, 4- и 6-летние мальчики. Приложение измеряет прогресс, и у каждого есть личный файл с личным прогрессом в обучении. Малышу действительно не бывает скучно. Одно из лучших подробных приложений. «Мать 2-х, 4-х и 6-ти летних мальчиков

Звуковые дорожки для предварительного просмотра приложения предоставлены bensound.com

Планы подписки

Бесплатная пробная версия
Бесплатные пробные версии могут быть недоступны быть объединены с любыми другими предложениями. Если вы или другой член вашей семьи были участником Agnitus в течение последних 12 месяцев или если ваш Способ оплаты, физический адрес или адрес электронной почты были связаны с членством Agnitus, вы не имеете права на получите бесплатную пробную версию на 7 дней.

Ежемесячный план: 6,99 долларов США в месяц
Вы можете начать бесплатную пробную версию для ежемесячного плана в любое время. Мы начнем выставлять счет за обучение на ваш метод оплаты, когда вы запустите бесплатную пробную версию для платного плана. Мы будем продолжать выставлять счет за обучение на ваш метод оплаты ежемесячно, пока вы не отмените его.

Годовой план: 47,99 долларов США в год
Вы можете начать бесплатную пробную версию нашего годового плана в любое время. Мы начнем выставлять счет за обучение на ваш метод оплаты, когда вы запустите бесплатную пробную версию для платного плана.После первоначальной 7-дневной пробной версии с вас будет сначала взиматься плата за весь год, а в конце года с вас будет снова взиматься плата за следующий год, если вы не отмените подписку до этого.

ABC Гипотеза | Нерешенные математические задачи

Kanijoman / Flickr / Creative Commons

• Рецензируемый математический журнал, наконец, опубликует спорное доказательство основной математической идеи. (Но это собственный журнал математика.)
• Математические доказательства могут пройти множество итераций и попыток, прежде чем они станут правильными.
• Гипотеза abc относится к 1980-м годам и является расширением последней теоремы Ферма.

---

Была ли наконец решена одна из основных нерешенных проблем теории чисел? Или в в 600-страничной пробе отсутствует ключевой элемент? Вердикт еще не вынесен, но доказательства, по крайней мере, , наконец, появятся в рецензируемом журнале.

Однако есть одна загвоздка: сам математик Шиничи Мотидзуки является одним из старших редакторов журнала.

Тем, кто не занимается академической математикой, трудно объяснить одновременно, насколько странно драматичной была эта ситуация и насколько огромным было бы успешное доказательство гипотезы abc. Nature сравнивает его с доказательством последней теоремы Ферма в 1994 году, которое было гигантской вехой в математике, а в 26 лет — самым последним доказательством того же уровня достижений.

Оба доказательства также включают единственную алгебраическую категорию, называемую диофантовыми проблемами.Это уравнения, для которых люди стремятся найти целочисленные решения, например частные случаи теоремы Пифагора, называемые троек Пифагора . Когда вы изучаете уравнение и вас интересуют только решения, которые являются целыми числами, это диофантова проблема.

Гипотеза abc имеет некоторые общие черты с теоремой Пифагора и другими диофантовыми проблемами, включая связь между a и b , сложенными вместе с результирующим c .Могут ли эти числа быть доведены до высоких показателей и при этом иметь очевидную взаимосвязь? Это то, что математики пытались доказать с тех пор, как математики впервые заметили это в середине 1980-х годов. И, по сути, эта гипотеза является продолжением последней теоремы Ферма.

Подробнее из Природа:

Гипотеза abc выражает глубокую связь между сложением и умножением целых чисел. Любое целое число можно разложить на простые числа, его «делители»: например, 60 = 5 x 3 x 2 x 2.Гипотеза примерно утверждает, что если много маленьких простых чисел делят два числа a и b , , то только несколько больших делят свою сумму, c .


Мотидзуки впервые опубликовал доказательство гипотезы abc длиной в роман Миченера в 2012 году, когда он бесцеремонно выложил в Интернет 500 страниц и сказал, что доказал это. Но это не первое чье-либо родео. Предыдущие публичные попытки доказать эту гипотезу оказались ошибочными.В этом нет ничего необычного в процессе доказательства сложных и знаковых идей, когда разные ученые часто повторяют один новый шаг за раз в зависимости от того, что делают их коллеги.

Когда впервые появилось доказательство Мотидзуки, другие математики пришли в негодование как от идеи доказательства гипотезы abc, так и от непонятной неясности самой работы. Мотидзуки изобрел фантомные леса абстрактных понятий, которые скрывают реальные математические идеи и обозначения, чтобы повесить на них свое очень длинное доказательство.В некотором смысле, попытка расшифровать доказательство потребовала изучения совершенно новой системы и обозначений.

На сегодняшний день никто не понял это доказательство в достаточной степени, чтобы подтвердить его и передать его структуру и логическую последовательность другим. Сам Мотидзуки — затворник и не особо помог пролить свет на его неясные механизмы.

Несколько лет назад математики были расстроены, узнав, что доказательство должно быть опубликовано в рецензируемом журнале, а в 2018 году два выдающихся математика заявили, что уверены, доказательство неверно.

Слухи о публикации были тогда ложными или, возможно, были отменены после протестов математиков. Но теперь доказательство действительно появится в каком-то специальном выпуске Publications Исследовательского института математических наук (RIMS) после того, что, по их словам, будет той же строгой рецензией, которую они сделали бы для любого. Речь идет не только о скандальном доказательстве, но и о том, что Мотидзуки является главным редактором RIMS .

Возможно, написание 500-страничного гиганта оживит дискуссию и окончательно и навсегда обнажит любые недостатки.Трудно сказать наверняка, когда сами математические идеи настолько далеки от нормы, что кажутся математикой аутсайдера . Любой, кто отправлял материалы для технических или математических публикаций, получил гигантские, сложные документы, авторы которых настаивают, что они доказали нечто грандиозное.

Правда редко бывает так прямолинейна.

Этот контент создается и поддерживается третьей стороной и импортируется на эту страницу, чтобы помочь пользователям указать свои адреса электронной почты. Вы можете найти больше информации об этом и подобном контенте на сайте piano.io.

Angle — Определение математического слова

Angle — Определение математического слова — Math Open Reference

Определение: фигура, образованная двумя линиями или лучами, расходящимися от общей точки (вершины).

Попробуй это Отрегулируйте угол ниже, перетащив оранжевую точку.

Атрибуты

Вершина	Вершина это общая точка, в которой соединяются две прямые или лучи.Точка B — это фигура выше — это вершина угла ∠ABC.
Ножки	Ножки (по бокам) угла — две линии, составляющие его. На рисунке выше отрезки AB и BC — стороны угла ∠ABC.
Интерьер	Внутренняя часть угла — это пространство в «губах» угла, простирающееся до бесконечности. Видеть Интерьер угла
Внешний	Все пространство в самолете, кроме интерьера. Видеть Интерьер угла

Определение угла

Угол можно определить двумя способами.

1. Как это: ∠ABC

   Символ угла, за которым следуют три точки, определяющие угол, при этом средняя буква является вершиной, а две другие — ногами. Таким образом, на рисунке выше угол будет ABC или ∠CBA. Пока вершина — это средняя буква, порядок не важен. Как стенография мы можем использовать символ «угол». Например, «ABC» будет читаться как «угол ABC».

2. Или так: ∠B

   Просто по вершине, если это не неоднозначно. Таким образом, на рисунке выше угол можно было бы назвать просто ‘∠B’

Измерение угла

Размер угла измеряется в градусах (см. Угловые измерения). Когда мы говорим «угол ABC», мы имеем в виду фактический угловой объект. Если мы хотим говорить о размере или измерении угла в градусах, мы должны сказать «мера угла ABC» — часто пишется m∠ABC.

Однако много раз мы будем видеть «ABC = 34 °».Собственно говоря, это ошибка. Должно быть написано m∠ABC = 34 °.

Типы уголков

Всего существует шесть типов углов, перечисленных ниже. Щелкните изображение, чтобы получить полное описание этого типа и соответствующего интерактивного апплета.

В тригонометрии

При использовании в тригонометрии углы обладают некоторыми дополнительными свойствами: Они могут иметь размер больше 360 °, могут быть положительными и отрицательными и располагаться на координатной сетке с осями x и y. Обычно они измеряются в радианах, а не в градусов.Подробнее об этом см. Определение и свойства угла (тригонометрия).

Уголок строительный

В главе «Конструкции» есть анимированные демонстрации различных конструкции углов, используя только циркуль и линейку.

Другие темы ракурса

Общие

Типы углов

Угловые отношения

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

.

No related posts.