СРАВНЕНИЕ ВРЕМЕНИ РАЗЛОЖЕНИЯ ПЕРИОДИЧЕСКОЙ ФУНКЦИИ В РЯД ФУРЬЕ В ПАКЕТАХ MATHCAD И MATLAB
Авторы:
М.А. Нифедов
М.П. Базилевский
Дата поступления:
22.06.2020
Рубрика:
8. ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ
Номер журнала (Том):
3(9) 2020
УДК:
УДК 519.683.8
Файл статьи:
Аннотация:
Целью данной работы является проведение сравнительного анализа времени разложения в ряд Фурье заданной периодической функции в пакетах Mathcad и MATLAB. Кратко рассмотрены основные теоретические сведения о разложении периодических функций в ряд Фурье. Для исследования пакетов Mathcad и MATLAB была поставлена задача разложения конкретной кусочно-заданной функции. Для этой функции была организована проверка условий теоремы Дирихле, которая позволила сделать вывод о допустимости её разложения в ряд Фурье. В пакетах Mathcad и MATLAB разработаны программы для разложения заданной функции в ряд Фурье. Первичное разложение заданной функции в пакетах Mathcad и MATLAB продемонстрировало на её концах явление Гиббса.
Ключевые слова:
ряд Фурье
разложение в ряд Фурье
теорема Дирихле
явление Гиббса
Mathcad
Matlab
Список цитируемой литературы:
1. Привалов И.И. Ряды Фурье: учебник для вузов. – М.: Издательство Юрайт, 2016. – 164 с.
2. Письменный Д.Т. Конспект лекций по высшей математике: полный курс. – М.: Айрис-пресс, 2006. – 608 с.
3. Медведева И.П., Багдуева Х.Н. Ряды: учебное пособие. – Иркутск: ИрГУПС, 2006. – 114 с.
4. Изосова Л.А., Изосов А.В., Грачёва Л.А. Элементы теории рядов: учебное пособие. – Магнитогорск: МГТУ, 2009. – 111 с.
5. Пчельников О.О., Новоселов И.М. Разложение функции в ряд Фурье при помощи персонального компьютера // Вестник Ижевской государственной сельскохозяйственной академии. 2012. – № 1 (30).
6. Гусенков А.В., Лебедев В.Д., Соколов А.М., Шадриков Т.Е. Применение разложения в ряд Фурье при расчете режимов работы полупроводникового преобразователя // Состояние и перспективы развития электро- и теплотехнологии (XVIII Бенардосовские чтения): материалы Международной научно-технической конференции. 2015. – С. 120-123.
7. Мельникова Е.Б., Лямина Н.В. Выявление методом разложения в ряд Фурье биологических ритмов гидробионтных сообществ // Ученые записки Таврического национального университета имени В.И. Вернадского. Серия: Биология, химия. 2013. – Т. 26 (65). – № 2. – С. 133-140.
8. Хазиев А.А., Лаушкин А.В., Постолит А.В., Васильева Л.С., Борисов Б.С. Экспресс-анализ моторных масел на основе инфракрасной спектроскопии с разложением в ряд Фурье // Транспорт. Транспортное сооружение. Экология. 2017. – № 2. – С. 116-125.
 2017. – Т. 1. – С. 159-162.
2017. – Т. 1. – С. 159-162.10. Носков С.И., Базилевский М.П. Построение регрессионных моделей с использованием аппарата линейно-булевого программирования. – Иркутск, 2018. – 176 с.
11. Базилевский М.П., Носков С.И. Программный комплекс построения линейной регрессионной модели с учётом критерия согласованности поведения фактической и расчетной траекторий изменения значений объясняемой переменной // Вестник Иркутского государственного технического университета. 2017. – Т. 21, № 9 (128). – С. 37-44.
12. Базилевский М.П., Носков С.И. Формализация задачи построения линейно-мультипликативной регрессии в виде задачи частично-булевого линейного программирования // Современные технологии. Системный анализ. Моделирование. 2017. – № 3 (55). – С. 101-105.
13. Баенхаева А.В., Базилевский М.П., Носков С.И. Моделирование валового регионального продукта Иркутской области на основе применения методики множественного оценивания регрессионных параметров // Фундаментальные исследования. 2016. – № 10-1. – С. 9-14.
2016. – № 10-1. – С. 9-14.
14. Базилевский М.П., Врублевский И.П., Носков С.И., Яковчук И.С. Среднесрочное прогнозирование эксплуатационных показателей функционирования Красноярской железной дороги // Фундаментальные исследования. 2016. – № 10-3. – С. 471-476.
15. Базилевский М.П. Сведение задачи отбора информативных регрессоров при оценивании линейной регрессионной модели по методу наименьших квадратов к задаче частично-булевого линейного программирования // Моделирование, оптимизация и информационные технологии. 2018. – Т. 6, № 1 (20). – С. 108-117.
16. Базилевский М.П. Отбор информативных регрессоров с учётом мультиколлинеарности между ними в регрессионных моделях как задача частично-булевого линейного программирования // Моделирование, оптимизация и информационные технологии. 2018. – Т. 6, № 2 (21). – С. 104-118.
17. Базилевский М.П. Синтез модели парной линейной регрессии и простейшей EIV-модели // Моделирование, оптимизация и информационные технологии. 2019. – Т. 7, № 1 (24). – С. 170-182.
– Т. 7, № 1 (24). – С. 170-182.
18. Базилевский М.П. Исследование двухфакторной модели полносвязной линейной регрессии // Моделирование, оптимизация и информационные технологии. 2019. – Т. 7, № 2 (25). – С. 80-96.
19. Mathcad [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Mathcad (дата обращения 11.05.2020)
20. MATLAB[Электронный ресурс].– Режим доступа: https://ru.wikipedia.org/wiki/MATLAB (дата обращения 11.05.2020)
|
MATHCAD
Сигнал прямоугольной формы можно описать следующим аналитическим выражением . (1)
Спектр такого сигнала s(t) с помощью ряда Фурье в тригонометрической форме имеет следующий вид:
Коэффициенты разложения ряда Фурье вычисляются по формулам:
где x(t) – периодический сигнал. Полученное аналитическое выражение сигнала x(t) в среде MathCAD будет иметь вид:
Для построения графика
сигнала x = f(t)
необходимо выбрать в главном меню программы MathCAD «Вид – Панели инструментов – График», далее на
появившейся панели «Graph» выбрать элемент «Декартов график», после чего на
рабочей области программы MathCAD появится область построения графика. По оси
ординат области построения графика необходимо ввести «x(t)», а по
оси абсцисс – «t». Далее двойным щелчком левой кнопки мыши по области
построения графика необходимо вызвать панель форматирования графика. Рис. График сигнала прямоугольной формы в среде MathCAD: A = 1, T = 50, τ = 25
Для записи разложения
сигнала в тригонометрический ряд Фурье потребуется вызвать панель «Calculus» или в главном меню выбрать «Вид – Панели
инструментов – Калькуляция». Полученное выражение для спектрального показания сигнала в общем виде для заданного числа гармоник N = 3 запишем следующим образом:
Чтобы добавить на график x = f(t) спектральную форму сигнала s = f(t), нужно выделить указателем мыши на оси ординат поле, где записана функция исходного сигнала x(t) и справа от неё ввести запятую, после этого ниже появится поле для ввода ещё одной функции, куда следует ввести s(t). Графики сигнала прямоугольной формы и его спектральное показание по первым трём гармоникам показаны на рисунке ниже.
Рис. Графики исходного сигнала прямоугольной формы x(t)
Аналогично строят графики
для пяти и семи гармоник. Для этого в программе расчёта гармоник нужно лишь
присвоить числу гармоник N новое значение, а программа автоматически пересчитает
спектр сигнала.
Рис. Графики исходного сигнала прямоугольной формы x(t) и его спектральное показание s(t) для числа гармоник N = 5
Рис. Графики исходного сигнала прямоугольной формы x(t) и его спектральное показание s(t) для числа гармоник N = 7
|
||||||||||||||||||||||
PTC Mathcad Prime 8 | Маткад
Что нового в PTC Mathcad Prime 8?
PTC Mathcad Prime — это отраслевой стандарт программного обеспечения для инженерной математики, позволяющий решать самые сложные задачи и обмениваться инженерными расчетами. А с PTC Mathcad Prime 8 инженерные расчеты стали еще лучше. В этом выпуске представлено ключевое приложение, символьный движок, числовой движок и улучшения удобства использования.
А с PTC Mathcad Prime 8 инженерные расчеты стали еще лучше. В этом выпуске представлено ключевое приложение, символьный движок, числовой движок и улучшения удобства использования.
Обновления приложений
Существует несколько обновлений функций на уровне приложений, которые включают важные функции, запрошенные пользователями.
- Теперь вы можете устанавливать предупреждения, когда пользовательские или системные идентификаторы, такие как переменные, константы и функции, переопределяются на вашем листе. Это позволяет избежать неосознанного изменения определения критических параметров.
- Мы добавили оператор частной производной в меню «Операторы», который можно использовать для определения вычислений, включающих частные производные.
- Вы можете независимо включать верхний и нижний колонтитулы или границу представления страницы с помощью новой функции отображения рамки.

- А для повышения удобства использования элемента управления вводом в поле со списком, добавленного в последнем выпуске, в Prime 8 вы можете копировать несколько значений и вставлять их в режим редактирования поля со списком, что упрощает создание элемента управления вводом в поле со списком.
Усовершенствования символьных и числовых движков
В Mathcad Prime 8 реализовано множество усовершенствований, ориентированных на клиентов, а также новых функций, отсутствовавших в предыдущих версиях Mathcad. Помимо общих улучшений ключевых слов, были значительно улучшены и расширены использование и производительность для интегральных функций, таких как Фурье, Лаплас и Ztrans и их обратные. Были добавлены два новых модификатора, позволяющие манипулировать факторами нормализации и колебаний для использования с ключевым словом Фурье. Операторы исчисления, такие как пределы, интегралы и производные, были улучшены и охватывают расширенные варианты использования. И теперь улучшена автоматическая маркировка неопределенных переменных в символьных результатах.
И теперь улучшена автоматическая маркировка неопределенных переменных в символьных результатах.
Обновления юзабилити
- Теперь вы можете видеть на вкладке рабочего листа, когда рабочий лист не сохранен, и можете закрыть рабочий лист непосредственно из его вкладки.
- Вы можете перемещать рабочие листы, чтобы изменить их порядок.
- Каждая вкладка теперь содержит меню правой кнопки мыши, которое обеспечивает доступ к полезным действиям, включая расчет, перемещение вкладки, копирование полного пути к файлу, открытие содержащей папки и закрытие этой или других вкладок.
- И есть несколько небольших обновлений удобства использования, таких как новая команда формата открытого текста и масштабирование с помощью Ctrl/Wheel.
Сохранить как устаревшее представление листа HTML
И, наконец, в устаревший конвертер листов добавлен новый параметр «Сохранить как HTML». Это позволяет вам создать представление вашего устаревшего рабочего листа PTC Mathcad перед его преобразованием в формат PTC Mathcad Prime и обращаться к нему, чтобы при необходимости переработать преобразованный рабочий лист.
Это позволяет вам создать представление вашего устаревшего рабочего листа PTC Mathcad перед его преобразованием в формат PTC Mathcad Prime и обращаться к нему, чтобы при необходимости переработать преобразованный рабочий лист.
Вы новичок в Mathcad Prime 8?
При загрузке PTC Mathcad Express и выборе 30-дневной полной функциональности вы получите доступ к полной версии PTC Mathcad Prime 8 на 30 дней.
Получить пробную версию / / /
Введение в ряды Фурье
Введение в ряды Фурье
| |||||||||||||||||||||||||||||||||||||
АУДИТОРИЯ | НАГРАДЫ | ЛЮДИ | ТРЕК | РАСПРОСТРАНЕНИЕ | ПУБЛИКАЦИИ | ||
Авторские права:
Университет
Южной Флориды, 4202 E Fowler Ave, Tampa, FL 33620-5350. Все права защищены. | ||





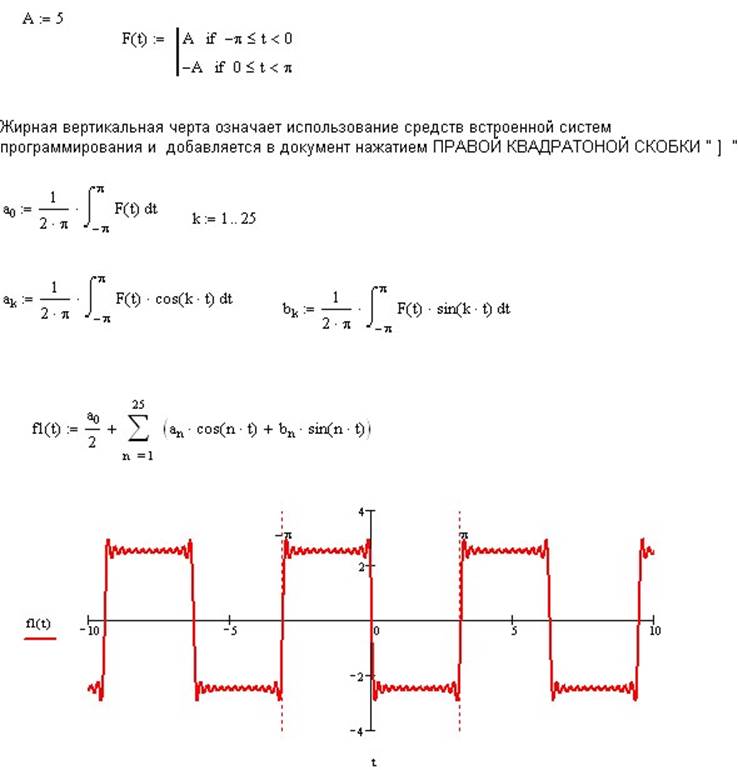 При этом автоматически обновится график зависимости s = f(t).
При этом автоматически обновится график зависимости s = f(t).
