Матлаб решение системы уравнений: 1.11 Решение систем линейных уравнений

alexxlab / / Разное

Содержание

1.11 Решение систем линейных уравнений

MATLAB позволяет работать с объектами линейной алгебры, т. е. векторами и матрицами, настолько просто, насколько это вообще возможно.

Яркий пример этому – решение систем линейных уравнений.

Пример:

Пусть дана система линейных уравнений

Решить систему с применением оператора обратного деления матриц < \ >.

Решение:

В матричной записи система имеет вид Ах = b, где

A = , b = , х =

– соответственно матрица из коэффициентов при незвестных, вектор-столбец из свободных членов и вектор-столбец из неизвестных.

Введем матрицу А и вектор-столбец свободных членов b:

>> А=[1 3 0;-2 -2 5;1 0 -5]

А =

1 3 0

-2 -2 5

1 0 -5

>> b=[-2;10;-9]

b =

-2

10

-9

Известно, что система имеет единственное решение, если определитель матрицы А не равен нулю (│A│ = det(A) ≠ 0). Вычислим определитель матрицы А:

>> disp(det(A))

-5

Определитель не равен нулю. Находим решение системы с помощью оператора обратного деления матриц < \ >:

>> x=А\b

x =

1

-1

2

Проверим полученное решение x1 = 1, x2

= -1, x3 = 2 подстановкой в систему уравнений:

>> disp(A*x)

-2.0000

10.0000

-9.0000

В результате проверки получен вектор-столбец свободных членов. Значит, система решена верно.

Найдем теперь решение системы х = A-1b с помощью обратной матрицы. Вначале вычислим обратную матрицу A-1:

>> A1=inv(A)

A1 =

-2. 0000 -3.0000 -3.0000

1.0000 1.0000 1.0000

-0.4000 -0.6000 -0.8000

Находим решение системы:

>> A1*b

ans =

1.0000

-1.0000

2.0000

Отметим, что решение системы с помощью обратной матрицы требует больше времени и памяти, к тому же этот способ может дать большую погрешность решения. Поэтому для решения линейных систем рекомендуется применять оператор обратного деления < \ >.

Пример:

Решить систему линейных уравнений

Решение:

>> A=[1 3 0;-2 -2 5;1 0 5]

A =

1 3 0

-2 -2 5

1 0 5

>> b=[-2 10 -9]

b =

-2 10 -9

>> disp(det(A))

35

Находим решение системы:

>> x=A\b’

x =

-7. 5714

1.8571

-0.2857

Заметим, что обратное деление произведено на вектор-столбец b‘, поскольку вектор b введен как вектор-строка. Получили приближенное решение системы. Вычислим обратную матрицу A-1:

>> disp(inv(A))

-0.2857 -0.4286 0.4286

0.4286 0.1429 -0.1429

0.0571 0.0857 0.1143

Точное решение системы и точная обратная матрица выражаются через рациональные дроби:

>> format rat

>> x=A\b’

x =

-53/7

13/7

-2/7

>> disp(inv(A))

-2/7 -3/7 3/7

3/7 1/7 -1/7

2/35 3/35 4/35

1. Какие окна имеет интерфейс MATLAB и каково их назначение

2. Какова структура командного окна Command Window

3. Как называется отображение в командном окне сеанса работы с системой На какие зоны подразделяется текстовое поле окна Command Window

4. Для чего служат в MATLAB клавиши <↑> и <↓>

5. Для чего применяется команда disp

6. Как можно ввести слишком длинную команду в окне C

ommand Window

7. Какая информация сохраняется в окнах Command History и Workspase после применения команды очистки экрана clc

8. Как получить справку по выбранной команде MATLAB

9. В каких форматах представляются в MATLAB вещественные числа

10. Какие форматы отображения вещественных чисел используются в MATLAB

11. Как в в MATLAB осуществляются операции с комплексными числами

12. В чем измеряются аргументы встроенных тригонометрических функций

13. Какая команда осуществляет векторизацию символьного выражения

14. Как MATLAB реагирует на ошибки ввода

15. Как обнаружить и устранить семантическую ошибку ввода

16. Как в MATLAB создаются векторы и матрицы

17. Как осуществляется просмотр и редактирование переменных в окне Workspase

18. Как в MATLAB осуществляются матричные и поэлементные операции над векторами и матрицами

19. Что вычисляют команды dot и cross

20. Как решается система линейных уравнений с помощью оператора обратного деления < \ >

Как решить систему линейных уравнений в matlab

Решение системы линейных алгебраических уравнений (СЛАУ) средствами MATLAB

. -1 , что означает A в степени -1.

2. Решение системы уравнений методом Гаусса.

Метод исключения Гаусса является одним из наиболее простых и эффективных методов. Алгоритм метода Гаусса основан на приведении матрицы А к треугольному виду (прямой ход) и последовательном вычислении неизвестных (обратный ход). Эти процедуры можно выполнять над невыраженными матрицами, в противном случае метод Гаусса неприменим.

Недостатком метода является накапливание погрешностей в процессе округления, поэтому метод Гаусса без выбора главных элементов используется обычно для решения сравнительно небольших (n < 100 — 200) систем уравнений с плотно заполненной матрицей и не близким к нулю определителем.

В MATLAB для решения систем уравнений (1) методом исключения Гаусса применяются следующие операторы:

Решение СЛАУ и матрицы в Matlab

Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и для этого необходимо знание нескольких базовых алгоритмов.

Также стоит отметить, что у каждого алгоритма, которым мы будем искать решение СЛАУ в Matlab, своя скорость нахождения этого решения, наличие или отсутствие условия выполнения алгоритма и т.д.

В традициях нашего сайта разберём на примере:

Решить систему линейных уравнений:

4*a + b — c = 6
a — b + c = 4
2*a — 3*b — 3*c = 4

Метод обратной матрицы в Matlab

Начнем с достаточно распространенного метода. Его суть состоит в том, что сначала необходимо выписать коэффициенты при a, b и c (то есть те коэффициенты, которые находятся слева) в одну матрицу, а свободный член (то есть то, что справа) в другую.

В итоге у нас получится 2 матрицы:

Для реализации этого метода (и следующих методов тоже) требуется одно условие: чтобы определитель матрицы, составленной из коэффициентов левой части не был равен нулю. Проверка на определитель:

После проверки условия можем перейти к следующему шагу: нахождение обратной матрицы. В Matlab для этого используется оператор inv .
А само решение СЛАУ в Matlab находится как перемножение найденной обратной матрицы на матрицу свободных членов:

Мы получили 3 значения, которые и соответствуют нашим коэффициентам: то есть a = 2, b = -1, c = 1 . Можете проверить, подставив полученные ответы в исходную систему, и убедиться, что мы решили СЛАУ правильно.

Также следует отметить, что матрицы нужно перемножать именно, как сделали мы, то есть слева обратная матрица, справа матрица свободных членов.

Если вы не все поняли, то советую вам почитать нашу статью по основам Matlab.

Метод Гаусса

Метод Гаусса в Matlab реализуется достаточно просто: для этого нам нужно всего лишь изучить один новый оператор.
(\) — левое деление.
При следующей записи:

Мы получим ответы на нашу исходную систему. Только заметьте, мы решили СЛАУ стандартным набором функций в Matlab, и желательно этот оператор использовать когда матрица коэффициентов квадратная, так как оператор приводит эту матрицу к треугольному виду. В других случаях могут возникнуть ошибки.

Метод разложения матрицы

Теперь поговорим о разложении матрицы. Нахождение решения через разложение матрицы очень эффективно. Эффективность обусловлена скоростью нахождения решения для данного вида систем и точностью полученных результатов.

Возможны следующие разложения:

  • разложение Холецкого
  • LU разложение
  • QR разложение

Разберём решение через LU и QR разложение, так как в задачах чаще всего встречается задание на решение именно через такие разложения.

Основное отличие этих двух разложений: LU разложение применимо только для квадратных матриц, QR &#8212; возможно и для прямоугольных.

LU разложение

Решим выше предложенную задачу через LU разложение:

QR разложение

И через QR разложение соответственно:

Отметим, что апостроф ( ‘ ) после Q означает транспонирование.

Стандартные функции Matlab

Так же Matlab предлагает функцию linsolve , с помощью которой возможно решить систему линейных алгебраических уравнений. Выглядит это так:

Как видите, ничего сложного тут нет, на то они и стандартные функции Matlab.

Повторение

Итак, сегодня мы с вами изучили несколько методов для решения СЛАУ в Matlab, как с помощью матриц, так и с помощью стандартных функций. Давайте их повторим на другом примере:

Решить систему линейных уравнений:
6*a — b — c = 0
a — 2*b + 3*d = 0
3*a — 4*b — 4*c = -1

  • Методом обратной матрицы:
  • Методом Гаусса:
  • LU разложение:
  • QR разложение:

На этом я с вами попрощаюсь, надеюсь, вы научились применять матрицы в Matlab для решения СЛАУ.

Документация

Одной из самых важных проблем в техническом вычислении является решение систем одновременных линейных уравнений.

В матричном обозначении общая проблема принимает следующую форму: Учитывая две матрицы A и b, действительно там существует уникальный матричный x, так, чтобы A x = b или x A = b?

Это поучительно, чтобы рассмотреть пример 1 на 1. Например, делает уравнение

имеет уникальное решение?

Ответ, конечно, является да. Уравнение имеет уникальное решение x = 3. Решение легко получено делением:

Решение обычно не получается путем вычисления инверсии 7, который равняется 7 –1 = 0.142857. и затем умножение 7 –1 21. Это было бы, больше работают и, если 7 –1 представлен конечному числу цифр, менее точных. Подобные факторы применяются к наборам линейных уравнений с больше чем одним неизвестным; MATLAB &#x00AE; решает такие уравнения, не вычисляя инверсию матрицы.

Несмотря на то, что это не стандартное математическое обозначение, MATLAB использует терминологию деления, знакомую в скалярном случае, чтобы описать решение общей системы одновременных уравнений. Два символа деления, наклонная черта ,/, и обратная косая черта , \, соответствуют этим двум функциям MATLAB mrdivide и mldivide . Эти операторы используются для двух ситуаций, где неизвестная матрица появляется слева или право на матрицу коэффициентов:

Обозначает решение матричного уравнения xA = b, полученное использование mrdivide .

Обозначает решение матричного уравнения Ax = b, полученное использование mldivide .

Думайте о “делении” обеих сторон уравнения Ax = b или xA = b A. Матрица коэффициентов A всегда находится в “знаменателе”.

Условия совместимости размерности для x = A\b потребуйте этих двух матриц A и b иметь одинаковое число строк. Решение x затем имеет одинаковое число столбцов как b и его размерность строки равна размерности столбца A . Для x = b/A , ролями строк и столбцов обмениваются.

На практике линейные уравнения формы Ax = b происходят более часто, чем те из формы xA = b. Следовательно, обратная косая черта используется намного более часто, чем наклонная черта. Остаток от этого раздела концентрируется на операторе обратной косой черты; соответствующие свойства оператора наклонной черты могут быть выведены из идентичности:

Матрица коэффициентов A не должно быть квадратным. Если A имеет размер m-by-n, затем существует три случая:

Квадратная система. Ищите точное решение.

Сверхрешительная система, большим количеством уравнений, чем неизвестные. Найдите решение методом наименьших квадратов.

Недоопределенная система, меньшим количеством уравнений, чем неизвестные. Найдите основное решение с в большей части m ненулевые компоненты.

Mldivide Алгоритм

mldivide оператор использует другие решатели, чтобы обработать различные виды содействующих матриц. Различные случаи диагностированы автоматически путем исследования матрицы коэффициентов. Для получения дополнительной информации смотрите раздел “Algorithms” mldivide страница с описанием.

Общее решение

Общее решение системы линейных уравнений Ax = b описывает все возможные решения. Можно найти общее решение:

Решение соответствующей гомогенной системы Ax = 0. Сделайте это использование null команда, путем ввода null(A) . Это возвращает базис для пробела решения к Ax = 0. Любое решение является линейной комбинацией базисных векторов.

Нахождение конкретного решения неоднородной системы Ax =b.

Можно затем записать любое решение Ax = b как сумма конкретного решения Ax =b, от шага 2, плюс линейная комбинация базисных векторов от шага 1.

Остальная часть этого раздела описывает, как использовать MATLAB, чтобы найти конкретное решение Ax =b, как на шаге 2.

Квадратные системы

Наиболее распространенная ситуация включает квадратную матрицу коэффициентов A и один правый вектор-столбец стороны b .

Невырожденная матрица коэффициентов

Если матричный A несингулярно, затем решение, x = A\b , одного размера с b . Например:

Можно проверить, что A*x точно равно u .

Если A и b являются квадратными и тот же размер, x= A\b также что размер:

Можно проверить, что A*x точно равно b .

Оба из этих примеров имеют точные, целочисленные решения. Это вызвано тем, что матрица коэффициентов была выбрана, чтобы быть pascal(3) , который является (несингулярной) матрицей полного ранга.

Сингулярная матрица коэффициентов

A квадратной матрицы сингулярен, если он не имеет линейно независимых столбцов. Если A сингулярен, решение Ax = b или не существует или не уникален. Оператор обратной косой черты, A\b , выдает предупреждение если A почти сингулярно или если это обнаруживает точную сингулярность.

Если A сингулярен и Ax =, b имеет решение, можно найти конкретное решение, которое не уникально путем ввода

pinv(A) псевдоинверсия A. Если Ax = b не имеет точного решения, то pinv(A) возвращает решение методом наименьших квадратов.

сингулярно, когда можно проверить путем ввода

Поскольку A не является полным рангом, он имеет некоторые равные нулю сингулярные значения.

Точные решения. Для b =[5;2;12] , уравнение Ax = b имеет точное решение, данное

Проверьте тот pinv(A)*b точное решение путем ввода

Решения методом наименьших квадратов. Однако, если b = [3;6;0] , Ax = b не имеет точного решения. В этом случае, pinv(A)*b возвращает решение методом наименьших квадратов. Если вы вводите

вы не возвращаете исходный вектор b .

Можно определить, имеет ли Ax =b точное решение путем нахождения, что строка уменьшала форму эшелона расширенной матрицы [A b] . Чтобы сделать так для этого примера, войти

Поскольку нижний ряд содержит все нули за исключением последней записи, уравнение не имеет решения. В этом случае, pinv(A) возвращает решение методом наименьших квадратов.

Сверхрешительные системы

В этом примере показано, как со сверхрешительными системами часто сталкиваются в различных видах аппроксимирования кривыми к экспериментальным данным.

Количество y измеряется в нескольких различных значениях времени t произвести следующие наблюдения. Можно ввести данные и просмотреть их в таблице со следующими операторами.

Попытайтесь моделировать данные с затухающей показательной функцией

y ( t ) = c 1 + c 2 e — t .

Предыдущее уравнение говорит что векторный y должен быть аппроксимирован линейной комбинацией двух других векторов. Каждый — постоянный вектор, содержащий все единицы, и другой вектор с компонентами exp(-t) . Неизвестные коэффициенты, c 1 и c 2 , может быть вычислен путем выполнения метода наименьших квадратов, который минимизирует сумму квадратов отклонений данных из модели. Существует шесть уравнений в двух неизвестных, представленных 6 2 матрица.

Используйте оператор обратной косой черты, чтобы получить решение методом наименьших квадратов.

Другими словами, метод наименьших квадратов к данным

y ( t ) = 0 . 4 7 6 0 + 0 . 3 4 1 3 e — t .

Следующие операторы оценивают модель в расположенном с равными интервалами шаге в t , и затем постройте результат вместе с исходными данными:

E*c не точно равно y , но различие может хорошо быть меньше погрешностей измерения в исходных данных.

Прямоугольный матричный A имеет неполный ранг, если это не имеет линейно независимых столбцов. Если A имеет неполный ранг, затем решение методом наименьших квадратов к AX = B не уникально. A\B выдает предупреждение если A имеет неполный ранг и производит решение методом наименьших квадратов. Можно использовать lsqminnorm найти решение X это имеет минимальную норму среди всех решений.

Недоопределенные системы

В этом примере показано, как решение недоопределенных систем не уникально. Недоопределенные линейные системы включают больше неизвестных, чем уравнения. Матричная операция левого деления в MATLAB находит основное решение методом наименьших квадратов, которое имеет в большей части m ненулевые компоненты для m — n матрица коэффициентов.

Вот небольшой, случайный пример:

Линейная система Rp = b вовлекает два уравнения в четыре неизвестные. Поскольку матрица коэффициентов содержит маленькие целые числа, уместно использовать format команда, чтобы отобразить решение в рациональном формате.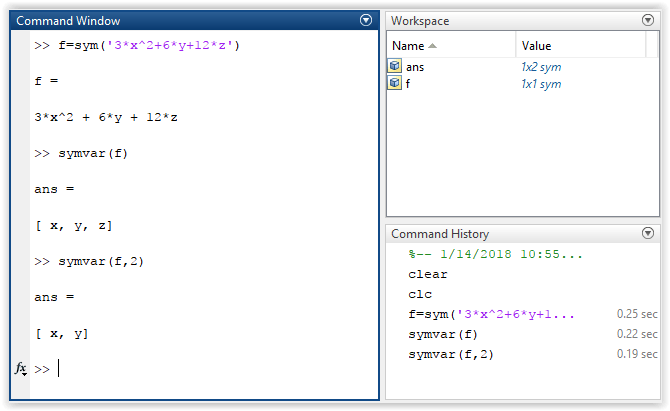 Конкретное решение получено с

Одним из ненулевых компонентов является p(2) потому что R(:,2) столбец R с самой большой нормой. Другим ненулевым компонентом является p(4) потому что R(:,4) доминирует после R(:,2) устраняется.

Полное общее решение недоопределенной системы может быть охарактеризовано путем добавления p к произвольной линейной комбинации пустых векторов пробела, которые могут быть найдены с помощью null функция с опцией, запрашивающей рациональный базис.

Можно проверить, что R*Z нуль и что остаточный R*x — b мал для любого векторного x , где

Начиная со столбцов Z пустые векторы пробела, продукт Z*q линейная комбинация тех векторов:

Z q = ( x ⇀ 1 x ⇀ 2 ) ( u w ) = u x ⇀ 1 + w x ⇀ 2 .

Чтобы проиллюстрировать, выберите произвольный q и создайте x .

Вычислите норму невязки.

Когда бесконечно много решений доступны, решение с минимальной нормой особенно интересно. Можно использовать lsqminnorm вычислить решение методом наименьших квадратов минимальной нормы. Это решение имеет наименьшее значение для norm(p) .

Решение для нескольких правых сторон

Некоторые проблемы касаются решения линейных систем, которые имеют ту же матрицу коэффициентов A , но различные правые стороны b . Когда различные значения b доступны одновременно, можно создать b как матрица с несколькими столбцами и решают все системы уравнений одновременно с помощью одной команды обратной косой черты: X = A\[b1 b2 b3 …] .

Однако иногда различные значения b не все доступны одновременно, что означает, что необходимо решить несколько систем уравнений последовательно. Когда вы решаете одну из этих систем уравнений с помощью наклонной черты (/) или обратная косая черта (\), оператор разлагает на множители матрицу коэффициентов A и использование это матричное разложение, чтобы вычислить решение. Однако в каждый последующий раз вы решаете аналогичную систему уравнений с различным b , оператор вычисляет то же разложение A , который является избыточным расчетом.

Решение этой проблемы состоит в том, чтобы предварительно вычислить разложение A , и затем снова используйте факторы, чтобы решить для различных значений b . На практике, однако, предварительное вычисление разложения этим способом может затруднить, поскольку необходимо знать, какое разложение вычислить (LU, LDL, Холесский, и так далее), а также как умножить факторы, чтобы решить задачу. Например, с LU-разложением необходимо решить две линейных системы, чтобы решить исходную систему Ax = b:

Вместо этого рекомендуемый метод для решения линейных систем с несколькими последовательными правыми сторонами должен использовать decomposition объекты. Эти объекты позволяют вам усилить выигрыши в производительности предварительного вычисления матричного разложения, но они не требуют знания того, как использовать матричные факторы. Можно заменить предыдущее LU-разложение на:

Если вы не уверены который разложение использовать, decomposition(A) выбирает правильный тип на основе свойств A , похожий на то, что делает обратная косая черта.

Вот простой тест возможных выигрышей в производительности этого подхода. Тест решает ту же разреженную линейную систему 100 раз с помощью и обратной косой черты (\) и decomposition .

Элементарные средства решения СЛУ MatLab

Урок 16. Численные методы Элементарные средства решения СЛУ
Функции для решения систем линейных уравнений с ограничениями
Решение СЛУ с разреженными матрицами
Точное решение, метод наименьших квадратов и сопряженных градиентов
Двунаправленный метод сопряженных градиентов
Устойчивый двунаправленный метод
Метод сопряженных градиентов
Квадратичный метод сопряженных градиентов
Метод минимизации обобщенной невязки
Квазиминимизация невязки — функция qmr
Вычисление нулей функции одной переменной

Минимизация функции одной переменной
Минимизация функции нескольких переменных
Аппроксимация производных
Аппроксимация Лапласиана
Аппроксимация производных конечными разностями
Вычисление градиента функции
Численное интегрирование
Метод трапеций
Численное интегрирование методом квадратур
Работа с полиномами
Умножение и деление полиномов
Вычисление полиномов
Вычисление производной полинома
Решение полиномиальных матричных уравнений
Разложение на простые дроби
Решение обыкновенных дифференциальных уравнений
Решатели ОДУ
Использование решателей систем ОДУ
Описание системы ОДУ
Дескрипторная поддержка параметров решателя
Пакет Partial Differential Equations Toolbox
Что нового мы узнали?

Решение систем линейных уравнений (СЛУ) относится к самой массовой области применения матричных методов, описанных в уроках 10-12.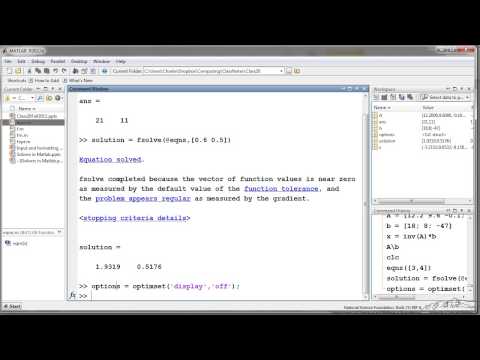

В этом разделе вы найдете ответы на вопросы, каким образом применяются указанные методы и какие дополнительные функции имеет система MATLAB для решения систем линейных уравнений.

Как известно, обычная СЛУ имеет вид:

а 11 X 1 , а 12 ,X 2 …, а 1n X n =b 1

Здесь а 11 , а, 2 ,…, а пп — коэффициенты, образующие матрицу А, которые могут иметь действительные или комплексные значения, x

1 , х 2 ,. .., х п — неизвестные, образующие вектор X, и b 1 , b 2 ,…, b п — .свободные члены (действительные или комплексные), образующие вектор В. Эта система может быть представлена в матричном виде как АХ=В, где А — матрица коэффициентов уравнений, X — искомый вектор неизвестных и В — вектор свободных членов. В зависимости от вида матрицы А и ее характерных особенностей MATLAB позволяет реализовать различные методы решения.

Для реализации различных алгоритмов решения СЛУ и связанных с ними матричных операций применяются следующие операторы: +,-,*,/, \, *, ‘ .

Как отмечалось ранее, MATLAB имеет два различных типа арифметических операций — поэлементные и для массивов (векторов и матриц) в целом. Матричные арифметические операции определяются правилами линейной алгебры.

Арифметические операции сложения и вычитания над массивами выполняются поэлементно. Знак точки «.» отличает операции над элементами массивов от матричных операций. Однако, поскольку операции сложения и вычитания одинаковы для матрицы и элементов массива, знаки «.+» и «.-» не используются. Рассмотрим другие операторы и выполняемые ими операции.

* — матричное умножение; С = А*В — линейное алгебраическое произведение матриц А и В:

 

Для случая нескалярных А и В число столбцов матрицы А должно равняться числу строк матрицы В. Скаляр может умножаться на матрицу любого размера.

 / — правое деление. Выражение Х=В/А дает решение ряда систем линейных уравнений АХ=В, где А — матрица размера тхп и В — матрица размера nxk;

 \ — левое деление. Выражение Х=В\А дает решение ряда систем линейных уравнений ХА=В, где А — матрица размера тхп и В — матрица размера nxk. Если А — квадратная матрица, то А\В — примерно то же самое, что и inv(A)*B, в остальных случаях возможны варианты, отмеченные ниже.

Если А — матрица размера пхп, а В — вектор-столбец с п компонентами или матрица с несколькими подобными столбцами, тогда Х=А\В — решение уравнения АХ=В, которое находится хорошо известным методом исключения Гаусса.

Если А — матрица размера тхп и тхп, а В представляет собой вектор-столбец с m компонентами или матрицу с несколькими такими столбцами, тогда система оказывается недоопределенной или переопределенной и решается на основе минимизации второй нормы невязок.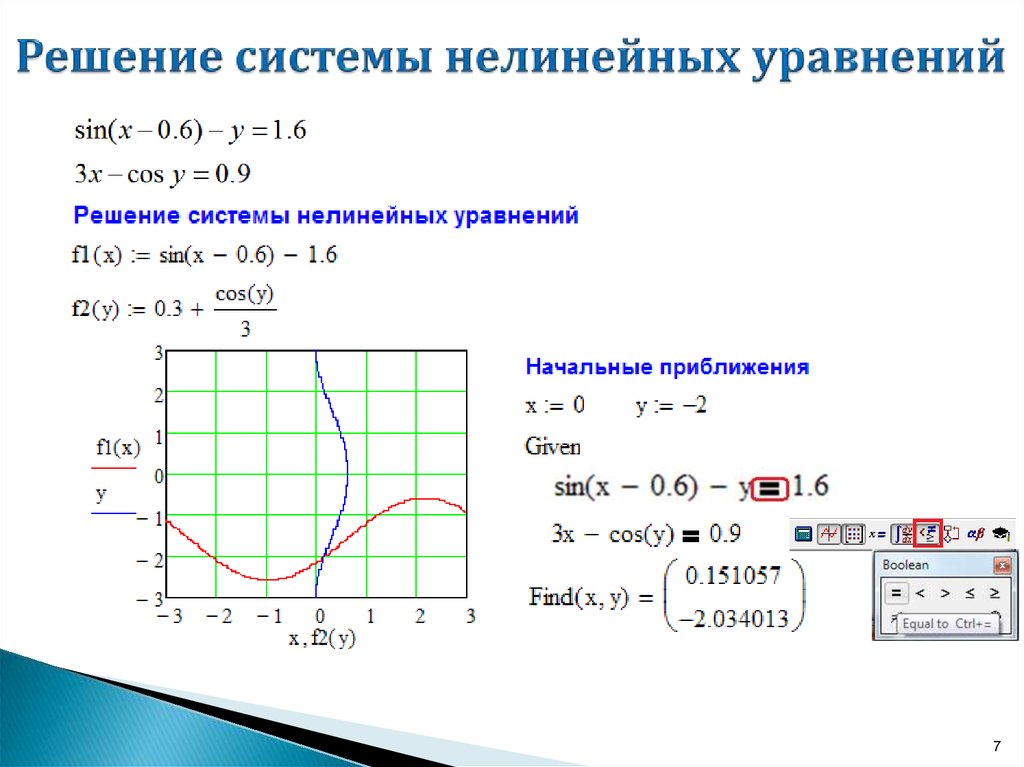 -1.

 ‘ — транспонирование матрицы, то есть замена строк столбцами и наоборот. Например, А’ — транспонированная матрица А. Для комплексных матриц транспонирование дополняется комплексным сопряжением. Транспонирование при решении СЛУ полезно, если в матрице А переставлены местами столбцы и строки.

При записи СЛУ в матричной форме необходимо следить за правильностью записи матрицы А и вектора В. Пример (в виде m-файла):

А-[2  1

0

1:

1    -3

2

4;

-5    0

-1

-7:

1    -6

2

6]:

В=[8  9

-5

0]:

Х1=В/А

Х2=В*А ^ -1

X3=B*inv(A)

Эта программа выдает результаты решения тремя способами:

X1 =

3. 0000 -4.0000-1.00001.0000

Х2 =

3.0000 -4.0000-1.00001.0000

X3 =

3.0000 -4.0000-1.00001.0000

Как и следовало ожидать, результаты оказываются одинаковыми для всех трех методов. При решении систем линейных уравнений, особенно с разреженной матрицей коэффициентов, полезно применение функций colmmd (colamd), symmmd (symamd), описанных ранее в уроке 12.

 

Нравится

Твитнуть

решение системы уравнений в матлабе

  • Программирование на C++ для финансовой инженерии
    Настоятельно рекомендуется тысячами студентов MFE. Охватывает основные темы C++ с приложениями для финансового инжиниринга. Узнать больше Присоединяйтесь!

    Python для финансов с введением в науку о данных
    Получите практическое понимание Python, чтобы читать, понимать и писать профессиональный код Python в первый рабочий день. Узнать больше Присоединяйтесь!

    Учебник по опционам, основанный на интуиции, для FE
    Идеально подходит для собеседований на начальном уровне и обучения в аспирантуре, специализирующихся на арбитражной торговле опционами и моделях оценки опционов. Узнать больше Присоединяйтесь!

JavaScript отключен. Для лучшего опыта, пожалуйста, включите JavaScript в вашем браузере, прежде чем продолжить.