Правило периметр прямоугольника: Как найти периметр прямоугольника, формула ⬅️

Содержание

Нахождение периметра прямоугольника. Периметр и площадь прямоугольника. Как найти периметр прямоугольника – онлайн-ресурсы

Прямоугольник обладает многими отличительными особенностями, исходя из которых, выработаны правила вычисления его различных числовых характеристик. Итак, прямоугольник:

Плоская геометрическая фигура;
Четырехугольник;
Фигура, у которой противоположные стороны равны и параллельны, все углы прямые.

Периметр – это общая длина всех сторон фигуры.

Вычисление периметра прямоугольника — довольно простая задача.

Все, что вам нужно знать, это ширину и длину прямоугольника. Поскольку прямоугольник имеет две равные длины и две равные ширины, измеряется только одна сторона.

Периметр прямоугольника равен удвоенной сумме 2-х его сторон длины и ширины.

P = (a + b) 2, где a — длина прямоугольника, b — ширина прямоугольника.

Так же периметр прямоугольника можно найти при помощи суммы всех сторон.

P= a+a+b+b, где а– длина прямоугольника, b – ширина прямоугольника.

Периметр квадрата — это длина стороны квадрата, умноженная на 4.

P = a 4, где a — длина стороны квадрата.

Дополнение: Нахождение найти площади и периметра прямоугольников

В программе обучения за 3 класс предусмотрено изучение многоугольников и их особенностей. Для того чтобы понять, как найти периметр прямоугольника и площадь, разберемся, что подразумевается под этими понятиями.

Основные понятия

Нахождение периметра и площади требует знания некоторых терминов. К ним относятся:

Прямой угол. Образуется из 2 лучей, имеющих общее начало в виде точки. При знакомстве с фигурами (3 класс) прямой угол определяют с помощью угольника.
Прямоугольник. Это четырехугольник, все углы которого являются прямыми. Его стороны называют длиной и шириной. Как известно, противоположные стороны этой фигуры равны.
Квадрат. Является четырехугольником, все стороны которого равны.

При знакомстве с многоугольниками их вершины могут называться АВСД. В математике принято именовать точки на чертежах буквами латинского алфавита. В названии многоугольника перечисляют все вершины без пропусков, например, треугольник ABC.

Вычисление периметра

Периметр многоугольника — это сумма длин всех его сторон. Эта величина обозначается латинской буквой P. Уровень знаний для предложенных примеров — 3 класс.

Задача №1: «Начертите прямоугольник 3 см шириной и 4 см длиной с вершинами ABCD. Найдите периметр прямоугольника ABCD».

Формула будет выглядеть так: P=AB+BC+CD+AD либо P=AB×2+BC×2.

Ответ: P=3+4+3+4=14 (см) либо P=3×2 + 4×2=14 (см).

Задача №2: «Как найти периметр прямоугольного треугольника ABC, если значения сторон равны 5, 4 и 3 см?».

Ответ: P=5+4+3=12 (см).

Задача №3: «Найдите периметр прямоугольника, одна сторона которого равна 7 см, а другая на 2 см длиннее».

Ответ: P=7+9+7+9=32 (см).

Задача №4: «Соревнования по плаванию проходили в бассейне, периметр которого составляет 120 м. Сколько метров проплыл участник соревнований, если ширина бассейна 10 м?».

В данной задаче стоит вопрос, как найти длину бассейна. Для решения найдите длины сторон прямоугольника. Ширина известна. Сумма длин двух неизвестных сторон должна составить 100 м. 120-10×2=100. Чтобы узнать расстояние, которое преодолел пловец, нужно разделить полученный результат на 2. 100:2=50.

Ответ: 50 (м).

Вычисление площади

Более сложной величиной является площадь фигуры. Для ее измерения используют мерки. Эталоном среди мерок являются квадраты.

Площадь квадрата со стороной 1 см равна 1 см². Квадратный дециметр обозначен как дм², а квадратный метр — м².

Области применения единиц измерения могут быть такими:

В см² измеряют маленькие предметы, например фотографии, обложки учебников, листы бумаги.
В дм² можно измерить географическую карту, оконное стекло, картину.
Для измерения пола, квартиры, земельного участка используют м².

Если начертить прямоугольник 3 см длиной и 1 см шириной и разбить на квадраты со стороной 1 см, то в нем поместится 3 квадрата, а значит, его площадь составит 3 см². Если прямоугольник разбит на квадраты, найдем периметр прямоугольника также без затруднений. В данном случае он равен 8 см.

Другой способ посчитать количество квадратов, вмещающихся в фигуру, — это использование палетки. Начертим на кальке квадрат площадью 1 дм², что составляет 100 см². Поместим кальку на фигуру и посчитаем число квадратных сантиметров в одном ряду. После этого выясним количество рядов, а затем перемножим значения. Значит, площадь прямоугольника — это произведение его длины и ширины.

Способы сравнения площадей:

На глаз. Иногда достаточно просто взглянуть на предметы, поскольку в некоторых случаях и невооруженным глазом видно, что одна фигура занимает больше места, как, например, учебник, лежащий на столе рядом с пеналом.
Наложение. Если фигуры совпадают при наложении, их площади равны. Если же одна из них полностью помещается внутри второй, то ее площадь меньше. Места, занимаемые тетрадным листом и страницей из учебника, можно сравнить, наложив их друг на друга.
По количеству мерок. Фигуры при наложении могут и не совпадать, однако иметь одинаковую площадь. Сравнить в этом случае можно, подсчитав количество квадратов, на которые разбита фигура.

Числа. Сравниваются численные значения, измеренные одной и той же меркой, например, в м².

Пример №1: «Швея сшила детское одеяло из квадратных разноцветных лоскутков. Один лоскуток длиной 1 дм, в ряду по 5 штук. Сколько дециметров ленты понадобится швее для обработки краев одеяла, если известна площадь 50 дм²?».

Чтобы решить задачу, нужно ответить на вопрос, как найти длину прямоугольника. Далее найдем периметр прямоугольника, составленного из квадратов. Из задачи ясно, что ширина одеяла — 5 дм, вычисляем длину, разделив 50 на 5, и получаем 10 дм. Теперь найдите периметр прямоугольника со сторонами 5 и 10. P=5+5+10+10=30.

Ответ: 30 (м).

Пример №2: «На раскопках обнаружен участок, где могут находиться древние сокровища. Сколько территории придется исследовать ученым, если известен периметр 18 м и ширина прямоугольника 3 м?».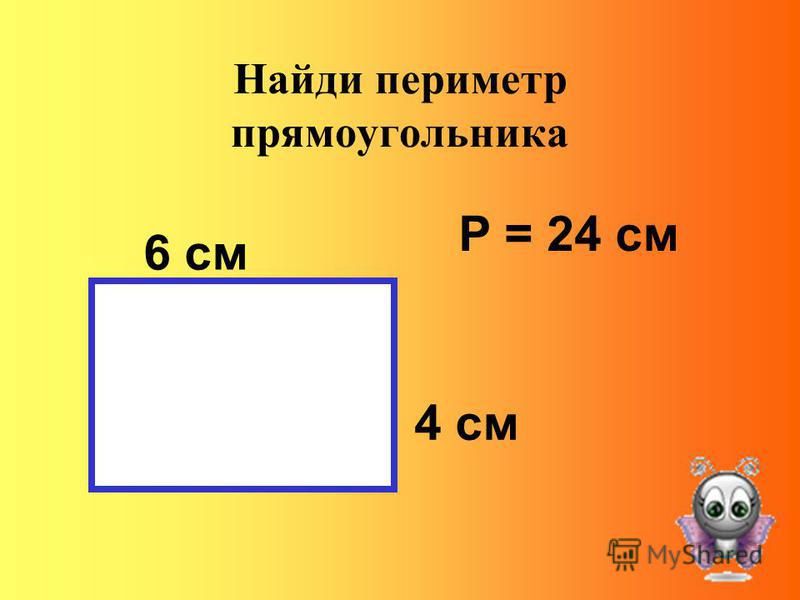

Определим длину участка, проделав 2 действия. 18-3×2=12. 12:2=6. Искомая территория будет также равна 18 м² (6×3=18).

Ответ: 18 (м²).

Таким образом, зная формулы, вычислить площадь и периметр не составит труда, а приведенные выше примеры помогут попрактиковаться в решении математических задач.

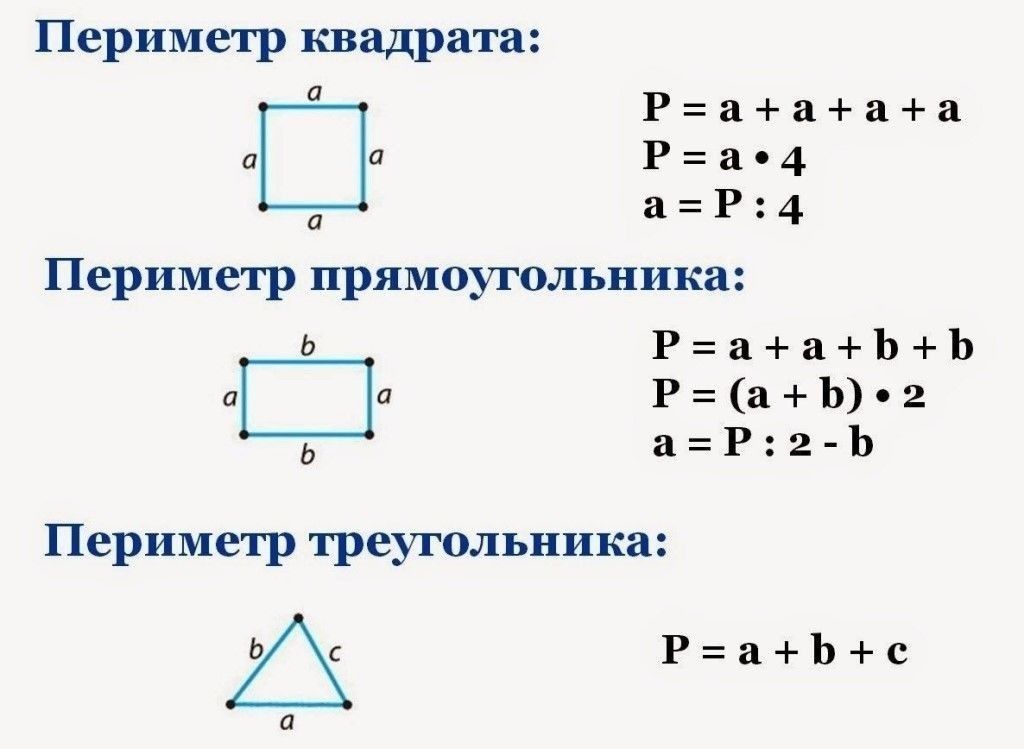
Достаточно узнать длину всех ее сторон и найти их сумму. Периметром называется совокупная длина границ плоской фигуры. Иными словами, это сумма длин ее сторон. Единица измерения периметра должна соответствовать единице измерения его сторон. Формула периметра многоугольника имеет вид Р = a + b + c…+ n, где Р — периметр, а вот а, b, с и n — длина каждой из сторон. Иначе вычисляется (или периметр круга): используется формула р = 2 * π * r, где r — радиус, а π — постоянное число, приблизительно равное 3,14. Рассмотрим несколько простых примеров, наглядно демонстрирующих, как найти периметр. В качестве образца возьмем такие фигуры как квадрат, параллелограмм и окружность.

Как найти периметр квадрата

Квадратом называется правильный четырехугольник, у которого равны все стороны и углы. Так как все стороны квадрата равны, сумму длин его сторон можно вычислить по формуле Р = 4 * a, где а — длина одной из сторон. Таким образом, со стороной 16,5 см равен Р = 4 * 16,5 = 66 см. Так же можно вычислить периметр равностороннего ромба.

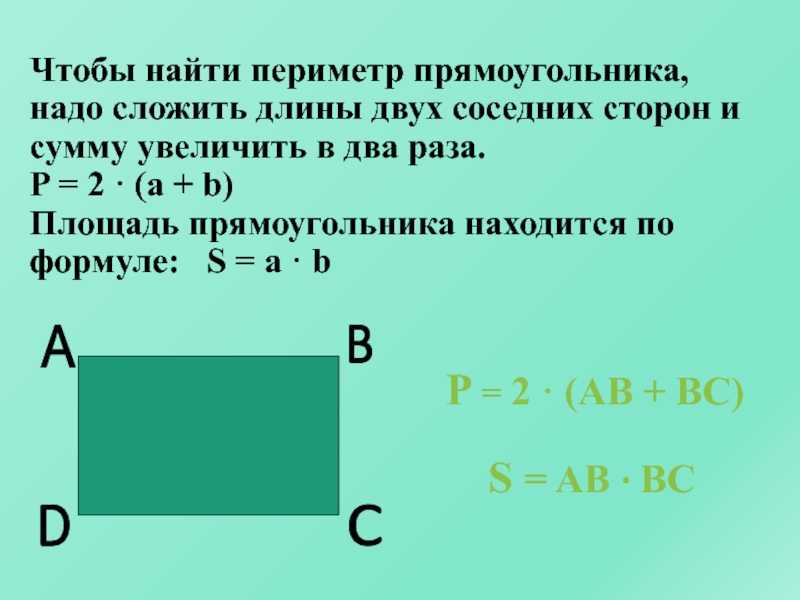
Как найти периметр прямоугольника

Прямоугольник — это четырехугольник, все углы которого равны 90 градусам. Известно, что в такой фигуре, как прямоугольник, длины сторон равны попарно. Если ширина и высота прямоугольника имеют одинаковую длину, то он называется квадратом. Обычно длиной прямоугольника называют наибольшую из сторон, а шириной — наименьшую. Таким образом, чтобы получить периметр прямоугольника, необходимо удвоить сумму его ширины и высоты: P = 2 * (а + b), где а — высота, а b — ширина. Имея в наличии прямоугольник, одна сторона которого является длиной и равна 15 см, а другая шириной с установленным значением в 5 см, мы получим периметр, равный Р = 2 * (15 + 5) = 40 см.

Как найти периметр треугольника

Треугольник образован тремя отрезками, которые соединяются в точках (вершинах треугольника), не лежащих на одной и той же прямой. Треугольник называется равносторонним, если равны все три его стороны, и равнобедренным, если равных сторон две. Чтобы узнать периметр необходимо длину его стороны умножить на 3: Р = 3 * a, где а — одна из его сторон. Если стороны треугольника не равны между собой, необходимо провести операцию сложения: Р = а + b + с. Периметр равнобедренного треугольника со сторонами 33, 33 и 44 соответственно будет равен: P = 33 + 33 + 44 = 110 см.

Как найти периметр параллелограмма

Параллелограмм — это четырехугольник с попарно параллельными противоположными сторонами. Квадрат, ромб и прямоугольник являются частными случаями фигуры. Противоположные стороны любого параллелограмма равны, поэтому для вычисления его периметра воспользуемся формулой P = 2 (а + b). В параллелограмме со сторонами 16 см и 17 см сумма сторон, или периметр, равна Р = 2 * (16 + 17) = 66 см.

Как найти длину окружности

Окружность является замкнутой прямой, все точки которой расположены на равном удалении от центра. Длина окружности и ее диаметр всегда имеют одинаковое отношение. Это отношение выражено константой, записывается при помощи буквы π и равняется примерно 3,14159. Узнать периметр круга можно по произведению радиуса на 2 и на π. Получается, что длина окружности с радиусом в 15 см будет равна Р = 2 * 3,14159 * 15 = 94,2477

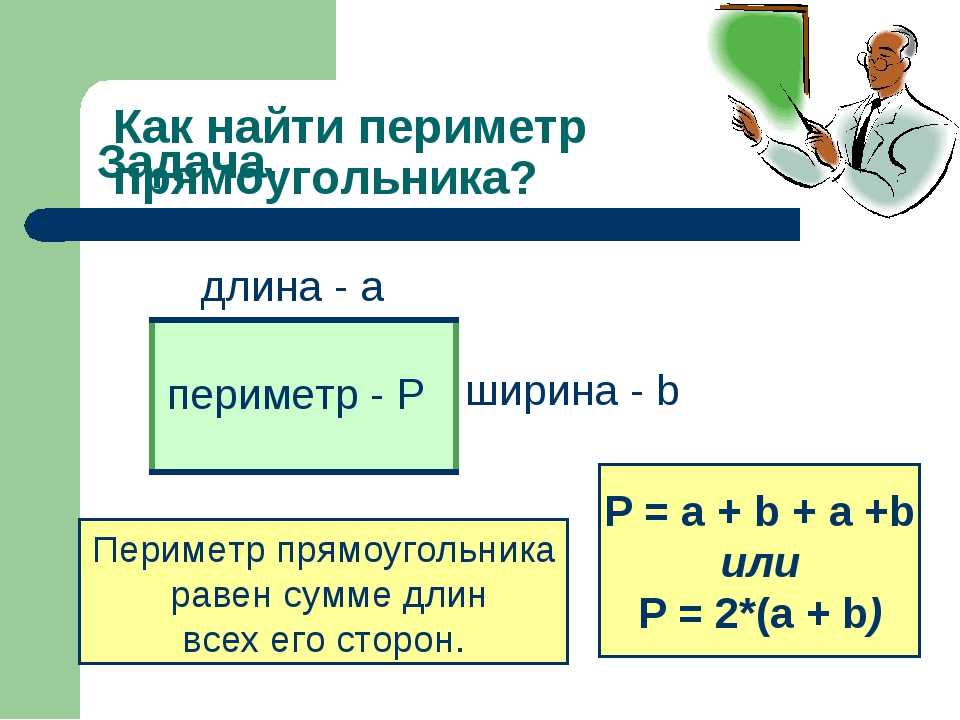
Ниже в статье вы узнаете что такое и как найти периметр прямоугольника если известны его стороны. А также как найти стороны прямоугольника, если известен его периметр. И ещё одна интересная строительная прикладная задача.

Немного теории:

Периметр — это длина геометрической фигуры по её внешней границе.

Периметр прямоугольника — это сумма длин его сторон.

Формулы для вычисления периметра прямоугольника: P = 2*(a+b) или P = a + a + b + b.

Резюмируем! Для того чтобы вычислить периметр прямоугольника необходимо сложить все его стороны.

Типовые математические и практические задачи:

Задача №1:

Исходные данные: Определить периметр прямоугольника с длинами сторон 5 см и 10 см.

Решение:

Согласно формуле периметр прямоугольника равен = 2 * (5 + 10) = 30 см.

Ответ: 30 см.

Задача №2:

Исходные данные: Определить стороны прямоугольника выраженные целыми числами, если периметр прямоугольника равен 10.

Решение:

По формуле определяем сумму длин сторон (a + b) = P / 2 = 10 / 2 = 5
Целыми значениями сторон могут быть только значения 1 + 4 = 5 и 2 + 3 = 5

Ответ: Длины сторон могут быть только 2 и 3 или 1 и 4.

Задача №3 (практическая):

Исходные данные: Определить число плинтусов в достаточном количестве для ремонта пола в комнате длиной 5 метров и шириной 3 метра, если длина одного плинтуса равна 3 метра.

Решение:

Периметр комнаты = 2 * (5 + 3) = 16 метров
Количество плинтусов = 16 / 3 = 5,33 штук
Обычно в строительных магазинах плинтусы продаются не погонными метрами, а поштучно. Поэтому принимаем следующее целое число. Это шесть.

Ответ: Количество плинтусов 6 штук.

В заключение:

Решение задачи вычисления периметра является достаточно простой математической задачей, но имеющей очень важное практическое значение например в строительстве или генеральном планировании территории.

На этой странице представлен самый простой онлайн калькулятор для расчета периметра прямоугольника. С помощью этой программы вы в один клик сможете найти периметр прямоугольника, если известны его длина и ширина.

Периметр — это сумма длин всех сторон многоугольника.

Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.
Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

Прямоугольник – это четырехугольник.
Все параллельные стороны равны
Все углы = 90º.
Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

1 способ. Складываем все стороны. P = a + а + b + b
2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

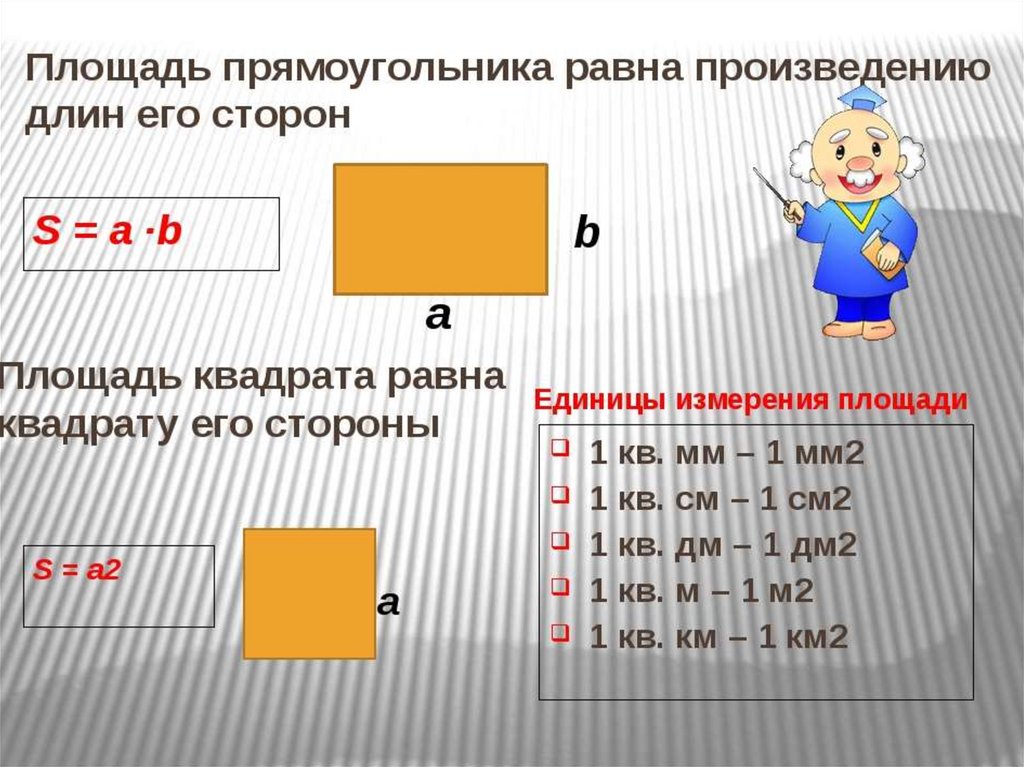
Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

Если в условии известна длина одной стороны и длина диагонали, то площадь найти можно, используя в таких задачах, теорему Пифагора, она позволяет найти длину стороны прямоугольного треугольника если известны длины двух других сторон.

: a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

Периметр — это сумма длин всех сторон многоугольника.

Для вычисления периметра геометрических фигур используются специальные формулы, где периметр обозначается буквой «P». Название фигуры рекомендуется писать маленькими буквами под знаком «P», чтобы знать чей периметр ты находишь.

Периметр измеряется в единицах длины: мм, см, м, км и т.д.

Отличительные особенности прямоугольника

Прямоугольник – это четырехугольник.
Все параллельные стороны равны
Все углы = 90º.
Например в повседневной жизни прямоугольник может встречаться в виде — книги, монитора, крышки от стола или двери.

Как вычислить периметр прямоугольника

Существует 2 способа его нахождения:

1 способ. Складываем все стороны. P = a + а + b + b
2 способ. Сложить ширину и длину, и умножить на 2. P = (a + b) · 2. ИЛИ Р = 2 · а + 2 · b. Стороны прямоугольника, которые лежат друг против друга (противолежащие), называются длиной и шириной.

«a» — длина прямоугольника, более длинная пара его сторон.

«b» — ширина прямоугольника, более короткая пара его сторон.

Пример задачи на подсчет периметра прямоугольника:

Вычислите периметр прямоугольника, есть его ширина равна 3 см., а длина — 6.

Запомни формулы вычисления периметра прямоугольника!

Полупериметр — это сумма одной длины и одной ширины.

Полупериметр прямоугольника — когда выполняешь первое действие в скобках – (a+b) .
Чтобы из полупериметра получить периметр, нужно его увеличить в 2 раза, т.е. умножить на 2.

Как найти площадь прямоугольника

Формула площади прямоугольника S= a*b

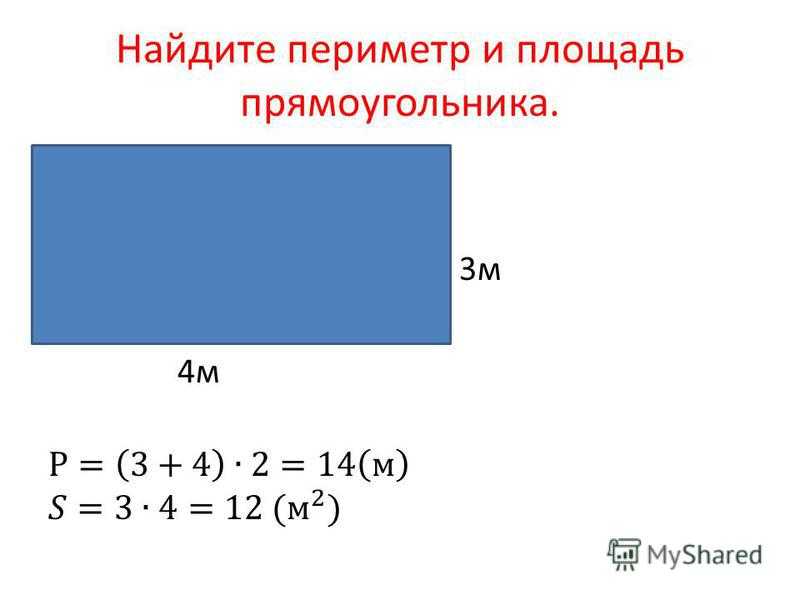
: a 2 + b 2 = c 2 , где a и b – стороны треугольника, а с – гипотенуза, самая длинная сторона.

Помни!

Все квадраты – прямоугольники, но не все прямоугольники – квадраты. Так как:
- Прямоугольник — это четырехугольник со всеми прямыми углами.
- Квадрат — прямоугольник, у которого все стороны равны.
Если ты находишь площадь, ответ всегда будет в квадратных единицах (мм 2 , см 2 , м 2 , км 2 и т.д.)

Как найти периметр прямоугольника. правило и решение… -reshimne.ru

Новые вопросы

Ответы

Формула тебе попутно — P=2(a+b) Пример | Так как нам известны ширина и длина прямоугольника, найти его периметр не составит труда. Ширина параллельна ширине, а длина длине. Таким образом, в обычном прямоугольнике 2 ширины и 2 длины.Складываем все стороны (3 + 3 + 6 + 6) = 18 см.

Урок № 43 Тема: Периметр прямоугольника | Поурочные планы по математике 2 класс

Цель урока: обеспечить усвоение учащимися правила нахождения периметра прямоугольника.

Задачи урока:

Организовать деятельность учащихся по закреплению понятия «периметр», для отработки умения нахождения периметра прямоугольника, закрепить знания о свойствах сторон прямоугольника;
содействовать развитию устных вычислительных навыков, логического мышления, внимания учащихся;
привить интерес к математике, воспитывать чувства дружбы и взаимопомощи.

Тип урока: урок закрепления знаний

Ход урока

1. Мобилизующее начало урока.

2. Проверка выполнения домашнего задания.

3. Актуализация опорных знаний.

А) игра «Молчанка»

Б) Математический диктант: (разночтением)

7+9

18-8

30+50

52+2

1дм6см =

35-5

9+7

14-9

6+8

В) Проверка.

Г) Работа с геометрическим конструктором.

4. Сообщение темы и целей урока.

Отгадайте, о какой фигуре говорится:

Если все углы прямые

И всего угла четыре

Стороны противоположны и равны

Этот четырехугольник назовем …..(прямоугольник)

Как вы думаете, на уроке? Правильно мы будем говорить о прямоугольнике.

Сегодня мы узнаем, что такое периметр, научимся находить периметр прямоугольника. Будем решать интересные задачи и примеры.

5 Работа над новым материалом.

1.Создание проблемной ситуации.

— На уроках познания мира мы изучали тему «План местности».

Так вот, нам сегодня предстоит опять погрузиться в эту тему.

Нам необходимо вычислить, какой длины надо поставить забор Матроскину, если его двор имеет прямоугольную форму. Длина участка – 30м, а ширина — 10 м

(Начертить план на доске)

Так, какой же длины будет забор?

Как узнать, чему равны две другие стороны?

Оформление записи на доске Периметр обозначается латинской буквой Р. Р=30+10+30+10=80(м)

Вывод: прямоугольник – это замкнутая ломаная. Вся ее длина (периметр) вычисляется сложением всех звеньев.

Чтение стр. 78.

6. Закрепление.

А) Работа с учебником.

а) Стр. 79 №3 устно

— Можем ли мы сразу, глядя на фигуру, найти её периметр?

— Что надо для этого сделать? (измерить стороны)

Измеряем длину (показать рукой). Измеряем ширину.

Золотое правило: измеряем от нуля.

Прочитайте, как нашли периметр фигур?

№ 4 стр. 79 коллективно, письменно

Длина – 3 см

Ширина – 2 см

Р — ?

Р= 3+3+2+2=10(см)

Р= 3+2+3+2= 10(см)

Ответ: Р=10см.

Физкультминутка

7 Работа в группах

— Мышонок задаёт задания. Найдите периметр прямоугольника.

(Четырем группам – разные прямоугольники)

Расскажите последовательность выполнения задания:

1. Измерим стороны прямоугольника

2. Найдем сумму длин всех его сторон

3. Сделаем запись на фигуре

1 группа

Длина 5 см

Ширина 4см

2 группа

Длина 6 см

Ширина 4см

3 группа

Длина 5 см

Ширина 3см

4 группа

Длина 6 см

Ширина 3см

Проверка:

— Какой периметр у вас получился? (ответы групп)

— А у кого еще такой ответ? Прекрасно! Поаплодируем!

—

8. Домашнее задание.

В домашнем задании будет задача №5, стр. 79 на нахождение периметра прямоугольника. Прочитайте и скажите, кто справиться с решением этой задачи?

9. Работа над пройденным материалом

Для вычисления периметра необходимо быстро и правильно вычислять. Покажите, как вы умеете считать.

— Решаем пример под №7 стр. 80 с комментированием у доски.

10. Подведение итогов. Рефлексия.

— Какую тему изучили? Что такое периметр? Как найти периметр?

Периметр прямоугольника – объяснение и примеры

Периметр прямоугольника – это общая длина всех его сторон.

Рассчитывается с помощью следующей формулы :

$\textrm{Периметр прямоугольника} = 2 ( \textrm{Длина} + \textrm{Ширина})$.

Периметр определяется как граница, окружающая фигуру . Его также можно определить как длину сторон фигуры. Прямоугольник — это четырехугольник (т. е. фигура с четырьмя сторонами), у которого противоположные стороны равны; поэтому нам нужно знать только его длину и ширину, чтобы найти периметр.

Что такое периметр прямоугольника?

Периметр прямоугольника равен общему расстоянию вокруг его границ . Другими словами, у прямоугольника четыре стороны, и если мы сложим все стороны, это даст нам периметр прямоугольника. Поскольку противоположные стороны прямоугольника равны, удвоение ширины и удвоение длины также даст нам тот же результат.

Как найти периметр прямоугольника

Рассмотрим изображение прямоугольника, приведенное ниже.

Здесь $X$ — длина прямоугольника, а $Y$ — ширина или ширина прямоугольника.

Периметр прямоугольника будет равен $ X+X+Y+Y$. Поскольку мы складываем стороны, единица измерения параметра будет такой же, как единица измерения каждой из сторон , т. е. метры, сантиметры, дюймы и т. д.

Формула периметра прямоугольника

Формула для периметра прямоугольника легко получить. Мы знаем, что противоположные стороны прямоугольника равны 9.0003 равны друг другу , поэтому мы можем написать уравнение для расчета периметра прямоугольника как:

Периметр прямоугольника = Длина + Ширина + Длина + Ширина

Если длина = $X$ и ширина = $Y$

Тогда периметр прямоугольника равен $ X\hspace{1мм}+\hspace{1мм}Y\hspace{1мм}+\hspace{1мм}X\hspace{1мм}+\hspace{1мм} Y$

Периметр прямоугольника $= 2 X\hspace{1мм} + \hspace{1мм}2 Y$

Периметр прямоугольника $= 2 (X\hspace{1мм} +\hspace{1мм} Y) $

Давайте рассмотрим пример :

Вычислите периметр прямоугольника для фигуры, приведенной ниже.

Итак, нам предоставлены значения одной длины и одной ширины прямоугольника. Мы знаем, что противоположные стороны прямоугольника конгруэнтны , поэтому мы можем записать длину $(X) = 7 см и ширину $(Y) = 11 см.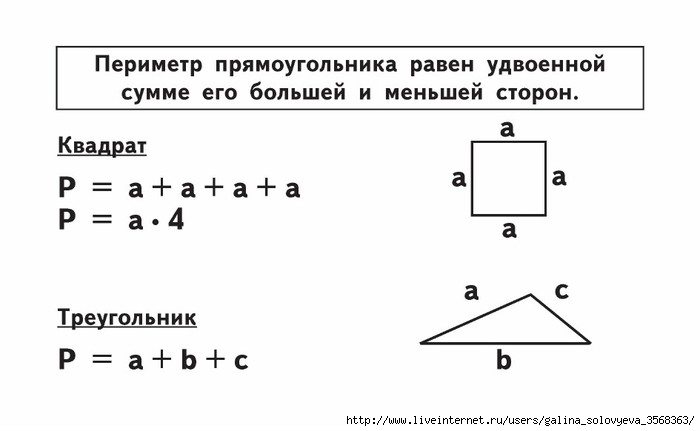 Периметр данного прямоугольника можно рассчитать как:

Периметр прямоугольника $= 2 (X \hspace{1mm}+\hspace{1mm} Y)$

Периметр прямоугольника $= 2 (7см \hspace{1мм}+\hspace{1мм} 11см)$

Периметр прямоугольника $= 2 (18 см)$

Периметр прямоугольника $= 36 \hspace{1мм} cm$

Применение периметра прямоугольника в реальной жизни

Периметр прямоугольника используется в многочисленных реальных приложениях .

Ниже приведены различные примеры:

Мы можем использовать периметр прямоугольника для определения или оценки длины прямоугольной области, такой как сад или белая доска.
Формула периметра также полезна при проектировании прямоугольного бассейна или шкафа прямоугольной формы.
Это также полезно в планах строительства офисов и домов, где нам нужно установить прямоугольную границу.

Пример 1

Вычислите периметр прямоугольника на рисунке ниже.

Решение
На приведенном выше рисунке показано, что длина одной стороны прямоугольника составляет $5$ см, а ширина $6$ см.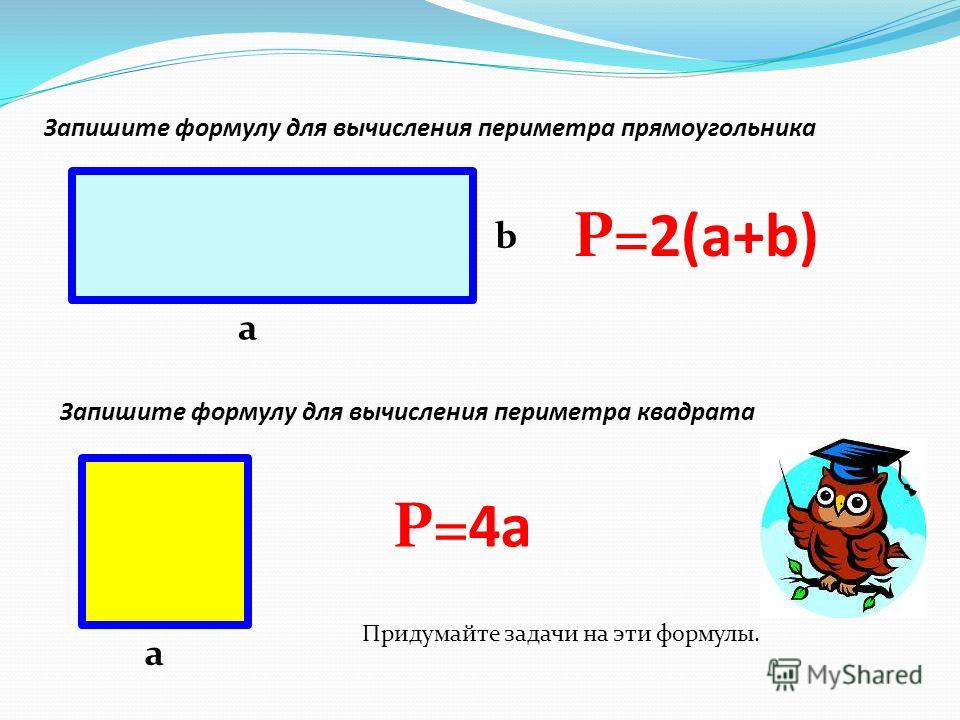
Мы знаем, что противоположные стороны прямоугольника равны , поэтому полный рисунок показан ниже:
Теперь мы можем вычислить периметр прямоугольника, используя либо определение периметра как суммы длин со всех сторон или по формуле, которую мы изучили ранее:
Периметр прямоугольника $= L \hspace{1мм}+W \hspace{1мм}+\hspace{1мм}L+\hspace{1мм}W$
Периметр прямоугольника $= 5 см\hspace{1мм} +\hspace{1мм}6 см \hspace{1мм}+\hspace{1мм}5 см+\hspace{1мм}6 см$
Периметр прямоугольника $= 22 см$
Альтернативное решение
Периметр прямоугольника $= 2 (W\hspace{1mm}+\hspace{1mm} L)$
Периметр прямоугольника $= 2 ( 6 см\hпробел{1мм}+\hпробел{1мм} 5 см)$
Периметр прямоугольника $= 2 ( 11 см)$
Периметр прямоугольника $= 22 \hпробел{1мм}см$
Пример 2
Длина прямоугольника $16$см, а ширина $10$ см. Чему будет равен периметр прямоугольника?
Решение
Мы равны , учитывая длину и ширину прямоугольника , и мы знаем, что противоположные стороны прямоугольника равны, поэтому периметр прямоугольника можно рассчитать как:
Периметр прямоугольника $= L\hspace{1мм} + \hspace{1мм}W +\hspace{1мм} L \hspace{1мм}+\hspace{1мм} W$
Периметр прямоугольника $= 16см \hspace{1мм}+\hspace{ 1мм} 10см\hпробел{1мм} +\hпробел{1мм} 16см +\hпробел{1мм} 10см$
Периметр прямоугольника $= 52 \hпробел{1мм}см$
Альтернативное решение
Периметр прямоугольника $= 2 (W\hspace{1мм}+\hspace{1мм} L)$
Периметр прямоугольника $= 2 ( 16\hspace{1мм} см+ \hspace{1мм}10 см)$
Периметр прямоугольника $= 2 ( 26 см)$
Периметр прямоугольника $= 52 \hspace{1mm}cm$
Вычисление периметра, когда известна площадь
В некоторых случаях вы можете знаете площадь прямоугольника и вас просят найти периметр.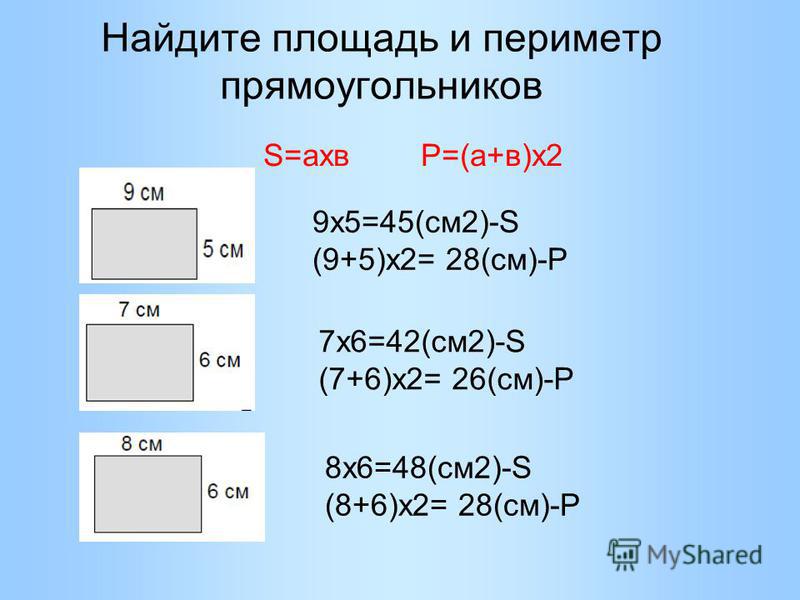 Для таких вопросов решение требует понимания и решение квадратного уравнения . Если вы хотите узнать, как решить квадратное уравнение, нажмите здесь.
Сначала вспомним формулу площади прямоугольника:
Площадь прямоугольника $= (Длина \x Ширина) = X \x Y$.
Давайте обсудим несколько примеров, где площадь прямоугольника равна и нам нужно вычислить периметр прямоугольника.
Пример 3
Если площадь прямоугольника составляет 24 квадратных дюйма, а ширина прямоугольника в 6 раз больше его длины, каков периметр прямоугольника? 9{2}$
$a = L = 2$
Итак, $y = W = 6a = 6\times2 = 12$
Длина $= 2$ дюймов и ширина $= 12$ дюймов
Периметр прямоугольника $= 2 ( W\hspace{1мм}+\hspace{1мм} L)$
Периметр прямоугольника $= 2 ( 12\hspace{1мм} +\hspace{1мм} 2)$
Периметр прямоугольника $= 2 ( 14 )$.
Периметр прямоугольника $= 28\hspace{1mm} дюймов$.
Пример 4
Прямоугольный сад площадью 32 квадратных метра.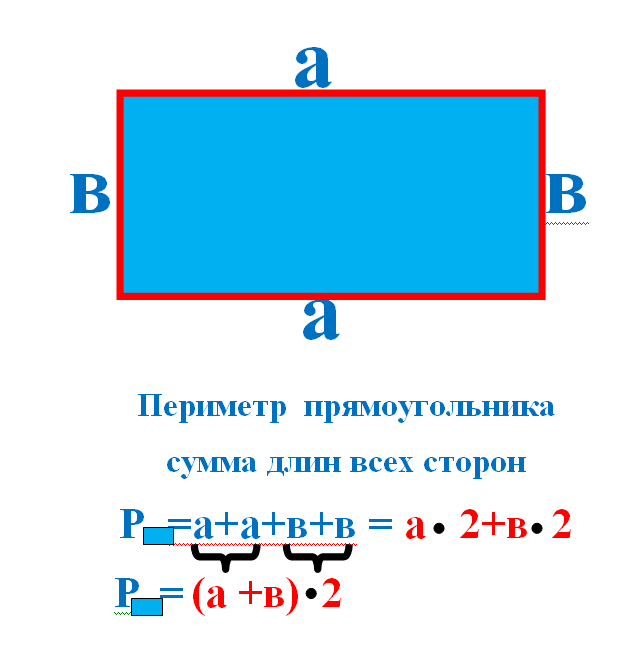 Длина на четыре единицы меньше ширины. Чему равен периметр сада? 9{2}\hspace{1мм} –\hspace{1мм} 8b \hspace{1мм}+\hspace{1мм}4b \hspace{1мм}–\hspace{1мм} 32 = 0$
$b (b – 8 ) +4 (b – 8) = 0$
$(b \hspace{1мм}–\hspace{1мм} 8) (b\hspace{1мм}+\hspace{1мм} 4) = 0$
Итак , $b = 8$ и $b = – 4$
Ширина не может быть отрицательной, поэтому ширина сада 8 метров.
Теперь мы можем легко вычислить значение длины.
$a = b\hspace{1мм} –\hspace{1мм} 4 = 8\hspace{1мм} –\hspace{1мм} 4 = 4$
Длина $= 4$ метра и ширина $= 8$ метров
Периметр сада $= 2 (W\hspace{1мм}+\hspace{1мм} L)$
Периметр сада $= 2 (8 м\hspace{1мм}+\hspace{1мм} 4 м)$
Периметр сада $= 2 ( 12 м)$
Периметр сада $= 24\hspace{1mm} метров$
Пример 5
Арчер планирует спроектировать прямоугольную доску для своего класса. Он хочет, чтобы общая площадь доски составляла $100$ квадратных сантиметров. Если длина доски будет на $10$ сантиметров меньше, чем удвоенная ширина, каков будет периметр доски в сантиметрах? 9{2} \hspace{1мм}–\hspace{1мм} 10b \hspace{1мм}+ \hspace{1мм}5b \hspace{1мм}- \hspace{1мм}50 = 0$
$b (b \hspace {1мм}–\hspace{1мм} 10) + 5(b \hspace{1мм}–\hspace{1мм} 10) = 0$
$(b \hspace{1мм}–\hspace{1мм} 10 )( b\hspace{1мм} +\hspace{1мм} 5) = 0$
$b = 10 \hspace{1мм} и\hspace{1мм} b = – 5$
Ширина может быть $-5$ или $10$, а так как ширина не может быть отрицательной, значение ширины равно $10$.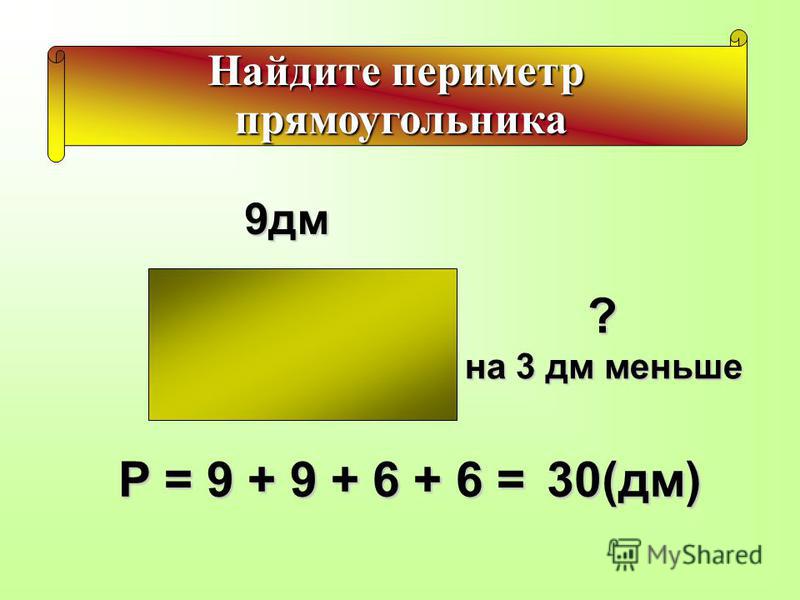
Если $b = 10 см$, то значение длины равно $a = 2(10)\hspace{1мм} -\hspace{1мм} 10 = 10 см$.
Теперь мы знаем значения ширины и длины прямоугольной доски. Имея эту информацию, мы можем рассчитать его периметр, подставив значения в формулу.
Периметр прямоугольной доски $= 2 L\hspace{1мм} +\hspace{1мм} 2 W = 2(10 см) + 2(10 см) = 40 \hspace{1мм}см$.
Практические вопросы:
Если длина и ширина прямоугольника равны $6 см$ и $8 см$ соответственно, каков будет периметр прямоугольника?
Если длина и ширина прямоугольника равны $10 см$ и $7 см$ соответственно, каков будет периметр прямоугольника?
Ахмад проектирует прямоугольный сад. Помогите Ахмаду рассчитать периметр сада по приведенным ниже данным. Длина сада $= 8 см$ и ширина $= 5 см$. Длина сада $= 6 см$ и ширина $= 9 см$. Площадь сада составляет $16$ квадратных метров, а ширина $= 8 м$
Натан планирует спроектировать прямоугольный бассейн на своем заднем дворе. Он хочет, чтобы общая площадь бассейна составляла 64 $ квадратных метра. Если длина доски будет на $4$ метра меньше ширины, то каким будет периметр бассейна в метрах?
Ключ ответа:
1. Мы знаем формулу периметра прямоугольника :
Периметр прямоугольника $= L \hspace{1mm}+\hspace{1mm} W\hspace{1mm} + \hspace{1мм} L +\hspace{1мм} W$
Периметр прямоугольника $= 6см\hspace{1мм} +\hspace{1мм} 8см\hspace{1мм} +\hspace{1мм} 6см \hspace{1мм }+\hspace{1mm} 8cm$
Периметр прямоугольника $= 28 \hspace{1mm}cm$
Альтернатива s решение
Периметр прямоугольника $= 2 ( L\hspace{1мм}+ \hspace{1мм}W)$
Периметр прямоугольника $= 2 ( 6\hspace{1мм} см+\hspace{1мм} 8 см)$
Периметр прямоугольника $= 2 ( 14 см)$
Периметр прямоугольника $= 28 \hspace{1mm}cm$
2. Мы знаем формулу периметра прямоугольника :
Периметр прямоугольника $ = L \hspace{1мм}+\hspace{1мм} W\hspace{1мм} +\hspace{1мм} L\hspace{1мм} +\hspace{1мм} W$
Периметр прямоугольника $= 10 см \hspace {1мм}+\hspace{1мм} 7 см \hspace{1мм}+\hspace{1мм} 10 см\hspace{1мм} +\hspace{1мм} 7 см$
Периметр прямоугольника $= 34 \hspace{1мм}см$
Альтернативное решение
Периметр прямоугольника $= 2 (L\hspace{1мм}+ \hspace{1мм}W)$
Периметр прямоугольника $= 2 ( 10 см + 7 см)$
Периметр прямоугольника $= 2 ( 17 см)$
Периметр прямоугольника $= 34\hпробел{1мм} см$
3.
Длина $= 8 см $ и ширина $= 5 см$
Мы можем рассчитать периметр прямоугольного сада на , используя формулу периметра .
Периметр прямоугольника $= 2 ( L\hspace{1мм}+\hspace{1мм} W)$
Периметр прямоугольника $= 2 ( 8 см\hspace{1мм}+\hspace{1мм} 5 см)$
Периметр прямоугольника $= 2 ( 13 см)$
Периметр прямоугольника $= 26 \hspace{1mm}cm$.
Длина $= 6 см$ и Ширина $= 9 см$
Мы можем вычислить периметр прямоугольного сада на , используя формулу периметра .
Периметр прямоугольника $ = 2 ( L\hspace{1mm}+\hspace{1mm} W)$ 9{2} $ and Width = $8m$
$A = L\times W$
$16 = L\times 8$
$L = 2 \hspace{1mm}m$
Теперь, когда у нас есть длину и ширину сада, мы можем теперь вычислить периметр по формуле .
Периметр прямоугольника $ = 2 ( L\hspace{1мм}+\hspace{1мм} W)$
Периметр прямоугольника $ = 2 ( 2 см+ 8 см)$
Периметр прямоугольника $ = 2 ( 10 см )$
Периметр прямоугольника $ = 20\hspace{1mm} см$ 9{2} \hspace{1мм}-\hspace{1мм} 6y \hspace{1мм}+ \hspace{1мм}2y \hspace{1мм}- \hspace{1мм}12 = 0$
$y (y \hspace {1мм}–\hspace{1мм} 6) + 2(y\hspace{1мм} –\hspace{1мм} 6) = 0$
$(y \hspace{1мм}– \hspace{1мм}6 )( y\hspace{1mm} +\hspace{1mm} 5) = 0$
Ширина может быть либо $-5$, либо $6$, и поскольку ширина не может быть отрицательной, значение ширины равно $6$.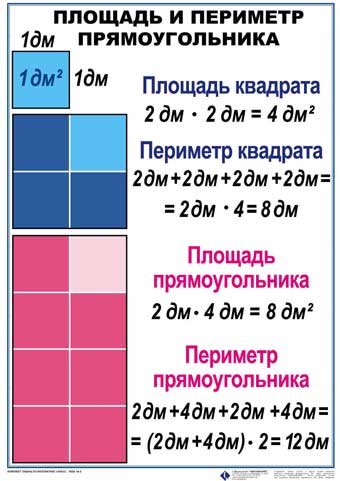
Итак, $y = W = 6$, тогда значение длины $L = W \hspace{1мм}-\hspace{1мм} 4 = 6\hspace{1мм} -\hspace{1мм} 4 = 2 \hspace {1мм} метров$
Теперь мы знаем значения ширины и длины прямоугольного бассейна. Затем мы можем вычислить его периметр с помощью , подставив значения в формулу .
Периметр бассейна $= 2 (L \hspace{1мм}+\hspace{1мм} W) = 2(2m \hspace{1мм}+\hspace{1мм} 6м) = 2(8m) = 16\ hspace{1mm} метров.$
Определение прямоугольника, площадь, формула, свойства и примеры
Содержание
Что такое прямоугольник?
Прямоугольник — это двумерная плоская фигура, имеющая четыре стороны и четыре внутренних угла. Противоположные стороны и углы имеют одинаковую меру. Он определяется как тип четырехугольника, имеющего четыре стороны и противоположные стороны, а углы равны и параллельны друг другу. Прямоугольный объект задается на основе двух параметров: длины и ширины. Самая длинная сторона прямоугольника считается длиной, а самая короткая сторона принимается за ширину.
В нашей повседневной жизни мы наблюдаем и используем различные предметы прямоугольной формы, такие как столы, книги, коробки, мобильные телефоны, стены, поля для крикета, экраны телевизоров или компьютеров, мебель, кровати, Almirah, двери и т. д. В этой статье , мы обсудим прямоугольник, его свойства, площадь прямоугольника, формулы, периметр прямоугольника и некоторые решенные примеры на его основе, чтобы получить четкое представление о понятиях прямоугольника.
Прямоугольник Определение
Прямоугольник определяется как любая двумерная замкнутая фигура, имеющая четыре стороны, а противоположные стороны и углы равны. Противоположные стороны видят параллель в том, что никогда не встречаются друг с другом. В прямоугольнике все четыре внутренних угла равны 90°. Вы можете наблюдать прямоугольник, его стороны и углы на рисунке, показанном ниже.
На приведенном выше рисунке показан прямоугольник ABCD, стороны которого имеют длины сторон AB = CD = l, AD = BC = b и AD || Британская Колумбия, AB || CD. Значения внутренних углов равны 90°.
Площадь прямоугольника
Площадь прямоугольника — это количество пространства, занимаемого внутри четырех сторон. Математически количество единичных квадратов, помещенных внутри прямоугольника, дает площадь прямоугольника. В нашей повседневной жизни мы наблюдаем множество прямоугольных объектов, также требуется нахождение их площадей. Мы можем взять в качестве примера множество прямоугольных объектов, таких как книги, столы, экраны ноутбуков, процессоры и т. д. Площадь прямоугольника зависит только от двух параметров, таких как длина и ширина. Площадь прямоугольника можно найти, используя приведенную ниже формулу блеска. Площадь прямоугольника выражается в квадратных единицах: кв. м, кв. см или кв. мм.
Площадь прямоугольника = длина × ширина
A = l × B Квадратные единицы
Форма прямоугольника
Как мы уже говорили, прямоугольник представляет собой двумерную замкнутую фигуру, имеющую четыре стороны. Противоположные стороны прямоугольника равны и параллельны друг другу, и он имеет четыре внутренних угла, равных 90°. Мы наблюдаем много прямоугольных форм, таких как стены, коробки, столы, кровати, экраны компьютеров/ноутбуков и т. д.
Формула площади прямоугольника
Площадь прямоугольника — это пространство, занимаемое внутри внешней границы прямоугольника. Площадь прямоугольника можно вычислить произведением длины на ширину. Предположим, что длина прямоугольника равна l, ширина прямоугольника равна b, площадь прямоугольника d представлена буквой A, тогда формула для вычисления площади прямоугольника представляет собой произведение длины и ширины. Площадь прямоугольника представлена в квадратных единицах.
Площадь прямоугольника = длина × ширина
92 × ширина
Формула прямоугольника
Формула для вычисления площади прямоугольника подробно обсуждалась выше. Формула площади прямоугольника есть произведение длины и ширины прямоугольника. Пусть длина прямоугольника равна L, ширина равна W, а площадь прямоугольника равна A. Тогда формулу площади прямоугольника можно представить в виде:
A = L × W квадратных единиц
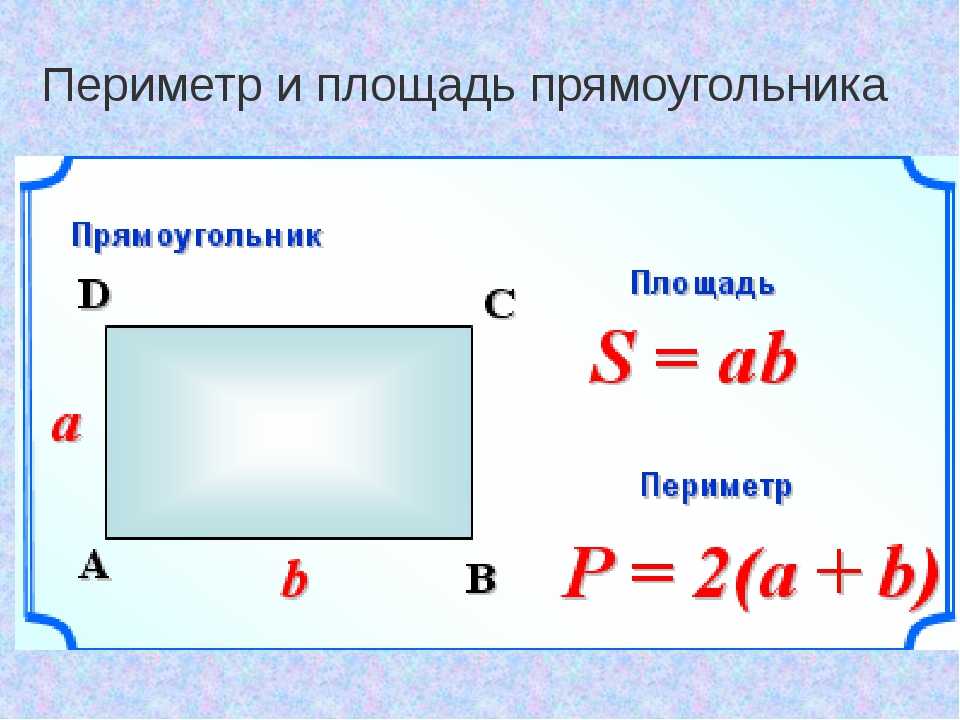
Формула периметра прямоугольника
Периметр прямоугольника – это общее расстояние от его внешних границ. Это удвоенная сумма длины и ширины прямоугольника. Периметр прямоугольника представляет собой линейное измерение его внешних сторон, а затем его добавляют, чтобы получить значение параметра прямоугольника. Он выражается в единицах длины, таких как м, см или мм.
Рассмотрим прямоугольник ABCD, как показано выше, длина которого равна l, а ширина равна b, тогда периметр прямоугольника ABCD представлен числом 9.0005
Периметр прямоугольника = 2 ( l + b)
Свойства прямоугольника
Прямоугольник имеет множество свойств, используемых в геометрии и других приложениях, посредством которых он задается. Важные свойства прямоугольника перечислены ниже.
Прямоугольник является разновидностью четырехугольника.
Противоположные стороны прямоугольника равны и параллельны друг другу
Значение внутреннего угла прямоугольника в каждой вершине равно 90°.
Сумма всех внутренних углов прямоугольника равна 360° (90°+90°+90°+90°).
Диагонали прямоугольника делят друг друга пополам.
Длина обеих диагоналей прямоугольника равна.
Длину диагоналей можно найти по теореме Пифагора. Длина диагонали со сторонами a и b равна, тогда диагональ = √( a ² + b ² ).
Поскольку стороны прямоугольника параллельны, его также называют параллелограммом.
Все прямоугольники определенно являются параллелограммами, но все параллелограммы не могут быть прямоугольниками.
Прямоугольник: Решенные примеры
1. Если длина прямоугольника 8 см, а ширина 5 см. Найдите площадь прямоугольника.
Решение: При l = 8 см и b = 5 см
тогда площадь прямоугольника A = l × b
A = 8 × 5
A = 40 кв. см
2. Ширина 2. длина прямоугольника 20 мм, а площадь прямоугольника 220 мм. Вычислите длину прямоугольника.
Решение: Дано b = 20 мм, A = 220 мм a и l =?
Мы знаем, что площадь прямоугольника = длина × ширина
A = l × b
220 = 20l
l = 220/20 = 11 мм
3. У Шьяма есть прямоугольная фоторамка размером 9 дюймов. в длину и 5 дюймов в ширину. Помогите Шьяму найти площадь фоторамки?
Решение: Мы знаем формулу для вычисления площади прямоугольника
Площадь прямоугольника = (Длина × Ширина).
Таким образом, площадь прямоугольной рамки = 9 × 5 = 45 квадратных дюймов
Следовательно, площадь фоторамки = 45 квадратных дюймов
4. Найдите периметр и площадь прямоугольника o с длина 17 см, ширина 13 см.
Решение: Дана длина = 17 см, ширина = 13 см
Периметр прямоугольника = 2 (длина + ширина)
= 2 (17 + 13) см
= 2 × 30 см
5 = 60 см 92 и L = 33M
A = L × B
660 = 33 × B B = 20 м
Следовательно, периметр прямоугольного графика = 2 (длина + ширина) = 2 (33 + 20) M
= 2×53 = 106 м

Решение: P = 2 (l + b)
Здесь Р = 48 см; b = 6 см
Следовательно, 48 = 2 (l + 6)
⇒ 48/2 = l + 6
⇒ 24 = l + 6
⇒ 24 – 6 = l
⇒ 9002 l 18 Следовательно, длина = 18 см
Теперь площадь прямоугольника = l × b = 18 × 6 см2 = 108 см2
7. Найдите ширину и периметр прямоугольника, если его площадь равна 96 см22
и длиной 12 см.
Решение: Учитывая, что A = 96 см2 и l = 12 см
A = l × b
Следовательно, 96 = 12 × b
96/12 = b
⇒ b = 8 см
Теперь P = 2 (l + b)
= 2 (12 + 8 )
= 2 × 20
= 40 см
8. Длина и ширина прямоугольного двора равны 75 м и 32 м. Найдите стоимость его выравнивания из расчета 3 долл. за м2. Также найдите расстояние, пройденное мальчиком за 4 круга двора.
Решение: Длина двора = 75 м
Ширина двора = 32 м
Периметр двора = 2 (75 + 32) м
= 2 × 107 м
= 214 м
Расстояние, пройденное мальчиком за 4 раунда = периметры двора
= 4 × 214
= 856 м
Известно, что площадь двора = длина × ширина
= 75 × 32 м22
= 2400 м22
, За 1 выравнивание затрат = 3$
Для 2400 м2 стоимость выравнивания = 3$ × 2400
= 7200
9. Сколько конвертов можно сделать из листа бумаги размером 100 см на 75 см, если для 1 конверта требуется лист бумаги размером 20 см на 5 см?
Решение: Площадь листа = 100 × 75 см2 = 7500 см2
Площадь конверта = 20 × 5 см = 100 см2
Количество конвертов, которые можно сделать = Площадь листа / Площадь конверта
= 7500/100 = 75 конвертов
10. Проволока в форме прямоугольника длиной 35 см и шириной 18 см сгибается в квадрат. Какова будет мера каждой стороны?
Решение: Периметр прямоугольника = 2 (35 + 18) см
= 2 × 53
= 106 см
Периметр квадрата со стороной x см =, Следовательно, периметр прямоугольника прямоугольник = периметр квадрата
106 см = 4x
⇒ x = 26,5
Следовательно, каждая сторона квадрата = 26,5 см
Прямоугольник: Часто задаваемые вопросы
Вопрос 1 Что такое прямоугольник?
Ответ – Прямоугольник – это замкнутая двумерная фигура, имеющая четыре стороны и четыре угла. Противоположные стороны параллельны и равны.
Que.2 Определите площадь прямоугольника?
Ответ – Площадь прямоугольника – это область, занимаемая под границей прямоугольника. Это продукт длины и ширины.
Que.3 Чему равен периметр прямоугольника?
Ответ – Периметр прямоугольника – это сумма длин сторон прямоугольника.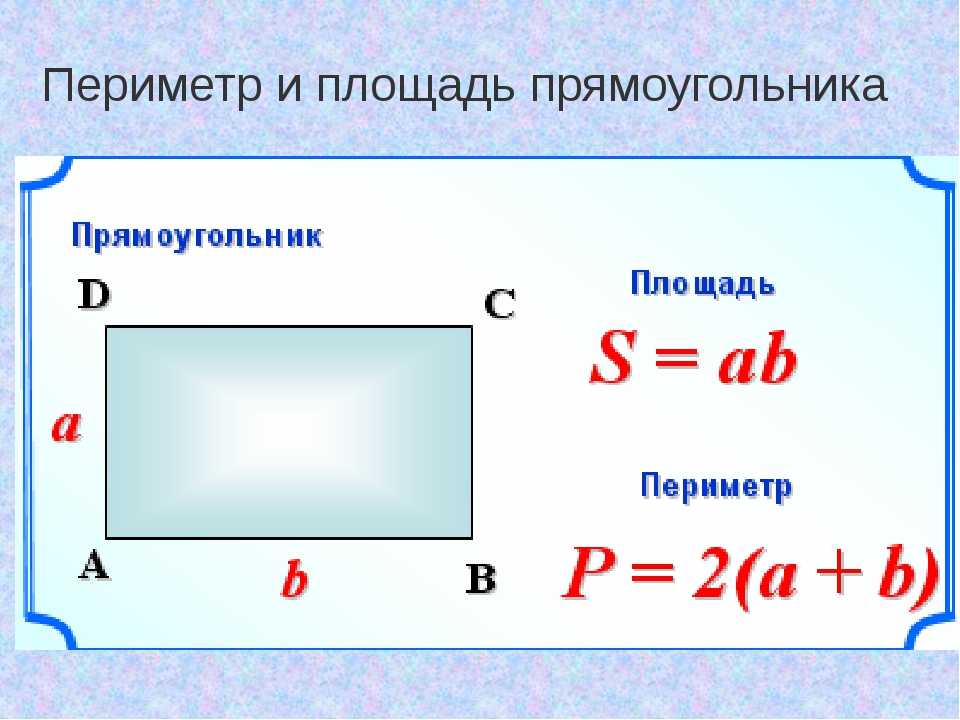 Он рассчитывается по формуле 2(l+b).
Que.4 Каковы диагонали прямоугольника?
Ответ – Диагонали – это линии, соединяющие противоположные вершины прямоугольника. Он равен по длине.
Объяснение для учителей, родителей и детей
Периметр фигуры – это размер вокруг ее края (периметр круга называется окружностью).
Этот блог является частью нашей серии блогов, предназначенных для объяснения основных математических понятий для тех, кто помогает детям начальной школы или в рамках домашнего обучения.
Что такое периметр?
Периметр фигуры – это общее измерение всех краев фигуры, например. треугольник имеет три ребра, поэтому его периметр равен сумме этих трех ребер, сложенных вместе.
Периметр квадрата легко вычислить, если известна одна сторона, так как все стороны имеют одинаковую длину; периметр квадрата со стороной 5 дюймов равен 20 дюймам, потому что 5 x 4 = 20. Периметр прямоугольника можно рассчитать, сложив длину и ширину и удвоив их.
Периметр прямоугольника длиной 5 дюймов и шириной 3 дюйма можно рассчитать как 5 + 3 + 5 + 3 (два участка длины + два участка ширины) или удвоить 5 + 3, то есть 16 дюймов.
Как измерить периметр фигуры
При измерении периметра более сложных фигур можно предложить детям подсвечивать каждое ребро, когда они складывают их вместе, чтобы убедиться, что они ничего не пропустили.
Когда мой ребенок узнает о периметре в начальной школе?
Периметр преподается, когда дети начинают изучать геометрию. Дети начинают с обучения измерению периметра простых двумерных фигур в 3-м классе. Дети также будут измерять и вычислять периметр многоугольников, в том числе находить периметр по длинам сторон, находить неизвестную длину стороны и показывать прямоугольники с одинаковым периметром
В 4-м классе дети применяют формулу периметра для прямоугольников в реальном мире и математические задачи.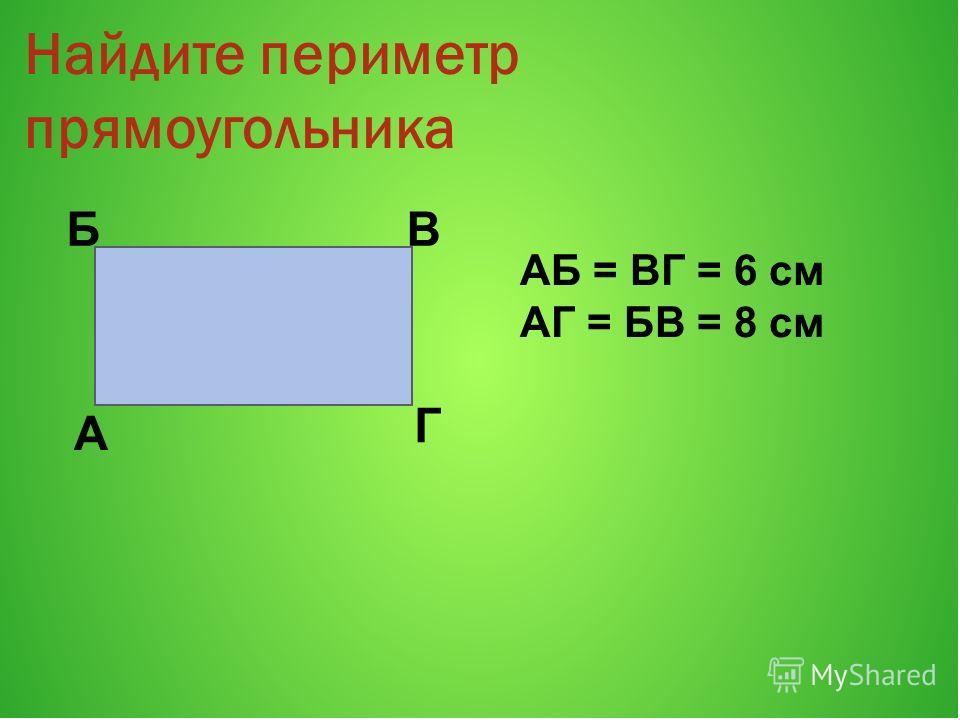 Например, найдите ширину прямоугольной комнаты, зная площадь пола и длину, рассматривая формулу площади как уравнение умножения с неизвестным коэффициентом 9.0040 .
Как периметр связан с другими областями математики?
Периметр наиболее тесно связан со свойствами форм, двухмерных и трехмерных форм и является одной из самых основных и важных частей геометрии.
Необходимо хорошее понимание того, как вычислить периметр фигуры, прежде чем дети смогут начать изучать более сложные геометрические понятия, такие как площадь и объем.
Хотите знать, как объяснить своим детям другие ключевые слова по математике? Посмотрите наши Математический словарь для детей , или попробуйте эти математические термины:
Что такое диаграмма Венна: объяснение для учителей, родителей и детей
Что такое разрядное значение: объяснение для учителей, родителей и детей
Что такое наивысшее Общий фактор: Объяснение для учителей, родителей и детей
Практические вопросы по периметру
1. Вычислите периметр этого квадрата.
(Ответ: 8 х 4 = 32 см)
2. Сэм нарисовал прямоугольник с периметром 28см. Его прямоугольник был длиной 10 см. Насколько он был широк?
(Ответ: 4 см)
3. Вот несколько фигур на квадратной сетке 1 см. а) Чему равен периметр фигуры А? б) Какая фигура имеет наименьший периметр?
(Ответ: а) 14 см б) Г)
4. Меган говорит: «Если два прямоугольника имеют одинаковый периметр, они должны иметь одинаковую площадь». Она права? Объясните откуда вы знаете.
(Ответ: Нет – периметр 20 см может быть 2 x 10 или 4 x 5)
5. Вот равносторонний треугольник внутри квадрата. Периметр треугольника равен 48 см. Чему равен периметр квадрата?
(Ответ: 64 см (48/3 = 16 (одна сторона треугольника) поэтому 16 x 4 = 64)
Что такое периметр в математике?
Расстояние вокруг периметра край фигуры
Как вычислить периметр?
Периметр можно найти, сложив длины каждой стороны фигуры.
Пример периметра?
Например, поле прямоугольной формы длиной 24 ярда и шириной 15 ярдов будет иметь периметр 78 ярдов.
Есть ли у вас ученики, которым нужна дополнительная помощь по математике?
Предоставьте учащимся четвертого и пятого классов больше возможностей для закрепления навыков обучения и практики с помощью персонализированного обучения элементарной математике с их собственным онлайн-репетитором по математике.
Каждый учащийся получает дифференцированное обучение, предназначенное для устранения индивидуальных пробелов в обучении, а организованное обучение гарантирует, что каждый учащийся учится в нужном темпе. Уроки соответствуют стандартам и оценкам вашего штата, плюс вы будете получать регулярные отчеты о каждом шаге.
Программы доступны для четвертого и пятого классов, и вы можете попробовать 6 уроков абсолютно бесплатно.
Содержание этой статьи изначально было написано учителем начальных классов Софи Бартлетт, а затем было отредактировано и адаптировано для школ США учителем математики начальных классов Кристи Кулешей.
No related posts.