Матпрофи решение интегралов: Онлайн калькулятор. Решение интегралов онлайн.

11-а, Решение интегралов

Решение интегралов. Рассказываем, как решать интегралы.

Интеграл – расширенное математическое понятие суммы. Решение интегралов или их нахождение называется интегрированием. Пользуясь интегралом можно найти такие величины, как площадь, объем, массу и другое. Решение интегралов (интегрирование) есть операция обратная диференциированию. Чтобы лучше представлять, что есть интеграл, представим его в следующей форме. Представьте. У нас есть тело, но пока не можем описать его, мы только знаем какие у него элементарные частицы и как они расположены. Для того, чтобы собрать тело в единое целое необходимо проинтегрировать его элементарные частички – слить части в единую систему. В геометрическом виде для функции y=f(x), интеграл представляет собой площадь фигуры ограниченной кривой, осью х, и 2-мя вертикальными линиями х=а и х=b .

Так вот площадь закрашенной области, есть интеграл от функции в пределах от a до b.

Не верится? Проверим на любой функции. Возьмем простейшую у=3. Ограничим функцию значениями а=1 и b=2. Построим: Итак ограниченная фигура прямоугольник. Площадь прямоугольника равна произведению длины на ширину. В наше случае длина 3, ширина 1, площадь 3*1=3. Попробуем решить тоже самое не прибегая к построению, используя интегрирование: Как видите ответ получился тот же. Решение интегралов – это собирание во едино каких-либо элементарных частей. В случае с площадью суммируются полоски бесконечно малой ширины. Интегралы могут быть определенными и неопределенными. Решить определенный интеграл значит найти значение функции в заданных границах. Решение неопределенного интеграла сводиться к нахождению первообразной. F(x) – первообразная. Дифференцируя первообразую, мы получим исходное подинтегральное выражение. Чтобы проверить правильно ли мы решили интеграл, мы дифференциируем полученный ответ и сравниваем с исходным выражением. Основные функции и первообразные для них приведены в таблице:

Таблица первообразных для решения интегралов

Основные приемы решения интегралов: Решить интеграл, значит проинтегрировать функцию по переменной. Если интеграл имеет табличный вид, то можно сказать, что вопрос, как решить интеграл, решен. Если же нет, то основной задачей при решении интеграла становиться сведение его к табличному виду. Сначала следует запомнить основные свойства интегралов:

Знание только этих основ позволит решать простые интегралы. Но следует понимать, что большинство интегралов сложные и для их решения необходимо прибегнуть к использованию дополнительных приемов. Ниже мы рассмотрим основные примеры решения интегралов. Приемы будет даны для общего ознакомления без примеров решения, чтобы не перегружать статью. Нужно понимать, что за 5 минут прочтения статьи решать все сложные интегралы вы не научитесь, но правильно сформированный каркас понимания, позволит сэкономить часы времени на обучение и выработку навыков по решению интегралов.

Основные приемы решения интегралов

1. Замена переменной. Для выполнения данного приема потребуется хороший навык нахождения производных.

2. Интегрирование по частям. Пользуются следующей формулой. Применения этой формулы позволяет казалось бы нерешаемые интегралы привести к решению.

3. Интегрирование дробно-рациональных функций.  — разложить дробь на простейшие  — выделить полный квадрат.  — создать в числителе дифференциал знаменателя.

4. Интегрирование дробно-иррациональных функций.  — выделить под корнем полный квадрат  — создать в числителе дифференциал подкоренного выважения. 5. Интегрирование тригонометрических функций.  При интегрировании выражений вида применяет формулы разложения для произведения. Для выражений  m-нечетное, n –любое, создаем d(cosx). Используем тождество sin

2+cos²=1 m,n – четные, sin²x=(1-cos2x)/2 и cos²x=(1+cos2x)/2 Для выражений вида:  — Применяем свойство tg²x=1/cos²x – 1

1. Разобраться в сути интегралов. Необходимо понять базовую сущность интеграла и его решения. Интеграл по сути есть сумма элементарных частей объекта интегрирования. Если речь идет об интегрирование функции, то интеграл есть площадь фигуры между графиком функции, осью х и границами интегрирования. Если интеграл неопределенный, то есть границы интегрирования не указаны, то решение сводиться к нахождению первобразной. Если интеграл определенный, то необходимо подставить значения границ в найденную функцию. 2. Отработать использование таблицы первообразных и основным свойства интегралов

. Необходимо научиться пользоваться таблицей первообразных. По множеству функций первообразные найдены и занесены в таблицу. Если мы имеем интеграл, которые есть в таблице, можно сказать, что он решен. 3. Разобраться в приемах и наработать навыки решения интегралов.Если интеграла не табличного вида, то его решение сводиться к приведению его к виду одного из табличных интегралов. Для этого мы используем основные свойства и приемы решения. В случае, если на каких то этапах применения приемов у вас возникают трудности и непонимания, то вы более подробно разбираетесь именно по этому приему, смотрите примеры подобного плана, спрашиваете у преподавателя. Дополнительно после решения интеграла на первых этапах рекомендуется сверять решение. Для этого мы дифференциируем полученное выражение и сравниваем с исходным интегралом. Отработаем основные моменты на нескольких примерах:

Примеры решения интегралов

Пример 1: Решить интеграл: Интеграл неопределенный. Находим первообразную. Для этого интеграл суммы разложим на сумму интегралов. Каждый из интегралов табличного вида. Смотрим первообразные по таблице. Решение интеграла: Проверим решение(найдем производную):

Пример 2. Решаем интеграл Интеграл неопределенный. Находим первообразную. Сравниваем с таблицей. В таблице нет. Разложить, пользуясь свойствами, нельзя. Смотрим приемы. Наиболее подходит замена переменной. Заменяем х+5 на t⁵. t⁵ = x+5 . Получаем. Но dx нужно тоже заменить на t. x= t⁵ — 5, dx = (t⁵ — 5)’ = 5t⁴. Подставляем: Интеграл из таблицы. Считаем: Подставляем в ответ вместо t , Решение интеграла:

Пример 3. Решение интеграла: Для решения в этом случае необходимо выделить полный квадрат. Выделяем:

В данном случае коэфециент ½ перед интегралом получился в результате замены dx на ½*d(2x+1). Если вы найдете производные x’ = 1 и ½*(2x+1)’= 1, то поймете почему так. В результате мы привели интеграл к табличному виду. Находим первообразную. В итоге получаем:

Как правильно решить интегралы

Практическое применение интегралов в жизни

Реальный мир не идеален и не прямолинеен. В нем нет геометрических форм без изъяна, нет движения без ускорения. И зависимости между величинами редко представлены прямой линией. Поэтому вычисления не обходятся без интегралов.

Определение

Интеграл — важнейшее понятие математики. Связано с необходимостью отыскивать функции по их производным и измерять объемы и площади, работу сил за какой-либо промежуток времени.

Множество частных случаев из жизни делают интегрирование не просто полезным, а необходимым действием. Интеграл поможет:

• рассчитать стоимость, изучив зависимость потребности от предложений;
• вычислить время выполнения работы, с учетом усталости людей;
• узнать, как изменяется долг по кредиту в течение времени;
• определить прирост жителей города

Место интегралам нашлось не только в физико-математических науках, но и в астрономии, экономике, медицине, биологии и архитектуре.

Понимая практическую значимость интегралов, легче усвоить базовые понятия и применять их в решении задач.

Из истории интегрирования

Интегрирование рассматривается, как сложение бесконечно малых частей бесконечное количество раз.

Интегральный расчет получен при определении площадей и объемов. Правила измерения квадратуры были известны древним ученым. В Египте и Вавилоне вычисляли площади круга и объем усеченной пирамиды.

Значительный вклад внесли древнегреческие ученые. Первый метод интегрирования назвали «исчерпание» по аналогии с водой, которую черпают кружкой из ведра. В Древней Греции Архимед объяснил задачу вычисления площади круга без знаний о числе «Пи».

Описание метода

Для нахождения площади круга в него вписываются геометрические фигуры. Высчитывается предел последовательности площадей этих фигур, который и принимается за площадь круга.

Данный способ вычисления площади рассматривает идею интегрирования. То есть нахождения предела безграничной суммы. Метод нашел применение в решении прикладных задач в разных научных областях.

Ньютон и Лейбниц сформулировали теорию интегрирования опираясь на законы дифференциального исчисления. Чтобы разобраться в классической теории нужно получить базовые знания.

Смысл интегрирования заключается в двух видах задач: геометрических и аналитико-алгебраических. В первом случае находят площади фигур, во втором подсчитывают суммарное значение переменной величины, принимающей различные значение единиц времени, длины и других измерений.

Понятие «Интеграл» в простом изложении

Термин «интеграл» произошел от латинского integer, то есть «целостный». Данный термин предложил математик Лейбниц еще в 17 веке.

Определение

Интеграл – это сложение маленьких частей и даже обозначение ∫ представляет собой вытянутую s, что означает сумму.

Интеграл – первообразная функции. Интегрирование – определение первообразной.

В математике интеграл вычисляет площадь, ограниченную кривой линией. Неопределенный интеграл – это вся фигура. Определенный интеграл – площадь некоторой части.

Запись интеграла функции:

х – аргумент, его можно заменить любой другой переменной, в отношении которой будет осуществляться интегрирование. d – бесконечно малое число. Сочетание «dx» называют приращением и рассматривают, как бесконечно малый «икс».

На рисунке криволинейная трапеция разбита на столбцы шириной х, число столбцов – d.

Неопределённый интеграл

Определение

Неопределенный интеграл – это сумма всех первообразных данной функции, которая не имеет границ интегрирования.

Сумма F(x)+C всех первоначальных функций f(x) на интервале а< x<b  является неопределенным интегралом от функции  f(x) на этом интервале и обозначается ∫f(x)dx .

Если функция F(x) является первообразной для f(x) , то по определению

∫ f(x)dx = F(x)+C 

∫ — знак интеграла, f(x)dx — подынтегральное выражение, f(x) — подынтегральная функция, х — переменная интегрирования, С — произвольная постоянная.

{b} f(x) d x \]

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Примеры вычисления интегралов

Найти неопределенный интеграл.

Часто при решении используют тригонометрические формулы.

Решение определенного интеграла.

Давайте рассмотрим несколько примеров вычисления интегралов:

Пример 1.

Пример 2.

Словарь базовых понятий.

Для понимания сути интеграла необходимо разбираться в базовых понятиях: функция, производная, приращение, предел.

Функция – отношение между элементами, где изменение одного элемента, повлечёт изменение другого.

Производная – функция, которая описывает скорость трансформации второй функции в каждой данной точке. Вторая функция называется первообразной. По сути — это предел отношения приращения функции к приращению аргумента.   Высчитывание проводят, используя таблицу производных со стандартными функциями.

Приращение – количественная степень изменения функции при вероятном изменении аргумента.

Предел – величина, к которой стремится значение функции, при стремлении аргумента к определённому значению.

Решение задач с интегралами могут показаться сложными. Выполнение практических заданий поможет преодолеть трудности.

Решение интегралов сводится к простым видоизменениям подынтегральной функции и поиску её в таблице интегралов.

Мы также можем отметить, что интегралы играют не последнюю роль в нашей жизни. В Биологических науках, к примеру, при их помощи узнают прирост популяции видов, в медицине используют в различных исследованиях, например, в томографии, в астрономии рассчитывают передвижение космических объектов и многое другое. Да и вообще трудно найти область, в которой не применяются данные методы вычисления.

ШКОЛЬНЫЙ ОКРУГ CAJON VALLEY UNION

НАЗВАН НАЦИОНАЛЬНЫМ ВЫСТАВОЧНЫМ ОКРУГОМ ЦИФРОВОЙ КОНВЕРГЕНЦИИ 2019 ГОДА

Подходящая для принтера версии

• Февраль 2019 г. Статьи

• Школьный округ Каджон-Вэлли
• Цифровой конвергенция Национальная витрина Район

от Miriam Rafteri «Современный учитель» назвал школьный округ Союза Кахон-Вэлли лучшим в 2019 году.Национальный выставочный район цифровой конвергенции.

Школьный округ Союза Кахон-Вэлли, являющийся Национальным демонстрационным округом, открыл свои классы 4 февраля для более чем 250 руководителей образования со всех концов Соединенных Штатов, объединенных участием в Национальной конференции по цифровой конвергенции и двумя общими целями: предоставить учащимся опыт, необходимый для процветать и служить всем ученикам.

 

Согласно пресс-релизу округа, школьный округ Cajon Valley Union School District удостоен награды за «революционный подход к предоставлению современного учебного опыта. Партнерство округа с сообществом для совместной работы над будущим обучения не только вдохновило руководителей образования по-новому взглянуть на свои подходы к современному обучению, но и предоставило информацию о передовых методах современного обучения в масштабе в рамках концепции цифровой конвергенции».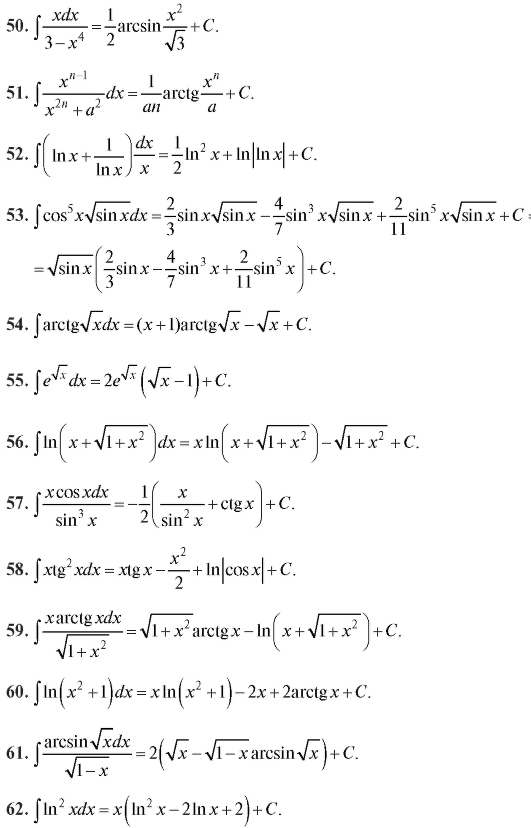

 

Посещения школ сосредоточены на Современной учебной программе округа, разработанной с учетом надежд сообщества на будущее обучения в Эль-Кахоне: поднять типы рабочих мест, важных для инфраструктуры местной экономики, и устранить только для колледжей менталитет и ожидания, которые, по словам округа, не подходят каждому учащемуся.

 

Более 250 руководителей учебных заведений увидели практический подход округа к предоставлению современных, реальных компетенций рабочей силы. Программа «Мир труда» предоставляет учащимся возможности для изучения карьерных возможностей, которые напрямую связаны с тем, что они изучают в школе, и соответствуют их сильным сторонам, интересам и ценностям. , синтезировать и делиться новыми идеями, а также исследовать практическое применение своих увлечений.

 

«За последний год передовые разработки Cajon Valley стали частью неотъемлемых волокон концепции цифровой конвергенции благодаря добавлению драйвера сообщества», — объясняет д-р Шон Смит, генеральный директор Modern Teacher.

«Добавление Community Driver дает руководителям округов нашей страны практический путь для эффективного партнерства со своими сообществами и обеспечения актуальности опыта учащихся, что является ярким примером школьного округа Cajon Valley Union».

 

По данным Департамента образования округа, в школьном округе Союза Кахон-Вэлли обучается более 17 000 учащихся классов K-8. Две трети из малообеспеченных семей участвуют в программе школьных обедов, а более трети изучают английский язык.

 

В разнообразном округе, в котором проживает много студентов-иммигрантов и беженцев, соотношение учителей и учащихся составляет 25 к 1, согласно данным Niche.com, но только 42% умеют читать и 34% умеют читать, что соответствует уровню C+ для ученых. Согласно рейтингу школ на сайте Dashboard штата Калифорния, учащиеся округа получили оценку ниже стандарта на 27,4 балла по английскому языку и на 53 балла ниже стандарта по математике, снизившись на 6,5 балла по математике.

 

Программа «Современный учитель» сотрудничает с округами, чтобы поддержать переход от традиционных классов к современным учебным средам в больших масштабах.