Синус, косинус и тангенс острого угла прямоугольного треугольника презентация, доклад
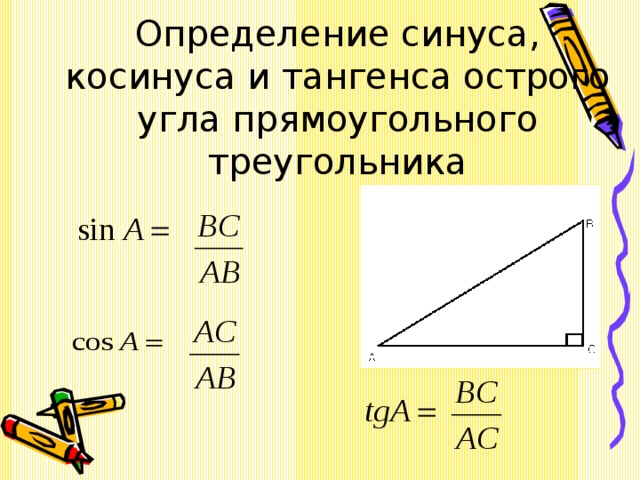
Синус, косинус и тангенс острого угла прямоугольного треугольника
Тригонометрические функции
sinA, sinα, sin60o
cosB, cosβ, cos30o
tgC, tgλ, tg45o
Знать:
Определение синуса, косинуса тангенса острых углов прямоугольного треугольника.
Уметь:
Находить данные функции для треугольника
Решать задачи на нахождение углов,
сторон прямоугольного треугольника
Применять
На уроках физики
Противолежащий катет данному углу, и прилежащий
катет к данному углу.
Синус угла
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе
Записать:
а) синус угла А ∆ DАЕ
б) синус угла С ∆ САD
в) синус угла А ∆СМА
Пример
Найти синус угла В и синус угла А прямоугольного треугольника АСВ, если АС=3см,ВС=4см и угол С = 90.
Синус острого угла есть отношение противолежащего катета к гипотенузе.
Найти: 1. синус углов А и К треугольника АКД 2.синус углов С и К треугольника СКД
1. SINA=8:10
SINK=6:10
2. SINC=8:9
SINK=5:9
С
А
К
Д
6
10
8
5
9
Решите задачу.
Найдите синус углов А и М треугольника АМС, уголС=90градусов, если АМ=17см, МС=8см.
Дано:
треугольник CMA, угол С=90,AM=17см,MC=8см.
SinA, SinМ.
Вопрос
Каким числом может быть синус острого угла
в прямоугольном треугольнике?
Может ли синус угла быть равен 2? 1.7? 0.3?
Синус угла всегда меньше 1.( 0.5, 0.9, 0.32)
Немного из истории тригонометрических функций
Отношение длины тени КС к длине гномона КМ(шест) солнечных часов
Меняется в зависимости от высоты Солнца.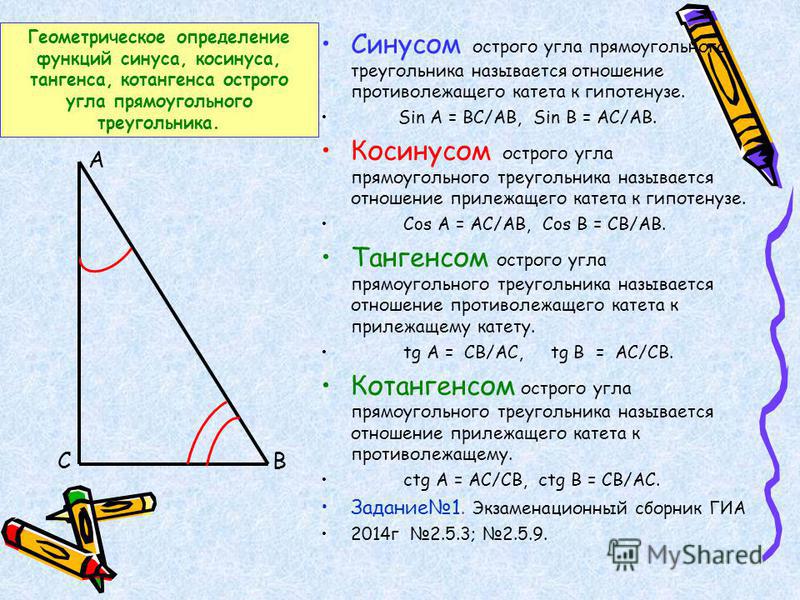
С такими данными составили таблицу, по которой определяли расстояние от Земли до Солнца.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Косинус есть отношение прилежащего катета к гипотенузе
Найти косинусы углов А и D треугольника АКD
6
C
B
Косинус есть отношение прилежащего катета к гипотенузе
CosA=
6
Косинус угла есть отношение прилежащего катета к гипотенузе.
Угол A равен углу K. Сравните косинусы и синусы этих углов
От чего зависят значения тригонометрических функций?
От величины угла?
От длин сторон треугольника?
От материала из которого сделан треугольник?
От расположения треугольника на плоскости?
Рассмотрим треугольники АРВ, АKТ и АОD.
Вывод:
Если в двух прямоугольных треугольниках острые углы равны, то косинусы этих углов равны.
Синус, косинус зависят только от величины угла.
Вопрос.
1.Каким числом может быть косинус угла ?
2.Может ли косинус данного угла быть равным 10? 1? 0,8?
3.От чего зависит косинус угла?
Тангенс угла. Определение.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
Тангенс угла есть отношение противолежащего катета к прилежащему
Найти тангенс угла А треугольника ABC с прямым углом B, если AB=24см, AC=25см
Синус угла, косинус угла,
тангенс угла
12
15
10
Конец урока
Домашнее задание
п.
66
Определения(учить)
№591в
Скачать презентацию
8 класс. Геометрия. Подобные треугольники. Практические приложения подобия треугольников. — Синус, косинус и тангенс острого угла прямоугольного треугольника.
Комментарии преподавателяСинус, косинус и тангенс острого угла прямоугольного треугольника
На этом уроке мы познакомимся с синусом, косинусом и тангенсом – тригонометрическими функциями, связывающими острый угол прямоугольного треугольника с катетами и гипотенузой этого треугольника. Это очень важные понятия, которые будут встречаться не только в геометрии, но и в алгебре, физике и во многих других науках.
Напомним основные сведения о прямоугольном треугольнике (см. Рис. 1).
Рис. 1
;
– катеты; – гипотенуза.
Также в прямоугольном треугольнике сумма острых углов равна : .
Для прямоугольного треугольника также верна теорема Пифагора: .
Введём теперь понятие синуса, косинуса и тангенса острого угла прямоугольного треугольника.
Определение
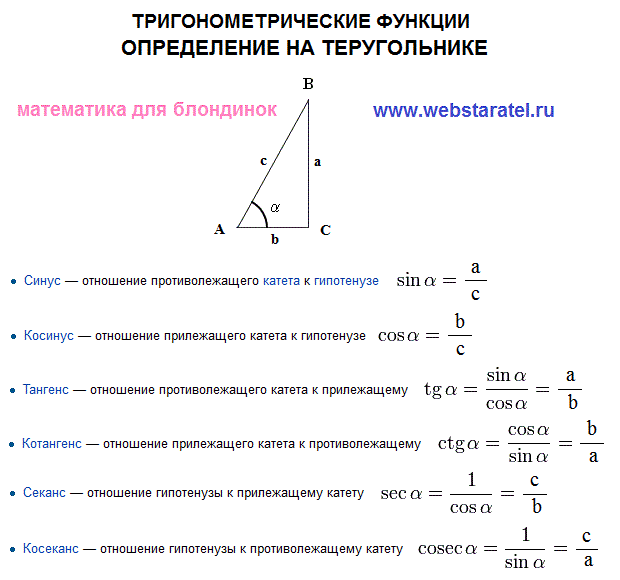
Синусом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к гипотенузе.
, .
Определение
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
, .
Определение
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего этому углу катета к прилежащему катету.
, .
С помощью введённых понятий можно находить катеты или гипотенузу.
Например, из формулы: . Аналогично: .
Также можно получить формулу для связи длин двух катетов: .
При решении задач очень важно знать соотношения между синусом, косинусом и тангенсом острого угла прямоугольного треугольника.
Рассмотрим следующие две формулы: . Так как сумма острых углов прямоугольного треугольника равна , то формула приобретает следующий вид:
Аналогично получаем: . Так как сумма острых углов прямоугольного треугольника равна , то формула приобретает следующий вид:
Докажем теперь важную формулу, связывающую тангенс с синусом и косинусом:
Доказательство
Запишем определение синуса и косинуса острого угла прямоугольного треугольника: , . Тогда: . Доказано.
Аналогично: .
Рассмотрим следующую важную задачу.
Задача
Даны прямоугольные треугольники . Кроме того, .
Доказать:.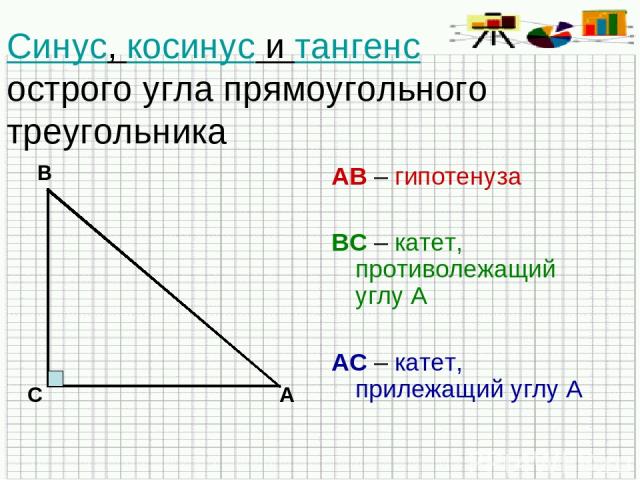
Доказательство
(так как оба треугольника прямоугольные с равными острыми углами). Значит, выполняется следующее соотношение: .
Отсюда получаем: .
.
.
Доказано.
Вывод: синус, косинус и тангенс не зависят от треугольника, а зависят только от угла.
Сформулируем и докажем одну из важнейших теорем, связывающих синус и косинус острого угла прямоугольного треугольника, – основное тригонометрическое тождество.
Основное тригонометрическое тождество: .
Примечание:
Доказательство
, тогда: (при доказательстве мы пользовались теоремой Пифагора: ).
Доказано.
Рассмотрим пример, иллюстрирующий связь тригонометрических функций.
Дано: – прямоугольный (), .
Найти:
Решение
Воспользуемся основным тригонометрическим тождеством: .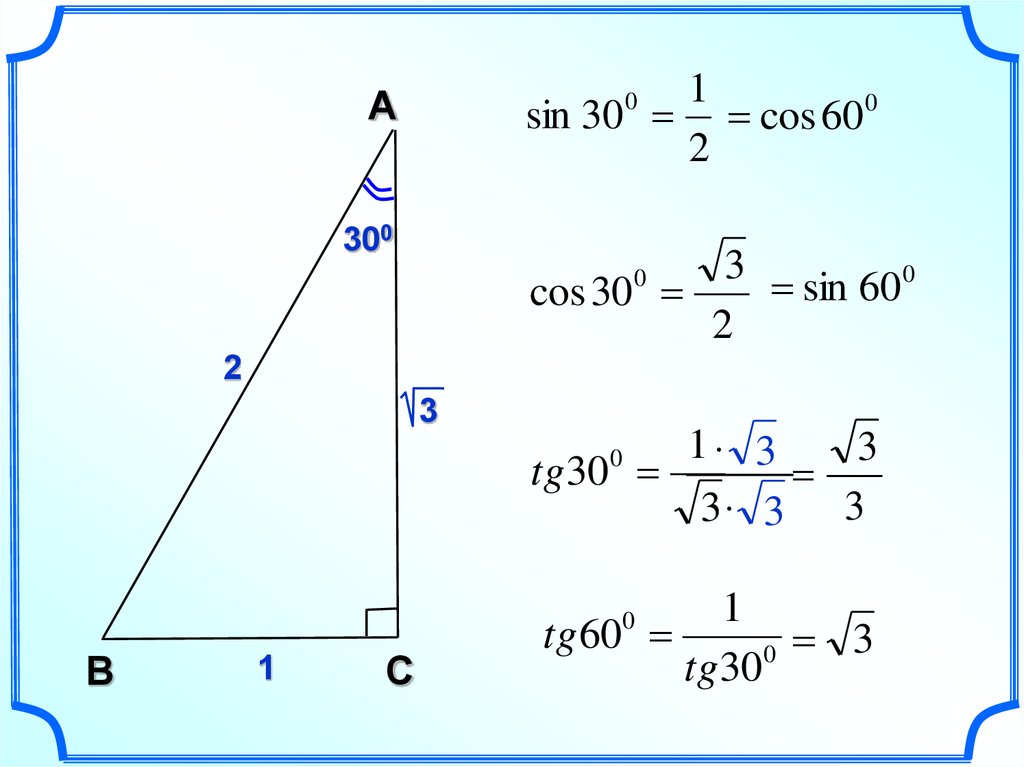
Подставим в него известное нам значение синуса: . Отсюда: . Так как косинус, по определению, – это отношение катета к гипотенузе, то он может быть только положительным, поэтому: .
Найдём теперь тангенс угла, пользуясь формулой: .
Ответ: .
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/8-klass/podobnye-treugolniki/sinus-kosinus-i-tangens-ostrogo-ugla-pryamougolnogo-treugolnika
http://www.youtube.com/watch?v=CvQYL11ce4c
http://www.funlib.ru/cimg/2014/102107/3325015
http://edu.convdocs.org/tw_files2/urls_25/7/d-6526/img4.jpg
http://player.myshared.ru/771881/data/images/img6.jpg
тригонометрия — когда использовать синус, косинус или тангенс
1 Я немного смущен тем, как вы предпочитаете использовать синус, косинус или тангенс. Взаимозаменяемы ли они, учитывая ту же информацию, что и у вас о прямоугольном треугольнике? Каковы обстоятельства, которые должны диктовать использование одного над другим? Или это предпочтение?
Я предполагаю, что, как и в части 2, у вас есть прямоугольный треугольник.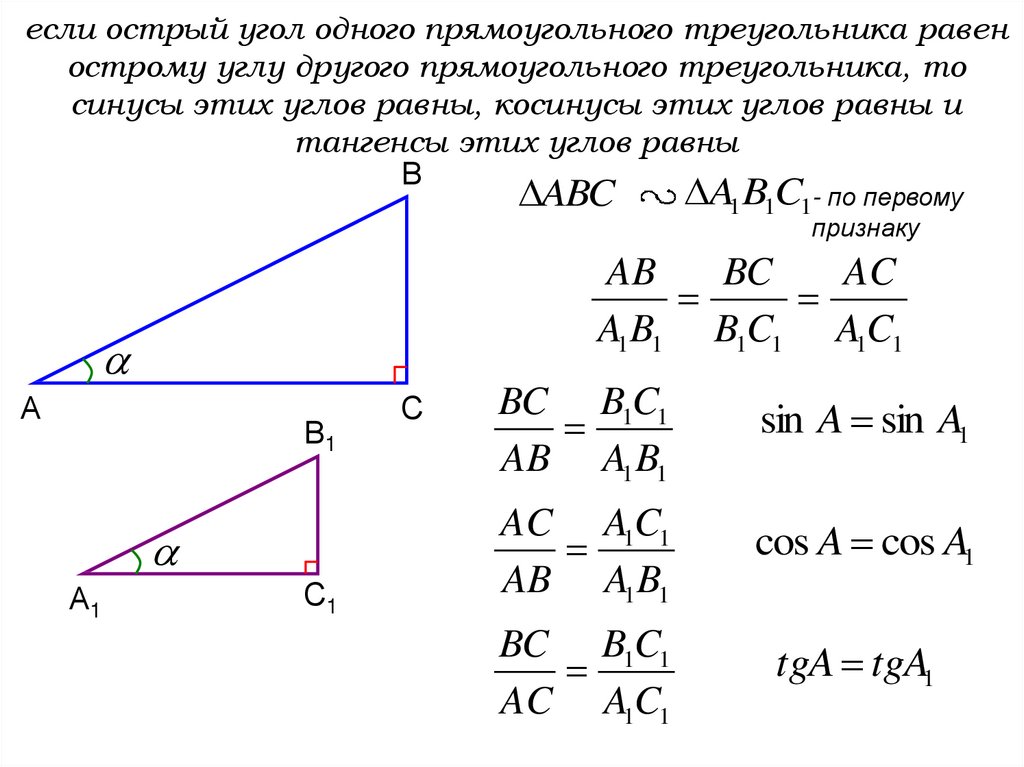
В этом случае вы можете определить угол по двум сторонам. В зависимости от того, какие у вас стороны, вы должны выбрать sin, cos или tan, как показано на схеме ниже.
$$\begin{выравнивание}
\sin d &= \frac{\text{противоположная сторона}}{\text{сторона гипотенузы}} \\
\cos d &= \frac{\text{прилежащая сторона}}{\text{сторона гипотенузы}} \\
\tan d &= \frac{\text{противоположная сторона}}{\text{прилегающая сторона}} \\
\end{выравнивание}$$ 92 х, \;\;\;
\text{где } \cot x = 1/\tan x, \mathrm{cosec}\,x=1/\sin x
\end{align}$$
2 Если вы знаете стороны, вы можете вычислить углы.
Да
Зная угол, можно вычислить длину сторон. Это правильное предположение?
Нет, см. правую часть схемы. У вас могут быть похожие треугольники, в которых все углы одинаковы, но длины сторон увеличены или уменьшены на какой-то фактор, как у матрешек.
Если подумать, то это имеет смысл, потому что все грех, кос или загар дают вам отношение между сторонами.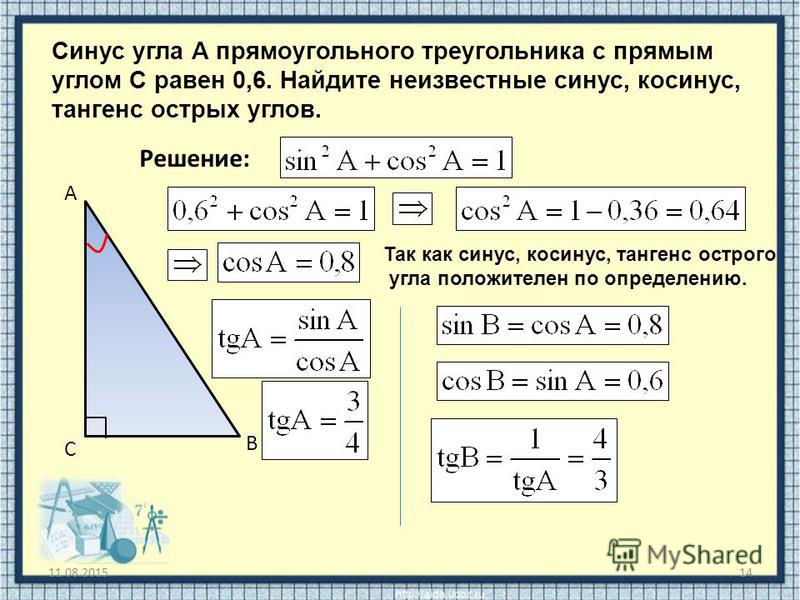
Итак, правильно ли предположить, что если вы знаете один из углов, кроме угла в 90 градусов и 1 длины одной стороны, вы можете определить синус, косинус и тангенс этого треугольника?
Строго говоря, мы говорим о синусе, косинусе и тангенсе углов, а не треугольников. Типичная постановка задачи состоит в том, что вам даны один из углов и одна из сторон прямоугольного треугольника. Затем вы можете определить длину другой стороны. Например. если у вас есть угол $d$ и противоположная сторона, вы можете изменить формулу синуса, чтобы найти сторону гипотенузы.
$$\begin{выравнивание} \sin d &= \frac{\text{противоположная сторона}}{\text{сторона гипотенузы}} \\ \text{сторона гипотенузы}\times\sin d &= \text{противоположная сторона} \\ \text{сторона гипотенузы} &= \frac{\text{противоположная сторона}}{\sin d} \end{align}$$
Также обратите внимание, что если у вас есть один угол и угол 90 градусов, вы можете вычислить третий угол, потому что сумма углов составляет 180 градусов.
Затем вы можете вычислить все стороны, но вам нужна хотя бы одна сторона, чтобы зафиксировать коэффициент масштабирования, как обсуждалось выше.
А зная две стороны всегда можно определить угол? Это верное предположение?
Да, верно. См. часть 1.
| ° ° ° | СИНУС, КОсинус и тангенс Вот мнемоническая фраза от Джайлза Марлоу из Уокинга, графство Суррей для тригонометрических соотношений синус (sin), косинус (cos) и тангенс (tan) любого неизвестного угла Ø в пределах прямоугольный треугольный:
Произносится « … Soaker Toe-Er … » где: Тригонометрия — это раздел математики, занимающийся измерением
стороны и углы треугольников. Натуральные таблицы используются для преобразования значений синуса, косинуса и тангенса в фактические степени и наоборот. Формулы отношений можно транспонировать (в Opp=Hyp*Sin, A=H*C и O=A*T), так что всегда можно найти (1) угол для любой две стороны и (2) сторона, заданная углом, и одна другая сторона. В противном случае Теорема Пифагора используется для нахождения стороны данной любые другие две стороны. Одна альтернативная мнемоника для соотношений: » O h H ек
— A другой H наш O f A лгебра! » Марк Олкок никогда не забывал вариацию своего старого учителя математики. » T или O il A C ar A всегда H пр. S оме O ил H энди Для непрямоугольного треугольника разные формулы отношений apply, что приводит к другой установленной мнемонике: » plus … A ll S tations T o C печь… » Чтобы понять его значение, рассмотрим различные тригонометрические соотношения. применительно к непрямоугольным треугольникам: Правило синусов для: (1) сторона, когда известны одна сторона и два угла, или (2) угол, зная один угол и две стороны: сторона a/sin A (т.е. угол A, противоположный стороне a) Правило косинусов для: (1) третья сторона, когда известны две стороны и прилежащий к ним угол A, или (2) угол A, когда известны все три стороны: сторона a²=b²+c²-(2bc * cos A) Также в непрямоугольном треугольнике один угол может быть тупым (т. sin Ø=sin(180°-Ø) и Косинус тупого угла отрицателен, потому что угол лежит в второй квадрант воображаемой окружности. Квадрант – это четверть круга, и измерение углов в против часовой стрелки направление между радиальным начальная точка X (эквивалентно 3 на циферблате) и другая радиальная точка P на круг, значения положительные для все функции угла Ø в 1-м квадранте (P лежит между 3-12 или Ø до 90°), но только синусы во 2-м квадранте (12-9, или 90-180°), только косинусы в 3-м квадранте (9-6) и только касательные в 4-м квадранте (6-3). Все остальные функции в каждом квадранте равны отрицательный . Это резюмируется в мнемоническом предложении: . » plus … A ll S tations T o C печь. |
А прямоугольный треугольник имеет три стороны
(два под углом 90° друг к другу обычно изображаются как горизонтальные и
вертикальные стороны, а оставшаяся третья сторона является гипотенузой ). синус угла есть отношение стороны против рассматриваемый угол и гипотенуза , а
косинус того же угла есть отношение между остальными оставшимися
сторона (т.е. та, что рядом с углом ) и гипотенуза, и тангенс того же угла есть отношение между противолежащим и
смежные стороны.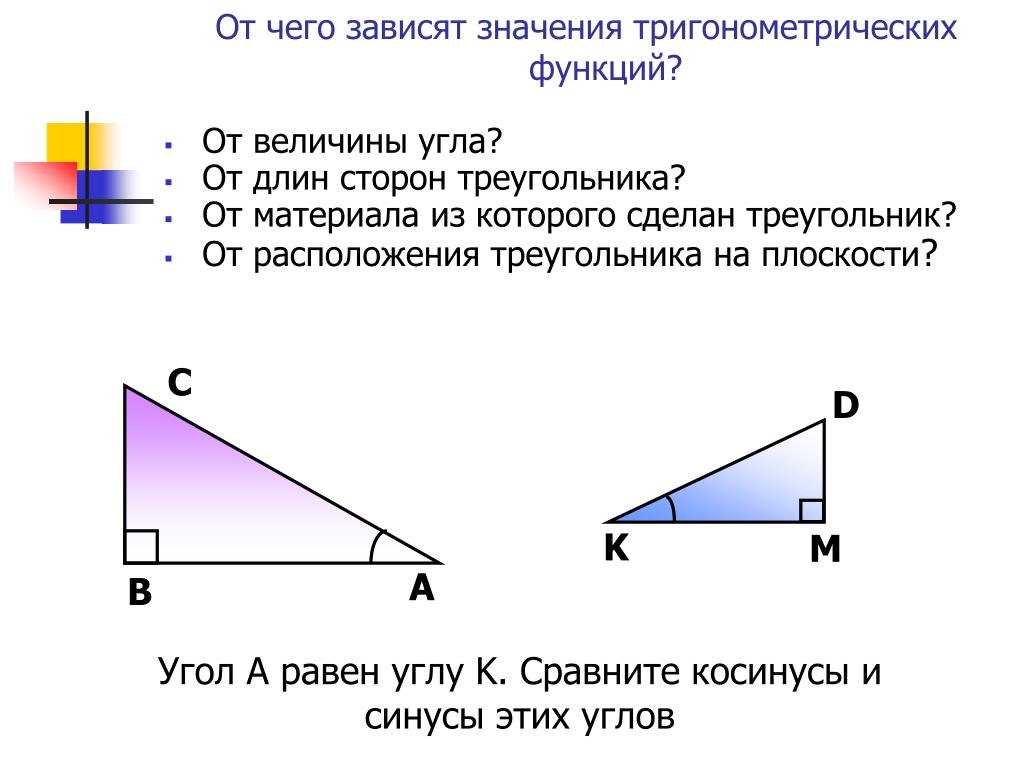
дал ему за то, что он запомнил правила tan, cos и sine таким образом…
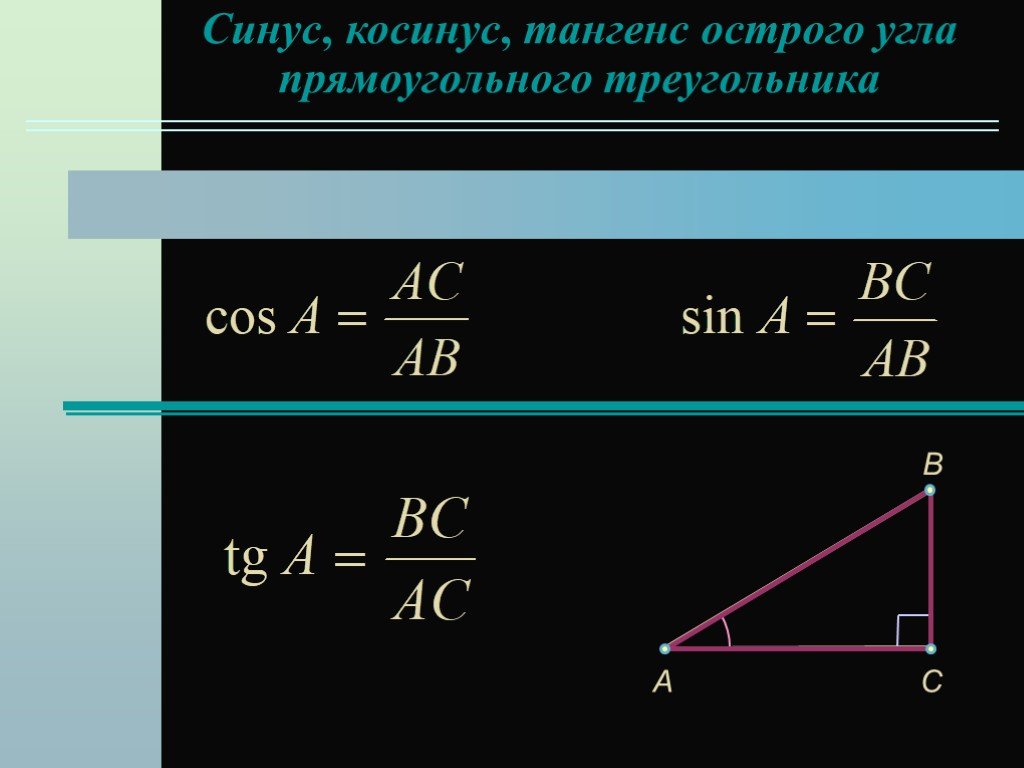е. больше 90%), после чего нужно вычесть его из
180° и сделать значение косинуса отрицательным : 