НОУ ИНТУИТ | Лекция | Матричная запись системы. Метод Гаусса. Метод Крамера. Матричный способ
< Лекция 10 || Лекция 5: 12345
Аннотация: В лекции рассмотрено использование ранее изученных методов для поиска решений системы линейных уравнений
Ключевые слова: определитель, Алгебраическим дополнением, алгебраические, коэффициенты, равенство, свободными членами, определителем системы, переменная, бесконечное множество, вывод, множитель, коэффициентами системы, система линейных уравнений, обратный, матричная форма, матрица, детерминант, совместность, расширенная матрица, выражение
Правило Крамера
Основные задачи изучения системы (3.1), «лекции 3» :
- Выяснить, является ли система (3.1) совместной или несовместной.
- Если система (3.1) совместна, то выяснить, является ли она определенной и найти решения.
Далее рассмотрим, в частности, систему трех уравнений первой степени с тремя неизвестными.
| ( 4.2) |
Составим из коэффициентов при неизвестных системы (4.2) определитель этой системы
Сложим все три полученных уравнения, умножив предварительно на соответствующие алгебраические дополнения, получим
(
4. 3) |
Коэффициенты при y и z в силу свойства определителя (см. «лекц. 1» , теорема 2) равны нулю, а коэффициент при х на основании тех же свойств (см. «лекц. 1» , теорема 1) равен , т.е. , поэтому равенство (4.3) примет вид:
| ( 4.4) |
| ( 4.5) |
Заметим, что определитель получается из определителя путем замены коэффициентов а11, а21, а31 при неизвестном х свободными членами или замены первого столбца коэффициентов при искомом х столбцом свободных членов.
| ( 4.6) |
Определители и получают из определителя системы заменой второго и третьего столбцов коэффициентов при y и z столбцом свободных членов.
Рассмотрим следующие случаи.
- . Тогда из равенств (4.4) и (4.5) находим решение системы (2) как
которые называют формулами Крамера.( 4.7) - и . Тогда система (4.2) либо не имеет решения, либо имеет бесконечное множество решений.
intuit.ru/2010/edi»>
. Тогда по крайней мере один из , или отличен от нуля и система (4.2) не имеет решения (система несовместна), что можно показать. Пусть, например, . Тогда равенство из (4.4) получаем или , что невозможно.Пример 1. Решить систему
Решение. Вычислим все определители.
Так как , то данная система имеет единственное решение, которое найдем по формулам Крамера (4.7):
т.е. (2, 0, -1) — искомое решение системы.
Решение. Вычислим определители
т.е. система решений не имеет (случай 2)
intuit.ru/2010/edi»>Пример 3. Решить системуРешение. Нетрудно убедиться в том, что и . Данная система не имеет решений, так как первое и третье уравнения противоречивы. Если умножить первое уравнение на 3 и вычесть из полученного уравнение третье, то придем к ложному равенству 0 = 3.
Пример 4. Решить систему
Решение. Нетрудно убедиться в том, что и . Так как второе уравнение получается из первого умножением на 2, то данная система равносильна системе двух уравнений относительно трех неизвестных
Так как
то можно найти решение последней системы
в которой переменная z является свободной, и, следовательно, исходная система имеет бесконечное множество решений, которое можно найти либо по формулам Крамера, либо методом исключений.
В результате получим (-5z/11; (7z+11)/11; z), где z может принимать произвольные значения.
Дальше >>
< Лекция 10 || Лекция 5: 12345
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов… Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства… Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Интересное: Искусственное повышение поверхности территории: Варианты искусственного повышения поверхности территории необходимо выбирать на основе анализа следующих характеристик защищаемой территории. Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Дисциплины:Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 2 из 5Следующая ⇒ Методом Гаусса решаются системы линейных уравнений, в которых число неизвестных может быть либо равно числу уравнений ( ), либо отлично от него ( ).
Система вида (13) называется ступенчатой, а система вида (14) – треугольной. Переход системы (2) к равносильной ей системе (13) или (14) называется прямым ходом метода Гаусса, нахождение неизвестных из последних систем – обратным ходом. Преобразования Гаусса удобно проводить, осуществляя преобразования не с самими уравнениями, а с матрицей их коэффициентов. Рассмотрим матрицу , (15) называемую расширенной матрицей системы (2), так как в ней кроме матрицы системы , дополнительно включен столбец свободных членов. 7) Векторы. Линейные операции над векторами. Направляющие косинусы и длина вектора. Условие коллинеарности двух векторов.Определение 3.1. Вектором называется направленный отрезок с начальной точкой и конечной точкой (который можно перемещать параллельно самому себе). Если даны начало вектора (точка А) и его конец (точка В), то вектор обозначается или .Определение 3.1. Длиной (или модулем) вектора называется число, равное длине отрезка , изображающего вектор. Определение 3.2. Нуль-вектором называется вектор, у которого конец совпадает с началом, он обозначается: . Направление нуль-вектора не определено. Можно считать, что нуль-вектор имеет любое желаемое в данный момент направление. Суммой двух векторов называется вектор, полученный по правилу «треугольника»: второй вектор откладывается так, чтобы его начало совпало с концом первого вектора . Суммой будет являться «замыкающий» вектор , начало которого совпадает с началом первого вектора , а конец – с концом второго вектора .
Свойства сложения векторов. 1. Коммутативный закон сложения: . 2. Ассоциативный закон сложения: . 3. . Определение 3.6. Противоположным к вектору называется такой вектор, что его сумма с равна нуль-вектору. Противоположный к вектор обозначается : . Определение 3.7. Разностью двух векторов называется сумма векторов и противоположного к : . Определение 3.8. Произведением вектора на действительное число называется вектор , коллинеарный вектору имеющий длину , направление которого совпадает с направлением вектора , если , и противоположно ему, если . Свойства умножения вектора на число. 1. Коммутативный закон: . 2. Ассоциативный закон: . 3. Дистрибутивный закон: . Доказательства этих свойств вытекают непосредственно из определения операции. Теорема 3.1. Два вектора и коллинеарны тогда и только тогда, когда или . Определение 3.9. Единичным называется вектор, длина которого равна единице. Вектор характеризуется длиной и направлением. Длина вектора (его модуль) вычисляется по формуле (8). Направление вектора в пространстве можно задать углами , которые составляет вектор с осями координат. Косинусы этих углов называются направляющими косинусами вектора. Пусть дан вектор . Тогда: ; ; , откуда: ; ; . (11) Подставляя в формулы (11) выражение (8) для , получим: ; ; (12) Возводя каждое из выражений (12) в квадрат и складывая, получим: . (13) Таким образом, среди трех углов независимыми являются только два, а третий определяется из соотношения (13). Замечание. Вектор в трехмерном пространстве задается тремя скалярными величинами. Это могут быть три координаты или два угла и длина вектора и т.д. Аналогично этому вектор в двумерном пространстве определяется двумя скалярными величинами: двумя координатами или углом и длиной и т.д. Пусть векторы и коллинеарны. В соответствии с теоремой 3.1 или , что означает для координат выполнение следующих соотношений: или . Выразив из этих равенств и приравняв, получим: или . (14) Таким образом, для того, чтобы два вектора и были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны. ⇐ Предыдущая12345Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства. Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
..
..МЕТОД ИСКЛЮЧЕНИЯ ГАУССА, МАТЕМАТИКА UNACADEMY
Исключение Гаусса в линейной и полилинейной алгебре — это процесс нахождения решений системы одновременных линейных уравнений путем сначала решения одного из уравнений для одной переменной, а затем подстановки выражения в оставшиеся уравнения. В результате получается новая система, в которой количество уравнений и переменных на единицу меньше, чем в исходной системе. Та же процедура применяется к другой переменной, и процесс редукции продолжается до тех пор, пока не останется только одно уравнение, в котором единственной неизвестной величиной является последняя переменная.
Решение уравнения позволяет «обратно заменить» значение в более раннем уравнении, которое содержит эту переменную и еще одну неизвестную, чтобы найти другую переменную. Этот процесс продолжается до тех пор, пока не будут оценены все исходные переменные. Весь процесс значительно упрощается с помощью матричных операций, которые можно выполнять с помощью компьютеров.
Метод исключения Гаусса-
Метод исключения Гаусса также называется алгоритмом сокращения строк для решения систем линейных уравнений. Он состоит из последовательности операций, выполняемых над соответствующей матрицей коэффициентов. Мы также можем использовать этот метод для оценки любого из следующего, приведенного ниже:
Ранг матрицы
Определитель данной квадратной матрицы
Обратная любая обратимая матрица
Чтобы выполнить сокращение строки на матрице, мы должны выполнить последовательность элементарных операций со строками, чтобы преобразовать любую матрицу , пока мы не получим нули (т.
е. нули) в нижнем левом углу этой матрицы, насколько это возможно. Это означает, что полученная матрица будет верхней треугольной матрицей. Есть три типа операций с элементарными строками; они следующие:
Замена двух строк местами и это может быть выражено с помощью обозначения ↔, например, R2 ↔ R3
Умножение строки на ненулевое число, например, R1 → kR2 где k — ненулевое число
Добавление кратного единице строки на другую строку, например, R2 → R2 + 3R1
Полученная матрица будет иметь вид эшелона строк. Говорят, что матрица имеет редуцированную ступенчатую форму, когда все старшие коэффициенты равны 1, а каждый столбец, содержащий старший коэффициент, имеет нули где-то еще. Эта окончательная форма будет уникальной; другими словами, он не зависит от последовательности операций над строками. Мы можем лучше понять это с помощью примеров, приведенных ниже.
Метод исключения Гаусса с примером-
Давайте посмотрим на пример метода исключения Гаусса с решением.
Вопрос: Решите следующую систему уравнений:
x + y + z = 2
x + 2y + 3z = 5
2x + 3y + 4z = 11
Решение:
Данной системой уравнений являются :
x + y + z = 2
x + 2y + 3z = 5
2x + 3y + 4z = 11
Теперь запишем эти уравнения в матричной форме.
Вычитание R1 из R2, чтобы получить новый элемент R2, то есть R2 → R2 – R1.
Отсюда получаем,
Теперь давайте проделаем еще одну операцию как R3 → R3 – 2R1
Теперь вычтите R2 из R1, чтобы получить новые элементы R1, то есть R1 → R1 – R2.
Вычтите R2 из R3, чтобы получить новые элементы R3, то есть R3 → R3 – R2.
Здесь
x – z = -1
y + 2z = 3
0 = 4
Следовательно, для данной системы уравнений существует 0 решений.
Решение системы уравнений-
Решение системы состоит в нахождении значения любого неизвестного значения, которое проверяет все уравнения, составляющие систему-
Существует единственное решение, тогда говорят, что система последовательная независимая система (СНГ).
Решений много, тогда говорят, что система является согласованной зависимой системой (CDS)
Если решений нет, то в этом случае она называется несогласованной системой (ИС).
Таким образом, решение системы уравнений методом исключения Гаусса состоит из элементарных операций над строками и столбцами расширенной матрицы для получения ее ступенчатого вида.
Заключение:
Исключение Гаусса в линейной и полилинейной алгебре — это процесс нахождения решений системы линейных уравнений для одновременной работы путем решения сначала одного из уравнений для одной переменной, а затем подстановки выражения в остальные уравнения.
В результате получается новая система, в которой количество уравнений и переменных на единицу меньше, чем в исходной системе. Та же процедура применяется к другой переменной, и процесс редукции продолжается до тех пор, пока не останется только одно уравнение, в котором единственной неизвестной величиной является последняя переменная. Решение уравнения позволяет «обратно заменить» значение в более раннем уравнении, которое содержит эту переменную и еще одну неизвестную, чтобы найти другую переменную. Этот процесс продолжается до тех пор, пока не будут оценены все исходные переменные. Весь процесс значительно упрощается с помощью матричных операций, которые можно выполнять с помощью компьютеров.
Игра на исключение Гаусса: Введение в линейную алгебру | Бретт Берри | Math Hacks
Прыжок из алгебры в страну матриц 🎉
Подпишитесь на Math Hacks в Instagram C исповедь: я люблю линейную алгебру. Ладно, может, это и не очень похоже на признание, но мне это нравится! Во многом из-за того, что линейная алгебра не похожа на остальную математику, она кажется загадкой.
Это может звучать безумно, но выслушайте меня.
Эта новая земля матриц и векторов может выглядеть и ощущаться пугающей, и на то есть веские причины: новые обозначения, новые правила, новые свойства. Все немного по-другому. Но, возможно, рассматривая это как головоломку, вы сможете преодолеть это новое препятствие в обозначениях.
Готовы попробовать?
Я считаю, что лучше всего начать с линейной алгебры с решения систем уравнений , потому что это то, что вы, вероятно, уже изучили. Помните методы замены и исключения?? Они звонят в колокол? Если нет, вы можете освежить свою память здесь. 🙂
Сегодня мы рассмотрим новый подход к решению систем уравнений, используя метод под названием Исключение Гаусса.
Что такое исключение Гаусса??
Исключение Гаусса — это метод, при котором мы переводим наши уравнения в матрицу и используем матрицу для решения системы (т.е. находим решения для каждой переменной, которые делают все уравнения верными).
Сегодня я шаг за шагом проведу вас через упрощенный пример (числа хорошо работают, так что шагов гораздо меньше!). Если вам нужен более подробный пример, посмотрите мой учебник на YouTube по исключению Гаусса ниже ⬇
Нажмите здесь, чтобы подписаться на «Математические лайфхаки» на YouTube 🎥Точно так же, как мы начинаем карточную игру путем перетасовки и раздачи карт, начало нашей игры «Исключение по Гауссу» начинается с преобразования наших уравнений в матрицу.
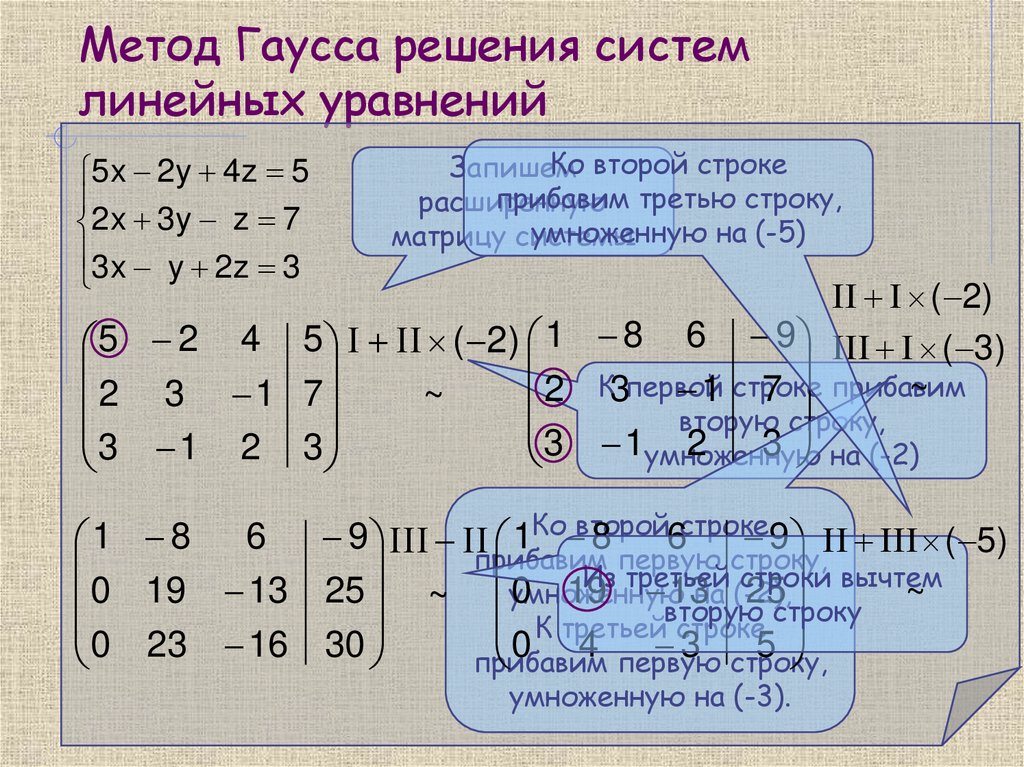
Вот система, которую мы собираемся решить:
Самое первое, что вам нужно понять, это то, что в нашей системе много скрытой информации. Красным цветом я добавлю нули и единицы заполнителя.
Далее мы отделим всю важную числовую информацию от посторонних символов. Теперь, выделенное красным цветом, вы найдете всю важную информацию, с которой мы будем работать:
Нам нужно переписать приведенные выше числовые значения в виде матрицы. Мы опустим буквы, знаки равенства и символы сложения (но не символы минус!) и просто напишем числа в точном порядке и в тех строках, в которых они указаны выше.
После этого мы добавим большие квадратные скобки, чтобы сгруппировать их вместе. Это наша матрица:
Как и в любой игре, мы должны соблюдать несколько правил:
- Вы можете поменять местами любые две строки
- Вы можете умножать или делить любую строку на значение
- Вы можете складывать или вычитать вместе любые две строки
*Примечание: вы можете комбинировать эти правила одним ходом.
Не волнуйтесь, если это пока не совсем понятно. Вы увидите, как они работают, когда мы будем работать с нашим примером.
Вы выигрываете, когда ваша матрица выглядит так:
Где символы # представляют собой любые числа, а остальная часть матрицы имеет нули во всех позициях, кроме диагональных. это называется Форма эшелона с уменьшенным рядом.
Начните с матрицы, которую вы создали на этапе настройки. Теперь мы собираемся использовать правила, чтобы довести эту матрицу до финиша!
Начальная матрицаХод 1: Поменять местами первую и вторую строки
Есть много разных способов привести эту матрицу в выигрышную форму, но я думаю, что самый простой способ начать — это поменять местами первую и вторую строки.
Таким образом, мы получаем 1 в первой позиции первой строки и 0 в первой позиции второй строки.
Шаг 2: прибавьте -2 раза ко второй строке к третьей строке
Одна вещь, которую мы можем сделать, это использовать несколько правил вместе за один шаг. В этом шаге мы умножим -2 на вторую строку и добавим эти продукты в третью строку. Это оставит вторую строку без изменений, но поможет нам получить ноль во второй позиции третьей строки.
Ход 3: Разделить третью строку на -3
Далее мы просто разделим третью строку на -3, чтобы получить 1 в третьей позиции третьей строки.
Движение 4: добавьте -2 раза к третьему ряду ко второму ряду
Теперь, когда у нас есть все нули в нижнем левом углу, окруженные диагональю 1, мы готовы начать работать над получением нулей в позициях над единицами.
👉 Но прежде чем мы это сделаем, я хочу сделать небольшое примечание: наша матрица в настоящее время находится в форме эшелона строк.
В этой форме вы можете перевести свою матрицу обратно в набор уравнений, если хотите, и легко сможете найти x, y и z. Сегодня мы работаем над преобразованием нашего уравнения в уменьшил форму эшелона строк , что означает, что мы хотим получить нули в позициях над единицами. Часто в линейной алгебре вас будут просить работать до сокращенной формы эшелона строк, поскольку это самая простая форма для чтения ответа.Хорошо, вернемся к нашей математике. В следующем шаге мы возьмем -2, умноженное на третью строку, и добавим ее ко второй строке, чтобы мы могли получить 0 в третьей позиции строки 2.
Шаг 5: добавить третью строку в первую строку
Далее , мы просто добавим третью строку к первой, поскольку -1 + 1 = 0, что поможет нам получить 0 в третьей позиции первой строки.
Ход 6: прибавим -2 раза ко второй строке к первой строке
Наконец, мы добавим -2 раза ко второй строке к первой строке, чтобы получить ноль во второй позиции первой строки.