Матрица 2х2
Обращение матрицы 2х2 возможно только при условии, что .
С помощью матрицы алгебраических дополнений
CT — транспонированная матрица алгебраических дополнений;
Полученная
матрица A−1 и
будет обратной. Сложность алгоритма
зависит от сложности алгоритма расчета
определителя Odet и
равна O(n²)·Odet.
Иначе говоря, обратная
матрица равна единице, делённой
на определитель исходной
матрицы и умноженной на транспонированную
матрицу алгебраических
дополненийэлементов
исходной матрицы. Ма́тричный
метод решения
(метод решения через обратную
матрицу) систем
линейных алгебраических уравнений с
ненулевым определителем состоит
в следующем.
Тогда её можно переписать в матричной форме: AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим
это матричное уравнение слева на A −
1 —
матрицу, обратную к матрице A:
Так как A −
1A = E,
получаем X = A −
1B.
Правая часть этого уравнения даст
столбец решений исходной системы.
Условием применимости данного метода
(как и вообще существования решения
неоднородной системы линейных уравнений
с числом уравнений, равным числу
неизвестных) является невырожденность матрицы
A.
Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0.
Пример решения неоднородной слау
Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.
Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.
Далее
найдём союзную
матрицу, транспонируем её
и подставим в формулу для нахождения
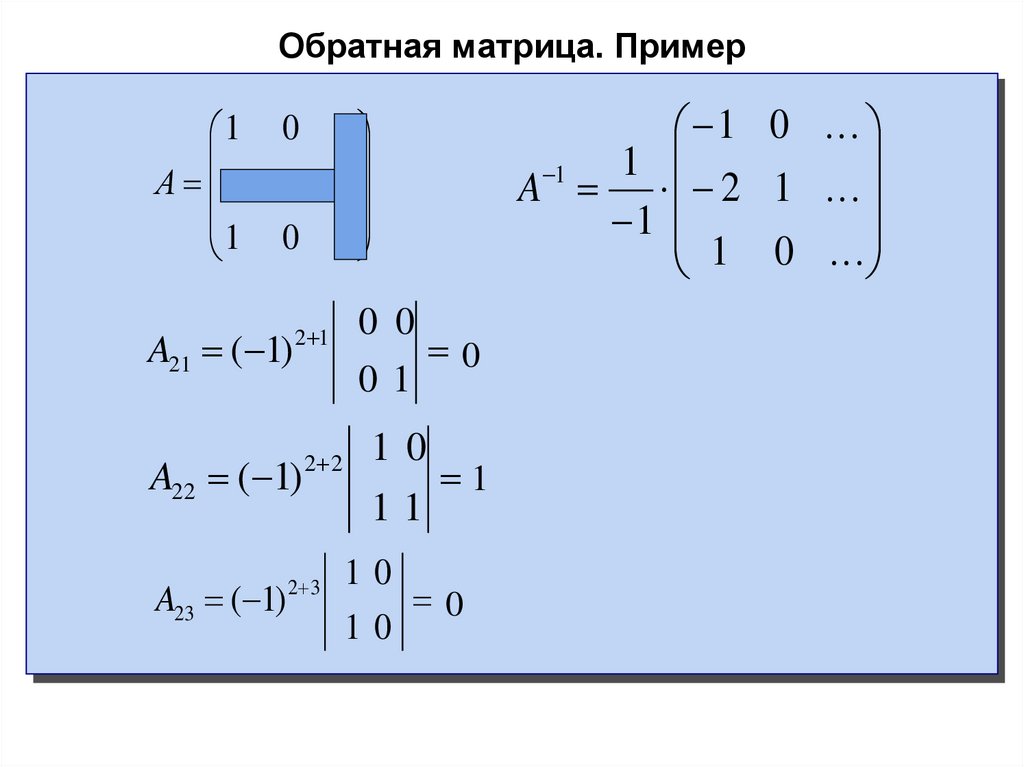
Подставляя переменные в формулу, получаем:
Осталось
найти неизвестные. Для этого перемножим обратную
матрицу и
столбец свободных членов.
Для этого перемножим обратную
матрицу и
столбец свободных членов.
Итак, x=2; y=1; z=4.
Вопрос 6.
Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы (причём для таких уравнений решение существует и единственно).
Метод Крамера состоит в том, что 1. мы последовательно находим главный определитель системы , т.е. определитель матрицы А
= det А
2. Вычисление n вспомогательных определителей i (i= ), которые получаются из определителя заменой i-го столбца столбцом свободных членов.
3. вычисление значения неизвестных x i = i / . Формула Крамера i
Если
главный определитель системы и
все вспомогательные определители i =
0 (i=
),
то система имеет бесчисленное множество
решений. Если главный определитель
системы =
0, а хотя бы один вспомогательный
определитель отличен от нуля, то система
несовместна.
Если главный определитель
системы =
0, а хотя бы один вспомогательный
определитель отличен от нуля, то система
несовместна.
Пример. Решить методом Крамера систему уравнений:
x1 + x2 + x3 + x4 = 5, x1 + 2x2 — x3 + 4x4 = -2, 2x1 — 3x2 — x3 — 5x4 = -2, 3x1 + x2 +2x3 + 11 x4 = 0. Решение. Главный определитель этой системы
значит, система имеет единственное решение. Вычислим вспомогательные определители i ( i = ), получающиеся из определителя путем замены в нем столбца, состоящего из коэффициентов при xi, столбцом из свободных членов:
Отсюда
x1 = 1/ =
1, x2 = 2/ =
2, x3 = 3/ =
3, x4 = 4/ =
-1, решение системы — вектор С=(1, 2, 3, -1)T.
Вопрос 7. Ме́тод Га́усса — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которого последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Метод состоит из 2х частей: 1) Прямой ход. Путем элементарных преобразований строк расширенной матрицы привести основную матрицу к треугольному виду.
2) Обратный ход. Путем движения по преобразованной системе снизу вверх выразить значения переменных.
Пример. Решить систему уравнений методом Гаусса: x + y — 3z = 2, 3x — 2y + z = — 1, 2x + y — 2z = 0. Решение. Выпишем расширенную матрицу данной системы
и произведем следующие элементарные преобразования над ее строками:
а) из ее второй и третьей строк вычтем первую, умноженную соответственно на 3 и 2:
~ ;
б) третью строку умножим на (-5) и прибавим к ней вторую:
.
В результате всех этих преобразований данная система приводится к треугольному виду: x + y — 3z = 2, -5y + 10z = -7, — 10z = 13. Из последнего уравнения находим z = -1,3. Подставляя это значение во второе уравнение, имеем y = -1,2. Далее из первого уравнения получим x = — 0,7.
алгоритм вычисления обратной матрицы
Вы искали алгоритм вычисления обратной матрицы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и инверсия матрицы, не
исключение.
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как алгоритм вычисления обратной матрицы,инверсия матрицы,как вычислить матрицу обратную,как вычислить обратную матрицу,как искать обратную матрицу,как найти обратную матрицу 2 на 2,как найти обратную матрицу 2х2,как найти обратную матрицу 3 на 3 пример с решением,как найти обратную матрицу методом присоединенной матрицы,как найти союзную матрицу,как находить матрицу обратную,как находить обратную матрицу,как находить обратные матрицы,как обратить матрицу 3 на 3,как посчитать обратную матрицу,как решать обратная матрица,как решать обратную матрицу,как решать обратные матрицы,как сделать проверку матрицы,как сделать проверку обратной матрицы,как считать обратную матрицу,какая матрица называется обратной,матпрофи обратная матрица,матрица обратная матрица примеры,матрица обратная матрица примеры с решением,матрицы инверсия,методом гаусса найти обратную матрицу,методом присоединенной матрицы найти обратные для следующих матриц,методы нахождения обратной матрицы,найти обратную матрицу методом гаусса,найти обратную матрицу пример,обратная матрица 3 порядка,обратная матрица второго порядка,обратная матрица матпрофи,обратная матрица метод гаусса,обратная матрица методом гаусса,обратная матрица методом гаусса примеры,обратная матрица пример,обратная матрица примеры,обратная матрица примеры с решением,обратной матрицы примеры,обратные матрицы как находить,обратные матрицы как решать,обратные матрицы примеры,пример найти обратную матрицу,примеры обратная матрица,способы нахождения обратной матрицы,формула обратной матрицы имеет вид,элементы обратной матрицы это.
Решить задачу алгоритм вычисления обратной матрицы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Обратная матрица 2×2 — Формула, ярлык, сопряженная 2×2
Прежде чем перейти к тому, как найти обратную матрицу 2×2, давайте вспомним значение обратной. В общем, инверсия действительного числа — это число, которое при умножении на данное число дает мультипликативную идентичность, равную 1. В матрицах инверсия матрицы A (обозначается A -1 ) равна матрица, которая при умножении на A дает единичную матрицу I. т. е. AA -1 = A -1 A = I. Но как найти обратную матрицу 2×2?
В матрицах инверсия матрицы A (обозначается A -1 ) равна матрица, которая при умножении на A дает единичную матрицу I. т. е. AA -1 = A -1 A = I. Но как найти обратную матрицу 2×2?
Давайте посмотрим формулу для нахождения обратной матрицы 2×2, а также некоторые другие способы ее нахождения. Здесь мы также можем увидеть несколько примеров нахождения обратной матрицы 2×2.
| 1. | Что является обратной матрицей 2×2? |
| 2. | Обратная формула матрицы 2×2 |
| 3. | шагов, чтобы найти обратную матрицу 2×2 |
| 4. | Нахождение обратной матрицы 2×2 с помощью операций со строками |
| 5. | Система решения уравнений 2×2 с использованием обратной |
| 6. | Часто задаваемые вопросы об обратной матрице 2×2 |
Что является обратной матрицей 2×2?
, обратная матрице 2×2 , скажем, A, является матрицей того же порядка, обозначаемой A -1 такое, что AA -1 = A -1 A = I, где I — единичная матрица порядка 2×2. т. е. I = \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{array}\right]\). Как правило, обратная матрица A находится по формуле (adj A)/(det A), где «adj A» — это «сопряженная матрица A», а «det A» — «детерминант A». Но в случае матрицы 2×2 A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), мы можем найти обратную, используя следующую формулу.
т. е. I = \(\left[\begin{array}{rr}1 & 0 \\ \\ 0 & 1 \end{array}\right]\). Как правило, обратная матрица A находится по формуле (adj A)/(det A), где «adj A» — это «сопряженная матрица A», а «det A» — «детерминант A». Но в случае матрицы 2×2 A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), мы можем найти обратную, используя следующую формулу.
Примечание: Поскольку ad — bc находится в знаменателе, он НЕ должен быть равен 0 для определения A -1 . т. е.
- Если ad — bc = 0, то A -1 НЕ существует, и в этом случае мы называем A сингулярной матрицей.
- Если ad — bc ≠ 0, то A -1 существует, и в этом случае мы называем A невырожденной матрицей.
Здесь мы подробно рассмотрим процесс нахождения определителя и сопряженной матрицы 2×2.
Определитель матрицы 2×2
Формула, обратная формуле матрицы 2×2, использует определитель матрицы. Мы знаем, что определитель матрицы 2×2 A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\) равен det(A) = объявление-BC . то есть, чтобы найти определитель, мы просто умножаем элементы каждой из двух диагоналей и вычитаем (произведение элементов главной диагонали является уменьшаемым).
то есть, чтобы найти определитель, мы просто умножаем элементы каждой из двух диагоналей и вычитаем (произведение элементов главной диагонали является уменьшаемым).
Примеры:
- Определитель A = \(\left[\begin{array}{rr}3 & 2 \\ \\ 1 & 5 \end{array}\right]\) = (3 × 5) — (2 × 1) = 15 — 2 = 13.
- Определитель B = \(\left[\begin{array}{rr}1 & -1 \\ \\ 0 & 2 \end{array}\right]\) = (1 × 2) — (-1 × 0) = 2 — 0 = 2,
Сопряженная матрица 2×2
Сопряженная матрица A является транспонированной матрицей кофакторов A. Но для нахождения сопряженной матрицы 2×2 нам не нужно мучиться с поиском кофакторов. Есть трюк, чтобы найти сопряженную матрицу 2×2. Для матрицы A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\) сопряженным является adj(A) = \(\ left[\begin{array}{rr}d & -b \\ \\ -c & a \end{массив}\right]\). т. е. найти сопряженную матрицу
- Поменять местами элементы главной диагонали.
- Просто поменять (но НЕ поменять местами) знаки элементов другой диагонали.

Пример: Сопряженным к матрице A = \(\left[\begin{array}{rr}3 & 2 \\ \\ 1 & 5 \end{array}\right]\) является adj A = \(\left[\begin{array}{rr}5 & -2 \\ \\ -1 & 3 \end{array}\right]\).
Обратная формула матрицы 2×2
Обратная любая матрица A находится по формуле A -1 = (adj A)/(det A). Мы уже знаем, как найти adj A и det A для матрицы 2×2. Для любой матрицы 2×2 A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), adj A = \(\left[\begin {массив}{rr}d & -b \\ \\ -c & a \end{массив}\right]\) и det A = 1/(ad — bc). Подставив эти значения в формулу A -1 = (adj A)/(det A),
- A -1 = [1/(ad — bc)] \(\left[\begin{array} {rr}d & -b \\ \\ -c & a \end{массив}\right]\)
Пример: Обратная матрица 2×2 A = \(\left[\begin{array}{rr}3 & 2 \\ \\ 1 & 5 \end{array}\right]\) равна
A -1 = [1/(3×5 — 2×1)] \(\left[\begin{array}{rr}5 & -2 \\ \\ -1 & 3 \end{массив} \right]\)
= (1/13) \(\left[\begin{array}{rr}5 & -2 \\ \\ -1 & 3 \end{массив}\right]\)
= \(\left[\begin{array}{rr}5/13 & -2/13 \\ \\ -1/13 & 3/13 \end{массив}\right]\)
шага, чтобы найти обратную матрицу 2×2
Мы уже видели формулу для нахождения обратной матрицы 2×2. Мы можем либо использовать эту формулу, либо просто выполнить следующие шаги вместо формулы, чтобы найти обратную матрицу 2×2. Шаги объяснены на примере, где мы собираемся найти обратную величину A = \(\left[\begin{array}{rr}1 & -1 \\ \\ 0 & 2 \end{array}\right] \).
Мы можем либо использовать эту формулу, либо просто выполнить следующие шаги вместо формулы, чтобы найти обратную матрицу 2×2. Шаги объяснены на примере, где мы собираемся найти обратную величину A = \(\left[\begin{array}{rr}1 & -1 \\ \\ 0 & 2 \end{array}\right] \).
- Шаг — 1: Найдите det A, просто перемножая элементы и вычитая их. Обратите внимание, что сначала нужно произвести произведение элементов главной диагонали.
det A = (1 × 2) — (-1 × 0) = 2 — 0 = 2, - Шаг — 2: Найдите adj A, поменяв местами элементы главной диагонали и знаки другой диагонали.
прил A = \(\left[\begin{array}{rr}2 & 1 \\ \\ 0 & 1 \end{array}\right]\). - Шаг — 3: Найдите обратную величину A по формуле A -1 = (adj A) / (det A) . т. е. разделить каждый элемент adj A на det A.
А -1 = \(\left[\begin{массив}{rr}2/2 и 1/2 \\ \\ 0/2 и 1/2 \end{массив}\right]\) = \(\ влево[\begin{массив}{rr}1 и 1/2 \\ \\ 0 и 1/2 \end{массив}\вправо]\)
Поиск обратной матрицы 2×2 с помощью операций со строками
Мы можем использовать элементарные операции со строками, чтобы найти обратную матрицу 2×2, A.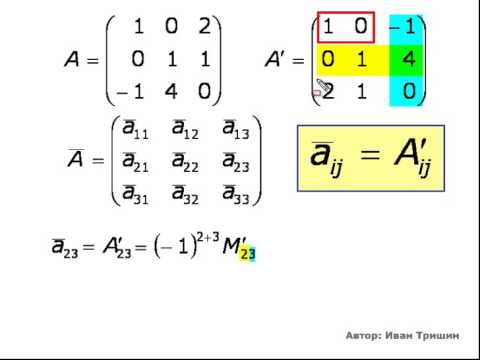 Процесс поясняется ниже на примере.
Процесс поясняется ниже на примере.
- Сначала запишем A и I (тождественная матрица порядка 2×2) как расширенную матрицу, разделенную линией, так что A находится слева, а I — справа.
- Применить операции со строками, чтобы левая матрица стала единичной матрицей I.
- Тогда правая матрица равна A -1 .
Система решения уравнений 2×2 с использованием обратной
Мы можем решить систему уравнений, используя обратную матрицу. Шаги, чтобы сделать то же самое, объясняются здесь с примером. Рассмотрим систему уравнений 2×2 x + 2y = 5 и 3x — 5y = -7.
- Шаг — 1: Запишите систему в виде AX=B.
\(\left[\begin{array}{rr}1 & 2 \\ \\ 3 & -5 \end{array}\right]\) \(\left[\begin{array}{rr}x \\ \\ y \end{массив}\right]\) = \(\left[\begin{array}{rr}5 \\ \\ -7 \end{массив}\right]\)
Здесь A = \(\left[\begin{array}{rr}1 & 2 \\ \\ 3 & -5 \end{array}\right]\), X = \(\left[\begin{array }{rr}x \\ \\ y \end{array}\right]\), и B = \(\left[\begin{array}{rr}5 \\ \\ -7 \end{array}\ Правильно]\).
- Шаг — 2: Найдите обратную матрицу 2×2. т. е. найти A -1 .
A -1 = [1/(1 × -5 — 2 × 3)] \(\left[\begin{array}{rr}-5 & -2 \\ \\ -3 & 1 \end{массив }\right]\) = \(\left[\begin{array}{rr}5/11 & 2/11 \\ \\ 3/11 & -1/11 \end{array}\right]\) - Шаг — 3: Найдите матрицу решения X, используя X = A -1 B.
X = \(\left[\begin{array}{rr}5/11 и 2/11 \\ \\ 3/11 & -1/11 \end{массив}\right]\) \(\left[\ begin{массив}{rr}5 \\ \\ -7 \end{массив}\right]\)
\(\left[\begin{array}{rr}x \\ \\ y \end{массив}\right]\)= \(\left[\begin{array}{rr}(25/11)+( -14/11) \\ \\ (15/11+7/11) \end{массив}\right]\)
\(\left[\begin{array}{rr}x \\ \\ y \end{array}\right]\)= \(\left[\begin{array}{rr}1 \\ \\ 2 \ конец {массив}\справа]\)
Следовательно, x = 1 и y = 2 являются решением данной системы уравнений.
Важные моменты об обратной матрице 2×2:
Вот несколько важных моментов об обратной матрице 2×2.
- A -1 не существует, когда det A = 0, т. е. матрица обратима, только если det A ≠ 0.
- Если A -1 является обратным A, то AA -1 = A -1 A = I.
- Обратная единичная матрица есть она сама. т. е. I -1 = I.
- -1 используется для решения системы уравнений.
☛ Связанные темы:
- Умножение матриц
- Формула матрицы
- Обратная матрица 3×3
- Калькулятор обратной матрицы 2×2
Часто задаваемые вопросы об обратной матрице 2×2
Что является обратной матрицей 2×2?
, обратная матрице 2×2 A, обозначается A -1 , где AA -1 = A -1 A = I. Если A = \(\left[\begin{array}{rr }a & b \\ \\ c & d \end{array}\right]\), тогда A -1 = [1/(ad — bc)] \(\left[\begin{array}{rr }d & -b \\ \\ -c & a \end{массив}\right]\).
Как найти обратную матрицу 2 на 2?
Чтобы найти обратную матрицу 2×2 A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\),
- Найти det A = объявление — до н.э.
- Найдите прил. A = \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\).
- Используйте формулу A -1 = (adj A)/(det A).
Что является примером матрицы 2×2 без обратной?
Матрица не имеет обратной, если ее определитель равен 0. A = \(\left[\begin{array}{rr}1 & 2 \\ \\2 & 4 \end{array}\right]\) является матрица без обратной, поскольку det A = (1 × 4) — (2 × 2) = 4 — 4 = 0,
Как найти обратную матрицу 2×2?
Если A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), то adj A можно найти, просто заменив главное диагональных элементов и изменением знаков других диагональных элементов. Кроме того, det A = ad — bc. Затем используйте A -1 = (adj A) / (det A).
Как найти обратную матрицу 2×2 с помощью сопряженной?
Если A является матрицей 2×2, ее обратной является A -1 = (adj A)/(det A).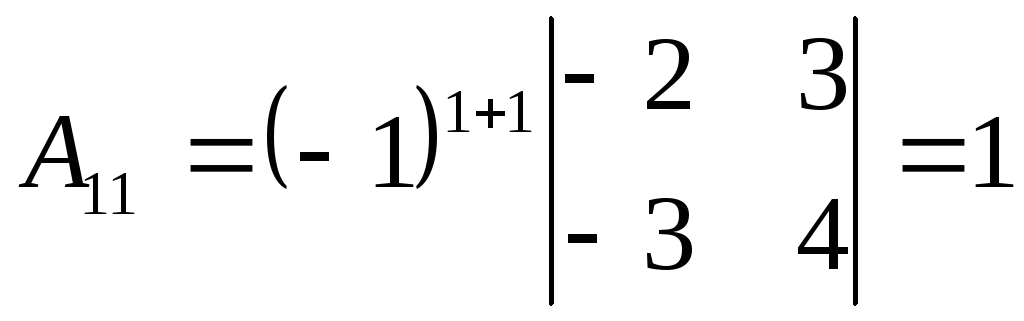 Если A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), то
Если A = \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\), то
- дет A = ad — bc
- прил A = \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\)
- A -1 = (adj A)/(det A) = [1/(ad — bc)] \(\left[\begin{array}{rr}d & -b \\ \\ -c & а \конец{массив}\справа]\)
Как найти обратную матрицу 2×2 с помощью определителя?
Определитель матрицы 2×2 \(\left[\begin{array}{rr}a & b \\ \\ c & d \end{array}\right]\) равен ad — bc. Его инверсия: [1/(ad — bc)] \(\left[\begin{array}{rr}d & -b \\ \\ -c & a \end{array}\right]\).
Есть ли у матрицы 2×2 обратная сторона?
Матрица 2×2 имеет обратную форму, только если ее определитель отличен от нуля. Если она равна нулю, то матрица не имеет обратной, и в этом случае она называется сингулярной матрицей.
Как найти обратную матрицу 2×2 с помощью элементарных операций со строками?
Чтобы найти обратную матрицу 2×2 A с помощью элементарных операций со строками,
- Запишите A и I (единичную матрицу) в одну матрицу, разделенную линией.

- Примените операции со строками, чтобы сделать левую матрицу равной I. 9{ – 1 } $, так что умножение матрицы на обратную дает единичную матрицу $ I $.
В этом уроке мы кратко рассмотрим, что такое обратная матрица, найдем обратную матрицу $ 2 \times 2 $ и формулу обратной матрицы $ 2 \ times 2 $. Там будет много примеров для вас, чтобы посмотреть. Проблемы с практикой последуют. Приятного обучения!
Что такое обратная матрица?
В матричной алгебре обратная матрица играет ту же роль, что и обратная величина в системах счисления. Обратная матрица — это матрица, на которую мы можем умножить другую матрицу, чтобы получить единичную матрицу (матричный эквивалент числа $1$) ! Чтобы узнать больше о матрице идентичности, пожалуйста, проверьте здесь.
Рассмотрим матрицу $ 2 \times 2 $, показанную ниже:
$ A = \begin{bmatrix} { a } & { b } \\ { c } & { d } \end {bmatrix} $
Мы обозначим , обратную этой матрицы, как $ A^{ – 1 } $ .

Мультипликативная обратная (обратная) в системе счисления и обратная матрица в матрицах играют одну и ту же роль. Кроме того, единичная матрица ($I$) (в области матриц) играет ту же роль, что и число один ($1$).
Как найти обратную матрицу 2 x 2
Так как же найти обратную матрицу $ 2 x 2 $?
Чтобы найти обратную матрицу, мы можем использовать формулу, которая требует выполнения нескольких пунктов перед ее использованием.
Чтобы матрица имела обратную , она должна удовлетворять $ 2 $ условиям:
- Матрица должна быть квадратной матрицей (количество строк должно быть равно количеству столбцов).
- Определитель матрицы (это скалярное значение матрицы из нескольких операций над ее элементами) не может быть $ 0 $.
Помните, что не все квадратные матрицы имеют обратную. Матрица, определитель которой равен $0$, не равна обратимая (не имеет обратной) и известна как сингулярная матрица .

Подробнее о сингулярных матрицах читайте здесь!
Мы рассмотрим изящную формулу для нахождения обратной матрицы $ 2 \times 2 $ ниже.
Формула обратной матрицы 2 x 2
Рассмотрим матрицу $ 2 \times 2 $, показанную ниже:
$ A = \begin{bmatrix} { a } & { b } \\ { c } & { d } \ end {bmatrix} $
Формула для обратной 9{ – 1 } = \frac{ 1 }{ad – bc} \begin{bmatrix} d & { – b } \\ { – c } & a \end {bmatrix} $
Количество $ ad – bc $ известен как определитель матрицы. Подробнее об определителе матриц $2\times2$ читайте здесь.
Другими словами, чтобы вычислить обратное, мы меняем местами $a$ и $d$, инвертируем $b$ и $c$ и делим результат на определитель матрицы!
Вычислим обратную матрицу $ 2 \times 2 $ ( Матрица $ B $ ), показанную ниже:
$ B = \begin{bmatrix} { 4 } & { – 2 } \\ { 3 } & { – 4 } \end {bmatrix} $
Прежде чем вычислять обратное значение, мы должны проверить $ 2 $ условия изложены выше.

- Это квадратная матрица?
Да, это квадратная матрица $ 2 \times 2 $!
- Определитель равен $ 0 $?
Вычислим определитель матрицы $ B $, используя формулу определителя для матрицы $ 2 \times 2 $. 9{ – 1 } = \begin{bmatrix} { – \frac{ 1 }{ 85 } } & { \ frac{ 5 }{ 34 } } \\ { – \ frac{ 3 }{ 17 } } & { – \ frac { 5 }{ 17 } } \end {bmatrix} $
Пример 2Дано $ A= \begin{bmatrix} 0 & { – 4 } \\ { – 1 } & 1 \end {bmatrix } $ and $ B= \begin{bmatrix} -\frac{ 1 }{ 4 } & -1 \\ -\frac{ 1 }{ 4 } & 0 \end {bmatrix}$, подтвердите, что матрица $ B $ обратная матрица $A$.
РешениеЧтобы матрица $B$ была обратной матрице $,A$, умножение матриц между этими двумя матрицами должно привести к единичной матрице (единичная матрица $2\times 2$). Если да, то $B$ является инверсией $A$.
Проверим:
$ A\times B= \begin{bmatrix} 0 & { – 4 } \\ { – 1 } & 1 \end {bmatrix} \times \begin{bmatrix} -\frac{ 1 } { 4 } & -1 \\ -\frac{ 1 }{ 4 } & 0 \end {bmatrix} $
$ = \begin{bmatrix} (0)(-\frac{1}{4}) + ( -4)(-\frac{1}{4}) & (0)(-1) + (-4)(0) \\ (-1)(-\frac{1}{4}) + (1 )(-\frac{1}{4}) & (-1)(-1) + (1)(0) \end {bmatrix} $
$ = \begin{bmatrix} { 1 } & { 0 } \\ { 0 } & { 1 } \end {bmatrix} $
9{– 1} $.
- Найдите обратную матрицу $ C $, показанную ниже:
$ C = \begin{bmatrix} { 2 } & { 1 } \\ { – 2 } & { 2 } \\ { 1 } & 7 \end {bmatrix } $ - Учитывая $ J = \begin{bmatrix} 1 & { 3 } \\ { – 2} & – 10 \end {bmatrix} $ и $ K = \begin{bmatrix} \frac{ 5 }{ 2 } & \frac{ 4 }{ 3 } \\ – \frac{ 1 }{ 2 } & – \frac{ 1 }{ 4 } \end {bmatrix} $, подтвердите, является ли матрица $ K $ обратной матрице $ J $.
- Эта матрица не имеет обратной .
Почему?
Потому что его определитель равен $ 0 $!Напомним, что определитель не может быть равен $0$, чтобы матрица имела обратную. Проверим значение определителя:
$ | Б | = ad – bc = ( – 4 )( 6 ) – ( 12 )( -2 ) = – 24 +24 = 0 $
Таким образом, эта матрица будет иметь обратную , а не !
- Эта матрица не имеет обратной .
 Напомним, что только квадратные матрицы имеют обратные ! Это , а не квадратная матрица. Это матрица $3\times 2$ с $3$ строками и $2$ столбцами. Таким образом, мы не можем вычислить обратную матрицу $C$.
Напомним, что только квадратные матрицы имеют обратные ! Это , а не квадратная матрица. Это матрица $3\times 2$ с $3$ строками и $2$ столбцами. Таким образом, мы не можем вычислить обратную матрицу $C$. Чтобы матрица $K$ была обратной матрице $J$, умножение матриц между этими двумя матрицами должно привести к единичная матрица ($ 2 \times 2 $ единичная матрица). Если да, то $K$ является инверсией $J$.
Проверим:
$ J\times K = \begin{bmatrix} 1 & { 3 } \\ { – 2} & – 10 \end {bmatrix} \times \begin{bmatrix} \frac{ 5 }{ 2 } & \frac{ 4 }{ 3 } \\ – \frac{ 1 }{ 2 } & – \frac{ 1 }{ 4 } \end {bmatrix} $
$ = \begin{bmatrix} (1) ( \ frac { 5 }{ 2 } ) + ( 3 ) ( — \ frac { 1 }{ 2 }) & ( 1 ) (\ frac { 4 }{ 3 } ) + ( 3 ) (- \ frac { 1 } { 4 } ) \\ ( – 2 )( \ frac { 5 }{ 2 } ) + (- 10 )(- \ frac { 1 }{ 2 } ) & (- 2 )(\ frac { 4 }{ 3 } ) + (- 10 )(- \frac{ 1 }{ 4 } ) \end {bmatrix} $
$ = \begin{bmatrix} { \frac{ 5 }{ 2 } – \ frac{ 3 }{ 2 } } & { \ frac{ 4 }{ 3 } – \ frac{ 3 }{ 4 } } \\ { – 5 + 5 } & { – \frac{ 8 }{ 3 } + \frac{ 5 }{ 2 } } \end {bmatrix} $
$ = \begin{bmatrix} { 1 } & { \frac{ 7 }{ 12 } } \\ { 0 } & { – \frac{ 1 }{ 6 } } \end {bmatrix} $
Это , а не $ 2 \times 2 $ единичная матрица!
Таким образом, Матрица $K$ НЕ является обратной Матрице $J$.

Ответы
- 9{ – 1 } = \begin{bmatrix} \frac{ 2 }{ 19 } & \frac{ 12 }{ 19 } \\ – \frac{ 36 }{ 19 } & \frac{ 12 }{ 19 } \end { bmatrix} $







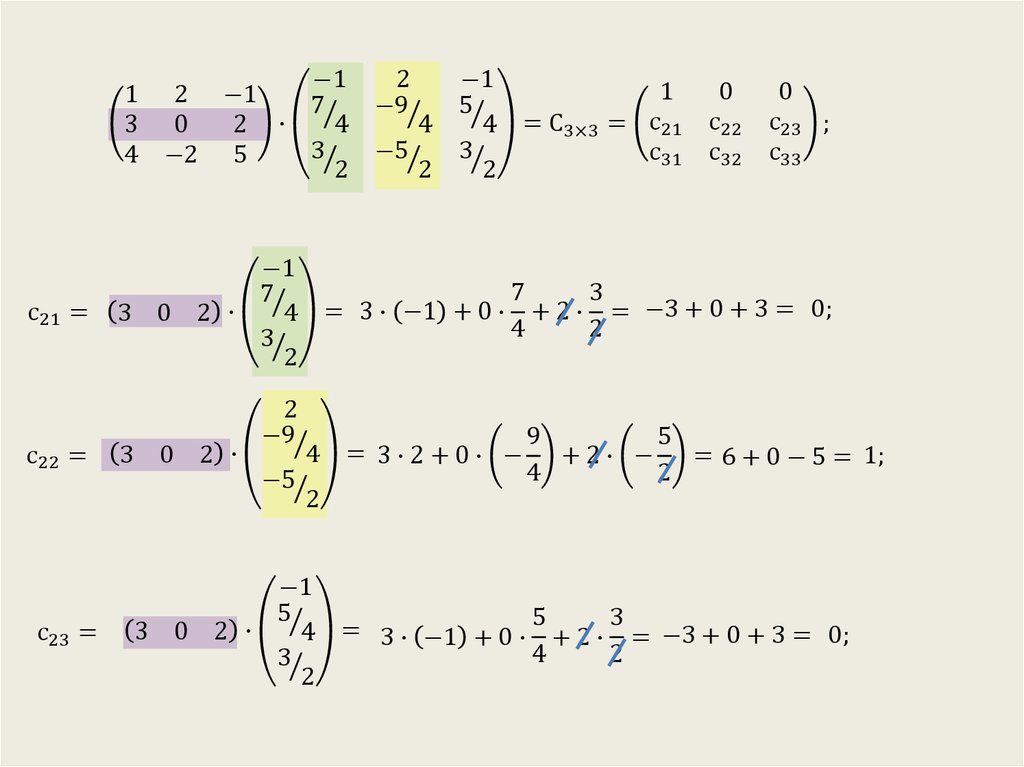 Напомним, что только квадратные матрицы имеют обратные ! Это , а не квадратная матрица. Это матрица $3\times 2$ с $3$ строками и $2$ столбцами. Таким образом, мы не можем вычислить обратную матрицу $C$.
Напомним, что только квадратные матрицы имеют обратные ! Это , а не квадратная матрица. Это матрица $3\times 2$ с $3$ строками и $2$ столбцами. Таким образом, мы не можем вычислить обратную матрицу $C$.