Матрица методом гаусса: Как решить методом Гаусса СЛАУ (систему линейных уравнений). Правила, примеры

alexxlab / / Разное

python — Построить обратную матрицу методом Гаусса

У вас несколько ошибок в коде.

  1. Вы конструируете правую часть как np.matrix, поэтому после np.hstack вы получаете тоже объект типа np.matrix. Это очень специальный вид массивов. В частности, итератор m возвращает не одномерные строки чисел, а двумерные массивы формы (1,6). В результате row[nrow] оказывается не числом, а одномерным массивом.

    В numpy есть специальная функция для построения единичной матрицы: np.eye(n) строит единичную матрицу размером n x n. Поэтому вам лучше конструировать m как m = np.hstack((matrix_origin, np.eye(len(matrix_origin)))

  2. Вы инициализировали n как число колонок в m: m = m.shape[1]. Но тогда вот эта строчка неверна: for row_ in range(k - 1, -1, -1) — у вас нет строк с номерами 5,4,3. Если

    n определяет число строк, то нужно присваивать вот так: n = m.shape[0]

  3. Но в таком случае сломается ваш код выделения правой части np.hsplit(m, n // 2)[1]. Я предлагаю использовать индексирование вместо hsplit: m[:, n:].copy() есть двумерный массив, каждая строка которого есть строка из m начиная с элемента с номером n, то есть элементы №№ 3,4 и 5. Как раз правая часть матрицы m. Метод copy() вызывается для того, чтобы не держать указатель на m, в противном случае m будет висеть в памяти до тех пор, пока «жив» указатель на результат функции inverse_matrix

После исправления этих ошибок получится что-то вроде

def inverse_matrix(matrix_origin):
    """
    Функция получает на вход матрицу, затем добавляет к ней единичную матрицу, 
    проводит элементарные преобразования по строкам с первоначальной, добиваясь получения слева единичной матрицы.
  В этом случае справа окажется матрица, которая является обратной к заданнй первоначально 
    """
    # Склеиваем 2 матрицы: слева - первоначальная, справа - единичная
    n = matrix_origin.shape[0]
    m = np.hstack((matrix_origin, np.eye(n)))
    
    for nrow, row in enumerate(m):
        # nrow равен номеру строки
        # row содержит саму строку матрицы
        divider = row[nrow] # диагональный элемент
        # делим на диагональный элемент:
        row /= divider
        # теперь вычитаем приведённую строку из всех нижележащих строк:
        for lower_row in m[nrow+1:]:
            factor = lower_row[nrow] # элемент строки в колонке nrow
            lower_row -= factor*row # вычитаем, чтобы получить ноль в колонке nrow
    # обратный ход:
    for k in range(n - 1, 0, -1):
        for row_ in range(k - 1, -1, -1):
            if m[row_, k]:
                # 1) Все элементы выше главной диагонали делаем равными нулю
                m[row_, :] -= m[k, :] * m[row_, k]
    return m[:,n:].
 
 copy()

Результат инвертирования вашей матрицы

array([[ 0.04128819,  0.09805945,  0.08980182],
       [ 0.15689513, -0.08790039, -0.01401625],
       [ 0.1734104 , -0.18025555,  0.206115  ]])

Я добавил jupyter notebook со своим вариантом, он быстрее на 10-15% за счёт выбора операций индексирования.

Схема решения линейных уравнений методом гаусса

Автор admin На чтение 14 мин Просмотров 1 Опубликовано Обновлено

Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Как решить систему линейных уравнений? Далее полезно изучить урок Правило Крамера. Матричный метод.

Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.

Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА. Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.

Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:

1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной).

Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решения любой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья Несовместные системы и системы с общим решением. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.

Вернемся к простейшей системе с урока Как решить систему линейных уравнений?

и решим ее методом Гаусса.

На первом этапе нужно записать расширенную матрицу системы:

. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.

Справка: рекомендую запомнить термины линейной алгебры.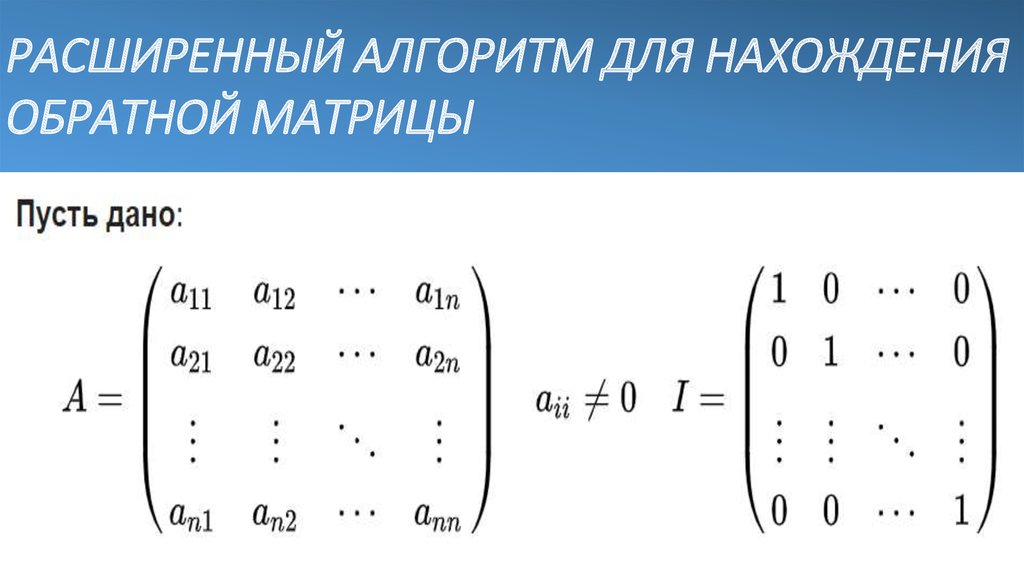 Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.

После того, как расширенная матрица системы записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями.

Существуют следующие элементарные преобразования:

1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:

2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу

. В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .

3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следует удалить. Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули.

4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля. Рассмотрим, например, матрицу

. Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.

5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число, отличное от нуля. Рассмотрим нашу матрицу из практического примера:

. Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2: . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ –

не изменилась

. Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

На практике так подробно, конечно, не расписывают, а пишут короче:

Еще раз: ко второй строке прибавили первую строку, умноженную на –2. Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:

«Переписываю матрицу и переписываю первую строку:

»

«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2:

, и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »

«Теперь второй столбец. Вверху –1 умножаю на –2:

. Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »

«И третий столбец. Вверху –5 умножаю на –2:

. Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »

Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.

Элементарные преобразования не меняют решение системы уравнений

! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать, если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!

Вернемся к нашей системе

. Она практически разобрана по косточкам.

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –2. И снова: почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.

(2) Делим вторую строку на 3.

Цель элементарных преобразований – привести матрицу к ступенчатому виду:

. В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид.

В результате элементарных преобразований получена эквивалентная исходной система уравнений:

Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса.

В нижнем уравнении у нас уже готовый результат:

.

Рассмотрим первое уравнение системы

и подставим в него уже известное значение «игрек»:

Ответ:

Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.

Решить методом Гаусса систему уравнений:

Запишем расширенную матрицу системы:

Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:

И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?

Сначала смотрим на левое верхнее число:

Почти всегда здесь должна находиться единица. Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:

Теперь первая строка у нас останется неизменной до конца решения. Уже легче.

Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:

Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2. Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2:

Результат записываем во вторую строку:

Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3. Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3:

Результат записываем в третью строку:

На практике эти действия обычно выполняются устно и записываются в один шаг:

Не нужно считать всё сразу и одновременно. Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО и ВНИМАТЕЛЬНО:

А мысленный ход самих расчётов я уже рассмотрел выше.

Далее нужно получить единицу на следующей «ступеньке»:

В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:

На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:

Для этого к третьей строке прибавляем вторую строку, умноженную на –2:

Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.

Последнее выполненное действие – причёска результата, делим третью строку на 3.

В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:

Круто.

Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.

В третьем уравнении у нас уже готовый результат:

Смотрим на второе уравнение:

. Значение «зет» уже известно, таким образом:

И, наконец, первое уравнение:

. «Игрек» и «зет» известны, дело за малым:

Ответ:

Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.

Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса. Но вот ответы обязательно должны получиться одинаковыми!

Решить систему линейных уравнений методом Гаусса

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так:
(1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.

Теперь слева вверху «минус один», что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).

Дальше алгоритм работает уже по накатанной колее:

(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.

(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.

(4) К третьей строке прибавили вторую строку, умноженную на 2.

(5) Третью строку разделили на 3.

Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде

, и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.

Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх. Да тут подарок получился:



Ответ:

.

Решить систему линейных уравнений методом Гаусса

Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.

В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:

Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод. В расширенной матрице системы на месте отсутствующих переменных ставим нули:

Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.

Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему:

.

Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.

Или еще такой условный пример:

. Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.

Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.

Дождливая осенняя погода за окном. Поэтому для всех желающих более сложный пример для самостоятельного решения:

Решить методом Гаусса систему четырёх линейных уравнений с четырьмя неизвестными.

Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.

Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением. Там же можно закрепить рассмотренный алгоритм метода Гаусса.

Пример 2: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание, что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.

Обратный ход:

Ответ: .

Пример 4: Решение: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.

Со второй «ступенькой» всё хуже, «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы

(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
Нужная вещь на второй ступеньке получена.
(5) К третьей строке прибавили вторую, умноженную на 6.
(6) Вторую строку умножили на –1, третью строку разделили на -83.

Обратный ход:

Ответ:

Пример 5: Решение: Запишем матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

Выполненные преобразования:
(1) Первую и вторую строки поменяли местами.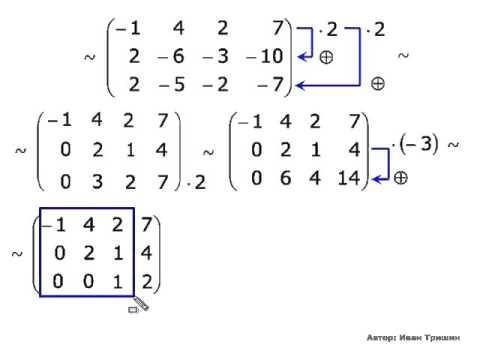
(2) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –2. К четвертой строке прибавили первую строку, умноженную на –3.
(3) К третьей строке прибавили вторую, умноженную на 4. К четвертой строке прибавили вторую, умноженную на –1.
(4) У второй строки сменили знак. Четвертую строку разделили на 3 и поместили вместо третьей строки.
(5) К четвертой строке прибавили третью строку, умноженную на –5.

Обратный ход:



Ответ:

(Переход на главную страницу)

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

Источник

[2/3] Полное руководство по исключению Гаусса | Адам Дхалла | Стартап

Часть 2 из 3: Как мы выражаем исключение и замену строк как умножение матриц.

Мы рассмотрели все базовые концепции исключения Гаусса в первой части этой мини-серии об исключении Гаусса. В этой статье рассказывается, как мы используем исключение Гаусса, чтобы превратить нашу матрицу коэффициентов A в верхний треугольник U, чтобы мы могли использовать обратную подстановку для решения системы. Мы также исследовали единичные случаи, которые могут из этого получиться.

[1/3] Полное руководство по методу исключения Гаусса

Часть 1 из 3: Что это значит и как мы [люди] его вычисляем, развороты, особые случаи, обмен строками и геометрическое…

adamdhalla .medium.com

Эту серию статей можно рассматривать как дополнение к проф. Курс Гилберта Стрэнга 18.06 по линейной алгебре — точнее, первые четыре лекции.

Какие операции по ликвидации?

При устранении есть две основные операции. Это устранение операции (комбинированный этап умножения/вычитания) и замена строк.

Мы пытаемся выразить эти операции как умножение матриц. Чтобы быть конкретным, на какую матрицу E нам нужно умножить A, чтобы выполнить исключение? Как насчет обмена строками? Это поможет нам приблизиться к последовательной формуле для выполнения исключения Гаусса.

Исключение как умножение матриц

Давайте посмотрим, как мы можем выразить исключение как умножение матриц, используя простую (2 x 2) систему.

Какая матрица E переводит нашу A на следующий шаг исключения? Какая матрица умножает первую строку на два и вычитает ее из второй строки?

Я дам ответ, а затем пройдусь по нему. Мы называем эту матрицу, цель которой состоит в том, чтобы превратить 4 в 0 на A (и, таким образом, превратить ее в верхний треугольник) E_21, поскольку она превращает элемент в пространстве (строка 2, столбец 1) в 0 , E является сокращением от Elementary Matrix — по определению, элементарная матрица — это матрица, которая отличается от идентичности только одним значением. Как вы увидите, это именно то, что они есть.

Давайте посмотрим, как это умножается на матрицу A, чтобы выполнить шаг исключения.

Так как верхняя строка остается неизменной после исключения, первая строка E совпадает с единичной матрицей. Во второй строке мы помещаем -2 в пробел (2, 1). Когда мы умножаем это, он умножает каждый элемент в строке 1 на 2 и вычитает его из элементов во второй строке, что аналогично вычитанию всей строки.

Эта матрица, умноженная на наши правые части b, также имеет тот же эффект вычитания верхней строки из нижней строки. Таким образом, мы умножаем и A, и b на E21, чтобы получить U и x. Алгебраически, Ax = b → EAx = Eb → Ux = c

Давайте рассмотрим более подробный пример (3 x 3), для которого требуются три разные матрицы исключения.

Если мы хотим превратить это в верхний треугольник, мы должны сделать три отдельных шага исключения. Сначала сделаем это привычным нам способом, а затем создадим соответствующие матрицы исключения.

Я не буду беспокоиться о правых частях здесь — если вы записываете все свои исключения в левой части, вы можете выполнять те же самые исключения в правой части постфактум — на самом деле, именно так большинство программистов такие языки, как MATLAB, выполняют исключение Гаусса.

Первый шаг умножает первую строку на 2 и вычитает ее из второй строки. Для второго шага , , мы также можем сделать позицию (3, 1) равной 0, умножив первую строку на 2 и вычтя из третьей строки. Выполнение обоих этих шагов дает нам:

для третьего и последнего шага, мы умножаем -1 на -1, поэтому при вычитании из 1 в последней строке мы получаем 0.

Мы достигли нашего верхняя треугольная матрица U. Теперь, как мы можем сделать эти три шага исключения, используя матрицы? В частности, три матрицы E21 (для присвоения (2, 1) разряда 0), E31 (для присвоения (3, 1) разряда 0) и E32 (для присвоения (3, 2) разряда 0).

Мы должны умножить эти три элементарные матрицы в том же порядке, что и исключение. Сначала два в первом столбце, затем один во втором столбце.

Они идут справа налево.

Итак, что это за элементарные матрицы? Я покажу их все одновременно и кратко объясню каждый из них; идея довольно интуитивна, и вы довольно быстро поймете.

Это то, чем является каждая из элементарных матриц. Трудно действительно объяснить, что они делают, кроме того, что я уже сделал, так как основной способ понять, как они работают, или больше, до считают, что они работают, — умножить их самостоятельно. Поэтому я настоятельно рекомендую потратить две минуты на то, чтобы умножить A на каждую из этих трех элементарных матриц (в указанном выше порядке) и увидеть, как A становится верхним треугольником U.

Полезное общее правило, если вы еще не поняли. Выяснилось, что нужно умножить некоторую строку i на некоторый множитель k и вычесть это из некоторой строки j, связанная с ней элементарная матрица Eji должна содержать -k в j-й строке i-го столбца. Прочтите это несколько раз (или лучше сами используйте пример), чтобы немного лучше его усвоить.

Поскольку умножение матриц ассоциативно ((AB)C = A(BC)), мы можем умножить эти три элементарные матрицы в одну матрицу E, которая переводит нашу матрицу A в верхнетреугольную форму U за одну операцию.

Здесь наше E (и вычисление для получения E) будет выглядеть примерно так:

Проблема с вычислением этого E заключается в том, что трудно узнать, как будет выглядеть E, до его умножения. Это усложняет вычисления, и наше решение этой проблемы будет представлено в последней статье этой серии, где мы предлагаем наиболее эффективный (и часто используемый) способ решения системы уравнений.

Перед этим нам нужно увидеть матричный эквивалент еще одного важного шага исключения: обмена строками.

Обмен строками как умножение матриц

Подобно тому, как элементарные матрицы выполняют исключение, матрицы перестановок выполняют обмен строк. Все матрицы перестановок чем-то напоминают искаженные матрицы идентичности — это имеет смысл, если подумать, поскольку обмен строками не меняет фактического содержимого в матрице — просто меняет их местами.

Вот пример матрицы, которая меняет местами 1-ю и 2-ю строки матрицы 3 x 3.

Матрица перестановок должна иметь 1 в каждой строке и каждом столбце и 0 во всех остальных местах. Вы можете умножить их, чтобы убедиться, что это работает; опять же, это единственный способ «получить» эти вещи.

Количество матриц перестановок для системы n x n равно n факториалу (n!) (с учетом единичной матрицы, которая представляет собой матрицу перестановок, которая ничего не делает). Следовательно, количество матриц перестановок для системы 3 x 3 равно 6. Здесь все они и что они делают; быстрый осмотр должен сделать очевидным то, что они делают.

Матрицы перестановок обладают несколькими интересными свойствами. Прежде всего, это «семейство» матриц — любая матрица перестановок, умноженная на другую матрицу перестановок, возвращает другую матрицу перестановок в том же «наборе». Кроме того, обратные матрицы перестановок являются их транспонированными.

Пока это все. В следующей статье мы будем манипулировать этими матрицами, чтобы найти наиболее эффективный способ решения этих систем с использованием инверсий и других инструментов.

Адам Дхалла учится в старшей школе из Ванкувера, Британская Колумбия, в настоящее время участвует в STEM и бизнес-сообществе ТКС . Он очарован внешним миром и в настоящее время изучает новые технологии для защиты окружающей среды. Чтобы не отставать,

Подпишитесь на его I nstagram и его LinkedIn . Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь.

Оценка нескольких матричных графиков Гаусса

. 2018 ноябрь;80(5):927-950.

doi: 10.1111/rssb.12278. Epub 2018 14 июня.

Юньчжан Чжу 1 , Лексин Ли 2

Принадлежности

  • 1 Статистический факультет Университета штата Огайо.
  • 2 Отдел биостатистики Калифорнийского университета в Беркли.
  • PMID: 30505211
  • PMCID: PMC6261498
  • DOI: 10.1111/rssb.12278

Бесплатная статья ЧВК

Юньчжан Чжу и др. J R Stat Soc Series B Stat Methodol. 2018 ноябрь

Бесплатная статья ЧВК

. 2018 ноябрь;80(5):927-950.

doi: 10. 1111/rssb.12278. Epub 2018 14 июня.

Авторы

Юньчжан Чжу 1 , Лексин Ли 2

Принадлежности

  • 1 Статистический факультет Университета штата Огайо.
  • 2 Отдел биостатистики Калифорнийского университета в Беркли.
  • PMID: 30505211
  • PMCID: PMC6261498
  • DOI: 10.1111/rssb.12278

Абстрактный

Данные с матричным значением, где единицей выборки является матрица, состоящая из строк и столбцов измерений, появляются во многих научных и деловых приложениях. Матричная гауссовская графическая модель является полезным инструментом для описания структуры условной зависимости строк и столбцов. В этой статье мы используем невыпуклую пенализацию для оценки нескольких графиков на основе матричных данных при матричном нормальном распределении. Мы предлагаем высокоэффективный алгоритм невыпуклой оптимизации, который можно масштабировать для графов с сотнями узлов. Мы устанавливаем асимптотические свойства оценщика, который требует менее строгих условий и имеет более точную границу ошибки вероятности, чем существующие результаты. Мы демонстрируем эффективность предложенного нами метода как с помощью моделирования, так и с помощью анализа реальной функциональной магнитно-резонансной томографии.

Ключевые слова: Условная независимость; гауссова графическая модель; Матричное нормальное распределение; Невыпуклая пенализация; функциональная магнитно-резонансная томография в состоянии покоя; Разреженность.

Цифры

Рисунок 1

Используются три типа графиков…

Рисунок 1

Три типа графиков, используемых в наших исследованиях моделирования

Рисунок 1

Три типа графиков, используемых в наших исследованиях моделирования

Рисунок 2

Предполагаемые сети подключения для…

Рисунок 2

Расчетные сети подключения для данных ABIDE. Левая панель предназначена для…

фигура 2

Расчетные сети подключения для данных ABIDE.

Левая панель предназначена для группы ASD, а правая панель — для обычного управления. Показаны 2% самых популярных ссылок, где серые ссылки являются общими для обеих групп, а красные ссылки уникальны для каждой группы.

Рисунок 3

Предполагаемые сети подключения для…

Рисунок 3

Расчетные сети подключения для данных СДВГ. Левая панель предназначена для…

Рисунок 3

Расчетные сети подключения для данных СДВГ. Левая панель предназначена для группы СДВГ, а правая — для обычного управления. Показаны 2% самых популярных ссылок, где серые ссылки являются общими для обеих групп, а красные ссылки уникальны для каждой группы.

Алгоритм 1

Алгоритм ММ и ADMM…

Алгоритм 1

Алгоритм ММ и алгоритм ADMM для решения (2).

Алгоритм 1

Алгоритм ММ и алгоритм ADMM для решения (2).

См. это изображение и информацию об авторских правах в PMC

Похожие статьи

  • Совместное изучение нескольких разреженных матричных гауссовских графических моделей.

    Хуан Ф., Чен С. Хуан Ф и др. IEEE Trans Neural Netw Learn Syst. 2015 ноябрь; 26 (11): 2606-20. doi: 10.1109/TNNLS.2014.2384201. Epub 2015 4 марта. IEEE Trans Neural Netw Learn Syst. 2015. PMID: 25751876

  • Совместная оценка множественных зависимых гауссовских графических моделей с приложениями к геномике мыши.

    Се Ю, Лю Ю, Валдар В. Се Ю и др. Биометрика. 2016 сен; 103 (3): 493-511. doi: 10.1093/biomet/asw035. Биометрика. 2016. PMID: 29038606 Бесплатная статья ЧВК.

  • Совместная оценка нескольких условных гауссовских графических моделей.

    Хуан Ф., Чен С., Хуан С.Дж. Хуан Ф и др. IEEE Trans Neural Netw Learn Syst. 2018 июль; 29 (7): 3034-3046. doi: 10.1109/TNNLS.2017.2710090. Epub 2017 28 июня. IEEE Trans Neural Netw Learn Syst. 2018. PMID: 28678717

  • РАЗРЕЖЕННАЯ УСЛОВНАЯ ГАУССОВА ГРАФИЧЕСКАЯ МОДЕЛЬ ДЛЯ АНАЛИЗА ГЕНЕТИЧЕСКИХ ДАННЫХ ГЕНОМИК.

    Инь Дж., Ли Х. Инь Дж. и др. Энн Appl Стат. 2011 декабрь; 5 (4): 2630-2650. дои: 10.1214/11-AOAS494. Энн Appl Стат. 2011. PMID: 22905077 Бесплатная статья ЧВК.

  • Выбор модели и оценка в матричной нормальной графической модели.

    Инь Дж., Ли Х. Инь Дж. и др. Дж мультивар анал. 2012 1 мая; 107:119-140. doi: 10.1016/j.jmva.2012.01.005. Дж мультивар анал. 2012. PMID: 22368309 Бесплатная статья ЧВК.

Посмотреть все похожие статьи

Цитируется

  • Расширение возможностей дифференциальных сетей с использованием байесовского анализа.

    Смит Дж., Араши М., Беккер А. Смит Дж. и др. ПЛОС Один. 2022 25 января; 17 (1): e0261193. doi: 10.1371/journal.pone.0261193. Электронная коллекция 2022. ПЛОС Один. 2022. PMID: 35077451 Бесплатная статья ЧВК.

  • Проверка гипотез для сетевых данных с помощью Power Enhancement.

    Ся Ю, Ли Л. Ся Ю и др. Стат Син. 2022;32:293-321. doi: 10.5705/сс.202019.0361. Стат Син. 2022. PMID: 35002179 Бесплатная статья ЧВК.

  • Сетевое моделирование в биологии: статистические методы для генных и мозговых сетей.

    Ван Ю.С.Р., Ли Л., Ли Дж.Дж., Хуан Х. Ван YXR и др. Стат. наук. 2021 фев; 36 (1): 89-108. дои: 10.1214/20-ст792. Стат. наук. 2021. PMID: 34305304 Бесплатная статья ЧВК.

  • Одновременный дифференциальный сетевой анализ и классификация матричных переменных данных с приложением к мозговым связям.

    Чен Х, Го И, Хэ И, Цзи Дж, Лю Л, Ши И, Ван И, Ю Л, Чжан Х; Инициатива нейровизуализации болезни Альцгеймера. Чен Х и др.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *