Угол 1 и угол 3 смежные. Что такое смежные углы
угол до развернутого, то есть равного 180°, поэтому для их нахождения вычтите из этого известную величину основного угла α₁ = α₂ = 180°-α.Из этого имеются . Если два угла одновременно являются и смежными, и равными, то они прямые. Если один из смежных углов является прямым, то есть составляет 90 градусов, то другой угол тоже прямой. Если один из смежных углов острый, то другой будет тупым. Аналогично, если один из углов тупой, то второй, соответственно, будет острым.
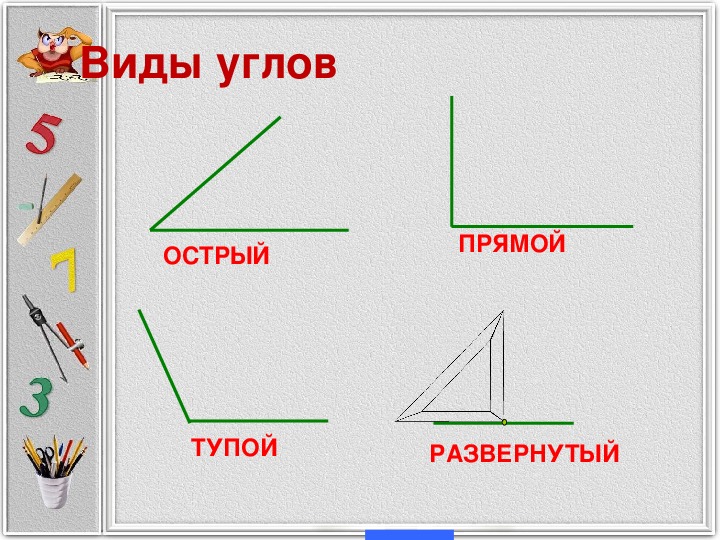
Острый угол – это такой, градусная мера которого меньше 90 градусов, но больше 0. Тупой угол имеет градусную меру больше 90 градусов, но меньше 180.
Другое свойство смежных углов формулируется так: если два угла равны, то углы, смежные с ними, также равны. Это , что если есть два угла, градусная мера для которых совпадает (например, она составляет 50 градусов) и при этом из них имеет смежный угол, то значения этих смежных углов тоже совпадают (в примере их градусная мера будет равна 130 градусам).
Источники:
- Большой Энциклопедический Словарь — Смежные углы
- угол 180 градусов
Слово « » имеет различные толкования. В геометрии угол – это часть плоскости, ограниченная двумя лучами, выходящими из одной точки – вершины. Когда речь идет о прямых, острых, развернутых углах, то подразумеваются именно геометрические углы.
Как и любые фигуры в геометрии, углы можно сравнивать. Равенство углов определяется с помощью движения. Угол нетрудно разделить на две равные части. Разделить на три части немного сложнее, но все же это можно сделать с помощью линейки и циркуля. Кстати, эта задача казалась довольно трудной. Описать, что один угол больше или меньше другого, геометрически несложно.
В качестве единицы измерения углов принят – 1/180
Два угла размещнные на одной прямой и имеющие одну вершину называются смежными.
Иначе — если сумма двух углов на одной прямой равна 180 градусам и одна сторона у них общая, то это смежные углы.
1 смежный угол + 1 смежный угол = 180 градусов.
Смежные углы -это два угла, у которых одна сторона общая, а две другие стороны в целом образуют прямую линию.
Сумма двух смежных углов всегда равна 180 градусам. К примеру, если один угол 60 градусов, то второй обязательно будет равен 120 градусам (180-60).
Углы АОС и ВОС являются смежными углами, потому что соблюдается все условия характеристики смежных углов:
1.ОС -общая сторона двух углов
2.АО -сторона угла АОС, ОВ -сторона угла ВОС. Вместе эти стороны образуют прямую линию АОВ.
3.Угла два и сумма их равна 180 градусов.
Вспоминая школьный курс геометрии, про смежные углы мы можем сказать следующее:
у смежных углов — одна сторона общая, а другие две стороны принадлежат одной прямой, то есть находятся на одной прямой. Если по рисунку, то углы СОВ и ВОА — это смежные углы, сумма которых всегда равна 180 , так как они разделяют развернутый угол, а развернутый угол всегда равен 180 .
Смежные углы понятие легкое в геометрии. Смежные углы, угол плюс угол дают 180 градусов в общей сумме.
Смежные углы, угол плюс угол дают 180 градусов в общей сумме.
Два смежных угла — это будет один развернутый угол.
Есть еще несколько свойств. Со смежными углами задачи решать и теоремы доказывать легко.
Смежные углы образуются при проведении луча из произвольной точки прямой. Тогда эта произвольная точка оказывается вершиной угла, луч — общей стороной смежных углов, а прямая от которой проведен луч — двумя оставшимися сторонами смежных углов. Смежные углы могут быть как одинаковыми в случае перпендикуляра, так и отличатся при наклонном луче. Легко понять, что сумма смежных углов равна 180 градусов или попросту прямой линии. По другому этот угол можно объяснить простым примером — вы сперва шли в одном направлении по прямой, потом передумали, решили вернуться назад и развернувшись на 180 градусов отправились по той же прямой в обратном направлении.
Итак, что же такое смежный угол? Определение:
Смежными называются два угла с общей вершиной и одной общей стороной, причем две другие стороны этих углов лежат на одной прямой.
И небольшой видео урок, где толково показано про смежные углы, вертикальные углы, плюс про перпендикулярные прямые, которые являются частным случаем смежных и вертикальных углов
Смежные углы — это углы, у которых одна сторона общая, а вторая является одной линией.
Смежные углы — это углы, зависящие друг от друга. То есть если общую строну слегка повернуть, то один угол уменьшится на сколько-то градусов и автоматически второй угол увеличится на столько же градусов. Это свойство смежных углов позволяет в Геометрии решать различные задачи и осуществлять доказательства различных теорем.
Общая же сумма смежных углов всегда равна 180 градусов.
Из курса геометрии, (насколько я помню за 6 класс) смежными называются два угла, у которых одна сторона общая, а другие стороны являются дополнительными лучами, сумма смежных углов равна 180. Каждый из двух смежных углов, дополняет другой до развернутого угла. Пример смежных углов:
Смежные углы это два угла с общей вершиной, одна из сторон которых общая, а оставшиеся стороны лежат на одной прямой (не совпадая).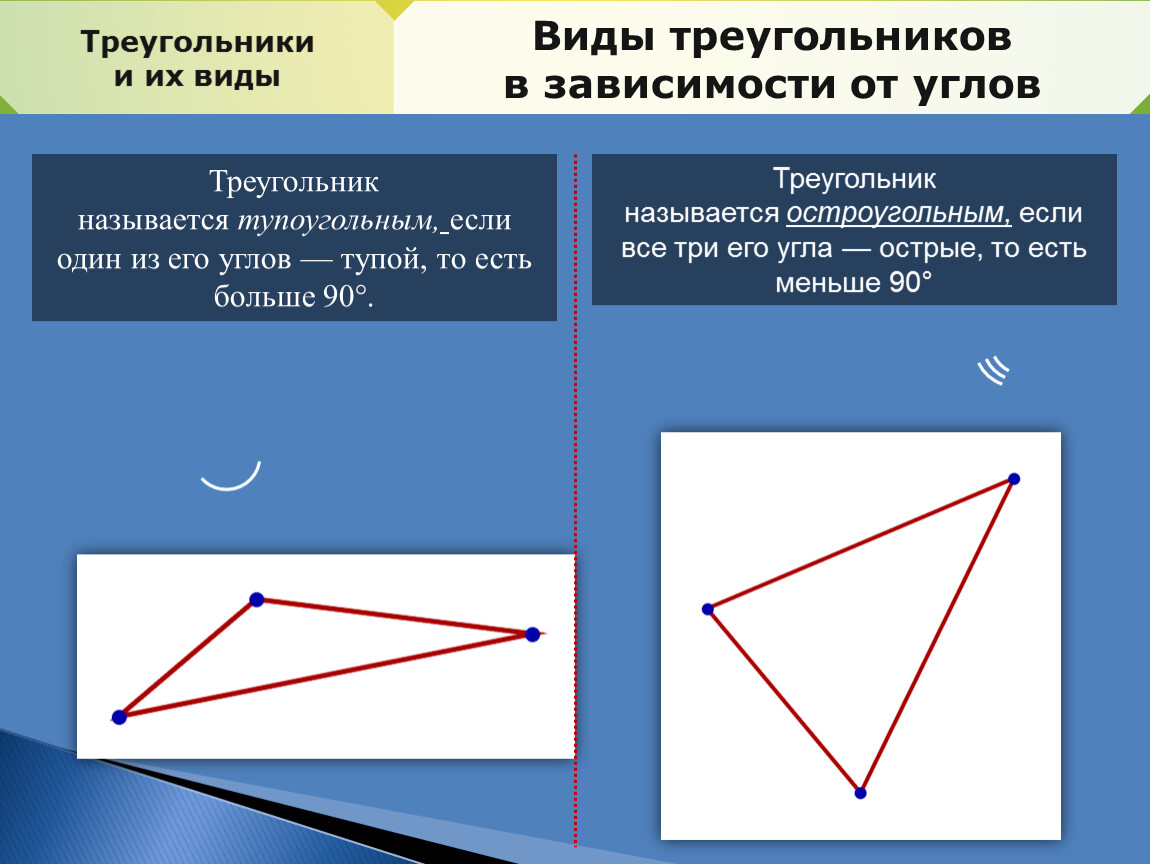 Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.
Сумма смежных углов равна ста восьмидесяти градусам. А вообще все это очень легко находится в гугле или учебнике геометрии.
1. Смежные углы.
Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.
Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.
Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.
Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).
Смежные углы могут иметь самые разнообразные положения (рис. 74).
Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°
Отсюда прямой угол можно определить как угол, равный своему смежному углу.
Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.
Например, если один из смежных углов равен 54°, то второй угол будет равен:
180° — 54° = l26°.
2. Вертикальные углы.
Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС- вертикальные; углы АОЕ и СОF — также вертикальные.
Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.
Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.
Таким же образом можно вычислить, чему равны ∠3 и ∠4.
∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;
∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.
Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.
Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.
Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.
Доказательство можно провести следующим образом (рис. 78):
∠a + ∠c = 180°;
∠b + ∠c = 180°;
(так как сумма смежных углов равна 180°).
∠a + ∠c = ∠b + ∠c
(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).
В это равенство входит один и тот же угол с .
Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b , т. е. вертикальные углы равны между собой.
3. Сумма углов, имеющих общую вершину.
На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.
∠1 + ∠2 + ∠3 + ∠4 = 180°.
На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т.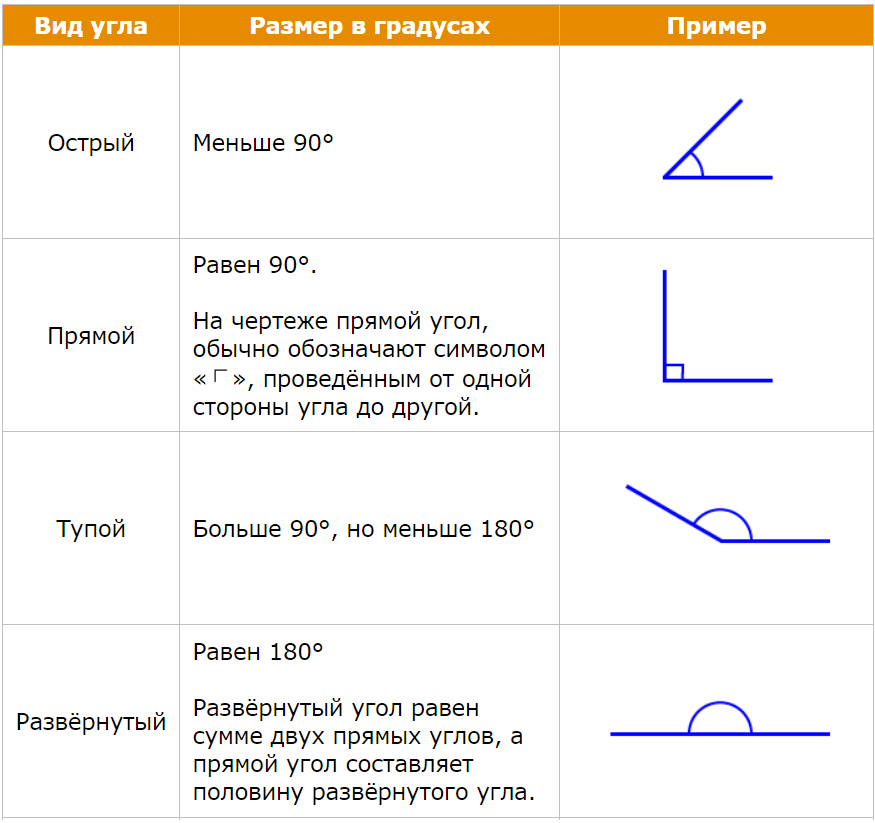 е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.
Геометрия — это весьма многогранная наука. Она развивает логику, воображение и интеллект. Конечно, из-за своей сложности и огромного количества теорем и аксиом, она не всегда нравится школьникам. Кроме этого, существует необходимость постоянно доказывать свои выводы, используя общепринятые стандарты и правила.
Смежные и вертикальные углы — это неотъемлемая составляющая геометрии. Наверняка многие школьники просто обожают их по той причине, что их свойства понятны и просты в доказательстве.
Образование углов
Любой угол образуется путем пересечения двух прямых или проведения двух лучей из одной точки. Они могут называться либо одной буквой, либо тремя, которые последовательно обозначают точки построения угла.
Углы измеряются в градусах и могут (в зависимости от их значения) по-разному называться. Так, существует прямой угол, острый, тупой и развернутый. Каждому из названий соответствует определенная градусная мера или ее промежуток.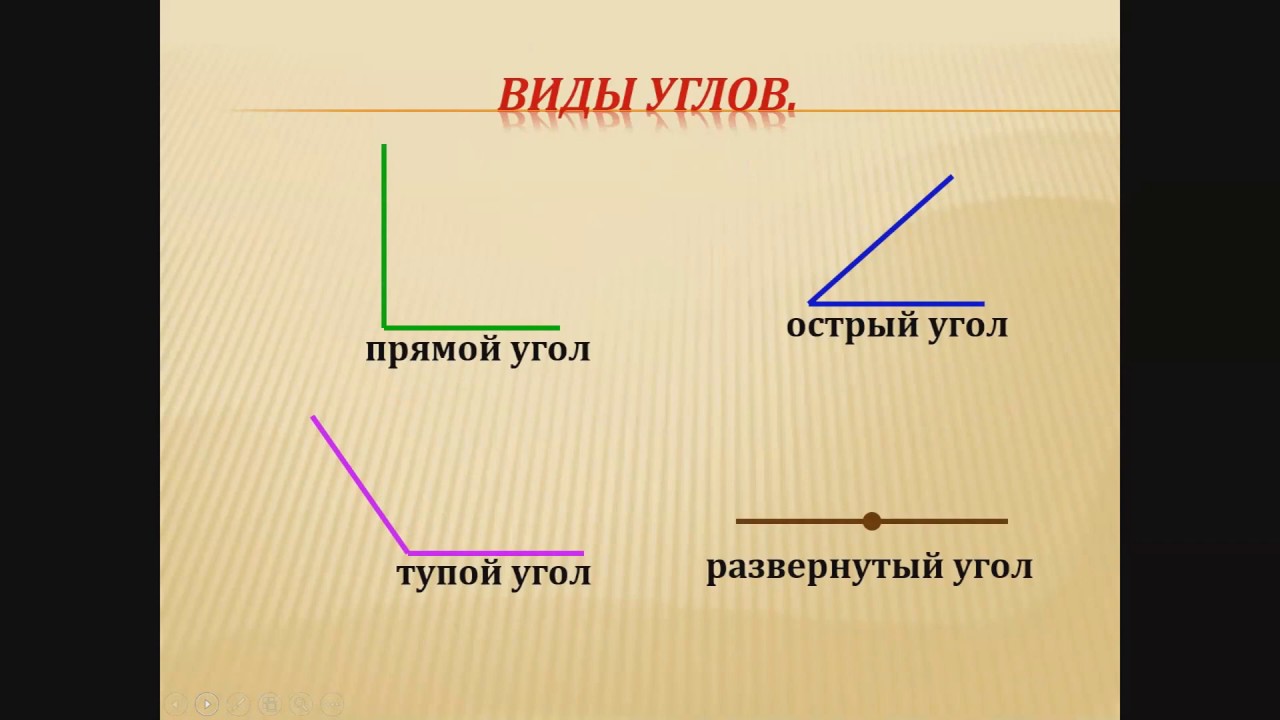
Острым называется угол, мера которого не превышает 90 градусов.
Тупым является угол, превышающий 90 градусов.
Угол называется прямым в том случае, когда его градусная мера равна 90.
В том случае, когда он образован одной сплошной прямой, и его градусная мера равна 180, его называют развернутым.
Углы, имеющие общую сторону, вторая сторона которых продолжает друг друга, называются смежными. Они могут быть как острыми, так и тупыми. Пересечение линией образует смежные углы. Свойства их следующие:
- Сумма таких углов будет равна 180 градусам (существует теорема, доказывающая это). Поэтому можно легко вычислить один из них, если известен другой.
- Из первого пункта следует, что смежные углы не могут быть образованы двумя тупыми или двумя острыми углами.
Благодаря этим свойствам, можно всегда вычислить градусную меру угла, имея значение другого угла или, по крайней мере, отношение между ними.
Вертикальные углы
Углы, стороны которых являются продолжением друг друга, называются вертикальными. В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
В качестве такой пары могут выступать любые их разновидности. Вертикальные углы всегда равны между собой.
Они образуются при пересечении прямых. Совместно с ними всегда присутствуют и смежные углы. Угол может быть одновременно смежным для одного и вертикальным для другого.
При пересечении произвольной линией также рассматривают еще несколько видов углов. Такая линия называется секущей, она и образует соответственные, односторонние и накрест лежащие углы. Они равны между собой. Их можно рассматривать в свете свойств, которые имеют вертикальные и смежные углы.
Таким образом, тема углов представляется довольно простой и понятной. Все их свойства легко запомнить и доказать. Решение задач не представляется сложным до тех пор, пока углам соответствует числовое значение. Уже дальше, когда начнется изучение sin и cos, придется запоминать множество сложных формул, их выводов и следствий. А до того времени можно просто наслаждаться легкими задачками, в которых необходимо найти смежные углы.
В процессе изучения курса геометрии понятия “угол”, “вертикальные углы”, “смежные углы” встречаются достаточно часто. Понимание каждого из терминов поможет разобраться в поставленной задаче и правильно ее решить. Что такое смежные углы и как их определять?
Смежные углы – определение понятия
Термин “смежные углы” характеризует два угла, образованных общим лучом и двумя дополнительными полупрямыми, лежащими на одной прямой. Все три луча выходят из одной точки. Общая полупрямая является одновременно стороной как одного, так и второго угла.
Смежные углы – основные свойства
1. Исходя из формулировки смежных углов, нетрудно заметить, что сумма таких углов всегда образует развернутый угол, градусная мера которого равна 180°:
- Если μ и η являются смежными углами, то μ + η = 180°.
- Зная величину одного из смежных углов (например, μ), можно легко вычислить градусную меру второго угла (η), используя выражение η = 180° – μ.
2. Данное свойство углов позволяет сделать следующий вывод: угол, являющийся смежным прямому углу, также будет прямым.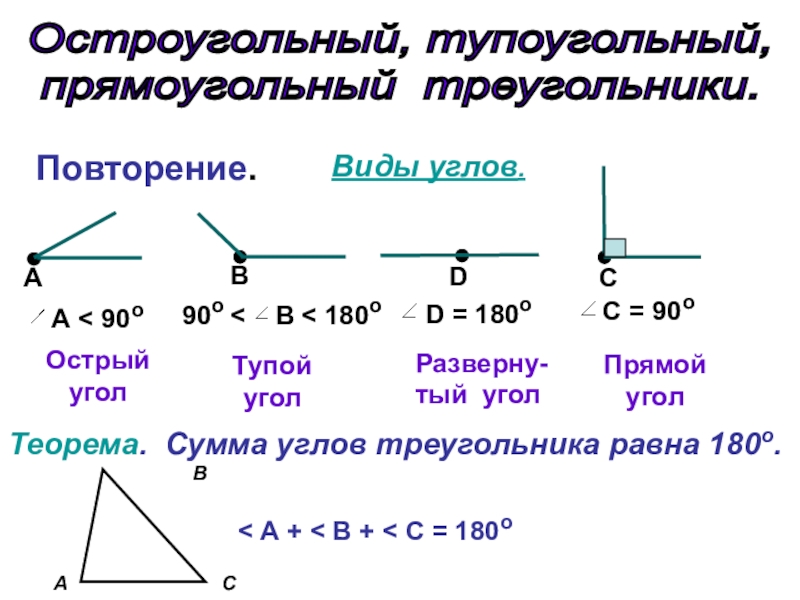
3. Рассматривая тригонометрический функции (sin, cos, tg, ctg), основываясь на формулах приведения для смежных углов μ и η справедливо следующее:
- sinη = sin(180° – μ) = sinμ,
- cosη = cos(180° – μ) = -cosμ,
- tgη = tg(180° – μ) = -tgμ,
- ctgη = ctg(180° – μ) = -ctgμ.
Смежные углы – примеры
Пример 1
Задан треугольник с вершинами M, P, Q – ΔMPQ. Найти углы, смежные углам ∠QMP, ∠MPQ, ∠PQM.
- Продлим каждую из сторон треугольника прямой.
- Зная о том, что смежные углы дополняют друг друга до развернутого угла, выясняем, что:
смежным для угла ∠QMP будет ∠LMP,
смежным для угла ∠MPQ будет ∠SPQ,
смежным для угла ∠PQM будет ∠HQP.
Пример 2
Величина одного смежного угла составляет 35°. Чему равна градусная мера второго смежного угла?
- Два смежных угла в сумме образуют 180°.
- Если ∠μ = 35°, то смежный ему ∠η = 180° – 35° = 145°.

Пример 3
Определить величины смежных углов, если известно, что градусная мера одного из низ втрое больше градусной меры другого угла.
- Обозначим величину одного (меньшего) угла через – ∠μ = λ.
- Тогда, согласно условию задачи, величина второго угла будет равна ∠η = 3λ.
- Исходя из основного свойства смежных углов, μ + η = 180° следует
λ + 3λ = μ + η = 180°,
λ = 180°/4 = 45°.
Значит первый один угол ∠μ = λ = 45°, а второй угол ∠η = 3λ = 135°.
Умение апеллировать терминологией, а также знание основных свойств смежных углов поможет справиться с решением многих геометрических задач.
| Урок учителя математики Истоминой Л. Г. Обобщающий урок по теме «Углы в нашей жизни» 5 класс. Цель урока: закрепление теоретического материала по теме «Углы»; обобщение знаний учащихся о видах углов; отработка навыков использования транспортира для построения и измерения углов. 1. Организационный момент Вступительное слово учителя о цели данного урока 2. Полетное повторение теоретического материала «цепочкой» 3. Практическая работа «Узнай меня» 4. Графический диктант. 5. Разноуровневая самостоятельная работа. Оценивание жетонами в форме треножника, четырехугольника, пятиконечной звезды 6. Знакомство с двухгранным углом 7. Словарная работа 8. Итог урока при помощи круг — сигнала «светофор». 1. Организационный момент . Вступительное слово учителя о цели данного урока. — Сегодня мы с вами в гостях в стране Углов, где есть президент Транспортир и его научный советник Градус. В мире углов иногда возникают научные споры о том, кто из них самый – самый угловажный. Поможем углам разрешить этот спор. А для этого, конечно, нужно все хорошо знать об углах. Господин Градус приготовил для вас вопросы и желает с вами познакомиться. 2. Полетное повторение теоретического материала «цепочкой». Ученики зачитывают вопрос и дают ответ. Что такое угол? Что называется сторонами угла и вершиной угла? Какие углы называются равными? Какие четыре вида углов вы знаете? Какой угол называется развернутым? Какой угол называют прямым? Какой угол называют острым? Какой угол называют тупым? Для чего служит транспортир? На сколько делений разделена шкала транспортира? Что такое градус? Сколько градусов содержит развернутый угол? Сколько градусов содержит прямой угол? Какой луч называется биссектрисой угла? Какие углы называются смежными? Чему равна сумма смежных углов? Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? 3. Практическая работа «Узнай меня» (на 2 варианта) 1 вариант 1. а) развернутые; б) прямые; в) острые; г) тупые. 2. Перечислите имеющие на чертеже углы: а) развернутые; б) тупые; в) прямые; г) острые; д) вертикальные; е) смежные. 3. Найдите, какие из данных углов равны углам, изображенным на чертеже. Запишите, какие углы равны и определите градусные меры равных углов, используя транспортир.
2 вариант 1. Из углов 1-7 определите: а) развернутые; б) прямые; в) острые; г) тупые. 2. Перечислите имеющие на чертеже углы: а) развернутые; б) тупые; в) прямые; г) острые; д) вертикальные; е) смежные. 3. Найдите, какие из данных углов равны углам, изображенным на чертеже. Запишите, какие углы равны и определите градусные меры равных углов, используя транспортир
4. «Верно ли данное утверждение». Если ученики отвечают «да», то рисуют прямую линию, если «нет», то линию в виде угла. Острый угол содержит 530 1030 — это острый угол. 890 – это тупой угол. 910 – это тупой угол. 1800 – это развернутый угол. 450 – прямой угол. Все прямые углы составляют половину развернутого. Два дополнительных друг другу луча образуют 900. Острый угол составляет часть прямой. Васе прямые углы равны между собой. В результате ответов получается такой рисунок: Предварительное оценивание происходит учениками в виде жетонов. 5. Разноуровневая самостоятельная работа. Скачать 142.46 Kb. Поделитесь с Вашими друзьями: |
Калькулятор тупоугольных треугольников
Создано Луцией Заборовской, доктором медицинских наук, кандидатом наук
Отзыв Габриэлы Диаз
Последнее обновление: 02 февраля 2023 г.
Содержание:- Что такое тупоугольный треугольник?
- Как определить, является ли треугольник тупоугольным?
- Как вычислить площадь тупоугольного треугольника?
- Как пользоваться калькулятором треугольника?
- Полный список калькуляторов площади треугольника:
- Часто задаваемые вопросы
Добро пожаловать в единственный и неповторимый калькулятор тупоугольных треугольников — больше не удивляйтесь; этот простой инструмент не только рассчитает площадь вашего треугольника, но и определит, действительно ли он тупой или нет !
Читайте дальше, чтобы узнать:
- Как вычислить площадь тупоугольного треугольника ; 🔺
- Как узнать, тупоугольный ли ваш треугольник ; и
- Как пользоваться калькулятором тупоугольных треугольников .

Что такое тупоугольный треугольник?
«Тупоугольный» описывает треугольник, который включает:
- 1x угол, который измеряет более 90 градусов (>90°), называемый тупым углом; и
- 2x угла, которые измеряют меньше 90 градусов (<90°), называются острыми углами.
Тупоугольный треугольник является одним из двух типов косоугольных треугольников — другой остроугольный.
Как определить, является ли треугольник тупоугольным?
Углы — это все, что вам нужно , чтобы определить, является ли треугольник тупым!
- Посмотрите на известные вам углы треугольника — если один из них больше 90 градусов, ваш треугольник тупоугольный . ✅
- Если вы знаете только 2 угла треугольника, используйте приведенное ниже уравнение:
Угол(α) = 180 - Угол(β) - Угол(γ)
Как вычислить площадь тупоугольного треугольника?
Вы можете вычислить площадь тупоугольного треугольника, используя каждое типичное уравнение площади треугольника.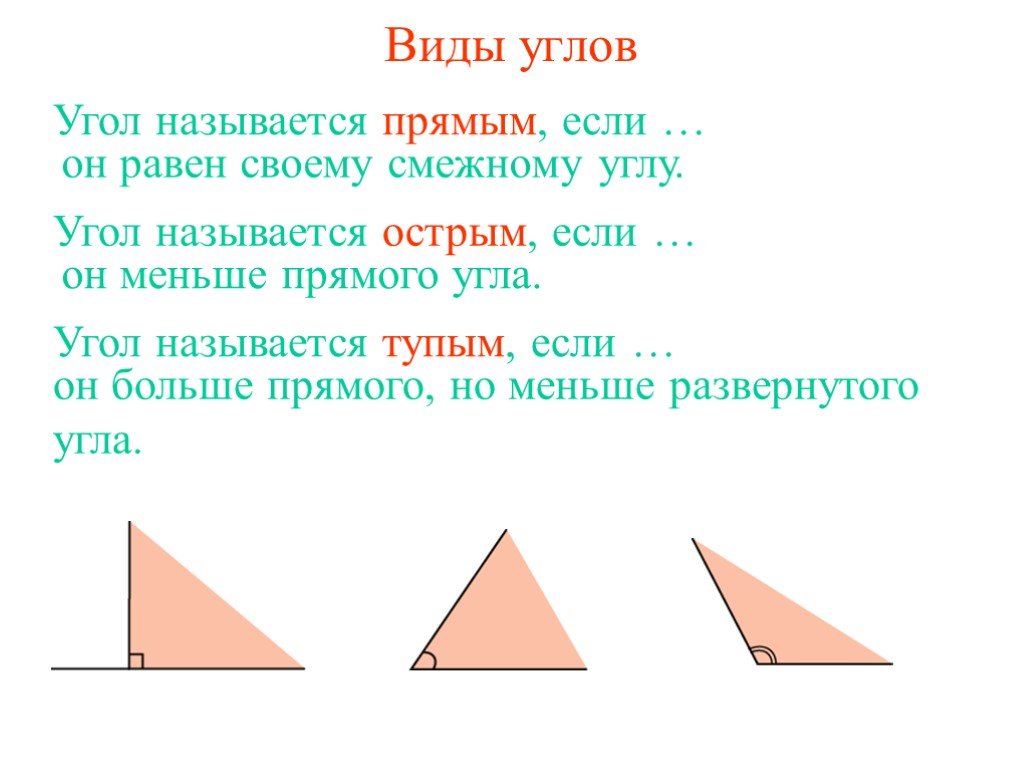
Приведем несколько примеров:
-
Площадь = 0,5 × Основание × Высота -
Площадь = 0,25 × √( (a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) -
Площадь = 0,5 × a × b × sin(γ)
Где:
-
a,bиc— длины сторон тупоугольного треугольника.
Как использовать калькулятор типа треугольник?
Наверное, это самая простая вещь на свете! 🌍
Введите один , два , или три угла вашего треугольника — наш калькулятор сторон тупоугольного треугольника сразу покажет вам ответ!
Помимо определения того, является ли ваш треугольник тупым, вы также можете использовать наш инструмент для вычисления его площади ! Идите вперед и выберите один из нескольких доступных вариантов.
Полный список калькуляторов площади треугольника:
Калькулятор тупоугольного треугольника является частью большой серии инструментов — узнай их все ! 🛠️
- Площадь треугольника;
- треугольник ААА;
- Средняя часть треугольника;
- Остроугольный треугольник;
- Центр окружности треугольника;
- Конгруэнтность треугольника;
- Косой треугольник;
- Основание треугольника;
- треугольник ААС;
- треугольник SAS;
- SSS треугольник; и
- Треугольник ASA.

Часто задаваемые вопросы
Какой тип треугольника имеет угол больше 90 градусов?
В тупоугольном треугольнике ровно один угол больше 90°, который называется тупым углом .
Два других угла тупоугольного треугольника острые — они меньше 90°.
Люция Заборовска, доктор медицинских наук, кандидат наук
Мой треугольник тупой?
Угол α
Угол β
Угол γ
Площадь тупоугольного треугольника
Высота
Посмотреть 18 подобных калькуляторов треугольников 🔺
30 60 90 треугольник45 45 90 треугольникПлощадь прямоугольного треугольника… Еще 15
Q2 2 Верно или неверно a Размер острого угла 90 b Размер тупого угла 90 c …
Перейти к
- Упражнение 5.1
- Упражнение 5.2
- Упражнение 5.
 3
3 - Упражнение 5.4
- Упражнение 5.5
- Упражнение 5.6
- Упражнение 5.7
- Упражнение 5.8
- Упражнение 5.9
- Зная наши цифры
- Целые числа
- Игра с числами
- Основные геометрические идеи
- Понимание элементарных форм
- Целые числа
- Фракции
- Десятичные
- Обработка данных
- Измерение
- Алгебра
- Соотношение и пропорция
- Симметрия
- Практическая геометрия
Главная >
Решения НЦЭРТ
Класс 6
Математика
>
Глава 5.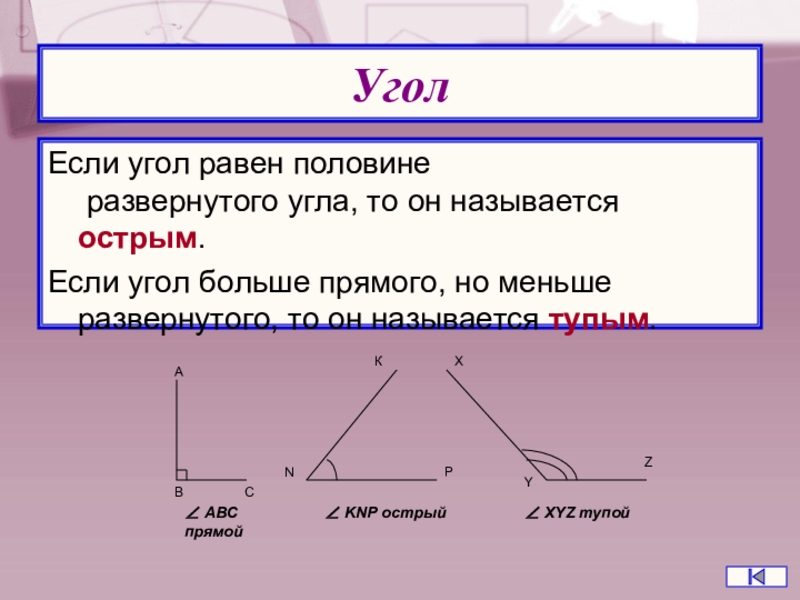 Понимание элементарных форм
>
Упражнение 5.4
>
Вопрос 3
Понимание элементарных форм
>
Упражнение 5.4
>
Вопрос 3
Вопрос 3 Упражнение 5.4
Q2) 2. Скажи Верно или Неверно:
(a) Размер острого угла < 90°.
(b) Величина тупого угла < 90°.
(c) Угол рефлекса > 180°.
(d) Размер одного полного оборота = 360°.
Ответ:
РЕШЕНИЕ:
(a) верно
(b) неверно, так как тупой угол всегда больше 90 градусов
(c) верно
(d) верно
true
Стенограмма видео
«»»Уважаемые студенты, давайте обсудим вопрос. Магнит был поднесен с разных сторон к игрушечной лодке, которая плавала по воде в ванне. Эффект, наблюдаемый в каждом случае, следующий: указано в столбце 1, а возможные причины этого влияют или упоминаются во втором столбце, нам нужно сопоставить утверждения, данные в столбце один, с утверждениями инструмента столбца. Итак, давайте прочитаем первое, что козел притягивается к магниту. Итак, если порт притягивается к магниту, что означает, что он сделан из магнитного материала.
Что состоит из магнитного материала? Сделаем вторую лодку, на которую не действует магнит. Итак, если на лодку не действует магнит, это означает, что она не является магнитным материалом или сделана из немагнитного материала. Итак, отметим, что эта третья лодка, сделанная из немагнитного материала, движется к магниту, когда А, заполненный магнитом, приближается к ее голове. Поэтому, когда Северный полюс приближается к его голове, это означает, что он будет от Южного полюса к Южному полюсу, потому что Южный полюс и Северный полюс так хорошо притягиваются друг к другу, что если победитель снабжен магнитом с Южным полюсом, он будет притягиваться к Северному полюсу. Итак, отметим, что не вся лодка оснащена магнитом с южным полюсом к носу.
Что удаляется от магнита, когда Северный полюс приближается к его голове. Итак, если его поднести к Северному полюсу, он будет удаляться, когда лодка будет направлена к Северному полюсу, потому что Северный полюс и не будут заменять друг друга, поэтому поэтому оба, если они снабжены магнитом под так, давайте напишем, что Сделаем последний, наливаем жидкости, не меняя своего направления.
Итак, давайте прочитаем первое, что козел притягивается к магниту. Итак, если порт притягивается к магниту, что означает, что он сделан из магнитного материала.
Что состоит из магнитного материала? Сделаем вторую лодку, на которую не действует магнит. Итак, если на лодку не действует магнит, это означает, что она не является магнитным материалом или сделана из немагнитного материала. Итак, отметим, что эта третья лодка, сделанная из немагнитного материала, движется к магниту, когда А, заполненный магнитом, приближается к ее голове. Поэтому, когда Северный полюс приближается к его голове, это означает, что он будет от Южного полюса к Южному полюсу, потому что Южный полюс и Северный полюс так хорошо притягиваются друг к другу, что если победитель снабжен магнитом с Южным полюсом, он будет притягиваться к Северному полюсу. Итак, отметим, что не вся лодка оснащена магнитом с южным полюсом к носу.
Что удаляется от магнита, когда Северный полюс приближается к его голове. Итак, если его поднести к Северному полюсу, он будет удаляться, когда лодка будет направлена к Северному полюсу, потому что Северный полюс и не будут заменять друг друга, поэтому поэтому оба, если они снабжены магнитом под так, давайте напишем, что Сделаем последний, наливаем жидкости, не меняя своего направления.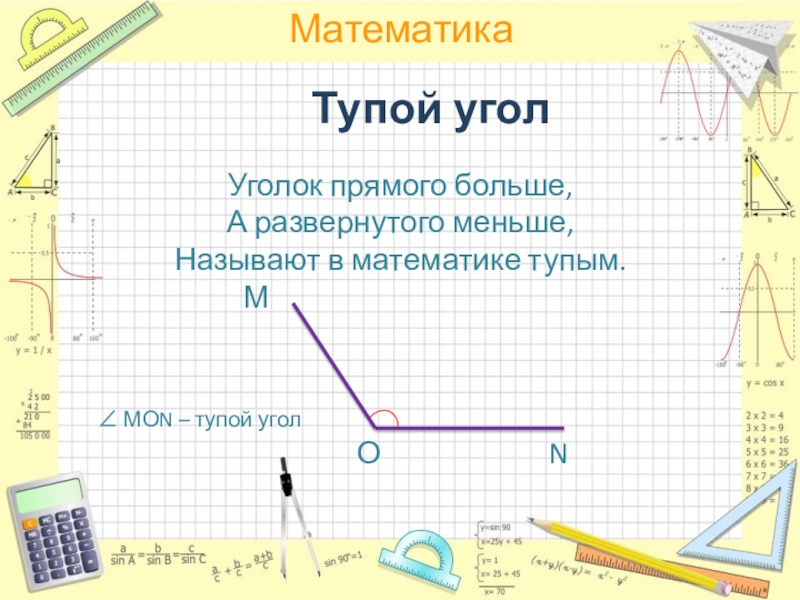 Лодка имеет маленький магнит, который подбирает ее длину, а полная лодка плывет, не меняя своего направления. Да. Итак, давайте отметим это
Лодка имеет небольшой идентификатор магнита. Вот почему он не изменит своего направления. Он будет плавать, не меняя своего направления.
Градиентная душа. Спасибо.
Ставьте лайк, чтобы получать больше обновлений.
Не стесняйтесь спрашивать раздел тысячи комментариев. Спасибо за просмотр видео студенты»»»
Лодка имеет маленький магнит, который подбирает ее длину, а полная лодка плывет, не меняя своего направления. Да. Итак, давайте отметим это
Лодка имеет небольшой идентификатор магнита. Вот почему он не изменит своего направления. Он будет плавать, не меняя своего направления.
Градиентная душа. Спасибо.
Ставьте лайк, чтобы получать больше обновлений.
Не стесняйтесь спрашивать раздел тысячи комментариев. Спасибо за просмотр видео студенты»»»
Связанные вопросы
Q4) Измерьте углы, указанные ниже, с помощью транспортира и запишите меру. (a) (b) (c) (d)
Q3) Запишите меры (а) некоторых острых углов. б) некоторые тупые углы (приведите не менее двух примеров…
Q5) Какой угол имеет большую меру? Сначала оцените, а затем измерьте. Мера угла A = мера …
В7) Заполните пропуски острыми, тупыми, прямыми или прямыми: (а) Угол, градусная мера которого меньше .

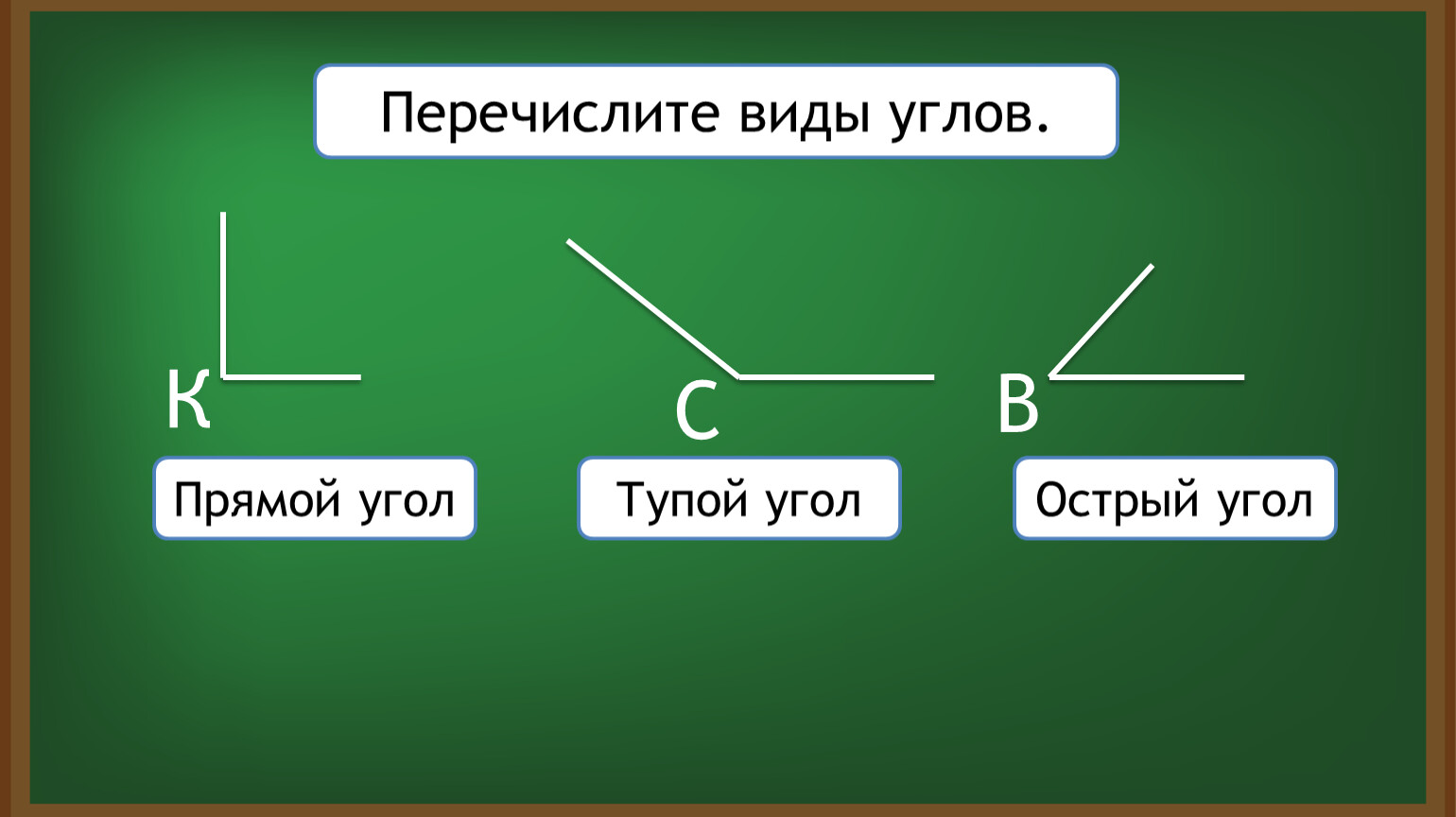


 Из углов 1-7 определите:
Из углов 1-7 определите: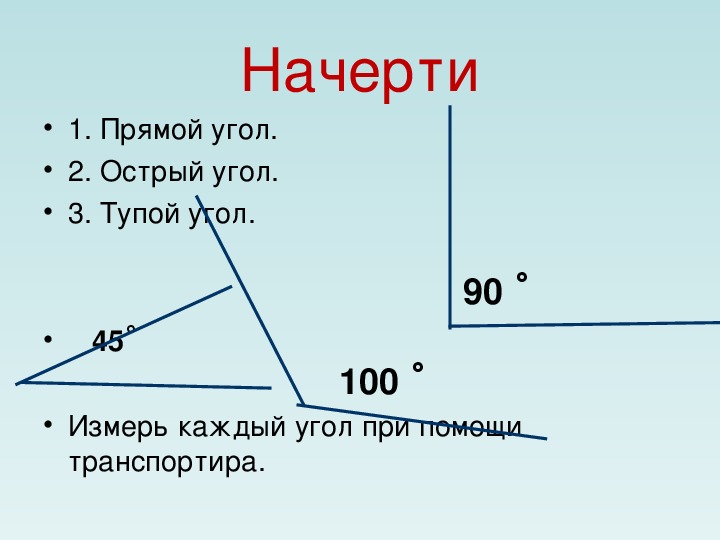 Графический диктант «Верно данное утверждение» (Взаимопроверка)
Графический диктант «Верно данное утверждение» (Взаимопроверка) org 2023
org 2023

 3
3