Матрица примеры: Примеры решения матриц с ответами

Примеры решения матриц с ответами

Простое объяснение принципов решения матриц и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

О чем статья

Алгоритм решения матриц

Теорема

Матрица – это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими буквами.

Есть два отличия между матрицами:

1. Комплексные матрицы.  Это когда хотя бы одно число равно  комплексному.
2. Действительные матрицы. Это когда в матрице содержаться действительные числа.

С матрицей можно выполнять самые наипростейшие действия: умножение, деление, сложение, вычитание и трансформация.

Сложение и вычитание

Данные действия можно совершать тогда, когда матрицы равны между собой, чтобы в конце получилось выражение аналогичной размерности. Сложение и вычитание выполняются по аналогии друг друга.

Пример 1

Задание

Даны две матрицы, найдите их  сумму.

   

   

Решение

Элемент первой строки складывается с элементом второй. Абсолютно также совершается вычитание, только вместо плюса, нужно поставить минус.

   

Пример 2

Задание

Даны две матрицы, найдите их разность.

   

Решение

   

   

   

Пример 3

Задание

Найдите C=2A +3B, если :

   

   

Решение

   

   

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Умножение

В математике умножать таблицу с числами можно абсолютно любую. В таком случае число умножается с показателем. Умножаем первое число на первой строке с числом второго столбца и так далее.

Пример

Задание

Даны две матрицы. Умножьте их друг на друга.

   

   

Решение

   

=

   

   

   

   

   

Матрицы можно перемножать друг на друга, только если количество столбцов в первой матрице, равно количеству строк второй. Элемент матрицы будет равняться сумме произведений (Aji), где i – строки в таблице; j – строки чисел второй таблицы.

Возведение матрицы в степень

Данную формулу используют лишь в случаях, если матрица стоит в квадратном выражении. Важно  знать, что степень должна быть у таких выражений натуральной!

   

Если число не будет натуральным, то это усложняет возведение матрицы в степень, так как степень n придётся умножить саму на себя n количество раз. Но если у Вас такой случай, то используется следующая формула.

   

Пример

Задание

Найдите

   

матрицы.

   

Решение

В первую очередь найдём, для этого нужно будет просто умножить её саму на себя.

   

   

   

После по формуле подставляем числовые значения.

   

Расчёт определителя

В математике линейной есть два понятия – определитель и детерминант. Определитель – это какое-либо число, которое ставится в соответствии с квадратной матрицей. Определитель используется при решении многих задач. Найти его можно с помощью формулы.

А детерминант находиться с помощью перемножения простых матриц, используются числа только с побочной и главной диагоналях.

Есть вероятность, что произведения матрицы будут значительно отличаться друг от друга. Если индекс чётный, то число будет со знаком плюс, если нечётный, то число будет со знаком минус. Обозначается определитель det А, а круглые скобки меняются на квадратные.

Пример 1

Дано

   

Решение

Пользуемся свойствам степеней – A^{3}=A^{2}*A

Возведём А в A^{2}

   

   

Далее используем свойство степеней

   

   

   

Ответ

   

Пример 2

Задание

Найдите определитель матрицы А.

   

Решение

   

   

   

Обратная матрица

Перед тем, как речь непосредственно пойдёт о самой обратной связи матрицы, давайте разберём алгоритм трансформирования матрицы. Во время трансформации столбцы и строки меняются местами.

Пример

Задание

Найти обратную матрицу А.

   

Решение

Приписываем к матрице А матрицу третьего ряда.

   

Переводим всё в единичную матрицу.

   

   

   

   

   

   

   

   

Ответ

   

   

Обратная матрица

Обратная матрица схожа с алгоритмом нахождения обратных чисел. К примеру, если умножить матричную таблицу на обратную матрицу, то в итоге мы получаем A*A(-1)=E. Но чтобы перейти уже к нахождению обратной матрицы, нам придётся найти её определитель. Мы рассмотрим самый простой способ – алгебраических дополнений.

Пример 1

Задание

В пример возьмём квадратную матрицу, она находиться с помощью следующей формулы:

   

, где

   

-транспортированные матрицы;|А| – определитель.

Рассмотрим самый простейший пример, где размер таблицы  2*2.

Найти обратную матрицу

   

Решение

Для начала находим определитель матрицы.

   

Если ответ равен нулю, то обратной матрицы нет! Так как наш ответ равен -2, то всё в порядке. Следующим действием нам нужно будет рассчитать матрицу миронов. Таблица элементов при этом не изменяется. Где прописан нужным нам элемент, нужно вычеркнуть строчку или столбец, оставшееся число и будет являться мироном.

   

Подставляем числа, возвращаясь к матрица, которая указана выше.

   

Всегда начинаем с левого верхнего угла и делаем следующее:

   

← линиями показано, что нужно и как зачеркнуть.

Как итог, у нас остаётся число 4

   

   

Теперь мы переходим к нахождению алгебраических дополнений.

Первым делом нужно поменять знаки у двух чисел в мироне.

   

  ← подчёркнуты те числа, у которых мы будем менять знаки.

   

, вот что у нас получилось.

И наконец-то мы переходим к завершающему этапу, к нахождению транспортированной матрице.

   

, вспоминаем формулу нахождения, и подставляем числовые значения

   

   

В завершении желательно проверить правильно ли мы нашли числовую таблицу. Это делать не обязательно, но рекомендуется, чтобы удостовериться в том, то ответ верный.

Пример 2

Задание

Найдите матрицу А.

   

Решение

Начинаем с определения матрицы.

   

   

Дело осталось за малым – осталось начти алгебраическое дополнение матрицы А:

   

   

   

   

   

   

   

   

   

Не забываем записать союзную матрицу:

   

И уже из неё находим обратную матрицу:

   

   

Получаем ответ

   

Средняя оценка 1.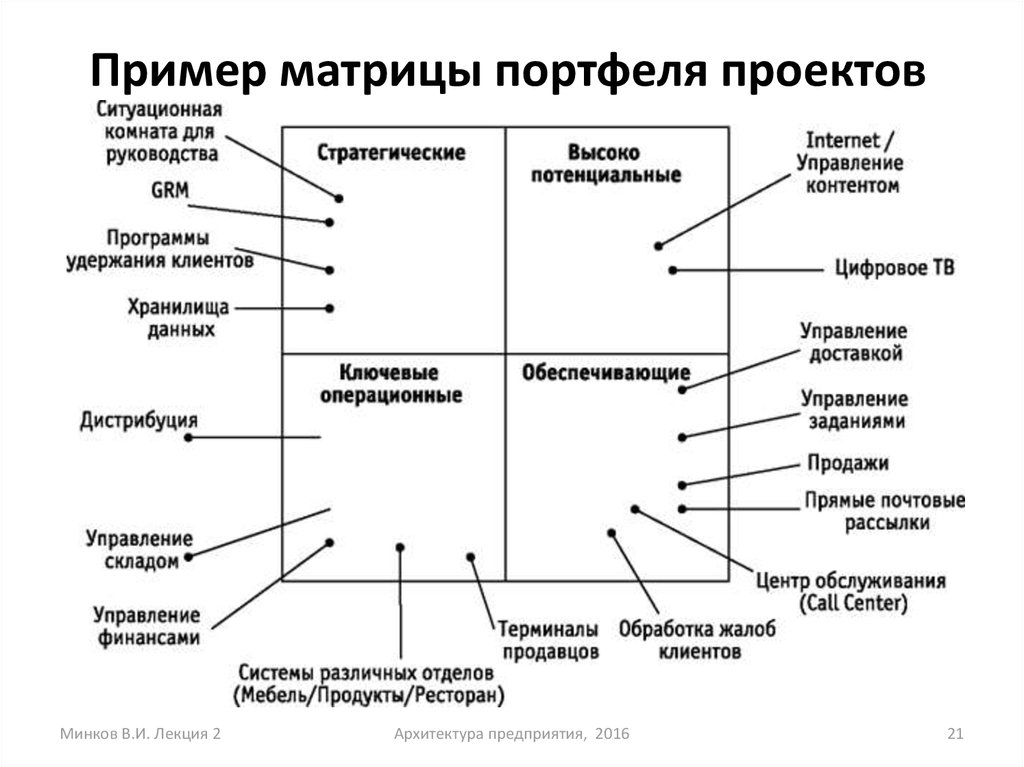 9 / 5. Количество оценок: 61

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

78422

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

Примеры решения матриц: виды матриц, формулы

Определение

Матрица — это математическая таблица с числовыми значениями. Обозначаются матрицы латинскими знаками.

Есть два вида матриц:

• Комплексные матрицы.  Одно из чисел равно комплексному.
• Действительные матрицы. Матрица в которой содержаться действительные числа.

С матрицей выполняют самые простейшие действия: умножение, деление, сложение, вычитание и трансформацию. Данные действия можно совершать тогда, когда матрицы схожи меж собой, чтобы в самом конце вышло выражение схожей размерности. Сложение и вычитание производятся подобно друг другу.

Эти числа, являются элементами матрицы. 

Матрицу можно записать в следующем виде:

\[A=\left(a_{\mathrm{ij}}\right)=\left\|a_{i j}\right\|\]

Квадратная матрица — это число строк, которое равно числу столбцов 

(m=n), при этом число n – это порядок матрицы.

Пример квадратной матрицы 3-го порядка: 

\[A=\left(\begin{array}{lll} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{array}\right)\]

Главная диагональ квадратной матрицы – это диагональ, которая состоит из a₂₁,a₂₂, a₂₃, идущая из левого верхнего угла этой матрицы в правый нижний угол. Побочной диагональю квадратной матрицы называется диагональ, составленная из элементов  идущая из правого верхнего угла этой матрицы в левый нижний угол.

В квадратной матрице, у которой все элементы, стоящие выше или ниже главной диагонали, равны нулю, называют треугольной, пример:

\[\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{array}\right)\]

Квадратная матрица, у которой все элементы, стоящие на верхней и нижней грани, равны нулю, является диагональной:

\[a_{i} \neq 0, a_{i j}=0\]

Для того чтобы получить квадратную диагональную матрицу с единичными элементами, нужно использовать букву E. {T}=\left(\begin{array}{lll} a_{11} & a_{21} & a_{31} \\ a_{12} & a_{22} & a_{32} \\ a_{13} & a_{23} & a_{33} \end{array}\right)\]

Матрица называется нулевой, если все ее элементы равны нулю.

Матрицы А и В называются равными, если они имеют одинаковую размерность, и все их соответствующие элементы совпадают.

Определитель матриц второго и третьего порядка

Определителем второго порядка квадратной матрицы называется число, равное:

\[ A=\left(\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right) \quad \Delta=|A|=\operatorname{det} A=\left|\begin{array}{ll} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right|=a_{11} a_{22}-a_{12} a_{21} \]

Суммой А + В двух матриц А=(а_ij) и В= (b_ij) одинакового размера m*n, называется матрица C=(c_ij), элементы которой c_ij=a_ij+ b_ij, для всех i=1,2,…,m и j=1,2…,n.

Задача

\[ \left(\begin{array}{rrr} 1 & 4 & 3 \\ 8 & -3 & 2 \end{array}\right)+\left(\begin{array}{rrr} 3 & 1 & 1 \\ 4 & -1 & 0 \end{array}\right)=\left(\begin{array}{rrr} 4 & 5 & 4 \\ 12 & -4 & 2 \end{array}\right) \]

Согласно правилу сложения матриц A+O=A, где A — произвольная матрица, а O — нулевая матрица того же размера, что и A.

Вычитание матриц

Разность двух матриц одинакового размера определяется с помощью операции умножения матрицы B на число —1 и последующего сложения матриц A и (—1) B т. е.

\[A-B=A+(-1) B\]

Некоторые свойства, присущие операциям над числами, справедливы и для операций над матрицами. В частности, из определений операций умножения матрицы на число и сложения матриц следует, что

\[A+B=B+A\]

Вышеуказанная формула показывает свойство коммуникативности при сложении матриц.

Доказательство. Так как операция сложения определена только для матриц одинакового размера, причем сумма матриц является матрицей того же размера, что и слагаемые матрицы, то очевидно, что размер матрицы

\[A+B=F\]

равен размеру матрицы

\[B+A=G\]

Докажем, что и все элементы матрицы F равны соответствующим элементам матрицы G. {k} a_{i s} b_{s j}\]

\[i=1,2, \ldots, m \text { и } j=1,2, \ldots, n .\]

Обратим внимание на размеры матрицы C, число строк матрицы-произведения совпадает с числом строк первой, а число столбцов — с числом столбцов второй из перемножаемых матриц (см. Рис. 1).

Пример. Вычислить произведение матриц AB, если

\[ A=\left(\begin{array}{rrr} 1 & 2 & 3 \\ 5 & 4 & -5 \end{array}\right), \quad B=\left(\begin{array}{rrr} 1 & 2 & 4 \\ 3 & -3 & 1 \\ 1 & 0 & 2 \end{array}\right) \]

Решение матриц:

Определим размер матрицы — произведения: 

\[\underset{2 \times 3}{A} \underset{3 \times 3}{B}=\underset{2 \times 3}{C} .\]

Далее, вычислим элементы матрицы — произведения:

\[ C=\left(\begin{array}{rrr} 1+6+3 & 2-6+0 & 4+2+6 \\ 5+12-5 & 10-12+0 & 20+4-10 \end{array}\right) =\left(\begin{array}{lll} 10 & -4 & 12 \\ 12 & -2 & 14 \end{array}\right) \]

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Обратная матрица

Прежде чем переходить к понятию обратного выражения матрицы, следует рассмотреть алгоритм её транспонирования. Во время операции строки и столбцы переставляются местами.

На рисунке представлен метод решения обратной матрицы:

Для вычисления матрицы приведем ее к верхнетреугольному виду, используя преобразования над строками матрицы и свойства определителя матрицы.

По аналогии обратная матрица сходна с обратными числами. Например, противоположной цифре 5 будет дробь 1/5 = 5 (-1) степени. Произведение этих чисел равно 1, выглядит оно так: 5*5 (-1) = 1. Умножение обычной матричной таблицы на обратную даст в итоге единичную: А* А (-1) = Е. Это аналог числовой единицы.

Но для начала нужно понять алгоритм вычисления обратной матрицы. Для этого находят её определитель. Разработано два метода решения: с помощью элементарных преобразований или алгебраических дополнений.

Более простой способ решения — путём алгебраических дополнений. Рассмотрим матричную таблицу А, обратная ей А (-1) степени находится по формуле:

Матрица обратного вида возможна только для квадратного размера таблиц 2*2, 3*3 и т. д. Обозначается она надстроенным индексом (-1). Задачу легче рассмотреть на более простом примере, когда размер таблицы равен 2*2.

На первом этапе выполняют действия:

Обратного выражения матрицы не может быть, если определитель равен нулю. В рассматриваемом случае он равен -2, поэтому всё в порядке.

2 этап: рассчитывают матрицу миноров, которая имеет те же значения, что и первоначальная. Под минором k-того порядка понимается определитель квадратной матрицы порядка k*k, составленный из её элементов, которые располагаются в выбранных k- столбцах и k-строках. При этом расположение элементов таблицы не меняется. Чтобы найти минор верхнего левого числа, вычёркивают строчку и столбец, в которых прописан этот элемент. Оставшееся число и будет являться минором. На выходе должна получиться таблица:

3 этап: находят алгебраические дополнения

4 этап: определяют транспонированную матрицу

Матрицы

Матрица представляет собой массив чисел:

Матрица
(у нее 2 строки и 3 столбца)

Мы говорим об одной матрице или нескольких матрицах .

Есть много вещей, которые мы можем с ними сделать…

Добавление

Чтобы сложить две матрицы: сложите числа в совпадающих позициях:

Вот расчеты:

3+4=7	8+0=8
4+1=5	6−9=−3

Две матрицы должны быть одинакового размера, т. е. строки должны совпадать по размеру, а столбцы должны совпадать по размеру.

Пример: матрица с 3 строки и 5 столбцов может быть добавлена ​​к другой матрице 3 строки и 5 столбцов .

Но его нельзя было добавить в матрицу с 3 строки и 4 столбца (столбцы не совпадают по размеру)

Отрицательное

Отрицательное значение матрицы также простое:

Вот расчеты:

−(2)=−2	−(−4)=+4
−(7)=−7	−(10)=−10

Вычитание

Чтобы вычесть две матрицы: вычтите числа в совпадающих позициях:

Вот расчеты:

3−4=−1	8−0=8
4−1=3	6−(−9)=15

Примечание: вычитание фактически определяется как сложение отрицательной матрицы: A + (−B)

Умножение на константу

Мы можем умножить матрицу на константу (значение 2 в этом случае) :

Вот расчеты:

2×4=8	2×0=0
2×1=2	2×−9=−18

Мы называем константу скаляром , поэтому официально это называется «скалярным умножением».

Умножение на другую матрицу

В число умножить две матрицы вместе немного сложнее… прочитайте Умножение матриц, чтобы узнать, как это сделать.

Деление

А деление? Ну, мы не на самом деле делим матрицы, мы делаем это так:

A/B = A × (1/B) = A × B ^-1

, где B ^-1 означает «обратное» значение B.

Таким образом, мы не делим, вместо этого мы умножить на обратное .

И есть специальные способы найти инверсию, узнайте больше в инверсии матрицы.

Транспонирование

Чтобы «транспонировать» матрицу, поменяйте местами строки и столбцы.

Мы ставим букву «Т» в верхнем правом углу, что означает транспонирование:

Обозначение

Матрица обычно обозначается заглавной буквой (например, A или B)

Каждая запись (или «элемент») обозначается строчной буквой с «нижним индексом» из строк, столбцов :

Строки и столбцы Итак, где строка, а где столбец? Ряды идут влево-вправо Столбцы идут вверх-вниз Чтобы помнить, что строки идут перед столбцами, используйте слово «дуга» : а р,с

Пример:

В =

Вот несколько примеров записей:

b _1,1 = 6 (запись в строке 1, столбец 1 равна 6)

b _1,3 = 24 (запись в строке 1 , столбец 3 равен 24)

b _2,3 = 8 (запись в строке 2, столбце 3 равна 8)

 

 

Свойства с примерами и специальными матрицами, которые образуют множественное число 7

2 Матрицы символизирует прямоугольный массив или таблицу, в которой числа/элементы организованы в строки и столбцы. Матрицы могут содержать любое количество столбцов и строк. Прямоугольный массив из m × n чисел (действительных или комплексных) в кадре из m горизонтальных линий (обозначается как 9).0256 строк ) и n вертикальных линий (названных столбцами ), называется матрицей, имеющей порядка m на n, и записывается как матрица m × n, как показано ниже.

\(A=\left[\begin{matrix}a_{11}&a_{12}&……&a_{1n}\\a_{21}&a_{22}&……&a_{2n}\\ .& .&.&.\\ .&.&.&.\\a_{m1}&a_{m2}&……&a_{mn}\end{matrix}\right] \)

\(\text{Здесь числа }a_{11},a_{12\ },\dots..\ \text{etc известны как элементы матрицы A} \)

Пример матрицы:

\(B=\begin{bmatrix}2&3&6\\3&4&5\\6&5&9\end{bmatrix}_{3\times3} \)

Приведенная выше матрица B имеет порядок 3 × 3. Следовательно, всего в матрице 9 элементов. Здесь горизонтальный массив идентифицируется как строки, а вертикальный массив распознается как столбцы.

Матрицы доступны во всех размерах, но их форма обычно остается неизменной. Размер матрицы называется ее размерностью, которая представляет собой общее количество строк и столбцов в назначенной матрице. Над матрицами могут выполняться различные операции, такие как сложение матриц, вычитание матриц, скалярное умножение матриц, умножение матриц, транспонирование матриц и т. д. Существуют различные типы матриц в зависимости от количества компонентов и организации элементов в матрицах.

В линейной алгебре существует множество типов матриц. Все типы матриц различаются по компонентам, порядку и определенному набору условий. Различные типы матриц: матрица-строка, матрица-столбец, одноэлементная матрица, прямоугольная матрица, квадратная матрица, единичная матрица, нулевая матрица, диагональная матрица и т. д. Существуют также некоторые специальные матрицы.

Какие бывают типы матриц?

В линейной алгебре существуют различные типы матриц. Все типы матриц различаются по компонентам, порядку и определенному набору условий. Различные типы матриц с примерами приведены ниже:

1. Матрица-строка: Любая матрица, имеющая одну строку и n столбцов, называется матрицей-строкой.

т.е. \(A=\left[a_{11}\dots..a_{1n}\right]_{1\times n} \)

Пример матрицы строк:

\(P=\begin{bmatrix }\ 1&-3&17\end{bmatrix} \)

2. Матрица-столбец: Любая матрица, имеющая m строк и один столбец, называется матрицей-столбцом.

т.е. \(A=\begin{bmatrix}a_{11}\\\vdots\\a_{m1}\end{bmatrix}_{m\times1}\)

Пример матрицы столбца:

\(Q=\begin{bmatrix}2\\3\\7\end{bmatrix}\)

3. Нулевая матрица или нулевая матрица: Любая матрица, в которой все компоненты равны нулю, называется нулевой матрицей. Она также распознается как нулевая матрица и обозначается O. нулевая матрица порядка 3 x 3.

4. Одноэлементная матрица: Любая матрица называется одноэлементной, если матрица имеет только один элемент.

т. е. \(A=\left[a_{ij}\right]_{ m\times n}\) является одноэлементной матрицей, если m = n = 1.

Пример одноэлементной матрицы:

\(\left [4\right],\left[7\right],\left[b\right]\) являются примерами одноэлементной матрицы.

5. Квадратная матрица: Любая матрица, в которой количество строк равно количеству столбцов, скажем «A», называется квадратной матрицей порядка n.

т. е. \(A=\left[a_{ij}\right]_{ m\times n}\) объявляется квадратной матрицей порядка n, если m = n.

Пример квадратной матрицы:

\(B=\begin{bmatrix}2&3&6\\3&4&5\\6&5&9\end{bmatrix}\)

6. Прямоугольная матрица:  Матрица идентифицируется как прямоугольная, если количество строк не совпадает с количеством столбцов.

Пример прямоугольной матрицы:

\(B=\begin{bmatrix}2&3&6&-1\\3&4&5&5\\6&5&9&-1\end{bmatrix}\)

Здесь мы видим, что есть четыре столбца и три строки в эта матрица, поэтому B является прямоугольной матрицей.

7. Горизонтальная матрица:  Матрица порядка m x n называется горизонтальной матрицей, если n > m. То есть, если количество столбцов больше, чем количество строк в горизонтальной матрице.

\(B=\begin{bmatrix}1&2&3&4\\4&3&2&1\end{bmatrix}\)

8. Вертикальная матрица:  Матрица порядка m x n называется вертикальной, если m > n. То есть, если количество строк больше, чем количество столбцов в вертикальной матрице.

\(B=\begin{bmatrix}1&1\\2&5\\3&6\\2&4\end{bmatrix}\)

9. Диагональная матрица:  Любая квадратная матрица, в которой все компоненты равны нулю, за исключением компонентов в главная диагональ называется диагональной матрицей.

т. е. \(A=\left[a_{ij}\right]_{n\times n}\) является диагональной матрицей, если \(a_{ij}=0\) для i не равно j.

Пример диагональной матрицы:

\(B=\begin{bmatrix}2&\ 0&\ \ 0\\0&\ 1&\ \ 0\\0&\ 0&-2\end{bmatrix}_{3\times3}\ )

\(P=\begin{bmatrix}1&0&0&0\\0&5&0&0\\0&\ 0&2&0\\0&0&0&4\end{bmatrix}\)

Здесь мы можем понять, что кроме диагональных элементов все остальные элементы равны до нуля. Следовательно, вышеупомянутый тип матрицы в математике является диагональной матрицей.

10. Прямоугольные диагональные матрицы: Прямоугольная диагональная матрица — это тип матрицы, которая также имеет одну ведущую диагональ с числами, а остальные записи — нули. Ведущая диагональ выбирается из самого большого квадрата в неквадратной матрице.

\(\begin{bmatrix}1&0&0&0&0\\0&4&0&0&0\\0&0&7&0&0\end{bmatrix}\)

11. Скалярная матрица: Диагональная матрица, в которой все главные диагональные компоненты равны, называется скалярной матрицей.

Пример скалярной матрицы:

\(B=\begin{bmatrix}2&\ 0&\ 0\\0&\ 2&\ 0\\0&\ 0&\ 2\end{bmatrix}_{3\times3}\)

\(B=\begin{bmatrix}-5&\ 0&\ 0\\0&\ -5&\ 0\\0&\ 0&-5\end{bmatrix}_{3\times3}\)

12. Единичная матрица или единичная матрица: Диагональная матрица, в которой все главные диагональные компоненты равны 1, называется единичной матрицей. Она также признается единичной матрицей. Единичная матрица порядка n обозначается I или \(I_{n}\).

Примеры матрицы идентичности:

\(I_2=\begin{bmatrix}1&\ \ 0\\0&\ \ 1\end{bmatrix}\)

\(B=\begin{bmatrix}1&0&0\\0&1&0\ \0&0&1\end{bmatrix}_{3\times3}\)

Узнать об определителях и сложении и вычитании алгебраических выражений

Специальные типы матриц

Существуют специальные типы матриц, которые применяются в передовых математических вычислениях и компьютерных технологиях:

1. Вырожденные и невырожденные матрицы: Любая квадратная матрица, определитель которой равен нулю называется сингулярной матрицей, а любая матрица, определитель которой не равен нулю, называется невырожденной матрицей.

Пример сингулярной матрицы:

\(B=\begin{bmatrix}1&\ 1&1\\1&1&1\\1&1&1\end{bmatrix}\left|B\right|=\begin{vmatrix}1&1&1\\1&1&1\\ 1&1&1\конец{vmatrix}=1\влево(1-1\вправо)-1\влево(1-1\вправо)+1\влево(1-1\вправо)\влево|B\вправо|=0+0 +0=0\)

Пример невырожденной матрицы:

\(B=\begin{bmatrix}2&\ 1&1\\1&2&1\\1&1&1\end{bmatrix}\left|B\right|=\begin{vmatrix}2&1&1\\1&2&1 \\1&1&1\end{vmatrix}=2\влево(2-1\вправо)-1\влево(1-1\вправо)+1\влево(1-2\вправо)\влево|B\вправо|=2 -0-1=1\)

Любая квадратная матрица называется треугольной матрицей , если элементы выше или ниже главной диагонали равны нулю. Существует 2 типа треугольных матриц, как показано ниже:

2. Верхнетреугольная матрица: Любая квадратная матрица, где указано \(A=\left[a_{ij}\right]_{n\times n}\), называется верхнетреугольной матрицей, если \(a_{ij}= 0\) ∀ i > j.

Пример верхней треугольной матрицы:

\(B=\begin{bmatrix}2&\ 3&\ \ 4\\0&\ 1&\ \ 5\\0&\ 0&-2\end{bmatrix}_{3\times3} \)

3. Нижняя треугольная матрица: Любая квадратная матрица, например \(A=\left[a_{ij}\right]_{n\times n}\), называется нижней треугольной матрицей, если \(a_{ ij}=0\) ∀ i < j. 9{’} (транспонировать A) \)тогда A называется кососимметричной матрицей.

Пример кососимметричной матрицы:

\(Q=\begin{bmatrix}\ 0&\ \ 3\\-3&\ \ 0\end{bmatrix}\)

Характеристики симметричных и кососимметричных матриц

• Для кососимметричной матрицы A все ее диагональные элементы равны нулю. то есть \(a_{ii\left(i=j\right)}=0\) ∀ i и j.
• Нулевая матрица / Нулевая матрица является как симметричной, так и кососимметричной матрицей.
• A+B и AB также являются симметричными матрицами. 9{\ тета} \).

  \(Q=\begin{bmatrix}0&\ -2+i\\2-i&\ \ \ \ \ 0\end{bmatrix}\)

  Подробнее о матрице преобразования

  Типы матриц в табличной форме

  The types of matrices with examples are given in the tabular form below:

  Type of Matrices	Matrix Representation Details	Matrix Example
  Row Matrix	\( A=\left[a_{ij}\right]_{1\times n}\)	\(P=\begin{bmatrix}\ 1&-3&17\end{bmatrix}\)
  Матрица столбцов	\(A=\left[a_{ij}\right]_{m\times1} \)	\(Q=\begin{bmatrix}2\\3\\7\end{bmatrix}\)
  Нулевая или нулевая матрица	\(A=\left[a_{ij}\right ]_{m\times n}\text{где }a_{ij}=0\)	\(B=\begin{bmatrix}0&0&0\0&0&0\0&0&0\end{bmatrix}_{3\times3}\)
  Одноэлементная матрица	\(A=\left[a_{ij}\right]_{m\times n}\text{где }m=n=1\)	\(\left[4\right],\left[7\right],\left[b\right]\)
  Горизонтальная матрица	\(A=\left[a_{ij}\right ]_{m\times n}\text{ где }n\gt m\)	\(B=\begin{bmatrix}1&2&3&4\\4&3&2&1\end{bmatrix}\)
  Вертикальная матрица	\ (A=\left[a_{ij}\right]_{m\times n}\text{, где }m>n\)	\(B=\begin{bmatrix}1&1\\2&5\\3&6\\ 2&4\end{bmatrix}\)
  Квадратная матрица	\(A=\left[a_{ij}\right]_{m\times n}\text{где }m=n\)	\(B=\begin{bmatrix}2&3&6\\3&4&5\\ 6&5&9\end{bmatrix}\)
  Диагональная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{где} a_{ij}=0\text { for } i\ne j\)	\(P=\begin{bmatrix}1&0&0&0\\0&5&0&0\\0&\ 0&2&0\\0&0&0&4\end{bmatrix}\)
  Скалярная матрица	\(A =\left[a_{ij}\right]_{n\times n}\text{ где }a_{ij}=\begin{Bmatrix}0&i\ne j\\k&i=j\end{Bmatrix}\) Здесь k — константа.	\(B=\begin{bmatrix}-5&\ 0&\ 0\\0&\ -5&\ 0\\0&\ 0&-5\end{bmatrix}_{3\times3}\)
  Идентичность или единичная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{, где }a_{ij}=\begin{Bmatrix}0&i\ne j\\1&i= j\end{Bmatrix}\)	\(B=\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}_{3\times3}\)
  Равная матрица	\(A =\left[a_{ij}\right]_{m\times n}\text{ и }B=\left[b_{ij}\right]_{r\times s}\text{ где}a_{ij }=b_{ij},\ m=r,\text{ и } n=s\)	\(A=\begin{bmatrix}2&-5\\2&\ 4\end{bmatrix},\ B=\begin{bmatrix}2&-5\\2&\ 4\end{bmatrix}\) Здесь A и B — равные матрицы.
  Верхняя треугольная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{ for }a_{ij}=0\ ∀\ i>j\)	\(B=\begin{bmatrix}2&\ 3&\ \ 4\\0&\ 1&\ \ 5\\0&\ 0&-2\end{bmatrix}_{3\times3}\)
  Нижний Треугольная матрица	\(A=\left[a_{ij}\right]_{n\times n}\text{ for }a_{ij}=0\ ∀\ i	\(B=\begin{bmatrix}2&\ 0&\ \ 0\\3&\ 1&\ \ 0\\4&\ 5&-2\end{bmatrix}_{3\times3}\)
  Единственное число Матрица	\(\left|A\right|=0\)	\(B=\begin{bmatrix}1&\ 1&1\\1&1&1\\1&1&1\end{bmatrix}\)
  Несингулярный Матрица	\(\left|A\right|\ne 0\)	\(B=\begin{bmatrix}2&\ 1&1\\1&2&1\\1&1&1\end{bmatrix}\)
  Симметричные матрицы 9{m} = O\), где O — нулевая матрица порядка n.	–

  Узнайте об определителе матрицы 4 x 4

  Важные моменты по типам матриц
  • Для матричных произведений матрицы должны быть совместимы. Это утверждает, что две матрицы A и B совместимы, если количество столбцов в A= количеству строк в B.
  • Если мы умножаем матрицу на скалярное значение, то это распознается как скалярное умножение.
  • Чтобы матрица была симметричной, она должна быть квадратной, т. е. иметь одинаковое количество строк и столбцов.
  • Если m=n, матрица считается квадратной.
  • Если m \ne n, матрица считается прямоугольной.
  • Здесь m обозначает количество строк, а n обозначает количество столбцов.
  • Диагональная матрица, в которой все главные диагональные компоненты равны 1, называется единичной матрицей. Она также распознается как единичная матрица, тогда как единичная матрица порядка n обозначается \(I\) или \(I_n\).
  • Единичная матрица, нулевая матрица или нулевая матрица, а также скалярная матрица являются примерами диагональной матрицы, поскольку во всех них неглавным диагональным элементам присваивается нуль.

  Мы надеемся, что приведенная выше статья о типах матриц поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным с математикой темам и другим подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.

  Часто задаваемые вопросы о типах матриц

  В.1 Каковы различные типы матриц?

  Ответ 1 Существуют следующие типы матриц: матрица-строка, матрица-столбец, одноэлементная матрица, прямоугольная матрица, квадратная матрица, единичная матрица, нулевая матрица, диагональная матрица и т. д.

  Q.2 Can вы добавляете матрицы с разными размерностями?

  Ответ 2 Для выполнения сложения или вычитания матриц они должны иметь одинаковый размер или размерность. Если сложение или разность двух матриц, имеющих разные размеры или размерности, не определены.

  No related posts.