Возведение матрицы в степень
|
|
|
|||||||||||||||||||||||||||||||
Частное решение.
Угол между ними.
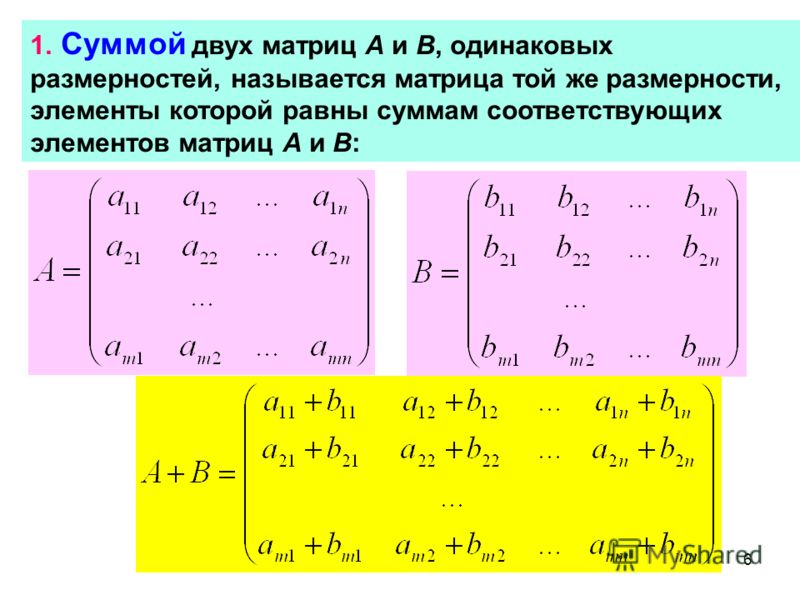
Матрица смежности онлайнЧто такое матрица Эйзенхауэра и как ее использовать
Матрица Эйзенхауэра — это классический метод тайм-менеджмента.
Он помогает правильно организовывать свои задачи и распределять время, чтобы укладываться в сроки и всё успевать.
Матрицу приоритетов Эйзенхауэра, как её называют американцы, придумал 34-й президент США Дуайт Эйзенхауэр, чтобы справляться со своими обязанностями и служить стране. Однако широкую известность метод получил после того, как о нём рассказал американский консультант Стивен Кови в книге «Семь навыков высокоэффективных людей».
В этой статье мы разберём, как матрица Эйзенхауэра помогает планировать время, зачем её приверженцы делят тетрадный лист на четыре квадрата и как применять матрицу в работе.
Чем полезна матрица Эйзенхауэра и как ей пользоваться
Иногда задач становится слишком много, и вы уже не знаете, как с ними справиться. Собаку нужно отвести к ветеринару, заболел зуб, на работе «горит» проект, нужно забрать из садика ребёнка. Матрица Эйзенхауэра позволяет не растеряться, правильно распределить дела и сделать всё вовремя.
В основе матрицы лежит простой принцип: важно расставить приоритеты и не делать лишнего.
Составьте список дел. Чтобы понять фронт работы на день, выпишите все дела на листок. Это поможет всё взвесить и правильно распределить время.
Рассортируйте задачи. Чтобы составить план по Эйзенхауэру, достаточно поделить лист бумаги на четыре части и распределить дела по срочности: сделать сразу, запланировать, поручить другим и не тратить время.
Это матрица Эйзенхауэра. Её можно начертить на простом листе. По сути, вы распределяете все дела на день на 4 квадрата: что сделать важно, что несрочно, что можно поручить коллегам и на что не стоит тратить время
Матрица Эйзенхауэра позволяет расставить приоритеты, понять, что действительно важно и не тратить время на ерунду. Ведь хороший тайм-менеджмент — это не «успевать всё», а «регулярно успевать делать то, что тебе важно». Если вы целый день носились с чужими задачами и ничего не успели из своего, это плохой тайм-менеджмент.
Квадрат 1: горящие задачи сделать первыми
Квадрат пожаров.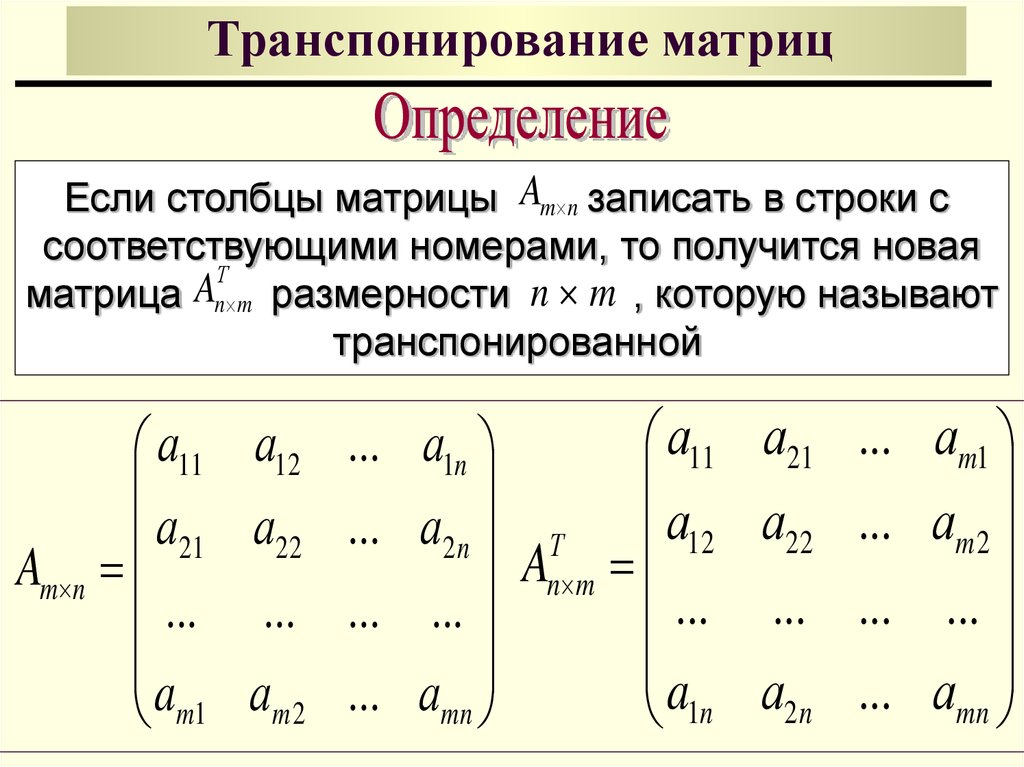
Это место для срочных и важных дел, которые внезапно возникли из-за форс-мажора или кризиса. Их отличительная черта — серьёзные последствия из-за срыва. Например, начальник лишил премии из-за вовремя не сданного отчёта.
На что обратить внимание. В этом квадрате всегда будут появляться дела — это неизбежно. Постоянная работа в авральном режиме приводит к хроническому стрессу и выгоранию.
Если количество «срочняков» не уменьшается, попробуйте устранить их источник. Например, договориться с руководством ставить задачи вовремя, а не в последний момент.
Квадрат 2: несрочные дела отложить на потом
Стратегический квадрат. Сюда попадают важные дела, за которые необязательно хвататься сразу — их можно сделать в течение дня. Главное — не забыть, чтобы не разгорелся новый «пожар».
На что обратить внимание. В идеале проводить в этом квадрате большую часть своего времени. Так вы будете чувствовать удовлетворение от своей работы и жизни в целом, не будете выгорать.
Задачи из этого квадрата — то, что делает ваш будущий успех.
Квадрат 3: делегировать или отказаться от неважных дел
Квадрат рутины. Сюда попадают срочные задачи, которые вместо вас может сделать кто-нибудь другой. Например, коллеги, друзья или родственники.
Сюда попадает рутина, которая отнимает время, выматывает и мешает делать «настоящую работу». Принцип простой — если можете нагрузить других, сделайте это.
На что обратить внимание. Третий квадрат очень коварный, его легко перепутать с первым квадратом. Вы можете наслаждаться галочками напротив закрытых пустяковых дел и попасть в иллюзию продуктивности, но при этом чувствовать, что просто суетитесь и занимаетесь совершенно не тем. Результат — хроническая неудовлетворённость и выгорание.
Такие дела лучше максимально автоматизировать или делегировать. Например, попросите купить продукты жену или сына вынести мусор.
Квадрат 4: ограничить время на ерунду
«Квадрат — чёрная дыра».
Сюда попадают задачи, которые не имеют ни ценности, ни дедлайнов и не стоят внимания. Например, полистать соцсети.
Чем больше вы заняты делами из четвёртого квадрата, тем глубже погружаетесь в «чёрную дыру». И уже не остаётся времени на важное.
На что обратить внимание. Переходите к делам из четвёртого квадрата в последнюю очередь, когда остальное сделано. Хорошая идея — наблюдать за тем, сколько времени вы находитесь в «чёрной дыре», и немного себя ограничивать. Например, смотреть только по серии «Игры престолов» в день или тратить по часу на соцсети.
Где составлять матрицу Эйзенхауэра
Эйзенхауэр планировал дела в ежедневнике. Сейчас не забыть о важном также помогают специальные программы и приложения.
Блокнот. Начертите четыре отдельных квадрата и разлинуйте их для записи задач. Для наглядности можно использовать разные цвета.
Матрицу Эйзенхауэра можно начертить в простом блокноте
Компьютер.
Для планирования задача подойдёт Word или Excel. Чтобы сделать таблицу нагляднее, можно выделить ячейки цветом по степени важности.
Матрица Эйзенхауэра в Excel
Приложения формата to-do list. Они созданы под смартфоны, поэтому список дел всегда будет под рукой. Здесь есть готовые шаблоны и напоминания о задачах, чтобы ничего не забыть.
Матрица Эйзенхауэра в Evernote. Приложение для смартфонов и компьютеров с возможностью бесплатной подписки. Есть готовый шаблон для планирования задач
Матрица Эйзенхауэра в 4.Do. Бесплатное мобильное приложение на Android с матрицей на русском языке. Главный плюс — можно добавлять напоминания о задачах
Матрица Эйзенхауэра в Focus Matrix. Бесплатное мобильное приложение для iOS на английском языке. Можно создать напоминания и отчёты по выполненным задачам
Как планировать дела: метод Эйзенхауэра
- Чтобы понять фронт работы на день, выпишите все дела на листок. Это поможет всё взвесить и правильно распределить время.
- Суть метода — сортировать задачи в зависимости от важности на четыре категории: сделать сразу, приступить позже, делегировать и не тратить время.
- Посвящайте день только срочным делам и проектам, в которых без вас не обойтись. Остальное подождёт.
- Если задачу может сделать кто-нибудь другой, делегируйте. Останется больше времени на по-настоящему важное.
Как успевать вдвое больше за то же время — онлайн-курсы от Академии iSpring
Матрица Эйзенхауэра — лишь один из инструментов тайм-менеджмента, который помогает не жить в огне.
Другие способы управлять временем, людьми и собой — в библиотеке онлайн-курсов Академии iSpring. Курсы для руководителей и личной эффективности помогут научиться правильно планировать проекты, управлять командой, проводить совещания и давать обратную связь подчинённым, чтобы зарядить их на результат и принести пользу бизнесу.
Используем быстрое возведение матриц в степень для написания очень быстрого интерпретатора простого языка программирования / Хабр
Недавно на хабре появилась неплохая статья про вычисление N-ного числа фибоначи за O(log N) арифметических операций.
Разумный вопрос, всплывший в комментариях, был: «зачем это может пригодиться на практике». Само по себе вычисление N-ого числа фибоначи может и не очень интересно, однако подход с матрицами, использованный в статье, на практике может применяться для гораздо более широкого круга задач.
В ходе этой статьи мы разберем как написать интерпретатор, который может выполнять простые операции (присвоение, сложение, вычитание и урезанное умножение) над ограниченным количеством переменных с вложенными циклами с произвольным количеством итераций за доли секунды (конечно, если промежуточные значения при вычислениях будут оставаться в разумных пределах). Например, вот такой код, поданный на вход интерпретатору:
loop 1000000000
loop 1000000000
loop 1000000000
a += 1
b += a
end
end
end
end
Незамедлительно выведет a = 1000000000000000000000000000, b = 500000000000000000000000000500000000000000000000000000, несмотря на то, что если бы программа выполнялась наивно, интерпретатору необходимо было бы выполнить октиллион операций.
Я полагаю, что у читателя есть представление о том, что такое матрица, и что такое произведение матриц. В рамках этой статьи мы будем использовать исключетельно квадратные матрицы и полагаться на очень важное свойство умножения квадратных матриц — ассоциативность.
Для простоты ограничим наш интерпретатор четырьмя переменными — A, B, C и D. Для представления состояния интерпретатора в заданный момент будем использовать вектор размера пять, первые четыре элемента которого будут содержать значения четырех переменных соответственно, а последний будет на протяжении всей работы интерпретатора равен единице.
(A, B, C, D, 1)
В начале работы интерпретатора будем полагать значения всех переменных равными нулю.
(0, 0, 0, 0, 1)
Допустим, что первая операция в коде программы содержит строку
A += 5
Эффект этой команды заключается в том, что значение переменной A увеличится на пять, в то время как значения остальных трех переменных не изменятся.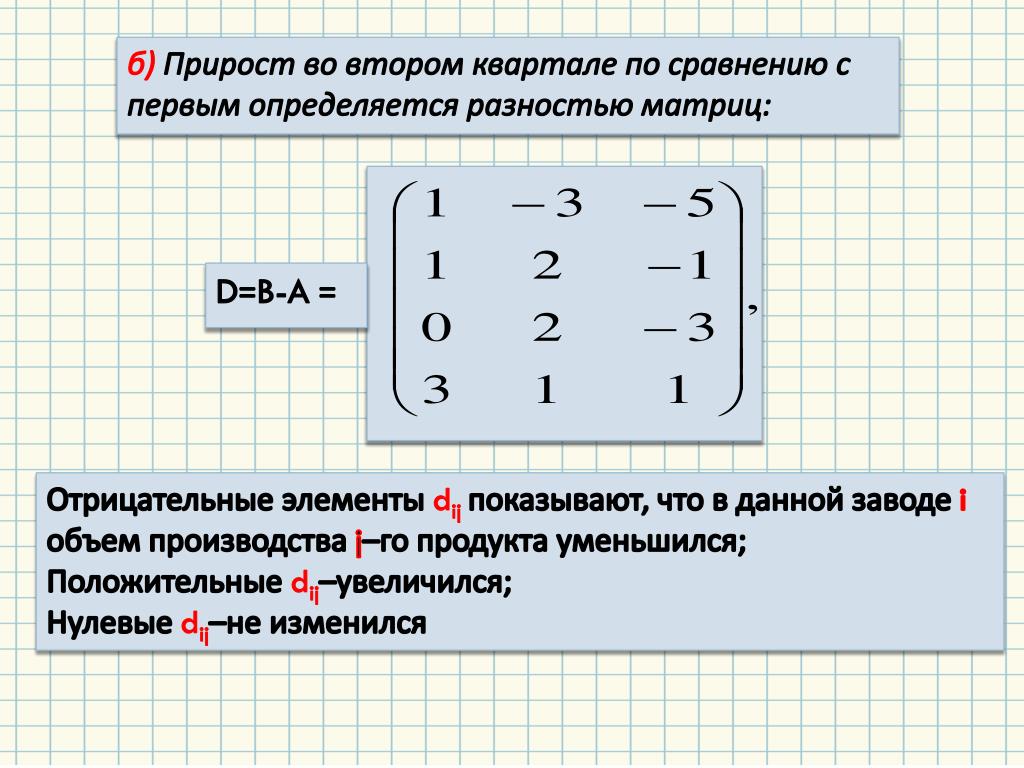
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 5 0 0 0 1
Если посмотреть на нее, можно заметить, что она почти идентична единичной матрице (которая, как известно, при умножении любого вектора на нее не меняет его значения), за исключением последнего элемента в первом столбце, который равен пяти. Если вспомнить, как происходит умножение вектора на матрицу, можно понять, что значения всех элементов, кроме первого, не изменятся, в то время как значение первого элемента станет равно
v[0] * 1 + v[4] * 5
Так как v[0] содержит текущее значение в переменной A, а v[4] всегда равен единице, то
v[0] * 1 + v[4] * 5 = A + 5
Если вектор текущего состояния умножить на эту матрицу, полученный вектор будет соответствовать состоянию, в котором A на пять больше, что и требовалось.
Если матрицу поменять немного, убрав единицу в первом элементе первой строки:
0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 5 0 0 0 1
Как и прежде, значения всех элементов кроме первого не изменятся, в то время как первый элемент станет равным v[4] * 5, или просто пяти.
Умножение вектора текущего состояния на такую матрицу эквивалентно выполнению команды
A = 5
Посмотрим на такую матрицу:
1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 0 1
Единственное отличие ее от единичной матрицы — это второй элемент в четвертой строке, который равен единице. Очевидно, что умножение вектора текущего состояния на эту матрицу не изменит значения в первом и последних трех элементах, в то время как значение второго элемента изменится на
v[1] * 1 + v[3] * 1
Так как v[1] содержит текущее значение переменной B, а v[3] содержит текущее значение переменной D, то умножение вектора состояния на такую матрицу эквивалентно выполнению команды B += D
Аналогично рассуждая можно понять, что умножение вектора состояния на следующую матрицу эквивалентно выполнению команды C *= 7
1 0 0 0 0 0 1 0 0 0 0 0 7 0 0 0 0 0 1 0 0 0 0 0 1
Перейдем к комбинированию команд. Пусть вектор v задает текущее состояние, матрица Ma соответствует команде A += 5, а матрица Mm соответствует команде A *= 7.
3
Мы вычисляем матрицу, соответствующую телу цикла, только один раз, после чего возводим ее в степень.
Рассмотренных примеров достаточно, чтобы начать работать над интерпретатором простого языка, поддерживающего присваивание, сложение, вычитание, умножение (только на константу) и циклы. Для этого мы научимся представлять любую такую программу в виде матрицы размера N+1 на N+1, где N — это количество переменных, которыми программа оперирует, после чего будем просто умножать вектор с начальным состоянием на эту матрицу.
Правила представления программы в виде матрицы очень просты:
1. Каждая отдельная команда представляется в виде матрицы, отличающейся от единичной одним элементом (или двумя для операции присваивания). Примеры таких матриц рассмотрены выше в этой статье.
2. Несколько подряд идущих команд представляются в виде матрицы, равной произведению матричного представления каждой отдельной команды.
3. Цикл представляется в виде матрицы, представляющей тело цикла, возведенной в степень количества итераций цикла.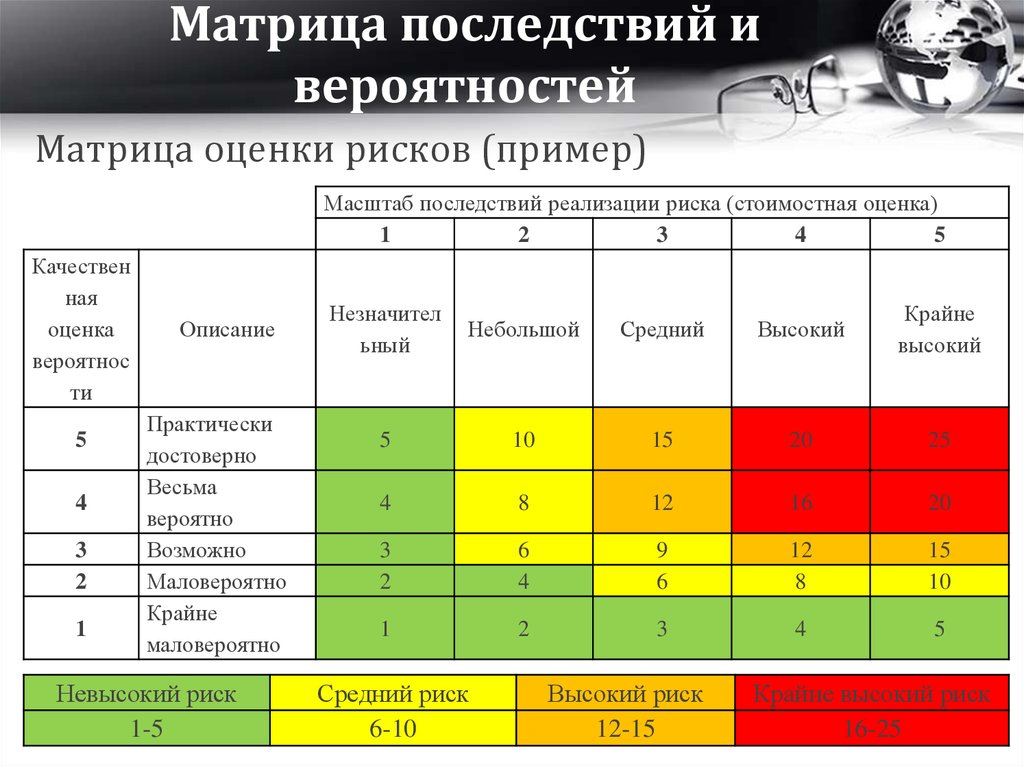
Если у нас есть функция identity, возвращающая единичную матрицу:
def identity():
return [[1 if i == j else 0 for j in range(REGS + 1)] for i in range(REGS + 1)]То фукнция, строящая матрицу для команды r1 += r2 (где r1 и r2 — переменные) может выглядеть так:
def addreg(r1, r2):
ret = identity()
ret[r2][r1] = 1
return retА для команды r += val (r — переменная, val — константа) вот так:
def addval(r, val):
ret = identity()
ret[REGS][r] = val
return retФункции для построения матриц других команд выглядят похоже — получается единичная матрица, в которой заменяется один элемент.
Интерпретатор без циклов теперь пишется очень просто — пусть матрица mat соответствует уже прочитанному коду. В начале она равна единичной матрице, потому что пустая программа не меняет состояния. Затем мы считываем команды по одной, разбиваем их на три элемента (левый операнд, оператор, правый операнд), и в зависимости от оператора домножаем матрицу, соответствующую всей программе, на матрицу, соответствующую текущей команде:
def doit():
mat = identity()
while True:
line = sys. stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur)
stdin.readline().lower()
tokens = line.split()
if tokens[0] == 'loop':
# тут будет код для циклов
elif tokens[0] == 'end':
return mat
else:
r1 = reg_names.index(tokens[0])
try:
r2 = reg_names.index(tokens[2])
except:
r2 = -1
if tokens[1] == '+=':
if r2 == -1: cur = addval(r1, long(tokens[2]))
else: cur = addreg(r1, r2)
elif tokens[1] == '-=':
....
mat = matmul(mat, cur)Осталось дело за малым — добавить поддержку циклов. Цикл возводит матрицу тела цикла в степень количества итераций цикла. Возведение в степень, как известно, требует только O(log N) операций, где N — это степень, в которую матрица возводится. Алгоритм возведения в степень очень прост:
1. Если степень равна нулю, вернуть единичную матрицу.
2. Если степень четная, пусть 2N, то можно рекурсивно вычислить M^N, а затем вернуть квадрат получившейся матрицы.
2N, и вернуть полученную матрицу, умноженную на M.
Так как каждые две итерации степень сокращается в двое, сложность такого алгоритма логарифмическая.
def matpow(m, p):
if p == 0: return identity()
elif p % 2 == 0:
tmp = matpow(m, p / 2)
return matmul(tmp, tmp)
else: return matmul(m, matpow(m, p - 1))В интерпретаторе теперь осталось добавить одну строку:
...
if tokens[0] == 'loop':
cur = matpow(doit(), long(tokens[1]))
...И интерпретатор готов.
Пример интерпретатора доступен на гитхабе. Весь код занимает меньше 100 строк.
Для теста скорости можно вернуться к уже упомянутым числам фибоначи. Например, такой код:
A = 1 B = 1 loop 100 C = A C += B A = B B = C end end
Вычислит 101-ое и 102-ое числа фибоначи:
A = 573147844013817084101, B = 927372692193078999176
Замена 100 на 1000000 вычислит миллион первое и миллион второе числа за четыре секунды.
Выполнение такой программы в лоб заняло бы гораздо больше, потому что программе приходится оперировать многотысячезначными числами. Если написать код, которому не приходится оперировать большими числами, например код для вычисления суммы арифметической прогрессии, приведенный в начале статьи, то количество итераций может уходить за рамки разумного, но код будет выполняться за доли секунды
loop 1000000000000000000000000000000000000000000000
loop 1000000000000000000000000000000000000000000000
loop 1000000000000000000000000000000000000000000000
a += 1
b += a
end
end
end
endНа практике этот подход может применяться, например, в оптимизирующих компиляторах, которые могут таким образом сворачивать циклы с большим количеством итераций, оперирующие на небольшом количестве переменных.
Online Calculator: Degree of Matrix
A 2 =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 5121 | 682 | 682 | 218 | 000 |
| 571 | 155 | 146 | 69 | ||
| 221 | 131 | 140 | 84 | ||
| 337 | 107 | 107 | 57 |
.
Расчет элементов матрицы:
S 11 11 11 11 11 11 11 11 . 12 * б 21 + а 13 * б 31 + а 14 * б 41 = 71 * 71 + 8 * 7 + 8 * 4 + 122 * 14; 
5 * 5 + 2 * 5 = 107;с 43 = a 41 * b 13 + a 42 * b 23 + a 43 * b 33 + a 44 * б 43 = 4 * 8 + 5 * 5 + 5 * 8 + 2 * 5 = 107;с 44 = а 41 * б 14 + а 42 * б 24 + а 43 * б 34 + а 44 * б 44 = 4 * 2 + 5 * 2 + 5 * 7 + 2 * 2 = 57;
A 3 =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 5121 | 682 | 682 | 218 | 000 |
| 571 | 155 | 146 | 69 | ||
| 221 | 131 | 140 | 84 | ||
| 337 | 107 | 107 | 57 |
| 000 | 370601 | 50924 | 50924 | 16816 | 000 |
| 42194 | 6883 | 6856 | 2612 | ||
| 17224 | 3936 | 3963 | 1852 | ||
| 25118 | 4372 | 4372 | 1751 |
Calculation of elements Матрицы:
С 11 = A 11 * B 11 + A 12 * B 21 + A 13 * B 31 + A 13 * B 31 + A 13 * B 31 + A 13 * B 31 + A 0147 41 = 71 * 5121 + 8 * 571 + 8 * 221 + 2 * 337 = 370601; C 12 = A 11 * B 12 + A 12 * B 22 + A 12 * B 22 + A 12 * B 22 + A * B 32 + A 14 * B 42 = 71 * 682 + 8 * 155 + 8 * 131 + 2 * 107 = 50924; C 13 = A 11 * B 13 = A 11 * B 13 = A 11 * B 13 = A 11 * B 13 = A а 12 * б 23 + а 13 * б 33 + а 14 * б 43 = 71 * 682 + 8 * 1509 + 8 * 14024;с 14 = a 11 * b 14 + a 12 * b 24 + a 13 * b 34 + a 14 * b 44 = 71 * 218 + 8 * 69 + 8 * 84 + 2 * 57 = 16816;с 21 = а 21 * б 11 + а 22 * б 21 + а 107 84 19 44 * 93 93 а 24 * б 41 = 7 * 5121 + 8 * 571 + 5 * 221 + 2 * 337 = 42194;с 22 = а 21 * б 12 + а 22 * б 22 + а 23 * б 32 + а 24 * б 42 = 7 * 682 + 7 * 1581 + 5; с 23 = a 21 * b 13 + a 22 * b 23 + a 23 * b 33 + a 24 * b 43 = 7 * 682 + 8 * 146 + 5 * 140 + 2 * 107 = 6856;с 24 = а 21 * б 14 + а 22 * б 24 + а 23 * б 34 + а 24 * б 44 = 7 * 218 + 8 * 69 + 5 * 84 + 2 * 57 = 2612 + a 32 * B 21 + A 33 * B 31 + A 34 * B 41 = 2 * 5121 + 571 + 8 * 221 + 727743743 = 2 * 5121 + 571 + 8 * 221 + 72 * 33743743 = 2 * 5121 + 571 + 8 * 221 + 727743 = 2 * 5121 + 571 + 8 * 221 + 72743; с 32 = а 31 * б 12 + а 32 * б 22 + а 33 * б 32 + 8 б 40147 42 = 2 * 682 + 5 * 155 + 8 * 131 + 7 * 107 = 3936;с 33 = а 31 * б 13 + а 32 * 1 б 29144 * б 33 + а 34 * б 43 = 2 * 682 + 5 * 146 + 8 * 140 + 7 * 107 = 3963 а 32 * б 24 + а 33 * б 34 + а 34 * б 44 = 2 * 218 + 5 * 69 + 8 * 852 = 19 * 852;0147 41 = a 41 * b 11 + a 42 * b 21 + a 43 * b 31 + a 44 * b 41 = 4 * 5121 + 5 * 571 + 5 * 221 + 2 * 337 = 25118;с 42 = a 41 * b 12 + a 42 * b 22 + a 43 * b 32 + a 44 * б 42 = 4 * 682 + 5 * 155 + 5 * 131 + 2 * 107 = 4372;с 43 = а 41 * б 13 + а 42 * б 23 + а 43 * б 33 + а 44 * б 43 = 4 * 682 + 7 = 2 * 1441 + 5; С 44 = A 41 * B 14 + A 42 * B 24 + A 43 * B 34 + A 44 * B 34 + A 44 44 944948 * B 34 + A 44 44 .
* 69 + 5 * 84 + 2 * 57 = 1751;
А 4 =
| 000 | 71 | 8 | 8 | 2 | 000 |
| 7 | 8 | 5 | 2 | ||
| 2 | 5 | 8 | 7 | ||
| 4 | 5 | 5 | 2 |
| 000 | 370601 | 50924 | 50924 | 16816 | 000 |
| 42194 | 6883 | 6856 | 2612 | ||
| 17224 | 3936 | 3963 | 1852 | ||
| 25118 | 4372 | 4372 | 1751 |
| 000 | 26838251 | 3710900 | 3710900 | 1233150 | 000 |
| 3068115 | 439956 | 439875 | 151370 | ||
| 1265790 | 198355 | 198436 | 73765 | 998 | 73765 | 936 | 73765 | 936 | 73765 | 36 | 73765 | 361829730 | 266535 | 266535 | 93086 |
Calculation of elements of the matrix:
с 11 = a 11 * b 11 + a 12 * b 21 + a 13 * B 31 + A 14 * B 41 = 71 * 370601 + 8 * 42194 + 8 * 17224 + 2 * 25118 = 26838251; S 12 = A .
+ а 12 * б 22 + а 13 * B 32 + A 14 * B 42 = 71 * 50924 + 8 * 6883 + 8 * 3936 + 2 * 4372 = 3710900; C 13 = A 9 * B 13 = A 9 * B 13 = A 9 * B 13 = A 9 * B 13 = A 9 * B 13 = A 9 ; A 12 * B 23 + A 13 * B 33 + A 14 * B 43 = 71 * 50924 + 8 * 6856 + 8 * 3963 + 2 * 4372 = 4372 = 4372 = 4372 = 4372 = 4372 = 4372 = 4372; 14 = а 11 * б 14 + а 12 * б 24 + а 13 * б 34 + а 14 * B 44 = 71 * 16816 + 8 * 2612 + 8 * 1852 + 2 * 1751 = 1233150; C 21 = A 21 * B 11 + A 22 * B 11 + A 22 * B 210148 + A 22 * B 210148 + A 21 * B 210148 + A 21 * B 11 + A 21 * B 11 + A 21 * B 210148 + A 21 * B A 23 * B 31 + A 24 * B 41 = 7 * 370601 + 8 * 42194 + 5 * 17224 + 2 * 25118 = 3068115; C 22 = A 9114 * * * * * * * * * * * * * * * * * * * * * * .
12 + а 22 * б 22 + а 23 * б 32 + а 24 * б 42 = 7 * 50924 + 8 * 6883 + 5 * 3936 + 2 * 4372 = 439956;с 23 = a 21 * b 13 + a 22 * b 23 + a 23 * b 33 + A 24 * B 43 = 7 * 50924 + 8 * 6856 + 5 * 3963 + 2 * 4372 = 439875; C 24 = A 21 * B 14 + A 21 * B 14 + A * * B 14 + A * .
24 + а 23 * б 34 + а 24 * б 44 = 7 * 16816 + 8 * 2612 + 5 * 1852 + 2 * 1751 = с159730147 31 = a 31 * b 11 + a 32 * b 21 + a 33 * b 31 + a 34 * b 41 = 2 * 370601 + 5 * 42194 + 8 * 17224 + 7 * 25118 = 1265790; C 32 = A 31 * B 12 + A 32 * B 22 + A 33 * B 22 + A 33 * B 22 + A 33 * B 22 + A 33 .
* б 42 = 2 * 50924 + 5 * 6883 + 8 * 3936 + 7 * 4372 = 198355;с 33 = а 31 * б 13 + a 32 * B 23 + A 33 * B 33 + A 34 * B 43 = 2 * 50924 + 5 * 686 + 86 * 396 + 836 + 86 + 836 + 86 + 86 + 86 + 86 + 86 + 86 + 86 + 86 * 396 + 836 + 86 * 396 + 836 + 836 + 86 * 396 + 86 * 396 + 836 + 836 + 86 * 396 + 86 * 396 + 836 + 836 + 86 * 396 + 86 * 396 + 86 * 396 + 86 * 396 + 86 * 396 + 86 * 343 * 346 + 86 * 34 * 433. 198436; C 34 = A 31 * B 14 + A 32 * B 24 + A 33 * B 34 + A 34 * B 34 + A 347 347 34 * B 34 + A 33 .
+ 5 * 2612 + 8 * 1852 + 7 * 1751 = 73765;с 41 = а 41 * б 11 + а 42 * б 21 + A 43 * B 31 + A 44 * B 41 = 4 * 370601 + 5 * 42194 + 5 * 17224 + 2 * 25118 = 1829730; o * b 12 + a 42 * b 22 + a 43 * b 32 + a 44 * b 42 = 4 * 50924 + 5 * 6883 + 5 * 3936 + 2 * 4372 = 266535;с 43 = а 41 * б 13 + а 42 * б 23 + а 43 * б 33 + A 44 * B 43 = 4 * 50924 + 5 * 6856 + 5 * 3963 + 2 * 4372 = 266535; С 44 = A 41 * B 147747 14747 14747 14747 14747 14747 14747 14747 14747 40147 40147.
* б 24 + а 43 * б 34 + а 44 * б 44 = 4 * 16816 + 5 * 2612 + 5 * 1852 + 12 * 9758;
Ответ:
| 000 | 26838251 | 3710900 | 3710900 | 1233150 | 3710900 | 1233150 | 0007 000
| 3068115 | 439956 | 439875 | 151370 | |||
| 1265790 | 198355 | 198436 | 73765 | |||
| 1829730 | 266535 | 266535 | 93086 |
Matrix Подход
Сопоставление результатов обучения по программе и курсовых занятий в матрице обеспечивает богатое графическое представление содержания программы и может использоваться в качестве отправной точки для оценки программы.
Геологические факультеты нескольких школ, в том числе Карлтонского колледжа, Колледжа Уильяма и Мэри и Университета штата Монтана, использовали «матричный подход» к оценке и пересмотру своих учебных планов и программ. Этот подход и варианты подробно описаны ниже.
Показать подпись
Скрыть
Матрица коммуникативных навыков геологического факультета Карлтонского колледжа. «a» указывает всегда, а «s» указывает иногда.
Перейти вниз к: Цели и предположения | Построение матриц | Использование вашей матрицы | Пример использования матричного подхода в разработке учебных программ | Ссылки и дополнительная литература
Преимущества матричного подхода
Этот подход имеет преимущества как для студентов, так и для преподавателей (см. Savina et al., 2001): стилей, формирование самосознания и коллегиальности.
Цели и допущения при таком подходе
- Студенты, проходящие обучение по программе получения степени, будут иметь предсказуемые возможности для ознакомления с идеями и практическими навыками в течение своей академической карьеры.
- Эти возможности будут предоставлены как в классе во время обязательных и факультативных курсов, так и вне класса во время внеклассных мероприятий, таких как экскурсии, наставничество сверстников и участие в студенческих организациях.
- Выпускники в рамках специальности должны владеть набором заранее определенных, специфичных для дисциплины навыков и иметь возможность практиковать эти навыки несколько раз в течение своей академической карьеры.
- Выпускники также должны были развить набор более общих навыков, таких как общение, анализ и количественные методы, как часть их опыта по специальности.
- Определение набора результатов обучения на уровне программы (PLLO) для программы на получение степени является отправной точкой для анализа пробелов, планирования учебного плана и программы, а также для разработки оценки программы.
Построение матриц
Изображение матрицы курса наук о Земле (Acrobat (PDF), 147 КБ, 4 сентября 14 г.) для Университета штата Монтана.
В своей основе матрица представляет собой визуальное представление соответствия между навыками, которыми должны обладать учащиеся, и возможностями, которые у них есть для их изучения. Представленная здесь форма помещает результаты обучения на уровне программы в левый столбец матрицы и группирует их по областям содержания, например, по предметным знаниям, навыкам решения проблем и коммуникативным навыкам. Вы можете построить несколько матриц, чтобы посмотреть на развитие навыков на нескольких уровнях детализации, как показано в матрицах ниже.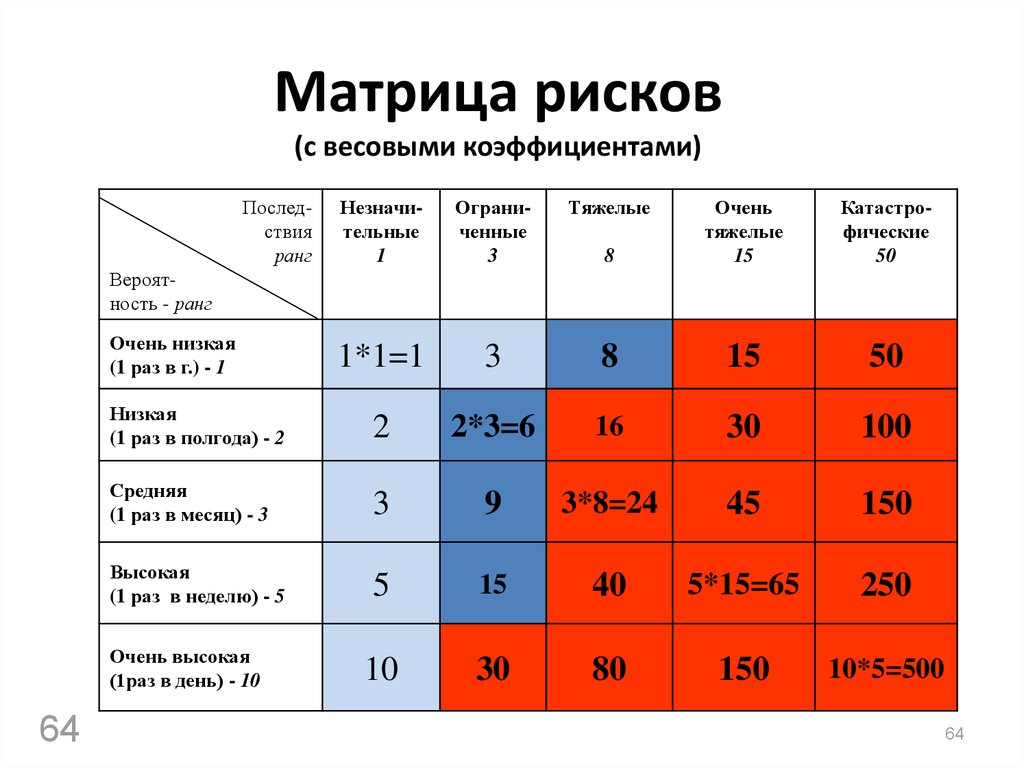
Это позволяет вам посмотреть, где в учебной программе практикуется каждый навык, и найти пробелы в учебной программе.
ПРИМЕР : В этом примере матрица учебного плана, построенная с использованием только необходимых курсов программы, была объединена с более полной матрицей, которая включала более широкий спектр мероприятий, спонсируемых отделом.
Матрица основного курса (Acrobat (PDF), 64 КБ, 4 сентября 14 г.), Матрица курса наук о Земле (Acrobat (PDF), 147 КБ, 4 сентября 14 г.). Предоставлено Дэвидом Могком из Университета штата Монтана
ПРИМЕР : Матрица программы, основанная на 10 результатах обучения по программе. Этот пример включает в себя основные ядра, обязательные курсы и дисциплинарные факультативы в списке возможностей обучения.
Дополнительная ссылка
Родс, Д.Д., 2011, Картирование учебных программ и результатов обучения для улучшения оценки программы: Геологическое общество Америки, рефераты с программами, т.
43, вып. 5, с. 300.
Пример матрицы программы (Excel 2007 (.xlsx) 22kB Sep4 14). Предоставлено Далласом Родесом из Южного университета Джорджии
Если вы начнете с пустого шаблона матрицы (Excel 51 КБ, 4 сентября 14 г.), это может помочь при построении матрицы, адаптированной к вашей программе.
Использование матрицы
Заполнив матрицу, вы можете приступить к разработке плана, чтобы оценить, на каком этапе находится программа с точки зрения достижения поставленных вами целей. Можно ли разумно ожидать, что ученики овладеют навыками, которые вы считаете важными, учитывая, как часто они практикуют каждый из них? Как работает то, что у вас есть сейчас? Какие навыки могут нуждаться в дополнительных возможностях для практики? Какие возможности существуют или могут быть созданы за пределами классной комнаты?
Пример использования матричного подхода при разработке учебных программ
В 2103 году Департамент наук о Земле Университета штата Монтана построил матрицу в рамках процесса пересмотра своей учебной программы бакалавриата.
Дэвид Могк предоставил подробный отчет (Curriculum by Design, часть первая и часть вторая) о том, как матричный подход использовался в этом процессе.
Ссылки и дополнительная литература
- Макдональд, Р. Хизер и Бейли, Кристофер М., 2000. Интеграция преподавания количественных навыков в учебную программу по геологии на факультете. Журнал образования в области наук о Земле, т. 48, н. 4, с. 482-486.
- Савина, Мэри Э., Бухвальд, К. Эдвард, Байс, Дэвид М. и Бордман, Шелби Дж., 2001 г. Матрица навыков как инструмент планирования учебной программы геологического факультета. Документ GSA № 79-0.
Матричная алгебра | GTPE
Массовый открытый онлайн-курс
- Обзор
- Содержание курса
- Требования и материалы
Обзор
Описание курса
Ваша способность применять понятия, которые мы представили в нашем предыдущем курсе, улучшается, когда вы можете выполнять алгебраические операции с матрицами.
В начале этого занятия вы увидите, как мы можем применить теорему об обратимой матрице, чтобы описать, как можно использовать квадратную матрицу для решения линейных уравнений. Эта теорема играет фундаментальную роль в линейной алгебре, поскольку она синтезирует многие понятия, введенные в первом курсе, в одно сжатое понятие.
Затем вы изучите теоремы и алгоритмы, которые позволят вам применять линейную алгебру способами, включающими две или более матриц. Вы изучите разделенные матрицы и матричные факторизации, которые появляются в большинстве современных применений линейной алгебры. Вы также изучите два приложения матричной алгебры: в экономике и в компьютерной графике.
Учащимся, посещающим этот курс, рекомендуется сначала пройти первый курс из этой серии — «Линейные уравнения».
Еще
Содержание курса
MATRIX OPERATIONS
INVERSE OF A MATRIX
INVERTIBLE MATRICES
APPLICATION: PARTITIONED MATRICES
APPLICATION: THE LU FACTORIZATION
APPLICATION: THE LEONTIF INPUT-OUTPUT MODEL
КОМПЬЮТЕРНАЯ ГРАФИКА
ПОДПРОСТРАНСТВА RN
РАЗМЕР И РАНГ
Подробнее
Требования и материалы
Необходимые условия
Рекомендуется
Требуется
Материалы
Требуется
- Интернет-соединение (желательно DSL, LAN или кабельное соединение)
- Программа для чтения PDF-файлов Adobe Acrobat (бесплатная загрузка доступна на странице get. adobe.com/reader/)
adobe.com/reader/)Еще
ИДЕНТИФИКАТОР КУРСА: DL 0051M
Контактный телефон для вопросов, связанных с курсом
Грегори Майер
Зарегистрироваться сейчас
Кому следует посещать
Этот курс предназначен для студентов старших курсов, старшеклассников, которые заинтересованы в карьере программа обучения или получения степени, включающая линейную алгебру, или работники отрасли, которые стремятся лучше понять линейную алгебру для развития своей карьеры.
Чему вы научитесь
- Обратимость матрицы с использованием теоремы об обратимой матрице
- LU-факторизация матрицы и применение LU-факторизации для решения систем уравнений
- Построение матриц преобразований для представления составных преобразований с однородными координатами, которые необходимы для приложений компьютерной графики
- Как построить базис подпространства
- Как вычислить координаты вектора в заданном базисе
- Как охарактеризовать матрицу, используя концепции ранга, пространства столбца и пустого пространства
Какую пользу вы получите
- Применение матричной алгебры, транспонирования матриц, нулевой и единичной матриц для решения и анализа матричных уравнений.
- Примените формальное определение инверсии и ее алгебраические свойства для решения и анализа линейных систем.
- Применение секционированных матриц для решения задач на обратимость матриц и умножение матриц.
- Применение теорем о ранге, базисе и обратимости матриц для описания матриц, подпространств и систем.
- Применение концепций матричной алгебры для моделирования, решения и анализа реальных ситуаций, включая Леонтифовскую модель ввода-вывода и компьютерную графику.
- Составьте или приведите примеры математических выражений, включающих векторы, матрицы и линейные системы линейных уравнений.
- Анализ математических утверждений и выражений, использующих линейные системы и матрицы. Например, для описания решений систем в терминах обратимости и подпространств.
Хотите просмотреть все массовые открытые онлайн-курсы?
Массовые открытые онлайн-курсы
Расписание курса было хорошо структурировано и включало лекции, обсуждения в классе и практические занятия под руководством знающих и увлеченных инструкторов.
Access (ADA)
Глобальный учебный центр Технологического института Джорджии и кампус Технологического института Джорджии в Саванне соответствуют требованиям Закона об американцах-инвалидах. Любой человек, которому требуется проживание для участия в любом курсе, предлагаемом GTPE, должен связаться с нами до начала курса.
Оценка
Курсы, которые являются частью сертификационных программ, включают обязательную оценку. Критерии прохождения определяются инструктором и предоставляются учащимся в начале курса.
Посещаемость
CEU присуждаются участникам, которые посещают не менее 80% запланированного времени занятий.
Гражданство
Управление безопасности исследований и соблюдения нормативных требований Технологического института Джорджии требует сохранения информации о гражданстве для тех, кто участвует в большинстве курсов GTPE. Информация о гражданстве получается непосредственно от учащегося во время регистрации и хранится в Системе студентов Технологического института Джорджии.
Кодекс поведения
Учащиеся, зачисленные на любую из программ профессионального образования Технологического института Джорджии, считаются членами сообщества Технологического института Джорджии и должны соблюдать все правила и процедуры, установленные Институтом, включая Кодекс поведения учащихся и академическую честь. Код.
Изменение и отмена курса
Полную информацию о правилах изменения и отмены курса см. в наших Условиях использования.
Сбор и хранение данных
Участники курсов GTPE должны заполнить онлайн-профиль, соответствующий требованиям безопасности Технологических исследований Джорджии. Собранная информация хранится в системе студентов Технологического института Джорджии. Следующие элементы данных считаются справочной информацией и собираются от каждого участника в рамках процесса регистрации и настройки профиля:
- Полное юридическое имя
- Адрес электронной почты
- Адрес доставки
- Название компании
Эти данные не публикуются в онлайн-справочной системе Технологического института Джорджии и, следовательно, в настоящее время недоступны для широкой публики.
Информация об учащемся используется только так, как описано в нашей Политике конфиденциальности. Данные GTPE не продаются и не предоставляются внешним организациям.
Конфиденциальные данные
Следующие элементы данных, если они находятся в студенческих системах Технологического института Джорджии, считаются конфиденциальной информацией и доступны только сотрудникам Технологического института Джорджии, которым это необходимо знать:
- Технический идентификатор Джорджии
- Дата рождения
- Гражданство
- Пол
- Этническая принадлежность
- Религиозные предпочтения
- Номера социального страхования
- Регистрационная информация
- Расписания занятий
- Записи о посещаемости
- Академическая история
В любое время вы можете отозвать свое согласие на получение маркетинговых электронных писем, а также запросить удаление ваших личных данных. Посетите нашу страницу GTPE EU GDPR для получения дополнительной информации.
Ненастная погода
Занятия и мероприятия, проводимые в Глобальном учебном центре Технологического института Джорджии в Атланте или кампусе Технологического института Джорджии в Саванне, могут быть закрыты или задержаны из-за ненастной погоды.
Глобальный учебный центр Технологического института Джорджии будет следовать указаниям главного кампуса Технологического института Джорджии в Атланте. Студенты, гости и преподаватели должны проверить домашнюю страницу Технологического института Джорджии , чтобы получить информацию о закрытии университетов или задержке открытия из-за ненастной погоды. Обратите внимание, что если кампус закрыт по каким-либо причинам, все классные занятия также отменяются.
Студенты, гости и преподаватели, посещающие занятия и мероприятия в Технологическом институте Джорджии, должны проверить домашнюю страницу Технологического института Джорджии, чтобы получить информацию о закрытии или задержке открытия из-за ненастной погоды.
Завершение программы
Сертификаты GTPE об окончании программы состоят из установленного количества обязательных и факультативных курсов, предлагаемых и пройденных в Технологическом институте Джорджии в течение последовательного шестилетнего периода.
Исключения, такие как запросы на замену или зачет за предшествующее образование, могут быть запрошены через форму петиции. Исключения не могут быть гарантированы.
Возврат средств
Полную информацию о правилах возврата средств см. в наших Условиях использования.
Курение и табачные изделия
Технологический институт Джорджии — это кампус без табака и курения. Использование сигарет, сигар, трубок, всех форм бездымного табака и любых других курительных устройств, в которых используется табак, строго запрещено. На территории кампуса нет специально отведенных мест для курения.
Специальные скидки
Курсы, на которые распространяются специальные скидки, будут соответствующим образом отмечены на странице курса. В процессе оформления заказа можно ввести только один код купона, и его нельзя активировать после завершения оформления заказа. Если вы уже зарегистрировались и забыли использовать код купона, вы можете запросить соответствующий возврат средств.
GTPE отменит любую транзакцию, в которой купон был использован не по назначению или не соответствовал требованиям. Если вы не уверены, можете ли вы использовать код купона, обратитесь к администратору курса.
ГТПО не имеет программы для пенсионеров. Тем не менее, Технологический институт Джорджии предлагает программу 62 лет и старше для жителей Джорджии в возрасте 62 лет и старше, которые заинтересованы в прохождении кредитных курсов. Эта программа не оплачивает некредитные курсы профессионального образования. Посетите страницу приема в бакалавриат Технологического института Джорджии, чтобы получить дополнительную информацию о программе бакалавриата, и страницу приема в аспирантуру Технологического института Джорджии, чтобы получить дополнительную информацию о программе магистратуры.
Как работают МООК?
МООК, предназначенные для онлайн-аудитории, доступны для всех, у кого есть подключение к Интернету, и регистрация на них бесплатна. Некоторые МООК можно начинать в любое время, другие – через регулярные промежутки времени, а их продолжительность варьируется от нескольких недель до нескольких месяцев.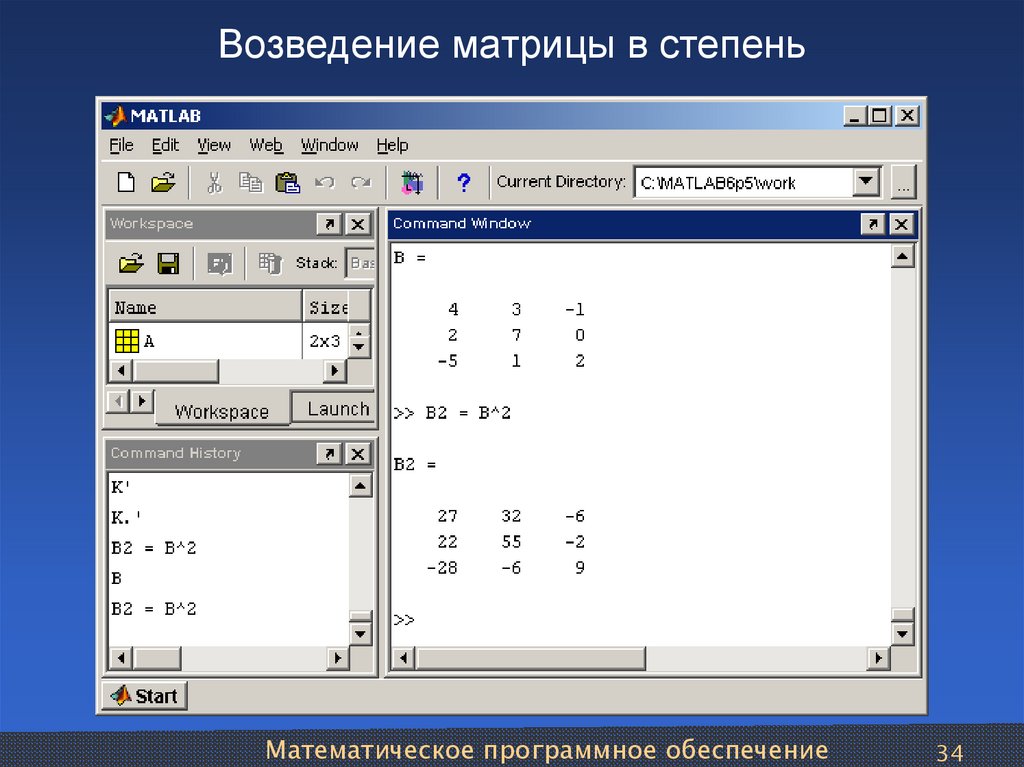
У вас будет доступ к широкому спектру онлайн-медиа и интерактивных инструментов, включая видеолекции, классные упражнения, обсуждения и оценки.
Кто может участвовать в МООК?
Любой, у кого есть подключение к Интернету, может зарегистрироваться. Курсы для малого и среднего бизнеса могут быть недоступны в небольшом числе стран из-за торговых ограничений или государственной политики.
Как записаться на МООК?
Посетите платформы поставщиков МООК — edX, Coursera или Udacity — для регистрации на МООК. Затем просмотрите предварительно записанные лекции, изучите материалы курса и выполните соответствующую работу, например викторины, а в некоторых случаях и окончательные проекты.
Сколько стоят МООК?
Большинство курсов бесплатны, хотя за получение сертификата об окончании взимается небольшая плата. Некоторые курсы засчитываются в университетский кредит, а некоторые, например наша онлайн-магистерская программа по компьютерным наукам, предлагают полную степень.
Эти кредитные курсы действительно имеют сборы и приложения, связанные с ними.
Могу ли я получить CEU за пройденный МООК?
Да, Технологический институт Джорджии предлагает CEU для некоторых завершенных курсов MOOC, пройденных через Coursera и edX. У вас есть возможность приобрести CEU после получения проверенного сертификата курса.
Что такое цифровой значок?
Цифровой бейдж является подтверждением того, что вы успешно завершили курс МООК. Вы можете отобразить свой цифровой значок в своих онлайн-профилях, чтобы коллеги и работодатели могли сразу увидеть ваши достижения.
Какие еще учетные данные доступны после прохождения МООК?
Вы можете заработать CEU, цифровые значки и подтвержденные сертификаты об окончании. Вы также можете использовать MOOC в качестве альтернативного пути для поступления на магистерские программы Технологического института Джорджии через программы MicroMasters «Аналитика: основные инструменты и методы» и онлайн-магистратуры в области компьютерных наук.