Матрица высшая математика примеры: Примеры решения задач

alexxlab / / Разное

Решение высшей математики онлайн

‹— Назад

        Определение 14.1   Матрицей размеров называется прямоугольная таблица чисел, содержащая строк и столбцов. Числа, составляющие матрицу, называются элементами матрицы.        

Обычно принято обозначать матрицы большими буквами, а саму таблицу чисел заключать в круглые скобки. Например,  — матрица размеров ,  — матрица размеров , или другими словами, матрица-столбец,  — матрица размеров , или матрица-строка.

Иногда вместо круглых скобок в записи матрицы используют квадратные или двойные прямые линии. Например, или .

Если элементы матрицы обозначаются буквами, то для этого обозначения используется та же буква, что и для обозначения матрицы, только не большая, а малая, и эта буква снабжается двумя индексами.

Например, матрицу размеров можно записать в виде

В этой записи означает, что элемент находится в строке с номером и столбце с номером , то есть первый индекс указывает номер строки, а второй — номер столбца. Например, в матрице

, .

Наряду с указанным обозначением элементов матрицы используется также обозначение , в котором номер строки указывает верхний индекс, а номер столбца — нижний.

Укажем основные типы матриц.

Если число строк матрицы равно числу столбцов, то матрица называется квадратной. Число строк или, что то же самое, число столбцов в ней называется порядком матрицы.

Если все элементы матрицы равны нулю, то матрица называется нулевой. Нулевая матрица обозначается обычной цифрой 0. Как правило, из контекста ясно, является ли этот 0 числом или матрицей.

Совокупность элементов квадратной матрицы, расположенных на отрезке, соединяющем левый верхний угол с правым нижним, называется главной диагональю матрицы.

Например, в матрице главную диагональ образуют числа . Отметим, что при обозначении элементов матрицы буквами с двумя индексами у элементов главной диагонали и только у них индексы будут равны друг другу. Так у квадратной матрицы порядка элементами главной диагонали являются элементы , .

Квадратная матрица, у которой все элементы вне главной диагонали равны нулю, называется диагональной. Примеры диагональных матриц:

Квадратная матрица называется верхней треугольной (нижней треугольной), если все ее элементы, стоящие ниже (выше) главной диагонали, равны нулю. Например, верхние треугольные матрицы:

Нижние треугольные матрицы:

Верхняя треугольная матрица иногда называется правой треугольной, а нижняя треугольная — левой треугольной.

Единичной матрицей называется диагональная матрица, у которой все элементы главной диагонали равны 1. Для обозначения единичной матрицы обычно используется буква . Порядок матрицы при этом обычно ясен из контекста. Например,  — единичная матрица третьего порядка.

Из определения единичной матрицы видно, что ее элементы равны нулю, если индексы различны, и равны 1, если индексы совпадают. В математике таким свойством обладает величина , называемая символом Кронекера:

Поэтому .

Две матрицы называются равными, если они имеют одинаковые размеры и элементы, стоящие на одинаковых местах, равны друг другу.

Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции

Раздел 3.

Линейная алгебра с элементами аналитической геометрии

Раздел 3. Линейная алгебра с элементами аналитической геометрии

6.

Матрицы, определители

6.1.

Основы линейной алгебры. Матрицы. Виды матриц. Операции над матрицами

Сегодня вы изучите вопросы

  1. Основы линейной алгебры

  2. Основные понятия линейной алгебры

  3. Понятие матрицы

Изучив тему занятия, вы сможете

  • умножать матрицу на число;

  • производить линейные операции над матрицами;

  • умножать матрицы;

  • возводить матрицы в натуральную степень.

Элементы линейной алгебры широко используются при решении большого числа прикладных экономических и управленческих задач. Успешное усвоение основных понятий данного занятия является основой для ее применения.

Основные понятия

6.1.1.

Матрица. Основные понятия

Матрицей размера называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,…, X, Y, Z, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: , где

 — номер строки;

 — номер столбца.

Например, матрица размеров имеет вид:

или в сокращенной записи

Например, матрица размеров имеет вид:

.

Наряду с круглыми скобками для обозначения матриц используются

и другие:

Две матрицы А и В одинаковой размерности называются равными, если при всех

Виды матриц

Матрица, состоящая из одного столбца, называется матрицей (вектором)-столбцом и обозначается , а состоящая из одной строки — матрицей (вектором)-строкой, соответственно обозначается .

Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n:

.

Элементы образуют главную диагональ квадратной матрицы порядка n, а элементы  — побочную диагональ.

Например,

 — квадратная матрица третьего порядка, элементами главной диагонали являются числа 1, 5, 9, а побочной — 7, 5 ,3.

Если все элементы, кроме элементов, образующих главную диагональ квадратной матрицы, равны нулю, то такая матрица называется диагональной.

Например,  — диагональная матрица третьего порядка.

Если у диагональной матрицы n-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей n-го порядка и обозначается буквой Е.

Например,  — единичная матрица третьего порядка.

Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О. Нулевая матрица имеет следующий вид:

.

В линейной алгебре матрицы Е и О играют такую же роль, какую играют числа 1 и 0 в арифметике.

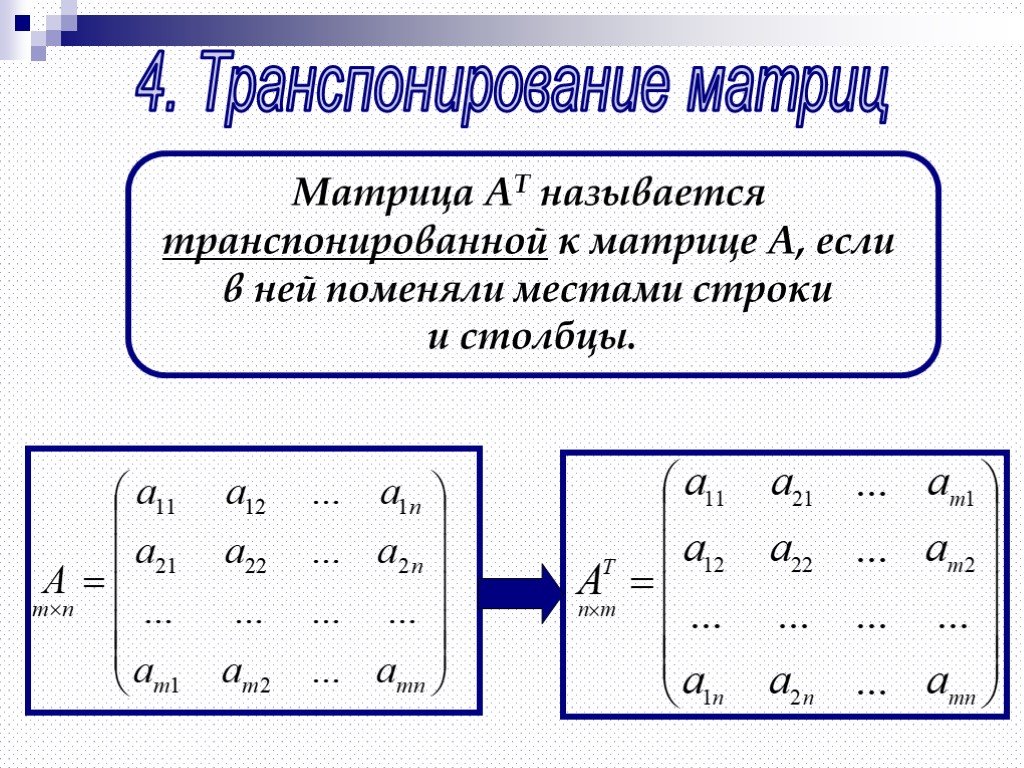
Матрица, полученная из данной матрицы А заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной и обозначается .

Пример 1. Так, если , то .

Транспонированная матрица обладает следующим свойством: .

6.1.2.

Действия над матрицами

Умножение матрицы на число

Пусть  — произвольная матрица,  — произвольное действительное число.

Произведением матрицы А на число называется новая матрица, каждый элемент которой равен произведению соответствующего элемента матрицы А на число , т.е.

.

Например,

Таким образом, можно выделить следующее следствие.

Общий множитель всех элементов матрицы можно выносить за знак матрицы.

Сложение и вычитание матриц

Эта операция определяется только для матриц одинаковой размерности (формата).

Суммой двух матриц А и В одинаковой размерности называется новая матрица С того же размера, каждый элемент которой равен сумме соответствующих (стоящих на одинаковых местах) элементов данных матриц.

Например, пусть А и В — матрицы размерности . Тогда по определению под суммой понимается

или .

Вышеприведенные действия над матрицами называются линейными.

Линейные операции над матрицами обладают следующими свойствами.

  1. Переместительность (коммутативность) умножения матрицы на число .

  2. Сочетательность (ассоциативность) со скалярным множителем .

  3. Переместительность (коммутативность) сложения матриц .

  4. Сочетательность (ассоциативность) сложения матриц .

  5. Распределительность (дистрибутивность) сложения матриц относительно умножения на число .

  6. Распределительность (дистрибутивность) относительно сложения чисел .

Таким образом, линейные операции над матрицами можно выполнять по аналогии с привычными правилами алгебры чисел.

Вычитание для матриц (как и для чисел) определяется как действие, обратное сложению. Разностью матриц А и В(А — В) одинаковой размерности называется такая матрица С, что

В + С = А.

Легко заметить, что матрица С, удовлетворяющая этому условию, всегда существует, и притом только одна. Ее элементы определяются равенствами

.

Таким образом, при вычитании матриц вычитаются соответствующие элементы этих матриц.

Например, .

Замечание. Знаки сравнения () для матриц любого формата лишены смысла.

Умножение матриц

Умножение матрицы А на матрицу В (рассматриваются именно в таком порядке) определено, если число столбцов первой матрицы равно числу строк второй матрицы. В этом случае матрица А называется согласованной с матрицей В.

Иначе говоря, если порядок матрицы А равен , то порядок согласованной с ней матрицы В должен быть , где  — любые натуральные числа.

Произведением матрицы на матрицу называется такая матрица , что

, где

Таким образом, для вычисления элемента , стоящего в строке и в столбце матрицы С, следует каждый элемент строки матрицы А умножить на соответственный элемент столбца матрицы В и результат сложить.

Примеры:

    1) .

    2) .

Умножение матриц обладает следующими свойствами:

    1) ;

    2) ;

    3) ;

    4) .

Заметим, что умножение матриц некоммутативно: .

Выше было определено, что операция умножения имеет место только для согласованных матриц А и В, при этом матрицы, взятые в ином порядке (В и А), могут оказаться несогласованными, тогда их произведение не определено. Но даже в том случае, когда согласованность матриц не нарушается, произведения АВ и ВА могут оказаться разными.

Например, для матриц

и имеем:

, но

.

Если АВ = ВА, то матрицы А и В называются перестановочными (коммутирующими). Очевидно, это может иметь место только в том случае, когда А и В — квадратные матрицы одного и того же порядка.

Например, коммутирующими являются матрицы

и .

Действительно,

,

то есть для данных матриц АВ = ВА.

Еще одно замечание: произведение двух матриц может быть нуль-матрицей, даже если ни один из сомножителей не является нуль-матрицей.

Например, пусть даны матрицы и . Найдем произведение АВ и ВА:

;

.

Отсюда следует, что умножение матриц обладает рядом свойств, не характерных для умножения действительных чисел, поэтому при действиях с матрицами необходимо проявлять осмотрительность и аккуратность.

В заключение, отметим свойства, присущие операции транспонирования:

    1) ;

    2) ;

    3) .

Возведение в степень

На основе определения произведения матриц умножать матрицу А на себя можно только в том случае, если это квадратная матрица.

Пусть k — целое неотрицательное число, тогда k-й степенью квадратной матрицы А называется матрица, которая вычисляется следующим образом:

Пример. Найти куб матрицы .

;

.

Контрольные вопросы

  1. Что называется матрицей? Перечислите виды матриц.

  2. Какую роль в линейной алгебре играют единичная и нулевая матрицы?

  3. Какая матрица называется диагональной?

  4. Дайте определение квадратной матрицы.

  5. Какая матрица называется транспонированной по отношению к данной?

  6. Для каких матриц определена операция сложения?

  7. Перечислите основные свойства сложения матриц.

  8. Какие матрицы называются коммутирующими между собой?

  9. Для каких матриц определена операция умножения?

  10. Перечислите основные свойства умножения матриц.

Задания для самостоятельной работы

Задание 1. Примеры для самоподготовки

(действия над матрицами)

  1. Найти сумму матриц

    +

    Ответ. 

  2. Найти сумму матриц

    +

    Ответ. 

  3. Найти сумму матриц

    +

    Ответ.  

  4. Найти разность матриц

     —

    Ответ. 

  5. Найти разность матриц

     —

    Ответ. 

  6. Найти произведение действительного числа на матрицу

    Ответ. 

  7. Найти произведение действительного числа на матрицу

    Ответ. 

  8. Найти произведение матриц

    ∙

    Ответ. 

  9. Найти произведение матриц

    ∙

    Ответ. 

  10. Найти произведение матриц

    ∙

    Ответ. 

Задание 2. Примеры для самопроверки

(отметьте правильный вариант ответа)

  1. Найти сумму матриц

    +

      1) ;

      2) ;

      3) ;

      4) ;

      5)

  2. Найти сумму матриц

    +

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  3. Найти сумму матриц

    +

      1) ;

      2) ;

      3) ;

      4) ;

      5)

  4. Найти разность матриц

     —

      1) ;

      2) ;

      3)

      4) ;

      5)

  5. Найти разность матриц

     —

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  6. Найти разность матриц

     —

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  7. Найти произведение действительного числа на матрицу

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  8. Найти произведение действительного числа на матрицу

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  9. Найти произведение действительного числа на матрицу

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  10. Найти произведение матриц

    ∙

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  11. Найти произведение матриц

    ∙

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  12. Найти произведение матриц

    ∙

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  13. Найти произведение матриц

    ∙

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  14. Найти произведение матриц

    ∙

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  15. Найти произведение матриц

    ∙

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

  16. Найти произведение матриц

    ∙ :

      1) ;

      2) ;

      3) ;

      4) ;

      5) .

M.5 Расширенные свойства матрицы | СТАТ ОНЛАЙН

Ортогональные векторы

Два вектора, x и y , являются ортогональными , если их скалярное произведение равно нулю.

Например,

\[ e \cdot f = \begin{pmatrix} 2 & 5 & 4 \end{pmatrix} * \begin{pmatrix} 4 \\ -2 \\ 5 \end{pmatrix} = 2* 4 + (5)*(-2) + 4*5 = 8-10+20 = 18\]

Векторы e и f не ортогональны.

\[ g \cdot h = \begin{pmatrix} 2 & 3 & -2 \end{pmatrix} * \begin{pmatrix} 4 \\ -2 \\ 1 \end{pmatrix} = 2*4 + ( 3)*(-2) + (-2)*1 = 8-6-2 = 0\]

Однако векторы g и h ортогональны. Ортогональность можно рассматривать как расширение перпендикуляра для более высоких измерений. Пусть \(x_1, x_2, \ldots , x_n\) будет m -мерных векторов. Тогда линейная комбинация из \(x_1, x_2, \ldots , x_n\) представляет собой любой m -мерный вектор, который может быть выражен как

\[ c_1 x_1 + c_2 x_2 + \ldots + c_n x_n \]

где \(c_1 , \ldots, c_n\) — все скаляры. Например:

\[x_1 =\begin{pmatrix}
  3  \\
  8 \\
  -2
\end{pmatrix},
x_2 =\begin{pmatrix}
  4  \\
  -2 \\
3
\end{pmatrix}\]

\[y =\begin{pmatrix}
  -5 \\
  12 \\
  -8
\end{pmatrix} = 1*\begin{pmatrix} 9{n} c_i x_i , c_i \in \mathbb{R} \} \]

Набор векторов \(x_1, x_2, \ldots , x_n\) является линейно независимым , если ни один из векторов в наборе не может быть выражена как линейная комбинация других векторов. Другой способ думать об этом — набор векторов \(x_1, x_2, \ldots , x_n\) линейно независимы, если единственным решением приведенного ниже уравнения является наличие \(c_1 = c_2 = \ldots = c_n = 0\ ), где \(c_1 , c_2 , \ldots , c_n \) — скаляры, а \(0\) — нулевой вектор (вектор, в котором каждая запись равна 0).

\[ c_1 x_1 + c_2 x_2 + \ldots + c_n x_n = 0 \]

Если набор векторов не является линейно независимым, то они называются линейно зависимыми .

Пример M.5.1

\[ x_1 =\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}, x_2 =\begin{pmatrix} 4 \\ -2 \\ 2 \end{pmatrix }, x_3 =\begin{pmatrix} 6 \\ 8 \\ -2 \end{pmatrix} \]

Существует ли вектор c , такой что

\[ c_1 x_1 + c_2 x_2 + c_3 x_3 = 0 \]

Чтобы ответить на вопрос выше, пусть:

\begin{align} 3c_1 + 4c_2 +6c_3 &= 0,\\ 4c_1 -2c_2 + 8c_3 &= 0,\\ -2c_1 + 2c_2 -2c_3 &= 0 \end{align}

Решение приведенной выше системы уравнений показывает, что единственно возможным решением является \(c_1 = c_2 = c_3 = 0\). Таким образом, \(\{ x_1 , x_2 , x_3 \}\) линейно независим. Один из способов решения системы уравнений показан ниже. Во-первых, вычтите (4/3) раз 1-е уравнение из 2-го уравнения.

\[-\frac{4}{3}(3c_1 + 4c_2 +6c_3) + (4c_1 -2c_2 + 8c_3) = -\frac{22}{3}c_2 = -\frac{4}{3}0 + 0 = 0 \стрелка вправо c_2 = 0 \]

Затем сложите 1-е и 3-е уравнения вместе и подставьте \(c_2 = 0\).

\[ (3c_1 + 4c_2 +6c_3) + 3*(-2c_1 + 2c_2 -2c_3) = -3c_1 + 10 c_2 = -3c_1 + 10*0 = 0 + 3*0 = 0 \Rightarrow c_1 = 0 \]

Теперь подстановка обоих \(c_1 = 0\) и \(c_2 = 0\) в уравнение 2 дает.

\[ 4c_1 -2c_2 + 8c_3 = 4*0 -2*0 + 8c_3 = 0 \Rightarrow c_3 = 0 \]

Итак, \(c_1 = c_2 = c_3 = 0\), и \(\{ x_1 , x_2 , x_3 \}\) линейно независимы.

9T X = \begin{pmatrix}
  -1  \\
  1\\
  -2
\end{pmatrix}  \begin{pmatrix}
x_1 & x_2 & x_3
\end{pmatrix} = -1 \begin{pmatrix}
  1  \\
  -8\\
  8
\end{pmatrix}+ 1
\begin{pmatrix}
  4  \\
  -2\\
  2
\end{pmatrix} — 2 \begin{pmatrix} 90 1  \\
  3 \\
 -2
\end{pmatrix} =
 \begin{pmatrix}
 -1*1 +1*4-2*1 \\
 -1*-8+1*-2- 2*3 \\
 -1*8+1*2-2*-2
\end{pmatrix}=
 \begin{pmatrix}
  0  \\
  0 \\
 0
\end{pmatrix}
\]

Норма вектора или матрицы

 Норма вектора или матрицы является мерой «длины» указанного вектора или матрицы. 2 } \] 9Т А х \leq 0\).

Последние заметки — инженерная математика

См. последние заметки по всем предметам здесь.

Матрицы

Матрица представляет собой набор чисел, расположенных в порядке строк и столбцов. Элементы матрицы необходимо заключать в круглые скобки или скобки.
Ниже показана матрица из 9 элементов.

Эта матрица [M] имеет 3 строки и 3 столбца. К каждому элементу матрицы [M] можно обращаться по номеру строки и столбца. Например, 23 =6

Порядок матрицы :  
Порядок матрицы определяется количеством строк и столбцов.
Порядок матрицы = количество строк × количество. столбцов
Следовательно, матрица [M] является матрицей порядка 3 × 3.

Транспонирование матрицы :  
Транспонирование [M] T матрицы m x n [M] представляет собой матрицу размера n x m, полученную путем замены строки и столбцы [M].
если A= [a ij ] mxn , то A T = [B IJ ] NXM, где B IJ = A JI

Свойства Transpept A Matrix:

  • (A T

    1 9081

    • . B) T = A T + B T
    • (AB) T = B T A T

    Singular and Nonsingular Matrix:  
     

    1. Singular Matrix: A квадратная матрица называется сингулярной матрицей, если ее определитель равен нулю, т. е. |A|=0
    2. Несингулярная матрица: Квадратная матрица называется невырожденной, если ее определитель отличен от нуля.

    Квадратная матрица: В квадратной матрице столько строк, сколько столбцов. т. е. количество строк = количество столбцов.
    Симметричная матрица: Квадратная матрица называется симметричной, если транспонирование исходной матрицы равно ее исходной матрице. т. е. (A T ) = A. 
    Кососимметричная: Кососимметричная (или антисимметричная, или антиметрическая[1]) матрица представляет собой квадратную матрицу, транспонирование которой равно ее отрицательному значению, т.е. (А Т ) = -А.
    Диагональная матрица: Диагональная матрица — это матрица, в которой все элементы вне главной диагонали равны нулю. Термин обычно относится к квадратным матрицам.
    Единичная матрица: Квадратная матрица, в которой все элементы главной диагонали равны единицам, а все остальные элементы равны нулю. Т = А Т А = I
    Идемпотентная матрица: Матрица называется идемпотентной, если A 2 = A
    Инволютивная матрица: Матрица называется инволютивной, если A 2 = I.

     

    Свойства сопряжения:  

    1. A(Adj A) = (Adj A) A = |A| I n
    2. Adj(AB) = (Adj B). (Adj A)
    3. |Adj A|= |A| n-1
    4. Adj(kA) = k n-1 Adj(A)

    Обратная квадратная матрица:

    Здесь |A| не должен быть равен нулю, значит, матрица A должна быть невырожденной.

    свойства обратного:

    1. (A -1 ) -1 = A
    2. (AB) -1 = B -1 A -1
    3. единственный. неособая квадратная матрица может иметь обратную.

    След матрицы:  
    Пусть A=[a ij ] nxn — квадратная матрица порядка n, то сумма диагональных элементов называется следом матрицы, которая обозначается tr(A). tr(A) = a 11 + a 22 + a 33 + ……….+ a nn . Помните, что след матрицы также равен сумме собственных значений матрицы. Например:

    Свойства следа матрицы:
    Пусть A и B — любые две квадратные матрицы порядка n, тогда

    1. tr(kA) = k tr(A), где k — скаляр. .
    2. tr(A+B) = tr(A)+tr(B)
    3. tr(A-B) = tr(A)-tr(B)
    4. tr(AB) = tr(BA)

    Решение системы линейных уравнений:  
    Линейные уравнения могут иметь три возможных решения:
     

    • Нет решения
    • Единственное решение
    • Бесконечное решение

    Ранг матрицы — это номер ранга матрицы: ненулевые строки в сокращенной форме строки или максимальное количество независимых строк или максимальное количество независимых столбцов.
    Пусть A — любая mxn матрица, содержащая квадратные подматрицы разных порядков. Говорят, что матрица имеет ранг r, если она удовлетворяет следующим свойствам:

    1. Она имеет хотя бы одну квадратную подматрицу порядка r с ненулевым определителем.
    2. Все определители квадратных подматриц порядка (r+1) или выше r равны нулю.

    Ранг обозначается как P(A).  
    , если A неособая матрица порядка n, то ранг A = n, т. е. P(A) = n.

    Свойства ранга матрицы:  
     

    1. Если A нулевая матрица, то P(A) = 0, т.е. ранг нулевой матрицы равен нулю.
    2. Если I n является единичной матрицей размера nxn, то P(A) = n.
    3. Ранг матрицы A mxn , P(A) ≤ min(m,n). Таким образом, P(A) ≤ m и P(A) ≤ n.
    4. P(A nxn ) = n, если |A| ≠ 0
    5. Если P(A) = m и P(B)=n, то P(AB) ≤ min(m,n).
    6. Если A и B — квадратные матрицы порядка n, то P(AB) ? П(А) + П(В) – п.
    7. Если A m×1 — ненулевая матрица-столбец, а B 1×n — ненулевая матрица-строка, то P(AB) = 1.
    8. Ранг кососимметричной матрицы не может быть равен единице .

    Система однородных линейных уравнений AX = 0 .
     

    1. X = 0 всегда является решением; означает, что все неизвестные имеют то же значение, что и ноль. (Это также называется тривиальным решением)
    2. Если P(A) = число неизвестных, единственное решение.
    3. Если P(A) < числа неизвестных, бесконечное число решений.

    Система неоднородных линейных уравнений AX = B .
     

    1. Если P[A:B] ≠P(A), решения нет.
    2. Если P[A:B] = P(A) = количество неизвестных переменных, единственное решение.
    3. Если P[A:B] = P(A) ≠ количество неизвестных, бесконечное количество решений.

    Здесь P[A:B] — ранг представления исключения Гаусса для AX = B. 
    Существует два состояния системы линейных уравнений:0018 Система уравнений, имеющая одно или несколько решений, называется согласованной системой уравнений.

  • Несовместимое состояние: Система уравнений, не имеющая решений, называется несовместимой системой уравнений.

Линейная зависимость и линейная независимость вектора:  

Линейная зависимость: Набор векторов X 1 ,X 2 ….X r к 1 ,k 2 …. .k r такое, что: k 1 X 1 + k 2 X 2 +……..k 9 9 r r 902 . 

Линейная независимость: Набор векторов X 1 ,X 2 ….X r называется линейно независимым, если для всех r скаляров k 1 ,k k r такое, что k 1 X 1 + k 2 X 2 +……..k r X r = 0, тогда k 1 = k 2 =……. = k r = 0. 
Как определить линейную зависимость и независимость?  
Пусть X 1 , X 2 ….X r — заданные векторы. Постройте матрицу с заданными векторами в качестве строк.
 

  1. Если ранг матрицы заданных векторов меньше числа векторов, то векторы линейно зависимы.
  2. Если ранг матрицы заданных векторов равен количеству векторов, то векторы линейно независимы.

 

Собственное значение и собственный вектор

Собственный вектор матрицы A — это вектор, представленный матрицей X такой, что при умножении X на матрицу A направление результирующей матрицы остается тем же, что и у вектора X.

Математически приведенное выше утверждение может быть представлено как:

AX = λX

, где A — произвольная матрица, λ — собственные значения, а X — собственный вектор, соответствующий каждому собственному значению.

Здесь мы видим, что AX параллелен X. Итак, X — собственный вектор.

Метод нахождения собственных векторов и собственных значений любой квадратной матрицы A 
Мы знаем, что

AX = λX

=> AX – λX = 0

=> (A – λI) X …..(1)

Приведенное выше условие будет верным, только если (A – λI) сингулярно. Значит,

|A – λI| = 0 …..(2)

(2) называется характеристическим уравнением матрицы.

Корнями характеристического уравнения являются собственные значения матрицы A.

Теперь, чтобы найти собственные векторы, мы просто подставляем каждое собственное значение в (1) и решаем его методом исключения Гаусса, то есть преобразуем расширенную матрицу (A – λI) = 0 в ступенчатую форму строк и решим линейную систему полученных таким образом уравнений.

Некоторые важные свойства собственных значений.0333

  • Собственные значения унитарных и ортогональных матриц имеют единичный модуль |λ| = 1
  • Если λ 1, =λ 2 …….λ n — собственные значения A, то kλ 1 , kλ 2 …….kλ n 90 kA
  • Если λ 1, λ 2 …….λ n — собственные значения A, то 1/λ 1 , 1/λ 2 …….1/λ являются собственными значениями A -1
  • Если λ 1, λ 2 …….λ n – собственные значения A, тогда λ 1 k , λ 2 k …….λ n собственные значения A 903 k
  • Собственные значения A = собственные значения A T (транспонирование)
  • Сумма собственных значений = след A (сумма диагональных элементов A)
  • Произведение собственных значений = |A|
  • Максимальное количество различных собственных значений A = размер A
  • Если A и B две матрицы одного порядка, тогда собственные значения AB = собственные значения BA

    • Вероятность

    Вероятность относится к степени возникновения событий. Когда происходит событие, такое как бросок мяча, выбор карты из колоды и т. д., то должна быть некоторая вероятность, связанная с этим событием.

    Основные термины:

    • Случайное событие: — Если эксперимент повторяется несколько раз в одинаковых условиях, если он не дает каждый раз один и тот же результат, но результат в испытании является одним из нескольких возможных исходов, то такой эксперимент называется случайным событием или вероятностным событием.
    • Элементарное событие — Элементарное событие относится к результату каждого выполненного случайного события. Всякий раз, когда выполняется случайное событие, каждый связанный с ним результат называется элементарным событием.
    • Пространство выборки — Пространство выборки относится к набору всех возможных исходов случайного события. Например, когда подбрасывается монета, возможные исходы — орел и решка.
    • Событие – Событие относится к подмножеству выборочного пространства, связанному со случайным событием.
    • Возникновение события – Говорят, что событие, связанное со случайным событием, произошло, если любое из принадлежащих ему элементарных событий является исходом.
    • Верное событие – Событие, связанное со случайным событием, называется достоверным, если оно всегда происходит всякий раз, когда выполняется случайное событие.
    • Невозможное событие – Событие, связанное со случайным событием, называется невозможным, если оно никогда не происходит при выполнении случайного события.
    • Составное событие — Событие, связанное со случайным событием, называется составным событием, если оно представляет собой непересекающееся объединение двух или более элементарных событий.
    • Взаимоисключающие события – Два или более события, связанные со случайным событием, считаются взаимоисключающими, если любое из них происходит, оно предотвращает возникновение всех других событий. Это означает, что никакие два или более события не могут происходят одновременно в одно и то же время.
    • Исчерпывающие события – Два или более события, связанные со случайным событием, называются исчерпывающими, если их объединение представляет собой выборочное пространство.

    Вероятность события – Если всего p возможных исходов, связанных со случайным экспериментом, и q из них являются благоприятными исходами для события A, то вероятность события A обозначается P(A ) и определяется как 

     P(A) = q/p

    Вероятность ненаступления события A, т. е. P(A’) = 1 – P(A)

    Примечание –

    • Если значение P(A) = 1, то событие A называется уверенным событием.
    • Если значение P(A) = 0, то событие A называется невозможным событием.
    • Кроме того, P(A) + P(A’) = 1

    Теоремы: P(A∪B) = P(A) + P(B) – P(A∩B)

  • P(A∪B) = P(A) + P(B), если A и B исключают друг друга
  • P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(B∩C)- P(C∩A) + P(A ∩B∩C)
  • P(A∩B’) = P(A) – P(A∩B)
  • P(A’∩B) = P(B) – P(A∩B)
  • Расширение теоремы умножения – Пусть A 1 , A 2 , …. ., A n — n событий, связанных со случайным экспериментом, тогда P(A 1 ∩A 2 ∩A 3 ….. A n ) = P(A 1 )P(A 2 /A 1 )P(A 3 /A 2 ∩A 1 ) ….. P(A n /A 1 ∩A 2 ∩A 3 ∩ ….. ∩A n-1 )

    • Total Закон вероятности — . Пусть S — выборочное пространство, связанное со случайным экспериментом, а E 1 , E 2 , …, E n — n взаимоисключающих и исчерпывающих событий, связанных со случайным экспериментом. Если A — любое событие, которое происходит с E 1 или E 2 или … или E n , то
     

     P(A) = P(E  1  )P(A/E  1  ) + P(E  2  )P(A/E  2  ) + ... + P(E  n  )P(A/E  n  )

    Условная вероятность  

    Условная вероятность P(A | B) показывает вероятность того, что событие ‘A’ произойдет при условии, что произошло событие B.

     

    Правило произведения:  
    Получено из приведенного выше определения условной вероятности путем умножения обеих сторон на P(B) 

     P(A ∩ B) = P(B) * P(A|B)

    Формула Байеса  

    Случайные величины  
    набор действительных чисел. Цель состоит в том, чтобы получить представление о результате конкретной ситуации, когда нам даны вероятности различных результатов.

    Дискретное распределение вероятностей – Если вероятности определены для дискретной случайной величины, которая может принимать только дискретный набор значений, то такое распределение называется дискретным распределением вероятностей.

    Непрерывное распределение вероятностей — Если вероятности определены для непрерывной случайной величины, которая может принимать любое значение между двумя числами, то такое распределение называется непрерывным распределением вероятностей.

    Кумулятивная функция распределения –  
    Подобно функции плотности вероятности, кумулятивная функция распределения действительнозначной случайной величины X или просто функция распределения оценивается в , представляет собой вероятность, которая примет значение меньше или равно .
    Для дискретной случайной величины,

    для непрерывной случайной переменной,

    Разнообразное распределение вероятности —

    Однородное распределение, также известное как Distrablibulation . .
    Он имеет непрерывную случайную переменную, ограниченную конечным интервалом, и его функция вероятности имеет постоянную плотность на этом интервале.
    Равномерная функция распределения вероятностей определяется как- 

       

    Ожидание: Среднее значение распределения, представленное как E[x].

    Разница:  .
    Для равномерного распределения

    Экспоненциальное распределение
    Для положительного действительного числа функция плотности вероятности случайной величины с экспоненциальным распределением задается следующим образом:

         

    , где R x 902 случайных величин.

    Биномиальное распределение:  

    Среднее = np, где p — вероятность успеха
    Дисперсия . = NP (1-P)

    Распределение Пуассона:


    Calculus:

    Ограничения, непрерывность и дифференциация

    Существуют предел-. левый предел и правый предел существуют и равны, т. е.

     

    Некоторые общие пределы –

       

    Правило Больницы –  
    Если данный предел имеет форму или, то есть оба и равны 0 или оба и равны, то предел может быть решен с помощью Правила Больницы .
    Если предел имеет форму, описанную выше, то правило Лопиталя гласит, что – 

    где и получено дифференцированием и .
    Если после дифференцирования форма все еще существует, то правило может применяться непрерывно, пока форма не будет изменена.

    Непрерывность 
    Говорят, что функция непрерывна в диапазоне, если ее график представляет собой одну непрерывную кривую.
    Формально, 
    Вещественнозначная функция называется непрерывной в точке области, если – 
    существует и равна .
    Если функция непрерывна в то- 

    Функции, которые не являются непрерывными, называются разрывными.

    Дифференцируемость 
    Производная действительной функции по это функция и определяется как – 

    Функция называется дифференцируемой , если производная функции существует во всех точках области определения. Для проверки дифференцируемости функции в точке должно существовать число
    .

    Если функция дифференцируема в точке, то она и непрерывна в этой точке.
    Примечание – Если функция непрерывна в точке, это не означает, что функция также дифференцируема в этой точке. Например, непрерывно в но не дифференцируемо в этой точке.

    Теорема Лагранжа о среднем значении  
     

    S . ) дифференцируема в открытом интервале a < x < b

    Тогда согласно теореме Лагранжа существует по крайней мере одна точка ‘c’ в открытом интервале (a, b) такая, что:

    Среднее Ролля Теорема о ценности  

    Предположим, что f(x) — функция, удовлетворяющая трем условиям:

    1) f(x) непрерывна на отрезке a ≤ x ≤ b

    2) f(x) дифференцируема на открытом отрезке a < x < b

    3) f(a) = f(b)

    Тогда согласно теореме Ролля существует по крайней мере одна точка ‘c’ в открытом интервале (a, b) такая, что:

    f ‘(c) = 0

    Неопределенные интегралы  

    • Определение: Пусть f(x) — функция. Тогда семейство всех ее первообразных называется неопределенным интегралом функции f(x) и обозначается ∫f(x)dx.
      Символ ∫f(x)dx читается как неопределенный интеграл от f(x) по x.
      Таким образом, ∫f(x)dx= ∅(x) + C.
      Таким образом, процесс нахождения неопределенного интеграла функции называется интегрированием функции.
       

    Основные формулы интегрирования –  

    1. ∫x n dx = (x n+1 /(n+1))+C
    2. ∫(1/x)dx = (log e |x|)+C
    3. ∫e x dx = (e x )+C
    4. ∫a x dx = ((a x )/(log e a))+C
    5. ∫sin(x)dx = -cos(x)+C
    6. ∫cos(x)dx = sin(x)+C
    7. ∫sec 2 (x)dx = tan(x)+C
    8. ∫cosec 2 (x)dx = -cot(x)+ C
    9. ∫sec(x)tan(x)dx = sec(x)+C
    10. ∫cosec(x)cot(x)dx = -cosec(x)+C
    11. ∫cot(x)dx = log |грех(х)|+С
    12. ∫tan(x)dx = log|sec(x)|+C
    13. ∫sec(x)dx = log|sec(x)+tan(x)|+C
    14. ∫cosec(x)dx = log|cosec(x)-cot(x)|+C

    Определенные интегралы:  
    Определенные интегралы являются продолжением неопределенных интегралов, определенные интегралы имеют пределы [a, b].

    No related posts.

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *