определения, свойства и примеры решения задач, формулы и онлайн калькуляторы
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Содержание:
- Равные матрицы
- Произведение матрицы на число
- Сумма матриц
- Произведение двух матриц
- Транспонирование матриц
- Свойства линейных операций:
- Свойства произведения матриц:
- Свойства транспонирования матриц:
Некоторые операции над матрицами, такие как сложение и вычитание, допускаются только для матриц одинакового размера.
Равные матрицы
Определение
Две матрицы называются равными, если они имеют одинаковые размеры и их соответствующие элементы равны:
$$A_{m \times n}=B_{m \times n} \Leftrightarrow a_{i j}=b_{i j}, i=\overline{1, m} ; j=\overline{1, n}$$
Пример
$A=\left( \begin{array}{cc}{2} & {3}\end{array}\right)$, $B=\left( \begin{array}{cc}{4-2} & {2+1}\end{array}\right)$. Эти матрицы равны, т.к. равны их размеры: $A_{1 \times 2}$ и $B_{1 \times 2}$, а также соответствующие элементы:
$a_{11}=2=b_{11}=4-2=2$; $a_{12}=3=b_{12}=2+1=3$
Эти матрицы равны, т.к. равны их размеры: $A_{1 \times 2}$ и $B_{1 \times 2}$, а также соответствующие элементы:
$a_{11}=2=b_{11}=4-2=2$; $a_{12}=3=b_{12}=2+1=3$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Пусть задана матрица $A=\left( \begin{array}{ll}{a} & {c} \\ {b} & {d}\end{array}\right)$ . Найти все элементы матрицы $A$, если известно, что она равна матрице $B=\left( \begin{array}{rr}{-1} & {3} \\ {0} & {0}\end{array}\right)$
Решение. Так как матрицы $A$ и $B$ равны, то равны и их соответствующие элементы, т.е. $a=-1, b=0, c=3, d=0$
Ответ. $a=-1, b=0, c=3, d=0$
Произведение матрицы на число
Определение
Произведением матрицы на число называется матрица, полученная из исходной умножением
каждого ее элемента на заданное число.
Пример
Задание. Пусть $A=\left( \begin{array}{r}{3} \\ {-1}\end{array}\right)$. Найти матрицу $2A$.
Решение. $2 A=2 \cdot \left( \begin{array}{r}{3} \\ {-1}\end{array}\right)=\left( \begin{array}{c}{2 \cdot 3} \\ {2 \cdot(-1)}\end{array}\right)=\left( \begin{array}{r}{6} \\ {-2}\end{array}\right)$
Ответ. $2 A=\left( \begin{array}{r}{6} \\ {-2}\end{array}\right)$
Подробная теория про умножение марицы на число по ссылке.
Сумма матриц
Определение
Суммой матриц $A$ и $B$ одного размера называется матрица $C = A+B$ такого же размера, получаемая из исходных путем сложения соответствующих элементов.
Пример
Задание. Найти $A+B$, если $A=\left( \begin{array}{rrr}{1} & {-2} & {4} \\ {2} & {0} & {-1}\end{array}\right)$, $B=\left( \begin{array}{lll}{5} & {2} & {3} \\ {4} & {6} & {2}\end{array}\right)$
Решение. $C=A+B=\left( \begin{array}{rrr}{1} & {-2} & {4} \\ {2} & {0} & {-1}\end{array}\right)+\left( \begin{array}{lll}{5} & {2} & {3} \\ {4} & {6} & {2}\end{array}\right)=$
$C=A+B=\left( \begin{array}{rrr}{1} & {-2} & {4} \\ {2} & {0} & {-1}\end{array}\right)+\left( \begin{array}{lll}{5} & {2} & {3} \\ {4} & {6} & {2}\end{array}\right)=$
$=\left( \begin{array}{rrr}{1+5} & {-2+2} & {4+3} \\ {2+4} & {0+6} & {-1+2}\end{array}\right)=\left( \begin{array}{ccc}{6} & {0} & {7} \\ {6} & {6} & {1}\end{array}\right)$
Ответ. $C=\left( \begin{array}{lll}{6} & {0} & {7} \\ {6} & {6} & {1}\end{array}\right)$
Операции умножение матрицы на число и сумма матриц называются линейными.
Свойства линейных операций:
Везде далее матрицы $A$, $B$ и $C$ — матрицы одного размера.- Ассоциативность $(A+B)+C=A+(B+C)$
- $A+\Theta=\Theta+A$, где $\Theta$ — нулевая матрица соответствующего размера.
- $A-A=\Theta$
- Коммутативность $A+B=B+A$
- Дистрибутивность $\lambda(A+B)=\lambda A+\lambda B$
- $(\lambda+\mu) A=\lambda A+\mu A$
- $(\lambda \mu) A=\lambda(\mu A)$
Произведение двух матриц
Определение
Произведением матрицы $A_{m \times n}$ на матрицу $B_{n \times k}$ называется матрица
$C_{m \times k}$ такая, что элемент матрицы $C$, стоящий в $i$-ой строке и $j$-ом столбце,
т. е. элемент $C_{ij}$, равен сумме произведений элементов $i$-ой строки матрицы $A$
на соответствующие элементы $j$-ого столбца матрицы $B$.
е. элемент $C_{ij}$, равен сумме произведений элементов $i$-ой строки матрицы $A$
на соответствующие элементы $j$-ого столбца матрицы $B$.
Пример
Задание.
Решение. Так как $A=A_{2 \times 3}$, а $B=B_{3 \times 1}$, то в результате получим матрицу размера $C=C_{2 \times 1}$, т.е. матрицу вида $C=\left( \begin{array}{c}{c_{11}} \\ {c_{21}}\end{array}\right)$ . Найдем элементы данной матрицы:
$c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}+a_{13} \cdot b_{31}=1 \cdot 1+2 \cdot 2+0 \cdot 3=5 $ $c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}+a_{23} \cdot b_{31}=3 \cdot 1+1 \cdot 2+(-1) \cdot 3=2 $
Таким образом, получаем, что:
$C=A B=\left( \begin{array}{l}{5} \\ {2}\end{array}\right)$
Все вычисления можно было сделать в более компактном виде:
$A B=\left( \begin{array}{ccc}{1} & {2} & {0} \\ {3} & {1} & {-1}\end{array}\right)_{2 \times 3} \cdot \left( \begin{array}{l}{1} \\ {2} \\ {3}\end{array}\right)_{3 \times 1}=\left( \begin{array}{c}{1 \cdot 1+2 \cdot 2+0 \cdot 3} \\ {3 \cdot 1+1 \cdot 2+(-1) \cdot 3}\end{array}\right)$
Ответ. Читать дальше: умножение матрицы на число. Некоторые
из операторов MathCad
имеют особые значения в применении к
векторам и матрицам. Например, символ
умножения * при применении к векторам означает
скалярное умножение и умножение матриц
— когда применяется к матрицам. Векторные
и матричные операторы доступны на панели Символьная.
Если результатом является вектор, то
это обязательно вектор-столбец, а не
вектор-строка. Таблица
7.1 Команды
работы с векторами и матрицами Обозначение Клавиши Пояснения x
* y Ctrl+* Векторное
произведение трехмерных векторов x
и y An ^ Степень
матрицы. |A| | Определитель
матрицы. А-1 – обратная
матрица – такая матрица, при умножении на
которую, исходная матрица A даёт в
результате единичную матрицу E: Е
— единичная
матрица — квадратная
матрица, элементыглавной
диагоналикоторой равны единице, а
остальные элементы равны нулю: Если
количество строк матрицы равно количеству
столбцов, то такая матрица называется квадратной. АТ — транспонированная
матрица — матрица,
полученная из исходной матрицызаменой строк на столбцы. Формально,
транспонированная матрица для матрицы
размеров— матрицаразмеров,
определённая как AT[i,j]
= A[j,i]. Например, и
max(V) — возвращает максимальный по значению
элемент матрицы V; min(V) — возвращает минимальный по значению
элемент матрицы V; cols(V) — возвращает число столбцов матрицы
V; rows(V) — возвращает число строк матрицы V; tr(V) — возвращает след (сумму диагональных
элементов) квадратной матрицы V; csort(V,n) — возвращает матрицу с переставленными
строками в соответствии с элементами
N-го столбца, расположенными по возрастанию; rsort(V,n) — возвращает матрицу с переставленными
столбцами в соответствии с элементами
N-ой строки, расположенными по возрастанию. Переставить
столбцы матрицы
по элементам первой строки, по элементам
второго столбца. Найти
сумму матриц
и. Найти
матрицу 2А+5В,
если
и. Найти
произведения матриц АВ и ВА,
если
и. Найти
значение матричного многочлена
,
если,
аЕ — единичная матрица третьего порядка. Дана
матрица
.
Найти обратную матрицу. Найти
матрицу
,
еслии. Вычислить
|А|, Ат,
В-1,
А3,
если Найти
максимальный элемент матрицы С=А*В. Пример
выполнения упражнения 1.
Для решения системы уравнений включим
панель инструментов Матрица: Вид — Панели
инструментов — Матрица или воспользуемся кнопкой на панели Математическая . Вводим
с клавиатуры функцию rsort,
вводим аргументы D и 0 (т.к. по умолчанию нумерация строк и
столбцов в MathCad
начинается с 0), щелкаем знак «=»,
получаем результат: Замечание 1 Работа с матрицами Python — это работа с двухмерными квадратными массивами, для которых дополнительно могут выполняться операции возведения в степень и перемножения. Матрицей является двумерный массив, который состоит из M строк и N столбцов. Матрицы могут использоваться при осуществлении математических вычислений. Пользователь может самостоятельно выполнить любые функции для работы с матрицами, такие как, умножение, сложение, транспонирование и так далее. На Python эти операции осуществить существенно легче, чем языках программирования более низкого уровня, например, на Си. Однако постоянное написание одних и тех же алгоритмов не является оптимальным вариантом, по этой причине была сформирована библиотека NumPy. Она может быть использована для сложных научных вычислительных процедур и способна предоставить специалисту набор функций по обработке двумерных массивов. Вместо написания десятков строчек кода для исполнения не сложных операций над матрицами, пользователь может просто воспользоваться одной из функций библиотеки NumPy. Сама библиотека реализована на Python, Cи и Фортране, и по этой причине функции могут работать даже более быстро, чем на чистом Python. Библиотека NumPy не является встроенной составляющей интерпретатора Python, поэтому перед импортом ее следует сначала установить. Для этого можно использовать утилиту pip, а именно, следует набрать следующую команду: píp ínstall numpy После установки библиотеки, она может быть подключена при помощи команды import. Для более удобной работы, можно переименовать numpy при импорте в np следующим образом:
ímport numpy as np Для того чтобы создать матрицу, следует использовать функцию array(), в которую будет передан список. Приведем пример формирования матрицы, в котором в качестве аргумента функции используется двумерный список: a = np.array([[3, 3, 3], [2, 5, 5]]) В качестве второго параметра может быть задан тип компонентов матрицы: a = np.array([[3, 3, 3],[2, 5, 5]], int) prínt(a) Последняя команда выводит на консоль следующую информацию: [[3 3 3] [2 5 5]] Необходимо так же отметить, что если поменять ínt на str, то тип компонентов изменится на строковый. В качестве типа компонентов матрицы могут использоваться ínt, float, bool, complex, bytes, str, buffers. Также могут быть использованы и другие типы NumPy, а именно: Для иллюстрации этих возможностей приведем следующие примеры: Для того чтобы узнать размер матрицы, необходимо использовать атрибут shape следующим образом: síze = a.shape prínt(síze) # Будет выведено сообщение (2, 3) Первое число, а именно двойка, является количеством строк, а второе число, то есть, тройка является количеством столбцов. Когда требуется сформировать матрицу, которая состоит лишь из нулей, следует использовать функцию zeros(): a_of_zeros = np.zeros((2,2)) prínt(a_of_zeros) Результатом данного кода будет следующее сообщение: [[0. 0.] [0. 0.]] Для получения строки двухмерной матрицы, следует просто выполнить обращение к ней как показано ниже: temp = a[0] prínt(temp) # Будет выведено сообщение [3 3 3] {T} $
{T} $7 Работа с матрицами
7.1 Векторные и матричные операции
 Для квадратной матрицы А и
целого положительного n
вычисляется n-я
степень матрицы А, при n
отрицательном n-я
степень обратной матрицы А.
Для квадратной матрицы А и
целого положительного n
вычисляется n-я
степень матрицы А, при n
отрицательном n-я
степень обратной матрицы А.
7.2 Функции, возвращающие специальные характеристики матриц
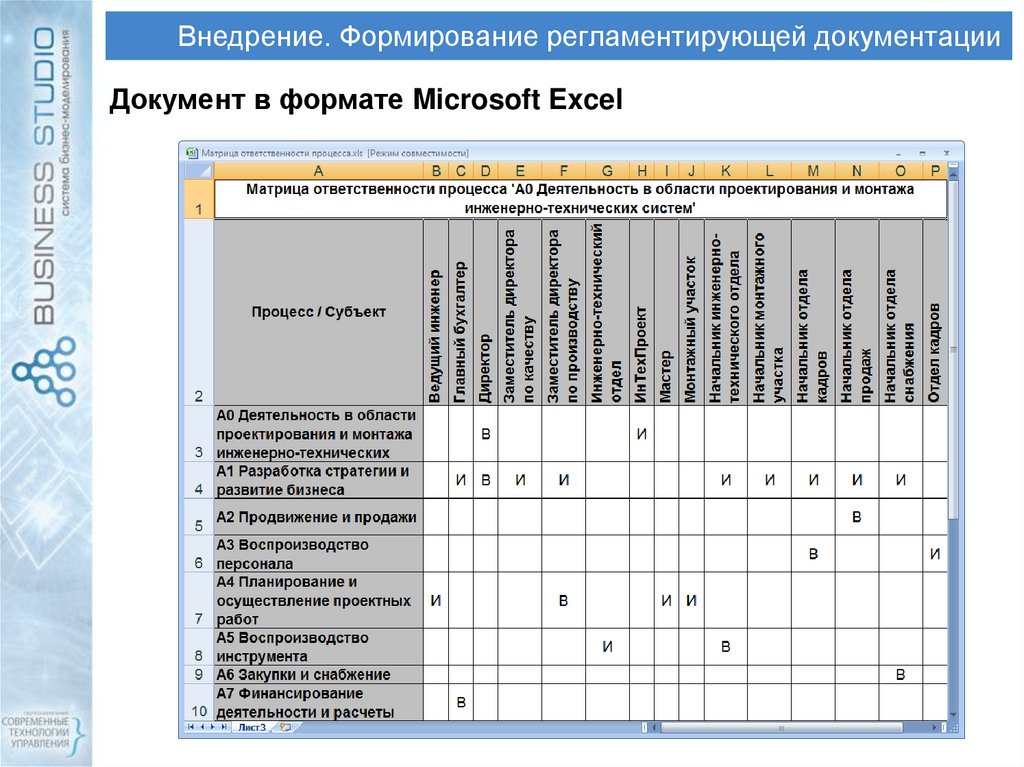
7.3 Упражнения к теме 7
 Вводим«D :=»,
далее можно воспользоваться комбинацией
клавиш: «Ctrl»
+ «M» или выбрать пиктограмму на панели Матрица .
На экране появляется менюВставка
матрицы (рис.
6.2). Вводим число столбцов 3 и число строк
3, щелкаем ОК.
Вводим элементы матрицы, перемещаясь
по таблице с помощью клавиши Tab.
Вводим«D :=»,
далее можно воспользоваться комбинацией
клавиш: «Ctrl»
+ «M» или выбрать пиктограмму на панели Матрица .
На экране появляется менюВставка
матрицы (рис.
6.2). Вводим число столбцов 3 и число строк
3, щелкаем ОК.
Вводим элементы матрицы, перемещаясь
по таблице с помощью клавиши Tab.Работа с матрицами Python
Введение
 Программисты используют матрицы, как правило, в научной сфере, но конечно их можно применять и для других целей, к примеру, для оперативной генерации уровней в видео играх.
Программисты используют матрицы, как правило, в научной сфере, но конечно их можно применять и для других целей, к примеру, для оперативной генерации уровней в видео играх.
Работа с матрицами Python
 Помимо этого, при выводе в консоль NumPy в автоматическом режиме форматирует вывод для того, чтобы он имел вид матрицы, а компоненты были расположены друг под другом.
Помимо этого, при выводе в консоль NumPy в автоматическом режиме форматирует вывод для того, чтобы он имел вид матрицы, а компоненты были расположены друг под другом.
arr = np. array([[3,3,3],[2,5,5]], str)
array([[3,3,3],[2,5,5]], str)
temp = arr[:,2]
print(temp) #
В результате будет выведено сообщение [‘3’ ‘5’].
Для того чтобы получить компонент, следует задать номер столбца и строки, в которых он расположен. К примеру, компонентом во второй строке и третьем столбце является цифра пять, что можно проверить следующим образом, помня, что нумерация отсчитывается от нуля:
arr = np.array([[3,3,3],[2,5,5]], str)
temp = arr[1][2]
prínt(temp) #
В результате будет выведено сообщение 5.
Для того чтобы выполнить операцию сложения матриц, следует просуммировать все их соответствующие компоненты. В Python для обозначения операции сложения применяется стандартный оператор «+». Приведем пример операции сложения матриц:
arr1 = np.array([[3,3,3],[2,5,5]])
arr2 = np.array([[2,4,2],[1,3,8]])
temp = arr1 + arr2
prínt(temp)
Результат сложения матриц будет следующим:
[[ 5 7 5]
[ 3 8 13]]
Здесь следует заметить, что суммировать можно только те матрицы, которые имеют равное количество строк и столбцов. В противном случае программа на Python выдаст ошибку ValueError.
В противном случае программа на Python выдаст ошибку ValueError.
Операция умножения матриц обладает сильными отличиями от сложения. Нельзя просто взять и выполнить перемножение соответствующих элементов двух матриц. Прежде всего матрицы обязаны являться согласованными, что означает равенство количества столбцов одной матрицы количеству строк другой и наоборот. В противном случае программа выпадет в ошибку. Умножение в библиотеке NumPy может быть исполнено при помощи метода dot(). Ниже приведен пример реализации операции умножения:
arr1 = np.array([[3,3],[2,5]])
arr2 = np.array([[2,4],[1,3]])
temp = arr1.dot(arr2)
prínt(temp)
В результате исполнения этого кода будет выдано сообщение: [[ 9 21]
[ 9 23]]
Функциональное программирование на примере работы с матрицами из теории линейной алгебры / Хабр
Вступление
В основе работы с матрицами (в данной статье мы будем рассматривать только двумерные матрицы) лежит мощная математическая теория из области линейной алгебры. Одно определение или действие следует из другого, одна функция вызывает другую. Поэтому для программной реализации функционала математических операций над матрицами функциональные языки подходят очень хорошо. В рамках данной статьи мы рассмотрим конкретные примеры на языке F# и дадим подробные комментарии, как это работает. Так как F# входит в семейство .NET, то полученный функционал можно без каким либо проблем использовать в других императивный языках, например C#.
Одно определение или действие следует из другого, одна функция вызывает другую. Поэтому для программной реализации функционала математических операций над матрицами функциональные языки подходят очень хорошо. В рамках данной статьи мы рассмотрим конкретные примеры на языке F# и дадим подробные комментарии, как это работает. Так как F# входит в семейство .NET, то полученный функционал можно без каким либо проблем использовать в других императивный языках, например C#.
Определение матрицы и реализация на F#
Матрицы являются базовой и важнейшей частью линейной алгебры. Матрицы часто используются в программировании, например в 3D-моделировании или гейм-девелопинге. Разумеется, велосипед уже давно изобретен и необходимые фреймворки для работы с матрицами уже готовы, и их можно и нужно использовать. Данная статья не ставит своей целью изобретение нового фреймворка, но показывает реализацию базовых математических операций для работы с матрицами в функциональном стиле с использованием языка программирования F#. По мере рассмотрения материала мы будем обращаться к математической теории матриц и смотреть, как ее можно реализовать в коде.
По мере рассмотрения материала мы будем обращаться к математической теории матриц и смотреть, как ее можно реализовать в коде.
Для начала вспомним, что такое матрица? Теория говорит нам следующее
Прямоугольная таблица чисел, содержащая m строк и n столбцов, называется матрицей размера m x n
Матрицы, как правило, обозначаются прописными буквами латинского алфавита и записываются в виде
Или коротко
Для работы с матрицами в F# создадим запись, основанную на двумерной таблице, которую в дальнейшем будем расширять полезными методами для того, чтобы совершать необходимые математические операции над ней.
type Matrix = { values: int[,] }
with
// здесь будем добавлять методы
end
Добавим вспомогательный метод для инициализации записи двумерным массивом
static member ofArray2D (values: int [,]) =
{ values = values }
Входным аргументом функции будет двумерный массив, а на ее выходе — запись типа Matrix. Ниже приведем пример инициализации записи.
Ниже приведем пример инициализации записи.
let a = array2D [[1;0;2]
[3;1;0]]
let A = Matrix.ofArray2D a
Две матрицы A=(aij) и B=(bij) называются равными, если они совпадают поэлементно, т.е. aij=bij для всех i=1,2…,m и j=1,2…n
Для реализации этого правила будем использовать переопределенный оператор == и добавим пару полезных функций, которые также понадобятся нам в дальнейшем.
static member sizes matrix =
let rows = matrix.values.[*,0].Length
let cols = matrix.values.[0,*].Length
(rows, cols)
static member isEquallySized matrix1 matrix2 =
let dim1 = Matrix.sizes matrix1
let dim2 = Matrix.sizes matrix2
(dim1 = dim2)
static member (==) (matrix1, matrix2) =
if not (Matrix.isEquallySized matrix1 matrix2) then false
else
not (matrix1.values
|> Array2D.mapi (fun x y v -> if matrix2. values.[x, y] <> v then false else true)
|> Seq.cast<bool>
|> Seq.contains false)
values.[x, y] <> v then false else true)
|> Seq.cast<bool>
|> Seq.contains false)
Давайте подробнее рассмотрим код выше. Как можно заметить, здесь есть три функции. Первая функция sizes возвращает размерность матрицы в виде кортежа. Так как мы работаем только с прямоугольными матрицами, то для получения количества строк мы берем полный срез первой колонки и возвращаем ее длину.
let rows = matrix.values.[*,0].Length
Аналогичным способом работает определение количества колонок — получаем полный срез первой строки и возвращаем ее длину.
Следующая функция isEquallySized сравнивает размерность двух матриц и возвращает true если они равны. Для этого она использует уже готовую функцию sizes и просто сравнивает результаты.
Оператор == для поэлементного сравнения двух матриц кажется сложнее, но сейчас вы увидите, что он также простой.
Перед тем, как сравнивать две матрицы, сравним их размерность. Если они не равны, то нет дальше смысла проводить проверку, так как уже понятно, что и матрицы будут не равны.
if not (Matrix.isEquallySized matrix1 matrix2) then false
Далее, на основе исходных матриц matrix1 и matrix2 мы формируем новую матрицу, заполненную true или false, в зависимости от того, совпадают ли соответствующие ячейки обеих матриц.
matrix1.values |> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true
Функция Array2D.mapi перебирает все элементы matrix1 и передает в обработчик три параметра
x — индекс строки
y — индекс колонки
v — содержимое ячейки
Содержимое ячейки v мы сравниваем с соответствующей ячейкой matrix2 и если они равны, то пишем true, иначе — false.
Если есть хоть одна ячейка с элементом false, то это означает, что матрицы не равны между собой.
Так как Array2D не содержит в себе методов для фильтрации или поиска, то реализуем это сами. Для этого разложим матрицу в линейный список
|> Seq.cast<bool>
И найдем хоть одно несовпадение
|> Seq.contains false
Функция Seq.contains вернет true если в разложенном списке будет найдено хоть одно значение false. Поэтому нам нужно инвертировать полученный результат, чтобы оператор == работал так, как мы хотим
else
not (matrix1.values
|> Array2D.mapi (fun x y v -> if matrix2.values.[x, y] <> v then false else true)
|> Seq.cast<bool>
|> Seq.contains false)
Матрица O называется нулевой или нуль-матрицей, если все ее элементы равны нулю.
static member O rows cols =
let array2d = Array2D.zeroCreate rows cols
{ values = array2d }
Пример использования этой функции
let AO = Matrix.O 5 5
Полагаю, что здесь нет ничего сложного, что требует пояснений, поэтому продолжаем.
Матрица, число строк которой равно числу столбцов и равно n, называется квадратной матрицей порядка n
Таким образом, квадратная матрица имеет вид.
В рамках этого правила мы создадим функцию, которая прямоугольную матрицу трансформирует в квадратную путем отсечения всех элементов, которые не попадают в квадрат.
static member toSquare matrix =
// получаем размерность исходной матрицы
let dim = Matrix.sizes matrix
// получаем количество колонок
let colCount: int = snd dim
// получаем количество строк
let rowCount: int = fst dim
// находим размер минимальной стороны
let length = System. Math.Min (colCount, rowCount)
// создаем пустой квадратный массив с размерностью
// равной наименешей стороне исходной матрицу
let zero = Array2D.zeroCreate length length
// копируем исходную матрицу в квадратную
let square = zero |> Array2D.mapi (fun x y _ -> matrix.values.[x, y])
// позвращаем полученную матрицу
{ values = square }
Math.Min (colCount, rowCount)
// создаем пустой квадратный массив с размерностью
// равной наименешей стороне исходной матрицу
let zero = Array2D.zeroCreate length length
// копируем исходную матрицу в квадратную
let square = zero |> Array2D.mapi (fun x y _ -> matrix.values.[x, y])
// позвращаем полученную матрицу
{ values = square }
Комментариев в исходном коде поясняют принцип работы функции, поэтому продолжим.
Квадратная матрица называется треугольной, если все ее элементы ниже главной диагонали равны нулю, т.е. треугольная матрица имеет вид
Ниже приведен код функции, который преобразует исходную матрицу в треугольную. Но в нашей функции мы будем работать с прямоугольной матрицей, то есть она может быть не квадратной. Читатель легко может модифицировать код функции так, чтобы она возвращала квадратную треугольную матрицу, используя функцию, которую мы рассмотрели ранее.
static member T matrix =
let values = matrix.values |> Array2D.mapi (fun x y v -> if y < x then 0 else v)
{ values = values }
Функция Array2D.mapi преобразовывает исходный двумерный массив в новый при помощи обработчика, который принимает три параметра
x — номер строки
y — номер колонки
v — содержимое ячейки
if y < x then 0 else v
Здесь мы делаем проверку, находится ли элемент ниже главной диагонали и если да, то заполняем ячейку 0. В противном случае — исходным значение из входной матрицы.
Ниже приведен пример использования этой функции.
let a = array2D [[1;2;3]
[4;5;6]
[7;8;9]
[10;11;12]]
let A = Matrix.ofArray2D a
let R = Matrix.triangular A
printfn "origin = \n %A" A.values
printfn "triangular = \n %A" R.values
Получаем следующий результат
origin = [[1; 2; 3] [4; 5; 6] [7; 8; 9] [10; 11; 12]] triangular = [[1; 2; 3] [0; 5; 6] [0; 0; 9] [0; 0; 0]]
Квадратная матрица называется диагональной, если все ее элементы, расположенные вне главной диагонали, равны нулю
static member D matrix =
let diagonal = matrix. values |> Array2D.mapi (fun x y v -> if x <> y then 0 else v)
{ values = diagonal }
values |> Array2D.mapi (fun x y v -> if x <> y then 0 else v)
{ values = diagonal }
Эта функция очень похожа на предыдущую, отличается только условие проверки. Ниже пример использования
let a = array2D [[1;2;3]
[4;5;6]
[7;8;9]
[10;11;12]]
let A = Matrix.ofArray2D a
let R = Matrix.D A
printfn "origin = \n %A" A.values
printfn "diagonal = \n %A" R.values
origin = [[1; 2; 3] [4; 5; 6] [7; 8; 9] [10; 11; 12]] diagonal = [[1; 0; 0] [0; 5; 0] [0; 0; 9] [0; 0; 0]]
Диагональная матрица является единичной и обозначается E, если все ее элементы, расположенные на главной диагонали, равны единице
Реализация такой матрицы на F# выглядит так
static member E rows cols =
let array2d = Array2D.init rows cols (fun x y -> if x = y then 1 else 0)
{ values = array2d }
Операции над матрицами при помощи F#
Над матрицами, как и над числами, можно производить ряд действий, причем некоторые из них аналогичны операциям над числами, а некоторые — специфические.
Суммой двух матриц Amn=(aij)и Bmn=(bij)одинаковых размеров называется матрица того же размера A+B=Cmn=(cij), элементы которой равны сумме элементов матриц A и B, расположенных на соответствующих местах
Пример, для заданных матриц A и B находим сумму A+B
Рассмотрим код для сложения двух матриц
static member (+) (matrix1, matrix2) =
if Matrix.isEquallySized matrix1 matrix2 then
let array2d = matrix1.values |> Array2D.mapi (fun x y v -> matrix2.values.[x, y] + v)
{ values = array2d }
else failwith "matrix1 is not equal to matrix2"
Перед тем, как складывать матрицы, нужно убедиться, что их размерность совпадает, в противном случае функция генерирует исключение. Ниже приведем пример использования данной функции
let a = array2D [[2;3]
[1;-5]
[0;6]]
let A = Matrix. ofArray2D a
let b = array2D [[-3;3]
[1;7]
[2;0]]
let B = Matrix.ofArray2D b
let R = A+B
printfn "A+B =\n %A" R.values
ofArray2D a
let b = array2D [[-3;3]
[1;7]
[2;0]]
let B = Matrix.ofArray2D b
let R = A+B
printfn "A+B =\n %A" R.values
A+B = [[-1; 6] [2; 2] [2; 6]]
Произведением матрицы A=(aij) на число k называется матрица kA=(kaij) такого же размера, что и матрица A, полученная умножением всех элементов матрицы A на число k
Пример, для заданной матрицы A находим матрицу 3A
static member (*) (value, matrix) =
let array2d = matrix.values |> Array2D.mapi (fun _ _ v -> v * value)
{ values = array2d }
Матрицу -A=(-1)*A будем называть противоположной матрице A. Из этого определения плавно переходим к следующему
Разностью матриц A и B одинаковых размеров называется сумма матрицы A и матрицы, противоположной к B
static member (-) (matrix1: Matrix, matrix2: Matrix) =
if Matrix. isEquallySized matrix1 matrix2 then
matrix1 + (-1)*matrix2
else failwith "matrix1 is not equal to matrix2"
isEquallySized matrix1 matrix2 then
matrix1 + (-1)*matrix2
else failwith "matrix1 is not equal to matrix2"
Две матрицы называются согласованными, если число столбцов первой равны числу строк второй
static member isMatched matrix1 matrix2 =
let row1Count = matrix1.values.[0,*].Length
let col2Count = matrix2.values.[*,0].Length
row1Count = col2Count
Проверка согласованности матриц требуется для их перемножения.
Произведением AB согласованных матриц Amn=(aij) и Bnp=(bjk) называется матрица Cmn=(cik), элемент cik которой вычисляется как сумма произведений элементов i-й строки матрицы A и соответствующих элементов k-го столбца матрицы B
Вычислить произведение матриц
Решение по определению произведения матриц
Рассмотрим код для умножения двух матриц
static member (*) (matrix1, (matrix2: Matrix)) =
if Matrix. isMatched matrix1 matrix2 then
let row1Count = matrix1.values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
let values = Array2D.zeroCreate row1Count col2Count
for r in 0..row1Count-1 do
for c in 0..col2Count-1 do
let row = Array.toList matrix1.values.[r,*]
let col = Array.toList matrix2.values.[*,c]
let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
values.[r,c] <- cell
{ values = values }
else failwith "matrix1 is not matched to matrix2"
isMatched matrix1 matrix2 then
let row1Count = matrix1.values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
let values = Array2D.zeroCreate row1Count col2Count
for r in 0..row1Count-1 do
for c in 0..col2Count-1 do
let row = Array.toList matrix1.values.[r,*]
let col = Array.toList matrix2.values.[*,c]
let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
values.[r,c] <- cell
{ values = values }
else failwith "matrix1 is not matched to matrix2"
Давайте разберемся с кодом подробнее.
Перед умножением нужно убедиться, что матрицы являются согласованными
if Matrix.isMatched matrix1 matrix2 then
Итоговая матрица будет иметь размерность, в которой количество строк такое же, как у первой матрицы и количество столбцов такое же, как у второй матрицы
let row1Count = matrix1.values.[*,0].Length let col2Count = matrix2.values.[0,*].Length // формируем пустой двумерный массив для сохранения результатов умножения let values = Array2D.zeroCreate row1Count col2Count
После этого мы последовательно перебираем все строки и все столбцы исходных матриц
for r in 0..row1Count-1 do
for c in 0..col2Count-1 do
let row = Array.toList matrix1.values.[r,*]
let col = Array.toList matrix2.values.[*,c]
Вычисляем итоговое значение каждой ячейки
let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
Функция List.fold2 на вход получает два списка (строку и колонку) и передает в обработчик следующие параметры
acc — аккумулятор, содержащий результат предыдущего вычисления
val1 — содержимое ячейки из первого массива. В нашем случае это строка из первой матрицы
val2 — содержимое ячейки из второго массива, то есть колонки второй матрицы
Так как матрицы являются согласованными, то мы уверены, что у нас не произойдет выхода за пределы массивов.
Обработчик добавляет к аккумулятору произведение ячеек из строк и столбца и полученное значение будет передано следующей итерации. Таким образом конечным итогом работы функции List.fold2 будет итоговое значение произведений двух матриц. Остается только заполнить им предварительно созданную пустую матрицу
values.[r,c] <- cell
Которая вернется как результат
{ values = values }Ниже приведем пример использования данной функции
let a = array2D [[1;0;2]
[3;1;0]]
let A = Matrix.ofArray2D a
let b = array2D [[-1;0]
[5;1]
[-2;0]]
let B = Matrix.ofArray2D b
let R = A*B
printfn "A*B =\n %A" R.values
A1*B1 = [[-5; 0] [2; 1]]
Если k ∈ N, то k-й степенью квадратной матрицы Aназывается произведение k матриц A
Рассмотрим код на F# для произведения матрицы в степень. Здесь будет использоваться хвостовая рекурсия для того, чтобы не переполнить стек при больших значениях степеней. Хвостовая рекурсия — это такая рекурсия, которая компилятором в итоге преобразуется в цикл. По возможности рекомендуется всегда использовать именно хвостовую рекурсию вместо обычной, но для этого нужно чтобы каждый кадр рекурсии возвращал итоговое вычисленное значение. Это значение обычно называется аккумулятором и передается в следующий кадр рекурсии. То есть, в отличие от обычной рекурсии, которая возвращает вычисленное значение вверх по стеку, хвостовая рекурсия передает вычисленное значение вниз по стеку. Каждый новый кадр рекурсии делает свои вычисления и добавляет их к уже ранее вычисленному значению, которое хранится в аккумуляторе. После того, как последний кадр рекурсии отработал, в аккумуляторе уже есть вычисленное значение, которое просто возвращается как результат.
Здесь будет использоваться хвостовая рекурсия для того, чтобы не переполнить стек при больших значениях степеней. Хвостовая рекурсия — это такая рекурсия, которая компилятором в итоге преобразуется в цикл. По возможности рекомендуется всегда использовать именно хвостовую рекурсию вместо обычной, но для этого нужно чтобы каждый кадр рекурсии возвращал итоговое вычисленное значение. Это значение обычно называется аккумулятором и передается в следующий кадр рекурсии. То есть, в отличие от обычной рекурсии, которая возвращает вычисленное значение вверх по стеку, хвостовая рекурсия передает вычисленное значение вниз по стеку. Каждый новый кадр рекурсии делает свои вычисления и добавляет их к уже ранее вычисленному значению, которое хранится в аккумуляторе. После того, как последний кадр рекурсии отработал, в аккумуляторе уже есть вычисленное значение, которое просто возвращается как результат.
Таким образом, компилятор может оптимизировать код и преобразовать его в обычный цикл.
// возводим матрицу в степень
// matrix - исходная матрица
// value - значение степени
static member (^^) (matrix, value) =
// внутренняя функция, которая реализует хвостовую рекурсию
// m - матрица
// p = значение степени
let inRecPow m p =
// рекурсивная функция
// acc - накопленный аккумулятор. имеет тип Matrix
// p - значение степени для текущего кадра
// с каждым кадром рекурсии это значение уменьшается на единицу
let rec recPow acc p =
// сравниваем текущую степень
match p with
| x when x > 0 ->
// вычисляем новое значение аккумулятора
// умножаем исходную матрицу на старый аккумулятор, то есть возводим в следующую степень
let nextAcc = acc*m
// рекурсивно вызываем функцию и передаем ей уменьшенное на единицу значение степени
recPow nextAcc (x-1)
// если степень достигла нуля, то возвращаем вычисленный аккумулятор
| _ -> acc
// создаем единичную матрицу, чтобы передать ее в качестве аккумулятор для вычисления степени
let dim = Matrix.sizes matrix
let colCount = snd dim
let rowCount = fst dim
let u = Matrix.E rowCount colCount
// вызываем рекурсивную функцию и передаем ей единичную матрицу в качестве аккумулятора
recPow u p
// вызываем функцию, реализующую хвостовую рекурсию для получения результата
let powMatrix = inRecPow matrix value
// возвращаем итоговую матрицу
{ values = powMatrix.
имеет тип Matrix
// p - значение степени для текущего кадра
// с каждым кадром рекурсии это значение уменьшается на единицу
let rec recPow acc p =
// сравниваем текущую степень
match p with
| x when x > 0 ->
// вычисляем новое значение аккумулятора
// умножаем исходную матрицу на старый аккумулятор, то есть возводим в следующую степень
let nextAcc = acc*m
// рекурсивно вызываем функцию и передаем ей уменьшенное на единицу значение степени
recPow nextAcc (x-1)
// если степень достигла нуля, то возвращаем вычисленный аккумулятор
| _ -> acc
// создаем единичную матрицу, чтобы передать ее в качестве аккумулятор для вычисления степени
let dim = Matrix.sizes matrix
let colCount = snd dim
let rowCount = fst dim
let u = Matrix.E rowCount colCount
// вызываем рекурсивную функцию и передаем ей единичную матрицу в качестве аккумулятора
recPow u p
// вызываем функцию, реализующую хвостовую рекурсию для получения результата
let powMatrix = inRecPow matrix value
// возвращаем итоговую матрицу
{ values = powMatrix. values }
values }
Код содержит подробные комментарии о том, как он работает. Требует небольшого пояснения, зачем используется единичная матрица? Она нужна для первого кадра рекурсии и служит в качестве базового значения аккумулятора, в котором будет накапливаться итоговый результат.
Ниже рассмотрим пример использования нашей функции
Вычислим следующее произведение
Где E — это единичная матрица. Так как мы не можем к матрице прибавить число, то мы должны прибавлять 3E.
// возвращает сумму матрицы и числа
static member (+) (matrix, (value: int)) =
let dim = Matrix.sizes matrix
let r = fst dim
let c = snd dim
// создаем единичную матрицу
let unit = Matrix.E r c
// умножаем единичную матрицу на число и прибавляем к входной матрице
value*unit + matrix
let a = array2D [[1;0]
[2;-1]]
let A = Matrix. 2 + 3 =
[[1; 0]
[4; -3]]
2 + 3 =
[[1; 0]
[4; -3]]
Матрица AT, столбцы которой составлены из строк матрицы A с теми же номерами и тем же порядком следования элементов, называется транспонированной к матрице A
static member transpose matrix =
let dim = Matrix.sizes matrix
let rows = fst dim
let cols = snd dim
// создаем нулевую матрицу для вычисления результатов
let tMatrix = Matrix.O cols rows
// копируем в нее данные из исходной матрицы
matrix.values |> Array2D.iteri(fun x y v -> tMatrix.values.[y, x] <- v)
// возвращаем результат
tMatrix
Пример использования
let a = array2D [[1;2;3]
[4;5;6]
[7;8;9]
[10;11;12]]
let A = Matrix.ofArray2D a
let R6 = Matrix.T A
printfn "origin = \n %A" A.values
printfn "transpose = \n %A" R.values
origin = [[1; 2; 3] [4; 5; 6] [7; 8; 9] [10; 11; 12]] transpose = [[1; 4; 7; 10] [2; 5; 8; 11] [3; 6; 9; 12]]
Итоги
В этот статье мы рассмотрели примеры реализации и использования матриц из теории линейной алгебры. А также основных математических операций над ними, с использованием функционального подхода на языке F#. Я надеюсь, что читатель смог оценить ту гибкость, которую дают функциональные языки.
А также основных математических операций над ними, с использованием функционального подхода на языке F#. Я надеюсь, что читатель смог оценить ту гибкость, которую дают функциональные языки.
Полный исходный код модуля матриц, фрагменты которого были рассмотрены в рамках статьи, вы сможете найти на гитхабе.
Github Matrix.fs
Работа с векторами и матрицами в MathCad
Похожие презентации:
3D печать и 3D принтер
Системы менеджмента качества требования. Развитие стандарта ISO 9001
Операционная система. Назначение и основные функции
Adobe Photoshop
AutoCAD история и возможности
Microsoft Excel
Облачные технологии
Корпорация Microsoft и ее особенности
Веб-дизайн
Тема 2. Пакеты прикладных программ
Работа с векторами и
матрицами
в MathCad
Массивы
одномерные
(векторы)
двумерные
(матрицы)
тензоры
a «My Name»
(многоиндексные)
1
M
V2 ( 1 2 3 )
V1 2
3
Индекс – порядковый номер элемента
1 2 3
4 5 6
7 8 9
Заполнение массивов
1. С помощью шаблона:
С помощью шаблона:
2. Поэлементно
m0 0 0
m1 0 3
m0 1 1
m1 0 3 m1 1 4 m1 2 5
m0 2 2
0 1 2
m
m1 2 5
3 4 5
m1 1 4
1 2
3. С использованием
и функций пользователя
0 переменных
m
00 33
i 0 1
j j
3
4T 5
0 1 2 3
T
ViV
i
0.50.5
i i 1 1 VV ( (11 1.5
MM
j j M
1.5))
i ji
j i i
1 0 1 2
4. Применение встроенных функций
6. Создание программ-функций
5. Чтение из внешнего файла
Матричные вычисления
элементарные действия
использование
программирования
создание, сложение,
использование
умножение,
суммирование
специальных функций элементов вложенного
извлечение данных
Реализация: операторы и встроенных алгоритмов
массива
панели Math: Calculator,
матричной алгебры
Matrix, Symbolic
ранг, единичная матрица,
сортировка
Реализация: главное меню
Insert (Вставка) Function
(Функция) (или
)
раздел Vector and Matrix
(Векторы и матрицы)
Операторы и функции для работы
с векторами и матрицами
V – вектор, M – матрица,
Z – скаляр
Векторные и матричные функции
Векторные функции
Функция
length(V)
Описание
Возвращает длину вектора
last(V)
Возвращает индекс последнего элемента
max(V)
Возвращает максимальный по значению элемент
min(V)
Возвращает минимальный по значению элемент
Re(V)
Возвращает вектор действительных частей
вектора с комплексными элементами
Im(V)
Возвращает вектор мнимых частей вектора с
комплексными элементами
Векторные и матричные функции
Функции для работы с матрицами
Функция
Описание
augment(M1,M2)
Объединяет в одну матрицы М2 и М2, имеющие
одинаковое число строк (объединение «бок о бок»)
stack(M1,M2)
Объединяет в одну матрицы М1 и М2, имеющие
одинаковое число столбцов, располагая М1 над М2
Создает единичную квадратную матрицу
identity(n)
размером n×n
Возвращает субматрицу, состоящую из всех
submatrix(M,ir,jr,ic,jc) элементов, содержащихся в строках с ir по jr и
столбцов с ic по jc
diag(V)
Re(M)
Im(M)
Создает диагональную матрицу, элемент главной
диагонали которой – вектор V
Возвращает матрицу действительных, мнимых
частей матрицы M с комплексными элементами
Векторные и матричные функции
Функции для работы с матрицами
Функция
Описание
Выводит значения того элемента матрицы N, который
lookup(r,M,N) занимает в ней такое же положение, что и скаляр r в
матрице M
Ищет в векторе или матрице A заданное значение z и
match(z,M) возвращает индексы его позиций в A
Функции, возвращающие специальные
характеристики матриц
Функция
Описание
cols(M)
Возвращает число столбцов матрицы М
rows(M)
Возвращает число строк матрицы М
rank(M)
Возвращает ранг матрицы М
tr(M)
Возвращает след (сумму диагональных элементов)
квадратной матрицы М
mean(M)
Возвращает среднее значение элементов массива М
median(M)
eigenvals(M)
Возвращает медиану элементов массива М
Возвращает вектор собственных значений квадратной
матрицы M
Функции сортировки
Функция
Описание
sort(V)
Сортировка элементов вектора в порядке возрастания
их значений
reverse(V)
Перестановка элементов вектора в обратном порядке
csort(M,n)
Перестановка строк матрицы М таким образом,
чтобы отсортированным оказался n-й столбец
rsort(M,n)
Перестановка столбцов матрицы М таким образом,
чтобы отсортированной оказалась n-я строка
Примеры
1 2
m1
3 1
1 2
m2
3 2
1 2
m1
1
m10 1 2
7 2
m1 m2
6 4
m11 0 3
1 4
( m1 m2)
9 2
Примеры
2
v 3
7
length( v) 3
last ( v) 2
max( v) 7
min( v) 2
Примеры
1 2
m1
3 1
1 2
m2
3 2
1 2 1 2
augment ( m1 m2)
3 1 3 2
1
3
M stack ( m1 m2)
1
3
3 1
submatrix( M 1 2 0 1)
1 2
2
1
2
2
3
submatrix( M 1 2 0 0)
1
Примеры
1 2
m1
3 1
1 2
m2
3 2
lookup ( 3 m1 m2) ( 3 )
1
lookup ( 1 m1 m2)
2
0
0
0
match ( 1 m1 ) 0
1
match ( 1 m1)
1
1
1
1
match ( 3 m2)
0
Примеры
9
3
V
5
2
2
3
sort ( V)
5
9
2
5
reverse ( V)
3
9
9
5
reverse ( sort ( V) )
3
2
1 5 7 2
M
0
7
4
2
0 7 4 2
csort ( M 2)
1
5
7
2
7 2 1 5
rsort ( M 1)
4
2
0
7
{4,1}
{4,1}
{5,1}
{4,1}
main( D Ta i h)
{201,2}
{4,1}
{4,1}
{1,2}
0
{5,1}
main( D Ta i h) 5
{5,1}
{5,1}
0
20
main(D Ta i h)5 1 20
20
20
Формат → Результат → Параметры отображения
English Русский Правила
Работа с матрицами
Компьютеры Работа с матрицами
просмотров — 92
Форматирование формул и текста
Ввод текста
Текст, помещенный в рабочий лист, содержит комментарии и описания и предназначен для ознакомления, а не для использования в расчетах. Программа MathCad определяет назначение текущего блока автоматически при первом нажатии клавиши ПРОБЕЛ. В случае если введенный текст не может быть интерпретирован как формула, блок преобразуется в текстовый и последующие данные рассматриваются как текст. Создать текстовый блок без использования автоматических средств позволяет команда insert > Text Region (Вставка > Текстовый блок).
Программа MathCad определяет назначение текущего блока автоматически при первом нажатии клавиши ПРОБЕЛ. В случае если введенный текст не может быть интерпретирован как формула, блок преобразуется в текстовый и последующие данные рассматриваются как текст. Создать текстовый блок без использования автоматических средств позволяет команда insert > Text Region (Вставка > Текстовый блок).
Иногда требуется встроить формулу внутрь текстового блока. Для этого служит команда Insert > Math Region (Вставка > Формула).
Для форматирования формул и текста в программе MathCad используется панель инструментов Formatting (Форматирование). С ее помощью можно индивидуально отформатировать любую формулу или текстовый блок, задав гарнитуру и размер шрифта͵ а также полужирное, курсивное или подчеркнутое начертание символов. В текстовых блоках можно также задавать тип выравнивания и применять маркированные и нумерованные списки.
В качестве средств автоматизации используются стили оформления. Выбрать стиль оформления текстового блока или элемента формулы можно из списка Style (Стиль) на панели инструментов Formatting (Форматирование). Для формул и текстовых блоков применяются разные наборы стилей.
Выбрать стиль оформления текстового блока или элемента формулы можно из списка Style (Стиль) на панели инструментов Formatting (Форматирование). Для формул и текстовых блоков применяются разные наборы стилей.
Чтобы изменить стиль оформления формулы или создать новый стиль, используется команда Format > Equation (Формат > Выражение). Изменение стандартных стилей Variables (Переменные) и Constants (Константы) влияет на отображение формул по всему документу. Стиль оформления имени переменной учитывается при ее определении. Так, переменные хил: рассматриваются как различные и не взаимозаменяемы.
При оформлении текстовых блоков можно использовать более обширный набор стилей. Настройка стилей текстовых блоков производится при помощи команды Format t Style (Формат > Стиль).
Векторы и матрицы рассматриваются в программе MathCad как одномерные и двумерные массивы данных. Число строк и столбцов матрицы задается в диалоговом окне Insert Matrix (Вставка матрицы), ĸᴏᴛᴏᴩᴏᴇ открывают командой Insert > Matrix (Вставка > Матрица). Вектор задается как матрица, имеющая один столбец.
Вектор задается как матрица, имеющая один столбец.
После щелчка на кнопке ОК в формулу вставляется матрица, содержащая вместо элементов заполнители. Вместо каждого заполнителя нужно вставить число, переменную или выражение.
Для матриц определены следующие операции: сложение, умножение на число, перемножение и прочие. Допустимо использование матриц вместо скалярных выражений: в этом случае предполагается, что указанные действия должны быть применены к каждому элементу матрицы, и результат также представляется в виде матрицы. К примеру, выражение М+ 3, где М — матрица, означает, что к каждому элементу матрицы прибавляется число 3. В случае если требуется явно указать крайне важность поэлементного применения операции к матрице, используют знак векторизации, для ввода которого служит кнопка Vectorize (Векторизация) на панели инструментов Matrix (Матрица). К примеру:
— обычное произведение матриц.
— поэлементное произведение матриц с
использованием векторизации.
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица).
Пара индексов, определяющих элемент матрицы, разделяется запятой. Иногда (к примеру, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки, к примеру М<0>. Для его ввода используется кнопка Matrix Column (Столбец) на панели инструментов Matrix (Матрица).
Чтобы задать общую формулу элементов матрицы, типа Мi,j : i + j,используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента͵ через запятую значение второго и через точку с запятой значение последнего элемента. Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, к примеру х := 0,0.01..1.
Точка с запятой при задании диапазона отображается как две точки (..). Диапазон можно использовать как значение переменной, к примеру х := 0,0.01..1.
В случае если разность прогрессии равна единице (то есть, элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают. К примеру, чтобы сформировать по приведенной выше формуле матрицу размером 6×6, перед этой формулой нужно указать i:= 0..5 j := 0..5. При формировании матрицы путем присвоения значения ее элементам, размеры матрицы можно не задавать заранее. Всем неопределенным элементам автоматически присваиваются нулевые значения. К примеру, формула М5,5 := 1 создает матрицу М размером 6´6, у которой все элементы, кроме расположенного в правом нижнем углу, равны 0.
Форматирование формул и текста
Ввод текста
Текст, помещенный в рабочий лист, содержит комментарии и описания и предназначен для ознакомления, а не для использования в расчетах. Программа MathCad определяет назначение текущего блока автоматически при первом нажатии… [читать подробенее]
Программа MathCad определяет назначение текущего блока автоматически при первом нажатии… [читать подробенее]
Рассмотрим простейшие операции матричной алгебры, реализованные в MathCAD в виде операторов, причем следует отметить, что их запись максимально приближена к математической форме записи. Наиболее часто используемые операции расположены на панели инструментов Матрица (Matrix)… [читать подробенее]
В MathCAD для работы с матрицами и векторами предназначена специальная панель инструментов Matrix. Чтобы отобразить панель Matrix необходимо щелкнуть по кнопке на математической панели Math. Рис.3. Панель инструментов Matrix Рассмотримназначение кнопок панели Matrix – определение… [читать подробенее]
Матрица – это двухмерный массив, который можно представить себе как совокупность строк (или совокупность столбцов). Положение элемента в массиве определяется двумя индексами: номером строки и номером столбца. Нумерация, как и для одномерных массивов, начинается с нуля…. [читать подробенее]
Положение элемента в массиве определяется двумя индексами: номером строки и номером столбца. Нумерация, как и для одномерных массивов, начинается с нуля…. [читать подробенее]
Глоссарий терминов, используемых в матричной алгебре: (жирный шрифт: наиболее важные для нас)
Глоссарий терминов, используемых в матричной алгебре: (жирный шрифт: наиболее важные для нас)( полужирный: самое важное для нас)
Возврат на главную страницу указателя
Совместимость:
Две матрицы совместимы (для умножения) если количество столбцов в первом равно количеству строк в второй. Это потому, что каждая строка (с j элементов) в первом матрица будет умножаться на каждый столбец (с i элементами) в вторая матрица. Чтобы поэлементный принцип работал, число элементов (столбцов) в первом должно быть равно количеству элементов (строк) во-вторых.Совместимость: «внутренних» терминов ( c1 должен быть равен r2) Размерность результата: «внешние» термины (r1 * с2)Эвристика: m x n * o x p приводит к NO GO, если n < > o. Делать они совпадают, где они касаются?
Определитель (Det):
Только квадратные матрицы . Дет А = · aij (-1)i+j Det M ij, где M ij — минор числа A с i-я строка и j-й столбец удалены. (Сумма по j для расширения по столбцам, что является обычным способом сделай это). Для больших матриц вычисление определителя выполняется по строке развязки. Определитель может сказать нам о количестве решений к набору уравнений (уникальных, бесконечных?) и различным другим полезным свойствам матрицы.Собственные значения:
Характеристические корни системы уравнений. В матричной форме собственные значения (l) определены так, что Det( A — l I) = 0 [характеристическое уравнение].Собственный вектор:Характеристическое уравнение будет многочлен от л степень n , где n — порядок (размер) матрицы. В демографии, доминирующим собственным значением является скорость роста населения, л , в то время как второе собственное значение дает коэффициент затухания (как быстро население вернется к равновесию после возмущения).
Вектор, u , такой, что A*u = l* u. Для матричных моделей правый и левый собственные векторы, соответствующие доминирующим собственным значением являются репродуктивных значения (левый собственный вектор, вектор-строка) и стабильное (st)возрастное распределение (правый собственный вектор, вектор-столбец).Идентификационная матрица:
Матрица обычно записывается как I , с 1 (единицы) на главной диагонали и нули в остальных местах.Обратное:
А -1 * А = I .Неснижаемый:Обратной матрицей называется та матрица, которая при предварительно умноженный на A , дает единичную матрицу. Обратное существует только когда матрица сингулярна (то есть имеет определитель).
Эквивалентно «сильно связанным» на диаграмме теории (см. Кейфиц, стр. 30). Каждая точка на графике (или в матрице) можно добраться из любой другой точки либо напрямую, либо через промежуточные узлы.Матрица Лесли:
Матрица возрастной классификации, используемая в анализе истории жизни. Оно имеет элементы только в верхнем ряду (плодовитость) и по поддиагональному (выживаемость). Чтобы получить стабильное возрастное распределение, матрица должна быть несокращаемый (сильно связанный) и примитивный .Умножение:
см. Совместимость. Выполнено ряд за столбцом, элемент за элементом. Произведение матрицы r x c * c x s представляет собой матрицу порядок (= размер) r x s (количество строк в первом по количеству столбцы во втором).Примитив :Итак, совместимость включает в себя два внутренних числа и «порядок» матрицы произведения включает два внешних числа.
Любая матрица, для которой А п (для некоторых произвольных n ) имеет только положительные элементы, называется примитивный. Примитивность неотрицательной неприводимой матрицы является достаточным условие стабильности. Для простой матрицы Лесли это означает, что при должны существовать как минимум две возрастные группы, у которых m i > 0 и которые имеют i относительно простые (например, для шестилетнего срока службы плодовитость только в возрастных классах 3 и 6 будет давать циклы, а не стабильную возрастное распределение).Единственное число :
Матрица, определитель которой равен нулю.
Нижний индекс:
Для матрицы A , a ij означает элемент в i-й строке и j-й столбец.Симметричный:A = {aij}, где {} означает «множество».
Матрица симметрична, если она равна своей транспонировать. То есть если А + А ‘.След :
Только квадратные матрицы . Сумма элементы главной диагонали.Транспонировать:
Для матрицы А , транспонировать А ‘ = {arc}’ = {acr} (используйте i и j в качестве индексов, если хотите). То есть элементы в строках из первых становятся элементами столбцов транспонирования.ИСПОЛЬЗОВАННАЯ ЛИТЕРАТУРА: Кейфиц, Н. 1985. С. 27–33 обсуждаются матрицы и графики, используемые в демографии.
Рафгарден, Дж. 1979. Приложение 3, стр. 579-590 In : Теория популяционной генетики. и эволюционная экология: введение. Макмиллан, Нью-Йорк
Серл, С.Р. 1966. Матричная алгебра для биологических наук. Wiley and Sons, NY
Вернуться к началу страницы2.1: Введение в матрицы — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 37846
- Рупиндер Секон и Роберта Блум
- Колледж Де Анза
Цели обучения
В этом разделе вы научитесь:
- Складывать и вычитать матрицы.

- Умножить матрицу на скаляр.
- Умножьте две матрицы.
Матрица представляет собой двумерный массив чисел, расположенных в строках и столбцах. Матрицы обеспечивают метод организации, хранения и работы с математической информацией. Матрицы имеют множество применений и использования в реальном мире. Матрицы представляют собой полезный инструмент для работы с моделями, основанными на системах линейных уравнений. Мы будем использовать матрицы в разделах 2.2, 2.3 и 2.4 для решения систем линейных уравнений с несколькими переменными в этой главе.
Матрицы используются в шифровании, которое мы рассмотрим в разделе 2.5, и в экономическом моделировании, рассмотренном в разделе 2.6. Мы снова используем матрицы в главе 4, в задачах оптимизации, таких как максимизация прибыли или дохода или минимизация затрат. Матрицы используются в бизнесе для планирования, маршрутизации транспорта и отгрузок, а также управления запасами.
Почти любое приложение, которое собирает данные и управляет ими, может применять матрицы. Использование матриц расширилось по мере увеличения доступности данных во многих сферах жизни и бизнеса. Они являются важными инструментами для организации данных и решения задач во всех областях науки, от физики и химии до биологии и генетики, метеорологии и экономики. В компьютерных науках за анимацией изображений в фильмах и видеоиграх стоит матричная математика.
Использование матриц расширилось по мере увеличения доступности данных во многих сферах жизни и бизнеса. Они являются важными инструментами для организации данных и решения задач во всех областях науки, от физики и химии до биологии и генетики, метеорологии и экономики. В компьютерных науках за анимацией изображений в фильмах и видеоиграх стоит матричная математика.
Информатика анализирует диаграммы сетей, чтобы понять, как вещи связаны друг с другом, например, отношения между людьми на веб-сайте социальной сети, отношения между результатами линейного поиска и то, как люди ссылаются с одного веб-сайта на другой. Математика для работы с сетевыми диаграммами относится к области «теории графов»; он использует матрицы для организации информации в графах, которые отображают соединения и ассоциации в сети. Например, если вы используете Facebook, Linked-In или другие сайты социальных сетей, эти сайты используют сетевые графики и матрицы для организации ваших отношений с другими пользователями.
Знакомство с матрицами
Матрица представляет собой прямоугольный массив чисел. Матрицы полезны при организации и обработке больших объемов данных. Чтобы получить некоторое представление о том, что такое матрицы, мы рассмотрим следующий пример.
Пример \(\PageIndex{1}\)
Fine Furniture Company производит стулья и столы на своих фабриках в Сан-Хосе, Хейворде и Окленде. Общий объем производства трех заводов в сотнях за 2014 и 2015 годы указан в таблице ниже.
| 2014 | 2015 | |||
| СТУЛЬЯ | СТОЛЫ | СТУЛЬЯ | СТОЛЫ | |
| САН-ХОСЕ | 30 | 18 | 36 | 20 |
| ХЕЙВОРД | 20 | 12 | 24 | 18 |
| ОКЛЕНД | 16 | 10 | 20 | 12 |
- Представим производство за 2014 и 2015 годы в виде матриц A и B.

- Найдите разницу в продажах между 2014 и 2015 годами.
- Компания прогнозирует, что в 2020 году производство на этих заводах удвоится по сравнению с 2014 годом. Каким будет производство в 2020 году?
Решение
а) Матрицы следующие:
\[A=\left[\begin{array}{ll}
30 и 18 \\
20 и 12 \\
16 & 10
\ end{массив}\right] \nonumber \]
\[\mathrm{B}=\left[\begin{array}{ll}
36 и 20 \\
24 и 18 \\
20 и 12
\ end{array}\right] \nonumber \]
б) Ищем матрицу \(B — A\). Когда две матрицы имеют одинаковое количество строк и столбцов, матрицы можно складывать или вычитать поэлементно. Таким образом, мы получаем
\[\mathrm{B}-\mathrm{A}=\left[\begin{array}{ll}
36-30 и 20-18 \\
24-20 и 18-12 \\
20- 16 & 12-10
\end{массив}\right]=\left[\begin{array}{ll}
6 & 2 \\
4 & 6 \\
4 & 2
\end{массив}\right ] \nonumber \]
c) Нам нужна матрица, вдвое превышающая матрицу 2014, т. е. \(2A\).
е. \(2A\).
Всякий раз, когда матрица умножается на число, каждая запись умножается на число.
\[2 \mathrm{A}=2\left[\begin{array}{ll}
30 и 18 \\
20 и 12 \\
16 и 10
\end{array}\right]=\left[\begin{array}{ll}
60 и 36 \\
40 & 24 \\
32 & 20
\end{array}\right] \nonumber \]
Прежде чем двигаться дальше, нам нужно ознакомиться с некоторыми терминами, связанными с матрицами. Числа в матрице называются элементами или элементами матрицы.
Всякий раз, когда мы говорим о матрице, нам нужно знать размер или размер матрицы. Размерность матрицы — это количество строк и столбцов в ней. Когда мы говорим, что матрица представляет собой «матрицу 3 на 4», мы говорим, что она имеет 3 строки и 4 столбца. Строки всегда упоминаются первыми, а столбцы — вторыми. Это означает, что матрица \(3 \times 4\) не имеет той же размерности, что и матрица \(4 \times 3\).
\[A=\left[\begin{array}{cccc}
1 & 4 & -2 & 0 \\
3 & -1 & 7 & 9 \\
6 & 2 & 0 & 5
\end{массив}\right] \nonumber \]
\[B=\left[\begin{array}{ccc}
2 & 9 & 8 \\
-3 & 0 & 1 \\
6 & 5 & -2 \\
-4 & 7 & 8
\end{array}\right] \nonumber \]
Матрица \(A\) имеет размеры \(3 \times 4\) и матрицу \(B\ ) имеет размеры \(4 \times 3\).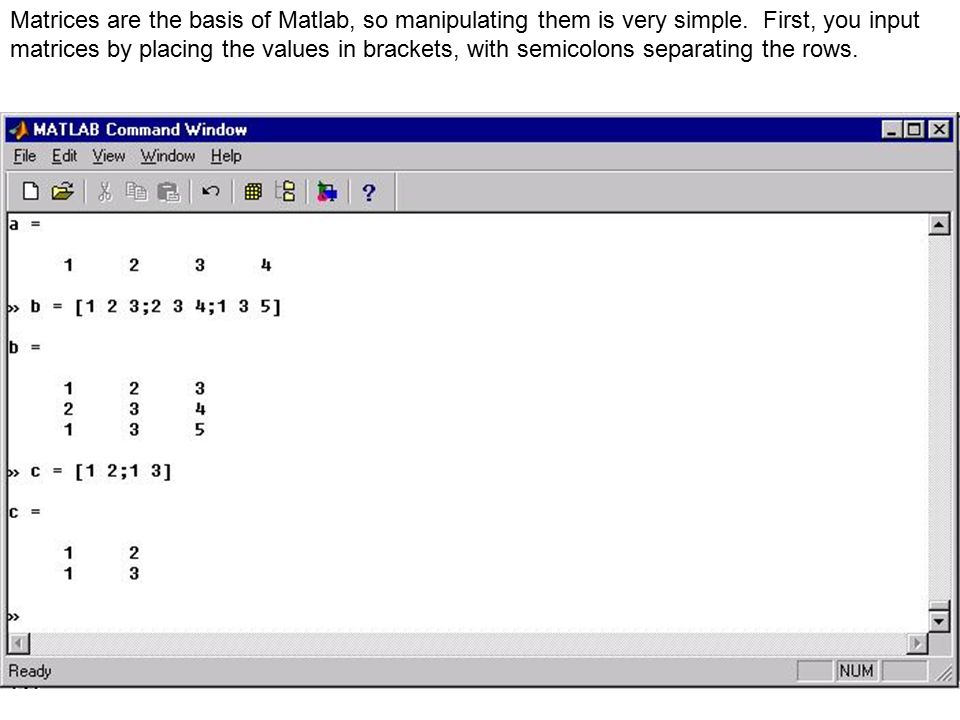
Матрица, в которой количество строк равно количеству столбцов, называется квадратной матрицей . Матрица, в которой все элементы равны нулю, называется нулевой матрицей . Квадратная матрица с единицами вдоль главной диагонали и нулями в остальных местах называется единичной матрицей . Когда квадратная матрица умножается на единичную матрицу того же размера, матрица остается прежней.
\[I=\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right] \nonumber \]
Матрица \(I\) представляет собой \(3 \x 3\) единичную матрицу
Матрица только с одной строкой называется матрицей строк или вектор-строка, и матрица только с одним столбцом называется матрицей-столбцом или вектором-столбцом . Две матрицы равны , если они имеют одинаковый размер и соответствующие элементы равны.
Мы можем выполнять арифметические операции с матрицами. Далее мы определим и приведем примеры, иллюстрирующие операции сложения и вычитания матриц, скалярного умножения и умножения матриц. Обратите внимание, что умножение матриц сильно отличается от того, что вы интуитивно ожидаете, поэтому обратите особое внимание на объяснение. Также обратите внимание, что возможность выполнения матричных операций зависит от того, совместимы ли матрицы по размеру или размерам для этой операции. Определение совместимых размеров различается для разных операций, поэтому внимательно запишите требования для каждой из них.
Обратите внимание, что умножение матриц сильно отличается от того, что вы интуитивно ожидаете, поэтому обратите особое внимание на объяснение. Также обратите внимание, что возможность выполнения матричных операций зависит от того, совместимы ли матрицы по размеру или размерам для этой операции. Определение совместимых размеров различается для разных операций, поэтому внимательно запишите требования для каждой из них.
Сложение и вычитание матриц
Если две матрицы имеют одинаковый размер, их можно сложить или вычесть. Операции выполняются над соответствующими записями.
Пример \(\PageIndex{2}\)
Даны матрицы \(A\), \(B\), \(C\) и \(D\), ниже
\[A=\left [\begin{array}{lll}
1 & 2 & 4 \\
2 & 3 & 1 \\
5 & 0 & 3
\end{массив}\right] \quad B=\left[\begin{ array}{lll}
2&-1&3\
2&4&2\
3 & 6 & 1
\end{массив}\right] \quad C=\left[\begin{array}{l}
4 \\
2 \\
3
\end{массив}\right] \ quad D=\left[\begin{array}{r}
-2 \\
-3 \\
4
\end{array}\right] \nonumber \]
Найти, если возможно.
- \(А+В\)
- \(С — Г\)
- \(А + Д.\)
Решение
Как мы упоминали ранее, сложение и вычитание матриц включают выполнение этих операций поэлементно.
а) Мы добавляем каждый элемент \(A\) к соответствующему элементу \(B\).
\[A+B=\left[\begin{array}{lll}
3 & 1 & 7 \\
4 & 7 & 3 \\
8 & 6 & 4
\end{array}\right] \nonumber \]
б) Так же, как и в задаче выше, мы выполняем вычитание элемент за элементом.
\[\mathrm{C}-\mathrm{D}=\left[\begin{array}{c}
6 \\
5 \\
-1
\end{array}\right] \nonumber \ ]
c) Сумма \(A + D\) не может быть найдена, потому что две матрицы имеют разные размеры.
Примечание. Две матрицы можно складывать или вычитать только , если они имеют одинаковую размерность.
Умножение матрицы на скаляр
Если матрица умножается на скаляр, каждая запись умножается на этот скаляр. Мы можем рассматривать скалярное умножение как умножение числа и матрицы для получения новой матрицы в качестве произведения.
Пример \(\PageIndex{3}\)
Имея матрицы \(A\) и \(C\) в приведенном выше примере, найдите \(2A\) и \(- 3C\).
Решение
Чтобы найти \(2A\), мы умножаем каждый элемент матрицы \(A\) на 2, а чтобы найти \(-3C\), мы умножаем каждый элемент C на -3. Результаты приведены ниже.
а) Умножаем каждую запись A на 2.
\[2 \mathrm{A}=\left[\begin{array}{ccc}
2 & 4 & 8 \\
4 & 6 & 2 \ \
10 & 0 & 6
\end{array}\right] \nonumber \]
b) Мы умножаем каждый элемент C на -3.
\[-3 C=\left[\begin{массив}{c}
-12 \\
-6 \\
-9
\end{array}\right] \nonumber \]
Умножение двух матриц
Умножить одну матрицу на другую не так просто, как сложение, вычитание, или скалярное умножение матриц. Из-за его широкого использования в прикладных задачах важно, чтобы мы хорошо его изучили. Поэтому постараемся изучить процесс поэтапно. Сначала начнем с нахождения произведения матрицы-строки и матрицы-столбца.
Пример \(\PageIndex{4}\)
Найти произведение \(AB\), заданное
\[A=\left[\begin{array}{lll}
2 & 3 & 4
\end{array}\right] \nonumber \]
и
\[B=\left[\begin{array}{l}
a \\
b \\
c
\end{array}\right]. \nonumber \]
Решение
Произведение представляет собой матрицу \(1 \times 1\), элементы которой получаются путем умножения соответствующих элементов и последующего формирования суммы.
\[\begin{align*}
\mathrm{AB} &=\left[\begin{array}{lll}
2 & 3 & 4
\end{массив}\right]\left[\begin{array}{l}
\mathrm{a} \\
\mathrm{b} \\
\mathrm{c}
\ end{массив}\right] \\[4pt] &=[2 (\mathrm{a}+3 \mathrm{b}+4 \mathrm{c})]
\end{align*} \nonumber \]
Обратите внимание, что \(AB\) является матрицей \(1 \times 1\), и ее единственный элемент — \(2a + 3b + 4c\).
Пример \(\PageIndex{5}\)
Найти произведение \(AB\), заданное
\[A=\left[\begin{array}{lll}
2 & 3 & 4
\end {массив}\справа] \номер\]
и
\[B=\left[\begin{array}{l}
5 \\
6 \\
7
\end{array}\right] \nonumber \]
Решение
Снова умножаем соответствующие записи и складываем.
\[\begin{align*} \mathrm{AB} &=\left[\begin{array}{lll}
2 & 3 & 4
\end{массив}\right]\left[\begin{массив }{l}
5 \\
6 \\
7
\end{массив}\right] \\[4pt] &=[2 \cdot 5+3 \cdot 6+4 \cdot 7]\\[4pt ] &=[10+18+28]\\[4pt] &=[56] \end{align*} \nonumber \]
Примечание. Чтобы произведение матрицы-строки и матрицы-столбца существовало, количество элементов в матрице-строке должно совпадать с количеством элементов в матрице-столбце.
Пример \(\PageIndex{6}\)
Найдите произведение AB, учитывая
\[A=\left[\begin{array}{lll}
2 & 3 & 4
\end{array}\ right] \nonumber \]
и
\[B=\left[\begin{array}{ll}
5 & 3 \\
6 & 4 \\
7 & 5
\end{array}\right ]. \номер\]
Решение
Мы знаем, как умножать матрицу-строку на матрицу-столбец. Чтобы найти произведение \(AB\), в этом примере мы умножим матрицу строк \(A\) на первый и второй столбцы матрицы \(B\), в результате чего получим \(1 \times 2\ ) матрица.
\[\mathrm{AB}=\left[\begin{array}{lll}
2 \cdot 5+3 \cdot 6+4 \cdot 7 и 2 \cdot 3+3 \cdot 4+4 \cdot 5
\end{массив}\right]=\left[\begin{array}{ll}
56 и 38
\end{массив}\right] \nonumber \]
Мы умножили матрицу \(1 \times 3\) на матрицу размера \(3 \times 2\). Таким образом, в отличие от сложения и вычитания, можно умножать две матрицы разной размерности, если количество элементов в строках первой матрицы равно количеству элементов в столбцах второй матрицы.
Пример \(\PageIndex{7}\)
Найти произведение \(AB\), учитывая:
\[A=\left[\begin{array}{lll}
2 & 3 & 4 \\
1 и 2 и 3
\end{array}\right] \nonumber \]
и
\[\mathrm{B}=\left[\begin{array}{ll}
5 & 3 \\
6 & 4 \\
7 & 5
\end{array}\right] \nonumber \]
Решение
На этот раз мы умножаем две строки матрицы \(A\) на два столбца матрицы \(B\). Поскольку количество записей в каждой строке \(A\) равно количеству записей в каждом столбце \(B\), произведение возможно. Делаем точно так же, как и в последнем примере. Единственное отличие состоит в том, что матрица \(A\) имеет на одну строку больше.
Делаем точно так же, как и в последнем примере. Единственное отличие состоит в том, что матрица \(A\) имеет на одну строку больше.
Умножаем первую строку матрицы \(A\) на два столбца \(B\), по одному, а затем повторяем процесс со второй строкой A. Получаем
\[\ mathrm{AB}=\left[\begin{array}{lll}
2 & 3 & 4 \\
1 & 2 & 3
\end{array}\right]\left[\begin{array}{ll}
5 и 3 \\
6 и 4 \\
7 и 5
\end{массив}\right]=\left[\begin{массив}{ll}
2 \cdot 5+3 \cdot 6+4 \ cdot 7 и 2 \cdot 3+3 \cdot 4+4 \cdot 5 \\
1 \cdot 5+2 \cdot 6+3 \cdot 7 и 1 \cdot 3+2 \cdot 4+3 \cdot 5
\end{массив}\right] \nonumber \]
\[\mathrm{AB}=\left[\begin{array}{ll}
56 и 38 \\
38 и 26
\end{массив} \right] \nonumber \]
Пример \(\PageIndex{8}\)
Найдите, если возможно:
- \(EF\)
- \(ФЭ\)
- \(ФХ\)
- \(ГХ\)
- \(HG\)
\[\mathrm{E}=\left[\begin{array}{ll}
1 & 2 \\
4 & 2 \\
3 & 1
\end{array}\right] \quad \mathrm {F}=\left[\begin{массив}{ll}
2 & -1 \\
3 & 2
\end{array}\right] \quad \mathrm{G}=\left[\begin{array}{lll}
4 & 1
\end{array}\ right] \quad \mathrm{H}=\left[\begin{array}{l}
-3 \\
-1
\end{array}\right] \nonumber \]
Решение
a ) Чтобы найти \(EF\), мы умножаем первую строку \(\left[\begin{array}{ll}
1 & 2
\end{array}\right]\)
E со столбцами \ (\left[\begin{array}{l}
2 \\
3
\end{array}\right] \text { и }\left[\begin{array}{l}
1 \\
-2
\end{array}\right]\) матрицы F, а затем повторите процесс, умножив две другие строки E на эти столбцы F. Результат будет следующим:
Результат будет следующим:
\[\mathrm{EF}=\left[\begin{array}{ll}
1 & 2 \\
4 & 2 \\
3 & 1
\end{массив}\right]\left[\begin{ array}{cc}
2 & -1 \\
3 & 2
\end{array}\right]=\left[\begin{array}{cc}
1 \cdot 2+2 \cdot 3 & 1 \ cdot-1+2 \cdot 2 \\
4 \cdot 2+2 \cdot 3 и 4 \cdot-1+2 \cdot 2 \\
3 \cdot 2+1 \cdot 3 и 3 \cdot-1+1 \cdot 2
\end{массив}\right]=\left[\begin{массив}{cc}
8 & 3 \\
14 & 0 \\
9 & -1
\end{array}\right] \nonumber \]
б) Произведение \(FE\) невозможно, так как матрица F имеет два элемента в каждой строке, а матрица E имеет по три записи в каждом столбце. Другими словами, матрица F имеет два столбца, а матрица E — три строки.
c) \[\mathrm{FH}=\left[\begin{array}{cc}
2 & -1 \\
3 & 2
\end{массив}\right]\left[\begin{array}{c}
-3 \\
-1
\end{массив}\right]=\left[\begin{array}{c}
2 \cdot-3+-1 \cdot-1 \\
3 \cdot-3+2 \cdot-1
\end{массив}\right]=\left[\begin{массив}{c}
-5 \\
-11
\end{array}\right] \nonumber \]
d) \[\mathrm{GH}=\left[\begin{array}{ll}
4 & 1
\end{array }\right]\left[\begin{array}{l}
-3 \\
-1
\end{array}\right]=\left[\begin{array}{l}
4 \cdot-3 +1 \cdot-1 \\
-1
\end{array}\right]=[-13] \nonumber \]
e) \[\mathrm{HG}=\left[\begin{array}{l}
-3 \\
-1
\end{array}\right]\left[\begin{array}{ll}
4 & 1
\end{array}\right]=\left[\begin{array}{ll}
-3 \cdot 4 & -3 \cdot 1 \\
-1 \cdot 4 & -1 \cdot 1
\end{массив}\right]=\left[\begin{массив}{cc}
-12 & -3 \\
-4 & -1
\end{array}\right] \nonumber \]
Мы суммируем некоторые важные свойства матричного умножения, которые мы наблюдали в предыдущих примерах.
Чтобы продукт \(\bf{AB}\) существовал:
- количество столбцов \(\bf{A}\) должно равняться количеству строк \(\бф{В}\)
- , если матрица \(\bf{A}\) имеет размерность \(\bf{m \times n}\) и матрица \(\bf{B}\) имеет размерность \(\ bf{n \times p}\) , то произведение \(\bf{AB}\) будет матрицей размерности \(\bf{m \times p}\) .
Умножение матриц не является коммутативным: если оба матричных произведения \(\bf{AB}\) и \(\bf{BA}\) существуют, большую часть времени \(\bf{AB} \) не будет равно \(\bf{BA}\) .
Пример \(\PageIndex{9}\)
По заданным ниже матрицам \(R\), \(S\) и \(T\) найдите \(2RS — 3ST\).
\[R=\left[\begin{array}{lll}
1 & 0 & 2 \\
2 & 1 & 5 \\
2 & 3 & 1
\end{массив}\right] \quad S=\left[\begin{array}{lll}
0 & -1 & 2 \\
3 & 1 & 0 \\
4 & 2 & 1
\end {array}\right] \quad T=\left[\begin{array}{lll}
-2 & 3 & 0 \\
-3 & 2 & 2 \\
-1 & 1 & 0
\end{ array}\right] \nonumber \]
Решение
Перемножаем матрицы R и S.
\begin{aligned}
&\mathrm{RS}=\left[\begin{array}{ccc}
8 & 3 & 4 \
23 & 9 & 9 \\
13 & 3 & 5
\end{массив}\right]\\
&\begin{массив}{l}
2 \mathrm{RS}=2\left[\begin{ array}{ccc}
8 & 3 & 4 \\
23 & 9 & 9 \\
13 & 3 & 5
\end{array}\right]=\left[\begin{array}{ccc}
16 & 6 & 8 \\
46 & 18 & 18 \\
26 & 6 & 10
\end{массив}\right] \\
\mathrm{ST}=\left[\begin{array}{ccc}
1&0&-2\
-9&11&2\
-15&17&4
\end{массив}\right] \\
3 \mathrm{ST}=3\left[\begin{array}{ccc}
1 & 0 & -2 \\
-9 & 11 & 2 \\
-15 & 17 & 4
\end{array}\right]=\left[\begin{array}{ccc}
3 & 0 & -6 \\
-27 & 33 & 6 \\
-45 & 51 & 12
\end{массив}\right]
\end{массив}
\end{выровненный}
Таким образом,
\[2 \mathrm{RS}-3 \mathrm{ST}=\left[\begin{ array}{ccc}
16 & 6 & 8 \
46 & 18 & 18 \ 92\), возможен только в том случае, если матрица является квадратной матрицей.
ИСПОЛЬЗОВАНИЕ МАТРИЦ ДЛЯ ПРЕДСТАВЛЕНИЯ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
В этой главе мы будем использовать матрицы для решения линейных систем. В разделе 2.4 нас попросят выразить линейные системы в виде матричного уравнения \(\bf{AX = B}\), где \(A\), \(X\) и \(B\) матрицы.
- Матрица \(A\) называется матрицей коэффициентов .
- Матрица \(X\) — это матрица с 1 столбцом, содержащим переменные.
- Матрица \(B\) — это матрица с 1 столбцом, содержащая константы.
Пример \(\PageIndex{11}\)
Проверить, что система двух линейных уравнений с двумя неизвестными:
\begin{array}{l}
a x+b y=h \\
c x+d y =k
\end{array}
можно записать как \(AX = B\), где
\[A=\left[\begin{array}{ll}
a & b \\
c & d
\end{массив}\right] \quad X=\left[\begin{array}{l}
x \\
y
\end{массив}\right] \text { и } B=\left[\ начало {массив} {l}
h \\
k
\end{array}\right] \nonumber \]
Решение
Если мы перемножим матрицы \(A\) и \(X\), то получим
\[A X =\left[\begin{array}{ll}
a & b \\
c & d
\end{массив}\right]\left[\begin{array}{l}
x \\
y
\ end{массив}\right]=\left[\begin{массив}{c}
a x+b y \\
c x+d y
\end{массив}\right] \nonumber \]
Если \(AX = B\) тогда
\[\left[\begin{array}{l}
a x+b y \\
c x+d y
\end{массив}\right]=\left[\begin{array}{l}
h \\
k
\end{массив}\right] \nonumber \]
Если две матрицы равны, то равны и их соответствующие записи. Отсюда следует, что
Отсюда следует, что
\begin{array}{l}
a x+b y=h \\
c x+d y=k
\end{array}
Пример \(\PageIndex{12}\)
Express следующую систему в виде матричного уравнения вида \(AX = B\).
\begin{array}{l}
2 x+3 y-4 z=5 \\
3 x+4 y-5 z=6 \\
5 x \quad-6 z=7
\end{array}
Решение
Эта система уравнений может быть выражена в форме \(AX = B\), как показано ниже.
\[\left[\begin{array}{ccc}
2 & 3 & -4 \\
3 & 4 & -5 \\
5 & 0 & -6
\end{array}\right]\ left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
5 \\
6 \\
7
\конец{массив}\право] \номер\]
Эта страница под названием 2.1: Introduction to Matrices распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Рупиндером Секоном и Робертой Блум с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Рупиндер Сехон и Роберта Блум
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- Матрица коэффициентов
- вектор-столбец
- размер
- элементов
- записей
- тождественная матрица
- вектор-строка
- источник@https://www.
 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html - квадратная матрица
- нулевая матрица
Матрицы и массивы — MATLAB & Simulink
Основное содержание
Open Live Script
MATLAB — это сокращение от «матричная лаборатория». В то время как другие языки программирования в основном работают с числами по одному, MATLAB® предназначен для работы в основном с целыми матрицами и массивами.
Все переменные MATLAB являются многомерными массивами , независимо от типа данных. А 9Матрица 0451 представляет собой двумерный массив, часто используемый для линейной алгебры.
Создание массива
Чтобы создать массив из четырех элементов в одной строке, разделите элементы запятой ( , ) или пробелом.
а = [1 2 3 4]
а = 1×4
1 2 3 4
Этот тип массива представляет собой вектор-строку .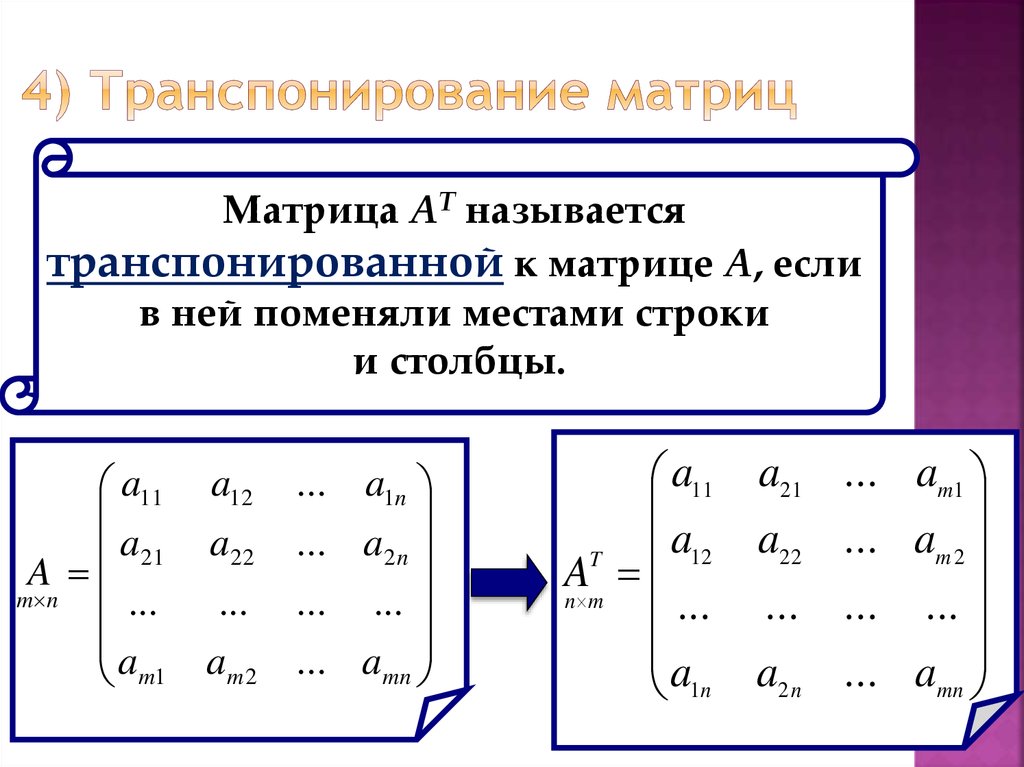
Чтобы создать матрицу из нескольких строк, разделите строки точкой с запятой.
а = [1 3 5; 2 4 6; 7 8 10]
а = 3×3
1 3 5
2 4 6
7 8 10
Другой способ создать матрицу — использовать функцию, например единиц , нулей или ранд . Например, создайте вектор-столбец 5 на 1 из нулей.
z = нули (5,1)
z = 5×1
0
0
0
0
0
Операции с матрицами и массивами
MATLAB позволяет обрабатывать все значения в матрице с помощью одного арифметического оператора или функции.
а + 10
анс = 3×3
11 13 15
12 14 16
17 18 20
sin(a)
ans = 3×3
0,8415 0,1411 -0,9589
0,9093 -0,7568 -0,2794
0,6570 0,9894 -0,5440
Чтобы транспонировать матрицу, используйте одинарную кавычку ( ' ):
ans = 3×3
1 2 7
3 4 8
5 6 10
Вы можете выполнить стандартное умножение матриц, которое вычисляет внутренние произведения между строками и столбцами, используя * оператор. Например, подтвердите, что матрица, умноженная на свою обратную, возвращает единичную матрицу:
Например, подтвердите, что матрица, умноженная на свою обратную, возвращает единичную матрицу:
p = a*inv(a)
p = 3×3
1,0000 0,0000 -0,0000
0 1,0000 -0,0000
0 0,0000 1,0000
Обратите внимание, что p не является матрицей целочисленных значений. MATLAB хранит числа как значения с плавающей запятой, а арифметические операции чувствительны к небольшим различиям между фактическим значением и его представлением с плавающей запятой. Вы можете отобразить больше десятичных цифр, используя формат команда:
формат длинный p = a*inv(a)
p = 3×3
0,999999999999996 0,000000000000007 -0,000000000000002
0 1.000000000000000 -0.000000000000003
0 0,000000000000014 0,999999999999995
Сбросьте отображение на более короткий формат, используя
формат short
формат влияет только на отображение чисел, а не на то, как MATLAB их вычисляет или сохраняет.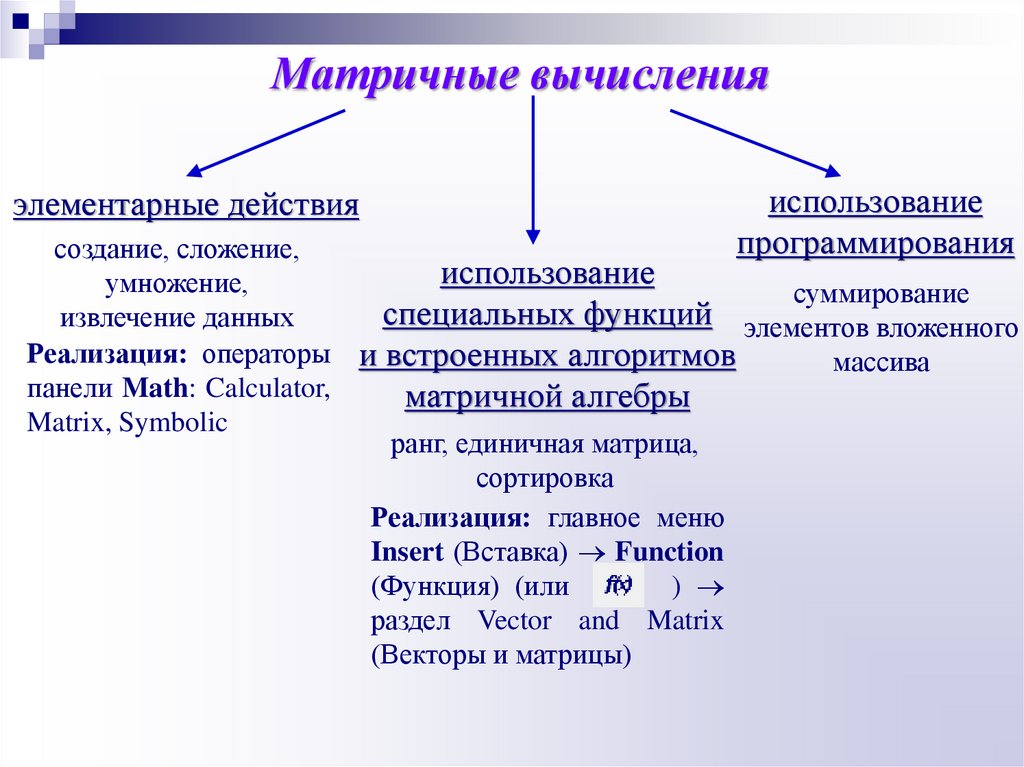
Чтобы выполнить поэлементное умножение, а не матричное умножение, используйте .* оператор:
p = a.*a
p = 3×3
1 9 25
4 16 36
49 64 100
Каждому из матричных операторов умножения, деления и возведения в степень соответствует оператор массива, работающий поэлементно. Например, возведите каждый элемент и в третью степень:
анс = 3×3
1 27 125
8 64 216
343 512 1000
Конкатенация
Конкатенация — это процесс объединения массивов для получения больших массивов. Фактически вы создали свой первый массив, объединив его отдельные элементы. Пара квадратных скобок [] — это оператор конкатенации.
А = [а, а]
А = 3×6
1 3 5 1 3 5
2 4 6 2 4 6
7 8 10 7 8 10
Объединение массивов рядом друг с другом с помощью запятых называется горизонтальная конкатенация. Каждый массив должен иметь одинаковое количество строк. Точно так же, когда массивы имеют одинаковое количество столбцов, вы можете объединить 90 451 по вертикали с 90 452, используя точку с запятой.
Каждый массив должен иметь одинаковое количество строк. Точно так же, когда массивы имеют одинаковое количество столбцов, вы можете объединить 90 451 по вертикали с 90 452, используя точку с запятой.
А = [а; а]
А = 6×3
1 3 5
2 4 6
7 8 10
1 3 5
2 4 6
7 8 10
Комплексные числа
Комплексные числа имеют как действительную, так и мнимую части, где мнимой единицей является квадратный корень из -1 .
sqrt(-1)
анс = 0,0000 + 1,0000i
Для представления мнимой части комплексного числа используйте i или j .
с = [3+4i, 4+3j; -i, 10j]
c = Комплекс 2×2 3.0000 + 4.0000i 4.0000 + 3.0000i 0,0000 - 1,0000i 0,0000 +10,0000i
Начало работы с MATLAB
Следующий
У вас есть модифицированная версия этого примера. Хотите открыть этот пример со своими правками?
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Веб-браузеры не поддерживают команды MATLAB.
Выберите веб-сайт, чтобы получить переведенный контент, где он доступен, и ознакомиться с местными событиями и предложениями. В зависимости от вашего местоположения мы рекомендуем вам выбрать: .
Вы также можете выбрать веб-сайт из следующего списка:
Европа
Свяжитесь с местным офисом
- Пробная версия ПО
- Пробная версия программного обеспечения
- Обновления продукта
- Обновления продукта
Матрица
Умножение Определено (стр. Так же, как и при добавлении матриц, размеры матриц имеют значение, когда мы умножаем. Для умножения матриц для работы столбцы второй матрицы должны иметь одинаковые номера элементов, как и строки первой матрицы.
Если, используя вышеуказанные матрицы, Б имел бы только две строки, его столбцы были бы слишком короткими для умножения
против строк A .
Затем « AB »
не существовало бы; продукт был бы «неопределенным».
Аналогично, если Б имел, скажем, четыре ряда или, альтернативно, если A имел две или четыре колонки, затем AB не существовало бы, потому что A и Б не было бы нужных размеров. Другими словами, для AB существовать (то есть, чтобы сам процесс умножения матриц был способный функционировать разумно), A должно иметь такое же количество столбцов, как Б имеет ряды; глядя на матрицы, строки A должны быть той же длины, что и столбцы B . Вы можете использовать этот факт для быстро проверить, определено ли данное умножение. Напишите продукт по размерам матрицы. В случае вышеуказанной проблемы A 23 года а Б это 32, так АВ есть (23)(32). Средние значения совпадают: …так что умножение определено. Кстати, вы помните, что AB , матрица продукта, была 22. Вы также можете увидеть это на размерах: Используя это, вы можете видеть, что ВА должна быть отличная от 9 матрица0016 АБ , потому что: Продукт ВА определено (то есть мы можем сделать умножение), но произведение, когда
матрицы перемножаются в таком порядке, будет 33,
не 22.
Умножение работает так же, как и в предыдущей задаче, проходя по рядам и вниз столбцы. Я не буду пытаться снова рисовать свои руки, но вы можете видеть вычисления в следующих цветах: Авторское право Элизабет Стапель 2003-2011 Все права защищены Тогда ответ: Умножение матриц
Вероятно, впервые Коммутативный
Собственность когда-либо
была проблема. Помните, когда они сделали большое дело, еще в средней школе
или ранее, примерно как « ab
= ба «или» 56
= 65″? Это «правило»
вероятно, казался довольно глупым в то время, потому что вы уже знали, что
порядок не имеет значения в умножении. << Предыдущая Топ | 1 | 2 | 3 | Возвращаться к индексу Далее >>
|
|
|
Матричная арифметика
Матричная арифметика Большая часть линейной алгебры включает в себя математические объекты, называемые матрицы . Матрица — это
конечный прямоугольный массив чисел:
Матрица — это
конечный прямоугольный массив чисел:
В этом случае числа являются элементами (или ). В общем записи будут элементы некоторого коммутативного кольца или поля.
В этом разделе я объясню операции с матрицами на примере. Я обсужу и докажу некоторые свойства этих операций. позже.
Размеры матриц. Матрица — это матрица с m строк и n столбцов. Иногда это выражается в том, что размеры матрицы .
Матрица называется n-мерный вектор-строка . Например, вот трехмерный вектор строки:
Точно так же матрица называется n-мерным вектором-столбцом . Вот Трехмерный вектор-столбец:
Матрица называется квадратом . матрица . Например, вот квадратная матрица:
Обратите внимание, что по соглашению число строк указывается первым, а
количество столбцов в секунду. Эта конвенция также применяется к ссылке
к конкретным элементам матриц. Рассмотрим
следующая матрица:
Эта конвенция также применяется к ссылке
к конкретным элементам матриц. Рассмотрим
следующая матрица:
Элемент является элементом в строке 2 и столбец 4, который является. (Обратите внимание, что первая строка строка 1, а не строка 0, и аналогично для столбцов.) Элемент — это элемент в строке 3 и столбце 3, то есть 13.
Равенство матриц. Две матрицы равны , если они имеют одинаковые размеры и соответствующие записи равны. Например, предположим
Затем, если я сопоставляю соответствующие элементы, я вижу, что , и .
Определение. Если R — коммутативное кольцо, то это набор матриц с записи в Р.
Примечание. Некоторые люди используют обозначение .
Например, это набор матриц с реальными элементами. представляет собой набор матриц с элементами в .
Сложение и вычитание матриц . Для этих
примеры, я предполагаю, что матрицы имеют записи в .
Вы можете добавлять (или вычитать) матрицы, добавляя (или вычитая) соответствующие записи.
Сложение матрицы ассоциативно — символически,
Это означает, что если вы добавляете несколько матриц, вы можете сгруппировать их любым удобным для вас способом:
Вот пример вычитания:
Обратите внимание, что сложение матриц равно коммутативному :
Символически, если A и B — матрицы одинаковой размерности, то
Конечно, вычитание матриц не является коммутативным.
Вы можете складывать или вычитать матрицы только с одинаковыми размерами. Эти две матрицы нельзя ни сложить, ни вычесть:
Сложение или вычитание матриц свыше . Вы добавляете или вычитаете матрицы, добавляя или вычитая соответствующие записи, но вся арифметика делается в .
Например, вот сложение и вычитание над :
Обратите внимание, что во втором примере были некоторые отрицательные числа. середине вычисления, но окончательный ответ был выражен
полностью с точки зрения элементов .
середине вычисления, но окончательный ответ был выражен
полностью с точки зрения элементов .
Определение. А ноль матрица — это матрица, все элементы которой 0.
Для каждой пары существует нулевая матрица. положительные размерности m и n.
Если вы добавите нулевую матрицу к другой матрице A, вы получите A:
В символах, если — нулевая матрица, а А — матрица одного размера, то
Говорят, что нулевая матрица представляет собой тождество . элемент для сложения матриц.
Примечание. В какой-то момент я могу просто написать «0» вместо » » (жирным шрифтом) для нуля матрица и полагаться на контекст, чтобы отличить ее от числа 0.
Умножение матриц на числа. Вы можете умножить матрицу на число путем умножения каждого элемента на количество. Вот пример с реальными числами:
Вещи работают таким же образом, но все
арифметика делается в . Вот
пример над:
Вот
пример над:
Обратите внимание, что, как обычно, я упростил мой окончательный ответ, чтобы все элементы матрицы были в наборе .
В отличие от операций, которые я обсуждал до сих пор, умножение матриц (умножение двух матриц) не работает так, как вы могли бы ожидать: Вы не просто перемножаете соответствующие элементы матриц, способ добавления соответствующих элементов для добавления матриц.
Чтобы объяснить умножение матриц, я сначала напомню вам, как вы возьми скалярное произведение двух векторов ; ты вероятно, видел это в курсе многомерного исчисления. (Если ты увидев это в первый раз, не волнуйтесь — это просто!) Вот пример скалярного произведения двух трехмерных векторов вещественных номера:
Обратите внимание, что векторы должны быть одного размера, а произведение номер . На самом деле это пример матрицы
умножение, и мы увидим, что технически результат должен быть
матрица. Но для скалярных произведений мы будем писать
Но для скалярных произведений мы будем писать
Если вы видели скалярные произведения в многомерном исчислении, вы, возможно, видел это написано так:
Но для того, что я буду делать дальше, я хочу различать ряд (первый) вектор и вектор-столбец (второй).
Перемножение матриц. Чтобы вычислить произведение двух матриц, возьмите точку произведения строк A со столбцами B. В этом примере Предположим, что все матрицы имеют действительные элементы.
На этом схематическом рисунке показано, как расположены строки первой матрицы. «точечное произведение» со столбцами второй матрицы для произвести 4 элемента продукта:
Вы можете видеть, что вы берете скалярные произведения строк из первая матрица с столбцами второй матрицы.
Чтобы умножение работало, матрицы должны иметь
совместимые размеры: количество столбцов в A должно равняться
количество строк B. Таким образом, если A является матрицей и B является матрицей, будет матрицей. Например,
это не сработает:
Таким образом, если A является матрицей и B является матрицей, будет матрицей. Например,
это не сработает:
Вы понимаете, почему? Строки первой матрицы имеют 4 элемента, но столбцы второй матрицы имеют 3 элемента. Вы не можете взять точку продукты, потому что записи не будут совпадать.
Вот еще два примера, опять же с использованием матриц с реальными элементами:
Вот пример с матрицами в формате . Вся арифметика делается в .
Обратите внимание, что я упрощаю окончательный результат, так что все записи в .
Если вы умножаете матрицу на нулевую матрицу, вы получаете нулевую матрицу:
В символах, если — нулевая матрица, а А — матрица совместим с ним для умножения, то
Умножение матриц требует небольшой практики, но это не сложно.
большой принцип, который нужно убрать, заключается в том, что вы берете скалярные произведения строк первой матрицы с столбцами первой матрицы
вторая матрица. Эта картина матричного умножения будет очень
важно для нашей работы с матрицами.
Эта картина матричного умножения будет очень
важно для нашей работы с матрицами.
Я должен сказать кое-что о моменте, который я упоминал ранее: почему бы и нет? умножать такие матрицы?
Вы могли бы определить умножение матриц таким образом, но к сожалению, это было бы бесполезно для приложений (таких как решение систем линейных уравнений). Или когда мы изучаем связь между матрицами и линейными преобразованиями, мы увидим что матричное умножение, которое мы определили с помощью скалярных произведений соответствует композиции преобразований. Таким образом, хотя определение «соответствующие элементы» кажется более простым, оно не соответствует тому, как используются матрицы.
Вот предварительный просмотр того, как матрицы связаны с системами линейных уравнения.
Пример. Напишите систему уравнений, которая соответствуют матричному уравнению
Две матрицы равны, если их соответствующие элементы равны, поэтому приравнять соответствующие записи:
Пример. Напишите следующую систему линейных
уравнения как уравнение умножения матриц:
Напишите следующую систему линейных
уравнения как уравнение умножения матриц:
Возьмите 9 коэффициентов переменных x, y и z в левой части и превратить их в матрицу. Положите переменные в трехмерный вектор-столбец. Сделайте 3 числа на с правой стороны в 3-мерные векторы-столбцы. Вот что мы получить:
Выполните умножение в левой части этого уравнения и вы увидите, как это представляет исходную систему.
Это действительно важно! позволяет представить систему уравнения как матричное уравнение. В конце концов, мы придумаем, как решить исходную систему, работая с матрицами.
Матрицы идентичности. Имеются специальные матрицы которые служат тождествами для умножения: Единичная матрица представляет собой квадратную матрицу с 1 вниз по главной диагонали — по диагонали с северо-запада на юго-восток — и 0 везде. За например, единичная матрица
Если I — тождество, а A — матрица, которая совместима для умножения с A, то
Например,
Умножение матриц подчиняется некоторым алгебраическим законам, которые вы знаете. знаком с. Например, умножение матриц ассоциативно : Если A, B и C являются матрицами и их
размеры совместимы для умножения, то
знаком с. Например, умножение матриц ассоциативно : Если A, B и C являются матрицами и их
размеры совместимы для умножения, то
Однако умножение матриц равно , а не . коммутативное вообще. То есть для всех матриц A, B.
Один тривиальный способ получить контрпример состоит в том, чтобы позволить A быть и позволить B быть . Тогда есть пока есть . Так как и имеют разные размерности, они не может быть равным.
Однако легко придумать контрпримеры, даже если и имеют те же размеры. За Например, рассмотрим следующие матрицы в:
Затем вы можете проверить, выполнив умножение, которое
Многие свойства матричной арифметики вполне ожидаемы.
— например, что сложение матриц коммутативно, или что матрица
умножение ассоциативно. Вы должны платить конкретно
внимание, когда что-то работает не так, как вы ожидаете и это
такой случай. Очень важно, что умножение матриц
не всегда коммутативный.
Транспонирует. Если A является матрицей, транспонирование матрицы A получается с помощью поменять местами строки и столбцы A. Например,
Обратите внимание, что транспонирование матрицы матрица.
Пример. Рассмотрим следующие матрицы с реальные записи:
(а) Вычислить.
(б) Вычислить.
(а)
(б)
Обратная матрица. обратная матрица A — это матрица, удовлетворяющая условию
Нет такой вещи, как матричное деление вообще, потому что некоторые матрицы не имеют обратных . Но если у A есть обратный, вы можете имитировать деление путем умножения на . Это часто бывает полезно при решении матричных уравнений.
Матрица, не имеющая обратной, называется называется единственное число .
Позже мы подробно обсудим обратные матрицы и то, как их найти. А пока вот формула, которую мы будем часто использовать.
А пока вот формула, которую мы будем часто использовать.
Предложение. Рассмотрим следующую матрицу с элементами в коммутативном кольце с единицей R.
Предположим, что обратимо в R. Тогда инверсия А
Примечание: число называется определитель матрицы. мы обсудим определители позже.
Помните, что не каждый элемент коммутативного кольца с единицей имеет обратную. Например, не определено в . Если мы имеем дело с реальными числами, то имеет мультипликативную обратную тогда и только тогда, когда это не ноль.
Доказательство. Чтобы показать, что формула дает обратный A, я должен проверить это и:
Это доказывает, что формула дает обратную матрицу.
Вот пример этой формулы для матрицы с реальными элементами. Заметь . Так
(Если у меня есть дробь вне матрицы, я могу не умножать
в матрицу, чтобы результат выглядел лучше. Вообще, если есть
является целым числом вне матрицы, я умножу его.)
Вообще, если есть
является целым числом вне матрицы, я умножу его.)
Напомним, что матрица, не имеющая обратной, называется сингулярной . Предположим, у нас есть вещественная матрица
Приведенная выше формула даст обратную, если обратима, что для действительных чисел означает . Таким образом, матрица вырождена, если .
Пример. Для каких значений x выполняется следующее вещественная матрица в единственном числе?
Матрица сингулярна — необратима — если
Решите для х:
Это дает или . Матрица единственное число для и для .
Будь осторожен! Следующая матрица сингулярна над :
Однако его определитель , который не равен нулю. Дело в том, что 2 — это , а не обратимое в , даже если он не равен нулю.
Пример. (а) Найти в .
(b) Найдите обратную следующую матрицу над .
(Вы должны умножать любые числа вне матрицы на матрицу, и упростите все числа в окончательном ответе в .)
(а) Поскольку в , у меня есть .
(b) Во-первых, определитель . Я увидел в (а), что . Так
Я уменьшил все числа в последнем шаг; например, в . В качестве проверки,
То есть, когда я умножаю обратную и исходную матрицу, я получаю тождественная матрица. Убедитесь сами, что это также работает, если я умножьте их в обратном порядке.
Мы обсудим решение систем линейных уравнений позже, а здесь пример этого, который ставит много идей, которые мы обсуждали вместе.
Пример. ( Решение системы уравнений) Решите следующую систему относительно x и y, используя обратную матрицу.
Запишите уравнение в матричной форме:
Используя формулу обратной матрицы, я нахожу, что
Умножьте обе части на обратную матрицу:
Слева квадратная матрица и обратная ей сокращаются, так как они
умножить на I. (Вы видите, как это похоже на «деление на
матрица»?) справа,
(Вы видите, как это похоже на «деление на
матрица»?) справа,
Следовательно,
Решение , .
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2020 Брюс Икенага
Умножение матриц
Цели
- Понимать композиции преобразований.
- Понимать взаимосвязь между матричными произведениями и композициями матричных преобразований.
- Освойте базовую алгебру с матрицами.
- Рецепт: умножение матриц (два способа).
- Фото: композиция трансформаций.
- Словарное слово: композиция .
В этом разделе мы изучаем композиции преобразований. Как мы увидим, композиция — это способ объединения трансформаций в цепочку. Композиция матричных преобразований соответствует понятию умножения двух матриц вместе. Мы также обсуждаем сложение и скалярное умножение преобразований и матриц.
Композиция означает то же самое в линейной алгебре, что и в исчислении. Вот определение.
Определение
Пусть T:Rn→Rm и U:Rp→Rn — преобразования. Их композиция представляет собой преобразование T◦U:Rp→Rm, определяемое
(Т◦U)(х)=Т(U(х)).
Составление двух преобразований означает объединение их в цепочку: T◦U — это преобразование, которое сначала применяет U, а затем применяет T (обратите внимание на порядок операций). Точнее, чтобы оценить T◦U на входном векторе x, сначала вы оцениваете U(x), затем берете этот выходной вектор U и используете его в качестве входного вектора T: то есть (T◦U)(x )=Т(U(x)). Конечно, это имеет смысл только тогда, когда выходы U являются действительными входами T, то есть когда диапазон U содержится в домене T.
RpxRnU(x)RmT◦U(x)UTT◦U Вот изображение композиции T◦U как «машины», которая сначала запускает U, затем получает его выходные данные и передает их в T; аналогичная картина есть в этом подразделе раздела 3. 1.
1.
Домен и домен композиции
- Чтобы можно было определить T◦U, кодовый домен U должен совпадать с доменом T.
- Домен T◦U является доменом U.
- Кодовый домен T◦U является кодовым доменом T.
Пример (функции одной переменной)
Интерактив: композиция матричных преобразований
Интерактивный: преобразование, определенное в шагах
Интерактивный: преобразование, определенное в шагах
Напомним из этого определения в разделе 3.1, что преобразование идентичности — это преобразование IdRn:Rn→Rn, определяемое IdRn(x)=x для каждого вектора x.
Окончательное свойство называется ассоциативностью . Разворачивая обе стороны, он говорит:
S◦(T◦U)(x)=S(T◦U(x))=S(T(U(x))=S◦T(U(x))=(S◦T)◦U (Икс).
Другими словами, как S◦(T◦U), так и (S◦T)◦U являются преобразованием, определяемым сначала применением U, затем T, затем S.
Композиция преобразований не коммутативна вообще. То есть, вообще говоря, T◦UB=U◦T, даже когда определены обе композиции.
То есть, вообще говоря, T◦UB=U◦T, даже когда определены обе композиции.
Пример (функции одной переменной)
Пример (Некоммутативная композиция преобразований)
В этом подразделе мы вводим кажущуюся несвязанной операцию с матрицами, а именно матричное умножение. Как мы увидим в следующем подразделе, умножение матриц в точности соответствует композиции соответствующих линейных преобразований. Сначала нам понадобится терминология.
Обозначение
Пусть A — матрица размера m × n. Обычно мы будем писать aij для записи в i-й строке и j-м столбце. Он называется i,j записью матрицы.
a11···a1j···a1n………ai1···aij···ain………am1···amj···amnEIIIGFJJJHjthcolumnithrowОпределение (умножение матриц)
Пусть A — матрица размера m×n, а B — матрица размера n×p. Обозначим столбцы матрицы B через v1,v2,…,vp:
B=C|||v1v2···vp|||D.
Продукт AB — матрица m×p со столбцами Av1, Av2,…, Avp:
AB=C|||Av1Av2···Avp|||D.
Другими словами, умножение матриц определяется столбец за столбцом или «распределяется по столбцам B».
Пример
Для определения векторов Av1,Av2,…,Avp количество строк B должно быть равно количеству столбцов A.
Размеры матриц в матричном произведении
- Для определения AB количество строк B должно быть равно количеству столбцов A.
- Произведение матрицы m×n и матрицы n×p является матрицей m×p.
Если B имеет только один столбец, то AB также имеет один столбец. Матрица с одним столбцом — это то же самое, что и вектор, поэтому определение произведения матриц обобщает определение произведения матриц на вектор из этого определения в разделе 2.3.
Если А — квадратная матрица, то мы можем умножить ее саму на себя; мы определяем его степень как
А2=ААА3=АААи т.д.
Правило строки-столбца для умножения матриц
Напомним из этого определения в Разделе 2.3, что произведение вектора-строки и вектор-столбца есть скаляр
Aa1a2···anBEIIGx1x2. ..xnFJJH=a1x1+a2x2+···+anxn.
..xnFJJH=a1x1+a2x2+···+anxn.
Следующая процедура нахождения матричного произведения гораздо лучше приспособлена к ручным вычислениям; предыдущее определение больше подходит для доказательства теорем, таких как эта теорема ниже.
Рецепт: Правило строки-столбца для умножения матриц
Пусть A — матрица размера m×n, пусть B — матрица размера n×p, и пусть C=AB. Тогда ij-я запись C — это i-я строка A, умноженная на j-й столбец B:
cij=ai1b1j+ai2b2j+···+ainbnj.
Вот схема:
a11···a1k···a1n………ai1···aik···ain………am1···amk···amnEIIIGFJJJHithrowb11···b1j· ··b1p………bk1···bkj···bkp………bn1···bnj···bnpEIIIIGFJJJJHjthcolumn=c11···c1j···c1p. ……..ci1···cij···cip………cm1···cmj···cmpEIIIGFJJJHijentryПример
Хотя умножение матриц удовлетворяет многим ожидаемым свойствам (см. конец раздела), нужно быть осторожным при выполнении матричных арифметических действий, так как есть несколько свойств, которые не выполняются в общем случае.
Предостережения по умножению матриц
- Умножение матриц некоммутативно: AB обычно не равно BA, даже если оба произведения определены и имеют одинаковый размер. См. этот пример.
- Умножение матриц не удовлетворяет закону сокращения: из AB=AC не следует B=C, даже если AB=0. Например,
К1000ЛК1234Л=К1200Л=К1000ЛК1256Л.
- Это возможно для AB=0, даже когда AB=0 и BB=0. Например,
К1010ЛК0011Л=К0000Л.
Хотя умножение матриц вообще не является коммутативным, существуют примеры матриц A и B с AB=BA. Например, это всегда работает, когда A является нулевой матрицей или когда A=B. Читателю предлагается найти другие примеры.
Пример (некоммутативное умножение матриц)
Порядок действий
Цель этого подраздела — показать, что умножение матриц соответствует композиции преобразований, то есть стандартная матрица для T◦U является произведением стандартных матриц для T и для U. Это должно быть трудно поверить, что наша сложная формула для умножения матриц на самом деле означает что-то интуитивное, например, «связывание двух преобразований вместе»!
Теорема
Пусть T:Rn→Rm и U:Rp→Rn — линейные преобразования, а A и B — их стандартные матрицы соответственно, поэтому A — матрица размера m×n, а B — матрица размера n×p. Тогда T◦U:Rp→Rm — линейное преобразование, а его стандартная матрица — произведение AB.
Тогда T◦U:Rp→Rm — линейное преобразование, а его стандартная матрица — произведение AB.
Доказательство
Сначала проверим линейность T◦U. Пусть u,v — векторы в Rp. Затем
T◦U(u+v)=T(U(u+v))=T(U(u)+U(v))=T(U(u))+T(U(v))=T ◦U(u)+T◦U(v).
Если c скаляр, то
T◦U(cv)=T(U(cv))=T(cU(v))=cT(U(v))=cT◦U(v).
Поскольку T◦U удовлетворяет двум определяющим свойствам в разделе 3.3, это линейное преобразование.
Теперь, когда мы знаем, что T◦U является линейным, имеет смысл вычислить его стандартную матрицу. Пусть C — стандартная матрица T◦U, поэтому T(x)=Ax,U(x)=Bx и T◦U(x)=Cx. По этой теореме в разделе 3.3 первый столбец C — это Ce1, а первый столбец B — Be1. У нас есть
T◦U(e1)=T(U(e1))=T(Be1)=A(Be1).
По определению, первый столбец произведения AB является произведением A на первый столбец B, то есть Be1, поэтому
Ce1=T◦U(e1)=A(Be1)=(AB)e1.
Отсюда следует, что C имеет тот же первый столбец, что и AB. Тот же аргумент, примененный к i-му стандартному вектору координат ei, показывает, что C и AB имеют один и тот же i-й столбец; поскольку у них одинаковые столбцы, это одна и та же матрица.
Тот же аргумент, примененный к i-му стандартному вектору координат ei, показывает, что C и AB имеют один и тот же i-й столбец; поскольку у них одинаковые столбцы, это одна и та же матрица.
Теорема оправдывает наш выбор определения произведения матриц. Это единственная причина, по которой матричные произведения определяются таким образом. Перефразируя:
Продукты и композиции
Матрица композиции двух линейных преобразований есть произведение матриц преобразований.
Пример (Композиция вращений)
Интерактив: композиция матричных преобразований
Интерактивный: преобразование, определенное в шагах
Напомним из этого определения в разделе 3.3, что единичная матрица — это матрица размера n × n, столбцы которой являются стандартными векторами координат в Rn. Единичная матрица является стандартной матрицей преобразования идентичности: то есть x=IdRn(x)=Inx для всех векторов x в Rn. Для любого линейного преобразования T:Rn→Rm имеем
ИКм◦T=T
, и по тому же признаку у нас есть для любой m × n матрицы A мы имеем
ИмА=А.
Аналогично имеем T◦IRn=T и AIn=A.
В этом подразделе мы опишем еще две операции, которые можно выполнять над преобразованиями: сложение и скалярное умножение. Затем мы переводим эти операции на язык матриц. Это аналогично тому, что мы сделали для композиции линейных преобразований, но гораздо менее тонко.
Определение
- Пусть T,U:Rn→Rm — два преобразования. Их сумма есть преобразование T+U:Rn→Rm, определяемое формулой
(Т+У)(х)=Т(х)+У(х).
Обратите внимание, что добавление преобразований определяется только в том случае, если оба преобразования имеют один и тот же домен и кодовый домен. - Пусть T:Rn→Rm — преобразование, а c — скаляр. Скалярное произведение числа c на T представляет собой преобразование cT:Rn→Rm, определяемое формулой
(сТ)(х)=с·Т(х).
Чтобы подчеркнуть, сумма двух преобразований T,U:Rn→Rm представляет собой еще одно преобразование, называемое T+U; его значение на входном векторе x является суммой выходов T и U.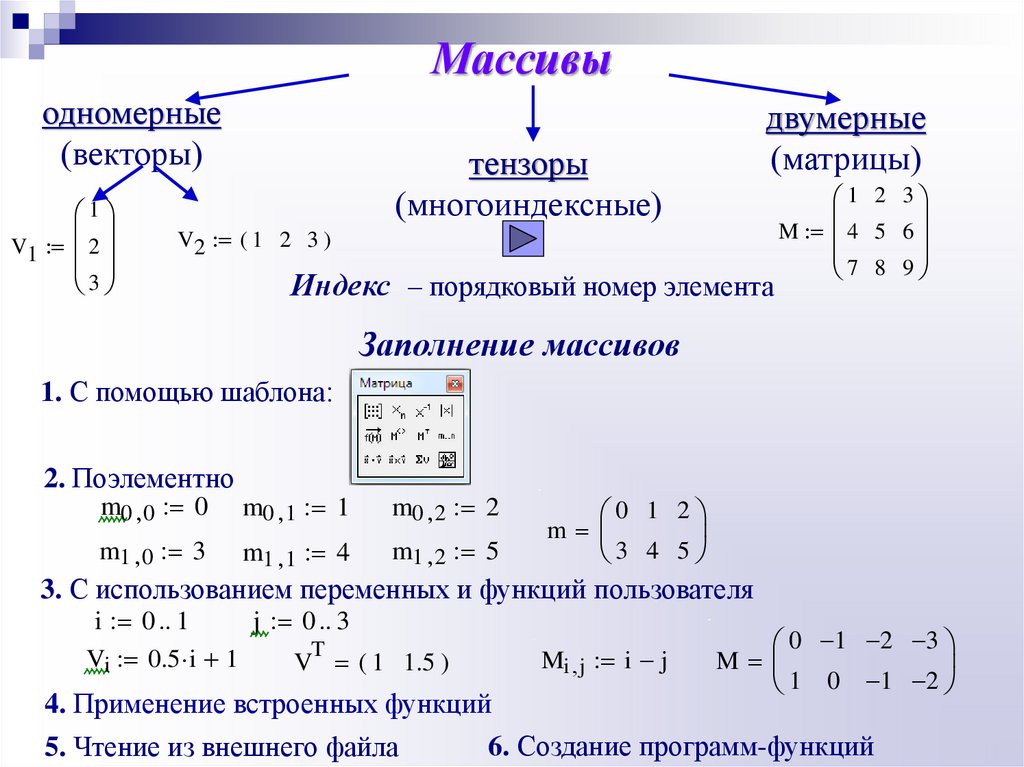 Точно так же произведение T на скаляр c является другим преобразованием, называемым cT; его значением на входном векторе x является вектор c·T(x).
Точно так же произведение T на скаляр c является другим преобразованием, называемым cT; его значением на входном векторе x является вектор c·T(x).
Пример (функции одной переменной)
В одном из приведенных выше свойств мы использовали 0 для обозначения преобразования Rn→Rm, которое равно нулю для каждого входного вектора: 0(x)=0 для всех x. Это называется нулевым преобразованием .
Приведем теперь аналогичные операции для матриц.
Определение
- Сумма двух матриц размера m×n представляет собой матрицу, полученную суммированием элементов A и B по отдельности:
Ka11a12a13a21a22a23L+Kb11b12b13b21b22b23L=Ka11+b11a12+b12a13+b13a21+b21a22+b22a23+b23L
Другими словами, элемент i,j матрицы A+B является суммой элементов i,j матрицы A и B. Обратите внимание, что сложение матриц определяется только тогда, когда обе матрицы имеют одинаковый размер. - Скалярное произведение скаляра c на матрицу A получается масштабированием всех элементов A на c:
cKa11a12a13a21a22a23L=Kca11ca12ca13ca21ca22ca23L
Другими словами, i,j элемент cA в c раз больше i,j элемента A.
Факт
Пусть T,U:Rn→Rm — линейные преобразования со стандартными матрицами A, B соответственно, и пусть c — скаляр.
- Стандартной матрицей для T+U является A+B.
- Стандартной матрицей для cT является cA.
Ввиду вышеизложенного следующие свойства являются следствием соответствующих свойств преобразований. Они также легко проверяются непосредственно из определений.
В одном из приведенных выше свойств мы использовали 0 для обозначения матрицы размера m×n, все элементы которой равны нулю. Это стандартная матрица нулевого преобразования, она называется нулевой матрицей .
Мы также можем комбинировать сложение и скалярное умножение матриц с умножением матриц. Поскольку умножение матриц соответствует композиции преобразований (теорема), следующие свойства являются следствием соответствующих свойств преобразований.
Большинство приведенных выше свойств легко проверить непосредственно из определений.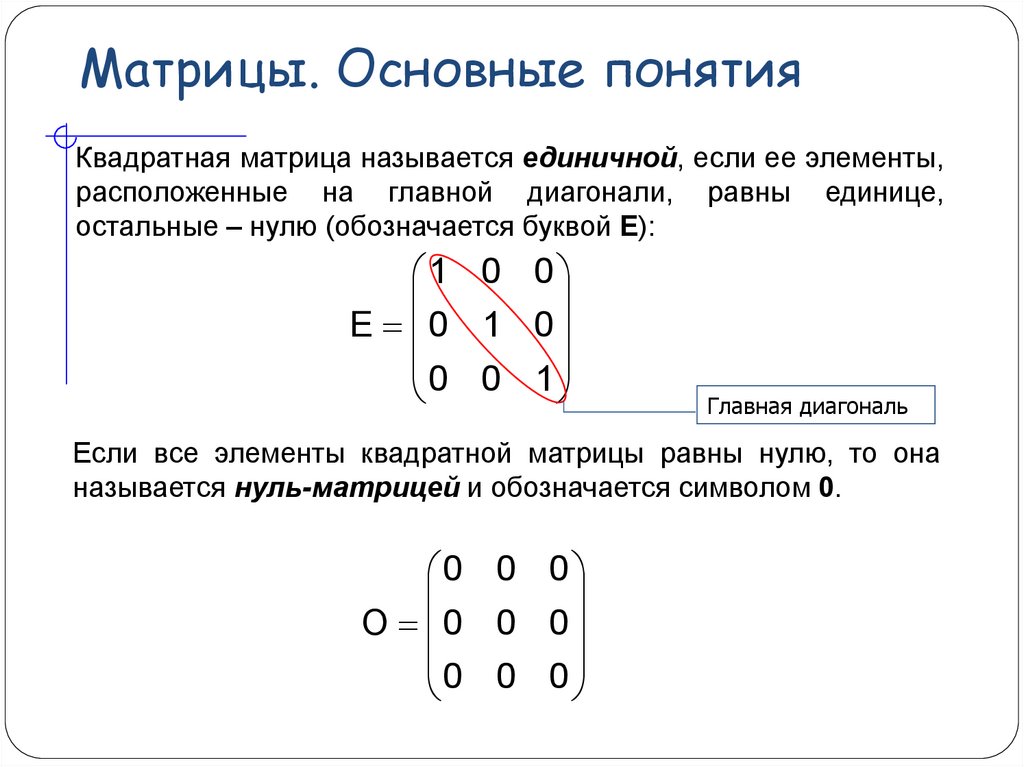

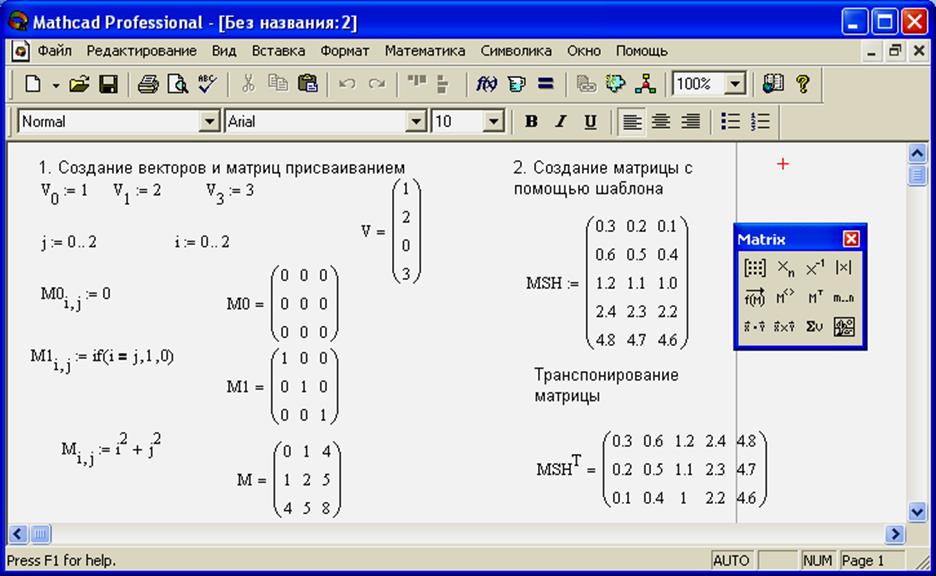 values.[x, y] <> v then false else true)
|> Seq.cast<bool>
|> Seq.contains false)
values.[x, y] <> v then false else true)
|> Seq.cast<bool>
|> Seq.contains false)

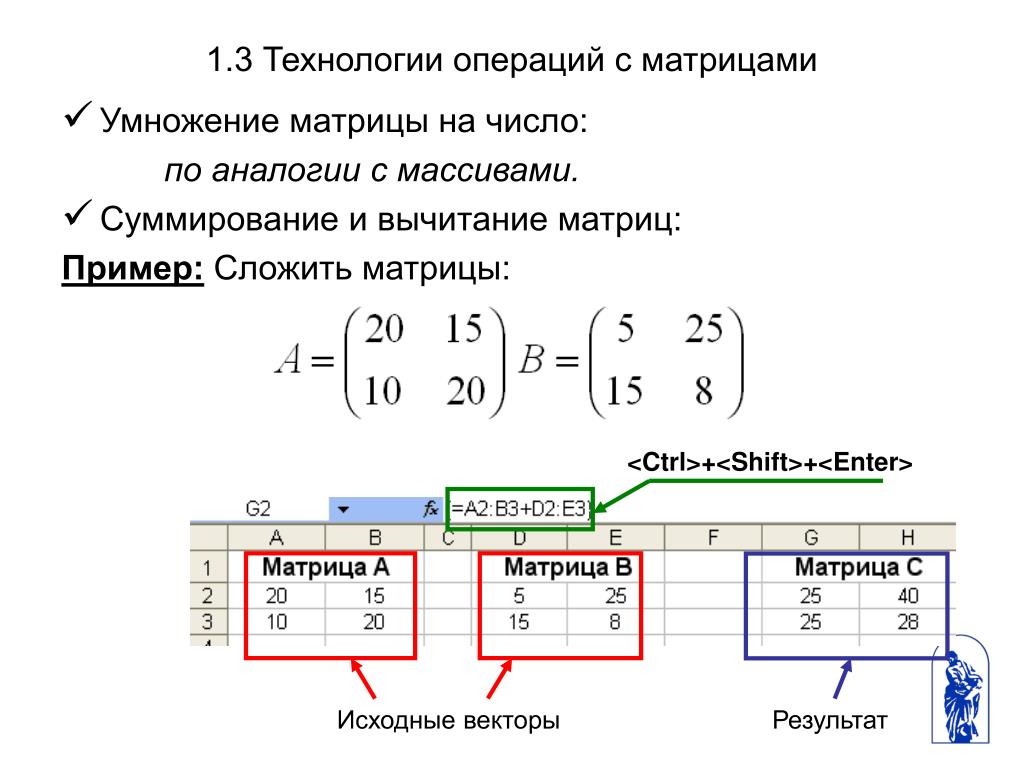 Math.Min (colCount, rowCount)
// создаем пустой квадратный массив с размерностью
// равной наименешей стороне исходной матрицу
let zero = Array2D.zeroCreate length length
// копируем исходную матрицу в квадратную
let square = zero |> Array2D.mapi (fun x y _ -> matrix.values.[x, y])
// позвращаем полученную матрицу
{ values = square }
Math.Min (colCount, rowCount)
// создаем пустой квадратный массив с размерностью
// равной наименешей стороне исходной матрицу
let zero = Array2D.zeroCreate length length
// копируем исходную матрицу в квадратную
let square = zero |> Array2D.mapi (fun x y _ -> matrix.values.[x, y])
// позвращаем полученную матрицу
{ values = square }
 values |> Array2D.mapi (fun x y v -> if x <> y then 0 else v)
{ values = diagonal }
values |> Array2D.mapi (fun x y v -> if x <> y then 0 else v)
{ values = diagonal }
 ofArray2D a
let b = array2D [[-3;3]
[1;7]
[2;0]]
let B = Matrix.ofArray2D b
let R = A+B
printfn "A+B =\n %A" R.values
ofArray2D a
let b = array2D [[-3;3]
[1;7]
[2;0]]
let B = Matrix.ofArray2D b
let R = A+B
printfn "A+B =\n %A" R.values
 isEquallySized matrix1 matrix2 then
matrix1 + (-1)*matrix2
else failwith "matrix1 is not equal to matrix2"
isEquallySized matrix1 matrix2 then
matrix1 + (-1)*matrix2
else failwith "matrix1 is not equal to matrix2"
 isMatched matrix1 matrix2 then
let row1Count = matrix1.values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
let values = Array2D.zeroCreate row1Count col2Count
for r in 0..row1Count-1 do
for c in 0..col2Count-1 do
let row = Array.toList matrix1.values.[r,*]
let col = Array.toList matrix2.values.[*,c]
let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
values.[r,c] <- cell
{ values = values }
else failwith "matrix1 is not matched to matrix2"
isMatched matrix1 matrix2 then
let row1Count = matrix1.values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
let values = Array2D.zeroCreate row1Count col2Count
for r in 0..row1Count-1 do
for c in 0..col2Count-1 do
let row = Array.toList matrix1.values.[r,*]
let col = Array.toList matrix2.values.[*,c]
let cell = List.fold2 (fun acc val1 val2 -> acc + (val1 * val2)) 0 row col
values.[r,c] <- cell
{ values = values }
else failwith "matrix1 is not matched to matrix2"
 values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
// формируем пустой двумерный массив для сохранения результатов умножения
let values = Array2D.zeroCreate row1Count col2Count
values.[*,0].Length
let col2Count = matrix2.values.[0,*].Length
// формируем пустой двумерный массив для сохранения результатов умножения
let values = Array2D.zeroCreate row1Count col2Count
 имеет тип Matrix
// p - значение степени для текущего кадра
// с каждым кадром рекурсии это значение уменьшается на единицу
let rec recPow acc p =
// сравниваем текущую степень
match p with
| x when x > 0 ->
// вычисляем новое значение аккумулятора
// умножаем исходную матрицу на старый аккумулятор, то есть возводим в следующую степень
let nextAcc = acc*m
// рекурсивно вызываем функцию и передаем ей уменьшенное на единицу значение степени
recPow nextAcc (x-1)
// если степень достигла нуля, то возвращаем вычисленный аккумулятор
| _ -> acc
// создаем единичную матрицу, чтобы передать ее в качестве аккумулятор для вычисления степени
let dim = Matrix.sizes matrix
let colCount = snd dim
let rowCount = fst dim
let u = Matrix.E rowCount colCount
// вызываем рекурсивную функцию и передаем ей единичную матрицу в качестве аккумулятора
recPow u p
// вызываем функцию, реализующую хвостовую рекурсию для получения результата
let powMatrix = inRecPow matrix value
// возвращаем итоговую матрицу
{ values = powMatrix.
имеет тип Matrix
// p - значение степени для текущего кадра
// с каждым кадром рекурсии это значение уменьшается на единицу
let rec recPow acc p =
// сравниваем текущую степень
match p with
| x when x > 0 ->
// вычисляем новое значение аккумулятора
// умножаем исходную матрицу на старый аккумулятор, то есть возводим в следующую степень
let nextAcc = acc*m
// рекурсивно вызываем функцию и передаем ей уменьшенное на единицу значение степени
recPow nextAcc (x-1)
// если степень достигла нуля, то возвращаем вычисленный аккумулятор
| _ -> acc
// создаем единичную матрицу, чтобы передать ее в качестве аккумулятор для вычисления степени
let dim = Matrix.sizes matrix
let colCount = snd dim
let rowCount = fst dim
let u = Matrix.E rowCount colCount
// вызываем рекурсивную функцию и передаем ей единичную матрицу в качестве аккумулятора
recPow u p
// вызываем функцию, реализующую хвостовую рекурсию для получения результата
let powMatrix = inRecPow matrix value
// возвращаем итоговую матрицу
{ values = powMatrix. values }
values }
 2 + 3 =
[[1; 0]
[4; -3]]
2 + 3 =
[[1; 0]
[4; -3]]
 Эвристика: m x n * o x p приводит к NO GO, если n < > o. Делать
они совпадают, где они касаются?
Эвристика: m x n * o x p приводит к NO GO, если n < > o. Делать
они совпадают, где они касаются? Характеристическое уравнение будет
многочлен от л
степень n , где n — порядок (размер) матрицы. В демографии, доминирующим собственным значением является скорость роста населения, л ,
в то время как второе собственное значение дает коэффициент затухания (как быстро население
вернется к равновесию после возмущения).
Характеристическое уравнение будет
многочлен от л
степень n , где n — порядок (размер) матрицы. В демографии, доминирующим собственным значением является скорость роста населения, л ,
в то время как второе собственное значение дает коэффициент затухания (как быстро население
вернется к равновесию после возмущения).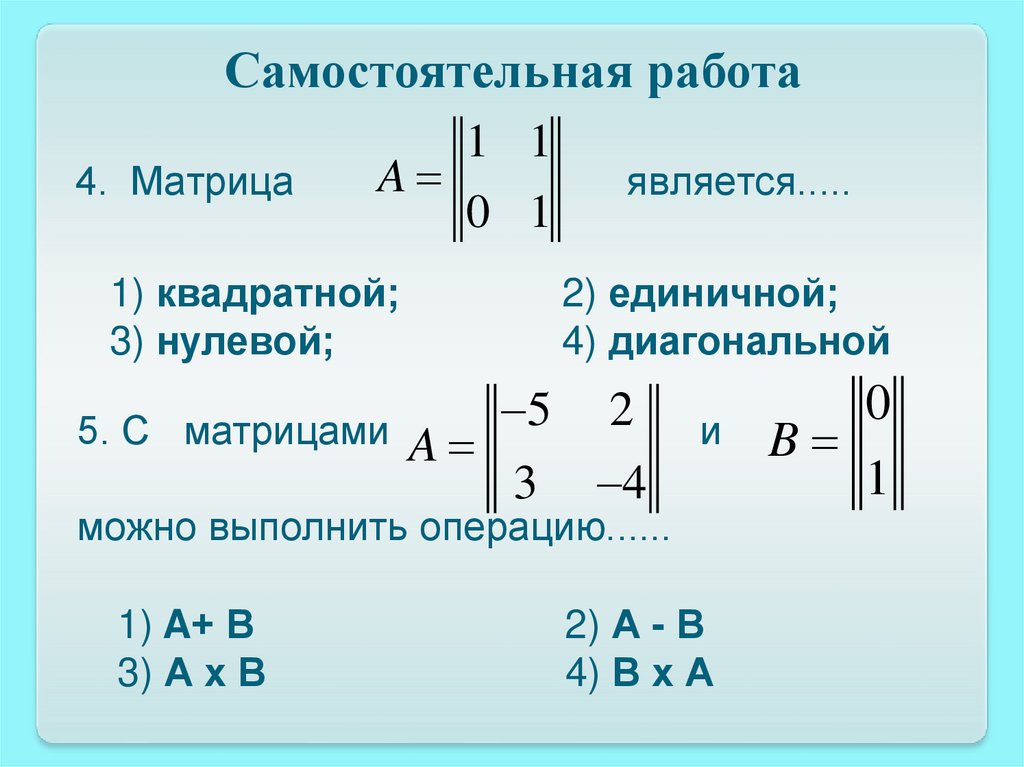 Обратной матрицей называется та матрица, которая при
предварительно умноженный на A , дает единичную матрицу. Обратное существует
только когда матрица сингулярна (то есть имеет определитель).
Обратной матрицей называется та матрица, которая при
предварительно умноженный на A , дает единичную матрицу. Обратное существует
только когда матрица сингулярна (то есть имеет определитель). Итак, совместимость включает в себя два внутренних числа
и «порядок» матрицы произведения включает два внешних числа.
Итак, совместимость включает в себя два внутренних числа
и «порядок» матрицы произведения включает два внешних числа. A = {aij}, где {} означает «множество».
A = {aij}, где {} означает «множество».

 deanza.edu/faculty/bloomroberta/math21/afm3files.html.html
deanza.edu/faculty/bloomroberta/math21/afm3files.html.html 2 из 3)
2 из 3) 
 В частности, умножение матриц не является «коммутативным»;
вы не можете изменить порядок факторов и ожидать, что в конечном итоге
такой же результат. (Вы должны ожидать увидеть «концептуальный» вопрос
относящийся к этому факту в вашем следующем тесте.)
В частности, умножение матриц не является «коммутативным»;
вы не можете изменить порядок факторов и ожидать, что в конечном итоге
такой же результат. (Вы должны ожидать увидеть «концептуальный» вопрос
относящийся к этому факту в вашем следующем тесте.)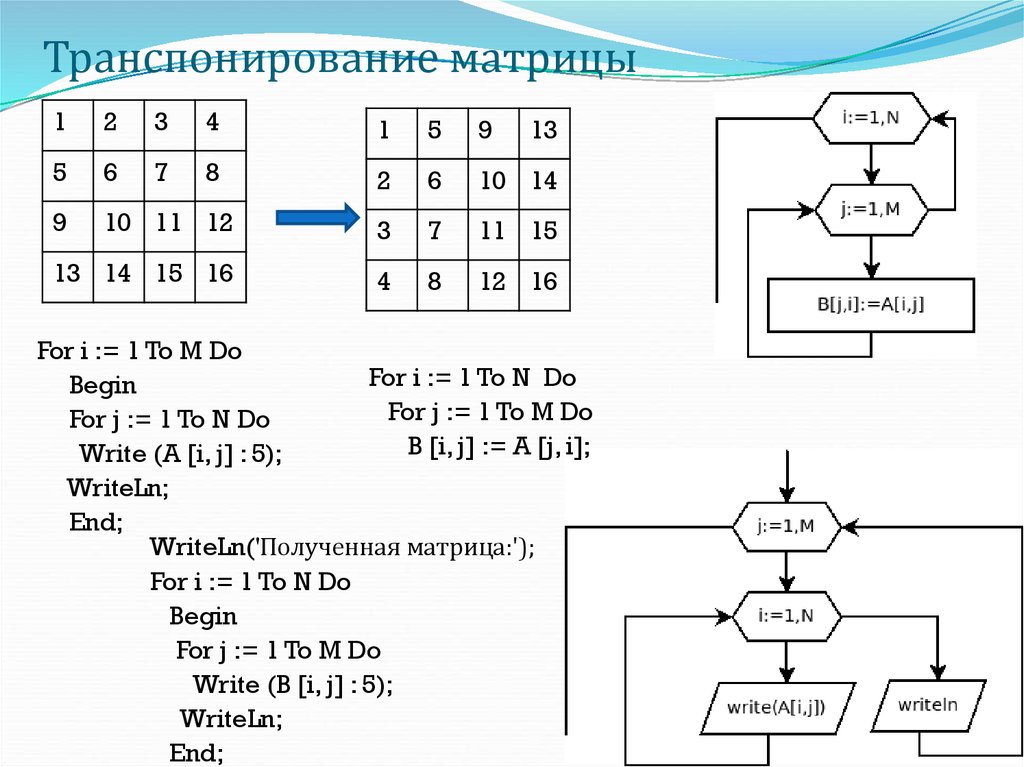 Знакомство с этими правилами
тогда было, вероятно, бессмысленно, так как приказ не имело значения за все, что вы тогда умножали. Ну а теперь Закон Коммутативности
имеет значение, потому что порядок имеет значение для умножения матриц.
Всегда помните, что для матриц AB почти наверняка не равно BA .
Знакомство с этими правилами
тогда было, вероятно, бессмысленно, так как приказ не имело значения за все, что вы тогда умножали. Ну а теперь Закон Коммутативности
имеет значение, потому что порядок имеет значение для умножения матриц.
Всегда помните, что для матриц AB почти наверняка не равно BA .