Математика Делимое и делитель
Материалы к уроку
30. Делимое, делитель.doc
69 KBСкачать30. Делимое, делитель.ppt
12.79 MBСкачать
Конспект урока
30. Делимое, делитель
|
Организационный этап
Мы в лес за наукой сегодня пойдём, Здравствуйте, дорогие ребята. Сегодня на уроке мы отправимся с вами в лесную школу. Отправляемся в путь!
Этап подготовки учащихся к активному сознательному усвоению знаний
Устный счёт
Звери и птицы пришли в школу учиться! Учиться считать, учиться решать. Ребята, кто же первым из лесной школы нас встретит — угадайте.
Спать ложится, снимет тапок И сосёт, как соску, лапу. А начнет капель звенеть, Просыпается. Медведь
Медведь школу открывает, Считать устно приглашает.
Задание 1 Зайцы по лесу бежали, У каждого волка 4 лапы, которые оставили 40 следов. 40:4=10. Значит, прошло 10 волков.
Задание 2 Сорока прожить может 27 лет. В 3 раза короче у ласточки век. Сколько лет может прожить ласточка? 9 лет 27:3=9
Задание 3 3 бельчонка маму – белку Каждому бельчонку досталось по 10 шишек.
Задание 4 Под берёзой 90 листиков лежат, Правильно, 10 мышат.
|
|
Этап усвоения новых знаний
Вспомните, как называются компоненты при делении? делимое делитель частное Отгадайте загадку: Хитрая плутовка Ребята, лиса принесла числовое выражение: 15:5=3. Чем является число 15? Чем является число 5? Чем является число 3? Компоненты при делении называются: делимое, делитель, частное.
Сейчас поиграем в математические прятки, я буду прятать число, а вы мне должны объяснить, как его найти. А поможет нам в этом знание математического правила о делении. Что такое деление? Деление — это действие, обратное умножению.
Как найти частное? Делимое разделить на делитель, получится частное.
Как найти делимое? Если делитель умножить на частное, то получится делимое.
Как найти делитель? Если делимое разделить на частное, то получится делитель. Сделаем вывод:
Я – Лиса-краса, могу всех обхитрить, а могу всё хорошо объяснить. Вы поняли, ребята, что при делении все три компонента: делимое, делитель и частное между собой взаимосвязаны.
|
|
Этап закрепления новых знаний
Ребята угадайте кто это? В лесу темно, Сова
Задание Выпишите и решите только те выражения, в которых надо найти частное. 4 + 3 5 · 2 6 : 3 8 – 4 4 > 3 12 : 2 Проверьте себя и оцените свои успехи.
12:2=6 Задание Сделайте вычисления, подчеркните делитель. 36:9 72:8 35:7 Проверьте себя и оцените свои успехи.
72:8= 9 — делитель – 8 35:7=5 — делитель – 7 Задание Сделайте вычисления, обведите делимое. 45:5= 20:2= 56:8= Проверяем.
20:2=10 — делимое – 20 56:8=7 — делимое – 56
Молодцы, ребята, вы справились с заданиями мудрой Совы.
|
|
Ребята, угадайте кто этот лесной житель? Сам он круглый, а не мяч,
Самостоятельная работа Решите числовые выражения. 96 : 3 84 : 7 88 : 4 78 : 6 85 : 5 Проверьте себя и оцените свои успехи.
84:7=(70+14):7=70:7+14:7=10+2=12 88:4=(80+8):4=80:4+8:4=20=2=22 78:6=(60+18):6=60:6+18:6=10+3=13 85:5=(50+35):5=50:5+35:5=10+7=17
Этап подведения итогов
Запомните: 1. 2. Если делимое разделить на частное, то получится делитель.
Рефлексия
Ребята, если вам всё понятно, нарисуйте листик красного цвета; если не совсем понятно, то листик желтого цвета; а если не понятно ничего – зелёный листик. Спасибо за работу! |
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Деление целых чисел. Делимое, делитель, частное.
Деление целых чисел отличается от деления натуральных чисел, только тем что у целых чисел нужно у частного посчитать знак. Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.
Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.
Термины и понятия частного целых чисел.
Чтобы выполнить деление целых чисел нужно вспомнить термины и понятия. В делении есть: делимое, делитель и частное целых чисел.
Делимое – это то целое число, которое делят. Делитель – это целое число, на которое делят. Частное – это результат деления целых чисел.
Можно сказать “Деление целых чисел” или “Частное целых чисел” смысл этих фраз один и тот же, то есть нужно поделить одно целое число на другое и получить ответ.
Деление берет свое начало из умножения. Рассмотрим пример:
3∙4=12
У нас есть два множителя 3 и 4. Но допустим нам известно, что есть один множитель 3 и результат умножения множителей их произведение 12. Как найти второй множитель? На помощь приходит деление.
12:3=4
Правило деления целых чисел.
Определение:
Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.
Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:
Плюс на плюс дает плюс.
“+ : + = +”
Минус на минус дает плюс.
“– : – =+”
Минус на плюс дает минус.
“– : + = –”
Плюс на минус дает минус.
“+ : – = –”
А теперь рассмотрим подробно каждый пункт правила деления целых чисел.
Деление целых положительных чисел.
Вспомним, что целые положительные числа это тоже самое, что натуральные числа. Мы пользуемся теми же правила, что и при делении натуральных чисел. Знак частного от деления целых положительных чисел всегда плюс. Иными словами, при делении двух целых чисел “плюс на плюс дает плюс”.
Пример:
Выполните деление 306 на 3.
Решение:
Оба числа имеют знак “+”, поэтому ответ будет со знаком “+”.
306:3=102
Ответ: 102.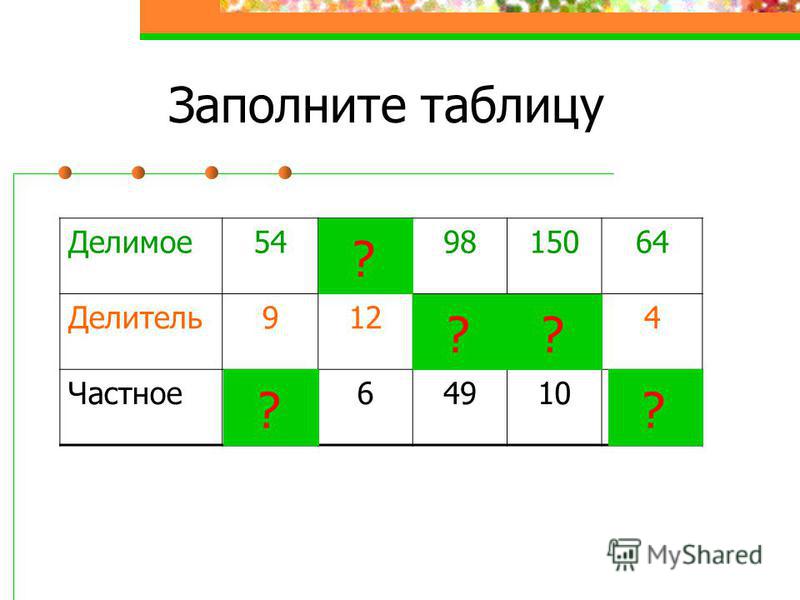
Пример:
Разделите делимое 220286 на делитель 589.
Решение:
Делимое 220286 и делитель 589 имеет знак плюс, поэтому частное тоже будет иметь знак плюс.
220286:589=374
Ответ: 374
Деление целых отрицательных чисел.
Правило деления двух отрицательных чисел.
Пусть у нас будут два отрицательных целых числа a и b. Нам нужно найти их модули и выполнить деление.
a:b=|a|:|b|
Результат деления или частное двух отрицательных целых чисел будет со знаком “+” или “минус на минус дает плюс”.
Рассмотрим пример:
Найдите частное -900:(-12).
Решение:
-900:(-12)=|-900|:|-12|=900:12=75
Ответ: -900:(-12)=75
Пример:
Выполните деление одного целого отрицательного числа -504 на второе отрицательное число -14.
Решение:
-504:(-14)=|-504|:|-14|=504:14=34
Записать выражение можно короче:
-504:(-14)=34
Деление целых чисел с разными знаками. Правило и примеры.

Правило:
При выполнении деления целых чисел с разными знаками, частное будет равно отрицательному числу.
Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.
Минус на плюс дает минус.
Плюс на минус дает минус.
Пример:
Найдите частное двух целых чисел с разными знаками -2436:42.
Решение:
-2436:42=-58
Пример:
Вычислите деление 4716:(-524).
Решение:
4716:(-524)=-9
Нуль деленный на целое число. Правило.
Правило:
При деление нуля на целое число ответ будет равен нулю.
Пример:
Выполните деление 0:558.
Решение:
0:558=0
Пример:
Разделите нуль на целое отрицательное число -4009.
Решение:
0:(-4009)=0
Правило:
На нуль делить нельзя.
Нельзя 0 разделить на 0.
Проверка частного деления целых чисел.
Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.
Проверка результата деления краткая формула:
Делитель ∙ Частное = Делимое
Рассмотрим пример:
Выполните деление и сделайте проверку 1888:(-32).
Решение:
Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число.
1888:(-32)=-59
А теперь выполним проверку найденного ответа:
1888 – делимое,
-32 – делитель,
-59 – частное,
Делитель умножаем на частное.
-32∙(-59)=1888
Вопросы по теме:
Что такое частное чисел?
Ответ: частное чисел – это результат деления деления двух чисел.
Как найти частное?
Ответ: нужно одно число поделить на другое, то есть делимое поделить на делитель и получим частное.
Чему равно частное от деления целых чисел?
Ответ: если целые числа делятся без остатка, то их частное равно целому числу. Иначе будет дробное число.
Что такое делимое и делитель?
Ответ: число которое делят называют делимым, а число на которое делят называют делителем.
Пример:
Найдите частное суммы и разности чисел 48 и 16.
Решение:
Находим сумму чисел 48 и 16.
48+16=64
Находим разность чисел 48 и 16.
48-16=32
Находим частное.
64:32=2
Ответ: 2.
Деление целых чисел. Делимое, делитель, частное. Что такое частное в математике
Частное, как результат деления Частное, как противопоставление общему Частное, как принадлежащее Частному лицу … Википедия
Результат деления … Большой Энциклопедический словарь
— [сн], частного, ср. (мат.). Число, полученное от деления одного числа на другое. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
(мат.). Число, полученное от деления одного числа на другое. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова
ЧАСТНОЕ, ого, ср. Результат, итог деления. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
Сущ., кол во синонимов: 1 термин (18) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Обвинение особый порядок производства в судебныхустановлениях дел о Ч. преступлениях; в более общем значении термин: Ч.обвинение обнимает собой все формы участия Ч. лиц в возбужденииуголовного преследования и в обличении обвиняемого на суде.… … Энциклопедия Брокгауза и Ефрона
частное — частное. Произносится [часное] … Словарь трудностей произношения и ударения в современном русском языке
частное — отношение коэффициент — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы отношениекоэффициент EN quotient … Справочник технического переводчика
ЧАСТНОЕ — результат операции деления; обозначается а:b, а/b или … Большая политехническая энциклопедия
Ого; ср. 1. Матем. Результат деления одной величины на другую. Найти ч. В частном получилось слишком большое число. 2. То, что представляет собой отдельную часть, особенность чего л. От частного к общему. Уделить внимание частному. * * * частное… … Энциклопедический словарь
1. Матем. Результат деления одной величины на другую. Найти ч. В частном получилось слишком большое число. 2. То, что представляет собой отдельную часть, особенность чего л. От частного к общему. Уделить внимание частному. * * * частное… … Энциклопедический словарь
частное — вынести частное определение существование / создание … Глагольной сочетаемости непредметных имён
Книги
- Частное право Древнего Рима , В. В. Макеев, А. Г. Головко. Предлагаемое издание является учебным пособием по римскому частному праву. Новационность содержания и структуры не имеет на сегодняшний день аналога, так как охватывает буквально все стороны…
- Частное расследование , Фридрих Незнанский. Талантливый ученый и инженер А. Н. Грамов создает уникальный психотропный генератор, при помощи которого можно влиять на человека, где бы он ни находился. По сути им создано новейшее…
Только тем что у целых чисел нужно у частного посчитать знак. Как посчитать знак частного целых чисел? Рассмотрим подробно в теме.
Термины и понятия частного целых чисел.
Чтобы выполнить деление целых чисел нужно вспомнить термины и понятия. В делении есть: делимое, делитель и частное целых чисел.
Делимое – это то целое число, которое делят. Делитель – это целое число, на которое делят. Частное – это результат деления целых чисел.
Можно сказать “Деление целых чисел” или “Частное целых чисел” смысл этих фраз один и тот же, то есть нужно поделить одно целое число на другое и получить ответ.
Деление берет свое начало из умножения. Рассмотрим пример:
У нас есть два множителя 3 и 4. Но допустим нам известно, что есть один множитель 3 и результат умножения множителей их произведение 12. Как найти второй множитель? На помощь приходит деление.
Правило деления целых чисел.
Определение:
Частное двух целых чисел равно частному их модулей, со знаком плюс в результате, если числа одинаковых знаков, и со знаком минус, если они разных знаков.
Важно учитывать знак частного целых чисел. Кратко правила деления целых чисел:
Плюс на плюс дает плюс.
“+ : + = +”
Минус на минус дает плюс.
“– : – =+”
Минус на плюс дает минус.
“– : + = –”
Плюс на минус дает минус.
“+ : – = –”
А теперь рассмотрим подробно каждый пункт правила деления целых чисел.
Деление целых положительных чисел.
Вспомним, что целые положительные числа это тоже самое, что натуральные числа. Мы пользуемся теми же правила, что и при делении натуральных чисел. Знак частного от деления целых положительных чисел всегда плюс . Иными словами, при делении двух целых чисел “плюс на плюс дает плюс ”.
Пример:
Выполните деление 306 на 3.
Решение:
Оба числа имеют знак “+”, поэтому ответ будет со знаком “+”.
306:3=102
Ответ: 102.
Пример:
Разделите делимое 220286 на делитель 589.
Решение:
Делимое 220286 и делитель 589 имеет знак плюс, поэтому частное тоже будет иметь знак плюс.
220286:589=374
Ответ: 374
Деление целых отрицательных чисел.
Правило деления двух отрицательных чисел.
Пусть у нас будут два отрицательных целых числа a и b. Нам нужно найти их модули и выполнить деление.
Результат деления или частное двух отрицательных целых чисел будет со знаком “+” или “минус на минус дает плюс”.
Рассмотрим пример:
Найдите частное -900:(-12).
Решение:
-900:(-12)=|-900|:|-12|=900:12=75
Ответ: -900:(-12)=75
Пример:
Выполните деление одного целого отрицательного числа -504 на второе отрицательное число -14.
Решение:
-504:(-14)=|-504|:|-14|=504:14=34
Записать выражение можно короче:
-504:(-14)=34
Деление целых чисел с разными знаками. Правило и примеры.
При выполнении деления целых чисел с разными знаками , частное будет равно отрицательному числу.
Не важно положительное целое число делим на отрицательное целое число или отрицательное целое число делим на положительное целое число, результат деления всегда будет равен отрицательному числу.
Минус на плюс дает минус.
Плюс на минус дает минус.
Пример:
Найдите частное двух целых чисел с разными знаками -2436:42.
Решение:
-2436:42=-58
Пример:
Вычислите деление 4716:(-524).
Решение:
4716:(-524)=-9
Нуль деленный на целое число. Правило.
При деление нуля на целое число ответ будет равен нулю.
Пример:
Выполните деление 0:558.
Решение:
0:558=0
Пример:
Разделите нуль на целое отрицательное число -4009.
Решение:
0:(-4009)=0
На нуль делить нельзя.
Нельзя 0 разделить на 0.
Проверка частного деления целых чисел.
Как говорилось ранее деление и умножение тесно связаны. Поэтому чтобы проверить результат деления двух целых чисел, нужно выполнить умножение делителя и частного в результате должно получиться делимое.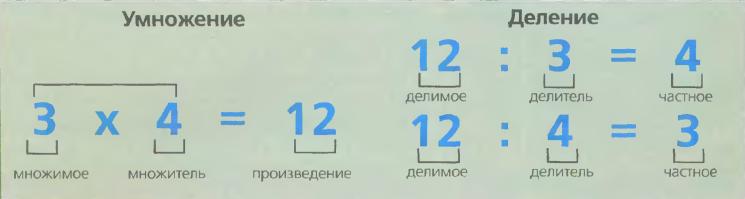
Проверка результата деления краткая формула:
Делитель ∙ Частное = Делимое
Рассмотрим пример:
Выполните деление и сделайте проверку 1888:(-32).
Решение:
Обращаем внимание на знаки целых чисел. Число 1888 положительное и имеет знак “+”. Число (-32) отрицательное и имеет знак “–”. Поэтому при делении двух целых чисел с разными знаками ответ будет отрицательное число.
1888:(-32)=-59
А теперь выполним проверку найденного ответа:
1888 – делимое,
-32 – делитель,
-59 – частное,
Делитель умножаем на частное.
-32∙(-59)=1888
Аноним
Давайте вспомним определение, что называется частным чисел.
Частное чисел — это результат деления одного числа на другое. Таким образом, частное чисел а и b будет число c, которое равно c = a: b. При этом число a будет делимым, а число — b делителем.
Иными словами, частное чисел — это математическая величина, которая получается в результате деления одного числа на другое. Частное двух чисел показывает нам, во сколько раз одно число больше другого.
a: b = c, где a — делимое; b — делитель; c — частное.
Частное двух чисел показывает нам, во сколько раз одно число больше другого.
a: b = c, где a — делимое; b — делитель; c — частное.
Аноним
Частное чисел
1. Введем определение этого понятия. Частным чисел называется результат деления одного из чисел на другое. Частное чисел — это математическая величина.
2. Наглядное представление: a / b = c.
- а — делимое;
- b — делитель;
- c — частное.
3. Пример 1. 156 / 2. Если поделить число 156 на 2, то в результатом будет число 78. В этом случае число 78 представляет собой частное двух чисел, результат от деления числа 156 на 2. 156 — делимое, 2 — делитель. Число 156 больше, чем число 2, в 78 раз. Данные умозаключения можно проверить, достаточно лишь выполнить операцию, обратную делению. 78 * 2 = 156. Верно.
4. Усложненный пример. 153214 / 2. 153214 — делимое, 2 — делитель.
- Делим 15 на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 15 полученное значение и получаем 1.
- Спускаем 3.
 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1.
13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1. - Спускаем 2. 12 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 12 полученное значение и получаем 0.
- Спускаем единицу, прописываем ноль. Спускаем 4. 14 делим на 2. Берем по 7. 7 * 2 = 14. Вычитаем из 14 полученное значение и получаем 0.
Неполное частное
Пример пункта 3 довольно прост. Так число 2 содержится в числе 156 ровно 78 раз.
Приведем пример: 157 / 3. 157 — делимое, 3 — делитель. При делении мы получаем, что число 3 содержится в числе 157, 52 раза, но образуется еще и остаток, который равен единице. В данном случае число 52 будем называть неполным частным. Число 1 — это остаток от деления числа 157 на 3.
Большинство людей, окончивших среднюю общеобразовательную школу, имеют достаточно хорошее представление о том, что такое частное чисел в математике. Но тем не менее, давайте дадим определение этому термину.
Частное числа: значение
Частное чисел — это математическая величина, полученная при делении одного числа на другое. Частное показывает нам, во сколько раз одно число больше другого.
Частное показывает нам, во сколько раз одно число больше другого.
Если записать операцию деления в виде простой формулы
- a: b = c,
то в ней a — это «делимое», b — это «делитель», а c — это и есть «частное».
Рассмотрим также пример с конкретными цифрами. Если мы поделим число 39 на 3, то в ответе получим число 13. В данном случае 13 — это частное, результат деления числа 39 на 3. Другими словами можно сказать, что число 39 больше, чем число 3, в 13 раз.
А давайте задумаемся, так ли это на самом деле? Чтобы понять, ошиблись мы или нет, произведем проверку и выполним действие, обратное делению. Как вы, наверное, уже догадались, это умножение. Умножим число 13 на 3. В ответе получается 39. Мы не ошиблись.
Неполное частное
О приведенном выше математическом примере можно сказать, что число 3 содержится в числе 39 ровно 13 раз. Однако в большинстве реальных случаев такой красивый и простой ответ получить невозможно. Сколько раз, например, число 3 содержится в числе 40?
Данная математическая операция записывается следующим образом:
- 40: 3 = 13 (1).

Что означает эта запись? Число 3 содержится в числе 40 тоже 13 раз, но при этом еще образуется остаток, равный 1. В данном случае число 13 называется «неполным частным», а число 1 — «остатком от деления».
Частное — это что такое? Можно услышать о множестве вещей и процессов, которые используются с этим словом. Что же оно значит?
Общая информация
Частное — это значит, что что-то принадлежит одному человеку или же относительно небольшой группе людей. Причем они объединены на добровольной основе, а не в приказном порядке (как пример можно в последнем случае привести коммунальные предприятия). А это, в свою очередь, обозначает определённую специфику. Также, когда говорят про частное, это может означать отдельный, весьма редкий или вообще единичный случай чего-то. Кроме этого, так называется одноименный математический оператор.
Как видите, слово «частное» — это весьма широко используемый инструмент нашего языка. Чтобы лучше понять его использование, давайте рассмотрим его применение на практике. Для полноты обзора будет уделено внимание и общему примеру, и частному. Итак, приступим.
Для полноты обзора будет уделено внимание и общему примеру, и частному. Итак, приступим.
Общий пример
Сейчас нами будет рассмотрена частная собственность. Как уже ранее говорилось, так называется всё, что принадлежит отдельному человеку или небольшой группе людей, которые объединились на добровольном основании. В качестве иллюстрации можно привести такое понятие, как дача. Что это? Так называют землю и постройки, которые принадлежат определённому человеку или группе (семье). Это на которую посторонним входить без разрешения хозяев запрещено. В случае нарушения к ним могут быть применены силовые методы для задержания с последующей передачей правоохранительным органам.
Частная собственность — это одна из основ капитализма, поэтому она охраняется со всей строгостью. Нарушение этого принципа подрывает устои современного капитализма и ведёт к различным, как правило негативным, последствиям. Хотя у нас защищен любой тип собственности, нажитый законным путём, так уж повелось, что именно частная представляет наибольший интерес для подавляющего количества людей.
Частный пример
А сейчас давайте рассмотрим использование этого слова с немного иной точки зрения. Только теперь для нас интерес будут представлять не физические лица, а юридические. Мы рассмотрим частное предприятие. Это означает, что оно принадлежит определённому человеку или группе и было создано на добровольческих основаниях. Но при этом оно не претендует на определённые материальные ценности. Так, есть объекты коммунальной собственности, например — парки. Они находятся в ведении коммунальных служб городов, где расположены.
Частные предприятия могут претендовать на определённое количество земли, необходимое для ведения деятельности, но это подразумевает использование только определённых типов территории. Причем следует отметить статус, который имеет юридическое лицо. Если взять, к примеру, гипотетическое село, и там одновременно будет действовать и частное, и В обоих могут состоять все жители. Но тем не менее у них будут различные полномочия и возможности, от которых уже будет зависеть осуществляемая деятельность и конечные цели.
Деление чисел — Математика и Английский
Делимое делитель частное правило 4 класс математика
Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.
Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:
Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:
2 + 2 + 2 = 2 · 3 = 6.
Для записи деления используется знак : (Двоеточие), который ставится между числами. Например:
Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак = (Равно), после которого записывается полученный результат:
Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?
Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.
Для этого разделим 9 на 3. Получим 3.
Решение можно записать так:
Ответ: 3 пучка.
Пример. Решить примеры на деление с помощью схем.
2) 12 : 4 = 3, 12: 3 = 4.
Делимое, делитель и частное
Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:
12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.
Частное — это число, которое получается в результате деления. Например, в записи:
4 — это частное. При этом сама запись 12 : 3 тоже называется Частным.
Эта запись читается так: частное двенадцати и трёх равняется четырём или двенадцать разделить на три равно четырём.
Проверка деления
Где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:
Решение можно записать так.
Izamorfix. ru
07.05.2017 10:58:14
2017-05-07 10:58:14
Источники:
Https://izamorfix. ru/matematika/arifmetika/delenie. html
ПНШ 4 класс. Математика. Учебник № 1, с. 54 | Умники и умницы » /> » /> .keyword { color: red; }
Делимое делитель частное правило 4 класс математика
156. «Маша, а числа при делении с остатком тоже имеют свои названия?» — спросил Миша.
«Да. Они называются делимое, делитель, НЕПОЛНОЕ ЧАСТНОЕ и остаток», — ответила Маша.
Используя следующую запись деления с остатком и объяснение Маши, дай названия всем участвующим в этом делении числам.
58 : 8 = 7 (ост. 2)
Какие названия тебе уже хорошо знакомы? Какие названия являются новыми?
Попробуй объяснить смысл термина «неполное частное».
Делимое — 58, делитель — 8, неполное частное — 7, остаток — 2.
Знакомы: делимое, делитель, остаток. Новое — неполное частное.
«Неполное частное» — это число, показывающее какое максимальное количество раз, делитель содержится в делимом.
157. Выполни деление нацело и деление с остатком.
60 : 10 = и 63 : 10 =
Как получить делимое 60, используя значение частного и делитель? Запиши соответствующее выражение и его значение.
Как получить делимое 63, используя неполное частное, делитель и остаток? Запиши соответствующее выражение и его значение.
60 : 10 = 6 63 : 10 = 6 (ост. 3)
Если делитель умножить на значение частного, то получится делимое: 10 • 6 = 60.
Если делитель умножить на неполное частное и к полученному результату прибавить остаток, то получится делимое: 10 • 6 + 3 = 63.
158. Выполни деление с остатком.
55 : 7 = 63 : 8 = 80 : 9 = 95 : 10 = 46 : 15 =
Убедись, что во всех приведённых выше случаях выполняется правило.
Если делитель умножить на неполное частное и к полученному результату прибавить остаток, то в итоге получится делимое.
Может ли это правило нарушиться при правильном выполнении деления с остатком?
Запиши данное правило в виде равенства буквенных выражений, обозначив буквой α — делимое, буквой b — делитель, буквой с — неполное частное, буквой d — остаток.
55 : 7 = 7 (ост. 6) 7 • 7 + 6 = 55
63 : 8 = 7 (ост. 7) 8 • 7 + 7 = 63
80 : 9 = 8 (ост. 8) 9 • 8 + 8 = 80
95 : 10 = 9 (ост. 5) 10 • 9 + 5 = 95
46 : 15 = 3 (ост. 1) 15 • 3 + 1 = 46
При правильном выполнении деления с остатком всегда выполняется правило: если делитель умножить на неполное частное и к полученному результату прибавить остаток, то в итоге получится делимое.
B • C + D = Α
Какие названия являются новыми.
E-razumniki. ru
21.04.2020 18:24:07
2020-04-21 18:24:07
Источники:
Https://e-razumniki. ru/pnsh-4-klass-matematika-uchebnik-1-s-54/
Урок 55. название чисел при делении — Математика — 2 класс — Российская электронная школа » /> » /> .keyword { color: red; }
Делимое делитель частное правило 4 класс математика
2. Как называется числовое выражение со знаком деление?
Глоссарий по теме:
Деление — это арифметическое действие, обратное умножению. С помощью деления по произведению и одному из множителей определяется второй множитель.
С помощью деления по произведению и одному из множителей определяется второй множитель.
Делимое — это число стоящее слева от знака деления, которое делим.
Делитель — это число стоящее справа от знака деления, число на которое делим делимое. (какими частями делим, дробим)
Частное — это число стоящее после знака равно, результат деления, числовое выражение со знаком деление.
Обязательная литература и дополнительная литература:
Моро М. И., Бантова М. А. и др. Математика 2 класс. Учебник для общеобразовательных организаций. М.; Просвещение, 2017. – с. 62. С. И. Волкова. Математика 2 класс. Тетрадь учебных достижений. Учебное пособие для общеобразовательных организаций. М.; Просвещение, 2018. – с. 44-47.
Теоретический материал для самостоятельного изучения
Запишем равенство, используя необходимое арифметическое действие:
10 яблок разложили на две тарелки поровну.
9 конфет раздали трём детям поровну.
8 тетрадей раздали четырём ученикам поровну.
Для того, чтобы выполнит задание, нам понадобилось действие деление.
Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.
Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!
Числа при делении имеют свои названия.
8 листьев раздали детям, по 2 листа каждому.
4 человека получили листья.
Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.
Компоненты деления: делимое, делитель, частное.
Найдите частное, если делимое – 6, делитель – 3.
Проверьте: 6 : 3 = 2
Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2
Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?
По сколько клубничек получил каждый ребёнок?
Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.
Ответ: по 3 клубнички получил каждый ребёнок.
Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.
Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.
Ответим на вопросы, поставленные в начале урока.
Число, которое делят, называется делимое.
Число, на которое делят делимое, называется делитель.
Результат деления – частное.
Числа, которые соединены знаком деления, тоже называются частное.
Выполним несколько тренировочных заданий.
1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.
А) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?
Проверьте: 15 : 3 = 5 (яб.).
15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.
3 – делитель. 5 – частное. Выражение 15:3 – частное.
Б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?
Частное — это число стоящее после знака равно, результат деления, числовое выражение со знаком деление.
Resh. edu. ru
21.07.2017 22:18:40
2017-07-21 22:18:40
Источники:
Https://resh. edu. ru/subject/lesson/4303/conspect/
Делимое, делитель, частное. | План-конспект урока по математике (2 класс) по теме:
— Ребята, какую тему вы изучали на прошлом уроке? (деление)
— Сегодня мы продолжим изучать эту тему.
А пока повторим то, что изучали на прошлых уроках.
— Что вы знаете о действии умножения и деления?
( они взаимно обратные)
Поэтому первое задание по таблице умножения с числом 2.
Умножив два на единицу,
Получим ДВОЙКУ — лебедь-птицу, 2х1=2
Спасает каждый ученик
От этих «птичек» свой дневник.
Известно детям в целом мире,
Что дважды два равно ЧЕТЫРЕ. 2х2=4
2х2=4
Им также следует учесть,
Что дважды три получим ШЕСТЬ. 2х3=6
Два на четыре — будет ВОСЕМЬ.
И всех ребят мы очень просим 2х4=8
Забыть капризы, ссоры, лень
Восьмого марта — в мамин день!
Нам два на пять умножить нужно, 2х5=10
И если все возмемся дружно,
Да поднатужимся, ребятки,
То сразу попадем в ДЕСЯТКУ!
О том, что дважды шесть — ДВЕНАДЦАТЬ, 2х6=12
Вам календарь расскажет, братцы,
А в нём подсказку вам дадут
Двенадцать месяцев в году!
Красиво два на семь умножить
Февральский праздник нам поможет, 2х7=14
День всех влюбленных, помню я, —
ЧЕТЫРНАДЦАТОГО, друзья!
А сколько будет дважды восемь,
Десятиклассников мы спросим.
Они подскажут нам ответ, 2х8=16
Ведь им уже ШЕСТНАДЦАТЬ лет!
Запомнить надо постараться,
Что дважды девять – ВОСЕМНАДЦАТЬ. 2х9=18
И очень просто догадаться,
Что дважды десять — будет ДВАДЦАТЬ! 2х10=20
№1.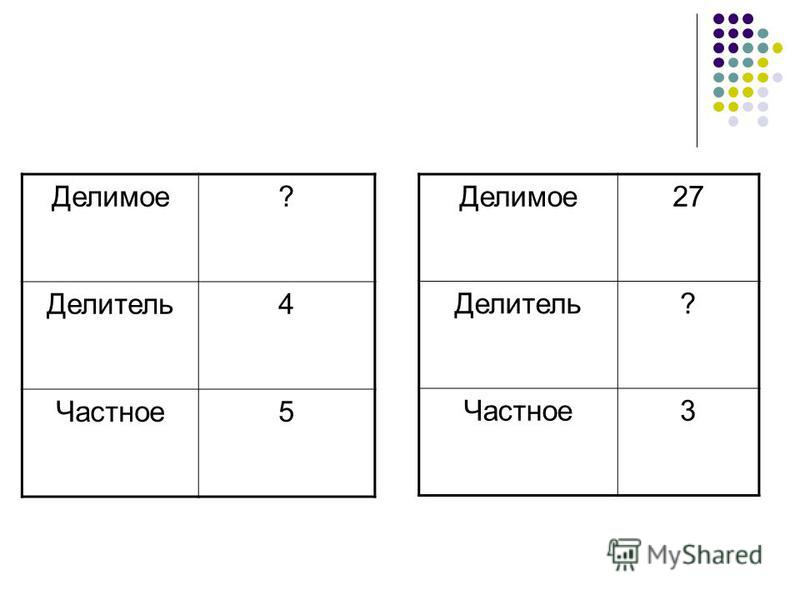
— Прочитайте выражение. Что интересного заметили?
— А что мы получаем если последовательно выполнить некоторую операцию и обратную ей операцию? (то, что было сначала)
— Чему равно значение этого выражения?
(Первая строчка с пояснением с места; Вторая строчка самостоятельно).
14:7Х7=14 32:8Х8=32 7Х5:5=7
6Х2:2=6 5Х9:9=5 4:2Х2=4
— У кого не так?
№2. 35:7=
-Давайте начнем заполнять.
Ребята, находим в первом столбике число 7, под этой строкой прикладываем линейку и находим в строке над линейкой число 35. Поднимаемся вверх по столбику с числом 35 до верхней строки. Какое число получили?(5)
Это и есть результат деления.
35:7=5
48:6= 8 25:5=5
Умножение Слагаемое, слагаемое, сумма
Вычитание Уменьшаемое, вычитание, сумма
Деление Множитель, множитель, произведение
Сложение
— Соедините короткие полоски с длинными.
Подумайте, по какому признаку вы будете соединять эти полоски.
— Что получилось? Что интересного заметили?
— Какую же цель мы поставим сегодня на уроке?
Что нового мы должны сегодня узнать?(как называются числа при делении)
-Ребята, число 35 называют делимым;
Число 7- делитель;
Выражение 35:7- называется частным.
— А как вы думаете, почему число 35 называется делимым?
— Что обозначает это слово?
-Раз мы познакомились с названиями компонентов и результатом действия деления, мы сможем читать выражения с действием деление, так как положено в математике.
1 способ:
Делимое -35
Делитель — 7
Найти частное 5
2 способ:
Частное 35 и 7 равно 5.
№3
— Прочитайте задание.
4:2=2 6:2=3 10:2=5 14:2=7
— Назовите в каждом равенстве делимое, делитель и частное.
— Что общего в этих примерах и чем они отличаются?
-Какой вывод мы сделаем?
№4
— Прочитайте задание
18:2= 9 18:3=6 18:6=3 18:9=2
— Что вы заметили?
№5
— Прочитайте задание.
Решите примеры самостоятельно. Подчеркните те примеры, в которых 2 является делителем и обведите те, в которых 2 является частным.
8:2=4 12:6=2 16:2=8 18:9=2
8:4=2 12:2=6 16:8=2 18:2=9
№6
А)18: b
Б)c:k
В)a:n
Г)m:d
№8 (а)
Прочитайте задачу.
Что в задаче обозначает 2? (2 набора открыток)
Что в задаче обозначает 8? (8 открыток в каждом наборе)
Что обозначает 7? (столько открыток она подарила)
Что нужно найти в задаче? (сколько открыток осталось у Ани)
Что нам для этого нужно знать? (сколько у нее было открыток, и сколько она подарила)
Мы знаем, сколько открыток подарила девочка? (да)
Знаем, сколько открыток было у Ани в начале? (нет)
Можем найти? (да)
Как? (нужно 8 умножить на 2)
Теперь нам известны все данные? (да)
Можем ответить на вопрос задачи? (можем)
Запишите решение задачи в тетрадь, составляя выражение.
8Х2-7= 9 (откр. )
)
Ответ запишите полный.
-Чему новому вы научились сегодня на уроке?
— Что было сложным на уроке?
— Кто хорошо понял новый материал?
— Кто не совсем хорошо понял?
Домашнее задание №8 (б), №9.
Презентация по математике на тему Делимое. Делитель (3 класс) доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по математике на тему Делимое. Делитель (3 класс), предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 14 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Делитель (3 класс), предмет презентации: Математика. Этот материал в формате pptx (PowerPoint) содержит 14 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Разминка
Зайцы по лесу бежали, Волчьи следы по дороге считали. Стая большая волков здесь прошла, Каждая лапа в снегу их видна. Оставили волки 40 следов. Сколько, скажите, здесь было волков?
40: 4 = 10 (в.)
27 : 3 = 9 (л.)
Сорока может прожить 27 лет, в 3 раза короче у ласточки лет . Сколько лет может прожить ласточка?
30 : 3 = 10 (ш.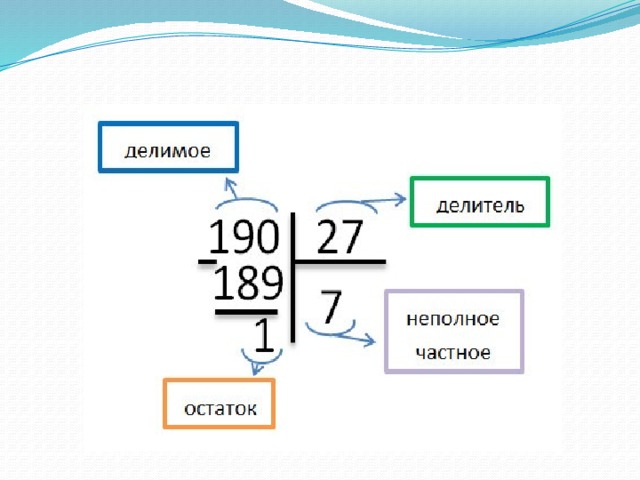 )
)
Три бельчонка маму-белку
Ждали около дупла.
Им на завтрак мама-белка
Тридцать шишек принесла.
Разделила на троих.
Сколько каждому из них?
Если вы были внимательны, то заметили, что все примеры решались с помощью деления.
Вспомним, как называются компоненты при делении.
15 : 5 = 3
Делимое
Делитель
Частное
Как найти частное?
15 : 5 = ?
Делимое разделить на делитель, получится частное.
Делимое
Делитель
Частное
Деление – действие обратное умножению.
Как найти делимое?
? : 5 = 3
Если делитель умножить на частное, то получится делимое.
Делимое
Делитель
Частное
Деление – действие обратное умножению. Как найти делитель?
Как найти делитель?
15 : ? = 3
Если делимое разделитель на частное, то получится делитель.
Делимое
Делитель
Частное
Сделаем вывод:
Если делитель умножить на частное, то получится делимое.
Если делимое разделитель на частное, то получится делитель.
а : b = c
Делимое
Делитель
Частное
При делении все 3 компонента: делимое, делитель и частное, -
между собой взаимосвязаны!
Назовите те выражения, в которых надо найти частное. Решите их.
40 + 3
80 — 4
12 : 2
5 х 2
14 > 13
60 : 3
= 6
= 20
Выполните устно вычисления, назовите делитель.
36 : 9
72 : 8
35 : 7
= 4
= 9
= 5
Выполните устно вычисления, назовите делимое.
45 : 5
20 : 2
56 : 8
= 9
= 10
= 7
Проверим себя!
Если делитель умножить на частное, то получится….
Если делимое разделить на частное, то получится….
делимое
делитель
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Делитель— определение, формула, свойства, примеры
Делитель — это число, которое делится на другое число. Без делителя мы не можем делить числа. При делении используются четыре важных термина: делимое, делитель, частное и остаток. Деление — это метод равномерного распределения предметов по группам. Число, которое необходимо разделить, называется делимым, а общее количество равных групп, на которые оно должно быть разделено, называется делителем. Число, которое не учитывается без образования группы, называется «остатком».
Деление — это метод равномерного распределения предметов по группам. Число, которое необходимо разделить, называется делимым, а общее количество равных групп, на которые оно должно быть разделено, называется делителем. Число, которое не учитывается без образования группы, называется «остатком».
| 1. | Что такое делитель? |
| 2. | Как найти делитель? |
| 3. | Формула делителя |
| 4. | Факты о делителях |
| 5. | Разница между делителем и множителями |
| 6. | Часто задаваемые вопросы о делителях |
Что такое делитель?
Делитель делит число на равные группы. Число, которое делится, называется делимым , а число, на которое оно делится, называется делителем .
Делитель Значение
Число, которое делится на другое число с остатком или без него, называется делителем.
Существуют разные способы записи задачи на деление. На следующем рисунке показаны различные способы выражения деления и показано, как идентифицировать делитель, делимое и частное.
Как найти делитель?
Без делителей деление невозможно. Это означает, что определить делитель довольно просто. Например, если нам нужно разделить число 35 на 5, его можно представить как 35 ÷ 5 = 7. Здесь число 35 — делимое, число 5 — делитель , а число 7 — частное .
Иногда мы знаем значение делимого и частного и нам нужно найти делитель. В этом случае мы используем формула делителя . Давайте узнаем о формуле делителя в следующем разделе.
Формула делителя
Формула делителя формируется для двух ситуаций — с остатком или без остатка:
- Если остаток равен 0, то Делитель = Дивиденд ÷ Частное.
- Если остаток не равен 0, то Делитель = (Дивиденд — Остаток) ÷ Частное
Пример 1: Найдите делитель, если делимое равно 48, а частное равно 4.
Решение: Мы знаем, что делимое = 48, частное = 4. Итак, применим формулу делителя Делитель = Делимое ÷ Частное. Подставляя известные значения в формулу, получаем Делитель = 48 ÷ 4 = 12. Следовательно, делитель = 12.
Пример 2: Найдите делитель, если делимое равно 59, частное 11, а остаток равен 4.
Решение: Мы знаем, что делимое = 59, частное = 11, остаток = 4. Итак, применим формулу делителя Делитель = (Дивиденд — Остаток) ÷ Частное. Подставив известные значения в формулу, получим, Делитель = (59- 4) ÷ 11 = 55 ÷ 11 = 5. Следовательно, делитель = 5.
Факты о делителях
Вот список некоторых фактов, связанных с делителем.
- Если частное равно делимому, то делитель равен 1. Например, 45 ÷ 1 = 45
- Когда делимое и делитель равны в задаче на деление, частное равно 1. Например, 45 ÷ 45 = 1
- Частное — это число, которое получается при делении делимого на делитель, а любое число, оставшееся после деления, называется остатком.

- Остаток всегда меньше делителя.
- Когда остаток равен нулю, это означает, что делитель полностью разделил делимое.
- Если делитель больше делимого, то результирующее число будет десятичным числом. Например, 45 ÷ 100 = 0,45 .
Разница между множителем и делителем
Мы знаем, что делитель — это число, на которое делится делимое. Когда делитель полностью делит делимое и не оставляет остатка, этот делитель также называется множителем этого числа. Таким образом, все делители числа являются делителями, но не всегда все делители должны быть делителями числа.
Пример 1: Множители 8 = 1, 2, 4 и 8. Это означает, что 8 полностью делится на 1, 2, 4, 8. Следовательно, все эти множители в данном случае являются делителями.
Пример 2: Разделите 12 на 5. Если мы разделим 12 на 5, мы получим 2 в частном, а остаток равен 2. Это означает, что 12 ÷ 5 = 2, остаток = 2. В этом случае делитель равен 5, но 12 не делится полностью на 5. Таким образом, 5 не является делителем 12, но является делителем 12, так как дает остаток 2.
Таким образом, 5 не является делителем 12, но является делителем 12, так как дает остаток 2.
Следовательно, все делители являются делителями, но не все делители являются факторами.
Важные советы по делителю
Ниже приведены некоторые важные советы, связанные с делителем, которые мы изучили в этой статье.
- Делитель не может быть равен нулю, потому что при делении числа на ноль результат не определен.
- Задача на деление остается верной, даже если поменять местами частное и делитель.
- Когда ноль делится на любой делитель, в частном всегда получается ноль.
☛Статьи по теме
- Раздел Формула
- Формула остатка делителя дивиденда
- Деление десятичных дробей
Часто задаваемые вопросы о делителях
Что такое делитель в математике?
Число, на которое делится другое число, называется делителем . Например, когда мы делим 20 на 4, мы получаем 5. Когда мы записываем это как 20 ÷ 4 = 5, здесь 4 — это число, на которое делится число 20. Следовательно, 4 называется делителем.
Например, когда мы делим 20 на 4, мы получаем 5. Когда мы записываем это как 20 ÷ 4 = 5, здесь 4 — это число, на которое делится число 20. Следовательно, 4 называется делителем.
Является ли число делителем самого себя?
Да, число является делителем самого себя, потому что число может полностью делиться само на себя. Это означает, что частное будет равно 1. Например, 23 ÷ 23 = 1
Что такое делитель в дроби?
Дробь представляется в виде p/q, (где q не равно 0). Здесь знаменатель q является делителем. Например, в дроби 6/2 знаменатель 2 является делителем.
Что такое формула делителя?
Мы используем формулу делителя, когда знаем значение делимого и частное. У нас есть два сценария, чтобы найти делитель.
- Если остаток равен 0, то Делитель = Делимое ÷ Частное.
- Если остаток не равен 0, то Делитель = (Дивиденд — Остаток) ÷ Частное
Чему равен делитель в факте деления 30 ÷ 15 = 2?
Делитель — это число, на которое делится другое число. Здесь 30 делится на 15. Следовательно, 15 — делитель.
Здесь 30 делится на 15. Следовательно, 15 — делитель.
В чем разница между делителем и дивидендом?
Делитель делит число на равные группы. Число, которое делится, называется делимым, а число, на которое оно делится, называется делителем. Например, в 72 : 6 = 12 72 — это делимое, а 6 — делитель.
Что такое наибольший общий делитель?
Наибольший общий делитель (НОД) относится к наибольшему положительному числу, являющемуся общим делителем данного набора положительных чисел. Он также известен как наивысший общий фактор (HCF) или наибольший общий фактор (GCF). Например, найдем наибольший общий делитель 10 и 22. Перечислим делители 10 и 22. Делители 10 = 1, 2, 5, 10. Делители 22 = 1, 2, 11, 22. общие делители 10 и 22 = 1, 2. Наибольший общий делитель = 2,
Разделение на: значение и шаги для деления чего-либо
Деление в математике — это одна из 4 основных арифметических операций, наряду со сложением, вычитанием и умножением (иногда возведением в степень). На простейшем уровне деление двух чисел — это операция по выяснению того, насколько одно число переходит в другое. Число, которое нужно разделить, называется делимым , число, которое выполняет деление, называется делителем , а результат операции называется 9.0208 частное . Стандартным символом операции деления является обел 〈÷〉 или обратная косая черта 〈/〉. В общем, деление считается операцией, обратной умножению.
На простейшем уровне деление двух чисел — это операция по выяснению того, насколько одно число переходит в другое. Число, которое нужно разделить, называется делимым , число, которое выполняет деление, называется делителем , а результат операции называется 9.0208 частное . Стандартным символом операции деления является обел 〈÷〉 или обратная косая черта 〈/〉. В общем, деление считается операцией, обратной умножению.
Деление часто интерпретируется в контексте разбиения большего числа на более мелкие равные части. Вот простой пример: выражение 6÷3 можно прочитать двояко. Во-первых, мы могли бы прочитать выражение как вопрос: «Сколько частей размера 3 нужно добавить, чтобы получить 6?» Мы можем переписать выражение как:
6=3+3
Требуется 2 группы размера 3, чтобы в сумме получить 6, поэтому наш ответ 6÷3=2. В качестве альтернативы мы могли бы прочитать 6÷3 как «Каков размер 3 равных частей, сумма которых равна 6?» Мы можем переписать это как
6=2+2+2:
Размер этих трех частей равен 2, поэтому ответ 6÷3=2.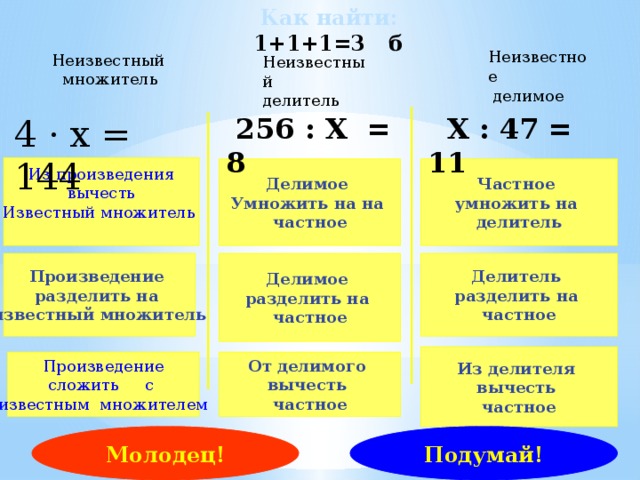 Обе интерпретации выражения деления дают один и тот же ответ, поэтому можно использовать любую из них.
Обе интерпретации выражения деления дают один и тот же ответ, поэтому можно использовать любую из них.
В отличие от сложения и умножения деление не является коммутативным; порядок чисел имеет значение. 6÷3 не то же самое, что 3÷6.
Деление полезно, потому что оно выбирает уникальную связь между тремя числами: делимое (число, которое нужно разделить), делитель (число, на которое делится) и частное (результат деления). В обычной элементарной алгебре деление на ноль (уравнения вида x÷0) не определено, хотя существуют расширения базовой алгебры, в которых деление на 0 четко определено.
Два вида деления
Хотите верьте, хотите нет, но на самом деле есть два вида деления, которые имеют разные свойства. Скорее всего, вы уже знаете об обоих, но вас учили, что это одно и то же. Первый вид деления называется евклидовым делением, а второй — алгебраическим делением.
Евклидово деление
Евклидово деление соответствует процессу деления двух целых чисел для получения частного и остатка .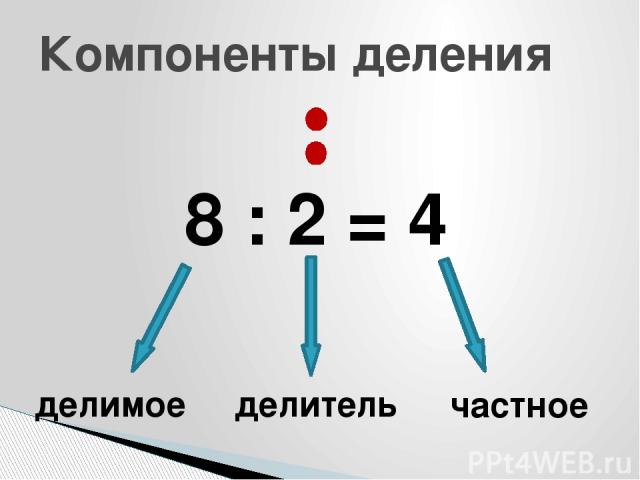 Это самая элементарная концепция деления, соответствующая интуитивному процессу деления дискретной величины на группы одинакового размера. Во многих случаях делитель не будет идеально вписываться в делимое, в результате чего остаток будет меньше, чем частное.
Это самая элементарная концепция деления, соответствующая интуитивному процессу деления дискретной величины на группы одинакового размера. Во многих случаях делитель не будет идеально вписываться в делимое, в результате чего остаток будет меньше, чем частное.
Допустим, у нас есть 10 яблок, и мы хотим разделить их поровну между 3 людьми. Мы начинаем с того, что даем каждому человеку по 1 яблоку. Когда у всех будет по одному яблоку, у нас останется 7 яблок. Проходим еще раз, давая каждому человеку по одному яблоку и у нас остается 4 яблока. Повторяем процесс еще раз, чтобы у каждого было по 3 яблока и осталось 1. Но теперь у нас осталось количество яблок, которое нельзя равномерно распределить между тремя людьми, если мы не разрезаем яблоко на кусочки. Сумма, которая осталась, в данном случае 1 яблоко – это наш остаток. Точно так же, если бы мы начали с 11 яблок, наш остаток был бы равен 2. Если бы мы начали с 12 яблок, наш остаток был бы равен 0 (нулю), потому что 3 равномерно переходит в 12 без остатка.
10 яблок делятся на 3 группы, остается 1 яблоко. Предоставлено: WikiCommons CC0 1.0
В общем, евклидово деление говорит нам, что для любых целых чисел a и b существует некоторое уникальное частное (q) и остаток (r), такие что:
a = bq +r, где 0≤ r ≤|б|
По сути, это уравнение говорит нам, что любое целое число a может быть записано как произведение двух целых чисел b и q плюс остаток r. Важно, чтобы остаток был меньше делителя. Следуя нашему предыдущему примеру с яблоками, подставив делимое (10), делитель (3), частное (3) и остаток (1), мы получим
10 = 3(3)+1
10 делится на три 3 раза с остатком 1. Как и другие формы деления, евклидово деление не определено в случаях деления на 0.
Алгебраическое деление
Евклидово деление полезно, когда все, с чем вам нужно работать, — это целые числа. Деление без остатка требует расширения системы счисления на рациональные и действительные числа. В результате деление определяет отношение только между тремя числами, делимым, делителем и частным.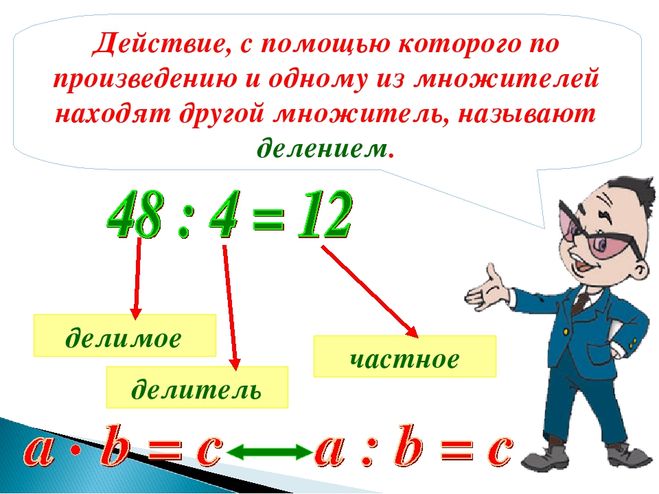
В тех случаях, когда деление 2 целых чисел не дает целого числа, частное выражается как некоторое рациональное число. Например, возьмем случай 11÷7. 11 не делится на 7 без остатка, поэтому ответ можно просто выразить рациональным числом 11/7. В этих случаях важно упростить полученную дробь. 11/7 — такое же рациональное число, как 22/14. Можно также преобразовать эту дробь в десятичную запись as 11/7 = 1,574
Разделить два рациональных числа просто. Скажем, у нас есть два рациональных числа p/q и r/s. Общая форма деления рациональных чисел такова:
p/q ÷ r/s = p/q × s/r
, где q, r и s ≠ 0. По существу, деление на рациональное число означает перестановку числителя и знаменателя второго числа и умножение дробей . В качестве числового примера:
7/5 ÷ 3/4 = 7/5 × 4/3 = 28/15
Это определение деления рациональных чисел гарантирует, что умножение является операцией, обратной делению. Точно так же деление действительных чисел может быть определено между тремя числами a, b и c так, что a/b=c и a=bc
Алгоритм деления
Длинное деление — это стандартный арифметический алгоритм, введенный для вычисления деления двух чисел. Длинное деление — это механическая процедура, которую можно использовать для деления любых двух чисел, чтобы получить десятичное представление частного.
Длинное деление — это механическая процедура, которую можно использовать для деления любых двух чисел, чтобы получить десятичное представление частного.
Сначала мы помещаем делимое (число, которое нужно разделить) в открытый прямоугольник, называемый скобкой деления, с делителем вне скобки. Например, представьте, что наше делимое равно 624, а наш делитель равен 4. Мы устанавливаем два числа как таковые:
Далее мы начнем с деления делимого на делитель, начиная с самой левой цифры в самой внутренней ячейке. 4 делится на 6 без остатка 1 раз, поэтому мы помещаем 1 сверху деления над 6, например:
Затем вы умножаете число сверху на делитель и помещаете полученное число под 6:
Следующим шагом является вычитание нижнего числа из соответствующего разряда, например:
Затем мы опускаем следующее число делителя, в данном случае 2, и делим это число на делитель:
Вы повторяете этот процесс, пока не закончатся цифры. Шаги алгоритма: «Разделить, умножить, вычесть, свести» (DMSB). В качестве мнемонического приема запомните фразу «папа, мама, сестра, брат». Завершение этого процесса для настоящей задачи должно дать вам дерево деления, которое выглядит следующим образом:
В качестве мнемонического приема запомните фразу «папа, мама, сестра, брат». Завершение этого процесса для настоящей задачи должно дать вам дерево деления, которое выглядит следующим образом:
Мы полностью разделили 624 и осталось 156 без остатка. В тех случаях, когда после перебора всех цифр делимого все еще остается остаток, есть два варианта. (1) Вы можете оставить ответ как есть и просто написать остаток рядом с частным. Или (2), вы можете поставить 0,000 рядом с делимым и продолжить деление в длинную сторону, добавляя десятичный разряд к частному справа над десятичной точкой в делимом. Продолжайте делить, пока не дойдете до точки, где ваш остаток равен 0. Для некоторых чисел вы получите десятичную дробь, которая повторяется бесконечно. Например, если вы разделите 10 на 3, используя длинное деление, вы получите 3,333… где тройки в конце повторяются бесконечно.
Используя этот метод, вы сможете разделить любые два числа, даже десятичные. Однако для некоторых номеров этот метод ограничен. Некоторые числа никогда не будут заканчиваться повторяющейся десятичной последовательностью, строка чисел после десятичной точки будет продолжаться вечно без повторяющихся последовательностей. Такие числа называются иррациональными числами, и их нельзя полностью записать в десятичной системе счисления, поскольку они имеют бесконечные разряды.
Некоторые числа никогда не будут заканчиваться повторяющейся десятичной последовательностью, строка чисел после десятичной точки будет продолжаться вечно без повторяющихся последовательностей. Такие числа называются иррациональными числами, и их нельзя полностью записать в десятичной системе счисления, поскольку они имеют бесконечные разряды.
Деление на 0
В большинстве математических систем деление на 0 не определено. Причина в том, что никакое число нельзя умножить на 0, чтобы получить делимое. Каждое число является коэффициентом 0 (каждое число, умноженное на 0, равно нулю), поэтому не существует уникального числа, удовлетворяющего делению на 0 случаев. Вот почему операция обычно остается неопределенной; потому что на самом деле не существует числа, удовлетворяющего выражению. Если делением на 0 является любое уравнение, имеющее форму a/0=b, решения не существует, потому что не существует такого b, что a=0×b
Поставьте задачу таким образом, скажем, у нас есть 10 файлов cookie, которые мы хотим разделить поровну между 0 людьми. Сколько файлов cookie получит каждый, если мы разделим 10 файлов cookie на 0 равных частей? Невозможно разделить 10 на 0 равных подмножеств (в базовой арифметике), поэтому вопрос в лучшем случае не определен, а в худшем — бессмысленен.
Сколько файлов cookie получит каждый, если мы разделим 10 файлов cookie на 0 равных частей? Невозможно разделить 10 на 0 равных подмножеств (в базовой арифметике), поэтому вопрос в лучшем случае не определен, а в худшем — бессмысленен.
На самом деле, если бы мы допустили деление на 0 в качестве допустимого выражения, то смогли бы доказать несколько нелепостей. Если деление на 0 правомерно, то можно доказать, что все числа равны друг другу. Начните с истинных выражений 0×1=0 и 0×2=0. С помощью подстановки выполняется следующее тождество:
0×1=0×2
разделить обе части на ноль, чтобы получить:
0/0×1=0/0×2
Упростить, чтобы получить:
1=2.
Те же самые рассуждения можно провести с любым числом, приведя к абсурдному выводу, что все числа равны друг другу. Это «доказательство» «работает», только если мы допускаем, что деление на 0 является законной операцией. Тот факт, что разрешение деления на 0 приводит к таким нелепостям, как приведенный выше аргумент, является одной из причин, по которой операция обычно считается неопределенной. Существует несколько расширенных математических систем, допускающих использование уравнений в форме а/0, но в большинстве из них символ «0» не означает строго ноль, как это обычно бывает. В исчислении при вычислении производных иногда остается выражение в форме 0/0. Это выражение называется неопределенной формой.
Существует несколько расширенных математических систем, допускающих использование уравнений в форме а/0, но в большинстве из них символ «0» не означает строго ноль, как это обычно бывает. В исчислении при вычислении производных иногда остается выражение в форме 0/0. Это выражение называется неопределенной формой.
Отдел
Искусство. 111. В умножении нам даны два множителя, и требуется найти их произведение. Умножая множители 4 и 6, мы получаем произведение 24. Но часто необходимо обратить этот процесс вспять. Число 24 и 90 314 одного из 90 315 факторов могут быть заданы, чтобы мы могли найти другой. Операция, посредством которой это осуществляется, называется Отдел . Мы получаем число 4, разделив 24 на 6. Величина, которую нужно разделить, называется делимым; дан множитель , делитель; а то, что равно 90 314, требует 90 315 частного.
112. ДЕЛЕНИЕ si Нахождение частного, которое умножается на делитель, дает делитель.
При умножении множитель всегда является числом. А произведение есть величина того же рода, что и множимое. Произведение 3 стержней на 4 равно 12 стержням. Когда мы подошли к делению, можно задать произведение и или множителей, чтобы найти другой: то есть
А произведение есть величина того же рода, что и множимое. Произведение 3 стержней на 4 равно 12 стержням. Когда мы подошли к делению, можно задать произведение и или множителей, чтобы найти другой: то есть
Делитель может быть числом , и тогда частное будет величиной того же вида, что и делимое; или же,
Делитель может быть величиной того же вида, что и делимое; и тогда частное будет числом.
Таким образом, 12 рухов/4 = 3 удилища. Но 12 стержней/3 стержня = 4.
А 12 стержней/24 = 1/2 стержня. И 12 стержней/24 стержня = 1/2.
В первом случае делитель, являющийся числом , показывает, на сколько частей нужно разделить делимое; и частное показывает, каковы эти части.
Если 12 стержней разделить на 3 части, то каждая будет иметь длину 4 стержня. А если 12 стержней разделить на 24 части, то каждая будет иметь длину половин стержня.
В другом случае, если делитель на 90 314 меньше делимого на 90 315, то первый показывает на 90 314, на какие 90 315 частей следует разделить последний; а частное показывает , сколько этих частей содержится в делимом. Другими словами, деление m в этом случае состоит в нахождении того, как часто одна величина содержится в другой .0315 .
Другими словами, деление m в этом случае состоит в нахождении того, как часто одна величина содержится в другой .0315 .Линия из 3 стержней, содержится в одном из 12 стержней, четыре раза по .
Но если делитель на 90 314 больше делимого на 90 315, но при этом является величиной того же рода, то частное показывает 90 314, какая часть 90 315 делителя равна делимому.
Таким образом, половина из 24 стержней равна 12 стержням.
113. Поскольку произведение делителя на частное равно делимому, частное можно найти, разложив делимое на два таких множителя, что один из них будет делителем. Другим, конечно, будет частное.
Предположим, что abd нужно разделить на a. Факторы a и bd будут давать дивиденды. Первый из них, являющийся делителем, может быть отложен. Другой — частное. Следовательно,
Когда делитель находится как множитель в делимом, деление выполняется с отменой этого множителя.
| Разделить | сх | дркс | дхси | абкси |
| По | с | др | день | топор |
Кот. | х | х | хх | на |
В каждом из этих примеров буквы, общие для делителя и делимого, откладываются, а остальные буквы образуют частное. Сразу видно, что произведение частного на делитель равно делимому.
114. Если буква повторяет в делимом, нужно позаботиться о том, чтобы отбрасываемый множитель был равен только делителю.
| Разделить | ааб | адддх | аааксххх |
| По | и | объявление | ахх |
| Кот. | аб | адрес | ахх |
В таких случаях очевидно, что мы не должны отбрасывать каждую букву в делимом, которое представляет собой сейри с единицей в делителе.
115. Если делимое состоит из любых множителей , удаление одного из них означает деление на него.
| Разделить | а(б + г) | а(б + г) | (б + х) (в + г) | (б + у) (г — з) х |
| По | и | б + д | б + х | д — з |
Кот.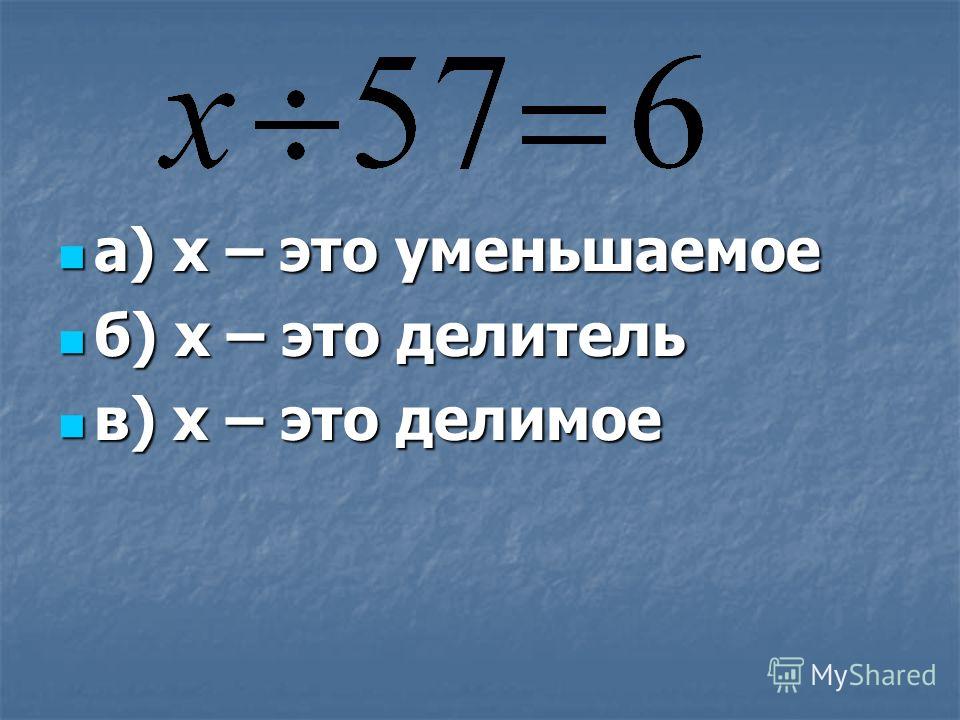 | б + д | и | в + г | (б + у) х |
116. При умножении, если множители содержат цифровых цифр , они умножаются друг на друга. (Статья 94.) Таким образом, 3a в 7b равно 21ab. Теперь, если обратить этот процесс вспять, то очевидно, что деление числа в произведении на число в одном из множителей даст число в другом множителе. Частное 21ab/3a равно 7b. Следовательно,
При делении, если перед буквами стоят цифры и коэффициенты , коэффициент при делимом надо разделить, на коэффициент делителя.
117. Когда простой множитель умножается на составной , первый входит в через каждые членов последнего. Таким образом, a в b + d есть ab + ad. Такое произведение легко снова разложить на исходные множители.
Таким образом, ab + ad = a.(b + d).
ab + ac + ah = a.(b + c + h).
Теперь, если все количество разделить на один из этих факторов, согласно статье 115, частное будет другим фактором.
Если делитель содержится в каждый срок сложного дивиденда, он должен быть отменен в каждом .
| Разделить | аб + акр | ааа + ау |
| По | и | и |
| Кот. | б + в | ах + у |
И если есть cvefficiency , то их надо разделить, в том числе и в каждом члене.
| Разделить | 6аб + 12ас | 12чх + 8 |
| По | 3а | 4 |
| Кот. | 2б + 4в | 3хх + 2 |
118. С другой стороны, если составное выражение , содержащее какой-либо множитель в каждом члене, разделить на другие величины, связанные своими знаками, то в частном получится этот множитель . См. первую часть предыдущей статьи.
119. В делении, как и в умножении, надо соблюдать осторожность, не смешивать терминов с факторами .
Таким образом, (ab + ac)/a = b + c.
Но (ab.ac)/a = aabc/a = abc.
И (ab + ac)/(b + c) = a.
Но (ab.ac)/(b.c) = aabc/bc = aa.
120. При делении следует соблюдать то же правило относительно знаков, что и при умножении; то есть, если делитель и делимое оба положительны или оба отрицательны, частное должно быть положительным: если одно положительное, а другое отрицательное, частное должно быть отрицательным.
Это видно из соображений, что произведение делителя и частного должно быть таким же, как делимое.
Если
+а.+б = +аб
-а.+б = -аб
+а.-б = -аб
-а.-аб = +аб
тогда
+аб/+а = +а
-аб/+б = -а
-аб/-б = +а
+аб/-б = -а
| Разделить | АБХ | 8а — 10ау | 6am.dh |
| По | -а | -2а | -2а |
| Кот. | -бх | -4 + 5 лет | -3м. дхм = -3дхм дхм = -3дхм |
121. Если в делимом нет букв делителя, деление выражается записью делителя под делимым в виде обычной дроби.
Это метод , обозначающий деление , а не фактическое выполнение операции. Но цели деления часто могут быть решены с помощью этих дробных выражений. Поскольку они имеют ту же природу, что и другие вульгарные дроби, их можно складывать, вычитать, умножать. См. следующий раздел.
122. Когда делимое представляет собой составную величину, делитель может быть либо помещен под целым дивидендом, как в предыдущих случаях, либо может быть повторен под каждым членом , взятым отдельно. Бывают случаи, когда удобно заменить одну из этих форм выражения на другую.
Таким образом, b + c, деленное на x, равно либо (b + c)/x, либо b/x + c/x.
Ибо очевидно, что половина суммы двух или более величин равна сумма половин tlievr . И тот же принцип применим к третьей, четвертой, пятой или любой другой части дивиденда.
Таким образом, a — b, деленное на 2, равно либо (a — b)/2, либо a/2 — b/2.
Для половина разности двух величин равна разности их половин .
123. Если или букв делителя находятся в каждом члене делимого, дробное выражение можно сделать более простым, отбросив равные множители из числителя и знаменателя.
124. Если делитель находится в некоторых условиях дивиденда, но не во всех; те, которые содержат делитель, могут быть разделены в соответствии со статьей 116, а другие представлены в виде дроби.
| Разделить | dxy + rx — dh | бм + 3 года |
| По | х | -б |
| Кот. | dy + r — dh/x | -м — 3г/б |
125. Частное любой величины, деленной на 9.0314 сам по себе или его аналог, очевидно, является единицей .
Кор. Если делимое на больше делителя на , то частное должно быть на больше единицы : Но если делимое на меньше делителя на , то частное должно быть на меньше единицы .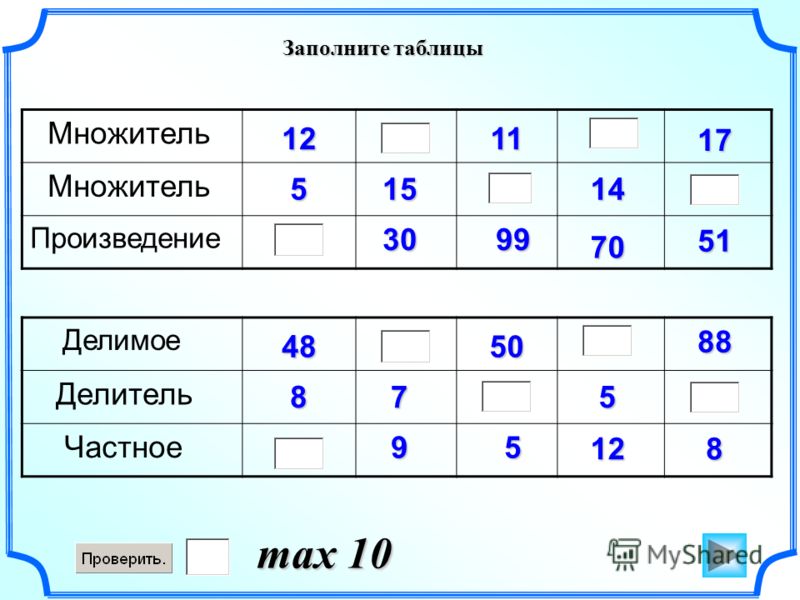
НЕРАЗБОРНЫЕ ПРИМЕРЫ.
1. Делим 18абы+6абх — 18ббм+24б, на 6б.
2. Разделить (a — 2h).(3m + y).x на (a — 2h).(3m + y)
3. Разделить топор — ры + ад — 4мы — 6 + а, на -а.
4. Разделить ard — 6a + 2r — hd + 6, на 2rd.
126. Из характера деления видно, что значение частного зависит как от делителя, так и от делимого. При заданном делителе чем больше делимое, тем больше частное. А при заданном делимом чем больше делитель, тем меньше частное. В некоторых последующих разделах алгебры, особенно в предметах о дробях, отношениях и пропорциях, будет важно иметь возможность определить, какое изменение произойдёт в частном при увеличении или уменьшении либо делителя, либо делимого.
Если данное делимое равно 24, а делитель 6 ; частное будет равно 4. Но можно предположить, что это же самое делимое умножается или делится на какое-то другое число до того, как оно будет разделено на 6. используется при делении 24. В каждом из этих случаев частное будет изменено.
127. Во-первых, если данный делитель содержится в данном делимом определенное число раз, то очевидно, что один и тот же делитель содержится,
В удвойте это делимое, в два раза больше ;
В утроить делимое, утроить столько раз.
То есть, если делитель остается тем же самым, , умножение на делимое на любую величину, фактически равно , умножение частного на эту величину.
Таким образом, если постоянный делитель равен 6, то 24/6 = 4 частное.
Умножая делимое на 2, 2,24/6 = 2,4.
Умножение на любое число n, n.24/6 = n.4.
128. Во-вторых, если данный делитель содержится в данном делимом определенное число раз, то один и тот же делитель содержится,
В половина , что дивиденд, в два раза меньше;
В одну треть делимого, в одну треть столько раз.
То есть, если делитель остается прежним, 90 314, делящее делимое 90 315 на любую другую величину, фактически равно 90 314, делящему частное 9. 0315 по этому количеству.
0315 по этому количеству.
Таким образом, 24/6 = 4
Разделив делимое на 2, (1/2)24/6 = (1/2).4
Деление на n, (1/n)24/6 = (1/n).4
129. В-третьих, если данный делитель содержится в данном делимом определенное число раз, то в одном и том же делимом
Дважды этот делитель содержится только в половине раз;
Три раза делитель содержится одна треть столько раз.
То есть, если делимое остается тем же самым, 90 314, умножая делитель 90 315 на любую величину, является, в числе прочего, результатом деления 90 314 частного 90 315 на эту величину.
Таким образом, 24/6 = 4
Умножение делителя на 2, 24/2,6 = 4/2
Умножение на n, 24/n.6 = 4/n
130. Наконец, если данный делитель содержится в данном делимом известное число раз, то в одном и том же делимом
Половина этот делитель содержится вдвое больше раз;
Одна треть делителя содержится в трижды раз.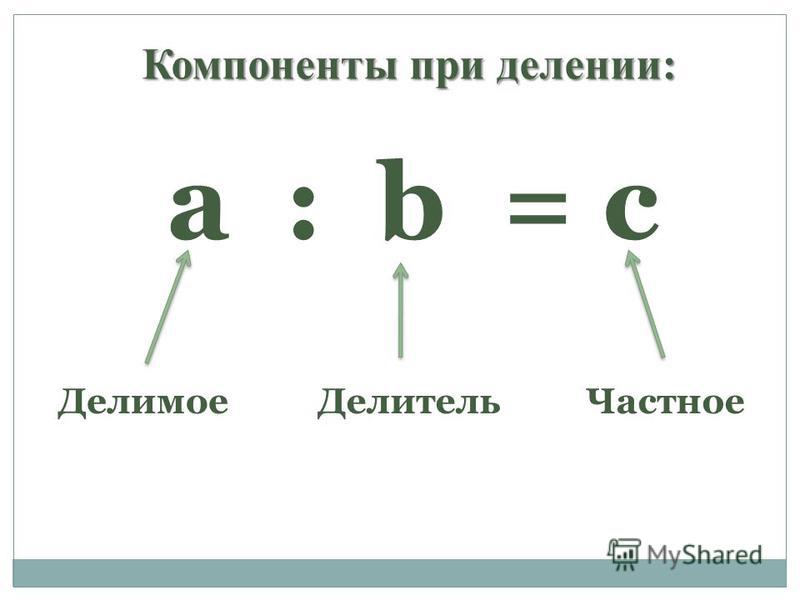
То есть, если делимое остается прежним, 90 314, делящее делитель 90 315 на любую другую величину, фактически равно 90 314, умножающему частное 90 315 на эту величину.
О способе выполнения деления, когда делитель и делимое равны , обе составные величины см. в одном из следующих разделов.
ТОП 9 в разделе что такое делитель ЛУЧШИЙ и НОВЕЙШИЙ
Вы задаетесь вопросом в разделе что такое делитель но в настоящее время нет ответа, поэтому позвольте kienthuctudonghoa.com обобщить и перечислить лучшие статьи с вопрос. ответьте на вопрос в делении чему равен делитель, что поможет вам получить наиболее точный ответ. Следующая статья призвана помочь вам сделать правильный выбор и получить больше полезной информации
Mục lục
- 1 1.Что такое делитель? – Определение, факты и примеры – SplashLearn
- 2 2. Делитель, дивиденд, значение частного в математике | Примеры – Byju’s
- 3 3.Дивизор – определение, формула, свойства, примеры – Cuemath
- 4 4.
 Термины, используемые в подразделе | Дивиденд | Делитель | Коэффициент | Остаток
Термины, используемые в подразделе | Дивиденд | Делитель | Коэффициент | Остаток - 5 5.Дивиденд, делитель, частное и остаток | Свойства деления
- 6 6. Части задачи на деление: делимое, делитель, частное и остаток
- 7 7. Как решать задачи на деление — Математический блог для дифференцирования
- 8 8. Что такое дивиденды и делители? – Научные науки
- 9 9.делить, делить, делимое, делитель – Математический словарь для детей
1.Что такое делитель? – Определение, факты и примеры – SplashLearn
- Автор: www.splashlearn.com
- Дата публикации: 6 вчера
- 0004 5
- Низкий рейтинг: 2
- Резюме: Делитель — это число, которое полностью или с остатком делится на другое число. Делитель представлен в уравнении деления как: Дивиденд ÷ Делитель …
См. Подробности
2. Делитель, дивиденд, частное Значение в математике | Примеры – Byju’s
- Автор: byjus.
 com
com - Дата публикации: 10 вчера
- Рейтинг: 5(1523 отзыва)
- Высшая оценка: 3
- Низкая оценка: 2
- Итог: Делитель — это целое число, которое делится на другое целое число для получения результата. Число, которое делится, называется делимым, а результат, полученный здесь, …
Подробнее
См. подробности
4. Термины, используемые в подразделе | Дивиденд | Делитель | Коэффициент | Остаток
- Автор: www.math-only-math.
 com
com - Дата поста: 13 вчера
- Рейтинг: 4 (1462 Обзоры)
- Высокий рейтинг: 4
- Низкий рейтинг: 1
- Сумма: Мы знаем, что дивизионные значения. большую группу объектов на более мелкие равные группы. Большая группа называется дивидендом. Число меньших равных …
Подробнее
5.Дивиденд, делитель, частное и остаток | Свойства Дивизиона
- Автор: www.math-onyly-math.com
- Дата поста: 12 вчера
- Рейтинг: 3 (521 обзоры)
- Высокий рейтинг: 4
-
- : 4
- : 4
- 1
- Итог: При делении мы увидим соотношение между делимым, делителем, частным и остатком.
 Число, которое мы делим, называется делимым.
Число, которое мы делим, называется делимым.
Подробнее
6. Части задачи на деление: делимое, делитель, частное и остаток
- Автор: www.youtube.com
- Дата поста: 28 вчера
- Рейтинг: 5 (298 Обзоры)
- Высокий рейтинг: 5
- 9003 394444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444444418 Резюме:
Подробнее
7. Как решать задачи на деление – Блог по математике для дифференцирования
- Автор: happynumbers.com
- Вчера 10084
- Рейтинг: 5(565 отзывов)
- Самый высокий рейтинг: 3
- Низкий рейтинг: 1
- Резюме: Дивиденд — это число, которое будет разделено. Делитель — это количество «людей», между которыми делится число.
 Частное — это ответ.
Частное — это ответ.
Подробнее
8.Что такое дивиденды и делители? – Наука
- Автор: sciencing.com
- Дата публикации: 9 вчера
- Рейтинг: 2 (1856 Обзоры)
- Высокий рейтинг: 3
- Низкий рейтинг: 1
- Св. , divisor – Математический словарь для детей
- Автор: www.amathsdictionaryforkids.com
- Дата публикации: 24 вчера
- Рейтинг: 3 1(1062 отзывов)0003 Высший рейтинг:
- Низкий рейтинг: 1
- Итог: число на равные части. • делимое: делимое число. • делитель или множитель: число, на которое делимое точно делится. ПРИМЕРЫ:
См. Подробности
Приведенная выше информация о вопросе в делении, что такое делитель , безусловно, помогла вам получить желаемый ответ, пожалуйста, поделитесь этой статьей со всеми. так что каждый может знать эту полезную информацию. Желаю тебе хорошего дня!
так что каждый может знать эту полезную информацию. Желаю тебе хорошего дня!
division
division| 5 класс ОТДЕЛЕНИЕ |
Что такое деление?
Точно так же, как умножение есть многократное сложение, деление — его обратное операция (обратное действие) — есть повторное вычитание . Если четверо из нас разделят стоимость пиццы по 12 долларов, каждый из нас заплатит по 3 доллара, потому что 12 : 4 = 3. Это означает, что мы можем разделить 12 долларов на 4 «пакета» из по 3 долларов каждый.
12 — 3 — 3 — 3 — 3 = 0
Но поскольку деление является операцией, обратной умножению , и повторное вычитание может занимать очень много времени, когда числа большие — мы использовать таблицы умножения , в сочетании с нашими знаниями о факторах и оценке , на помогают нам эффективно делить чисел.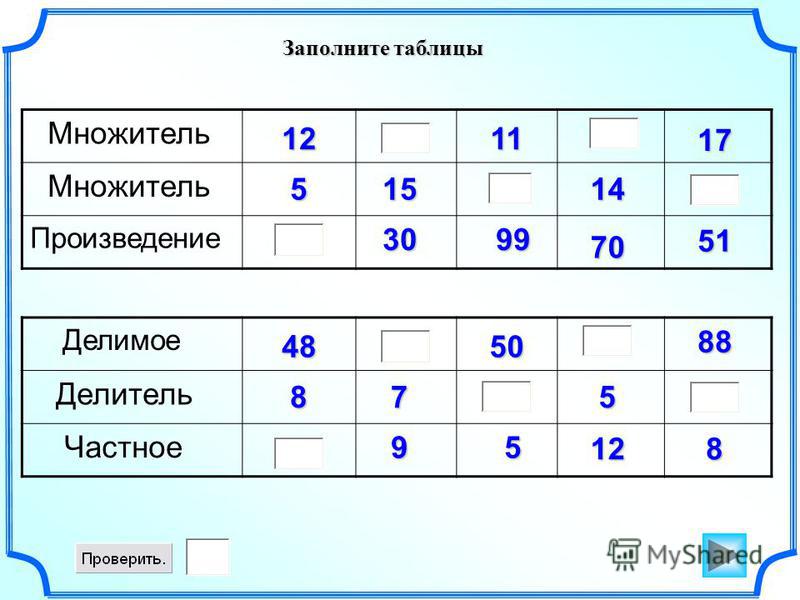
Дробь означает деление . Три четверти означает 3 ÷ 4 , что, конечно, то же самое, что и
¾ или 0,75 . Это говорит нам о том, что деление изменяется или преобразует в дробь в десятичное или целое или смешанное число . Когда мы делим большое число на малое, мы получаем либо смешанное число, либо целое число. Когда мы делим малое число на большое число, мы получаем дробь или десятичную дробь.
Примеры
Словарь разделов
Поскольку математика — это язык, мы должны уделять особое внимание словам, которые мы используем для обозначения различных чисел и символов в нашей работе. Мы используем 3 термина — множитель, множимое и произведение — для обозначения частей выражения умножения. Мы используем 4 термина для определения частей деления выражения.
Дивиденд — это число на , которое нужно разделить на . Если деление представить как дробь, это числитель . Число , делящее на , называется делителем или знаменателем (в дроби). Результат или ответ называется частным . Иногда остается 90 324 остатка 90 325, который, как следует из его названия, равен 90 324, оставшимся после 90 325, как только мы нашли все количество пакетов размером с делитель, которое мы можем отделить от делимого. Всякий раз, когда мы делим нечетное число на четное, в остатке будет 1, потому что любое нечетное число на 1 больше, чем предшествующее ему четное число.
Если деление представить как дробь, это числитель . Число , делящее на , называется делителем или знаменателем (в дроби). Результат или ответ называется частным . Иногда остается 90 324 остатка 90 325, который, как следует из его названия, равен 90 324, оставшимся после 90 325, как только мы нашли все количество пакетов размером с делитель, которое мы можем отделить от делимого. Всякий раз, когда мы делим нечетное число на четное, в остатке будет 1, потому что любое нечетное число на 1 больше, чем предшествующее ему четное число.
В первом примере выше:
делимое = 7, делитель = 3 , частное = 2 и остаток = 1 .
Допустим, трое из нас хотят поровну разделить 7 батончиков. После того, как каждый из нас возьмет по 2 батончика, останется одного на . Вот почему называется остатком . Каждый из нас получит одну треть этого последнего оставшегося батончика, что составит справедливую долю из 7 батончиков = 2 и трети батончика по каждый. Если бы наша пицца стоила 13 долларов вместо 12, то равная доля стоимости составила бы 13 ÷ 4 = 3¼ или 3,25 . После платим $3 каждый, осталось бы еще доллара на 1 доллар, чтобы заплатить . Когда каждый из нас платит еще ¼ или 25 центов, выплачивается последний доллар.
Если бы наша пицца стоила 13 долларов вместо 12, то равная доля стоимости составила бы 13 ÷ 4 = 3¼ или 3,25 . После платим $3 каждый, осталось бы еще доллара на 1 доллар, чтобы заплатить . Когда каждый из нас платит еще ¼ или 25 центов, выплачивается последний доллар.
Во второй дроби выше — та, в которой 15 + 2 в числителе.
Мы переписали или перегруппировали 17 как 15 + 2 , потому что 15 = 5 × 3 — кратно 5 и, следовательно, делится на 5 — и поскольку мы пытаемся разделить на 5 — это хорошая вещь!! 15 тоже наибольшее целое число, кратное 5 , которое мы можем вычесть из 17, и это то, что нам нужно. Когда мы делим на 15 на 5, мы получаем 3 — целую числовую часть частного. У нас есть остатка от 2 , который должен быть , разделенным на 5 — так что наш ответ. Обратите внимание на оставшуюся часть 2 с правой стороны.
Если бы пятеро из нас делили такси стоимостью 17 долларов, каждый из нас должен был бы внести по 3,40 доллара
потому что две пятых доллара = 40 центов.
что делать с остатком?
Есть 2 способа справиться с остатком. Мы можем выразить частное как смешанное число с дробной частью остатка над делителем, или мы можем написать R2 рядом с частным, как в примере справа выше.
Оценка коэффициентов
Помните, что деление — это операция, обратная умножению, поэтому, когда мы делим одно число на другое, мы ищем наибольшее целое число, кратное делителю , что мы можем вычесть из делимого . Это означает, что мы должны лучше знать наши мультипликаторы. В приведенном выше примере мы вычитаем 15 из 17, потому что знаем, что в 17 целых 3 пакета по 5. Две оставшиеся части мы разбиваем на 10-пятых, которые затем делим на 5 пакетов по 2/5 в каждом.
В приведенных выше примерах делители и делимые являются небольшими числами. Когда мы работаем с с большими числами , часто помогает округлить оба из них, поэтому мы можем оценить или угадать , сколько раз одно делится на другое.
Когда мы работаем с с большими числами , часто помогает округлить оба из них, поэтому мы можем оценить или угадать , сколько раз одно делится на другое.
Пример:
Оценить путем округления, затем найти частное от 123 ÷ 19
Мы округлить 123 до 120 — мы округлить 19 до 20 .
Теперь мы думаем, что 120 ÷ 20 = 6 . Это наш пробный коэффициент .
Умножаем на 6 × 19 , чтобы получить 114 .
Это мы вычитаем из 123 для остатка 9
а так как 9 меньше 19 — делитель, то он остается остатком.
Наш пробный коэффициент (оценка) равен 6 , фактический коэффициент равен .
Иногда наше первое пробное частное или оценка слишком велики из-за округления. Как только мы умножаем его на делитель, мы видим, что произведение будет больше, чем делимое, поэтому мы уменьшаем его до меньшего числа.
Пример:
Оценить путем округления, затем найти частное от 92 ÷ 32
Для оценки округляем 92 до 90 и 32 до 30 .
Теперь думаем, что 90 ÷ 30 = 3 . Итак, наша оценка или пробное частное равно 3 .
Но когда мы умножаем 3 × 32 , мы получаем 96 , что равно 9.0324 больше , чем 92.
Это означает, что 3 слишком большой . Частное должно быть меньше 3. Оно должно быть 2.
Правила делимости
Эти правила помогают нам найти делители заданных чисел:
Число делится на:
2 если это четное число (оканчивается на 0, 2, 4, 6 или 8) | 3 , если сумма его цифр делится на 3 |
4 если последние две цифры делятся на 4 | 5 если оно оканчивается на 5 или 0 |
6 если оно делится на 2 и на 3 | 8 , если последние три цифры делятся на 8 |
9 , если сумма его цифр делится на 9 | 10 если он заканчивается на 0 |
примеры
| а) 531 делится на 3, так как 5 + 3 + 1 = 9 | б) 9516 делится на 4, так как 16 делится на 4 |
| в) 1128 делится на 6, так как четно и сумма его цифр = 12 (делится на 3) | г) 5024 делится на 8, так как 024 делится на 8. |
| e) 576 делится на 9, так как сумма цифр = 18, которая делится на 9. |
.
Деление больших дивидендов на двузначные делители
Допустим, нам нужно разделить 189 на 17. Мы видим, что частное будет больше 10
потому что 10 × 17 = 170. В таком случае мы должны обратить пристальное внимание на разрядное значение
.
числа в частном. Вот что мы делаем:
Последовательность операций:
ДЕЛИТЬ, УМНОЖАТЬ, ВЫЧИТАТЬ
Это подводит нас к первому остатку. Если на правом конце в делимом есть неподвижных числа , мы приводим одно из них вниз к присоединяем к первому остатку . Это становится новым дивидендом . Теперь мы повторяем последовательность операций до тех пор, пока у нас не останется остаток, меньший делителя, и не останется неразделенных чисел в начальном делимом. Если бы наши дивиденды здесь были 1890, мы продолжили бы деление, опустив 0 вниз, чтобы встретить 2 в остатке, а затем мы разделили бы 20 на 17.
Это становится новым дивидендом . Теперь мы повторяем последовательность операций до тех пор, пока у нас не останется остаток, меньший делителя, и не останется неразделенных чисел в начальном делимом. Если бы наши дивиденды здесь были 1890, мы продолжили бы деление, опустив 0 вниз, чтобы встретить 2 в остатке, а затем мы разделили бы 20 на 17.
Чтобы проверить нашу работу при делении, мы умножаем частное на делитель , затем добавляем остаток к получаем делимое .
Еще один пример и готово:
Краткое изложение шагов в разделе
1. Для однозначных делителей используйте пробное частное, разделите, умножьте и вычтите.
2. Для двузначных делителей выровняйте числовые столбцы, оцените, а затем разделите, как в пункте 1.
3. Выразите остатки дробями или буквой «R» в верхнем регистре и значением остатка.
Теперь возьмите карандаш, ластик и блокнот, скопируйте вопросы,
выполните практические упражнения, затем проверьте свою работу с решениями.
Если вы застряли, просмотрите примеры в уроке, а затем повторите попытку.
Практика
1) Разложите делимое как наибольшее кратное делителя + что-то и найдите частное.
Оформите ответы в виде смешанных чисел.
| а) 25 ÷ 7 = | б) 39 ÷ 8 = | в) 125 ÷ 11 = | г) 56 ÷ 5 = |
2) Разделить. Покажите все свои работы.
| а) 2 563 ÷ 14 = | б) 3 494 ÷ 28 = | в) 12 540 ÷ 11 = | г) 756 ÷ 35 = |
.
Решения
1) Разложите делимое как произведение делителя плюс что-нибудь, затем найдите частное.
Оформите ответы в виде смешанных чисел.
| а) 25 ÷ 7 = (21 + 4) ÷ 7 = | б) 39 ÷ 8 = (32 + 7) ÷ 8 = | в) 125 ÷ 11 = (121 + 4) ÷ 11 = | г) 56 ÷ 5 = (55 + 1) ÷ 5 = |
2) Разделить. Покажите все свои работы.
| а) 2 563 ÷ 14 = | б) 3 494 ÷ 28 = | в) 12 540 ÷ 11 = | d) 756 ÷ 35 = |
( Арифметический индекс MathRoom )
5.
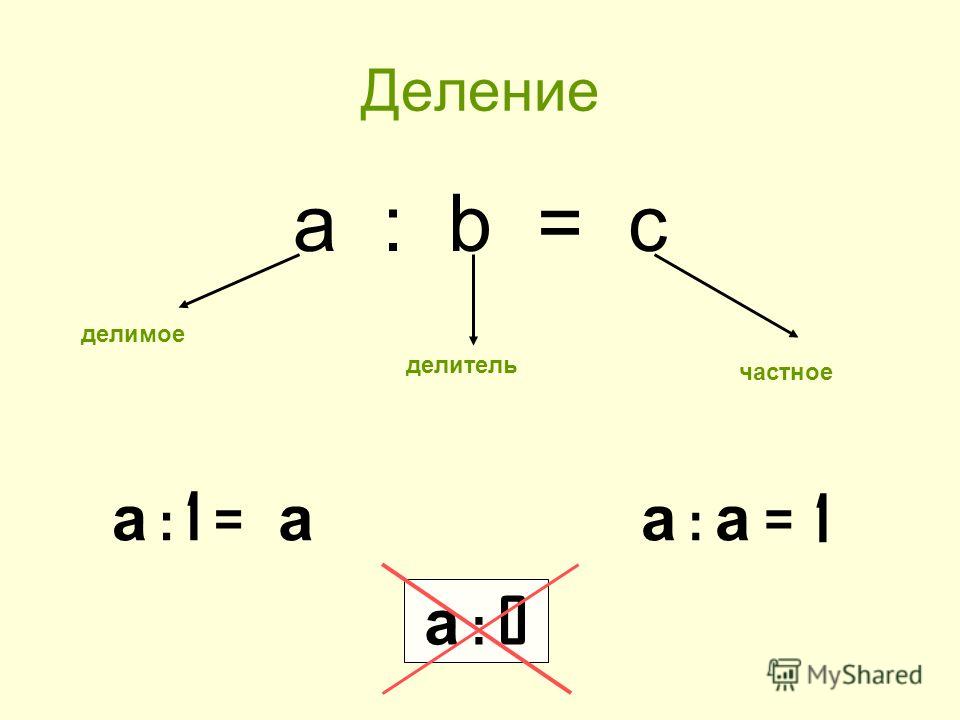 5: Деление десятичных знаков — Математика LibreTexts
5: Деление десятичных знаков — Математика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 22491
- Дэвид Арнольд
- Колледж Редвудс
В этом и последующих разделах мы используем термины делитель , делимое , частное и остаток .
Делитель, делимое, частное и остаток
Эта схема напоминает читателям о положении этих терминов в процессе деления.
Теперь, когда эти термины определены, мы начинаем обсуждение деления десятичных чисел. Предположим, что мы хотим разделить 637 на 100. Мы могли бы сделать это в виде дроби, преобразовать результат в смешанную дробь, а затем смешанную дробь в десятичную форму.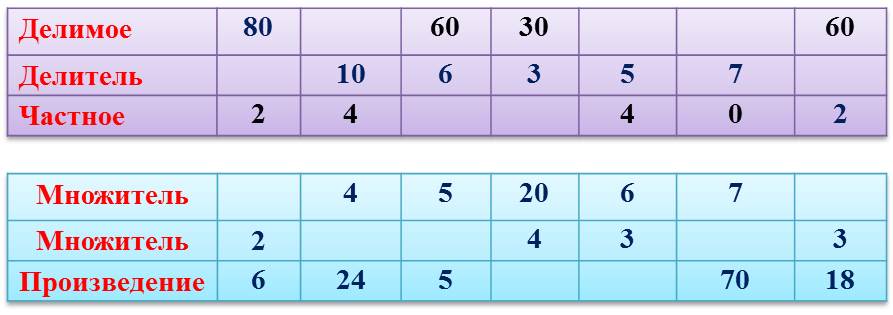
\[\frac{637}{100} = 6 \frac{37}{100} = 6,37\номер\]
Мы также можем организовать деление так же, как деление двух целых чисел.
Обратите внимание, что добавление двух нулей после запятой в делимом не меняет значения 637. Далее, обратите внимание, что мы действуем так, как будто мы делим два целых числа, помещая десятичную точку в частном непосредственно над десятичной запятой в делимом. дивиденд.
Эти наблюдения приводят к следующему алгоритму.
Деление десятичной дроби на целое число
Чтобы разделить десятичное число на целое, выполните следующие действия:
- Настройте деление в длинную, как при делении двух целых чисел.
- Выполните деление так, как если бы оба числа были целыми числами, добавляя нули справа от десятичной точки в делимом, если это необходимо для завершения деления.
- Поместите запятую в частном непосредственно перед запятой в делимом.
Пример 1
Разделите 23 на 20.
Решение
Расположите, как при делении целых чисел, используя длинное деление, добавив достаточное количество нулей справа от десятичной точки в делимом, чтобы завершить деление.
Следовательно, 23 разделить на 20 равно 1,15.
Добавление нулей справа от запятой
Обычно сразу не видно, сколько нулей справа от запятой нужно в делимом. Эти нули обычно добавляются на каждом шаге деления, пока деление не будет завершено или пока пользователь не захочет завершить процесс и принять только оценку частного.
Пример 2
Разделить: 155,2 ÷ 25.
Решение
Расположите, как при делении целых чисел с помощью длинного деления, и начните.
У нас все еще есть ненулевой остаток. Добавление еще одного нуля не дает никакого результата.
Однако, если мы добавим еще один дополнительный ноль, деление завершится с нулевым остатком.
Таким образом, 155,2 разделить на 25 будет 6,208.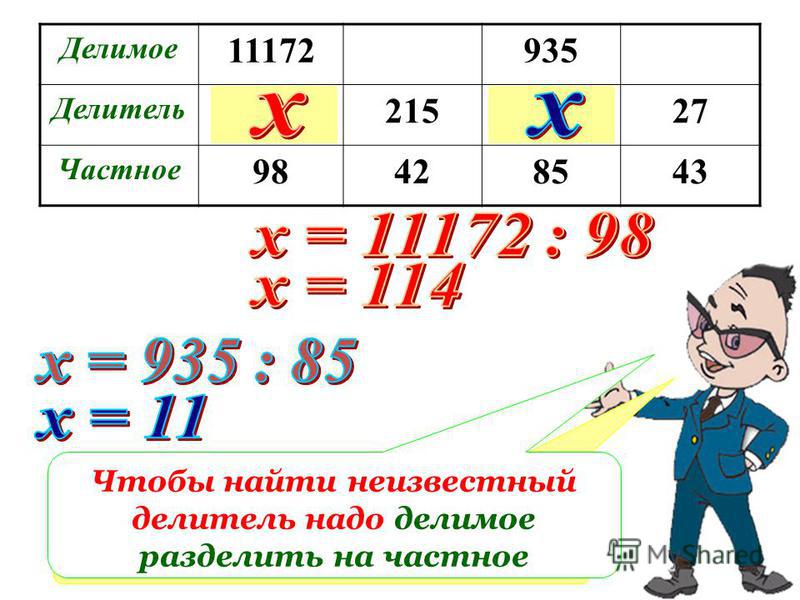
Упражнение
Разделить: 42,55 ÷ 23
- Ответить
1,85
Десятичные делители Когда делитель содержит десятичную точку, нам нужно немного поработать, прежде чем мы начнем процесс деления. Предположим, что мы хотим разделить 1,25 на 2,5. В дробной форме мы могли бы начать с
.\[ \frac{1.25}{2.5},\номер\]
затем удалите десятичные дроби из знаменателя, умножив и числитель, и знаменатель на 10. Примечание: Помните, что при умножении на 10 десятичная точка сдвигается на один разряд вправо.
\[ \begin{выровнено} \frac{1.25}{2.5} = \frac{1.25 \cdot 10}{2.5 \cdot 10} \\ = \frac{12.5}{25} \end{выровнено}\nonumber \ ]
Таким образом, деление 1,25 на 2,5 эквивалентно делению 12,5 на 25. Это мы умеем делать.
Таким образом, 1,25 разделить на 2,5 равно 0,5.
Письмо Математика
Никогда не пиши .5. Всегда добавляйте начальные нули на место единиц и пишите 0,5.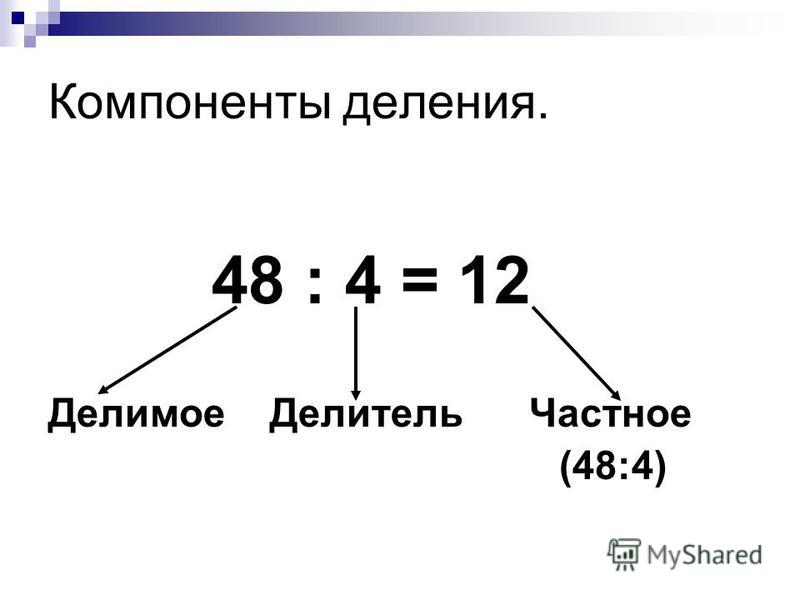
Вместо того, чтобы работать в виде дроби, мы можем позаботиться о расположении десятичной точки в рамках длинного деления. Начните с:
Переместите запятую в делителе в конец делителя, затем переместите запятую в делимом на такое же количество знаков.
Таким образом, деление становится
, и мы действуем, как описано выше, чтобы найти частное. Это обсуждение мотивирует следующий алгоритм.
Деление на десятичный делитель
Если делитель содержит десятичную дробь, выполните следующие действия:
- Переместите десятичную дробь в конец делителя.
- Переместите десятичную дробь в делимом на равное количество знаков.
Затем мы можем завершить деление, используя правила деления десятичной дроби на целое число.
Пример 3
Разделить: \(\overline{ )4.392}\)
Решение
Переместить десятичную дробь в делителе в конец делителя. Переместите десятичную дробь в делимом на равное количество знаков (два разряда) вправо.
Теперь мы можем следовать алгоритму деления десятичного числа на целое число.
Таким образом, 4,392 разделить на 0,36 равно 12,2.
Упражнение
Разделить: \(0,45 \overline{)36,99}\)
- Ответ
82,2
Деление десятичных чисел со знаком
Правила деления десятичных чисел со знаком идентичны правилам деления целых чисел.
Подобные знаки. Частное двух десятичных чисел с одинаковыми знаками положительно. То есть:
\[\frac{(+)}{(+)} = + \text{ and } \frac{(-)}{(-)} = +\nonnumber \]
В отличие от знаков. Частное двух десятичных чисел с разными знаками отрицательно. То есть:
\[\frac{(+)}{(-)} = — \text{ and } \frac{(-)}{(+)} = -\nonumber \]
Пример 4
Разделить: −0,03 ÷ 0,024.
Решение
Сначала разделим величины. Переместите десятичную дробь в делителе в конец делителя. Переместите десятичную дробь в делимом на равное количество знаков (три знака) вправо. Обратите внимание, что для этого требуется дополнительный конечный нуль в делимом.
Переместите десятичную дробь в делимом на равное количество знаков (три знака) вправо. Обратите внимание, что для этого требуется дополнительный конечный нуль в делимом.
Тогда наша задача принимает следующий вид:
\[ 24 \overline{24 )30}\)
Теперь мы можем следовать алгоритму деления десятичного числа на целое число. Обратите внимание, что мы должны добавить два нуля в конце делимого, чтобы завершить деление с нулевым остатком.
Наконец, поскольку частное разных знаков отрицательно, -0,03, деленное на 0,024, равно -1,25. То есть
\[ \frac{-0,03}{0,024} = -1,25.\nonumber \]
Упражнение
Разделить: −0,0113 ÷ 0,05
- Ответ
−0,226
Округление
Иногда точное десятичное представление дроби не требуется, и приближение более чем достаточно.
Пример 5
Преобразование 4/7 в десятичное число. Округлите ответ до сотых.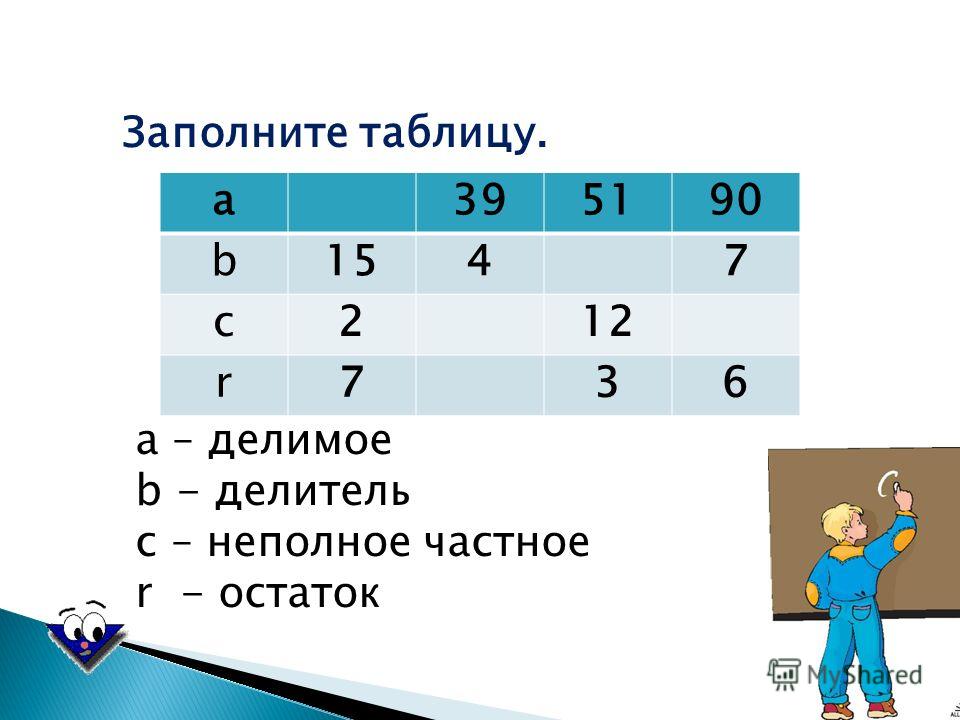
Решение
Нам нужно перевести деление на один разряд дальше сотых.
Чтобы округлить до сотых, сначала определите цифры округления и проверки.
Поскольку «проверочная цифра» меньше 5, оставьте цифру округления и усеките ее. Следовательно, с точностью до сотых, 4/7 ≈ 0,57.
Упражнение
Преобразование 5/7 в десятичную дробь. Округлите ответ до сотых.
- Ответить
0,71
Деление на степени десяти 93 = 10 \cdot 10 \cdot 10 = 1000 \end{aligned}\nonumber \]
Степени десяти
В выражении 10 n показатель степени соответствует количеству нулей в ответе. Следовательно, 10 n будет 1, за которой следуют n нулей.
Таким образом, 10 4 = 10 000, 10 5 = 100 000 и т. д. Показатель степени говорит нам, сколько нулей будет после 1.
Разделим 123456,7 на 10000.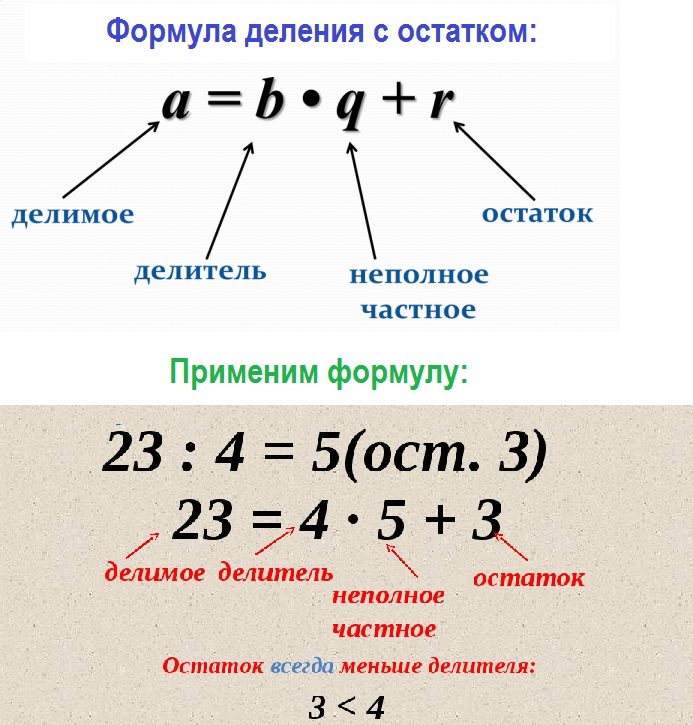 результат: 123456,7 разделить на 1000 будет 123,4567. При делении на 1000 запятая сдвигается на 3 знака влево!
результат: 123456,7 разделить на 1000 будет 123,4567. При делении на 1000 запятая сдвигается на 3 знака влево!
Это обсуждение приводит к следующему результату.
Деление десятичного числа на степень десяти
Деление десятичного числа на 10 n приведет к перемещению десятичной точки n знаков влево.
Пример 6
Упрощение: 123456,7 ÷ 10 4
Решение
Деление на 10 4 (или эквивалентно, 4 знака после запятой) сдвигается влево на 10,00. Таким образом, 123456,7 ÷ 10 4 = 12,34567.
Упражнение
Упрощение: 123456,7 ÷ 10 2
- Ответ
1234.567
Порядок работы
Напоминаем читателям о Правилах , определяющих порядок работы s.
Правила, определяющие порядок операций
При вычислении выражений действуйте в следующем порядке.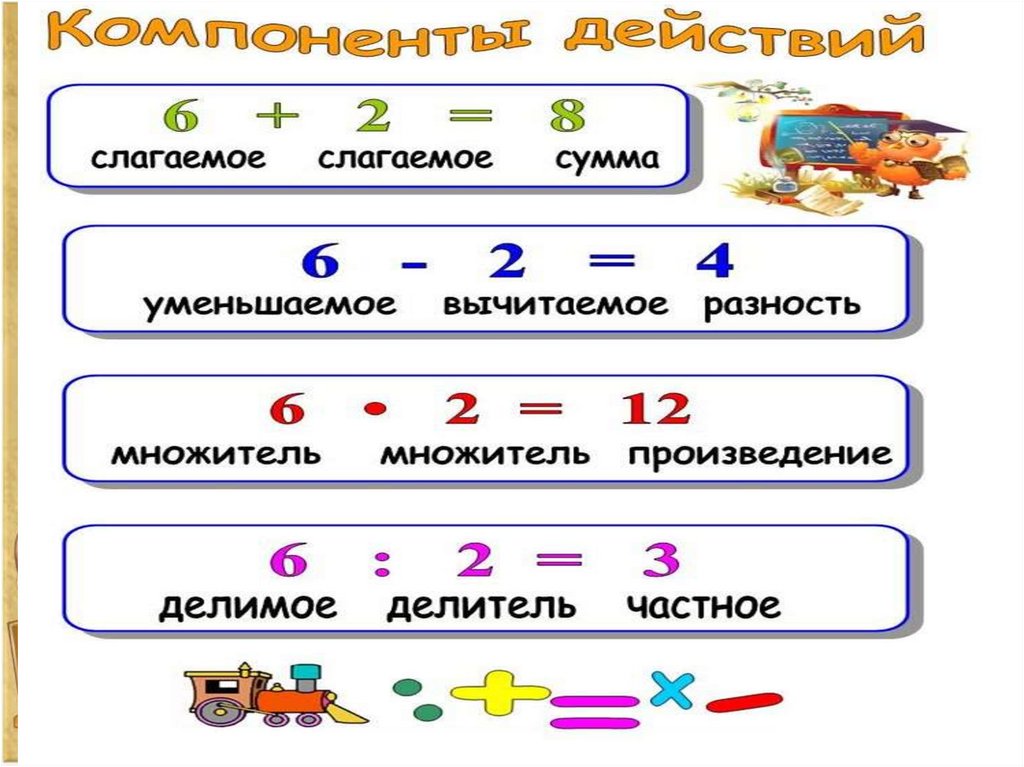
- Сначала вычислить выражения, содержащиеся в символах группировки. Если символы группировки являются вложенными, сначала вычислите выражение в самой внутренней паре символов группировки.
- Вычислить все показатели степени, встречающиеся в выражении.
- Выполнить все операции умножения и деления в порядке их появления в выражении, двигаясь слева направо.
- Выполняйте все сложения и вычитания в порядке их появления в выражении, двигаясь слева направо.
Кроме того, при наличии дробей:
Выражения дробей
Если присутствует дробное выражение, упростите числитель и знаменатель по отдельности, а затем разделите.
Пример 7
Оценить ab/(c + d), учитывая, что a = 2,1, b = -3,4, c = -1,3 и d = 1,1.
Решение
Напомним, что хорошей практикой является подготовка выражения для подстановки с использованием круглых скобок.
\[ab/(c + d) = (~)(~)/((~) +(~)) \nonumber \]
Подставьте данные значения для a, b, c и d, затем используйте Правила , руководящие порядком операций , чтобы упростить результирующее выражение.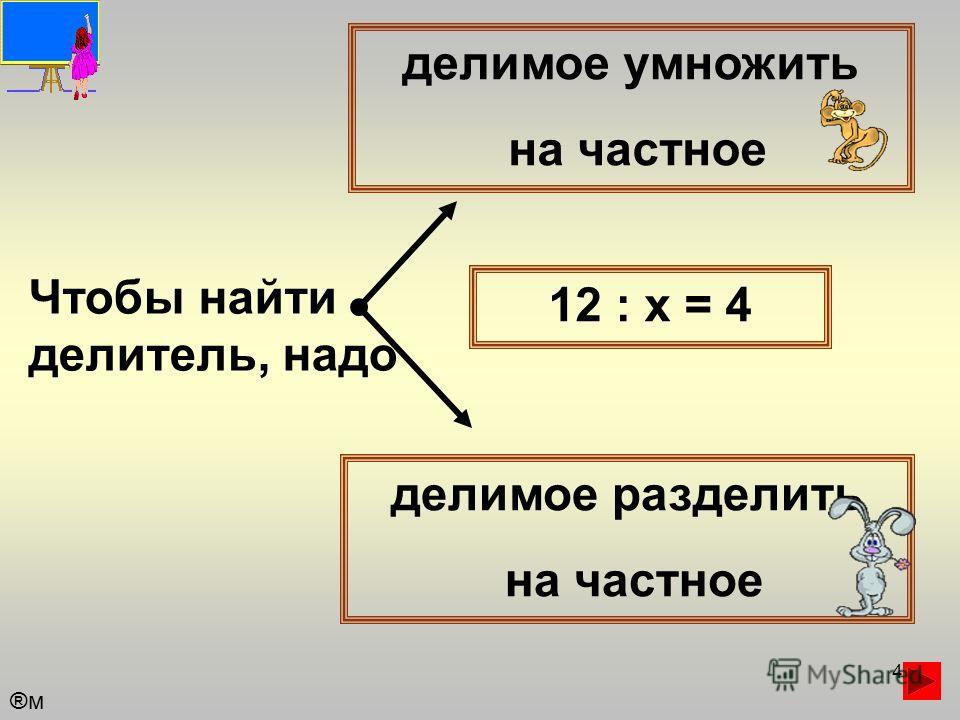
\[ \begin{align} ab/(c+d) = (2.1)(-3.4)/((-1.3)+(1.1)) ~ & \textcolor{red}{2.1, -3.4,-1.3 , 1.1 \text{ для } a, b, c, d.} \\ = (2.1)(-3.4)/(-0.2) ~ & \textcolor{red}{ \text{ Скобки: } (-1.3) + (1.1) = -0,2.} \\ = -7,14/(-0,2) ~ & \textcolor{red}{ \text{ Умножить: } (2,1)(-3,4) = -7,14.} \\ =35,7 ~ & \textcolor{red}{ \text{ Разделить: } -7,14/(-0,2) = 35,7} \end{выравнивание}\nonumber \]
Упражнение
Если a = −2,1, b = 1,7, c = 4 и d = 0,05, оцените:
\[\frac{a+b}{cd}\nonumber \]
- Ответ
−2
Пример 8
При заданных a = 0,1 и b = −0,3 вычислить выражение значений, затем используйте Правила , определяющие порядок операций , чтобы упростить результирующее выражение.
\[ \begin{align} \frac{a+2b}{2a+b} = \frac{(0.1)+2(-0.3)}{2(0.1)+(-0.3)} ~ & \textcolor {red}{ \text{ 0,1 для } a,~ -0,3 \text{ для } b.} \end{aligned}\nonumber \]
Упростите числитель, упростите знаменатель, затем разделите.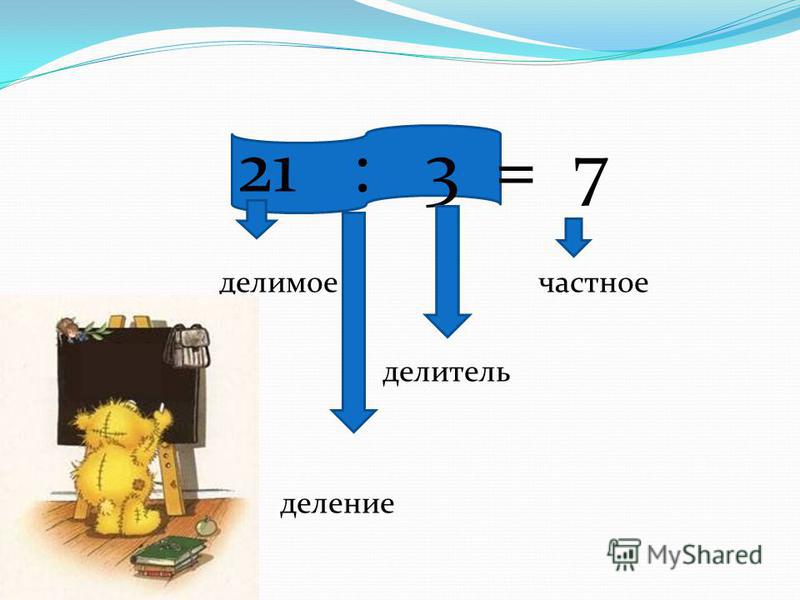
\[ \begin{aligned} = \frac{0,1+(-0,6)}{0,2+(-0,3)} ~ & \textcolor{red}{ \begin{aligned} \text{ Числитель: } 2(- 0,3) = -0,6. \\ \text{ Знаменатель: } 2(0,1)=0,2. \end{выровнено}} \\ = \frac{-0,5}{-0,1} ~ & \textcolor{red}{ \begin{aligned} \text{ Числитель: } 0,1 + (-0,6)=-0,5 \\ \ текст {Знаменатель:} 0,2 + (-0,3) = -0,1. \end{выровнено}} \\ =5 ~ & \textcolor{red}{ \text{ Разделить: } -0,5/(-0,1)=5.} \end{выровнено}\nonumber \]
Упражнение
Если a = 0,5 и b = −0,125, оцените:
\[ \frac{2a-b}{a+2b}\nonumber \]
- Ответ
4,5
Упражнения
В упражнениях 1-16 разделите числа.
1. \(\frac{39}{52}\)
2. \(\frac{16}{25}\)
3. \(\frac{755.3}{83}\)
4. \(\frac{410.4}{76}\)
5. \(\frac{333}{74}\)
6. \(\frac{117}{65}\)
7. \(\frac{32.12}{73}\)
8. \(\frac{12.32}{44}\)
9. \(\frac{37.63}{71}\)
10 .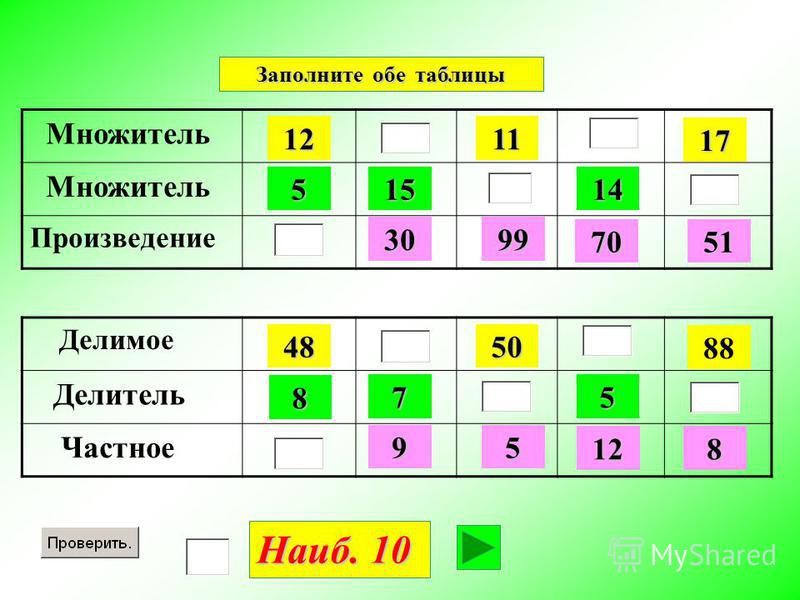 (\frac{17}{25}\)
(\frac{17}{25}\)
14. \(\frac{18}{75}\)
15. \(\frac{229.5}{51}\)
16. \(\ frac{525.6}{72}\)
В упражнениях 17-40 разделите десятичные дроби.
17. \(\frac{0,3478}{0,47}\)
18. \(\frac{0,4559}{0,97}\)
19. \(\frac{1.694}{2.2}\)
20. \(\frac{1.008}{1.8}\)
21. \(\frac{43.61}{4.9}\)
22. \(\frac{22,78}{3,4}\)
23. \(\frac{1,107}{0,41}\)
24. \(\frac{2,465}{0,29}\)
25. \(\frac{2,958}{0,51}\)
26. \(\frac{5,141}{0,53}\)
27. \(\frac{71,76}{7,8}\)
28. \( \frac{14.08}{8.8}\)
29. \(\frac{0.8649}{0.93}\)
30. \(\frac{0.3901}{0.83}\)
31. \(\frac {0,6958}{0,71}\)
32. \(\frac{0,1829}{0,31}\)
33. \(\frac{1,248}{0,52}\)
34. \(\frac{6,375} {0,85}\)
35. \(\frac{62,56}{9,2}\)
36. \(\frac{28,08}{7,8}\)
37. \(\frac{6,278}{8,6 }\)
38. \(\frac{3.185}{4.9}\)
39. \(\frac{2.698}{7. 1}\)
1}\)
40. \(\frac{4.959}{8.7}\ )
В упражнениях 41-64 разделите десятичные дроби.
41. \(\frac{−11.04}{1.6}\)
42. \(\frac{−31.27}{5.3}\)
43. \(\frac{−3.024}{5.6}\)
44. \(\frac{−3.498}{5.3}\)
45. \(\frac{−0.1056}{0.22}\ )
46. \(\frac{−0,2952}{−0,72}\)
47. \(\frac{0,3204}{−0,89}\)
48. \(\frac{0,3306}{−0,38 }\)
49. \(\frac{−1,419}{0,43}\)
50. \(\frac{−1,625}{−0,25}\)
51. \(\frac{−16,72} {−2,2}\)
52. \(\frac{−66,24}{9,2}\)
53. \(\frac{−2,088}{−0,87}\)
54. \(\frac{ −2,025}{−0,75}\)
55. \(\frac{−1,634}{−8,6}\)
56. \(\frac{−3,094}{3,4}\)
57. \(\frac{−0,119}{0,85}\ )
58. \(\frac{0,5766}{−0,62}\)
59. \(\frac{−3,591}{−6,3}\)
60. \(\frac{−3,016}{5,8 }\)
61. \(\frac{36,96}{−4,4}\)
62. \(\frac{−78,26}{−8,6}\)
63. \(\frac{−2,156} {−0,98}\)
64. \(\frac{−6,072}{0,66}\)
В упражнениях 65-76 разделите десятичную дробь на заданную степень 10.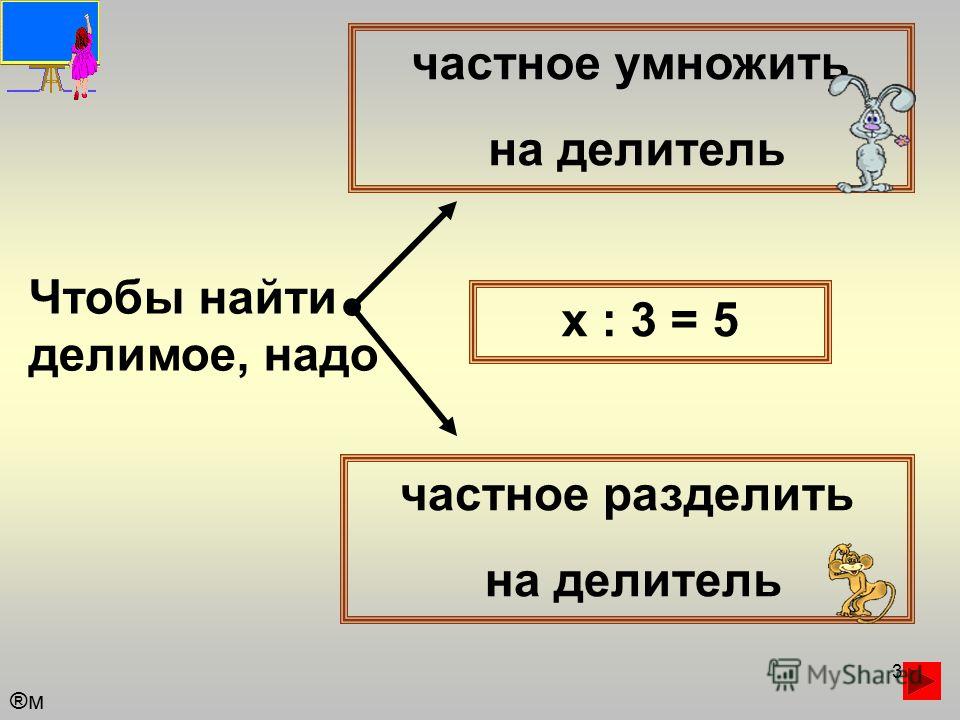
65. \(\frac {524.35}{100}\) 94}\)
75. \(\frac{113.02}{1000}\)
76. \(\frac{520.77}{1000}\)
77. Вычислить частное 52/83 и округлить ваш ответ с точностью до десятых.
78. Вычислите частное 43/82 и округлите ответ до десятых.
79. Вычислите частное 51/59 и округлите ответ до десятых.
80. Вычислите частное 17/69 и округлите ответ до десятых.
81. Вычислите частное 5/74 и округлите ответ до сотых.
82. Вычислите частное 3/41 и округлите ответ до сотых.
83. Вычислите частное 5/94 и округлите ответ до сотых.
84. Вычислите частное 3/75 и округлите ответ до сотых.
85. Вычислите частное 7/72 и округлите ответ до сотых.
86. Вычислите частное 4/57 и округлите ответ до сотых.
87. Вычислите частное 16/86 и округлите ответ до десятых.
88. Вычислите частное 21/38 и округлите ответ до десятых.
В упражнениях 89-100 упростите данное выражение.
89.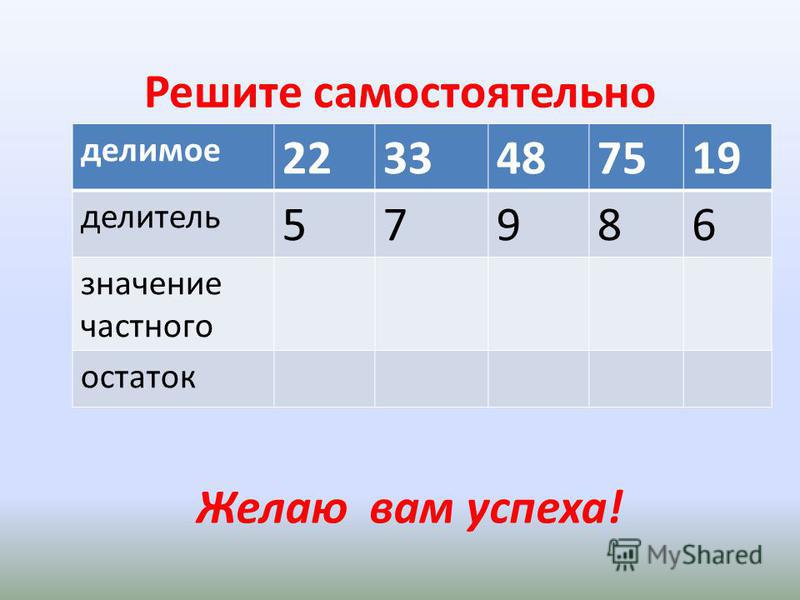 \(\frac{7,5 \cdot 7,1 − 19,5}{0,54}\)
\(\frac{7,5 \cdot 7,1 − 19,5}{0,54}\)
90. \(\frac{1,5(−8,8) − (−18,6)}{1,8}\)
91. \(\frac{17,76 — (-11,7)}{0,52}\)
92. \(\frac{-14,8 — 2,1}{2,62}\)
93. \(\frac{-18,22 — 6,7} {14,75 − 7,75}\)
94. \(\frac{1,4 − 13,25}{−6,84 − (−2,1)}\)
95. \(\frac{−12,92}\nonumber \]
103. Учитывая a = −5,8, b = 10,37, c = 4,8 и d = 5,64, оцени и упрости следующее выражение:
\[\frac{a − b}{c − d}\nonumber \]
104. Учитывая a = −10,79, b = 3,94, c = −3,2 и d = −8,11, оцените и упростите следующее выражение:
\[\frac{a − b}{ c − d}\nonumber \]
105. Учитывая a = −1,5, b = 4,7, c = 18,8 и d = −11,75, оцените и упростите следующее выражение.
\[\frac{ab − c}{d}\номер\]
106. Учитывая a = 9,3, b = 6,6, c = 14,27 и d = 0,2, оцените и упростите следующее выражение.
\[\frac{ab − c}{d}\номер \]
107. Биодизельные установки. Около 180 биодизельных заводов работают примерно в 40 штатах.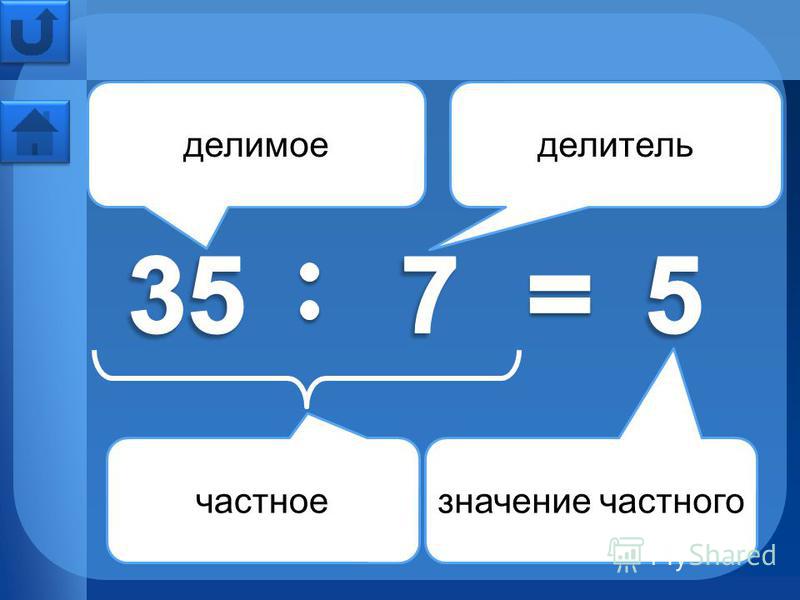 Каково среднее количество заводов по производству биодизельного топлива в штатах, в которых они есть? Ассошиэйтед Пресс-Таймс-Стандарт 02.01.10 Молодая биотопливная промышленность заканчивает год на суровой ноте .
Каково среднее количество заводов по производству биодизельного топлива в штатах, в которых они есть? Ассошиэйтед Пресс-Таймс-Стандарт 02.01.10 Молодая биотопливная промышленность заканчивает год на суровой ноте .
108. Грибок летучих мышей. Грибок под названием «синдром белого носа» убил около 500 000 летучих мышей по всей стране. Это означает, что около 2 400 000 фунтов жуков не съедается за год, говорит биолог Лесной службы Бекки Юинг. Сколько фунтов насекомых съедает средняя летучая мышь ежегодно? Associated Press-Times-Standard 02.05.09
109. Задолженность по патентам. В Ведомстве США по патентам и товарным знакам 6000 экспертов имеют накопившуюся задолженность по 770 000 новых нерассмотренных заявок на патенты. Сколько заявлений нужно каждому экзаменатору наверстать? Округлите ответ до десятых. Associated Press-Times-Standard 5/5/09
110. Дела идут хорошо. Крупная медицинская страховая компания Wellpoint, Inc. , владелец Anthem Blue Cross, за последние три месяца 2009 года заработала 536 миллионов долларов. Каков был средний месячный доход страховой компании за этот период? Округлить до миллиона. Associated Press-Times-Standard 09.02.10 Секретарь HHS просит Anthem Blue Cross оправдать повышение ставки.
, владелец Anthem Blue Cross, за последние три месяца 2009 года заработала 536 миллионов долларов. Каков был средний месячный доход страховой компании за этот период? Округлить до миллиона. Associated Press-Times-Standard 09.02.10 Секретарь HHS просит Anthem Blue Cross оправдать повышение ставки.
111. Кибератаки. Пентагон потратил 100 миллионов долларов за шестимесячный период на реагирование и устранение ущерба от кибератак и других проблем с компьютерной сетью. Какова средняя сумма денег, потраченная в месяц за это время? Округлите ответ до сотых долей миллиона. Associated Press-Times-Standard 19.04.09
112. Ежедневное молоко. Средняя калифорнийская корова может производить 2305 галлонов молока в год. Сколько молока может дать корова каждый день? Округлите ответ до ближайшей сотой доли галлона. www.moomilk.com/faq.htm
113. Почта СМИ. Для продвижения своего бизнеса Тереза отправляет несколько посылок через Media Mail. Одна упаковка весом 2 кг. стоит 2,77 доллара, еще одна упаковка весом 3 фунта. стоит 3,16 доллара, а третья упаковка весом 5 фунтов. стоит 3,9 доллара4 на почту. Какова была средняя стоимость пересылки посылки за фунт? Округлите результат до копейки. www.usps.com/prices/media-mailprices.htm
Одна упаковка весом 2 кг. стоит 2,77 доллара, еще одна упаковка весом 3 фунта. стоит 3,16 доллара, а третья упаковка весом 5 фунтов. стоит 3,9 доллара4 на почту. Какова была средняя стоимость пересылки посылки за фунт? Округлите результат до копейки. www.usps.com/prices/media-mailprices.htm
Ответы
1. 0,75
3. 9.1
5. 4.5
7. 0,44
9. 0,53
11. 1,5
13 130002 9. 0,53
. 0,68
15. 4,5
17. 0,74
19. 0,77
21. 8,9
23. 2,7
25. 5,8
27. 9,2
29. 0,93
0002 31. 0,9833. 2,4
35. 6,8
37. 0,73
39. 0,38
41. −6,9
43. -0,54
45. –0,48
43,54
45. –0,48
43,569
45. –0,48
43. 49. −3.3
51. 7.6
53. 2,4
55. 0,19
57. −0,14
59. 0,57
61. -8,4
63. 2,2
65,5,2435
6766. 0,56394
69.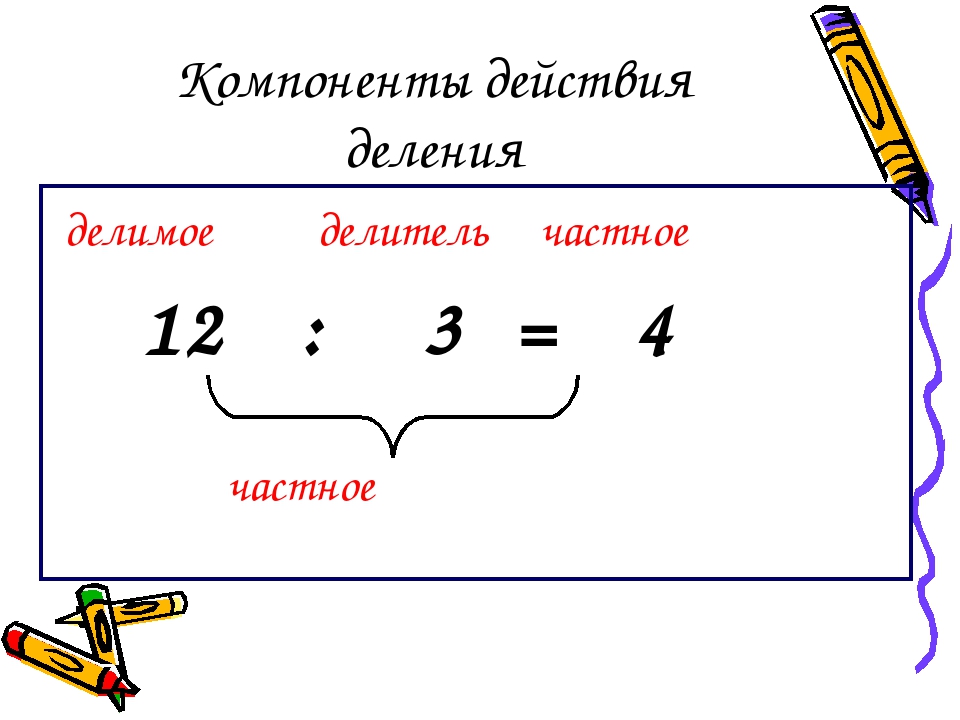






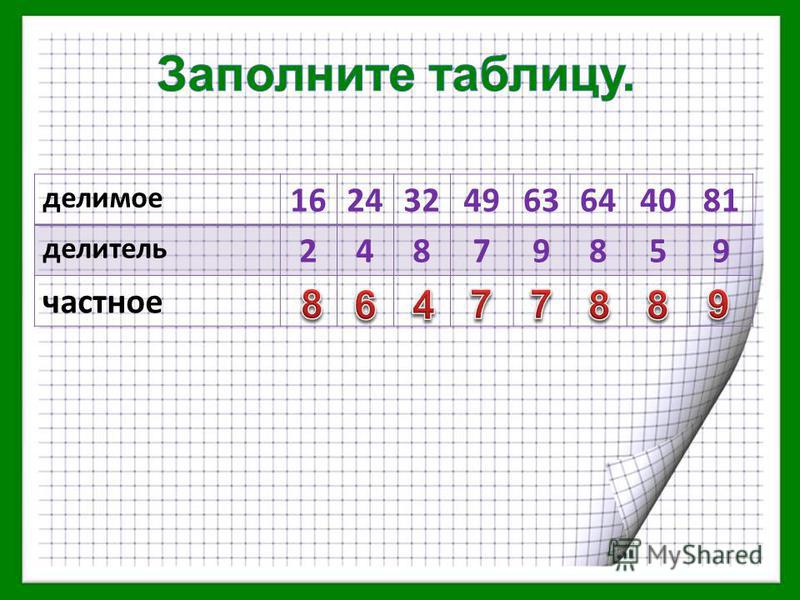 Если делитель умножить на частное, то получится делимое.
Если делитель умножить на частное, то получится делимое. 13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1.
13 делим на 2. Берем по 6. 6 * 2 = 12. Вычитаем из 13 полученное значение и получаем 1.

 Термины, используемые в подразделе | Дивиденд | Делитель | Коэффициент | Остаток
Термины, используемые в подразделе | Дивиденд | Делитель | Коэффициент | Остаток com
com com
com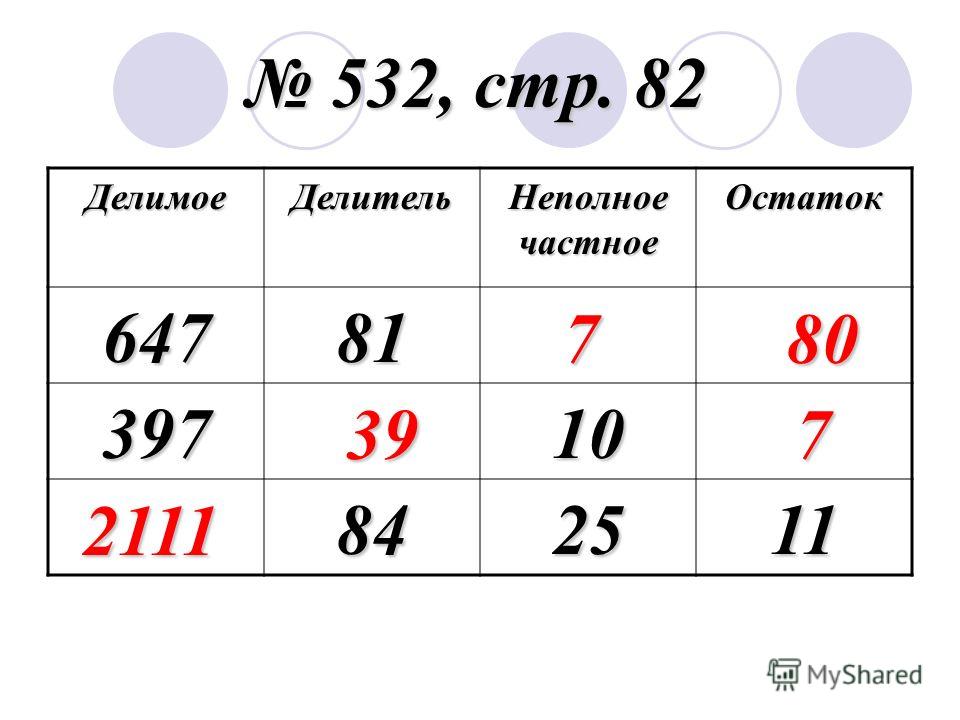 Число, которое мы делим, называется делимым.
Число, которое мы делим, называется делимым.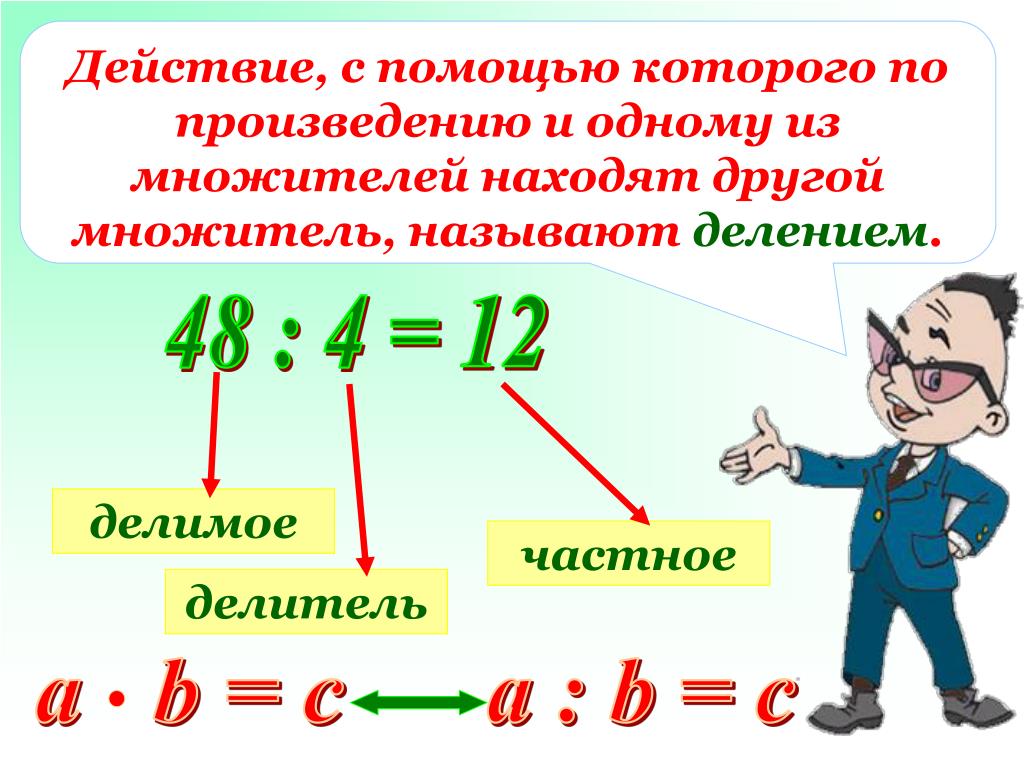 Частное — это ответ.
Частное — это ответ.