Матрицы примеры решения задач, формулы и онлайн калькуляторы
Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .
Выполним произведения в более компактном виде:
$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$
Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .
Матрицы примеры решения задач, формулы и онлайн калькуляторы
Задание. Вычислить $A B$ и $B A$,
если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Вычислить $A B$ и $B A$,
если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .
Выполним произведения в более компактном виде:
$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$
Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .
Матрицы примеры решения задач, формулы и онлайн калькуляторы
Задание. Вычислить $A B$ и $B A$,
если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Вычислить $A B$ и $B A$,
если $A=\left( \begin{array}{rr}{1} & {-1} \\ {2} & {0} \\ {3} & {0}\end{array}\right), B=\left( \begin{array}{ll}{1} & {1} \\ {2} & {0}\end{array}\right)$
Решение. Так как $A=A_{3 \times 2}$ , а $B=B_{2 \times 2}$ , то произведение возможно и результатом операции умножения будет матрица $C=C_{3 \times 2}$ , а это матрица вида $C=\left( \begin{array}{cc}{c_{11}} & {c_{12}} \\ {c_{21}} & {c_{22}} \\ {c_{31}} & {c_{32}}\end{array}\right)$ .
Вычисли элементы матрицы $C$ :
$ c_{11}=a_{11} \cdot b_{11}+a_{12} \cdot b_{21}=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_{12}=a_{11} \cdot b_{12}+a_{12} \cdot b_{22}=1 \cdot 1+(-1) \cdot 0=1 $
$ c_{21}=a_{21} \cdot b_{11}+a_{22} \cdot b_{21}=2 \cdot 1+0 \cdot 2=2 $
$ c_{22}=a_{21} \cdot b_{12}+a_{22} \cdot b_{22}=2 \cdot 1+0 \cdot 0=2 $
$ c_{31}=a_{31} \cdot b_{11}+a_{32} \cdot b_{21}=3 \cdot 1+0 \cdot 2=3 $
$ c_{31}=a_{31} \cdot b_{12}+a_{32} \cdot b_{22}=3 \cdot 1+0 \cdot 0=3 $
Итак, $C=A B=\left( \begin{array}{rl}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ .
Выполним произведения в более компактном виде:
$=\left( \begin{array}{rrr}{1 \cdot 1+(-1) \cdot 2} & {1 \cdot 1+(-1) \cdot 0} \\ {2 \cdot 1+0 \cdot 2} & {2 \cdot 1+0 \cdot 0} \\ {3 \cdot 1+0 \cdot 2} & {3 \cdot 1+0 \cdot 0}\end{array}\right)=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$
Найдем теперь произведение $D=B A=B_{2 \times 2} \cdot A_{3 \times 2}$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin{array}{rr}{-1} & {1} \\ {2} & {2} \\ {3} & {3}\end{array}\right)$ . В обратном порядке умножить данные матрицы невозможно, так как количество столбцов матрицы $B$ не совпадает с количеством строк матрицы $A$ .
Матрицы, определители, системы линейных уравнений (Лекция №12)
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так
.
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице
число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше
примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая
матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все элементы которой равны нулю, называется
.
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
.
Квадратная
матрица, у которой все элементы, кроме, быть может, стоящих
на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .
Например, или .
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если и , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно
сопоставить такую матрицу B из
n строк и m столбцов, у которой каждая
строка является столбцом матрицы A с
тем же номером (следовательно, каждый столбец является строкой матрицы A с тем же номером).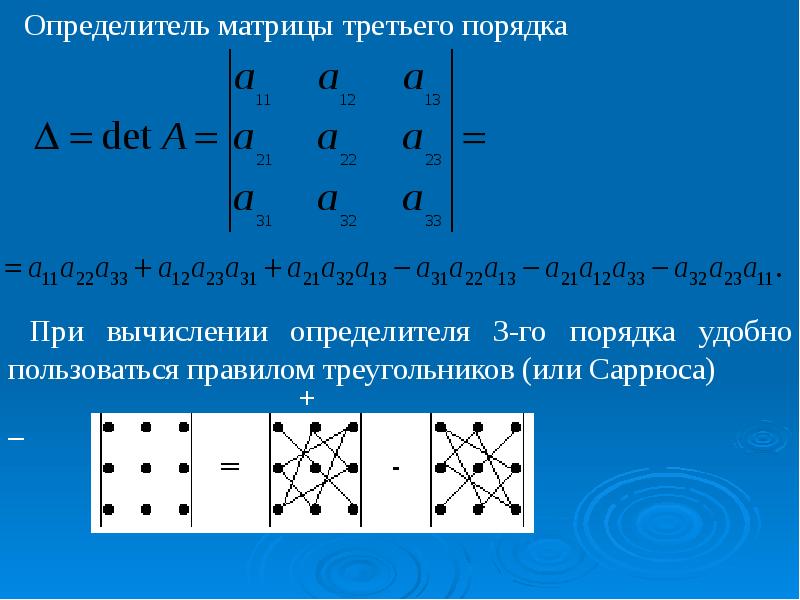 Итак,
если , то .
Итак,
если , то .
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице
Связь между матрицей A и её транспонированной можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
или
Примеры. Найти сумму матриц:
Найти сумму матриц:
- .
- — нельзя, т.к. размеры матриц различны.
- .
Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .
Для любых чисел a и b и матриц A и B выполняются равенства:
- .
Примеры.
- .
- Найти 2A-B, если , .
.
- Найти C=–3A+4B.
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A не матрицу B называется новая матрица C=AB,
элементы которой составляются следующим образом:
Эта операция осуществляется по своеобразному
закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть
согласованы. Перемножать можно только те матрицы, у которых число столбцов
первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки
первой равна высоте столбца второй). Произведением
матрицы A не матрицу B называется новая матрица C=AB,
элементы которой составляются следующим образом:
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.
В
общем случае, если мы умножаем матрицу A = (aij) размера m×n на
матрицу B = (bij) размера n×p, то получим матрицу C
размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате
произведения элементов i-ой строки матрицы A на соответствующие элементы j-го
столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
.
Примеры.
- Пусть
Найти элементы c12, c23 и c21 матрицы C.
- Найти произведение матриц.
.
- .
- — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
- Пусть
Найти АВ и ВА.
Найти АВ и ВА.
, B·A – не имеет смысла.

Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.
Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если , то
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана
матрица второго порядка – квадратная матрица, состоящая из двух строк и двух
столбцов .
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом: a11a22 – a12a21.
Определитель обозначается символом .
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
- .
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
.
Таким образом,
эта формула даёт разложение определителя третьего порядка по элементам первой
строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению
определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
- .
- .
- Решите уравнение..
.
(x+3)(4x-4-3x)+4(3x-4x+4)=0.
(x+3)(x-4)+4(-x+4)=0.
(x-4)(x-1)=0.
x1 = 4, x2 = 1.
Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
примеры, алгоритм умножения на вектор, число, свойства произведения
Произведение двух матриц
Определение 1Произведение матриц (С= АВ) — операция только для согласованных матриц А и В, у которых число столбцов матрицы А равно числу строк матрицы В:
C⏟m×n=A⏟m×p×B⏟p×n
Пример 1Даны матрицы:
- A=a(ij) размеров m×n;
- B=b(ij) размеров p×n
Матрицу C, элементы cij которой вычисляются по следующей формуле:
cij=ai1×b1j+ai2×b2j+. ..+aip×bpj, i=1,…m, j=1,…m
..+aip×bpj, i=1,…m, j=1,…m
Вычислим произведения АВ=ВА:
А=121012, В=100111
Решение, используя правило умножения матриц:
А⏟2×3×В⏟3×2=121012×100111=1×1+2×0+1×11×0+2×1+1×10×1+1×0+2×10×0+1×1+2×1==2323⏟2×2
В⏟3×2×А⏟2×3=100111×121012=1×1+0×01×2+0×11×1+0×20×1+1×00×2+1×10×1+1×21×1+1×01×2+1×11×1+1×2=121012133⏟3×3
Произведение АВ и ВА найдены, но являются матрицами разных размеров: АВ не равна ВА.
Свойства умножения матриц
Свойства умножения матриц:
- (АВ)С = А(ВС) — ассоциативность умножения матриц;
- А(В+С) = АВ + АС — дистрибутивность умножения;
- (А+В)С = АС + ВС — дистрибутивность умножения;
- λ(АВ)=(λА)В
Проверяем свойство №1: (АВ)С = А(ВС):
(А×В)×А=1234×5678×1002=19224350×1002=194443100,
А(В×С)=1234×56781002=1234×512716=194443100.
Пример 2Проверяем свойство №2: А(В+С) = АВ + АС:
А×(В+С)=1234×5678+1002=1234×66710=20264658,
АВ+АС=1234×5678+1234×1002=19224350+1438=20264658.
Произведение трех матриц
Произведение трех матриц АВС вычисляют 2-мя способами:
- найти АВ и умножить на С: (АВ)С;
- либо найти сначала ВС, а затем умножить А(ВС).
Перемножить матрицы 2-мя способами:
4375×-289338-126×7321
Алгоритм действий:
- найти произведение 2-х матриц;
- затем снова найти произведение 2-х матриц.
1). АВ=4375×-289338-126=4(-28)+3×384×93+3(-126)7(-28)+5×387×93+5(-126)=2-6-621
2). АВС=(АВ)С=2-6-6217321=2×7-6×22×3-6×1-6×7+21×2-6×3+21×1=2003.
Используем формулу АВС=(АВ)С:
1). ВС=-289338-1267321=-28×7+93×2-28×3+93×138×7-126×238×3-126×1=-10914-12
2). АВС=(АВ)С=7321-10914-12=4(-10)+3×144×9+3(-12)7(-10)+5×147×9+5(-12)=2003
Ответ: 4375-289338-1267321=2003
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать заданиеУмножение матрицы на число
Определение 2Произведение матрицы А на число k — это матрица В=Аk того же размера, которая получена из исходной умножением на заданное число всех ее элементов:
bi,j=k×ai,j
Свойства умножения матрицы на число:
- 1×А=А
- 0×А=нулевая матрица
- k(A+B)=kA+kB
- (k+n)A=kA+nA
- (k×n)×A=k(n×A)
Найдем произведение матрицы А=4290 на 5.
Решение:
5А=542905×45×25×95×0=2010450
Умножение матрицы на вектор
Определение 3Чтобы найти произведение матрицы и вектора, необходимо умножать по правилу «строка на столбец»:
- если умножить матрицу на вектор-столбец число столбцов в матрице должно совпадать с числом строк в векторе-столбце;
- результатом умножения вектора-столбца является только вектор-столбец:
АВ=а11а12⋯а1nа21а22⋯а2n⋯⋯⋯⋯аm1аm2⋯аmnb1b2⋯b1n=a11×b1+a12×b2+⋯+a1n×bna21×b1+a22×b2+⋯+a2n×bn⋯⋯⋯⋯am1×b1+am2×b2+⋯+amn×bn=c1c2⋯c1m
- если умножить матрицу на вектор-строку, то умножаемая матрица должна быть исключительно вектором-столбцом, причем количество столбцов должно совпадать с количеством столбцов в векторе-строке:
АВ=аа⋯аbb⋯b=a1×b1a1×b2⋯a1×bna2×b1a2×b2⋯a2×bn⋯⋯⋯⋯an×b1an×b2⋯an×bn=c11c12⋯c1nc21c22⋯c2n⋯⋯⋯⋯cn1cn2⋯cnn
Пример 5Найдем произведение матрицы А и вектора-столбца В:
АВ=240-213-10112-1=2×1+4×2+0×(-1)-2×1+1×2+3×(-1)-1×1+0×2+1×(-1)=2+8+0-2+2-3-1+0-1=10-3-2
Пример 6Найдем произведение матрицы А и вектора-строку В:
А=320-1, В=-1102
Решение:
АВ=3201×-1102=3×(-1)3×13×03×22×(-1)2×12×02×20×(-1)0×10×00×21×(-1)1×11×01×2=-3306-22040000-1102
Ответ: АВ=-3306-22040000-1102
Как решать матрицы
Математическая матрица представляет собой упорядоченную таблицу элементов. Размерность матрицы определяется числом ее строк m и столбцов n. Под решением матриц понимается множество обобщающих операций, производимых над матрицами. Различают несколько типов матриц, к некоторым из них не применим ряд операций. Существует операция сложения для матриц с одинаковой размерностью. Произведение двух матриц находится, только если они согласованны. Для любой матрицы определяется детерминант. Также матрицу можно транспонировать и определить минор ее элементов.
Размерность матрицы определяется числом ее строк m и столбцов n. Под решением матриц понимается множество обобщающих операций, производимых над матрицами. Различают несколько типов матриц, к некоторым из них не применим ряд операций. Существует операция сложения для матриц с одинаковой размерностью. Произведение двух матриц находится, только если они согласованны. Для любой матрицы определяется детерминант. Также матрицу можно транспонировать и определить минор ее элементов.Запишите заданные . Определите их размерность. Для этого посчитайте количество столбцов n и строк m. Если для одной матрицы m = n, матрица считается квадратной. Если все элементы матрицы равны нулю – матрица нулевая. Определите главную диагональ матриц. Ее элементы располагаются с левого верхнего угла матрицы до правого нижнего. Вторая, обратная диагональ матрицы является побочной.
Проведите транспонирование матриц. Для этого замените в каждой матрице элементы строк на элементы столбцов относительно главной диагонали. Элемент а21 станет элементом а12 матрицы и наоборот. В итоге из каждой исходной матрицы получится новая транспонированная матрица.
Элемент а21 станет элементом а12 матрицы и наоборот. В итоге из каждой исходной матрицы получится новая транспонированная матрица.
Сложите заданные матрицы, если они имеют одинаковую размерность m х n. Для этого возьмите первый элемент матрицы а11 и сложите его с аналогичным элементом b11 второй матрицы. Результат сложения запишите в новую матрицу на ту же позицию. Затем сложите элементы а12 и b12 обоих матриц. Таким образом заполните все строки и столбцы суммирующей матрицы.
Определите, являются ли заданные матрицы согласованными. Для этого сравните число строк n в первой матрицы и число столбцов m второй матрицы. Если они равны, выполните произведение матриц. Для этого попарно умножьте каждый элемент строки первой матрицы на соответствующий элемент столбца второй матрицы. После чего найдите сумму этих произведений. Таким образом, первый элемент результирующей матрицы g11 = а11* b11 + а12*b21 + а13*b31 + … + а1m*bn1. Выполните умножение и сложение всех произведений и заполните результирующую матрицу G.
Найдите определитель или детерминант для каждой заданной матрицы. Для матриц второго порядка — размерностью 2 на 2 – определитель находится, как разница произведений элементов главной и побочной диагоналей матрицы. Для трехмерной матрицы формула определителя: D = а11* а22*а33 + а13* а21*а32 + а12* а23*а31 — а21* а12*а33 — а13* а22*а31 — а11* а32*а23.
Для нахождения минора определенного элемента вычеркните из матрицы строку и столбец, где расположен данный элемент. Затем определите детерминант полученной матрицы. Это и будет минор элемента.
Линейная алгебра на Python. [Урок 5]. Обратная матрица и ранг матрицы
Пятый урок посвящен нахождению обратной матрицы, ее свойствам, а также определению ранга матрицы
Обратная матрицаОбратной матрицей A-1 матрицы A называют матрицу, удовлетворяющую следующему равенству:
где – E это единичная матрица.
Для того, чтобы у квадратной матрицы A была обратная матрица необходимо и достаточно чтобы определитель |A| был не равен нулю. Введем понятие союзной матрицы. Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.
Введем понятие союзной матрицы. Союзная матрица A* строится на базе исходной A путем замены всех элементов матрицы A на их алгебраические дополнения.
Исходная матрица:
Союзная ей матрица A*:
Транспонируя матрицу A*, мы получим так называемую присоединенную матрицу A*T:
Теперь, зная как вычислять определитель и присоединенную матрицу, мы можем определить матрицу A-1, обратную матрице A:
➣ Численный пример
Пример вычисления обратной матрицы. Пусть дана исходная матрица A, следующего вида:
Для начала найдем определитель матрицы A:
Как видно из приведенных вычислений, определитель матрицы не равен нулю, значит у матрицы A есть обратная. Построим присоединенную матрицу, для этого вычислим алгебраические дополнения для каждого элемента матрицы A:
Союзная матрица будет иметь следующий вид:
Присоединенная матрица получается из союзной путем транспонирования:
Находим обратную матрицу:
➤ Пример на Python
Решим задачу определения обратной матрицы на Python. Для получения обратной матрицы будем использовать функцию inv():
Для получения обратной матрицы будем использовать функцию inv():
>>> A = np.matrix('1 -3; 2 5')
>>> A_inv = np.linalg.inv(A)
>>> print(A_inv)
[[ 0.45454545 0.27272727]
[-0.18181818 0.09090909]]Рассмотрим свойства обратной матрицы.
Свойство 1. Обратная матрица обратной матрицы есть исходная матрица:
➤Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> A_inv = np.linalg.inv(A)
>>> A_inv_inv = np.linalg.inv(A_inv)
>>> print(A)
[[1. -3.]
[2. 5.]]
>>> print(A_inv_inv)
[[1. -3.]
[2. 5.]]Свойство 2. Обратная матрица транспонированной матрицы равна транспонированной матрице от обратной матрицы:
➤ Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
-3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]Свойство 3. Обратная матрица произведения матриц равна произведению обратных матриц:
➤ Пример на Python
>>> A = np.matrix('1. -3.; 2. 5.')
>>> B = np.matrix('7. 6.; 1. 8.')
>>> L = np.linalg.inv(A.dot(B))
>>> R = np.linalg.inv(B).dot(np.linalg.inv(A))
>>> print(L)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]]
>>> print(R)
[[ 0.09454545 0.03272727]
[-0.03454545 0.00727273]]Ранг матрицыРанг матрицы является еще одной важной численной характеристикой. Рангом называют максимальное число линейно независимых строк (столбцов) матрицы. Линейная независимость означает, что строки (столбцы) не могут быть линейно выражены через другие строки (столбцы). Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.
Ранг матрицы можно найти через ее миноры, он равен наибольшему порядку минора, который не равен нулю. Существование ранга у матрицы не зависит от того квадратная она или нет.
Вычислим ранг матрицы с помощью Python. Создадим единичную матрицу:
>>> m_eye = np.eye(4) >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 1.]]
Ранг такой матрицы равен количеству ее столбцов (или строк), в нашем случае ранг будет равен четырем, для его вычисления на Python воспользуемся функцией matrix_rank():
>>> rank = np.linalg.matrix_rank(m_eye) >>> print(rank) 4
Если мы приравняем элемент в нижнем правом углу к нулю, то ранг станет равен трем:
>>> m_eye[3][3] = 0 >>> print(m_eye) [[1. 0. 0. 0.] [0. 1. 0. 0.] [0. 0. 1. 0.] [0. 0. 0. 0.]] >>> rank = np.P.S.linalg.matrix_rank(m_eye) >>> print(rank) 3
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Использование матриц при решении системы уравнений (Алгебра 2, Матрицы) — Mathplanet
Матрицы могут использоваться для решения систем уравнений, но сначала нужно освоить, чтобы найти обратную матрицу, C -1 .
Матрицы C будут иметь обратную матрицу C -1 тогда и только тогда, когда определитель матрицы C не равен нулю.
$$ if \: c = \ begin {bmatrix} a & b \\ c & d \ end {bmatrix} \; \; \; \ begin {vmatrix} a & b \\ c & d \ end {vmatrix} \ neq 0 \\ \\ \\ then \: C ^ {- 1} = \ frac {1} {ad-bc} \ begin { bmatrix} d & -b \\ -c & a \ end {bmatrix} $$
Теперь мы на примере покажем, как решать системы уравнений с использованием матриц и обратных матриц. {- 1} = \ frac {1} {3 \ cdot -1-1 \ cdot 2} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} = $$
{- 1} = \ frac {1} {3 \ cdot -1-1 \ cdot 2} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} = $$
$$ = — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} $$
Следующий шаг — умножить обе части матричного уравнения на обратную матрицу:
$$ — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} \ begin {bmatrix} 3 & 1 \\ 2 & -1 \ end {bmatrix } \ cdot \ begin {bmatrix} x \\ y \\ \ end {bmatrix} = — \ frac {1} {5} \ begin {bmatrix} -1 & -1 \\ -2 & 3 \ end {bmatrix} \ begin {bmatrix} 5 \\ 0 \ end {bmatrix} $$
$$ — \ frac {1} {5} \ begin {bmatrix} -5 & 0 \\ 0 & -5 \ end {bmatrix} \ cdot \ begin {bmatrix} x \\ y \ end {bmatrix} = — \ frac {1} {5} \ begin {bmatrix} -5 \\ -10 \ end {bmatrix} $$
$$ \ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix} \ cdot \ begin {bmatrix} x \\ y \ end {bmatrix} = \ begin {bmatrix} 1 \\ 2 \ end { bmatrix} $$
Наше решение — (1,2), самый простой способ проверить, правы ли мы, — это подставить наши значения в наши исходные уравнения.
Видеоурок
Пример выше в видеоформате.
Решение матричных уравнений
А матричное уравнение уравнение, в котором переменная обозначает матрица .
Вы можете решить более простые матричные уравнения, используя матрица сложения а также скалярное умножение .
Примеры 1:
Решить для матрицы Икс : Икс + [ 3 2 1 0 ] знак равно [ 6 3 7 — 1 ]
Икс + [ 3 2 1 0 ] — [ 3 2 1 0 ] знак равно [ 6 3 7 — 1 ] — [ 3 2 1 0 ] Икс + [ 0 0 0 0 ] знак равно [ 6 — 3 3 — 2 7 — 1 — 1 — 0 ] Икс знак равно [ 3 1 6 — 1 ]
Примеры 2:
Решить для матрицы Икс : Икс — [ — 9 — 3 6 0 ] знак равно [ 4 0 12 — 10 ]
Икс — [ — 9 — 3 6 0 ] знак равно [ 4 0 12 — 10 ] Икс — [ — 9 — 3 6 0 ] + [ — 9 — 3 6 0 ] знак равно [ 4 0 12 — 10 ] + [ — 9 — 3 6 0 ] Икс — [ 0 0 0 0 ] знак равно [ 4 + ( — 9 ) 0 + ( — 3 ) 12 + 6 — 10 + 0 ] Икс знак равно [ — 5 — 3 18 — 10 ]
Решение систем линейных уравнений с использованием матриц: Матричные уравнения можно использовать для
решать системы линейных уравнений
используя левую и правую части уравнений.
Примеры 3:
Решите систему уравнений с помощью матриц: { 7 Икс + 5 y знак равно 3 3 Икс — 2 y знак равно 22
7 Икс + 5 y знак равно 3 3 Икс — 2 y знак равно 22 → [ 7 Икс + 5 y 3 Икс — 2 y ] знак равно [ 3 22 ]
Запишите матрицу слева как произведение коэффициентов и переменных.
[ 7 5 3 — 2 ] [ Икс y ] знак равно [ 3 22 ]
↑ ↑ ↑
коэффициент Переменная постоянный матрица матрица матрица
Сначала найдите обратную матрицу коэффициентов. Обратное
[
7
5
3
—
2
]
является
Обратное
[
7
5
3
—
2
]
является
1 7 ( — 2 ) — ( 3 ) ( 5 ) [ — 2 — 5 — 3 7 ] знак равно — 1 29 [ — 2 — 5 — 3 7 ] знак равно [ 2 29 5 29 3 29 — 7 29 ]
Затем умножьте каждую сторону матричного уравнения на
обратная матрица
. Поскольку матричное умножение нет коммутативной, обратная матрица должна быть слева на каждый сторона матричного уравнения.
Поскольку матричное умножение нет коммутативной, обратная матрица должна быть слева на каждый сторона матричного уравнения.
[ 2 29 5 29 3 29 — 7 29 ] [ 7 5 3 — 2 ] [ Икс y ] знак равно [ 2 29 5 29 3 29 — 7 29 ] [ 3 22 ]
[ 1 0 0 1 ] [ Икс y ] знак равно [ 4 — 5 ]
В
единичная матрица
слева подтверждает, что обратная матрица была рассчитана правильно.
[ Икс y ] знак равно [ 4 — 5 ]
Решение ( 4 , — 5 ) .
Использование матриц для решения систем уравнений
Матричные уравнения
Матрицымогут использоваться для компактного написания и работы с системами множественных линейных уравнений.
Цели обучения
Определить, как матрицы могут представлять систему уравнений
Основные выводы
Ключевые моменты
- Если [latex] A [/ latex] является матрицей [latex] m \ times n [/ latex], а [latex] x [/ latex] обозначает вектор-столбец (например, [latex] n \ times 1 [/ latex] матрица) [латекс] n [/ latex] переменных [latex] x_1, x_2,…, x_n [/ latex] и [latex] b [/ latex] представляет собой [латекс] m \ times 1 [/ latex ] Вектор-столбец, то матричное уравнение имеет вид: [latex] Ax = b [/ latex].

Ключевые термины
- матрица : прямоугольное расположение чисел или членов, имеющее различное использование, такое как преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.
Матрицы можно использовать для компактного написания и работы с системами уравнений. Как мы узнали в предыдущих разделах, матрицами можно манипулировать так же, как и нормальным уравнением. Это очень полезно, когда мы начинаем работать с системами уравнений.Полезно понять, как организовать матрицы для решения этих систем.
Написание системы уравнений с матрицами
Можно решить эту систему, используя метод исключения или замены, но также можно сделать это с помощью матричной операции. Прежде чем приступить к настройке матриц, важно сделать следующее:
- Убедитесь, что все уравнения написаны одинаково, то есть переменные должны быть в одном порядке.

- Убедитесь, что одна сторона уравнения — это только переменные и их коэффициенты, а другая сторона — просто константы.
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: [latex] X [/ latex] — это матрица, представляющая переменные системы, а [latex] B [/ latex] — это матрица, представляющая константы. Используя матричное умножение, мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как:
[латекс] \ displaystyle A \ cdot X = B [/ латекс]
Чтобы решить систему линейных уравнений с использованием обратной матрицы, пусть [latex] A [/ latex] будет матрицей коэффициентов, пусть [latex] X [/ latex] будет переменной матрицей, и пусть [latex] B [/ latex ] — постоянная матрица.
Учитывая систему:
[латекс] \ displaystyle \ begin {align} x + 8y & = 7 \\ 2x-8y & = — 3 \ end {align} [/ latex]
Матрица коэффициентов:
[латекс] A = \ begin {bmatrix} 1 & 8 \\ 2 & -8 \ end {bmatrix} [/ latex]
Матрица переменных:
[латекс] \ displaystyle X = \ begin {bmatrix} x \\ y \ end {bmatrix} [/ latex]
Постоянная матрица:
[латекс] \ displaystyle B = \ begin {bmatrix} 7 \\ -3 \ end {bmatrix} [/ latex]
Таким образом, чтобы решить систему [latex] AX = B [/ latex], для [latex] X [/ latex] умножьте обе стороны на обратную величину [latex] A [/ latex], и мы получим решение:
[латекс] \ Displaystyle X = (A ^ {- 1}) B [/ латекс]
Если существует обратный [латекс] \ left (A ^ {- 1} \ right) [/ latex], эта формула решит систему.
Если матрица коэффициентов необратима, система может быть несовместимой и не иметь решения, или быть зависимой и иметь бесконечно много решений.
Матрицы и операции со строками
Две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.
Цели обучения
Объясните, как использовать операции со строками и почему они создают эквивалентные матрицы
Основные выводы
Ключевые моменты
- Элементарная операция со строкой — это любое из следующих действий: переключение строк (перестановка двух строк в матрице), умножение строк (умножение строки матрицы на ненулевую константу) или сложение строк (добавление к одной строке матрицы до некоторого числа, кратного другой строке).
- Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы.

Ключевые термины
- пространство строки : набор всех возможных линейных комбинаций его векторов-строк.
- эквивалент строки : В линейной алгебре, когда одна матрица может быть заменена другой последовательностью элементарных операций со строкой.
Элементарные операции со строками (ERO)
В линейной алгебре две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.В качестве альтернативы, две матрицы [latex] m \ times n [/ latex] эквивалентны строкам тогда и только тогда, когда они имеют одинаковое пространство строк. Пространство строк матрицы представляет собой набор всех возможных линейных комбинаций ее векторов-строк. Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы. Две матрицы одинакового размера эквивалентны строкам тогда и только тогда, когда соответствующие однородные системы имеют одинаковый набор решений или, что эквивалентно, матрицы имеют одно и то же нулевое пространство. Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).
Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).
Операция элементарной строки — это любой из следующих трех ходов:
- Переключение строк (перестановка): поменять местами две строки матрицы.
- Умножение строк (масштаб): умножение строки матрицы на ненулевую константу.
- Сложение строк (сводная): прибавить к одной строке матрицы несколько значений, кратных другой строке.
Создание эквивалентных матриц с использованием элементарных операций со строками
Поскольку матрица по существу является коэффициентами и константами линейной системы, три операции со строками сохраняют матрицу.Например, замена двух строк просто означает изменение их положения в матрице. Кроме того, при решении системы линейных уравнений методом исключения, умножение строк будет таким же, как умножение всего уравнения на число для получения аддитивных обратных величин, так что переменная сокращается. Наконец, добавление строк аналогично методу исключения, когда для получения переменной выбирается сложение или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод для решения системы уравнений.
Наконец, добавление строк аналогично методу исключения, когда для получения переменной выбирается сложение или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод для решения системы уравнений.
Пример 1: Покажите, что эти две матрицы эквивалентны строкам:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & -1 & 0 \\ 2 & 1 & 1 \ end {pmatrix} \ quad B = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ латекс]
Начните с [latex] A [/ latex], добавьте вторую строку к первой:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 2 & 1 & 1 \ end {pmatrix} [/ latex]
Затем умножьте вторую строку на 3 и вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 3 & 3 & 2 \ end {pmatrix} [/ latex]
Наконец, вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ latex]
Вы можете видеть, что [latex] A = B [/ latex], что мы достигли с помощью серии элементарных операций со строками.
Сокращение строк: решение системы линейных уравнений
В редукторе рядов, линейная система:
[латекс] \ displaystyle x + 3y-2z = 5 \\ 3x + 5y + 6z = 7 \ 2x + 4y + 3z = 8 [/ latex]
Представлен в виде расширенной матрицы:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {pmatrix} [/ latex]
Затем эта матрица модифицируется с использованием операций с элементарными строками до тех пор, пока она не достигнет уменьшенной формы эшелона строк.
Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.
Существует несколько конкретных алгоритмов сокращения строк расширенной матрицы, простейшими из которых являются исключение Гаусса и исключение Гаусса-Жордана. Это вычисление может быть выполнено вручную (с использованием трех типов ERO) или на калькуляторе с использованием матричной функции «rref» (сокращенная форма эшелона строк).
Окончательная матрица представлена в виде уменьшенного ряда строк и представляет систему [латекс] x = -15 [/ latex], [latex] y = 8 [/ latex] [latex] z = 2 [/ latex].
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 0 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {pmatrix} [/ latex]
Упрощение матриц с помощью операций со строками
Используя элементарные операции, метод исключения Гаусса приводит матрицы к форме эшелона строк.
Цели обучения
Используйте операции с элементарными строками, чтобы представить матрицу в упрощенной форме
Основные выводы
Ключевые моменты
- Поскольку элементарные операции со строками сохраняют пространство строк матрицы, пространство строк формы эшелона строк такое же, как и у исходной матрицы.
- Существует три типа операций с элементарными строками: меняют местами две строки, умножают строку на ненулевой скаляр и добавляют к одной строке скалярное значение, кратное другой.

- На практике обычно не рассматривают системы в терминах уравнений, а вместо этого используют расширенную матрицу (которая также подходит для компьютерных манипуляций).
Ключевые термины
- расширенная матрица : Матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же элементарных операций со строками для каждой из данных матриц.
С помощью конечной последовательности элементарных операций со строками, называемых исключением по Гауссу, любую матрицу можно преобразовать в форму эшелона строк. Это преобразование необходимо для решения системы линейных уравнений.
Прежде чем углубляться в детали, следует упомянуть несколько ключевых терминов:
- Расширенная матрица : расширенная матрица — это матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же операций с элементарной строкой для каждой из данных матриц.

- Форма верхнего треугольника : Квадратная матрица называется верхней треугольной, если все элементы ниже главной диагонали равны нулю. Треугольная матрица — это нижняя или верхняя треугольная матрица. Матрица, имеющая одновременно верхний и нижний треугольники, является диагональной матрицей.
- Элементарные операции со строками : Поменять местами строки, добавить строки или умножить строки.
Исключение по Гауссу
- Напишите расширенную матрицу для линейных уравнений.
- Используйте элементарные операции со строками в расширенной матрице [latex] [A | b] [/ latex], чтобы преобразовать [latex] A [/ latex] в форму верхнего треугольника. Если на диагонали находится ноль, переключайте строки, пока на его месте не окажется ненулевое значение.
- Используйте обратную замену, чтобы найти решение.
Пример 1: Решите систему методом исключения Гаусса:
[латекс] \ displaystyle 2x + y-z = 8 \\ -3x-y + 2z = -11 \ -2x + y + 2z = -3 [/ latex]
Запишите расширенную матрицу:
[латекс] \ left [\ begin {array} {rrr | r} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \ end {array} \ right] [/ latex]
Используйте элементарные операции со строками, чтобы уменьшить матрицу до уменьшенной формы эшелона строк:
[латекс] \ left [\ begin {array} {rrr | r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \ end {array} \ right ] [/ латекс]
Используя элементарные операции со строками для получения сокращенной формы эшелона строк (‘rref’ в калькуляторе), решение системы отображается в последнем столбце: [latex] x = 2, y = 3, z = -1 [/ latex] .
Решение систем линейных уравнений с использованием матриц
Если нужно, просмотрите матрицы , матричные операции со строками а также решение систем линейных уравнений перед прочтением этой страницы.
В матричный метод решения систем линейных уравнений — это просто метод устранения в маскировке. При использовании матриц запись становится немного проще.
Предположим, у вас есть система линейных уравнений, например:
{ 3 Икс + 4 y знак равно 5 2 Икс — y знак равно 7
Первый шаг — преобразовать это в матрицу.Убедитесь, что все уравнения имеют стандартную форму
(
А
Икс
+
B
y
знак равно
C
)
, и используйте коэффициенты каждого уравнения для формирования каждой строки матрицы. Это может помочь вам разделить правый столбец пунктирной линией.
Это может помочь вам разделить правый столбец пунктирной линией.
[ 3 4 2 — 1 | 5 7 ]
Далее мы используем матричные операции со строками изменить 2 × 2 матрицу слева на единичная матрица .Во-первых, мы хотим получить ноль в строке 1 , Столбец 2 . Итак, добавляем 4 раз Строка 2 грести 1 .
[ 11 0 2 — 1 | 33 7 ] → добавлен ( 4 × Строка 2 ) к Строка 1
Далее мы хотим
1
в верхнем левом углу.
[ 1 0 2 — 1 | 3 7 ] → разделенный Строка 1 от 11
Теперь нам нужен ноль в нижнем левом углу.
[ 1 0 0 — 1 | 3 1 ] → добавлен ( — 2 × Строка 1 ) к Строка 2
Наконец, мы хотим
1
в строке
2
, Столбец
2
.
[ 1 0 0 1 | 3 — 1 ] → умноженный Строка 2 от — 1
Теперь, когда у нас есть 2 × 2 Слева единичная матрица, мы можем считать решения из правого столбца:
Икс знак равно 3 y знак равно — 1
Тот же метод можно использовать для
п
линейные уравнения в
п
неизвестные; в этом случае вы создадите
п
×
(
п
—
1
)
матрица и используйте операции со строками матрицы, чтобы получить тождество
п
×
п
матрица слева.
Важная заметка: Если уравнения, представленные исходной матрицей, представляют собой параллельные линии, вы не сможете получить единичную матрицу, используя операции со строками. В этом случае решения либо не существует, либо существует бесконечно много решений системы.
матричных уравнений | Суперпроф
Чтобы понять матричные уравнения, вы должны знать, как умножить две матрицы.Допустим, вам показан результат умножения двух матриц (
), и вас попросят найти матрицу B, и вам предоставлены матрицы A и C, как вы их найдете? С помощью матричного уравнения. В матричном уравнении неизвестное — это матрица. Это означает, что вы обозначите неизвестную матрицу как матрица X .A · X = B
Чтобы решить, убедитесь, что матрица обратима, если это так, предварительно умножьте (умножьте влево) обе стороны на матрицу, обратную A.
Если уравнение имеет тип X · A = B , члены должны умножаться после умножения вправо, поскольку умножение матриц не является коммутативным.
1. Учитывая матрицы
. Решите уравнение: A · X = BНайдите определитель указанной выше матрицы.
, это означает, что существует обратный2.Учитывая матрицы
. Решите уравнение: X · A + B = C, это означает, что существует обратная00053. Решите матричное уравнение:
A · X + 2 · B = 3 · C
, это означает, что существует обратное 4. Решите матричное уравнение:
Решите матричное уравнение:
преобразовать систему уравнений в линейную систему из матричное уравнение, а затем решено.
Нужен учитель математики?
Понравилась статья?
Загрузка…Хамза
Привет! Я Хамза и я из Пакистана. Мои хобби — чтение, письмо и игра в шахматы. В настоящее время я учусь на программе бакалавриата по химической инженерии.
Решение матричных уравнений за один этап с помощью резистивных матриц точек пересечения
Значение
Линейная алгебра используется практически во всех научных и инженерных дисциплинах, например. ж., физика, статистика, машинное обучение и обработка сигналов. Решение матричных уравнений, таких как линейная система или уравнение с собственным вектором, выполняется путем факторизации матриц или итерационного умножения матриц на обычных компьютерах, что требует больших вычислительных ресурсов. Вычисления в оперативной памяти с аналоговой резистивной памятью продемонстрировали высокую эффективность использования времени и энергии за счет реализации умножения матрицы на вектор за один шаг по закону Ома и закону Кирхгофа. Однако решение матричных уравнений за одну операцию остается открытой проблемой.Здесь мы показываем, что схема обратной связи с перекрестной резистивной памятью может решать алгебраические задачи, такие как системы линейных уравнений, собственные векторы матриц и дифференциальные уравнения, всего за один шаг.
ж., физика, статистика, машинное обучение и обработка сигналов. Решение матричных уравнений, таких как линейная система или уравнение с собственным вектором, выполняется путем факторизации матриц или итерационного умножения матриц на обычных компьютерах, что требует больших вычислительных ресурсов. Вычисления в оперативной памяти с аналоговой резистивной памятью продемонстрировали высокую эффективность использования времени и энергии за счет реализации умножения матрицы на вектор за один шаг по закону Ома и закону Кирхгофа. Однако решение матричных уравнений за одну операцию остается открытой проблемой.Здесь мы показываем, что схема обратной связи с перекрестной резистивной памятью может решать алгебраические задачи, такие как системы линейных уравнений, собственные векторы матриц и дифференциальные уравнения, всего за один шаг.
Abstract
Обычные цифровые компьютеры могут выполнять расширенные операции с помощью последовательности элементарных булевых функций из 2 или более битов. В результате сложные задачи, такие как решение линейной системы или решение дифференциального уравнения, требуют большого количества вычислительных шагов и широкого использования модулей памяти для хранения отдельных битов.Для ускорения выполнения таких сложных задач вычисления в памяти с резистивной памятью представляют собой многообещающее направление благодаря хранению аналоговых данных и физическим вычислениям в памяти. Здесь мы показываем, что массив точек пересечения резистивных запоминающих устройств может напрямую решать систему линейных уравнений или находить собственные векторы матрицы. Эти операции выполняются всего за один шаг благодаря физическим вычислениям по законам Ома и Кирхгофа, а также благодаря подключению с отрицательной обратной связью в схеме коммутации.Алгебраические задачи демонстрируются на оборудовании и применяются к классическим вычислительным задачам, таким как ранжирование веб-страниц и решение уравнения Шредингера за один шаг.
В результате сложные задачи, такие как решение линейной системы или решение дифференциального уравнения, требуют большого количества вычислительных шагов и широкого использования модулей памяти для хранения отдельных битов.Для ускорения выполнения таких сложных задач вычисления в памяти с резистивной памятью представляют собой многообещающее направление благодаря хранению аналоговых данных и физическим вычислениям в памяти. Здесь мы показываем, что массив точек пересечения резистивных запоминающих устройств может напрямую решать систему линейных уравнений или находить собственные векторы матрицы. Эти операции выполняются всего за один шаг благодаря физическим вычислениям по законам Ома и Кирхгофа, а также благодаря подключению с отрицательной обратной связью в схеме коммутации.Алгебраические задачи демонстрируются на оборудовании и применяются к классическим вычислительным задачам, таким как ранжирование веб-страниц и решение уравнения Шредингера за один шаг.
Задачи линейной алгебры, такие как решение систем линейных уравнений и вычисление собственных векторов матриц, лежат в основе современных научных вычислений и задач, требующих обработки большого количества данных. Традиционно эти проблемы в форме матричных уравнений решаются матричными факторизациями или итеративным матричным умножением (1, 2), которые являются дорогостоящими в вычислительном отношении с полиномиальной временной сложностью, например.г., O ( N 3 ), где N — размер проблемы. Поскольку обычные компьютеры все чаще сталкиваются с ограничениями масштабирования технологии комплементарного металл-оксид-полупроводник (КМОП) (3), а также из-за затрат энергии и задержки при перемещении данных между памятью и вычислительными блоками (4), улучшая вычисления производительность с увеличением аппаратных ресурсов становится сложной и неэкономичной. Чтобы обойти эти фундаментальные ограничения, вычисления в памяти недавно стали многообещающим методом для проведения вычислений на месте, т.е.е., в блоке памяти (5). Одним из примеров являются вычисления в массивах точек пересечения, которые могут ускорить умножение матрицы на вектор (MVM) по закону Ома и закону Кирхгофа с аналоговой и реконфигурируемой резистивной памятью (5⇓⇓ – 8).
Традиционно эти проблемы в форме матричных уравнений решаются матричными факторизациями или итеративным матричным умножением (1, 2), которые являются дорогостоящими в вычислительном отношении с полиномиальной временной сложностью, например.г., O ( N 3 ), где N — размер проблемы. Поскольку обычные компьютеры все чаще сталкиваются с ограничениями масштабирования технологии комплементарного металл-оксид-полупроводник (КМОП) (3), а также из-за затрат энергии и задержки при перемещении данных между памятью и вычислительными блоками (4), улучшая вычисления производительность с увеличением аппаратных ресурсов становится сложной и неэкономичной. Чтобы обойти эти фундаментальные ограничения, вычисления в памяти недавно стали многообещающим методом для проведения вычислений на месте, т.е.е., в блоке памяти (5). Одним из примеров являются вычисления в массивах точек пересечения, которые могут ускорить умножение матрицы на вектор (MVM) по закону Ома и закону Кирхгофа с аналоговой и реконфигурируемой резистивной памятью (5⇓⇓ – 8). MVM в памяти был адаптирован для нескольких задач, включая сжатие изображений (5), разреженное кодирование (6) и обучение глубоких нейронных сетей (7, 8). Однако решение матричных уравнений, таких как линейная система Ax = b , за одну операцию остается открытой проблемой.Здесь мы показываем, что схема обратной связи, включающая реконфигурируемую резистивную решетку в точках пересечения, может обеспечить решение алгебраических задач, таких как системы линейных уравнений, собственные векторы матрицы и дифференциальные уравнения, всего за один шаг.
MVM в памяти был адаптирован для нескольких задач, включая сжатие изображений (5), разреженное кодирование (6) и обучение глубоких нейронных сетей (7, 8). Однако решение матричных уравнений, таких как линейная система Ax = b , за одну операцию остается открытой проблемой.Здесь мы показываем, что схема обратной связи, включающая реконфигурируемую резистивную решетку в точках пересечения, может обеспечить решение алгебраических задач, таких как системы линейных уравнений, собственные векторы матрицы и дифференциальные уравнения, всего за один шаг.
Резистивная память — это двухполюсные элементы, которые могут изменять свою проводимость в ответ на приложенное напряжение (9, 10). Благодаря своему энергонезависимому и реконфигурируемому поведению резистивные запоминающие устройства широко исследовались и разрабатывались для запоминающих устройств (11, 12), логики с отслеживанием состояния (13⇓ – 15), вычислений в памяти (5, 6, 16, 17), и нейроморфные вычислительные приложения (7, 8, 18, 19). Резистивная память включает в себя различные концепции устройств, такие как резистивная коммутационная память (RRAM, ссылки 9⇓⇓ – 12), память с изменением фазы (PCM, ссылка 20) и магнитная память с передачей вращения по крутящему моменту (21). Реализованные в архитектуре массива точек пересечения, резистивная память может естественным образом ускорить операции с большим объемом данных с улучшенной эффективностью времени / энергии по сравнению с классическими цифровыми вычислениями (5, 6, 17). Также недавно было показано, что итерированные операции MVM с резистивными массивами точек пересечения могут решать системы линейных уравнений в сочетании с цифровыми компьютерами с плавающей запятой (22).Чем выше желаемая точность решения, тем больше итераций требуется для завершения операции. Однако итерация поднимает фундаментальный предел для достижения высокой вычислительной производительности с точки зрения энергии и задержки.
Резистивная память включает в себя различные концепции устройств, такие как резистивная коммутационная память (RRAM, ссылки 9⇓⇓ – 12), память с изменением фазы (PCM, ссылка 20) и магнитная память с передачей вращения по крутящему моменту (21). Реализованные в архитектуре массива точек пересечения, резистивная память может естественным образом ускорить операции с большим объемом данных с улучшенной эффективностью времени / энергии по сравнению с классическими цифровыми вычислениями (5, 6, 17). Также недавно было показано, что итерированные операции MVM с резистивными массивами точек пересечения могут решать системы линейных уравнений в сочетании с цифровыми компьютерами с плавающей запятой (22).Чем выше желаемая точность решения, тем больше итераций требуется для завершения операции. Однако итерация поднимает фундаментальный предел для достижения высокой вычислительной производительности с точки зрения энергии и задержки.
Результаты
Схемы пересечения для решения системы линейных уравнений.

Рис. 1 A показывает предлагаемую схему обратной связи для решения системы линейных уравнений за один шаг, а аппаратная схема на печатной плате показана в приложении SI , рис.S1. Схема представляет собой матрицу узлов RRAM, каждое из которых состоит из пакета металл-изолятор-металл со слоем HfO 2 между верхним электродом из Ti и нижним электродом из C (15). Устройства показывают установленный переход от высокого сопротивления к низкому сопротивлению, когда положительное напряжение выше порогового значения V set применяется к Ti-электроду, и переход сброса от низкого сопротивления к высокому сопротивлению, когда отрицательное напряжение выше порогового значения V сброс применяется к Ti-электроду.Многоуровневая работа также возможна путем выполнения установленного перехода при переменном максимальном (согласованном) токе I C или выполнения перехода в сброс при переменном максимальном напряжении В stop (23), как показано в приложении SI , Рис. S2. Массив точек пересечения 3 × 3 на рисунке может выполнять MVM с разомкнутым контуром, то есть путем приложения вектора напряжения V к столбцам и измерения вектора тока I в строках без соединений строка-столбец, разрешенных посредством операционные усилители (ОУ), которые показаны в приложении SI , рис.S3. Измеренные токи дают скалярное произведение I = A · V между приложенными аналоговыми напряжениями и матрицей A значений проводимости RRAM в матрице точек пересечения. Результаты свидетельствуют о небольшой ошибке, обычно менее 8%, в основном из-за нелинейности проводимости в резистивных устройствах с перекрестными точками. Это соответствует предыдущим результатам, в которых точность MVM оказалась удовлетворительной (5), хотя и не соответствовала полностью цифровым операциям с одинарной и двойной точностью.
S2. Массив точек пересечения 3 × 3 на рисунке может выполнять MVM с разомкнутым контуром, то есть путем приложения вектора напряжения V к столбцам и измерения вектора тока I в строках без соединений строка-столбец, разрешенных посредством операционные усилители (ОУ), которые показаны в приложении SI , рис.S3. Измеренные токи дают скалярное произведение I = A · V между приложенными аналоговыми напряжениями и матрицей A значений проводимости RRAM в матрице точек пересечения. Результаты свидетельствуют о небольшой ошибке, обычно менее 8%, в основном из-за нелинейности проводимости в резистивных устройствах с перекрестными точками. Это соответствует предыдущим результатам, в которых точность MVM оказалась удовлетворительной (5), хотя и не соответствовала полностью цифровым операциям с одинарной и двойной точностью.
Решение систем линейных уравнений с массивом точек пересечения резистивных устройств. ( A ) Схема пересечения для решения линейной системы или инвертирования положительной матрицы. Элементы RRAM (красные цилиндры) расположены в точках пересечения между строками (синие полосы) и столбцами (зеленые полосы). ( Вставка , Справа ) Экспериментальные значения проводимости, отображающие элементы матрицы A . Единицы преобразования между матрицами / векторами с действительным знаком и физическими реализациями были: G 0 = 100 мкс, В 0 = 1 В и I 0 = 100 мкА для проводимости RRAM, входное / выходное напряжение и выходной / входной ток соответственно.Другие случаи также следуют этому соглашению, если не указано иное. ( B ) Схемы для вычисления скалярного произведения I = G · V по закону Ома и для вычисления скалярного деления V = — I / G с помощью TIA. ( C ) Измеренное решение линейной системы с вектором входного тока I = [0,2; 1; 1] I 0 . Экспериментальные выходные напряжения дают решение, очень близкое к аналитическому.( D ) Измеренное решение для линейных систем, а именно выходное напряжение, как функция параметра β , управляющего входным током, задаваемым I = β · [0,2; 1; 1] I 0 с −1 ≤ β ≤ 1. Экспериментальные решения (цветные кружки) сравниваются с аналитическими решениями (цветные линии) системы, что подтверждает точность физического расчета. ( E ) Обратная экспериментальная матрица A −1 , а именно измеренные выходные напряжения в трех последующих экспериментах с входным током I = [1; 0; 0] I 0 , [0; 1; 0] I 0 и [0; 0; 1] I 0 соответственно.Также показано аналитическое решение. ( Вставка ) Матричное произведение AA -1 очень близко к единичной матрице U , таким образом поддерживая экспериментальную инверсию.
Работа MVM является следствием физического закона Ома I = G · В , где G — проводимость устройства, В — приложенное напряжение, а I — измеренный ток ( Рис.1 B , Верх ).С другой стороны, обратная операция V = — I / G может быть получена для заданных I и G , просто нагнетая ток I в заземленном узле резистивного устройства. и измерение потенциала В, во втором узле. Это физическое разделение выполняется трансимпедансным усилителем (TIA) на рис. 1 B ( Bottom ), где ток вводится в узел инвертирующего входа OA, а проводимость обратной связи G соединяет вход и выходные узлы ОА.Дифференциальное входное напряжение В + — В — на ОУ минимизировано высоким коэффициентом усиления ОУ, тем самым устанавливая виртуальное заземление ( В — = 0) на инвертирующем входе. node (24, 25) и включение физического разделения. Это обеспечивает основу для схемы на рис. 1 A , которая решает систему линейных уравнений, выраженную матричной формулой: Ax = b, [1] где A — невырожденная квадратная матрица, отображаемая с поперечными значениями проводимости. -точечные устройства RRAM, b — известный вектор, а x — неизвестный вектор.В этой схеме входные токи I = — b прикладываются к рядам точек пересечения, подключенным к узлам виртуальной земли OA. В результате токи вынуждены автоматически распределяться между резистивными элементами в массиве точек пересечения, чтобы установить выходной потенциал В , удовлетворяющий A · V + I = 0, [2], что подразумевает В = — A −1 · I = x . Схема, аналогичная показанной на рис. 1 A ранее была представлена в отчете International Roadmap for Devices and Systems (25) и предложена исх.26, хотя не было продемонстрировано возможности решения линейной системы с помощью экспериментов или моделирования.
Чтобы продемонстрировать концепцию на рис. 1 A , мы измерили выходные напряжения в матрице точек пересечения RRAM 3 × 3 на рис. 1 A , где также показана матрица проводимости. Все матрицы, принятые в экспериментах в этой работе, приведены в приложении SI, таблица S1. Вектор тока [ I 10 ; I 20 ; I 30 ] с I 10 = 20 мкА, I 20 = 100 мкА, и I 30 = 100 мкА, был применен к строкам массива, и результирующий потенциал в столбцах массива, т.е.е., [ V 10 ; В 20 ; V 30 ], было измерено, как показано на фиг. 1 C . Хорошее согласие (с относительными ошибками в пределах 3%) с аналитическим решением поддерживает функциональность цепи обратной связи, показанной на рис. 1 A для решения матричного уравнения в уравнении. 1 . Схема была дополнительно продемонстрирована путем линейного изменения входных токов в соответствии с I i = β I i 0 , где i = 1, 2 или 3, а β было изменяется равномерно в диапазоне от -1 до 1.Результаты представлены на рис. 1 D , где показаны измеренные выходные напряжения в сравнении с аналитическими решениями x = A -1 b . Ошибка остается ниже 10% для | β | > 0,5 ( SI Приложение , рис. S4). Примечательно, что уравнение. 1 физически решается всего за один шаг благодаря физическому MVM в массиве точек пересечения и соединению обратной связи, заставляющему виртуальное заземление в рядах точек пересечения.
Та же концепция может быть расширена для вычисления инверсии матрицы A , удовлетворяющей AA -1 = U , где U — единичная матрица.Столбец i -й столбца A -1 может быть измерен как выходное напряжение, когда столбец i -й столбец U применяется в качестве входа, таким образом реализуя инверсию матрицы за N шагов. На рис. 1 E показаны измеренные элементы A −1 в сравнении с аналитически решенными элементами обратной матрицы, а относительные ошибки вычислены в приложении SI , рис. S5. Рис. 1 E (, вставка ) показывает, что экспериментальный продукт AA -1 хорошо аппроксимирует U , что дополнительно поддерживает вычисленную инверсию матрицы.
Схема на рис. 1 A — это, по сути, оператор инверсии матрицы, который можно использовать для решения линейных систем и инверсий матриц, в то время как массив точек пересечения без обратной связи является оператором матрицы, который, естественно, может использоваться для выполнить MVM. Поскольку схема инверсии матрицы является системой с отрицательной обратной связью, стабильность выходного напряжения требует, чтобы коэффициент усиления контура ( G контур ) каждого контура обратной связи был отрицательным (27). Анализ показывает, что условие G loop <0 выполняется, когда все знаки диагональных элементов A −1 положительны ( SI Приложение , рис.S6). Следуя этому руководству, была решена система линейных уравнений и инверсия матрицы 5 × 5, при этом матрица была реализована в виде массива дискретных резисторов в точках пересечения. Небольшая относительная погрешность около нескольких процентов в этом идеальном случае с дискретными резисторами свидетельствует о том, что высокая точность может быть достигнута с помощью точных и линейных устройств резистивной памяти ( SI Приложение , рис. S7).
Решение линейной системы с положительными и отрицательными коэффициентами.
Поскольку в резистивном элементе проводимость может быть только положительной, схема на рис.1 может решать только линейные системы с положительной матрицей коэффициентов. Для решения линейных систем с неположительными коэффициентами следует принять схему со смешанной матрицей, показанную на рисунке 2. Здесь матрица A разделена на два массива точек пересечения согласно A = B — C, где B и C оба положительны. На рис.2 A показана реализация массива с двумя точками пересечения, где входной ток I разделен схемой на два компонента I B и I C = I — I B , передаваемый в ряды виртуальной земли B и C , соответственно.Аналоговые инверторы позволяют инвертировать напряжение между столбцами B и C . Исходя из закона Ома и закона тока Кирхгофа, выходное напряжение В OA определяется как B · V + C (−V) + I = 0, [3] или A · V + I = 0, который решает линейную систему уравнения. 1 с I = — b .
Рис. 2.Обращение смешанной матрицы. ( A ) Схема двух массивов точек пересечения для инверсии матриц, где два массива точек пересечения содержат элементы матриц B ( Bottom ) и C ( Top ) с A = B — C .Напряжение в матрице C инвертируется в другой с помощью аналоговых инверторов, в то время как входной ток вводится в линии виртуальной земли и разделяется на две матрицы. ( B ) Измеренные значения матриц A , B и C , при A = B — C . В эксперименте матрица B была реализована в виде массива точек пересечения RRAM, а матрица C была реализована в виде массива точек пересечения дискретных резисторов.( C ) Измеренные значения обратной матрицы A -1 как функция аналитически рассчитанных элементов A -1 . Поскольку A −1 является положительной матрицей, ее можно инвертировать с помощью единственного массива точек пересечения, как показано на рисунке 1. ( D ) Значения проводимости для матрицы A −1 , реализованные в элементах RRAM. , как функция экспериментальных значений A −1 в C .Чтобы устройства работали в области высокой проводимости, была реализована матрица A -1 с G 0 = 500 мкс для проводимости RRAM. ( E ) Измеренные элементы матрицы ( A −1 ) −1 как функция аналитических расчетов. I 0 = 500 мкА и В 0 = 1 В использовались для входного тока и выходного напряжения соответственно. ( F ) Измеренные элементы матрицы ( A −1 ) −1 как функция с исходной матрицей A , демонстрируя замечательную точность, несмотря на накопленные ошибки по двум последовательным процессам инверсии и устройству -процесс программирования.
Мы экспериментально продемонстрировали инверсию смешанной матрицы 3 × 3 A с двумя матрицами B и C , реализованными в массиве RRAM и массиве резисторов, соответственно. Значения A , B и C показаны на рисунке 2 B , а на рисунке 2 C показаны измеренные элементы A −1 как функция аналитического результаты, демонстрирующие хорошую точность. Чтобы дополнительно поддержать инверсию физической матрицы, мы инвертировали A -1 , которая является положительной матрицей, с одним массивом точек пересечения.Для этой цели элементы A -1 были сначала отображены как значения проводимости в массиве RRAM с использованием алгоритма программирования и проверки с ошибкой менее 5% ( SI Приложение , рис. S8). Хотя алгоритм программирования и проверки применялся к отдельному устройству RRAM за раз, массив точек пересечения подходит для параллельного программирования, чтобы значительно сократить время инициализации массива (28, 29). На рис. 2 D показаны измеренные значения проводимости RRAM как функция целевых значений, полученных из экспериментального A -1 на рис.2 С . Инверсия A -1 , т. Е. ( A -1 ) -1 , была вычислена схемой инверсии матриц, показанной на фиг.1 A , что дало результаты на фиг. E . Вычисленное ( A −1 ) −1 сравнивается с исходной матрицей A на рис.2 F , которая поддерживает хорошую точность двойных инверсий ( A −1 ) −1 = А .Относительные ошибки вышеуказанных операций указаны в приложении SI , рис. S9.
Подобно схеме с одиночной точкой пересечения на фиг. 1 A , условие отрицательной обратной связи применяется к смешанной матрице A . Кроме того, поскольку матрица точек пересечения B непосредственно участвует в обратной связи с обратной связью с OA, матрица B также должна удовлетворять условию G loop <0. В качестве предложения для практических приложений. , опорная матрица B , удовлетворяющая условию G loop , может быть принята в схеме со смешанной матрицей, в то время как матрица C может быть свободно расположена с помощью массива точек пересечения RRAM с условием C = B — A .Чтобы продемонстрировать общность этой концепции, одномерное стационарное уравнение Фурье для диффузии тепла было решено с помощью схемы с перекрестными точками ( SI Приложение , рис. S10 и S11). Используя метод конечных разностей, дифференциальное уравнение сначала преобразуется в систему линейных уравнений, где характеристическая матрица A является смешанной трехдиагональной матрицей. Входные токи соответствуют известному термину, а именно рассеиваемой мощности в одномерной структуре.Решение дает профиль температуры вдоль эталонной структуры, которая решает численное уравнение Фурье.
Ключевым параметром для описания устойчивости решения линейной системы является число обусловленности κ матрицы (30). Число обусловленности отражает стабильность решения x при небольших изменениях известного члена b в уравнении. 1 , где чувствительность к возмущениям увеличивается с увеличением числа обусловленности. Чтобы изучить влияние числа обусловленности на решение линейных систем в массивах резистивной памяти, мы смоделировали схемное обращение трех матриц 10 × 10 с увеличением числа обусловленности.Чтобы проверить стабильность решения, случайное изменение 0,1 или -0,1 было добавлено к каждому элементу в члене b уравнения Ax = b , где b — это i -й столбец единичная матрица U , x — это i -й столбец A -1 , а i был прогнут от 1 до 10 для вычисления всей обратной матрицы. Результаты представлены в приложении SI, приложение , рис. S12, что указывает на то, что ошибка вычисления увеличивается с увеличением числа обусловленности матрицы.
Влияние числа обусловленности также было проверено в экспериментах путем выполнения двойного обращения матрицы с большим числом обусловленности ( κ = 16,9) по сравнению с матрицей с κ = 9,5 на рис. 2. Номера условий для всех матриц в эксперименте сведены в SI Приложение , Таблица S1. Как показано в Приложении SI , рис. S13, матрица с большим значением κ успешно инвертируется дважды, хотя ошибки вычислений больше, чем в случае на рис.2 ( SI Приложение , рис. S14). Следует отметить, что рассматриваемые в данной работе матрицы хорошо подготовлены. Для плохо обусловленной матрицы с чрезвычайно высоким числом обусловленности должны потребоваться дополнительные схемы, возможно, включая итерационные алгоритмы уточнения, которые могут поддерживаться обычным цифровым компьютером (22) или реализованы в массиве резистивной памяти (26). Погрешность, вызванная тепловым шумом и дробовым шумом компонентов в схеме пересечения, также увеличивается с увеличением числа условий, хотя представляет гораздо менее значительную проблему ( SI Приложение , рис.S15).
Схемы коммутации для вычисления собственных векторов.
Решение линейной системы в уравнении. 1 можно дополнительно расширить до вычисления собственных векторов с помощью физических вычислений в массиве точек пересечения. Уравнение для собственного вектора имеет вид Ax = λx, [4] где A — вещественная квадратная матрица, λ — ее собственное значение, а x — соответствующий собственный вектор. Рис. 3 A показывает схему собственного вектора, состоящую из самоуправляемой цепи обратной связи, где вектор напряжения V , сформированный в столбцах точек пересечения, формирует вектор тока I = A · V , при этом проводимость матрицы точек пересечения, отображающей матрицу A .Выходные токи преобразуются в напряжения с помощью TIA с резисторами обратной связи G λ , отображающими известное собственное значение λ . Затем выходные сигналы TIA инвертируются и возвращаются в столбцы точек пересечения. Комбинируя закон Ома и закон Кирхгофа, получаем — A · V / G λ = — V , следовательно, A · V = G λ 902 V , который удовлетворяет уравнению. 4 . Поскольку физические напряжения и токи могут иметь только действительные значения, схема собственных векторов применяется только к действительным собственным значениям и собственным векторам. Для положительной матрицы, согласно теореме Перрона – Фробениуса (31), наивысшее собственное значение должно быть положительным действительным числом, а его собственный вектор также состоит из положительных действительных чисел. В результате собственный вектор наивысшего собственного значения положительной матрицы всегда может быть решен с помощью перекрестной схемы. Если собственный вектор самого низкого отрицательного собственного значения действительный, его также можно измерить, удалив аналоговые инверторы в цепи обратной связи ( SI Приложение , рис.S16 A ). Обратите внимание, что схема собственного вектора на рис. 3 A работает автономно, подобно генератору с положительной обратной связью, благодаря активным TIA, устанавливающим вектор напряжения В . Расчеты собственного вектора и PageRank. ( A ) Схема пересечения для решения уравнения собственных векторов Ax = λx , где x — собственный вектор, а λ — наивысшее положительное собственное значение положительной матрицы. вставка.Чтобы предотвратить нарушение при установке / сбросе проводимости RRAM, выходные напряжения OA были ограничены до ± 0,2 В. ( B ) Измеренные собственные векторы, соответствующие самому высокому положительному собственному значению и самому низкому отрицательному собственному значению, как функция нормированных собственных векторов полученные аналитическими решениями. Наивысшее положительное собственное значение и наименьшее отрицательное собственное значение были сохранены как проводимость обратной связи G λ TIA с проводимостью 940 и 331 мкс, соответственно.( C ) Система из четырех веб-страниц с соответствующими ссылками. Стрелка, указывающая со страницы i на страницу j , указывает на ссылку j на странице i , поэтому важность веб-страницы можно определить по количеству стрелок, указывающих на эту страницу. ( D ) Матрица ссылок для системы в C . Сумма элементов в каждом столбце равна 1, а все диагональные элементы равны нулю, поскольку страницы не ссылаются на себя. Единица преобразования была G 0 = 684 мкс для проводимости RRAM, чтобы минимизировать нелинейность RRAM.Наивысшее положительное собственное значение равно 1, что соответствует резисторам обратной связи с проводимостью G 0 . ( E ) Измеренный собственный вектор, представляющий оценки важности четырех страниц, как функция аналитически решенного нормализованного собственного вектора. Схема собственного вектора на рис. 3 A была экспериментально продемонстрирована для массива точек пересечения RRAM со значениями проводимости G , отображая матрицу A (рис. 3 A , вставка ) путем вычисления собственные векторы для наивысшего положительного собственного значения ( λ + = 9.41) и наименьшее отрицательное собственное значение ( λ — = −3,31). На рис. 3 B показаны измеренные значения собственных векторов как функции нормированных собственных векторов, полученных с помощью аналитических решений. Пропорциональность между экспериментальными и рассчитанными собственными векторами на рисунке указывает на правильное физическое вычисление собственных векторов. Хотя ограничение решения самыми высокими / самыми низкими собственными значениями может показаться неудобным, оказывается, что для многих приложений используются только самые высокие положительные или самые низкие отрицательные собственные значения.Например, в алгоритме PageRank (32, 33), который дает оценки важности веб-страниц для их ранжирования, собственный вектор матрицы ссылок вычисляется для наивысшего положительного собственного значения. Последний всегда равен 1, поскольку матрица связей является стохастической матрицей (33). На Фиг.3 C показан пример четырех страниц с соответствующими ссылками, а на Фиг.3 D показана соответствующая матрица ссылок, которая была реализована как значения проводимости массива точек пересечения RRAM 4 × 4.Используя схему собственного вектора на рис. 3 A , был решен собственный вектор матрицы ссылок для вычисления оценок важности страниц. Рис. 3 E показывает экспериментальные оценки по сравнению с аналитическими оценками, демонстрируя хорошую точность физического вычисления собственного вектора. Реальный случай PageRank описан в приложении SI , рис. S17. Анализ схемы собственных векторов на рис.3 A показывает, что G петля в идеале должна быть равна 1 ( SI Приложение , рис.S18), что, однако, никогда не может быть полностью удовлетворено в практических схемах. На практике G λ может быть экспериментально выбран так, чтобы G петля была немного больше 1, что позволяет правильно решить собственный вектор с приемлемой ошибкой. Фактически, хотя выход изначально увеличивается из-за цикла G > 1, нелинейность схемы, возникающая из-за насыщения выхода TIA, уменьшает цикл G до 1.С другой стороны, установка G loop меньше 1 приводит к нулевому выходному напряжению, чего, таким образом, следует избегать. Аналогично Рис. 2 A , решение для собственных векторов может быть расширено до смешанной матрицы A с помощью техники разделения с двумя массивами точек пересечения, соединенными аналоговыми инверторами ( SI Приложение , Рис. S16 B ). Мы проверили физическое вычисление собственных векторов для решения одномерного не зависящего от времени уравнения Шредингера: HΨ = EΨ, [5] где H — оператор Гамильтона, E — собственное значение энергии, а Ψ — соответствующая собственная функция.Уравнение 5 может быть численно решена методом конечных разностей, давая задачу на собственный вектор, заданную уравнением. 4 , где A — трехдиагональная матрица коэффициентов, x — вектор значений в дискретных позициях, а λ — наивысшее / наименьшее собственное значение. Уравнение Шредингера было решено для квадратной потенциальной ямы, показанной на рис. 4 A , которая была разделена поровну на 32 сегмента ( SI Приложение , рис. S19 и S20).На фиг. 4 B показана трехдиагональная смешанная матрица A 33 × 33, описывающая уравнения собственных векторов. Матрица A, разбита на две положительные трехдиагональные матрицы B и C , которые отображаются в значениях проводимости двух массивов точек пересечения, соответственно. Собственный вектор был рассчитан для основного состояния с энергией E = -4,929 эВ, что соответствует наименьшему отрицательному собственному значению задачи. Собственные значения и собственные векторы, полученные путем численного решения на цифровом компьютере, также указаны в Приложении SI , рис.S19. На рис. 4 C показан собственный вектор, полученный с помощью схемы смоделированного собственного вектора, в сравнении с аналитически вычисленным собственным вектором. Физически вычисленная волновая функция хорошо согласуется с численным решением, которое дополнительно поддерживает физические вычисления в схемах пересечения точек для реальных приложений. Решение уравнения Шредингера в схеме пересечения точек. ( A ) Прямоугольная яма потенциала V ( x ), принятая в уравнении Шредингера.Потенциальная яма имеет глубину -5 эВ и ширину 2 нм, в то время как решение проводится с общей шириной 3,2 нм, дискретизированной в 32 равных интервалах. ( B ) Матрица A размером 33 × 33, полученная из пространственной дискретизации уравнения Шредингера, и две положительные матрицы B и C , реализованные в массивах точек пересечения, с A = В — С . Единица преобразования 100 мкс для 7,6195 эВ была принята в матрицах B и C .Две матрицы проводимости имеют одну и ту же цветовую полосу. Собственное значение в основном состоянии составляет -4,929 эВ, что отображается на проводимость (65 мкСм) резисторов обратной связи TIA. ( C ) Дискретная собственная функция основного состояния, полученная как смоделированное выходное напряжение в схеме пересечения по сравнению с аналитическими решениями. Обратите внимание, что пиковое напряжение составляет около 1,5 В напряжения питания ОУ из-за насыщения. Массивы точек пересечения позволяют решать широкий набор задач алгебры, от линейных систем до задач на собственные векторы, тем самым обеспечивая физическое решение дифференциальных уравнений, описывающих реальные проблемы в промышленности, экономике и здравоохранении.Решение основано на чрезвычайно простых схемных элементах, таких как коммерчески доступные OA и современные резистивные запоминающие устройства, такие как RRAM и PCM. Для сравнения, предыдущие решения линейных систем с использованием подхода квантовых вычислений (34, 35) менее привлекательны, поскольку квантовые схемы обычно работают при криогенных температурах и требуют специального оборудования и некоммерческих технологий. Другие предлагаемые решения с архитектурой нейронных сетей (36) или аналоговыми ускорителями на основе КМОП (37) основаны на итерационных операциях, что приводит к полиномиальному времени вычислений и стоимости.Напротив, массив точек пересечения позволяет быстро решить всего за один шаг без итераций. Время вычислений ограничено временем установления ОУ, которое может достигать нескольких наносекунд в передовой КМОП-технологии (38). Чтобы оправдать ожидания практических приложений, схему коммутации следует масштабировать, чтобы продемонстрировать выполнимость схемы. Чтобы продемонстрировать масштабируемость схемы пересечения, решение системы линейных уравнений для матрицы коэффициентов модели 100 × 100 при моделировании показано в приложении SI , рис.S21. Результаты показывают, что линейная система точно решается схемой, которая поддерживает пригодность схемы коммутации для решения реальных проблем. Поскольку матричные коэффициенты хранятся в реальных наноразмерных устройствах с присущими им стохастическими вариациями, схема пересечения обеспечивает только приблизительное решение линейной задачи. Чтобы оценить влияние вариаций устройства, мы включили случайное отклонение проводимости каждого перекрестного устройства для матрицы 100 × 100 и рассчитали относительные ошибки выходных напряжений ( SI Приложение , рис.S22). Результаты моделирования показывают относительно низкие ошибки (около 10%) даже с отклонением в 10%. Таким образом, высокоточное хранение значений проводимости с помощью методов программирования и проверки имеет важное значение для повышения точности решения в зависимости от конкретных приложений. Нелинейная проводимость в резистивном элементе, физически возникающая из-за прыжковой проводимости и локального джоулева нагрева, также влияет на точность решения. Линейность проводимости может быть максимизирована путем увеличения проводимости устройства (5), что, однако, приводит к более высокому требованию энергии для перенастройки и работы схемы пересечения.Развитие технологии резистивной памяти, направленной на более высокую точность многоуровневого размещения и лучшую линейность проводимости, может улучшить схему пересечения для вычислений линейной алгебры в памяти. По мере увеличения масштаба схемы коммутации паразитное сопротивление из-за плотной разводки межсоединений в массиве памяти может стать дополнительной проблемой. Чтобы оценить влияние паразитного сопротивления, мы смоделировали ту же линейную систему 100 × 100 из SI Приложение , рис.S21 с дополнительным паразитным сопротивлением провода ( SI Приложение , рис. S23). Для справки параметры межсоединений были взяты из Международной дорожной карты технологий для полупроводников на 65- и 22-нм технологических узлах (39). Относительные ошибки находятся в пределах ∼10 и 30% для узлов 65 и 22 нм соответственно. Эти результаты предполагают, что существует компромисс между масштабированием и точностью схемотехнических решений задач алгебры. Следует также отметить, что ошибки вычислений по существу продиктованы соотношением сопротивлений между сопротивлением устройства и паразитным сопротивлением.В результате точность вычислений может быть улучшена за счет увеличения сопротивления запоминающих устройств, что, в свою очередь, может вызвать проблему нелинейности проводимости, которая также влияет на точность вычислений. Мы пришли к выводу, что существует сложный компромисс между масштабированием, паразитным сопротивлением и нелинейностью устройства для оптимизации операций (40, 41). В этом сценарии трехмерная интеграция памяти точки пересечения, где плотность не обязательно приводит к увеличению сопротивления межсоединений, может повысить устойчивость точности вычислений к паразитному сопротивлению (42). Хотя отсутствие итераций является очень привлекательной особенностью для быстрых вычислений, время, необходимое для программирования индивидуальных матричных коэффициентов в памяти, также следует учитывать для всесторонней оценки технологии. Хотя время записи в наших устройствах было относительно большим с целью точной настройки значений проводимости (см., Например, приложение SI, приложение , рис. S8), время программирования в реальном приложении могло бы быть значительно ускорено благодаря параллельному программирование (28, 29), схемы аналогового программирования (43), в дополнение к субнаносекундной коммутации устройств RRAM (44) и устройств PCM (45).Кроме того, согласно концепции вычислений в памяти, одни и те же данные могут часто повторно использоваться для вычислений (42), таким образом, время программирования может играть незначительную роль в общем времени вычислений. Хотя точность нашей схемы нельзя сравнивать с точностью решения с плавающей запятой в высокоточном цифровом компьютере, важно отметить, что требуемая точность может быть не высокой для всех приложений. На самом деле существует много случаев, когда задача линейной алгебры должна быть решена за короткое время, с низким бюджетом энергии и с достаточной устойчивостью к ошибкам.Например, в алгоритмах машинного обучения коэффициенты классификации / распознавания могут рассчитываться с некоторой погрешностью. Сетевые коэффициенты могут быть получены с помощью псевдообратной матрицы (46), вычисление которой может быть ускорено нашим подходом. Другим примером является ранжирование веб-страниц, где вычисленные оценки веб-сайтов должны отображаться в правильном порядке, хотя некоторые неточности все же могут допускаться для отдельных оценок. Для аналогичных типов приложений наши схемы могут предоставить решение с отличным компромиссом между точностью, скоростью и потреблением энергии. В заключение были представлены решения задач линейной алгебры в резистивных массивах точек пересечения. Такие задачи, как системы линейных уравнений, собственные векторы матриц и дифференциальные уравнения, решаются ( i ) за один шаг (и инверсия матрицы за N шагов), ( ii ) in situ в массиве памяти точек пересечения, и ( iii ) через физические законы, такие как закон Ома, закон Кирхгофа и механизмы обратной связи в схемах с обратной связью. Предлагаемые вычисления в памяти прокладывают путь для будущих приблизительных вычислительных систем в памяти для решения практических задач с большими данными с огромной экономией времени и энергии для широкого спектра реальных приложений. Подробная информация о производстве и характеристиках устройства, проектировании схем и методах измерения приведена в Приложении SI . Эта работа получила финансирование от Европейского исследовательского совета в рамках программы исследований и инноваций Европейского Союза Horizon 2020 (Соглашение о гранте 648635). Эта работа была частично выполнена на Polifab, предприятии по микро- и нанотехнологии Миланского политехнического университета. Автор: З.С., Г.П., Д.И. спланированное исследование; Z.S., G.P., E.A., A.B., W.W. и D.I. проведенное исследование; З.С., Г.П., Д.И. проанализированные данные; и З.С. и Д. написал газету. Авторы заявляют об отсутствии конфликта интересов. Эта статья представляет собой прямое представление PNAS. Эта статья содержит вспомогательную информацию на сайте www.pnas.org/lookup/suppl/doi:10.1073/pnas.1815682116/-/DCSupplemental. Раздел матриц QuickMath позволяет выполнять арифметические операции с матрицами. В настоящее время вы можете складывать или вычитать матрицы, умножать две матрицы, умножать матрицу на скаляр и возводить матрицу в любую степень. Матрица — это прямоугольный массив элементов (обычно называемых скалярами), которые располагаются в строках и столбцах.Они имеют множество применений в математике, включая преобразование координат и решение линейных систем уравнений. Вот пример матрицы 2×3: Арифметический набор команд позволяет складывать или вычитать матрицы, выполнять умножение матриц и скалярное умножение, а также возводить матрицу в любую степень. Матрицы добавляются и вычитаются друг из друга поэлементно.Например, при добавлении двух матриц A и B элемент в строке i, столбце j матрицы A добавляется к элементу строки i, столбцу j матрицы B, чтобы получить элемент в строке i, столбце j ответа. Следовательно, вы можете складывать и вычитать только матрицы одного размера. Умножение матриц немного сложнее. Предположим, что две матрицы A и B перемножаются, чтобы получить третью матрицу C. Элемент в строке i, столбце j в C находится путем взятия строки i из A и умножения ее на столбец j из B.Две матрицы можно перемножить, только если количество столбцов в первой равно количеству строк во второй. Умножение матрицы на скаляр просто включает в себя умножение каждого элемента на этот скаляр, в то время как возведение матрицы в положительную целочисленную степень может быть достигнуто путем серии умножений матриц. В настоящее время нет секции расширенной арифметики, хотя она может быть введена в будущем. Перейти на страницу арифметики Команда инверсии позволяет найти инверсию любой неособой квадратной матрицы.Обратной квадратной матрице A является другая матрица B того же размера, что A B = B A = I Перейти на обратную страницу Команда определителя позволяет вам найти определитель любой неособой квадратной матрицы. Например, если A является матрицей 3 x 3, то ее определитель может быть найден следующим образом: det (A) = a 1,1 A 1,1 — a 1,2 A 1,2 + a 1,3 A 1,3 , где a i, j — это элемент A в строке i, столбце j, а A i, j — матрица, построенная из A путем удаления строки i и столбца j. Перейти на страницу детерминанта Когда мы перечисляем строки и столбцы данной матрицы, мы считаем строки сверху вниз.
снизу и подсчитывать столбцы слева направо. Так как матрица представляет собой массив
чисел, мы часто видим матрицы, используемые для записи информации, особенно если строки
и столбцы матрицы можно понимать как представляющие категории. Таким образом, мы
безусловно, может использовать матрицы для записи соответствующей информации о системе
линейные уравнения — коэффициенты при переменных, а также константы на
правая часть уравнений системы. Рассмотрим систему Мы принимаем здесь соглашение об использовании переменных с индексами, а не
отдельные буквенные переменные, чтобы избежать возможных трудностей с количеством
доступные буквы. Мы строим матрицу 2 x 3, называемую расширенной матрицей для
система, где каждая строка представляет информацию для определенного уравнения и
каждый столбец представляет либо коэффициенты переменной, либо константы на
правая часть уравнений. Запишем эту матрицу следующим образом. Обратите внимание на соответствие между строками этой матрицы и уравнениями в
система, а также соответствие между столбцами матрицы и
коэффициенты и постоянные члены в уравнениях. Вертикальная линия не имеет
реальная цель, за исключением того, чтобы служить визуальным напоминанием о местонахождении равного
знаков в системе и, следовательно, разделение между коэффициентами
переменные и константы в правой части уравнений. Перед
углубившись в использование этих расширенных матриц, представляющих системы, мы будем
сделайте паузу, чтобы изложить некоторую терминологию и обозначения.Напомним, что в методе
исключения у нас было три операции, которые мы могли использовать для получения эквивалентных
системы линейных уравнений. У нас есть похожий набор строковых операций, которые
выполняем по матрицам. Мы говорим, что две матрицы эквивалентны строкам, если одна матрица
полученный из другого некоторой последовательностью строковых операций. Эти операции
следующим образом: Операции со строками: Выполнение любой последовательности этих операций приводит к эквивалентной строке
матрица. Обратите внимание на сходство между этими операциями и операциями, используемыми в
метод устранения. Мы используем аналогичное сокращенное обозначение для обозначения
выполнение также определенной строковой операции. Обозначение для операций со строками Обсуждение
Методы
Благодарности
Сноски
Выполнение матричных операций с помощью программы «Пошаговое решение математических задач»
Матрицы
Что такое матрица?
1 2 3
4 5 6
Арифметика
Обратный
Определитель
Матрица — это прямоугольный массив чисел, упорядоченный по строкам и столбцам. Мы называем
каждое число в этом массиве является элементом матрицы. Когда мы пишем матрицу, мы
обычно заключают массив в скобки. Матрицы (множественное число) бывают разных размеров,
определяется количеством строк и количеством столбцов. Если матрица имеет n
строк и m столбцов, то мы говорим, что размер матрицы m x n ,
прочтите «м по н». Ниже приведены примеры матриц различных размеров.
В случае, если матрица представляет собой расширенную матрицу, представляющую систему
линейные уравнения, выполнение строковой операции над матрицей эквивалентно
выполнение соответствующей операции над системой уравнений.

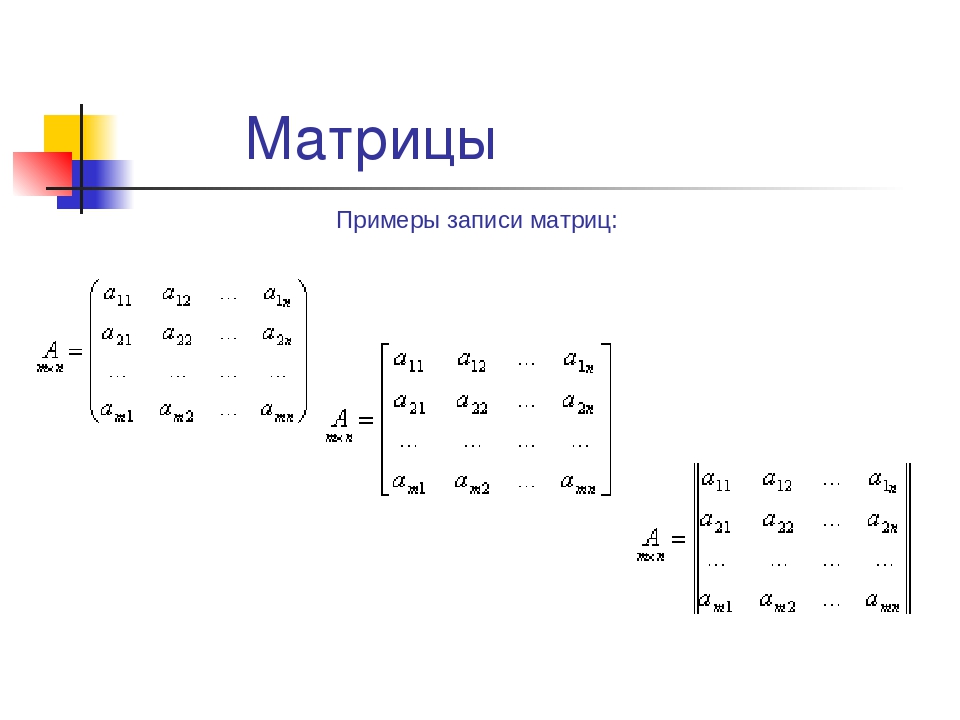
 -3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
-3.; 2. 5.')
>>> L = np.linalg.inv(A.T)
>>> R = (np.linalg.inv(A)).T
>>> print(L)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]]
>>> print(R)
[[ 0.45454545 -0.18181818]
[ 0.27272727 0.09090909]] linalg.matrix_rank(m_eye)
>>> print(rank)
3
linalg.matrix_rank(m_eye)
>>> print(rank)
3



