Сложение
Матрицы можно как складывать, так и вычитать друг из друга. Они должны иметь одинаковую размерность, иначе будет выдано сообщение об ошибке. Каждый элемент суммы двух матриц равен сумме соответствующих элементов матриц-слагаемых.
Задание 2. Получите сумму и разность двух матриц.
Введите две матрицы:
Выполните следующие операции:
Сохраните изменения в документе.
Кроме сложения матриц, MathCAD поддерживает операцию сложения матрицы со скаляром. Каждый элемент результирующей матрицы равен сумме соответствующего элемента исходной матрицы и скалярной величины.
Задание 3. Выполните операции сложения и вычитания матрицы со скаляром.
Введите матрицу и скаляр:
Выполните следующее операции:
Сохраните изменения в документе.

1.3. Умножение
При умножении следует помнить, что матрицу размерности M×N допустимо умножать только на матрицу размерности N×P (P может быть любым). В результате получается матрица размерности M×P.
Задание 4. Выполните операцию умножения двух матриц.
Введите две матрицы:
Получите скалярное произведение двух матриц. Чтобы ввести символ умножения можно воспользоваться клавишей со звездочкой или кнопкой на палитре Матрицы (Matrix):
Сохраните изменения в документе.
Можно умножать вектор на матрицу-строку и наоборот, строку на вектор. Аналогично сложению матрицы со скаляром определяется умножение и деление матрицы на скалярную величину.
Задание 5. Самостоятельно выполните следующие операции:
1.4. Определитель квадратной матрицы
Определитель
матрицы обозначается стандартным
математическим символом. Чтобы ввести
оператор определителя можно нажать
кнопку Вычисление
определителя (Determinant) на палитре Матрицы
(Matrix).
В результате появится местозаполнитель,
в который следует поместить матрицу.
Чтобы ввести
оператор определителя можно нажать
кнопку Вычисление
определителя (Determinant) на палитре Матрицы
(Matrix).
В результате появится местозаполнитель,
в который следует поместить матрицу.
Задание 6 . Реализуйте следующий пример:
1.5. Модуль вектора
Модуль вектора обозначается тем же символом, что и определить матрицы. По определению, модуль вектора равен квадратному корню из суммы квадратов его элементов.
1.6. Скалярное произведение векторов
Скалярное произведение векторов определяется как скаляр, равный сумме попарных произведений соответствующих элементов. Векторы должны иметь одинаковую размерность. Скалярное произведение двух векторов равно:
u·v=|u|·|v|·cos(Ө), где Ө — угол между векторами. Если векторы
ортогональны, то скалярное произведение
равно нулю. Скалярное произведение двух
векторов можно умножить на третий
вектор.
Скалярное произведение двух
векторов можно умножить на третий
вектор.
Задание 7. Выполните следующие примеры и проанализируйте полученные результаты:
1.7. Векторное произведение
Векторное произведение двух векторов u и v с углом Ө между ними равно вектору с модулем u×v=|u|·|v|·sin(Ө), направленным перпендикулярно плоскости векторов u и v. Обозначают векторное произведение символом ×, который можно ввести кнопкой Векторное произведение (Cross Product) палитры Матрица (Matrix).
Задание 8. Получите векторное произведение двух векторов:
1.8. Сумма элементов вектора и след матрицы
Если нужно вычислить
сумму всех элементов вектора, то можно
использовать вспомогательный оператор,
задаваемый кнопкой Сумма
элементов вектора (Vector Sum) на панели Матрица
(Matrix). Этот оператор чаще оказывается полезным
не в векторной алгебре, а при организации
циклов с индексированными переменными.
Этот оператор чаще оказывается полезным
не в векторной алгебре, а при организации
циклов с индексированными переменными.
Сумма диагональных элементов квадратной матрицы называется следом матрицы. Данная операция организована в виде встроенной функции tr.
Задание 9. Получите сумму элементов вектора A и след квадратной матрицы B, если вектор и матрица имеют следующие элементы:
НОУ ИНТУИТ | Лекция | Умножение разреженных матриц
Аннотация: В лекции рассматриваются типовые алгоритмы, применяемые в работе с плотными и разреженными матрицами. Рассказывается о некоторых форматах хранения этих матриц. Рассматриваются основные свойства матриц, методы решения СЛАУ, прямые и итерационные методы.
Ключевые слова: матрица, система линейных уравнений, вектор, норма, параметр, итерация, точность, компонент, Главная диагональ, представление, сходимость, дискретизация, выражение, радиус, решение системы линейных уравнений, функция, градиент, анализ, модель вычислений, операции
intuit.ru/2010/edi»>Цель лекции: Основной целью лекции является применение полученные знания о разработке и отладке параллельных программ в реализации численных алгоритмов для работы с матрицами.Презентация к лекции
Видеозапись лекции — (объем — 707 МБ).
Прямые методы решения СЛАУ
Методы решения систем линейных алгебраических уравнений (СЛАУ) относятся к численным методам алгебры. При формальном подходе решение подобных задач не встречает затруднений: решение системы можно найти, раскрыв определители в формуле Крамера.
Однако при непосредственном раскрытии определителей решение системы с n неизвестными требует арифметических операций; уже при n порядка 20 такое число операций недоступно для современных компьютеров.
При сколько-нибудь больших n применение методов с таким порядком числа операций будет невозможно и в обозримом будущем. Другой причиной, по которой этот классический способ неприменим даже при малых n, является сильное влияние на окончательный результат округлений при вычислениях.
Методы решения алгебраических задач можно разделить на точные и итерационные. Классы задач, для решения которых обычно применяют методы этих групп, можно условно назвать соответственно классами задач со средним и большим числом неизвестных. Изменение объема и структуры памяти вычислительных систем, увеличение их быстродействия и развитие численных методов приводят к смещению границ применения методов в сторону систем более высоких порядков.
Например, в 80-х годах прошлого века точные методы применялись для решения систем до порядка 104, итерационные – до порядка 107, в 90-х – до порядков 105 и 108 соответственно. Современные суперкомпьютеры способны использовать точные методы при решении еще больших систем.
(
7. 1) 1) |
В матричном виде система может быть представлена как
| ( 7.2) |
где есть вещественная матрица размера ; b и x — вектора из n элементов.
Под задачей решения системы линейных уравнений для заданных матрицы А и вектора b мы будем считать нахождение значения вектора неизвестных x, при котором выполняются все уравнения системы.
Метод исключения Гаусса
В первую очередь рассмотрим алгоритмыы, предназначенные для решения системы
(
7. 3) 3) |
с произвольной квадратной матрицей А. Основой для всех них служит широко известный метод последовательного исключения неизвестных, или же метод Гаусса
Метод Гаусса основывается на возможности выполнения преобразований линейных уравнений, которые не меняют при этом решение рассматриваемой системы (такие преобразования носят наименование эквивалентных). К числу таких преобразований относятся:
- умножение любого из уравнений на ненулевую константу,
- перестановка уравнений,
- прибавление к уравнению любого другого уравнения системы.
Метод Гаусса включает последовательное выполнение двух этапов. На первом этапе, который называется прямой ход, исходная система линейных уравнений при помощи последовательного исключения неизвестных приводится к верхнему треугольному виду.
Последовательный алгоритм
Прямой ход состоит в последовательном исключении неизвестных в уравнениях решаемой системы линейных уравнений.
На итерации i, метода производится исключение неизвестной i для всех уравнений с номерами k, больших i(т.е.) Для этого из этих уравнений осуществляется вычитание строки i, умноженной на константу с тем, чтобы результирующий коэффициент при неизвестной в строках оказался нулевым – все необходимые вычисления могут быть определены при помощи соотношений:
| ( 7.4) |
В итоге приходим к системе с верхней треугольной матрицей
При выполнении прямого хода метода Гаусса строка, которая используется для исключения неизвестных, носит наименование ведущей, а диагональный элемент ведущей строки называется ведущим элементом. Как можно заметить, выполнение вычислений является возможным только, если ведущий элемент имеет ненулевое значение. Более того, если ведущий элемент
имеет малое значение, то деление и умножение строк на этот элемент может приводить к накоплению вычислительной погрешности и вычислительной неустойчивости алгоритма.
Избежать подобной проблемы можно, если при выполнении каждой очередной итерации прямого хода метода Гаусса определить коэффициент с максимальным значением по абсолютной величине в столбце, соответствующем исключаемой неизвестной, т. е.
е.
и выбрать в качестве ведущей строку, в которой этот коэффициент располагается (данная схема выбора ведущего значения носит наименование метода главных элементов).
Обратный ход алгоритма состоит в следующем. После приведения матрицы коэффициентов к верхнему треугольному виду становится возможным определение значений неизвестных. Из последнего уравнения преобразованной системы может быть вычислено значение переменной
, после этого из предпоследнего уравнения становится возможным определение переменной
и т.д. В общем виде выполняемые вычисления при обратном ходе метода Гаусса могут быть представлены при помощи соотношений:
Оценим трудоемкость метода Гаусса. При выполнении прямого хода число операций составит
Для выполнения обратного хода потребуется
intuit.ru/2010/edi»>Таким образом, общее время выполнения метода Гаусса при больших n можно оценить какгде время выполнения одной операции.
Параллельный алгоритм
При внимательном рассмотрении метода Гаусса можно заметить, что все вычисления сводятся к однотипным вычислительным операциям над строками матрицы коэффициентов системы линейных уравнений. Как результат, в основу параллельной реализации алгоритма Гаусса может быть положен принцип распараллеливания по данным. В качестве базовой подзадачи можно принять тогда все вычисления, связанные с обработкой одной строки матрицы A и соответствующего элемента вектора b. Рассмотрим общую схему параллельных вычислений и возникающие при этом информационные зависимости между базовыми подзадачами.
Для выполнения прямого хода метода Гаусса необходимо осуществить итерацию по исключению неизвестных для преобразования матрицы коэффициентов A к верхнему треугольному виду. Выполнение итерации i, , прямого хода метода Гаусса включает ряд последовательных действий. Прежде всего, в самом начале итерации необходимо выбрать ведущую строку, которая при использовании метода главных элементов определяется поиском строки с наибольшим по абсолютной величине значением среди элементов столбца i, соответствующего исключаемой переменной . Зная ведущую строку, подзадачи выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной .
Выполнение итерации i, , прямого хода метода Гаусса включает ряд последовательных действий. Прежде всего, в самом начале итерации необходимо выбрать ведущую строку, которая при использовании метода главных элементов определяется поиском строки с наибольшим по абсолютной величине значением среди элементов столбца i, соответствующего исключаемой переменной . Зная ведущую строку, подзадачи выполняют вычитание строк, обеспечивая тем самым исключение соответствующей неизвестной .
При выполнении обратного хода метода Гаусса подзадачи выполняют необходимые вычисления для нахождения значения неизвестных. Как только какая-либо подзадача i, , определяет значение своей переменной , это значение должно быть использовано всеми подзадачам с номерами k, : подзадачи подставляют полученное значение новой неизвестной и выполняют корректировку значений для элементов вектора b.
Выделенные базовые подзадачи характеризуются одинаковой вычислительной трудоемкостью. Однако размер матрицы, описывающей систему линейных уравнений, является существенно большим, чем число потоков в программе (т.е.,), и базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько строк матрицы. При этом применение последовательной схемы разделения данных для параллельного решения систем линейных уравнений приведет к неравномерной вычислительной нагрузке между потоками: по мере исключения (на прямом ходе) или определения (на обратном ходе) неизвестных в методе Гаусса для большей части потоков все необходимые вычисления будут завершены и они окажутся простаивающими. Возможное решение проблемы балансировки вычислений может состоять в использовании ленточной циклической схемы для распределения данных между укрупненными подзадачами. В этом случае матрица A делится на наборы (полосы) строк вида
(см. рис. 7.1).
Однако размер матрицы, описывающей систему линейных уравнений, является существенно большим, чем число потоков в программе (т.е.,), и базовые подзадачи можно укрупнить, объединив в рамках одной подзадачи несколько строк матрицы. При этом применение последовательной схемы разделения данных для параллельного решения систем линейных уравнений приведет к неравномерной вычислительной нагрузке между потоками: по мере исключения (на прямом ходе) или определения (на обратном ходе) неизвестных в методе Гаусса для большей части потоков все необходимые вычисления будут завершены и они окажутся простаивающими. Возможное решение проблемы балансировки вычислений может состоять в использовании ленточной циклической схемы для распределения данных между укрупненными подзадачами. В этом случае матрица A делится на наборы (полосы) строк вида
(см. рис. 7.1).
Рис. 7.1. Ленточная схема
intuit.ru/2010/edi»>Сопоставив схему разделения данных и порядок выполнения вычислений в методе Гаусса, можно отметить, что использование циклического способа формирования полос позволяет обеспечить лучшую балансировку вычислительной нагрузки между подзадачами.Итак, проведя анализ последовательного варианта алгоритма Гаусса, можно заключить, что распараллеливание возможно для следующих вычислительных процедур:
- поиск ведущей строки,
- вычитание ведущей строки из всех строк, подлежащих обработке,
- выполнение обратного хода.
Оценим трудоемкость рассмотренного параллельного варианта метода Гаусса. Пусть n есть порядок решаемой системы линейных уравнений, а p, , обозначает число потоков. При разработке параллельного алгоритма все вычислительные операции, выполняемые алгоритмом Гаусса, были распределены между потоками параллельной программы. Следовательно, время, необходимое для выполнения вычислений на этапе прямого хода, можно оценить как
Следовательно, время, необходимое для выполнения вычислений на этапе прямого хода, можно оценить как
Подставив выражение получим, что время выполнения вычислений для параллельного варианта метода Гаусса описывается выражением:
Теперь можно оценить величину накладных расходов, обусловленных организацией и закрытием параллельных секций. Пусть – время, необходимое на организацию и закрытие параллельной секции. Параллельная секция создается при каждом выборе ведущей строки, при выполнении вычитания ведущей строки из остальных строк линейной системы, подлежащих обработке, а также при выполнении каждой итерации обратного хода метода Гаусса. Таким образом, общее число параллельных секций составляет .
Сводя воедино все полученные оценки можно заключить, что время выполнения параллельного метода Гаусса описывается соотношением
(
7.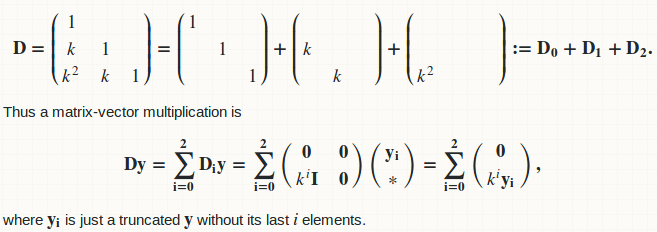 5) 5) |
Связь метода Гаусса и LU-разложения
LU-разложение — представление матрицы A в виде
| ( 7.6) |
где L — нижняя треугольная матрица с диагональными элементами, равными единице, а U — верхняя треугольная матрица с ненулевыми диагональными элементами. LU-разложение также называют LU-факторизацией. Известно [4], что LU-разложение существует и единственно, если главные миноры матрицы A отличны от нуля.
Алгоритм LU-разложения тесно связан с методом исключения Гаусса. В самом деле, пусть мы решаем систему уравнений вида (7. 2). Непосредственно проверяется, что преобразования k-го шага метода Гаусса равносильны домножению системы (7.2) слева на матрицу
2). Непосредственно проверяется, что преобразования k-го шага метода Гаусса равносильны домножению системы (7.2) слева на матрицу
где — множители Гаусса из (7.4). Как было рассмотрено в п. 7.1.1, прямой ход метода Гаусса преобразует исходную систему уравнений к виду
с верхней треугольной матрицей U. Зная матрицы , можно записать матрицу U и вектор c как
Обозначим Можно непосредственно проверить, что
Отсюда получаем .
Таким образом, матрицу L можно получить как нижнюю треугольную матрицу коэффициентов Гаусса, а матрицу U — как верхнюю треугольную матрицу, получаемую в результате работы метода Гаусса. При этом очевидно, что трудоемкость получения LU-факторизации будет такой же-.
ru/2010/edi»>Рассмотренный нами алгоритм LU-факторизации реализован с помощью исключения по столбцу. Следует отметить, что можно сформулировать аналогичный алгоритм, основанный на исключении по строке. В самом деле, основная идея алгоритма с помощью исключения по столбцу заключается в том, что на i-й итерации ведущая строка с подходящими множителями вычитается из строк, лежащих ниже, чтобы занулить все элементы матрицы, расположенные в i-м столбце ниже диагонали. Между тем возможно и другое: на каждой i-й итерации можно вычитать из i-й строки все строки, расположенные выше, умноженные на подходящие коэффициенты, так, чтобы занулить все элементы i-й строки левее диагонали. При этом элементы матрицы L ниже главной диагонали и элементы матрицы U на главной диагонали и выше нее можно вычислять на месте матрицы А. Как и в случае исключения по столбцу, приведенная схема требует проведения операцийРассмотрим теперь еще один способ LU-факторизаци, называемый компактной схемой. Пусть матрица допускает LU-разложение (7.6), где
Пусть матрица допускает LU-разложение (7.6), где
т.е. при а при . Из соотношения (7.6) следует, что
Преобразуем эту сумму двумя способами:
Отсюда находим
Оценка числа операций данного алгоритма LUфакторизаци также составляет
Если разложение (7.6) получено, то решение системы (7.2) сводится к последовательному решению двух систем уравнений с треугольными матрицами (обратный ход)
| ( 7.7) |
Обратный ход требует операций.
Как следует из приведенных оценок, вычислительная сложность метода исключения Гаусса и метода LU-разложения одинакова. Однако если необходимо решить несколько систем с одинаковыми матрицами коэффициентов, но различными векторами свободных членов (правая часть СЛАУ), то метод LU-разложения окажется предпочтительным, так как в этом случае нет необходимости производить разложение матрицы коэффициентов многократно. Достаточно лишь сохранить полученные треугольные матрицы в памяти и, подставляя различные вектора свободных членов, получать решения методами прямой и обратной подстановки. Это позволит значительно сократить объем вычислений по сравнению с методом Гаусса.
Однако если необходимо решить несколько систем с одинаковыми матрицами коэффициентов, но различными векторами свободных членов (правая часть СЛАУ), то метод LU-разложения окажется предпочтительным, так как в этом случае нет необходимости производить разложение матрицы коэффициентов многократно. Достаточно лишь сохранить полученные треугольные матрицы в памяти и, подставляя различные вектора свободных членов, получать решения методами прямой и обратной подстановки. Это позволит значительно сократить объем вычислений по сравнению с методом Гаусса.
линейная алгебра — Автоматическая оптимизация умножения матрицы на вектор 0-1
Вопрос:
Существует ли установленная процедура или теория для генерации кода, который эффективно применяет умножение матрицы на вектор, когда матрица плотная и заполнена только нулями и те? В идеале оптимизированный код должен систематически использовать ранее вычисленную информацию, чтобы уменьшить дублирование работы.
Другими словами, у меня есть матрица $M$, и я хочу выполнить предварительное вычисление на основе $M$, чтобы сделать вычисление $Mv$ максимально эффективным, когда я позже получу вектор $v$.
$M$ — прямоугольная плотная бинарная матрица, известная во время компиляции, тогда как $v$ — неизвестный действительный вектор, известный только во время выполнения.
Пример 1: (скользящее окно)
Позвольте мне использовать простой небольшой пример, чтобы проиллюстрировать мою точку зрения. Рассмотрим матрицу, $$M = \begin{bmatrix}1 & 1 & 1 & 1 & 1\\ & 1 & 1 & 1 & 1 & 1 \\ & & 1 & 1 & 1 & 1 & 1\\ & & & 1 & 1 & 1 & 1 & 1\end{bmatrix}.$$ Предположим, мы применяем эту матрицу к вектору $v$, чтобы получить $w = Mv$. Тогда записи результата: \начать{выравнивать} w_1 &= v_1 + v_2 + v_3 + v_4 + v_5\\ w_2 &= v_2 + v_3 + v_4 + v_5 + v_6\\ w_3 &= v_3 + v_4 + v_5 + v_6 + v_7\\ w_4 &= v_4 + v_5 + v_6 + v_7 + v_8 \end{выравнивание}
Стандартное умножение матрицы на вектор будет выполняться именно таким образом. Однако большая часть этой работы является избыточной. Мы могли бы выполнить те же вычисления матрицы с меньшими затратами, отслеживая «нарастающую сумму» и добавляя/вычитая, чтобы получить следующее число: \начать{выравнивать} w_1 &= v_1 + v_2 + v_3 + v_4 + v_5\\ w_2 &= w_1 + v_6 — v_1\\ w_3 &= w_2 + v_7 — v_2\\ w_4 &= w_3 + v_8 — v_3 \end{align}
Пример 2: (иерархическая структура)
В предыдущем примере мы могли просто отслеживать промежуточную сумму. Однако обычно требуется создать и сохранить дерево промежуточных результатов. Например, рассмотрим
$$M = \begin{bmatrix}1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 \\ & & & & & 1 & 1 & 1 & 1 & 1\\ 1 & 1 \\ & & & & 1 & 1 \\ & & 1 & 1 \\ & & & & & & & 1 & 1\end{bmatrix}$$
Можно эффективно вычислить $w = Mv$, используя дерево промежуточных результатов:
Однако обычно требуется создать и сохранить дерево промежуточных результатов. Например, рассмотрим
$$M = \begin{bmatrix}1 & 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & 1 & 1 & 1 \\ & & & & & 1 & 1 & 1 & 1 & 1\\ 1 & 1 \\ & & & & 1 & 1 \\ & & 1 & 1 \\ & & & & & & & 1 & 1\end{bmatrix}$$
Можно эффективно вычислить $w = Mv$, используя дерево промежуточных результатов:
- Вычислить $w_5$ и $w_7$ и сложить их, чтобы получить $w_3$.
- Вычислить $w_4$ и $w_6$ и сложить их, чтобы получить $w_2$.
- Добавьте $w_2$ и $w_3$, чтобы получить $w_1$
Структуру в приведенных выше примерах легко увидеть, но для реальных матриц, которые меня интересуют, структура не так проста.
Пример 3: (низкий ранг)
Чтобы прояснить некоторую путаницу, матрицы обычно не разрежены. В частности, метод, решающий эту проблему, должен уметь находить эффективные методы применения матриц, в которых большие блоки заполнены единицами. Например, рассмотрим
$$M = \begin{bmatrix}1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & & & \\ 1 & 1 & 1 & 1 & & \\ 1 & 1 & 1 & 1 & & \end{bmatrix}. $$
$$
Эту матрицу можно разложить как разность двух матриц ранга 1, $$M = \begin{bmatrix}1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 & 1 & 1 & 1\end{bmatrix} — \begin{bmatrix}& & & & & & \\ & & & & & & \\ & & & & 1 & 1 \\ & & & & & 1 & 1 \\ & & & & & 1 & 1\end{bmatrix}$$
, поэтому его действие на вектор $w := Mv$ можно эффективно вычислить с помощью \начать{выравнивать} w_1 &= v_1 + v_2 + v_3 + v_4 + v_5 + v_6 \\ w_2 &= w_1 \\ w_3 &= w_2 — v_5 — v_6 \\ w_4 &= w_3 \\ w_5 &= w_4. \end{align}
Мотивация:
Я работаю над численным методом для некоторой обработки изображений, и есть несколько больших плотных матриц $0-1$ с различными структурами, которые фиксированы на все времена. Позже эти матрицы нужно будет применить ко многим неизвестным векторам $v_i$, которые будут зависеть от ввода пользователя. Прямо сейчас я использую карандаш и бумагу, чтобы придумать эффективный код для каждой матрицы, но мне интересно, можно ли автоматизировать этот процесс.
Редактировать: (постскриптум)
Все ответы здесь до сих пор (по состоянию на 05.09.15) интересны, но ни один из них не отвечает на вопрос так удовлетворительно, как я надеялся. Вероятно, окажется, что это сложный исследовательский вопрос, и никто не знает хорошего ответа.
Поскольку время истекло, я присуждаю награду за ответ EvilJS, поскольку он отвечает на правильный вопрос. Однако хотелось бы, чтобы ответ содержал более четкие и подробные объяснения.
ответ транисстора устанавливает связь между этим вопросом и проблемой умножения логической матрицы на вектор (OMv) в Интернете, но эта связь не совсем то, что задает этот вопрос. В частности, следующее предположение на самом деле не подходит (выделено мной жирным шрифтом), 9{2 — \varepsilon})$ для некоторого $\varepsilon > 0$.
Вопрос о том, существуют или нет субквадратичные алгоритмы для всех матриц, ортогонален вопросу поиска максимально быстрого алгоритма для конкретной матрицы. Большинство матриц 0-1 выглядят как случайный шум и (если я должен предположить), вероятно, не имеют субквадратичных алгоритмов. Однако тот факт, что есть действительно плохие матрицы, не мешает мне найти быстрый алгоритм на хорошей матрице, например, матрице «скользящего окна».
Большинство матриц 0-1 выглядят как случайный шум и (если я должен предположить), вероятно, не имеют субквадратичных алгоритмов. Однако тот факт, что есть действительно плохие матрицы, не мешает мне найти быстрый алгоритм на хорошей матрице, например, матрице «скользящего окна».
ответы vzn, первый ответ, второй ответ интересны (и, на мой взгляд, не заслуживают такого количества отрицательных голосов), но они не относятся к вопросу по причинам, обсуждаемым там в комментариях.
Анимация Демонстрация умножения матриц, Онлайн-вычисления, онлайн-калькулятор, онлайн-расчет калькулятора
Категория: Алгебраический
Помогите изменить
Введите данные матрицы здесь:
Скорость:
SlowFast
Некоторые примеры Пример 1: Умножение квадратной матрицы 3-го порядкаПример 2: Умножение квадратной матрицы 2-го порядкаПример 3: Умножение квадратной матрицы 1-го порядкаПример 4: Единичная матрица, умноженная влево Квадратная матрица 3-го порядкаПример 5: Единичная матрица, умноженная справа 3 Квадратная матрица порядкаПример 6: Умножение единичной матрицы справа на матрицу 3×2Пример 7: Матрица единиц, умноженная влево Матрица 3×2Пример 8: Квадратная матрица 3-го порядка левого множителя матрицы 2×3Пример 9: Матрица 3×2, умноженная справа Квадратная матрица 3-го порядкаПример 10: 3-мерный вектор-столбец, умноженный справа Квадратная матрица 3-го порядкаПример 11: 3-мерный вектор-столбец, умноженный справа Квадратная матрица 3-го порядкаПример 12: Матрица 3 x 2, умноженная на 2 x 3 матрицаПример 13: Диагональная матрицаПример 14: Элементарная матрица умножается влево, две строки меняются местамиПример 15: Элементарная матрица умножается вправо, меняются местами два столбцаПример 16: Элементарная матрица умножается налево, а элементы строки умножаются на два. Пример 17 : Элементарная матрица умножается справа, а элементы столбца умножаются на 2. Пример 18: Умножение элементарной матрицы влево, один элемент строки, умноженный на 2, добавляется к другой строке. Пример 19: Элементарная матрица умножается справа, один элемент столбца умножается на 2 и добавляется к другому столбцу. Пример 20: Умножение вектора-строки на вектор-столбец.
Пример 17 : Элементарная матрица умножается справа, а элементы столбца умножаются на 2. Пример 18: Умножение элементарной матрицы влево, один элемент строки, умноженный на 2, добавляется к другой строке. Пример 19: Элементарная матрица умножается справа, один элемент столбца умножается на 2 и добавляется к другому столбцу. Пример 20: Умножение вектора-строки на вектор-столбец.
1
2
3
4
5
6
7
8
1
2
3
4
5
9000 23
4
5
9000 2 2 34
5
9000 2 34
5 9000 9000 2
00057
8
1
2
3
4
5
6
7
+
9000 + 9000 ++
9000 + 9000 ++
9000 ++
9000 ++
9000 +×
=
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
Описание приложения
На этой странице демонстрируется арифметика умножения левой и правой матриц с помощью анимации.