Площади геометрических фигур формулы: Как найти площадь фигуры, формула

Содержание

ВЫЧИСЛЕНИЕ ПЛОЩАДИ ГЕОМЕТРИЧЕСКОЙ ФИГУРЫ, ЗАДАВАЕМОЙ НА КЛЕТЧАТОЙ БУМАГЕ

Авторы
Руководители
Файлы работы
Наградные документы

Зарипова Д.М. 1

Кильмаматова З.М. 1

1МБОУ СОШ№1

Автор работы награжден дипломом победителя III степени

Диплом школьникаСвидетельство руководителя

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

ВВЕДЕНИЕ

Площадь – это величина, характеризующая размер геометрической фигуры. Расположенный на плоскости многоугольник занимает какую-то ее часть. Размер этой части плоскости и будет равен площади многоугольника. Определение площадей геометрических фигур является одной из древнейших задач геометрии, которая и в настоящее время имеет важное практическое значение. Так, например, определение границы земельного участка, и, в конечном итоге вычисление площади земельного участка является одной из основных задач кадастра объектов недвижимости. Картографо-геодезическое обеспечение кадастра направлено на решение указанной задачи. Точность кадастровых работ регламентирована соответствующими нормативными документами. Площадь земельного участка и конечная стоимость земельного участка связаны между собой. Вполне очевидно, что с увеличением стоимости земель должны возрастать требования к точности определения координат точек границы участка. Повышение точности определения координат поворотных точек границ земельных участков может быть достигнуто с использованием современных технологий и средств измерений (спутниковая технология, электронные тахеометры и т.д.). Таким образом, данная проблема имеет прикладное значение, ее понимание, прежде всего, важно для тех, кто осваивает навыки в области геодезии, картографии и кадастра и других областях, связанных с нахождением площади фигур.

Объект исследования – геометрия, предмет исследования – площади геометрических фигур. Цель исследования: овладеть практическими навыками, техническими приёмами, которые потребуются для вычисления площадей геометрических фигур. Задачи исследования:1. Ознакомить с различными формулами вычисления .площадей геометрических фигур.2.Ознакомить с понятием определителей, свойствами определителей, формулой вычисления площади треугольника с помощью определителя.3. Ознакомить с формулой Пика.4.Вычислить площади геометрических фигур, задаваемых на системе координат, различными способами. Выявить слабые и сильные стороны этих способов.

ГЛАВА I. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Рассмотрим систему из трех линейных уравнений относительно трех неизвестных

Определение. Определителем третьего порядка, соответствующим матрице системы, назовем число

D, равное Для того, чтобы вычислить определитель третьего порядка применяют две вычислительные схемы, позволяющие вычислять определители третьего порядка без особых хлопот.

Эти схемы известны как «правило треугольника» (или «правило звездочки») и «правило Саррюса». Правило треугольника: сначала перемножаются и складываются элементы, соединенными на схеме линиями

т.е. получаем сумму произведений: a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂. Обратите внимание, что перемножаются элементы, соединенные одной линией, прямой или ломанной, а потом полученные произведения складываются. Затем перемножаются и складываются элементы, соединенные на схеме

т.е. получаем другую сумму произведений a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂. И, наконец, чтобы вычислить определитель, из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:

D=(a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁

+a₂₁a₁₃a₃₂)-(a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂). Правило Саррюса: к определителю справа дописывают два первых столбца, а затем считают сумму произведений элементов определителя в одном направлении и из нее вычитают сумму произведений элементов в другом направлении (Рис.

1):

Рис. 1 Свойства определителей 3 порядкатакже помогают в вычислениях определителей:Свойство 1. Величина определителя не изменяется при замене строк столбцами.Свойство 2. При перестановке двух строк (столбцов) между собой, величина определителя меняет знак.Свойство 3. Определитель с двумя одинаковыми (пропорциональными) строками (столбцами) равен нулю.Свойство 4. Если все элементы некоторой строки (столбца) содержат одинаковый множитель, то этот множитель можно вынести за знак определителя.Свойство 5. Если все элементы некоторой строки (столбца) есть сумма равного числа слагаемых, то определитель будет равен сумме определителей, в которых элементы указанной строки (столбца) записываются отдельными слагаемыми.Свойство 6. Если все элементы некоторой строки (столбца) равны нулю, то весь определитель тоже равен нулю.Свойство 7. Величина определителя не изменится, если к элементам некоторой строки (столбца) добавить соответствующие элементы другой строки (столбца), предварительно умножив их на один и тот же множитель.

Миноры и алгебраические дополненияРассмотрим определитель третьего порядка

вычеркнем из определителя одну строку и один столбец, например, первую строку и второй столбец. Из оставшихся элементов составим определитель второго порядка

номер которого (индекс у D) определяется номерами вычеркнутых строки (первой) и столбца (второй). Если из определителя вычеркнуть другие строку и столбец, например, третий и третий, соответственно, то оставшиеся элементы будут также составлять определитель второго порядка, номер которого теперь будет другой –

Определение. Определитель, который получается вычеркиванием одной строки и одного столбца из исходного определителя называется минором основного определителя. Очевидно, что определитель третьего порядка имеет 9 различных миноров второго порядка, т.е. каждый элемент определителя имеет минор.

Определение. Назовем алгебраическим дополнением любого элемента определителя

D минор этого элемента, взятый со знаком плюс, если сумма номеров элемента четная и минус в противном случае .

Теорема 1. Определитель D равен сумме произведений элементов любого столбца или строки на их алгебраические дополнения Очевидно, что для определителя третьего порядка можно записать шесть различных равенств (по трем столбцам и по трем строчкам). Теорема 2. Суммы, произведений элементов для любого столбца (строки) на алгебраические дополнения другого столбца (строки) определителя, равна нулю.Доказательство. Возьмем сумму произведений алгебраических дополнений первой строки на элементы третьей строки. Получим

Разложение определителя по строке или столбцу дает нам правило вычисления любых определителей высоких порядков (четвертого и выше). Определение . Определителем n -го порядка называется число равное алгебраической сумме

_гдеA_ij=(-1)^i+jD_ij есть алгебраические дополнения элемента a_ij, а D_ij— есть соответствующие миноры, т. е. определители ( n-1 )-го порядка, получающиеся из исходного определителя вычеркиванием первой строки и n -го столбца, на пересечение которых находится элемент a_ij. Рассмотренные приемы позволяют вычислять определители любых порядков.

При нахождении площадей фигур можно пользоваться следующими приёмами:

1.Площадь треугольника с вершинами в точках вычисляется по формуле:

2.Площадь любого треугольника, нарисованного на клетчатой бумаге, легко посчитать, представив её как сумму или разность площадей прямоугольных треугольников и прямоугольников, стороны которых идут по линиям сетки, проходящим через вершины нарисованного треугольника.

3. Любой сложный многоугольник можно представить составленным из более простых многоугольников. В этом случае его площадь равна сумме площадей, входящих многоугольников.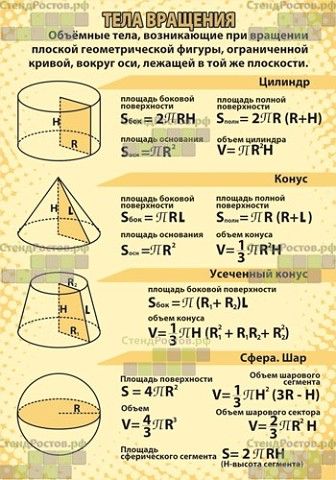

4.Можно воспользоваться формулой Пика Чтобы оценить площадь многоугольника на клетчатой бумаге, достаточно подсчитать, сколько клеток покрывает этот многоугольник (площадь клетки мы принимаем за единицу). Точнее, если S – площадь многоугольника, — число клеток, которые целиком лежат внутри многоугольника, и — число клеток, которые имеют с внутренностью. Будем рассматривать только такие многоугольники, все вершины которых лежат в узлах клетчатой бумаги – в таких, где пересекаются линии сетки многоугольника хоть одну общую точку. Для вычисления площади такого многоугольника можно воспользоваться следующей теоремой: Теорема Пика. Пусть — число целочисленных точек внутри многоугольника, — количество целочисленных точек на его границе, — его площадь. Тогда справедлива

формула Пика: .Доказательство теоремы Пика. Сначала заметим, что формула Пика верна для единичного квадрата. Действительно, в этом случае мы имеем . Рассмотрим прямоугольник со сторонами, лежащими на линиях решетки.

Пусть длины его сторон равны и . Имеем в этом случае и, по формуле Пика, Рассмотрим теперь прямоугольный треугольник с катетами, лежащими на осях координат. Такой треугольник получается из прямоугольника со сторонами и , рассмотренного в предыдущем случае, разрезанием его по диагонали. Пусть на диагонали лежат целочисленных точек. Тогда для этого случая и получаем, что Теперь рассмотрим произвольный треугольник. Его можно получить, отрезав от прямоугольника несколько прямоугольных треугольников и, возможно, прямоугольник (Рис. 2 и Рис. 3). Поскольку и для прямоугольника, и для прямоугольного треугольника формула Пика верна, мы получаем, что она будет справедлива и для произвольного треугольника.

Рис. 2 Рис. 3

_{Остается сделать последний шаг: перейти от треугольников к многоугольникам. Любой многоугольник можно разбить на треугольники (например, диагоналями). Поэтому нужно просто доказать, что при добавлении любого треугольника к произвольному многоугольнику формула Пика остается верной.} Пусть многоугольник и треугольник имеют общую сторону. Предположим, что для формула Пика справедлива, докажем, что она будет верна и для многоугольника, полученного из добавлением . Так как и имеют общую сторону, то все целочисленные точки, лежащие на этой стороне, кроме двух вершин, становятся внутренними точками нового многоугольника. Вершины же будут граничными точками. Обозначим число общих точек через и получим — число внутренних целочисленных точек нового многоугольника, — число граничных точек нового многоугольника. Из этих равенств получаем Так как мы предположили, что теорема верна для и для по отдельности, то Что и требовалось доказать. Теорема Пика — классический результат комбинаторной геометрии и геометрии чисел.

Пример. Для многоугольника на рисунке (Рис. 3) (желтые точки), (синие точки, не забудьте о вершинах!), поэтому квадратных единиц.

Рис. 3

Задание B3. Найдите площади фигуры, изображенной на клетчатой бумаге с размером клетки 1 см 1 см (Рис. 4). Ответ дайте в квадратных сантиметрах.

Рис. 4

ГЛАВА II. ПРАКТИЧЕСКАЯ ЧАСТЬ

Задача 1. Вычислить площадь .

1 способ.Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 5) и определяем координаты вершин данного треугольника: .

Рис. 5

Применим формулу :

Ответ: 8 кв.ед.

2 способ.Решение. Решим задачу с помощью формулы Проведем высоту CD к стороне AB (Рис. 6):

Рис. 6

Ответ: 8 кв.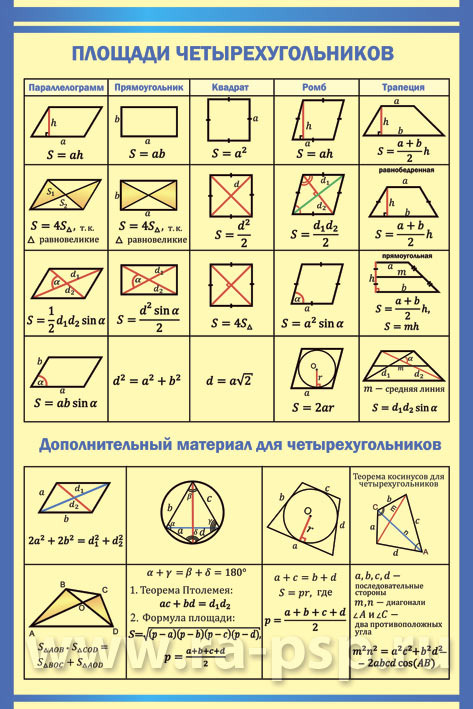 ед.

3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 7).

Рис. 7

Ответ: 8 кв.ед.

4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 8).

Рис. 8

Ответ: 8 кв.ед.

Применить метод «полных» клеток нельзя.

Задача 2. Вычислить площадь трапеции (Рис. 9).

Рис. 9

1 способ.Решение. Решим задачу с помощью определителя. Для этого вводим вспомогательную прямоугольную систему координат (Рис. 10), разбиваем трапецию на треугольники, например, , с помощью вспомогательных построений, определяем координаты вершин полученных треугольников: .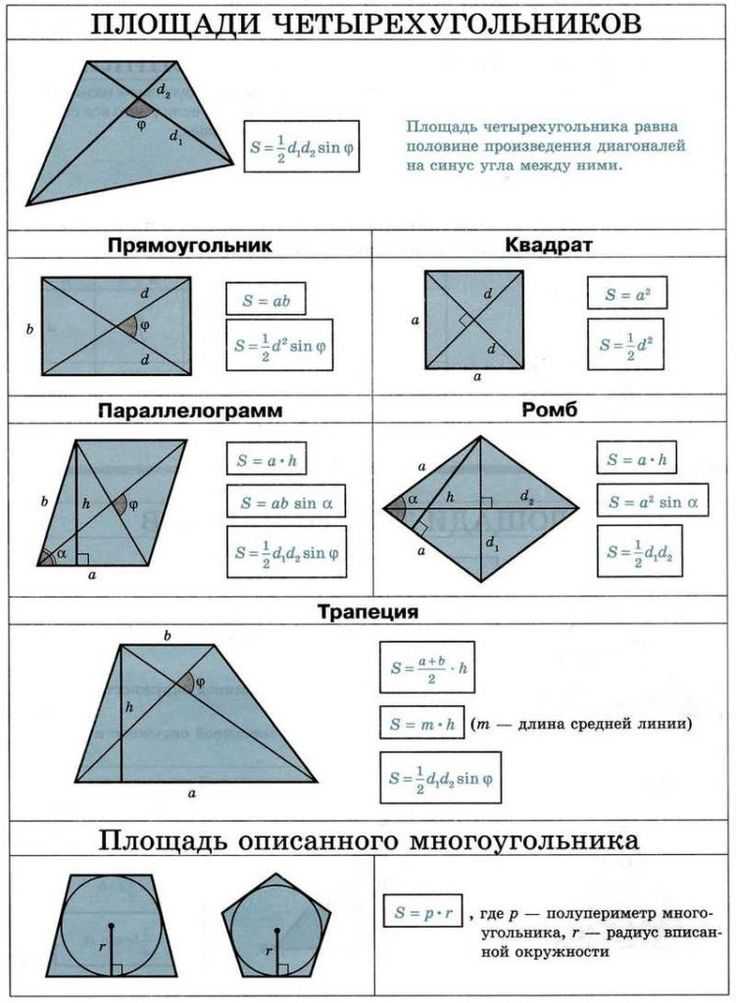

Рис. 10

Первый определитель вычисляем, замечая, что в первой строке только один элемент не равен нулю, а второй – разложением по второй строке.

Ответ: 10,5 кв.ед.2 способ. Решение. Решим задачу с помощью формулы

Ответ: 10,5 кв.ед.

3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 11).

Рис. 11

Ответ: 10,5 кв.ед.

4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 12).

_{Рис. 1}2

Ответ: 10,5 кв.ед.

_{5 способ.}Решение. Применим метод «полных» клеток (Рис. 13).

_{Рис. 1}3

Ответ: 10,5 кв.ед.

Задача 3. Вычислить площадь четырехугольника.

1 способ.Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 14) и определяем координаты вершин данного четырехугольника: .

Рис. 14

Применим формулу . Первый определитель вычисляем по правилу треугольника, второй – по правилу Саррюса (Рис. 15).

Рис. 15

Ответ: 5 кв.ед.

2 способ.Решим задачу с помощью формулы

Ответ: 5 кв.ед.

_{3 спо}соб. Решим задачу с помощью способа «вырезания» (Рис. 16). Достроим прямоугольник

Рис. 16

Ответ: 5 кв.ед.

4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 17).

Рис. 17

Ответ: 5 кв.ед.

Применить метод «полных» клеток нельзя.

_{Задача 4. Вычислить площадь треугольника (Рис. 18).}

Рис. 18

1 способ.Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 19) и определяем координаты вершин данного треугольника: .

Рис. 19

Применим формулу и приведем определитель к треугольному виду, предварительно переставляя местами первую и последнюю строки:

Ответ: 6 кв. ед.

2 способ.Решение. Решим задачу с помощью формулы Проведем высоту BD к стороне AC (Рис. 20):

Рис.20

Ответ: 6 кв.ед.

3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 21).

Рис. 21

Ответ: 6 кв.ед.

4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 22).

Рис. 22

Ответ: 6 кв.ед.

Применить метод «полных» клеток нельзя.

Задача 5. Вычислить площадь четырехугольника (Рис. 23).

_{Рис. 23}

1 способ. Решение. Решим задачу с помощью определителя. Введем вспомогательную прямоугольную систему координат (Рис. 24) и определяем координаты вершин данного четырехугольника: .

Рис. 24

Применим формулу :

Ответ: 10 кв.ед.

2 способ.Решение. Так как

_{Решим задачу с помощью формулы}

Ответ: 10 кв.ед.

3 способ.Решение. Решим задачу с помощью способа «вырезания». Достроим прямоугольник (Рис. 25).

Рис. 25

Ответ: 10 кв.ед.

4 способ.Решение. Решим задачу с помощью формула Пика:. Выделим узловые внутренние и граничные точки фигуры (Рис. 26).

Рис. 26

Ответ: 10 кв. ед.

Применить метод «полных» клеток нельзя.

ЗАКЛЮЧЕНИЕ

Результаты исследования предсьавлены в Таблице 1:

Рациональные (Р)/нерациональные (Н) способы, Н/П (не применим)
№ способа	Способ		Задача 1	Задача 2	Задача 3	Задача 4	Задача 5
1 способ		Определитель	Р	Р	Р	Р	Н/П
2 способ		По формулам площадей	Н	Р	Р	Р	Р
3 способ		Метод «вырезания»	Н	Н	Р	Р	Н/П
4 способ		Формула Пика	Р	Р	Р	Р	Н/П
5 способ		Метод «полных» клеток	Р	Н	Р	Р	Н/П

Таблица 1

В процессе исследования была изучена справочная, научно-популярная литература. В результате исследований появилась возможность расширить свои знания о решении задач на клетчатой бумаге, определить классификацию исследуемых задач, убедиться в их многообразии способов вычисления площади многоугольников, нарисованных на клетчатом листке Рассмотренные задачи имеют различный уровень трудности – от простых до олимпиадных. Каждый может найти среди них задачи посильного уровня сложности, отталкиваясь от которых, можно будет переходить к решению более трудных.

Рассмотренный предмет исследования достаточно многогранен, задачи на клетчатой бумаге многообразны, методы и приёмы их решения также разнообразны. Исследуемые фигуры часто требуют применения векторной геометрии, теоремы Пифагора. К рациональным способам вычисления площади фигуры можно отнести формулу Пика, вычисление площади с помощью определителя. Универсальным способом можно назвать способ вычисления по формулам площадей, значит, возникает необходимость знать всё разнообразие формул.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ

1. НОУ «ИНТУИТ» Лекция Определители – Режим доступа http://www.intuit.ru/ (дата обращения 09.06.2017)

2. Формула Пика. Математические этюды — Режим доступа: http://www.etudes.ru/ru/etudes/pick/ (дата обращения 09.06.2017)

3.Васильев Н. Б. Вокруг формулы Пика // Квант. — 1974. — № 12 стр.39-43

4. Матвеева Н. М.; Валеева А. А. Методическое пособие разработано для проведения практических занятий со студентами 4-го курса, обучающихся по специальности «Почвоведение» — Режим доступа: http://dspace.kpfu.ru/ (дата обращения 09.06.2017)

Просмотров работы: 1353

Формулы площадей геометрических фигур.

Площадь геометрических фигур. 9 класс. ОГЭ

3.а) Боковая сторона равнобедренного треугольника равна 34, а основание равно 60. Найдите площадь этого треугольника.

Б) Боковая сторона равнобедренного треугольника равна 25, а основание равно 48. Найдите площадь этого треугольника.

в)Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.

г) Боковая сторона равнобедренного треугольника равна 50, а основание равно 60. Найдите пл Периметр равнобедренного треугольника равен 216, а боковая сторона – 78. Найдите площадь треугольника.

д)Периметр равнобедренного треугольника равен 392, а боковая сторона – 100. Найдите площадь треугольника.

е)Периметр равнобедренного треугольника равен 324, а боковая сторона – 82. Найдите площадь треугольника

4. А)В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45∘. Найдите площадь треугольника.

б) В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45∘. Найдите площадь треугольника.

в) В прямоугольном треугольнике гипотенуза равна 8, а один из острых углов равен 45∘. Найдите площадь треугольника

г)В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45∘. Найдите площадь треугольника.

5.а)В треугольнике со сторонами 16 и 2 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?

б) В треугольнике со сторонами 15 и 3 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 1. Чему равна высота, проведённая ко второй стороне?

в) В треугольнике со сторонами 2 и 4 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 2. Чему равна высота, проведённая ко второй стороне?

6. а). Площадь равнобедренного треугольника равна 196√3. Угол, лежащий напротив основания, равен 120∘. Найдите длину боковой стороны.

Б) Площадь равнобедренного треугольника равна 625√3. Угол, лежащий напротив основания, равен 120∘ 3. Найдите длину боковой стороны.

В) Площадь равнобедренного треугольника равна 4√3. Угол, лежащий напротив основания, равен, 120∘. Найдите длину боковой стороны.

Б) Площадь прямоугольного треугольника равна . Один из острых углов равен 60∘. Найдите длину катета, лежащего напротив этого угла.

В) Площадь прямоугольного треугольника равна Один из острых углов равен 60∘. Найдите длину катета, лежащего напротив этого угла.

Г) Площадь прямоугольного треугольника равна 882√ 3. Один из острых углов равен 60∘. Найдите длину катета, прилежащего к этому углу.

Д) Площадь прямоугольного треугольника равна 512√3. Один из острых углов равен 30∘. Найдите длину катета, лежащего напротив этого угла.

е) Площадь прямоугольного треугольника равна 722√3. Один из острых углов равен 30∘. Найдите длину катета, лежащего напротив этого угла.

ё)Площадь прямоугольного треугольника равна . Один из острых углов равен 30∘. Найдите длину катета, прилежащего к этому углу.

ж)Площадь прямоугольного треугольника равна 50√3. Один из острых углов равен 60∘. Найдите длину катета, прилежащего к этому углу.

з) Площадь прямоугольного треугольника равна 2450√3/3. Один из острых углов равен 30∘. Найдите длину катета, прилежащего к этому углу

е) Площадь прямоугольного треугольника равна 50√3. Один из острых углов равен 30∘. Найдите длину гипотенузы.

7. Найдите площадь трапеции, изображённой на рисунке.

8.а) Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 6.

б)

Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 5.

9.а) В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.

б)В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 2. Найдите площадь трапеции.

10.а) Боковые стороны AB и CD трапеции ABCD равны соответственно 36 и 39, а основание BC равно 12. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

б) Боковые стороны AB и CD трапеции ABCD равны соответственно 24 и 30, а основание BC равно 6. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.

11.а)Основания трапеции равны 1 и 13, одна из боковых сторон равна 15√2, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.

б)Основания трапеции равны 6 и 20, одна из боковых сторон равна 13√2, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.

в)Основания трапеции равны 6 и и 10, одна из боковых сторон равна 23√2, а угол между ней и одним из оснований равен 135∘. Найдите площадь трапеции.

12.а) Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.

13.а) б)Найти площадь трапеции

14.а) Основания равнобедренной трапеции равны 2 и 14, а её боковые стороны равны 10. Найдите площадь трапеции.

б) Основания равнобедренной трапеции равны 8 и 18, а её боковые стороны равны 13. Найдите площадь трапеции.

в)Основания равнобедренной трапеции равны 5 и 15, а её боковые стороны равны 13. Найдите площадь трапеции.

15.а) В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

б) В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

16. Найдите площадь параллелограмма

17. а)Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.

б)Площадь параллелограмма ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.

в)Площадь параллелограмма ABCD равна 140. Точка E – середина стороны AD. Найдите площадь трапеции AECB.

18.а) а Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.

б)Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.

в)Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=12, а расстояние от точки K до стороны AB равно 9.

19.а) 26. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.

б)Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.

в)Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=7 и HD=24 Диагональ параллелограмма BD равна 51. Найдите площадь параллелограмма.

20.а) Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=19, а расстояние от точки K до стороны AB равно 7.

21.а) Сторона ромба равна 9, а расстояние от центра ромба до неё равно 1. Найдите площадь ромба.

б) Сторона ромба равна 18, а расстояние от центра ромба до неё равно 5. Найдите площадь ромба.

22.а) Площадь ромба равна 27, а периметр равен 36. Найдите высоту ромба.

б) Площадь ромба равна 54, а периметр равен 36. Найдите высоту ромба.

в)Площадь ромба равна 15, а периметр равен 20. Найдите высоту ромба.

г) Площадь ромба равна 72, а периметр равен 36. Найдите высоту ромба.

д) Площадь ромба равна 48, а периметр равен 32. Найдите высоту ромба.

23.а) Периметр ромба равен 116, а один из углов равен 30∘. Найдите площадь ромба.

б) Периметр ромба равен 60, а один из углов равен 30∘. Найдите площадь ромба.

в) Периметр ромба равен 32, а один из углов равен 30∘. Найдите площадь ромба.

24.а) Найдите площадь ромба, если его диагонали равны 14 и 6.

б) Найдите площадь ромба, если его диагонали равны 45 и 2.

в) Найдите площадь ромба, если его диагонали равны 4 и 6.

25.а) Сторона ромба равна 50, а диагональ равна 80. Найдите площадь ромба.

б) Сторона ромба равна 29, а диагональ равна 42. Найдите площадь ромба.

в) Сторона ромба равна 65, а диагональ равна 104. Найдите площадь ромба.

26.а) Периметр квадрата равен 160. Найдите площадь квадрата.

б)Периметр квадрата равен 60. Найдите площадь квадрата

27.а). Площадь прямоугольного земельного участка равна 11 га, ширина участка равна 100 м. Найдите длину этого участка в метрах.

б) Площадь прямоугольного земельного участка равна 20 га, ширина участка равна 200 м. Найдите длину этого участка в метрах.

28.а)Найдите площадь квадрата, если его диагональ равна 20.

б)Найдите площадь квадрата, если его диагональ равна 50

29.а)Картинка имеет форму прямоугольника со сторонами 19 см и 32 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1080 см². Какова ширина окантовки? Ответ дайте в сантиметрах

б)Картинка имеет форму прямоугольника со сторонами 20 см и 23 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 1258 см². Какова ширина окантовки? Ответ дайте в сантиметрах.

30. Пол комнаты, имеющей форму прямоугольника со сторонами 4 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек?

31.Сколько досок длиной 4 м, шириной 20 см и толщиной 30 мм выйдет
из бруса длиной 80 дм, имеющего в сечении прямоугольник размером
30 см × 40 см?

o 32. Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

33Найти площадь фигуры

34а)Две трубы, диаметры которых равны 7 см и 24 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.

б)Две трубы, диаметры которых равны 36 см и 48 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.

в)Две трубы, диаметры которых равны 63 см и 84 см, требуется заменить одной, площадь поперечного сечения которой равна сумме площадей поперечных сечений двух данных. Каким должен быть диаметр новой трубы? Ответ дайте в сантиметрах.

35.Найдите площадь квадрата, описанного вокруг окружности радиуса: а) 83Б)15

Площади геометрических фигур

Конфигурация

Название фигуры

Формула

Правило

Треугольник

Площадь треугольника равна половине произведения его стороны на высоту, проведённую к этой стороне

Треугольник

Площадь треугольника равна половине произведения двух его сторон на синус угла между ними

Треугольник

Площадь треугольника равна корню квадратному из произведения полупериметра этого треугольника и разностей полупериметра и всех его сторон

Треугольник

Площадь треугольника равна отношению произведения квадрата его стороны на синусы прилежащих углов к удвоенному синусу противолежащего угла

Треугольник

Площадь треугольника равна отношению произведения квадрата его высоты на синус угла, из вершины которого проведена эта высота, к удвоенному произведению синусов двух других углов

Треугольник

Площадь треугольника равна произведению квадрата его полупериметра на тангенсы половин всех углов треугольника

Прямоугольный треугольник

Площадь прямоугольного треугольника равна половине произведения его катетов

Равнобедренный треугольник

Площадь равнобедренного треугольника равна половине произведения его основания на корень квадратный из разности квадратов боковой стороны и половины основания

Равносторонний треугольник

Площадь равностороннего треугольника равна четверти произведения квадрата стороны этого треугольника и квадратного корня из трёх

Равносторонний треугольник

Площадь равностороннего треугольника равна отношению квадрата его высоты к квадратному корню из трёх

Треугольник

Площадь треугольника равна отношению произведения всех его сторон к четырём радиусам, описанной около него окружности

Треугольник

Площадь треугольника равна удвоенному произведению квадрата радиуса, описанной около него окружности, и синусов всех его углов

Треугольник

Площадь треугольника (многоугольника) равна произведению его полупериметра и радиуса окружности, вписанной в этот треугольник (многоугольник)

Треугольник

Площадь треугольника равна произведению квадрата радиуса вписанной окружности на котангенсы половин всех углов треугольника

Прямоугольник

Площадь прямоугольника равна произведению двух соседних его сторон

Квадрат

Площадь квадрата равна квадрату его стороны

Квадрат

Площадь квадрата равна половине квадрата его диагонали

Параллелограмм

Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне

Параллелограмм

Площадь параллелограмма равна произведению двух соседних его сторон на синус угла между ними

Ромб

Площадь ромба равна произведению квадрата его стороны на синус одного из его углов

Ромб (дельтоид)

Площадь ромба (как и дельтоида) равна половине произведения его диагоналей

Трапеция

Площадь трапеции равна произведению полусуммы её оснований на высоту

Трапеция

Площадь трапеции равна произведению её средней линии на высоту

Выпуклый четырёхугольник

Площадь выпуклого четырёхугольника равна половине произведения его диагоналей на синус угла между ними

Вписанный четырёхугольник

Площадь четырёхугольника, вписанного в окружность, равна корню квадратному из произведения разностей полупериметра этого четырёхугольника и всех его сторон

Круг

Площадь круга равна произведению числа «пи» на квадрат радиуса

Круг

Площадь круга равна четверти произведения числа «пи» на квадрат диаметра

Площадь геометрических фигур — Введение, типы, формулы, примеры и часто задаваемые вопросы

Площадь фигур

Площадь фигур – это пространство, окруженное или ограниченное границей периметра данных геометрических фигур. Это измерение, которое определяет величину двумерной формы или плоской пластинки в плоскости. Форма пластинки включает в себя двумерные фигуры, которые можно легко нарисовать на плоскости, такие как квадрат, прямоугольник, треугольник, параллелограмм, трапеция и т. д. Площади таких форм, как квадрат, прямоугольник, треугольник, параллелограмм, трапеция, круг составляют диапазон покрытые ими в пространстве. В этой статье вы изучите площади геометрических фигур, формулы площадей для различных фигур, площадь двумерных фигур, площадь трехмерных фигур и т. д.

Многоугольники

Многоугольник — это двумерная фигура, состоящая из прямых линий. Некоторыми примерами многоугольников являются треугольник, пятиугольник, шестиугольник, квадрат, прямоугольник и т. д. Само название этих фигур определяет общее количество сторон, включенных в форму. Например, у треугольника 3 стороны, а у прямоугольника 4 стороны. Таким образом, любая фигура, состоящая из соединения трех линий, называется треугольником, тогда как фигуры, состоящие из соединения четырех линий, называются четырехугольником. Область — это диапазон внутри границы/периметра, который необходимо исследовать.

Площадь двумерных фигур

В геометрии двумерные фигуры определяются как плоские фигуры или формы, которые включают две меры, такие как длина и ширина. В двумерных формах нет толщины. Площадь и периметр — две разные меры, используемые для измерения плоских фигур. Двухмерное можно легко нарисовать на обычной бумаге. Некоторыми примерами двумерных фигур являются прямоугольник, треугольник, квадрат, трапеция и т. д.

Площадь двумерных фигур Формула-

Обычно площадь фигур определяется как количество цвета краски, необходимое для покрытия любой поверхности. с одним пальто. Вот методы расчета площади на основе сторон, включенных в форму, как описано ниже:

[Изображение скоро будет загружено]

Здесь вы можете увидеть формулы площади для различных фигур в табличном формате.

Shapes	Area	Terms
Circle	π × r²	R indicates the radius of a circle
Треугольник	½ × ширина × высота	B указывает на ширину, тогда как H указывает на высоту
прямоугольник	L × w	L указывает на длину.	B обозначает ширину, а h обозначает высоту0030 (A+B) — это длина параллельных сторон, тогда как H — высота трапеции
Эллипс	π AB	ЗДЕСЬ A = ½ Минор Акс	, a = ½ Минор. b= 1/2 малой оси

Площадь трехмерных фигур

Трехмерные фигуры — это твердые формы, которые сохраняют трехмерность, такую как длина, ширина и высота. Две разные меры, используемые для определения трехмерности формы – это объем и площадь поверхности. Как правило, мы получаем трехмерные фигуры путем вращения двухмерных фигур. Основное различие между 2-мерными и 3-мерными формами заключается в том, что 3-мерные фигуры имеют толщину, тогда как 2-мерные формы не имеют толщины. Если вы хотите определить площадь поверхности любых твердых фигур, то ее можно легко определить по площади 2 d фигур.

Площадь трехмерных фигур Formula-

В соответствии с международной системой единиц (СИ) стандартной единицей площади является квадратный метр (м²). Например, некая фигура площадью 4 квадратных метра будет иметь такие же площади, как и четыре таких квадрата. Площадь поверхности твердых форм определяется как мера общей площади, которую покрывает поверхность объекта.

Здесь вы можете увидеть формулы площади для всех фигур в табличном формате.

0030

R = радиус, если круговое основание

H = высота цилиндра

Shapes	Formula	Terms
Cube	6a²	‘a’ = length of the edge
Rectangular prism	2 (WL + HL + HW)	1 = длина, W = ширина, H = высота
Цилиндр	2π R (H + R)	2π R (H + R)
Конинг	πr (R + L)	R = Radius, если циркулярная база l = nle height
Sphere	4Πr²	r = radius of spheres
Hemisphere	3Πr²	r= radius of the hemisphere

Включая площадь плоских фигур, дополнительная переменная, т. е. высота переменной, принимается во внимание при расчете площади поверхности фигур.

Исследуйте круг радиусом r и нарисуйте бесконечные концентрические круги. Теперь от центра круга к его границе нарисуйте отрезок, равный радиусу круга, вместе с этим отрезком. Будет сформирован треугольник с основанием, эквивалентным длине окружности, и высотой, эквивалентной радиусу внешней окружности, т.е. r. Таким образом, площадь можно рассчитать как ½ × основание × высота, т. е. ½ * 2πr².

Решенные примеры-

1. Вычислите площадь кругового пути, радиус которого равен 7 см.

Решение:

Радиус окружности = 7 см (дано)

Как мы знаем, площадь круга равна πr²

Соответственно,

Площадь = π × r × r

Площадь = 22/7 × 7 × 7

Площадь = 154 квадратных метра

2. Какова будет ширина прямоугольника, если его площадь 72 см, а длина 8 см.

Решение:

Как сейчас,

Площадь прямоугольника = длина × ширина

Учитывая, что площадь = 72 см, а длина = 8 см

Пусть ширина прямоугольника равна

Как мы сейчас,

Площадь прямоугольника = длина × ширина

Соответственно,

A = l × b

72 = 8 × a

72 = 8a

a = 72/9

a= 8 см

Следовательно, ширина прямоугольника 8 см.

3. Вычислите площадь конуса, радиус которого равен 4 см, а высота равна 3 см’

Решение:

Радиус конуса = 4 см и высота конуса = 3 см ( Gven)

Как мы теперь знаем, площадь конуса равна πr(r + l)

Наклонная высота = l \[\ sqrt{4²+3²}\] = \[\sqrt{25}\] = 5 см

Площадь конуса = πr(r + l)

A = 22/7 × 4 (4 + 5)

A = 22/7 × 4(9)

A = 22/7 × 36

A = 113,14 см²

Время викторины

Соотношение их площадей.

1: 3²
1: 4²
1: K²
1: 2K²
9034

. удваивается?

Он увеличится два раза
. высота которого равна 2\[\sqrt{3}\]см
1. \[\sqrt{3}\]см²
2. 2\[\sqrt{3}\]см²
3. 3\[\sqrt{3}\]см
  9\03334
Калькулятор площади — Площадь любой геометрической фигуры
Калькулятор площади — это универсальный калькулятор, который вычисляет площадь всех геометрических фигур. Основываясь на выбранной вами фигуре, наш калькулятор площади быстро найдет площадь и вернет вам результат. Кроме того, вы можете выбрать, в каких квадратная единица вы хотели бы измерить это ( квадратных метров , квадратных дюймов , квадратных футов ).
Что такое область в математике? Определение площади
В математике количество квадратных единиц, необходимых для покрытия поверхности замкнутой фигуры, мы называем площадью. Как геометрический термин площадь происходит от латинского языка 1560-х годов, что означает «открытая или закрытая поверхность, содержащаяся в определенном наборе пределов».
Если вы посмотрите вокруг себя, вы найдете применение этой области во многих ситуациях. Бывший. Вы хотите построить бассейн или не уверены, какой размер ковра подойдет для вашей комнаты. Во всех этих случаях вы можете использовать формулу площади, чтобы вычислить и найти размеры, выраженные в квадратных футах, квадратных метрах, квадратных дюймах и т. д..
Как рассчитать площадь?
Существует общее правило расчета площади любой формы, так что давайте посмотрим.
Когда мы хотим вычислить площадь определенной фигуры, сначала нам нужно поместить фигуру на воображаемую сетку, в которой каждый квадрат сетки равен 1 квадратной единице.
Пример: Мы хотим покрасить стену, но не знаем площадь стены. Во-первых, представьте, что стена представляет собой одну огромную сетку с маленькими квадратами, и все, что вам нужно сделать, это посчитать, сколько этих квадратов находится внутри сетки.
Предположим, мы измеряем его в квадратных метрах, и всего в сетке 6 квадратов. Это число указывает на то, что площадь стены (сколько пространства содержится внутри стены) равна 6 квадратных метров.
Стена имеет прямоугольную форму, а как насчет круглой, многоугольной или треугольной формы? Как вычислить их площадь? Все эти аспекты мы рассмотрим в следующих разделах.
Формула площади квадрата 9{2}})
Формула площади треугольника
У каждого треугольника три стороны, и чтобы вычислить его площадь, нам нужно знать длину всех трех сторон. {2}} 9{2}}{4\pi}
C – длина границы круга
Формула площади сектора
Сектор является частью круга. Он представляет собой пространство, ограниченное двумя радиусами и углом между ними. Таким образом, пространство, которое сектор занимает внутри круга, также считается площадью сектора. Каждый сектор имеет два типа: второстепенный и основной. Малый сектор — это часть, меньшая полукруга, в отличие от большого сектора, который больше полукруга.
Рассчитываем 9{2}\theta
θ – угол между двумя радиусами
r – радиус окружности
Формула площади эллипса
Эллипс не является идеальной окружностью; таким образом, расстояние от центра до соответствующих окружностей не является постоянным. Линия, соединяющая две дальние точки эллипса, называется большой осью. Линия с меньшим расстоянием между двумя точками называется малой осью. Площадь эллипса можно вычислить, умножив половину большой оси на половину малой оси.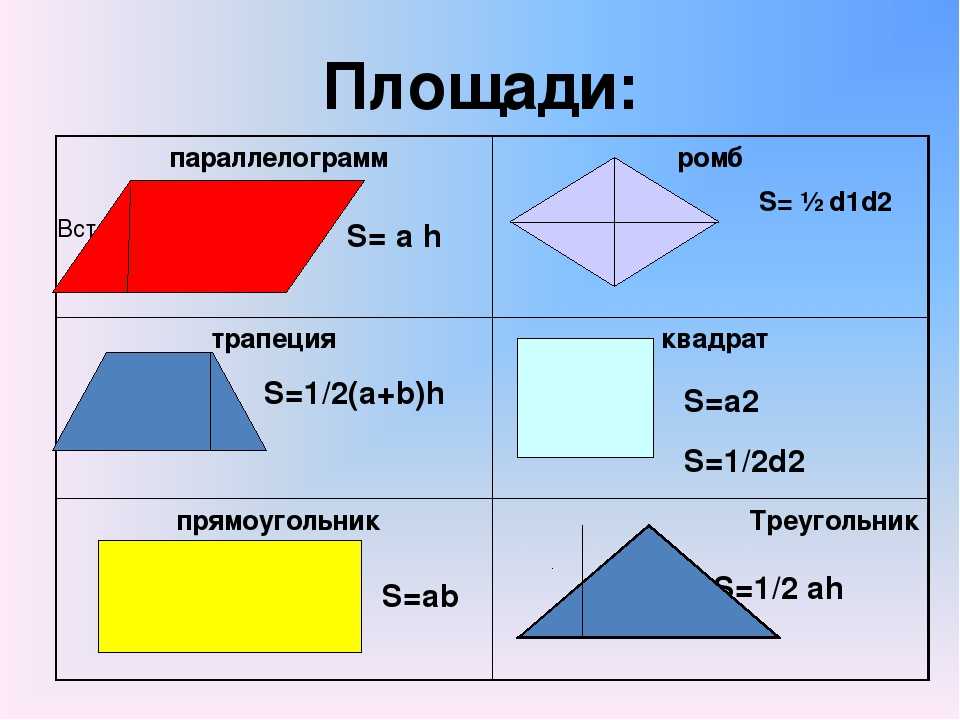
Площадь эллипса = \pi \times a \times b
π – число PI
a – большая ось
b – малая ось
Формула площади трапеции
Чтобы найти площадь трапеции, достаточно знать длину двух параллельных сторон и расстояние между ними (высоту). Также есть калькулятор для расчета параметров трапеции.
Площадь трапеции = \frac{1}{2} (a + b) h
a – основание 1
b – основание 2
h – расстояние между двумя основаниями
Формула площади параллелограмма
Параллелограмм – это четырехугольник с двумя парами параллельных сторон. Например, ромб, квадрат и прямоугольник являются параллелограммами. Все они имеют две пары параллельных линий, которые ограничивают пространство и образуют геометрическую фигуру.
Измерим площадь параллелограмма , умножив длину его основания на его высоту (высоту):
Площадь параллелограмма = b \×h
b – одно из его оснований
h – расстояние между основаниями
Второй метод: Вы можете рассчитать площадь параллелограмма, используя длину его диагоналей:
Площадь параллелограмма = \frac{1}{2} \times d1 \times d2 \times sin(x)
d1 – диагональ 1
d2 – диагональ 2
x – угол между двумя диагоналями
Площадь формулы ромба
Ромб – параллелограмм, у которого все стороны равны. Однако он отличается от квадрата, потому что ромб не обязательно должен иметь все четыре прямых угла между сторонами.
Мы можем вычислить площадь ромба тремя различными способами или воспользоваться нашим калькулятором площади:
Используя длину основания и высоту:
Формула площади ромба = b \×h
b – основание
h – длина высоты
Через длину диагоналей ромба: 9{2} \times sin(A)
сторона – одна из сторон ромба (неважно какая, потому что все они равны)
A – угол между двумя сторонами
Площадь ромба формула воздушного змея
Воздушный змей – это четырехугольник с четырьмя углами, двумя диагоналями и четырьмя сторонами (две пары равных смежных сторон). Он очень похож на ромб.
Для вычисления площади воздушного змея существует только одна формула, и она выглядит так же, как и для ромба:
Площадь воздушного змея = \frac{1}{2} \times d1 \times d2
Мы получим площадь воздушного змея, умножив две его диагонали и разделив это число на 2.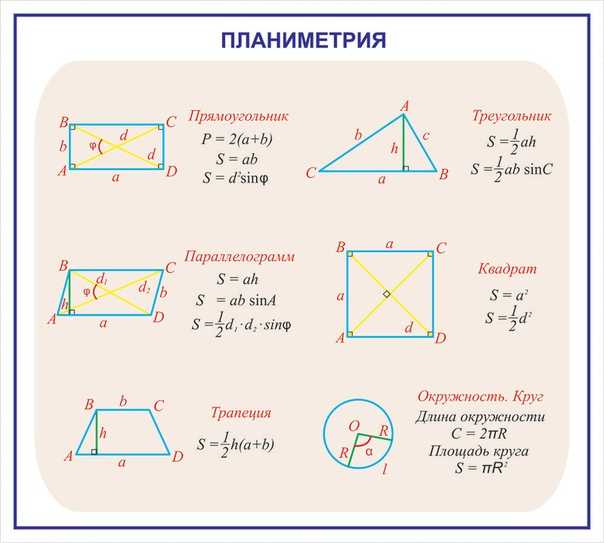
Формула площади пятиугольника
Пятиугольник — это двумерный многоугольник с 5 сторонами.
Рассчитаем площадь пятиугольника по любой из этих двух формул или воспользуемся нашим калькулятором площади:
Площадь пятиугольника = \frac{5}{2} \times s \times a
s – длина одного из стороны пятиугольника 9{2} \times (1 + \sqrt{2})
s – сторона восьмиугольника
Формула площади кольца
Предположим, мы нарисовали две концентрические окружности с точным центром разного радиуса. В этом случае два круга образуют форму, подобную кольцу, которое называется кольцом. Поскольку кольцо основано на радиусе обоих кругов, для расчета площади кольца нам нужно знать площадь меньшего и большего круга. Зная их площади, мы можем легко вычесть площадь меньшего круга из большего круга и получить площадь кольца. 9{2})
Площадь четырехугольника формула
Четырехугольник представляет собой замкнутую фигуру с четырьмя линиями.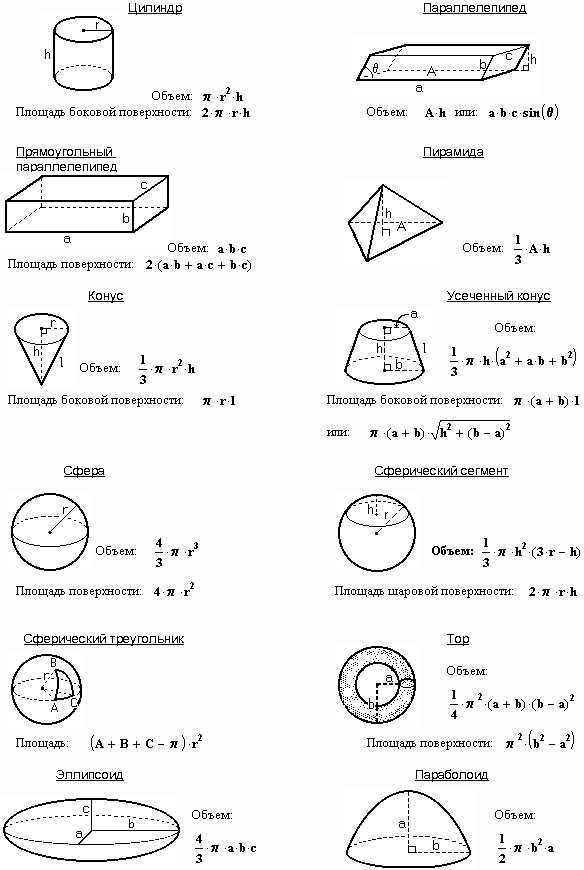 Если четырехугольник имеет все линии одинаковой длины, мы называем его правильным четырехугольником. Однако, если линии разного размера, такой четырехугольник называется неправильным.
Площадь четырехугольника можно вычислить, разделив его на два треугольника:
Площадь четырехугольника = \frac{1}{2} \times d \times (Sum of h)
d – одна из его диагонали
Сумма h – сумма всех его высот
Формула площади правильного многоугольника
Правильный многоугольник – это многоугольник с равными сторонами и углами. Например, это квадрат, правильный пятиугольник, равносторонний треугольник и многое другое.
У каждого из них есть специальная формула расчета площади, но это универсальная формула площади правильного многоугольника:
Площадь правильного многоугольника = (количество сторон × длина одной стороны × апофема) / 2
Также, кроме упомянутых калькуляторов площади, есть еще один — калькулятор площади поверхности конуса.
No related posts.