Умножение степеней отрицательных: Свойства отрицательных степеней. Как умножать отрицательные степени. Деление отрицательных степеней. Степени чисел

§ 8. Степень с отрицательным целым показателем

Класс

• 1 класс

• 2 класс

  • Математика
  • Английский язык

• 3 класс

  • Английский язык
  • Русский язык
  • Математика

• 4 класс

  • Математика
  • Русский язык
  • Английский язык

• 5 класс

  • Биология
  • Английский язык
  • Русский язык
  • Математика

• 6 класс

  • Математика
  • Биология
  • Английский язык
  • Русский язык

• 7 класс

  • Химия
  • Английский язык
  • Русский язык
  • Физика
  • Математика
  • Биология

• 8 класс

  • Английский язык
  • Биология
  • Химия
  • Математика
  • Физика
  • Русский язык

• 9 класс

  • Химия
  • Биология
  • Английский язык
  • Физика
  • Русский язык
  • Математика

• 10 класс

  • Биология
  • Математика
  • Физика
  • Химия
  • Английский язык

• 11 класс

  • Химия
  • Английский язык
  • Биология

8 КЛАСС

§ 8.

n. Упростить.

Упростить левую часть и сравнить с правой частью уравнения.

Упростить левую часть и сравнить с правой частью уравнения.

Упростить левую часть и сравнить с правой частью уравнения.

Вопросники:

Вопрос:

Вопрос:

Вопрос:

Пропуски:

возведениепроизведениеделениеумножениеделениепроизведение

Последовательности:

Степень с натуральным показателем — intmag24.ru

Степень с натуральным показателем — это произведение из нескольких одинаковых множителей. 
Например: 2 × 2 × 2 = 2³ = 8

• Пишется: сначала записывается повторяющийся множитель, а над ним указывается сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку.
• Читается: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».

где:
a — основание степени; в выражении 2³ основанием степени является число 2.
n — показатель степени; в выражении 2³ показателем степени является число 3. 

В данной статье рассмотрена степень с натуральным показателем. То есть, показателем степени является натуральное число (натуральные числа —  это целые числа, которые больше нуля, например, 1, 2, 3 и т.д.).

Степень числа a с натуральным показателем n — это выражение вида an, которое равно произведению n множителей, каждый из которых равен

Степень числа с показателем 1  есть само это число. Соответственно, если у числа отсутствует показатель, то надо считается, что показатель равен единице.
Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1

Если возвести 0 в какую-нибудь степень, то получится 0.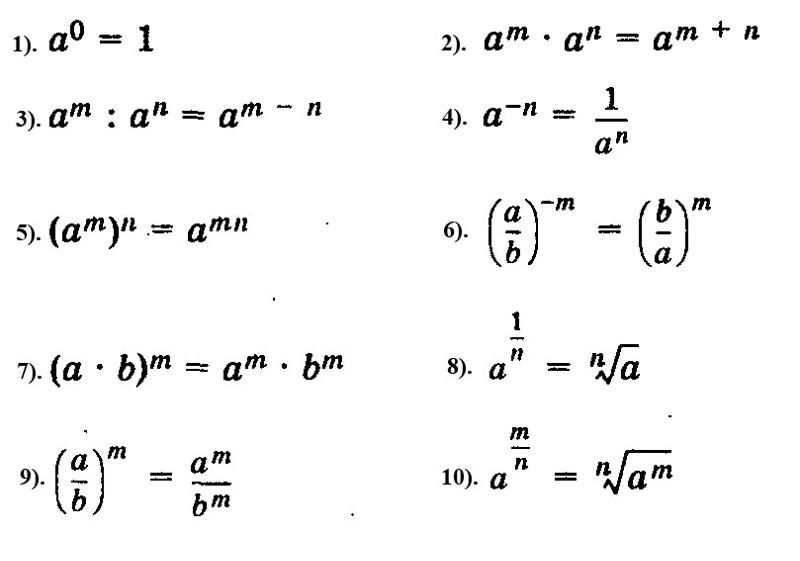 Действительно, сколько бы раз ничего не умножалось на само себя получится ничего.

• Пример 1. Возвести число 3 во вторую степень. Получим: 3
  2 = 3 × 3 = 9
• Пример 2. Возвести число 2 в четвертую степень. Получим: 2⁴ =2 × 2 × 2 × 2 = 16

Возведение в степень числа 10

Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.

• 10¹ = 10
• 10² = 10 × 10 = 100
• 10³ = 10 × 10 × 10 = 1000
• 10⁴ = 10 × 10 × 10 × 10 = 10000

Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.

• Число 10 имеет один нуль, значит, число 10 в виде степени  будет представлено как 10¹: 10 = 10¹
• Число 100 содержит два нуля, значит, число 100 в виде степени с основанием 10 будет представлено как 10²: 100 = 10² и т. д. 

Возведение в степень отрицательного числа

При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.
Это делается для того, чтобы поставить правильный знак при взведении в четную или нечетную степень.

Рассмотрим примеры: возведем число (-2) в четную и нечетную степень.

(−2)² = (−2) × (−2) = 4

• Если мы не заключим в скобки число −2, то мы будем вычислять выражение −2² или -(2²), которое будет равно −4: сначала выполняется операция возведения в степень, а затем выполняется взятие противоположного значения. 
• Если мы число -2 заключаем в скобки, то выполняем операцию возведения в степень с учетом знака: сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.

(−2)³ = (−2) × (−2) × (−2) = −8

(−2)⁴ = (−2) × (−2) × (−2) × (−2) = 16

Таким образом, при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.

Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным.

Нахождение значений выражений

При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.

Пример 1. Найти значение выражения 2 + 5²
Сначала выполняется возведение в степень: 5² = 25.
Затем этот результат складывается с числом 2: 2 + 5² = 2 + 25 = 27

Пример 2. Найти значение выражения −6² × (−12)
Сначала выполняется возведение в степень: заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус: −6

2  = −36 
Затем полученное  значение умножим на (−12): −6² × (−12) = −36 × (−12) = 432

Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.

Пример 3. Найти значение выражения (3² + 1 × 3) − 15 + 5
Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3.
Далее выполняется вычитание и сложение в порядке их следования: (3

2 + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2

Свойства степеней

Свойство 1: произведение степеней

При умножении степеней с одинаковыми основаниями, основание мы оставляем без изменений, а показатели степеней складываем:

an × am = an + m

a — основание степени
m, n — показатели степени, любые натуральные числа.

Пример. 2²×2³= 2²⁺³= 2⁵

Свойство 2: частное степеней

При делении степеней с одинаковыми основаниями, основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.

an : am = an — m

a — любое число, не равное нулю
m, n — любые натуральные числа такие, что m > n

Пример. 2⁷:2³= 2^7-3= 2⁴

Свойство 3: возведение степени в степень

При возведении степень в степень основание степени остается неизмененным, а показатели степеней умножаются друг на друга.

(an)m = an × m

a — основание степени
m, n — показатели степени, натуральное число/

Пример. (3²)² = 3⁴ = 81

Свойство 4: возведение в степень произведения

При возведении в степень произведения каждый из множителей возводится в степень. Затем полученные результаты перемножаются.

(a × b)n = an × bn

a, b — основание степени
n — показатели степени, натуральное число

Пример. (2×4)³= 2³×4³=8+64=72

Свойство 5: возведение в степень частного

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.

(a : b)n = an : bn

a, b — основание степени, b ≠ 0, 
n — показатель степени, натуральное число

Пример. (6:2)³= 6³:2³=216:8=27

Возведение в степень обыкновенных дробей

Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.

Пример.(1/6)³= 1³/6³

Возведение в степень десятичных дробей

При возведении в степень десятичной дроби её необходимо заключить в скобки.
Например, возведём в третью степень десятичную дробь -1,5. Показатель степени является нечётным числом, значит ответ будет отрицательным и равен -3,375.

Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:
(15/10)³=(3/2)³= 3³/2³

 

2??? равно ???(-4)(-4)??? или ???16???.

Как применить показатель степени к отрицательному основанию

Пройти курс

Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого. 🙂

Учить больше

Нахождение степеней отрицательных оснований

Пример

Упростите выражение. 94???

???(-1)(-1)(-1)(-1)???

???1???

Получите доступ к полному курсу Алгебра 2

Начать

Изучение математикиКриста Кинг 25 ноября 2020 г. математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра II, показатели, степени, отрицательные основания, показатели степени по отрицательным основаниям, степени отрицательных оснований

0 лайков

math — Как умножить число с отрицательной степенью в python

Когда я пытаюсь умножить это на отрицательное целое число, оно просто возвращает ошибку

Я использую:

A = np.array([[1, 2,0], [2,4,-2], [0,-2,3]])

• питон
• математика

7

Судя по скриншоту, это домашнее задание.

Итак, он запрашивает обратную матрицу

. В математике это записывается как 9(-1)

 импортировать numpy как np
A = np.массив([[1,2,0], [2,4,-2], [0,-2,3]])
np.linalg.inv(A)
 

 массив([[-2. , 1.5 , 1. ],
       [1,5, -0,75, -0,5],
       [ 1. , -0. 5 , 0. ]])
 

0

В numpy вы не можете повышать целые числа отрицательными целочисленными степенями (прочитайте это).

В python оператор ** возвращает значение без ошибок.

 В [6]: А = 20
В [7]: напечатать (A ** -1)
0,05
 

Вы также можете использовать pow() ,

 В [1]: A = 20
В [2]: pow(20, -1)
Выход[2]: 0,05
 

Если вы работаете с матрицами, рекомендуется убедиться, что они являются экземплярами типа numpy.matrix , а не более общего типа numpy.ndarray .

 импортировать numpy как np
M = np.matrix([[ ... ]])
 

Чтобы преобразовать существующий общий массив в матрицу, вы также можете передать его в np.asmatrix() .

Если у вас есть матрица instance M , один из способов получить обратную M.I

Чтобы избежать проблемы «целые числа не разрешены», убедитесь, что dtype вашей матрицы является числом с плавающей запятой, а не целым числом (укажите dtype = float в вызове matrix() или asmatrix() )

1

Чтобы вставить мощность как отрицательное значение, предположите другую переменную и назовите ее «pow» и назначьте это отрицательное значение.