Матрицы для чайников: умножение, сложение, вычитание. Как решать, с чего начать

Разреженные матрицы (sparse matrix) для чайников

Автор Роман Котюбеев

В одной из статей по Apache Spark я говорил о разреженных (sparse) матрицах, но не вдавался в подробности. Многих сбивают с толку эти разреженные матрицы, поскольку формат их хранения отличается от плотных матриц. Тем не менее, разреженные матрицы очень часто используются в Data Science, поскольку их хранение менее затратное. Сегодня мы шаг за шагом рассмотрим переход от плотных матриц к разреженным, начав со списка координат (COOrdinate list) и закончив сжатым хранением строкой (CSR) и столбцом (CSC).

Локальные векторы: плотные и разреженные

Допустим, что у нас имеется матрица (см. рисунок ниже). При беглом взгляде осознаем, что в ней много нулей (возможно, это матрица c категориальными значениями) А что если бы это была матрица 1000×1000? А матрица 100000×500000 со всеми этими нулями? Нет смысла хранить матрицу, где большая часть элементов – это нули. Поэтому пришли к так называемым разреженным матриц (sparse matrix).

Плотная матрица

Разреженные матрицы представляют в различных форматах:

• координатный список (Coordinate List),
• сжатое хранение строкой (Compressed Sparse Row),
• сжатое хранение столбцом (Compressed Sparse Column),
• список списков (List of lists),
• словарь ключей (Dict of keys)

Мы расскажем о первых трех, так как они встречаются чаще.

Список координат (Coordinate List)

Возможно, самый очевидный формат хранения разреженных матриц является список координат. Такой формат представляет собой триплет (строка, столбец, значение). При этом, хранятся только ненулевые значения. Например, матрицу выше можно записать следующим образом:

Представление списка координат

В этом формате еще хранится размерность матрицы. Подразумевается, что не записанные значения являются нулями.

Улучшаем, применив правило row-major order

Мы можем еще улучшить список координат. Давайте вместо того чтобы хранить каждый индекс строки, будем хранить количество ненулевых значений на каждой строке. Вот, что случится, после применения данного правила:

Улучшенный список координат

Подобное правило примененное к строкам называется порядок по строкам (row-major mode). Ничто не мешает применить его к столбцам, тогда это будет порядок по столбцам (column-major order)

[1].

Как можно заметить, теперь мы храним меньше данных: в данном примере меньше на два элемента по сравнению с оригинальным списком координат.

А что насчет компьютера? Получается, что он хранит три массива и размерность разреженной матрицы. Тогда как извлечь отдельные строки (поскольку это row-major order) из нее? Алгоритм извлечения p-й строки достаточно прост. Допустим, нам нужна 3-я строка (не забываем про счет с 0), т.е. последняя строка (0,0,0,1,0,3,0), тогда требуется:

1. Определить количество n ненулевых элементов выше p-й строки. Выполнить эту процедуру путем суммирования элементов в векторе Не-0 в строке вплоть до p-й строки. Для 3-й строки получается 1 + 3 + 0 = 4, значит количество ненулевых элементов выше 3-й строки равно 4.
2. Определить количество k элементов в p-й строке. Это значение равно p-му элементу вектора Не-0 в строке. Для 3-е строки это значение равно 2.
3. Дойти до элемента n + 1 векторов Столбец и Значение. В нашем случае это 4 + 1 = 5.
4. Взять k пар элементов векторов Столбец и Значение. В нашем случае это пары (3, 1) и (5, 3).
5. Вернуть вектор размера N (где N – это количество строк) с заполненными соответствующими парами, а остальные элементы заполняются нулями. В нашем случае это a[3] = 1 и a[5] = 3, а все остальное — это нули.

Сжатое хранение строкой (Compressed Sparse Row, CSR)

А что если мы захотим извлечь строку 2-ю, потом 1-ю, потом снова 2-ю и т. д. Исходя из алгоритма, происходит суммирование элементов вектора

Не-0 в строке каждый раз при извлечение очередной строки. Так, может быть, сразу и заменим вектор Не-0 в строке на кумулятивную сумму количества ненулевых элементов в строке и назовем новый вектор Кумулята Не-0 в строке. Тогда получится такой результат:

Формат CSR

И вот снова требуется получить p-ю строку, например, 3-ю. Тогда алгоритм ее получения будет следующим:

1. Определить количество ненулевых элементов выше p-й строки. Это просто (p — 1)-й элемент вектора Кумулята Не-0 в строке. Для 3-й строки — это 4.
2. Определить количество ненулевых элементов в строке p. Это количество равно разнице между p-м и (p-1)-м элементами вектора Кумулята Не-0 в строке. Для 3-й строки эта разница между 3-м и 2-м элементами, т.е. 6 — 4 = 2.
3. Шаги 3, 4, 5 такие же, как и выше.

В первом шаге нужно добавить условие при извлечении 0-ю строки:

Если требуется 0-я строка, вернуть 0 — поскольку выше этой строки ничего нет.

Такой формат хранения называется сжатое хранение строкой (Compressed Sparse Row, CSR).

Сжатое хранение столбцом (Compressed Sparse Column, CSC)

В задачах машинного обучения (machine learning) наиболее распространенной практикой является извлечение столбцов (признаков) нежели строк. С точки зрения математики строки и столбцы матрицы эквивалентны, поэтому правила выше можно применять к столбцам. Такая форма представления называться сжатое хранение столбцом (Compressed Sparse Column, CSC).

Если мы будем считать кумуляту по столбцам, т.е. по правилу порядка по столбцам (column-major order), то получим следующее:

Формат CSC

При извлечении столбца считаем то, что левее и правее необходимого. И также возвращается 0 на первом шаге алгоритма при извлечении 0-го столбца.

Еще больше подробностей о векторах, матрицах и других структурах данных с примерами из Data Science вы узнаете на специализированном курсе по машинному обучению «PYML: Введение в машинное обучение на Python» в лицензированном учебном центре обучения и повышения квалификации разработчиков, менеджеров, архитекторов, инженеров, администраторов, Data Scientist’ов и аналитиков Big Data в Москве.

Смотреть расписание

Записаться на курс

Источники

1. https://en.wikipedia.org/wiki/Row-_and_column-major_order

Математика для чайников. Матрицы и основные действия над ними. Матрицы, действия над матрицами. Обратная матрица. Ранг матрицы Виды матриц и действия над ними

Матрицы. Действия над матрицами. Свойства операций над матрицами. Виды матриц.

Матрицы (и соответственно математический раздел — матричная алгебра) имеют важное значение в прикладной математике, так как позволяют записать в достаточно простой форме значительную часть математических моделей объектов и процессов. Термин «матрица» появился в 1850 году. Впервые упоминались матрицы еще в древнем Китае, позднее у арабских математиков.

Матрицей A=A mn порядка m*n называется прямоугольная таблица чисел, содержащая m — строк и n — столбцов .

Элементы матрицы a ij , у которых i=j, называются диагональными и образуют главную диагональ .

Для квадратной матрицы (m=n) главную диагональ образуют элементы a 11 , a 22 ,…, a nn .

Равенство матриц.

A=B , если порядки матриц A и B одинаковы и a ij =b ij (i=1,2,…,m; j=1,2,…,n)

Действия над матрицами.

1. Сложение матриц — поэлементная операция

2. Вычитание матриц — поэлементная операция

3. Произведение матрицы на число — поэлементная операция

4. Умножение A*B матриц по правилу

строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)

A mk *B kn =C mn причем каждый элемент с ij матрицы C mn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элемеенты j-го столбца матрицы B , т.е.

Покажем операцию умножения матриц на примере

5. Возведение в степень

m>1 целое положительное число. А — квадратная матрица (m=n) т.е. актуально только для квадратных матриц

6. Транспонирование матрицы А. Транспонированную матрицу обозначают A T или A»

Строки и столбцы поменялись местами

Пример

Свойства опрераций над матрицами

(A+B)+C=A+(B+C)

λ(A+B)=λA+λB

A(B+C)=AB+AC

(A+B)C=AC+BC

λ(AB)=(λA)B=A(λB)

A(BC)=(AB)C

(λA)»=λ(A)»

(A+B)»=A»+B»

(AB)»=B»A»

Виды матриц

1. Прямоугольные: m и n — произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1 . Например, (1 3 5 7) — во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1 . Например

5. Диагональная матрица: m=n и a ij =0 , если i≠j . Например

6. Единичная матрица: m=n и

7. Нулевая матрица: a ij =0, i=1,2,…,m

j=1,2,…,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

9. Симметрическая матрица: m=n и a ij =a ji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно

A»=A

Например,

10. Кососимметрическая матрица: m=n и a ij =-a ji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем a ii =-a ii )

Ясно, A»=-A

11. Эрмитова матрица: m=n и a ii =-ã ii (ã ji — комплексно — сопряженное к a ji , т.е. если A=3+2i , то комплексно — сопряженное Ã=3-2i )

Назначение сервиса . Матричный калькулятор предназначен для решения матричных выражений, например, таких как, 3A-CB 2 или A -1 +B T .

Инструкция . Для онлайн решения необходимо задать матричное выражение. На втором этапе необходимо будет уточнить размерность матриц.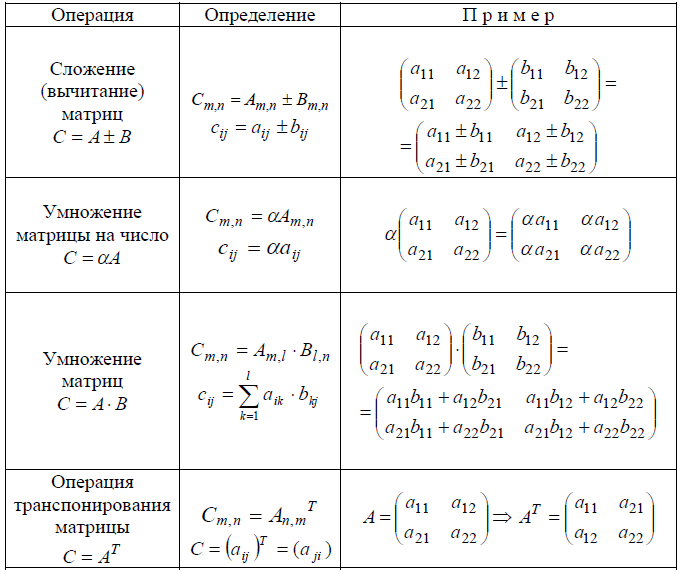 (-1)

Матрица — прямоугольная числовая таблица, имеющая m строк и n столбцов, поэтому схематически матрицу можно изображать в виде прямоугольника.

Нулевой матрицей (нуль-матрицей) называют матрицу, все элементы которой равны нулю и обозначают 0.
Единичной матрицей называется квадратная матрица вида

Две матрицы A и B равны , если они одинакового размера и их соответствующие элементы равны.
Вырожденной матрицей называется матрица, определитель которой равен нулю (Δ = 0).

Определим основные операции над матрицами .

Сложение матриц

Определение . Суммой двух матриц A=||a i k || и B=||b i k || одинакового размера называется матрица C=||c i k || тех же размеров, элементы которой находятся по формуле c i k =a i k +b i k . Обозначается C=A+B .

Пример 6 . .
Операция сложения матриц распространяется на случай любого числа слагаемых. Очевидно, что A+0=A .
Еще раз подчеркнем, что складывать можно только матрицы одинакового размера; для матриц разных размеров операция сложения не определена.

Вычитание матриц

Определение . Разностью B-A матриц B и A одинакового размера называется такая матрица C , что A+C=B .

Умножение матриц

Определение . Произведением матрицы A=||a i k || на число α называется матрица C=||c i k ||, получающаяся из A умножением всех ее элементов на α , c i k =α·a i k .

Определение . Пусть даны две матрицы A=||a i k || (i=1,2,…,m; k=1,2,…,n) и B=||b i k || (k=1,2,…,n; j=1,2,…,p), причем число столбцов A равно числу строк B . Произведением A на B называется матрица C=||c i k ||, элементы которой находятся по формуле .
Обозначается C=A·B .
Схематически операцию умножения матриц можно изобразить так:

а правило вычисления элемента в произведении:

Подчеркнем еще раз, что произведение A·B имеет смысл тогда и только тогда, когда число столбцов первого сомножителя равно числу строк второго, при этом в произведении получается матрица, число строк которой равно числу строк первого сомножителя, а число столбцов равно числу столбцов второго. Проверить результат умножения можно через специальный онлайн-калькулятор .

Пример 7 . Даны матрицы и . Найти матрицы C = A·B и D = B·A.
Решение. Прежде всего заметим, что произведение A·B существует, так как число столбцов A равно числу строк B.

Заметим, что в общем случае A·B≠B·A , т.е. произведение матриц антикоммутативно.
Найдем B·A (умножение возможно).

Пример 8 . Дана матрица . Найти 3A 2 – 2A.
Решение.

.
; .
.
Отметим следующий любопытный факт.
Как известно, произведение двух отличных от нуля чисел не равно нулю. Для матриц подобное обстоятельство может и не иметь места, то есть произведение ненулевых матриц может оказаться равным нуль-матрице.

Матрицей размерности называется прямоугольная таблица, состоящая изэлементов, расположенных вm строках и n столбцах.

Элементы матрицы (первый индексi − номер строки, второй индекс j − номер столбца) могут быть числами, функциями и т. п. Матрицы обозначают заглавными буквами латинского алфавита.

Матрица называется квадратной , если у нее число строк равно числу столбцов (m = n ). В этом случае число n называется порядком матрицы, а сама матрица называется матрицей n -го порядка.

Элементы с одинаковыми индексами образуютглавную диагональ квадратной матрицы, а элементы (т.е. имеющие сумму индексов, равнуюn +1) − побочную диагональ .

Единичной матрицей называется квадратная матрица, все элементы главной диагонали которой равны 1, а остальные элементы равны 0. Она обозначается буквой Е .

Нулевая матрица − это матрица, все элементы которой равны 0. Нулевая матрица может быть любого размера.

К числу линейных операций над матрицами относятся:

1) сложение матриц;

2) умножение матриц на число.

Операция сложения матриц определена только для матриц одинаковой размерности.

Суммой двух матриц А и В называется матрица С , все элементы которой равны суммам соответствующих элементов матриц А и В :

.

Произведением матрицы А на число k называется матрица В , все элементы которой равны соответствующим элементам данной матрицы А , умноженным на число k :

Операция умножения матриц вводится для матриц, удовлетворяющих условию: число столбцов первой матрицы равно числу строк второй.

Произведением матрицы А размерности на матрицу В размерности называется матрицаС размерности , элементi -ой строки и j -го столбца которой равен сумме произведений элементов i -ой строки матрицы А на соответствующие элементы j -го столбца матрицы В :

Произведение матриц (в отличие от произведения действительных чисел) не подчиняется переместительному закону, т.е. в общем случае А В В А .

1.2. Определители. Свойства определителей

Понятие определителя вводится только для квадратных матриц.

Определителем матрицы 2-го порядка называется число, вычисляемое по следующему правилу

.

Определителем матрицы 3-го порядка называется число, вычисляемое по следующему правилу:

Первое из слагаемых со знаком «+» представляет собой произведение элементов, расположенных на главной диагонали матрицы (). Остальные два содержат элементы, расположенные в вершинах треугольников с основанием, параллельным главной диагонали (и). Со знаком «-» входят произведения элементов побочной диагонали () и элементов, образующих треугольники с основаниями, параллельными этой диагонали (и).

Это правило вычисления определителя 3-го порядка называется правилом треугольников (или правилом Саррюса).

Свойства определителей рассмотрим на примере определителей 3-го порядка.

1. При замене всех строк определителя на столбцы с теми же номерами, что и строки, определитель своего значения не меняет, т.е. строки и столбцы определителя равноправны

.

2. При перестановке двух строк (столбцов) определитель меняет свой знак.

3. Если все элементы некоторой строки (столбца) нули, то определитель равен 0.

4. Общий множитель всех элементов строки (столбца) можно вынести за знак определителя.

5. Определитель, содержащий две одинаковые строки (столбца), равен 0.

6. Определитель, содержащий две пропорциональные строки (столбца), равен нулю.

7. Если каждый элемент некоторого столбца (строки) определителя представляет сумму двух слагаемых, то определитель равен сумме двух определителей, в одном из которых в том же столбце (строке) стоят первые слагаемые, а в другом − вторые. Остальные элементы у обоих определителей одинаковые. Так,

.

8. Определитель не изменится, если к элементам какого-либо его столбца (строки) прибавить соответствующие элементы другого столбца (строки), умноженные на одно и то же число.

Следующее свойство определителя связано с понятиями минора и алгебраического дополнения.

Минором элемента определителя называется определитель, полученный из данного вычеркиванием той строки и того столбца, на пересечении которых этот элемент расположен.

Например, минором элемента определителя называется определитель .

Алгебраическим дополнением элементаопределителя называется его минор, умноженный на, гдеi − номер строки, j − номер столбца, на пересечении которых находится элемент . Алгебраическое дополнение обычно обозначается. Для элементаопределителя 3-го порядка алгебраическое дополнение

9. Определитель равен сумме произведений элементов какой-либо строки (столбца) на соответствующие им алгебраические дополнения.

Например, определитель можно разложить по элементам первой строки

,

или второго столбца

Свойства определителей применяются для их вычисления.

Определение. Матрицей называется множество чисел, которое составляет прямоугольную таблицу, состоящее изmстрок иnстолбцов

коротко матрицу обозначают так:

где элементы данной матрицы,i– номер строки,j– номер столбца.

Если в матрице число строк равно числу столбцов (m = n ), то матрица называетсяквадратной n -го порядка, а в противном случае –прямоугольной.

Если m = 1 и n > 1, то получаем однострочную матрицу

которая называется вектор-строкой , если, жеm >1 иn =1, то получаем одностолбцовую матрицу

которая называется вектор-столбцом .

Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называется диагональной.

Диагональная матрица, у которой элементы главной диагонали равны единице, называется единично, обозначаетсяE .

Матрица, полученная из данной заменой ее строки столбцом с тем же номером, называется транспонированной к данной. Обозначается.

Две матрицы иравны, если равны между собой элементы, стоящие на одинаковых местах, то есть если

при всех i иj (при этом число строк (столбцов) матрицA иB должно быть одинаковым).

1°. Суммой двух матрицA =(a ij ) иB =(b ij ) с одинаковым количествомm строк иn столбцов называется матрицаC =(c ij ), элементы которой определяются равенством

Сумму матриц обозначают C =A +B .

Пример.

2 0 . Произведением матрицыA =(a ij ) на числоλ называется матрица, у которой каждый элемент равен произведению соответствующего элемента матрицыA на числоλ :

λA =λ (a ij )=(λa ij ), (i =1,2…,m ; j =1,2…,n).

Пример.

3 0 . Произведением матрицыA =(a ij ), имеющейm строк иk столбцов, на матрицуB =(b ij ), имеющейk строк иn столбцов, называется матрицаC =(c ij ), имеющаяm строк иn столбцов, у которой элементc ij равен сумме произведений элементовi -ой строки матрицыA иj -го столбца матрицыB , то есть

При этом число столбцов матрицы A должно быть равно числу строк матрицыB . В противном случае произведение не определено. Произведение матриц обозначается A*B =C.

Пример.

Для произведения матриц не выполняется равенство между матрицами A * B иB * A , в общем случае одна из них может быть не определена.

Умножение квадратной матрицы любого порядка на соответствующую единичную матрицу не меняет матрицу.

Пример. Пусть,, тогда согласно правилу умножения матриц имеем

,

откуда заключаем, что

Определители и их свойства.

Пусть дана квадратная матрица третьего порядка:

Определение. Определителем третьего порядка, соответствующим матрице (1), называется число, обозначаемое символом

и определяемое равенством

Чтобы запомнить, какие произведения в правой части равенства (2) берутся со знаком «+», а какие со знаком «-«, полезно использовать следующее правило треугольников.

Пример.

Сформулируем основные свойства для определителей третьего порядка, хотя они присущи определителям любого порядка.

1. Величина определителя не изменится, если его строки и столбцы поменять местами, т. е.

2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.

3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.

4. Умножение всех элементов одного столбца или одной строки определителя на любое числоλ равносильно умножению определителя на это числоλ .

5. Если все элементы некоторого столбца или некоторой строки определителя равны нулю, то и сам определитель равен нулю.

6. Если элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.

7. Если каждый элементn -го столбца (n -ой строки) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один вn -ом столбце (n -ой строке) содержит первые из упомянутых слагаемых, а другой — вторые; элементы, стоящие на остальных местах, у всех трех определителей одни и те же.

Например,

8 0 . Если к элементам некоторого столбца (строки) определителя прибавить соответствующие элементы другого столбца (строки), умноженные на любой общий множитель, то величина определителя не изменится.

Например,

Минором некоторого элемента определителя называется определитель, получаемый из данного определителя вычеркиванием строки и столбца, на пересечении которых расположен этот элемент.

Например, минором элемента а 1 определителяΔ является определитель 2-го порядка

Алгебраическим дополнением некоторого элемента определителя называется минор этого элемента, умноженный на (-1) p , гдер — сумма номеров строки и столбца, на пересечении которых расположен этот элемент.

Если, например, элемент а 2 находятся на пересечении 1-го столбца и 2-ой строки, то для негор =1+2=3 и алгебраическим дополнением является

9 0 . Определитель равен сумме произведений элементов какого–либо столбца или строки на их алгебраические дополнения.

10 0 . Сумма произведений элементов какого–либо столбца или какой–либо строки определителя на алгебраические дополнения соответствующих элементов другого столбца или другой строки равны нулю.

Возникает вопрос, можно ли для квадратной матрицы А подобрать некоторую матрицу, такую что умножив на нее матрицу А в результате получить единичную матрицу Е , такую матрицу называют обратной к матрице А.

Определение. Матрицаназывается обратной квадратной матрицеA, если.

Определение. Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. В противном случае квадратная матрица называется вырожденной.

Всякая невырожденная матрица имеет обратную.

Элементарными преобразованиями матриц являются:

перестановка местами двух параллельных рядов матрицы;

умножение всех элементов матрицы на число, отличное от нуля;

прибавление ко всем элементами ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

Матрица В , полученная из матрицыА с помощью элементарных преобразований, называетсяэквивалентной матрицей.

Для невырожденной квадратной матрицы

третьего порядка обратная матрица А -1 может быть вычислена по следующей формуле

здесь Δ — определитель матрицы А ,A ij – алгебраические дополнения элементовa ij матрицыА.

Элемент строки матрицы называется крайним , если он отличен от нуля, а все элементы строки, находящиеся левее него, равны нулю. Матрица называетсяступенчатой , если крайний элемент каждой строки находится правее крайнего элемента предыдущей строки. Например:

Не ступенчатая; — ступенчатая.

Матрицей называется прямоугольная таблица, заполненная некоторыми математическими объектами. По большей части мы будем рассматривать матрицы с элементами из некоторого поля, хотя многие предложения сохраняют силу, если в качестве элементов матриц рассматривать элементы ассоциативного (не обязательно коммутативного) кольца.

Чаще всего элементы матрицы обозначаются одной буквой двумя индексами, указывающими «адрес» элемента — первый йндекс дает номер строки, содержащей элемент, второй — номер столбца. Таким образом, матрица (размеров ) записывается в форме

Матрицы, вставленные из чисел, естественно возникают при рассмотрении систем линейных уравнений

Входные данные для этой задачи — это множество коэффициентов, естественно составляющих матрицу

и совокупность свободных членов, образующих матрицу , умеющую лишь один столбец. Искомым является набор значений неизвестных, который, как оказывается, удобно представлять тоже в виде матрицы состоящей из одного столбца.

Важную роль играют так называемые диагональные матрицы. Под этим названием подразумеваются квадратные матрицы, имеющие все элементы равными нулю, кроме элементов главной диагонали, т. е. элементов в позициях

Диагональная матрица D с диагональными элементами обозначается

Матрица, составленная из элементов, находящихся на пересечениях нескольких выбранных строк матрицы А и нескольких выбранных столбцов, называется субматрицей для матрицы А. Если — номера выбранных строк и — номера выбранных столбцов, то соответствующая субматрица есть

В частности, строки и столбцы матрицы можно рассматривать как ее субматрицы.

Матрицы связаны естественным образом с линейной подстановкой (линейным преобразованием) переменных. Под этим названием понимается переход от исходной системы переменных к другой, новой, связанных по формулам

Линейная подстановка переменных задается посредством матрицы коэффициентов

Среди систем линейных уравнений наибольшее значение имеют системы, в которых число уравнений равно числу неизвестных. Среди линейных подстановок переменных основную роль играют подстановки, в которых число исходных и новых переменных одинаково. В этих ситуациях матрица коэффициентов оказывается квадратной, т. е. имеющей одинаковое число строк и столбцов; это число называется порядком квадратной матрицы.

Вместо того чтобы говорить «матрица, состоящая из одной строки», и «матрица, состоящая из одного столбца», говорят короче: строка, столбец.

Как умножать матрицы друг на друга

Умножение матриц очень полезно при решении систем уравнений. Это связано с тем, что вы можете умножить матрицу на обратную по обе стороны от знака равенства, чтобы в конечном итоге получить переменную матрицу с одной стороны и решение системы с другой.

К сожалению, перемножить две матрицы вместе не так просто, как перемножить соответствующие элементы. Каждый элемент каждой матрицы в какой-то момент умножается на каждый член другой.

При умножении матриц матрицы записываются рядом друг с другом без промежуточного символа. Если вы хотите перемножить матрицы A и B, чтобы получить их произведение AB, количество столбцов в A должно совпадать с количеством строк в B. Каждый элемент в первой строке A умножается на каждый соответствующий элемент из первого столбца B , а затем все эти продукты складываются вместе, чтобы получить элемент в первой строке, первом столбце AB. Это известно как скалярное произведение первой строки A с первым столбцом B. Чтобы найти значение в первой строке, позиции второго столбца, возьмите скалярное произведение первой строки A со вторым столбцом B. путем умножения каждого элемента в первой строке A на каждый элемент во втором столбце B, а затем сложить все эти продукты вместе. В конце концов, после того как будут вычислены все возможные скалярные произведения, ваша новая матрица должна иметь то же количество строк, что и A, и то же количество столбцов, что и B.

Например, чтобы умножить матрицу A с 3 строками и 2 столбцами на матрицу B с 2 строками и 4 столбцами, вы берете скалярное произведение первой строки A с каждым из столбцов B, получая 4 члена в первый ряд произведения АВ. Взяв скалярное произведение второй строки A с каждым из столбцов B, мы получим вторую строку произведения AB, содержащую еще 4 термина. И то же самое касается создания последнего ряда AB. В итоге вы получите матрицу из 3 строк и 4 столбцов.

Если матрица A имеет размеры m x n , а матрица B имеет размеры n x p, то AB является матрицей m- x -p . Этот рисунок дает вам визуальное представление матричного умножения.

Умножение двух совпадающих матриц.

Когда вы умножаете матрицы, вы не умножаете соответствующие части, как при сложении или вычитании. Кроме того, при умножении матриц AB не равно BA. На самом деле, только потому, что вы можете умножить А на В, не означает, что вы можете умножьте B на A. Количество столбцов в A может быть равно количеству строк в B, но количество столбцов в B может не равняться количеству строк в A. Например, вы можете умножить матрицу с 3 строки и 2 столбца на матрицу с 2 строками и 4 столбцами. Однако вы не можете выполнить умножение по-другому, потому что вы не можете умножить матрицу с 2 строками и 4 столбцами на матрицу с 3 строками и 2 столбцами. Если вы попытаетесь получить скалярное произведение, перемножив правильные термины вместе, а затем сложив их произведения, где-то по пути у вас закончатся термины!

Вот пример умножения матриц. Скажем, в задаче вас просят умножить следующие две матрицы:

.

Сначала проверьте, можете ли вы перемножать две матрицы. Матрица A равна 3 x 2, а B равна 2 x 4, поэтому вы можете перемножить их, чтобы получить матрицу 3 x 4 в качестве ответа. Теперь вы можете перейти к скалярному произведению каждой строки первой матрицы с каждым столбцом второй.

Процесс умножения АВ.

На этом рисунке показан процесс. Вы можете начать с умножения каждого члена в первой строке A на последовательные члены в столбцах матрицы B. Обратите внимание, что умножение каждой записи в первой строке на соответствующую запись в первом столбце и сложение этих произведений вместе дает вам строку один, столбец вход. Точно так же, умножая каждую запись во второй строке на соответствующую запись в третьем столбце, вы получаете запись второй строки и третьего столбца.

Вынимаем весь пух, матрица продукта

Эту статью можно найти в категории:

• Предварительное исчисление,

Линейная алгебра для чайников | Wiley

• Загрузить флаер продукта
• Описание
• Цифровая пробная копия
• Об авторе
• Разрешения
• Содержание
• Скачано

Выбранный тип: Мягкая обложка

Количество:

$19. 99

Цифровая оценочная копия

Запросить цифровую оценочную копию

Мэри Джейн Стерлинг

ISBN: 978-0-470-43090-3 июль 2009 г. 384 страницы

• Электронная книга

  Всего от 12 долларов США

• Распечатать

  Всего от 19,99 долл. США

Электронная книга com are delivered on the VitalSource platform. To download and read them, users must install the VitalSource Bookshelf Software.</li><li>E-books have DRM protection on them, which means only the person who purchases and downloads the e-book can access it.</li><li>E-books are non-returnable and non-refundable.</li><li>To learn more about our e-books, please refer to our&nbsp;<a href="https://www.wiley.com/wiley-ebooks" target="_blank">FAQ</a>.</li></ul>» data-original-title=»» title=»»/>

$12,00

Мягкая обложка

19,99 $

Загрузить рекламный проспект

Загрузить рекламный проспект

Загрузить флаер продукта для загрузки PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание. Загрузить флаер продукта — загрузить PDF в новой вкладке. Это фиктивное описание.

Описание

Ученитесь:

• Решение линейных уравнений алгебры
• Поместите данные в порядок
• . Определите значения

• 9999
• . Ваше практическое руководство по практическому применению линейной алгебры

  Линейная алгебра заставляет вас чувствовать себя потерянным? Не беспокойтесь это простое в использовании руководство объясняет, как и почему решать задачи линейной алгебры на простом английском языке. От матриц до векторных пространств и линейных преобразований — вы поймете ключевые понятия и увидите, как они связаны со всем, от генетики до питания и вымирания пятнистых сов.

  • Выстраивание основ Откройте для себя несколько различных подходов к организации чисел и уравнений и решайте системы уравнений алгебраически или с помощью матриц
  • Связывайте векторы и линейные преобразования однородные системы
  • Вычисление определителей посмотреть, как выполнять функцию определителя на матрицах разных размеров и воспользоваться правилом Крамера
  • Оттачивайте свои навыки работы с векторными пространствами определяйте свойства векторных пространств и их подпространств и наблюдайте за линейным преобразованием в действии
  • Работайте с собственными значениями и собственными векторами определяйте и находите собственные значения и собственные векторы и понимайте, как они взаимодействуют с конкретными матрицами

  Откройте книгу и найдите:

  • Теоретические и практические способы решения задач линейной алгебры
  • Определения терминов повсюду и в глоссарии
  • Новые взгляды на операции
  • Как линейная алгебра связывает вместе векторы, матрицы, детерминанты и линейные преобразования
  • Реальные приложения матриц и определителей

  Об авторе

  Мэри Джейн Стерлинг является автором многочисленных книг для чайников . Она преподает в Университете Брэдли в Пеории, штат Иллинойс, где в течение почти 30 лет читает курсы по алгебре, исчислению и другим математическим дисциплинам.

  Разрешения

  Запросить разрешение на повторное использование контента с этого сайта

  Содержание

  Введение.

  Часть I: Выстраивание основ линейной алгебры.

  Глава 1: Дать имя линейной алгебре.

  Глава 2: Ценность привлечения векторов.

  Глава 3: Освоение матриц и матричной алгебры.

  Глава 4. Систематизация систем уравнений.

  Часть II: Связанные векторы и линейные преобразования.

  Глава 5: Выстраивание линейных комбинаций.

  Глава 6: Исследование матричного уравнения Ax = b.

  Глава 7: Знакомство с гомогенными системами и линейной независимостью.

  No related posts.