Вычитание векторов 2 способа: Вычитание векторов — урок. Геометрия, 9 класс.

Сложение и вычитание векторов – правила

4.6

Средняя оценка: 4.6

Всего получено оценок: 685.

Обновлено 11 Января, 2021

4.6

Средняя оценка: 4.6

Всего получено оценок: 685.

Обновлено 11 Января, 2021

Сложение и вычитание векторов – это одно из немногих действий на стыке математики и геометрии. Дело в том, что выражения из векторов можно складывать и вычитать арифметически, ориентируясь только на буквенные обозначения векторов, но для того, чтобы получить числовой результат или его геометрическое отображение придется выполнить ряд построений. Разберемся подробнее в правилах сложения и вычитания векторов.

Материал подготовлен совместно с учителем высшей категории Харитоненко Натальей Владимировной.

Опыт работы учителем математики — более 33 лет.

Что такое вектор?

Вектор – это отрезок с направлением.

Вектор и луч часто путают и допускают грубую ошибку. Вектор – это направленный отрезок, а любой отрезок имеет величину, то есть его можно измерить линейкой.

Луч имеет начало и направление, но он бесконечен, то есть измерить его невозможно. Так же, как нельзя и складывать лучи между собой или луч с вектором.

Вектор иногда помещают в декартову систему координат. Тогда, проведя перпендикуляры к каждой из осей, можно получить проекции вектора на оси Ох и Оу. Каждая из этих проекций будет отрезком. При этом, если из проекций составить прямоугольник, то его гипотенуза и будет начальным вектором. Это иногда используется при сложении векторов.

Рис. 1. Вектор в системе координат.

Сложение и вычитание векторов

Способов и методов сложения векторов всего два. Существует и третий, но его не считают отдельным методом, так как он вытекает из первых двух. Но мы его рассмотрим отдельно, чтобы не возникало вопросов при дальнейшем изучении темы.

Правило многоугольника

Для того, чтобы сложить векторы правилом многоугольника, необходимо параллельным переносом совместить конец первого вектора с началом второго, конец второго с началом третьего и так далее, пока не кончатся векторы, которые необходимо сложить.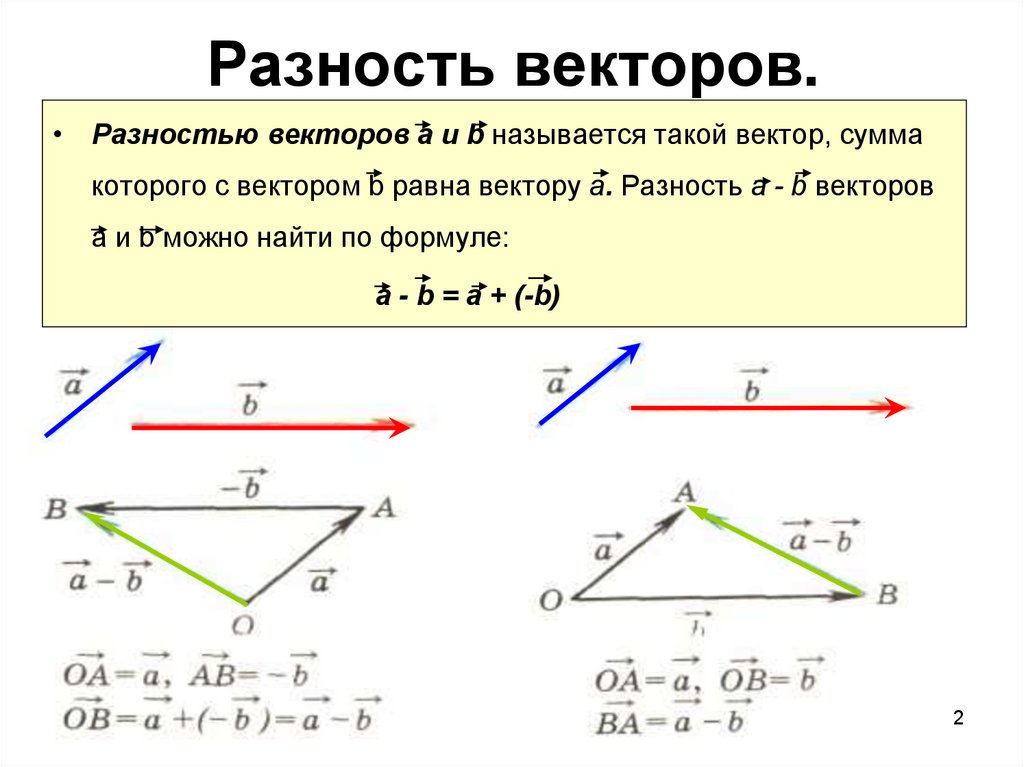

После этого нужно начало первого вектора соединить с концом последнего последнего вектора и указать направление. Получившийся вектор будет направлен в сторону последнего из участвовавших в сложении.

Складывать таким способом можно любое количество векторов. Если так складывается только два вектора, то способ называют правилом треугольника

Нужно понять и запомнить, что у отрезка одна определяющая величина: размер. У вектора определяющих величин две: размер и направление. Поэтому нельзя менять направление вектора и его размер. Любые действия нужно осуществлять с помощью параллельного переноса, то есть без изменения направления.

Рис. 2. Правило многоугольника.

Правило параллелограмма

Правило параллелограмма сложнее, его можно применять только для 2 векторов. Если вам нужно этим способом сложить большее количество векторов, например, три, то действие выполняют в следующем порядке:

• Складывают два любых вектора правилом параллелограмма. Результатом будет некий вектор и у нас остается еще один, который в сложении не участвовал.
• Получившийся и оставшийся векторы складывают по тому же правилу.
• Этот процесс можно повторять столько раз, сколько требуется по условию задачи.

Само правило параллелограмма заключается в том, что начала двух векторов совмещаются. После этого получившуюся фигуру достраивают до параллелограмма. Диагональ, которая выходит из начала двух векторов и есть результат сложения. Вектор должен быть направлен в противоположную сторону от совмещенного начала двух векторов.

Для того чтобы вычесть векторы любым способом, направление вектора, который является вычитаемым, меняют на противоположное. Получившиеся векторы складывают любым из методов.

Рис. 3. Правило многоугольника.

Сложение в декартовой системе

В декартовой системе все векторы раскладывают на проекции, после чего отрезки проекций складывают: проекции на ось Ох отдельно, на ось Оу отдельно. После из получившихся двух проекций снова собирают вектор.

Что мы узнали?

Мы узнали, что такое вектор. Поговорили о правилах сложения и вычитания векторов. Обсудили, чем отличается вектор от луча и обсудили метод действий с векторами в декартовой системе координат.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

• Нина Трофимова

  8/10

• Vlad Turlov

  10/10

• Никита Негин

  10/10

• Evgeniy Salakov

  10/10

• Артем Карнаух

  8/10

Оценка статьи

4.6

Средняя оценка: 4.6

Всего получено оценок: 685.

---

А какая ваша оценка?

Вычитание векторов / Векторы / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Векторы
5. Вычитание векторов

Разность векторов и — вектор, сумма которого с вектором равна вектору .

Разность векторов и обозначается так: .

Задача на построение разности векторов (1 способ)

Даны векторы и . Построить вектор .

Дано: и .

Построить: .

Решение:

От произвольной точки

О откладываем векторы = и = .

По правилу треугольника + = или + = , то есть сумма векторов и равна . По определению разности векторов это означает, что = , следовательно, вектор — искомый.

Противоположный вектор

Пусть — произвольный ненулевой вектор.

Вектор называется противоположным вектору , если векторы и имеют равные длины и противоположно направлены.

Вектор = является противоположным вектору = . Вектором, противоположным нулевому вектору, считается нулевой вектор.

Вектор, противоположный вектору , обозначается так: .

Сумма противоположных векторов и равна нулевому вектору, т.е. .

Теорема

Для любых векторов и справедливо равенство .

Доказательство

Дано: и .

Доказать: .

Доказательство:

По определению разности векторов . Прибавим к обеим частям этого равенства вектор , получим:

или (т.к. ), следовательно, . Теорема доказана.

Задача на построение разности векторов (2 способ)

Даны векторы и . Построить вектор .

Дано: и .

Построить: .

Решение:

От произвольной точки

О откладываем векторы = . Затем от точки А отложим =.

По теореме о разности векторов , поэтому , следовательно, вектор — искомый.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Понятие вектора

Равенство векторов

Откладывание вектора от данной точки

Сумма двух векторов

Законы сложения векторов. Правило параллелограмма

Сумма нескольких векторов

Произведение вектора на число

Применение векторов к решению задач

Средняя линия трапеции

Векторы

Правило встречается в следующих упражнениях:

7 класс

Задание 758, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 764, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 765, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 785, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 802, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 904, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 906, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 908, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 925, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 10, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

3.

2 Сложение и вычитание векторов: графические методы

Цели обученияВекторы в двух измеренияхСложение векторов: метод «голова к хвосту»Вычитание векторовУмножение векторов и скаляровРазложение вектора на компоненты

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Понимание правил сложения, вычитания и умножения векторов
• Применение графических методов сложения и вычитания векторов для определения смещения движущихся объектов

Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:

• 3.A.1.1 Учащийся может выразить движение объекта, используя описательные, математические и графические представления. (Ст. 1.5, 2.1, 2.2)
• 3.A.1.3 Учащийся способен анализировать экспериментальные данные, описывающие движение объекта, и может выражать результаты анализа, используя описательные, математические и графические представления. (П.5.1)

Рис. 3.8 Смещение можно определить графически, используя масштабную карту, например, карту Гавайских островов. Путешествие с Гавайев на Молокаи состоит из нескольких этапов или сегментов пути. Эти сегменты могут быть добавлены графически с помощью линейки, чтобы определить общее двухмерное перемещение пути. (Источник: Геологическая служба США)

Векторы в двух измерениях

Вектор – это величина, которая имеет величину и направление. Например, перемещение, скорость, ускорение и сила — все это векторы. В одномерном или прямолинейном движении направление вектора может быть задано просто знаком плюс или минус. Однако в двух измерениях (2-d) мы указываем направление вектора относительно некоторой системы отсчета, то есть системы координат, используя стрелку, длина которой пропорциональна величине вектора и указывает направление вектора.

На рис. 3.9 показано такое графическое представление вектора на примере полного перемещения человека, идущего по городу, рассматриваемого в книге «Кинематика в двух измерениях: введение».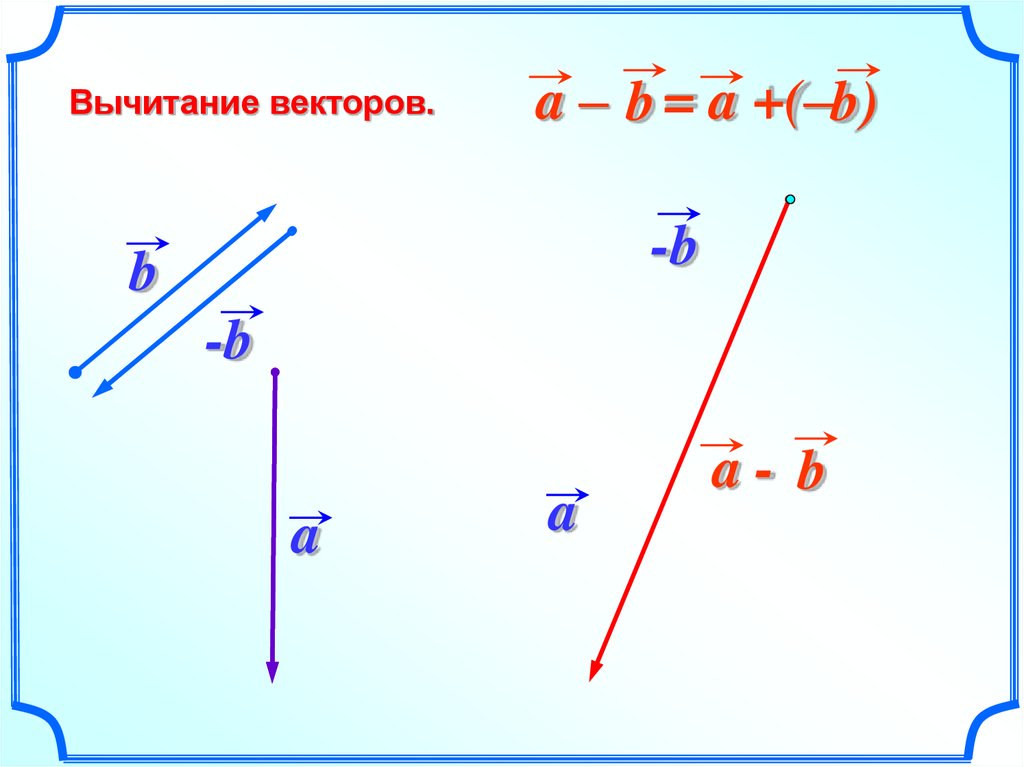 Мы будем использовать обозначение, что жирный шрифт, такой как размер DD 12{D} {}, обозначает вектор. Его величина представлена ​​символом, выделенным курсивом, размером DD 12{D} {}, а его направление размером θθ 12{θ} {}.

Векторы в этом тексте

В этом тексте мы будем представлять вектор с переменной, выделенной жирным шрифтом. Например, мы представим количественную силу вектором FF размером 12{F} {}, который имеет как величину, так и направление. Величина вектора будет представлена ​​переменной, выделенной курсивом, например размером FF 12{F} {}, а направление переменной будет задано углом θθ размером 12{θ} {}.

Рисунок 3.9 Человек идет девять кварталов на восток и пять кварталов на север. Водоизмещение составляет 10,3 блока при угле 29,1°29,1° размером 12{«29» «.» «1°»} {} к северу от востока.

Рисунок 3.10 Чтобы графически описать результирующий вектор для человека, идущего по городу, показанному на рисунке 3.9, нарисуйте стрелку, представляющую вектор полного смещения DD размером 12{D} {}.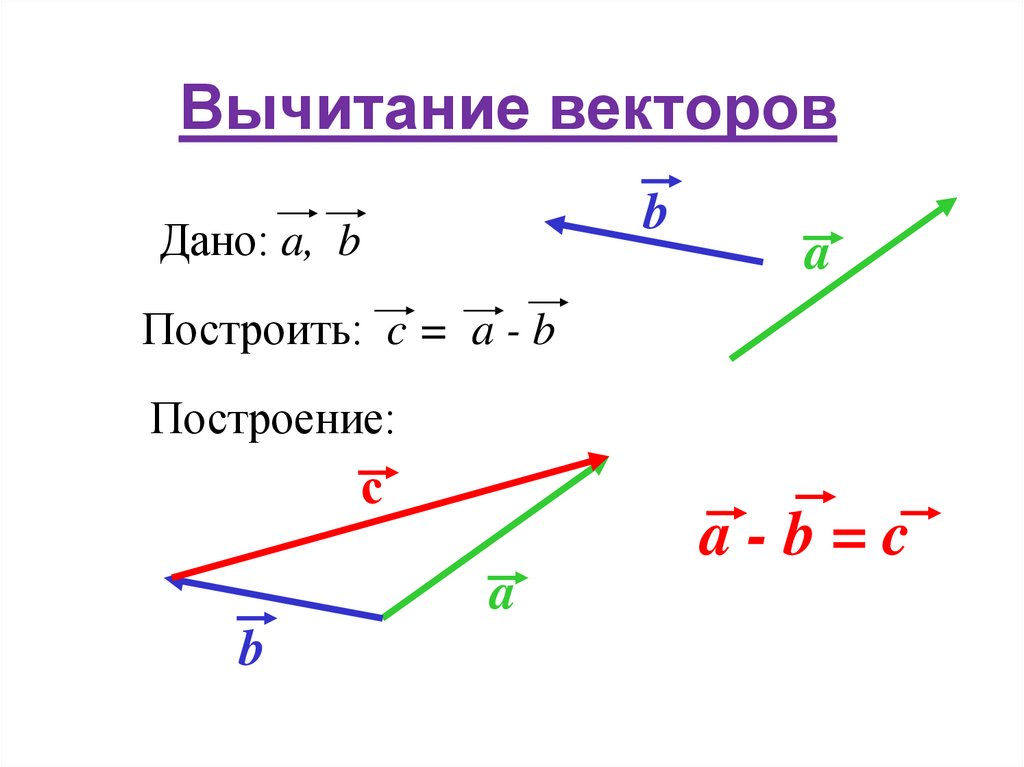 С помощью транспортира начертите линию под углом θθ величиной 12{θ} {} относительно оси восток-запад. Длина DD size 12{D} {} стрелки пропорциональна модулю вектора и измеряется линейкой вдоль линии. В этом примере величина DD размера 12{D} {} вектора составляет 10,3 единицы, а направление θθ размера 12{θ} {} равно 29.1°29.1° размер 12{«29» «.» 1 rSup { размер 12{°} } } {} к северу от востока.

Сложение векторов: метод «голова к хвосту»

Метод «голова к хвосту» — это графический способ добавления векторов, описанный на рис. 3.11 ниже и в следующих шагах. Хвост вектора — это начальная точка вектора, а начало (или кончик) вектора — это конечный заостренный конец стрелки.

Рисунок 3.11 Метод «голова к хвосту»: Метод «голова к хвосту» графического сложения векторов проиллюстрирован для двух перемещений человека, идущего по городу, рассмотренных на рисунке 3.9.. (a) Нарисуйте вектор, представляющий смещение на восток. (b) Нарисуйте вектор, представляющий смещение на север. Хвост этого вектора должен исходить из головы первого вектора, указывающего на восток. (c) Нарисуйте линию от конца вектора, указывающего на восток, до начала вектора, указывающего на север, чтобы сформировать сумму или результирующий вектор, размер DD 12{A} {}. Длина стрелки D,D размера 12{A}{} пропорциональна модулю вектора и составляет 10,3 единицы. Его направление, описываемое как угол по отношению к востоку (или горизонтальной оси) θθ размером 12{θ} {}, измеряется с помощью транспортира и составляет 29.1°29.1° размер 12{«29» «.» 1°} {}.

Шаг 1. Нарисуйте стрелку, представляющую первый вектор (девять блоков на восток), используя линейку и транспортир .

Рисунок 3.12

Шаг 2. Теперь нарисуйте стрелку, представляющую второй вектор (пять блоков на север).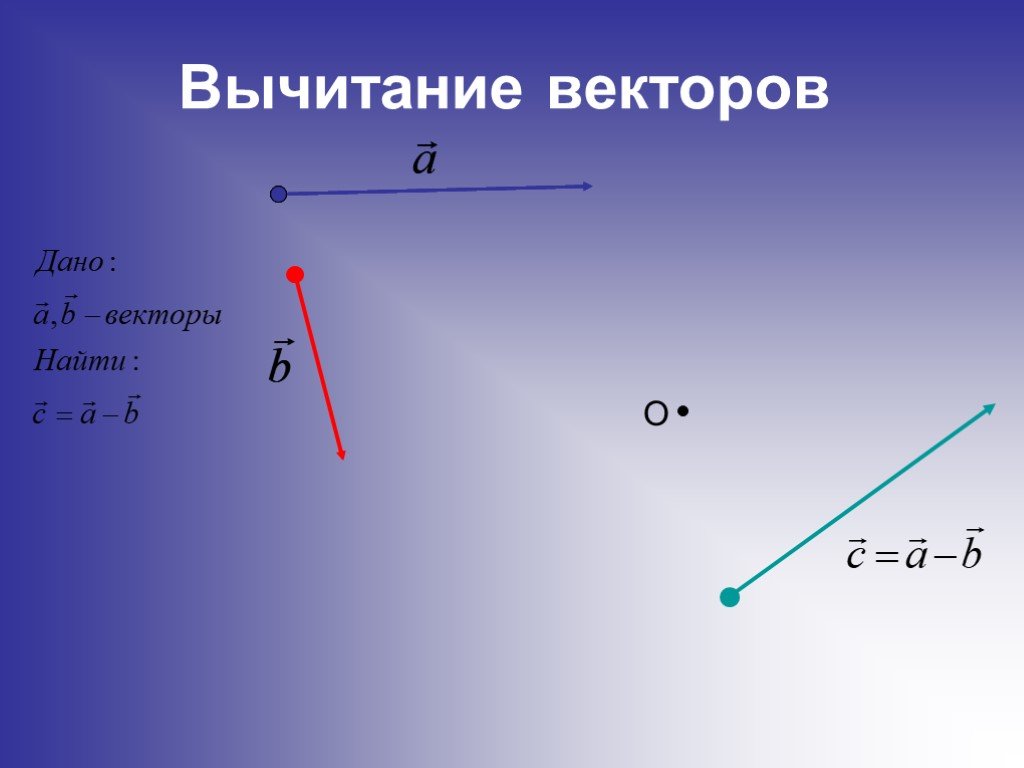 Поместите конец второго вектора в начало первого вектора .

Рисунок 3.13

Шаг 3. Если имеется более двух векторов, продолжайте этот процесс для каждого добавляемого вектора. Обратите внимание, что в нашем примере у нас есть только два вектора, поэтому мы закончили размещать стрелки от кончика к хвосту.

Шаг 4. Проведите стрелку от конца первого вектора к началу последнего вектора . Это результат или сумма D других векторов.

Рисунок 3.14

Шаг 5. Чтобы получить величину равнодействующей, измерьте ее длину линейкой. Обратите внимание, что в большинстве вычислений мы будем использовать теорему Пифагора для определения этой длины.

Шаг 6. Чтобы определить направление равнодействующей, измерьте угол, который она образует с системой отсчета, используя транспортир. Обратите внимание, что в большинстве расчетов мы будем использовать тригонометрические отношения для определения этого угла.

Точность графического сложения векторов ограничена только точностью, с которой могут быть выполнены чертежи, и точностью измерительных инструментов. Это справедливо для любого количества векторов.

Пример 3.1 Графическое сложение векторов с использованием метода «голова к хвосту»: прогулка женщины . Сначала она проходит 25,0 м в направлении 49,0°49,0° размера 12{«49» «.» «0°»} {} к северу от востока. Затем она проходит 23,0 м курсом 15,0°15,0° размер 12{«15» «.» «°°»} {} к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0° к югу от востока.

Стратегия

Представьте каждый вектор смещения графически со стрелкой, пометив первый размер AA 12{A} {}, второй размер BB 12{B} {} и третий размер CC 12{C} {} , делая длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад.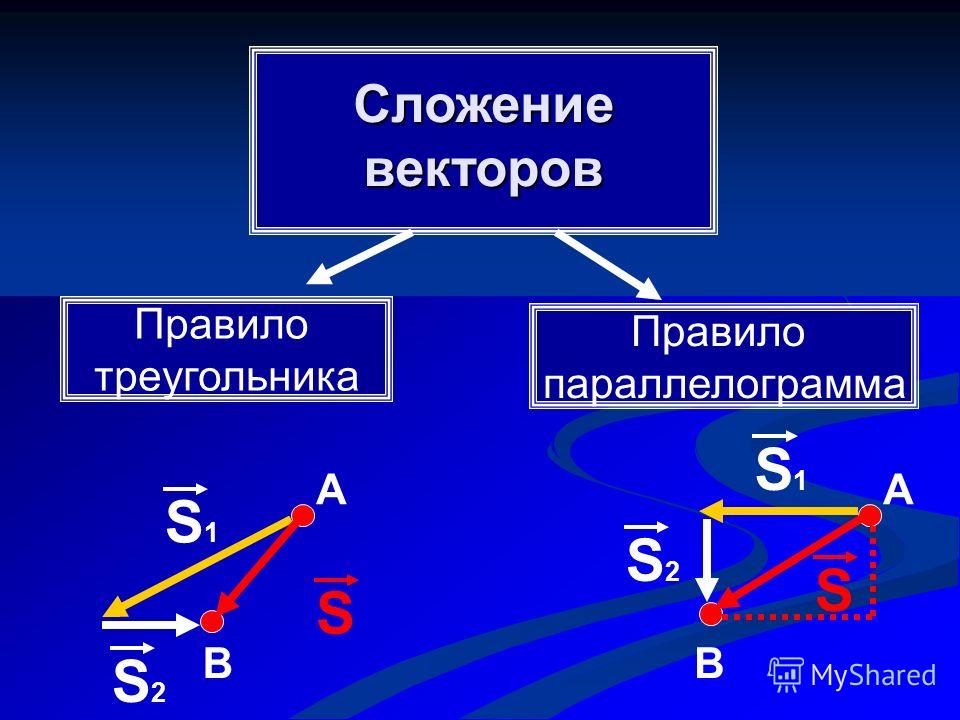 Описанный выше метод «голова к хвосту» позволяет определить величину и направление результирующего смещения, обозначаемого размером RR 12{R} {}.

Решение

(1) Нарисуйте три вектора смещения.

Рисунок 3.15

(2) Разместите векторы от начала до конца, сохранив их первоначальную величину и направление.

Рисунок 3.16

(3) Нарисуйте результирующий вектор, размер RR 12{R} {}.

Рисунок 3.17

(4) Используйте линейку для измерения величины RR размера 12{R} {} и транспортир для измерения направления RR размера 12{R} {}. Хотя направление вектора можно указать разными способами, проще всего измерить угол между вектором и ближайшей горизонтальной или вертикальной осью. Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх ногами и измеряем угол между осью, направленной на восток, и вектором.

Рисунок 3.18

В этом случае видно, что полное смещение RR размера 12{R} {} имеет величину 50,0 м и лежит в направлении 7,0°7,0° размера 12{7 «.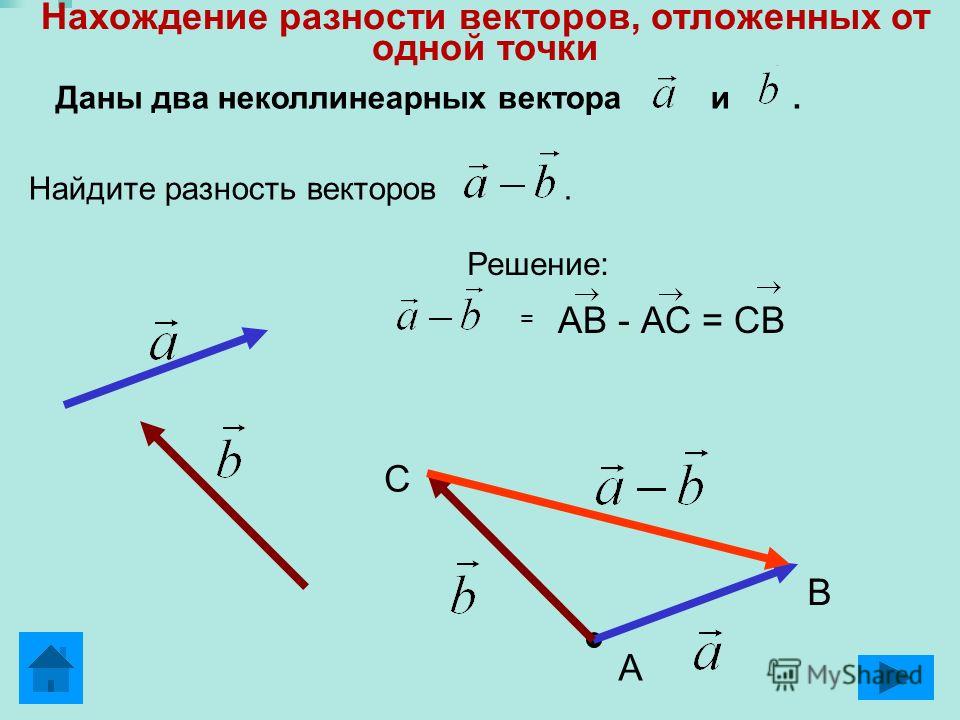 » 0°} {} к югу от востока. Используя его величину и направление, этот вектор можно выразить как R=50,0 мR=50,0 м, размер 12{R» = 50″ «.» «0 м»} {} и θ=7,0°θ=7,0° размер 12{θ=7 «.» «0°»} {} к югу от востока.

Обсуждение

Графический метод сложения векторов «голова к хвосту» работает для любого количества векторов. Также важно отметить, что результирующая не зависит от порядка добавления векторов. Следовательно, мы можем добавлять векторы в любом порядке, как показано на рис. 3.19.и мы все равно получим то же решение.

Рисунок 3.19

Здесь мы видим, что при добавлении одних и тех же векторов в другом порядке результат будет таким же. Эта характеристика верна в любом случае и является важной характеристикой векторов. Сложение векторов коммутативно. Векторы можно добавлять в любом порядке.

3.1 А+В=В+А.А+В=В+А. size 12{«A+B=B+A»} {}

Это верно и для сложения обычных чисел — вы получите тот же результат, если сложите 2+32+3 size 12{«2+3» } {} или же 3+23+2 размер 12{«3+2»} {}, например.

Вычитание векторов

Вычитание векторов — это прямое расширение сложения векторов. Чтобы определить вычитание, скажем, мы хотим вычесть BB размером 12{B} {} из Размер AA 12{A} {} , пишется A–BA–B size 12{ «A» «-B»} {} — сначала мы должны определить, что мы подразумеваем под вычитанием. минус вектора BB определяется как –B–B; то есть графически отрицательное значение любого вектора имеет ту же величину, но противоположное направление , как показано на рис. 3.20. Другими словами, BB размера 12{B} {} имеет ту же длину, что и –B–B размера 12{«-» «B»} {}, но указывает в противоположном направлении. По сути, мы просто переворачиваем вектор так, чтобы он указывал в противоположном направлении.

Рис. 3.20 Отрицательное значение вектора — это просто другой вектор той же величины, но направленный в противоположном направлении. Таким образом, размер BB 12{B} {} является минусом размера –B–B 12{ital «-B»} {}; он имеет ту же длину, но противоположное направление.

Затем вычитание вектора BB из вектора AA просто определяется как добавление –B–B к AA. Обратите внимание, что вычитание вектора — это добавление отрицательного вектора. Порядок вычитания не влияет на результат.

3.2 А – В = А + (–В). А – В = А + (–В). размер 12{ жирный «A – B = A + » \( жирный «–B» \) } {}

Это аналогично вычитанию скаляров, например, 5 – 2 = 5 + (–2)5 – 2 = 5 + (–2) размер 12{«5 – 2 = 5 + » \( «–2» \) } {}. Опять же, результат не зависит от порядка, в котором производится вычитание. Когда векторы вычитаются графически, используются описанные выше методы, как показано в следующем примере.

Пример 3.2. Графическое вычитание векторов: женщина, плывущая на лодке

Женщина, плывущая на лодке ночью, следует указаниям к пристани. Инструкции гласили, что сначала нужно пройти 27,5 м в направлении 66,0°66,0° размером 12{«66» «.» 0°} {} к северу-востоку от ее текущего местоположения, а затем пройдите 30,0 м в направлении 112°112° размера 12{«112″°} {} к северу от востока (или 22,0°22,0° размера 12{«22» «. » 0°} {} к западу от севера). Если женщина совершит ошибку и поедет в направлении , противоположном , на втором этапе поездки, где она окажется? Сравните это место с расположением дока.

Рисунок 3.21

Стратегия

Мы можем представить первый этап пути с помощью вектора AA, а второй этап пути с помощью вектора Размер каретки 12{B} {}. Пристань расположена в точке A + BA + B. Если женщина по ошибке едет в направлении , противоположном , для второго этапа путешествия, она проедет расстояние BB (30,0 м) в направлении 180°–112°. =68°180°–112°=68° к югу от востока. Мы представляем это как –B–B, как показано ниже. Вектор –B–B имеет ту же величину, что и BB, но направлен в противоположную сторону. Таким образом, она окажется в точке A+(–B)A+(–B) или A–BA–B.

Рисунок 3.22

Мы выполним сложение векторов, чтобы сравнить местоположение причала, A + BA + B size 12{ ital «A «»+ «B} {}, с местоположением, в которое по ошибке прибыла женщина, A + (–B)A + (–B) размер 12{ жирный «A + » \(жирный «–B» \) } {}.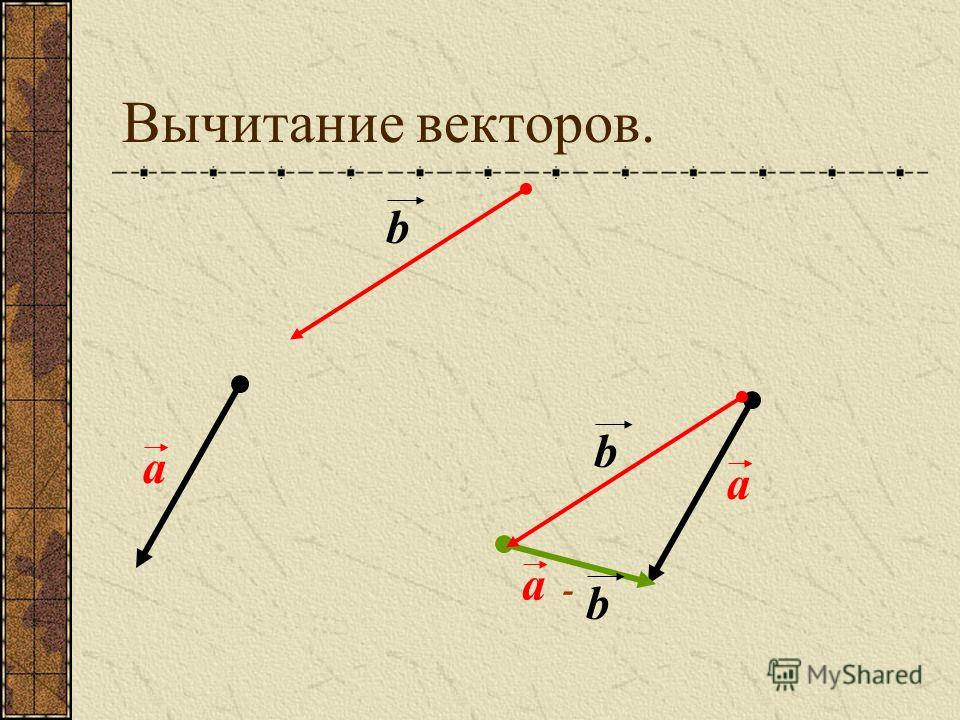

Решение

(1) Чтобы определить место, куда случайно попала женщина, начертите векторы AA размером 12{A} {} и –B–B.

(2) Разместите векторы лицом к хвосту.

(3) Нарисуйте результирующий вектор RR размером 12{R} {}.

(4) С помощью линейки и транспортира измерьте величину и направление RR размера 12{R} {}.

Рисунок 3.23

В этом случае R=23,0 мR=23,0 м размер 12{R»=23″ «.» «0 м»} {} а также θ=7,5°θ=7,5° размер 12{θ=7 «.» «5° к югу от востока»} {} к югу от востока.

(5) Чтобы определить местоположение дока, мы повторяем этот метод, добавляя векторы размера AA 12{A} {} и размера BB 12{B} {}. Получаем результирующий вектор R’R’ размера 12{R’} {}.

Рисунок 3.24

В этом случае R = 52,9 мР = 52,9 м, размер 12{R» = 52″ «.» «9 м»} {} и θ=90,1°θ=90,1° размер 12{θ=»90″ «.» «1° к северу от востока»} {} к северу от востока.

Мы видим, что женщина окажется на значительном расстоянии от пристани, если она отправится в противоположном направлении на второй этап поездки.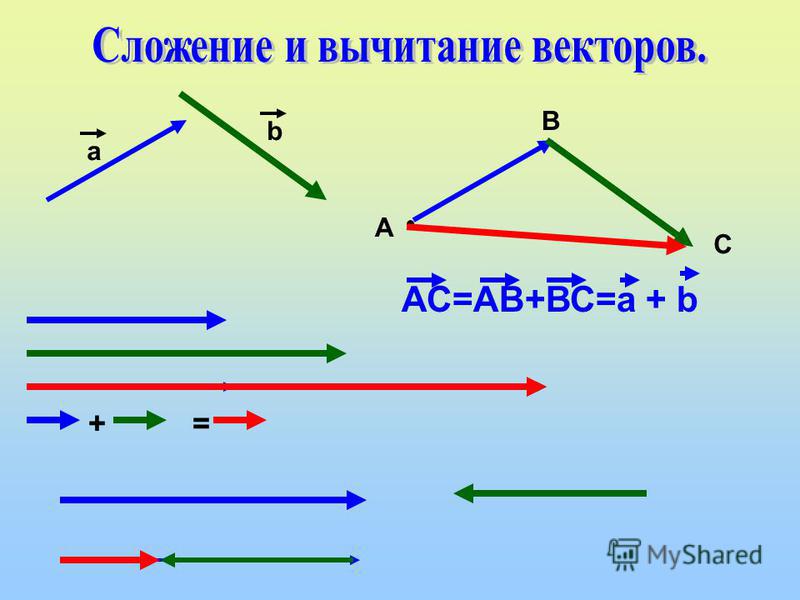

Обсуждение

Поскольку вычитание вектора аналогично сложению вектора с противоположным направлением, графический метод вычитания векторов работает так же, как и сложение.

Умножение векторов и скаляров

Если бы мы решили пройти в три раза больше на первом этапе пути, рассматриваемого в предыдущем примере, то мы бы прошли 3 × 27,5 м3 × 27,5 м размером 12{«3 » умножить на » 27″ «.» «5 м»} {}, или 82,5 м, в направлении 66,0°66,0° размер 12{«66» «.» 0 {размер 12{°} } } {} к северу от востока. Это пример умножения вектора на положительную скалярную величину. Обратите внимание, что величина меняется, но направление остается прежним.

Если скаляр отрицательный, то умножение вектора на него изменяет величину вектора и дает новому вектору в противоположном направлении . Например, если умножить на -2, величина удвоится, но изменится направление.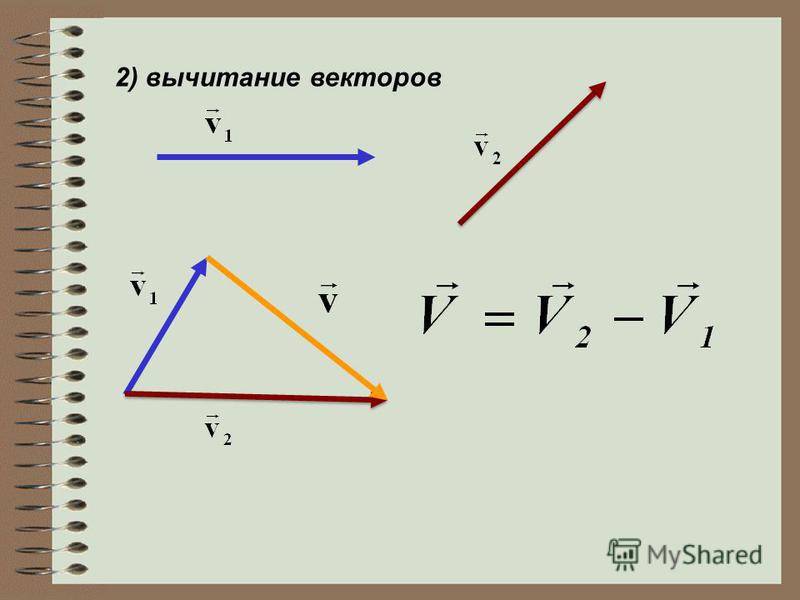 Мы можем обобщить эти правила следующим образом: когда векторный размер AA 12{A} {} умножается на скалярный размер cc 12{c} {}

• , модуль вектора становится абсолютным значением размера cc 12{ c} {}размер AA 12{A} {},
• , если cc size 12{A} {} положителен, направление вектора не меняется, и
• , если размер копий 12{A} {} отрицательный, направление меняется на противоположное.

В нашем случае c=3c=3размер 12{c=3} и A=27,5 мА=27,5 мразмер 12{«A= 27,5 м»}. Векторы умножаются на скаляры во многих ситуациях. Обратите внимание, что деление является обратным умножению. Например, деление на два равносильно умножению на значение (1/2). Правила умножения векторов на скаляры такие же, как и при делении; просто рассматривайте делитель как скаляр между нулем и единицей.

Разложение вектора на компоненты

В приведенных выше примерах мы добавляли векторы для определения результирующего вектора. Однако во многих случаях нам нужно будет сделать обратное.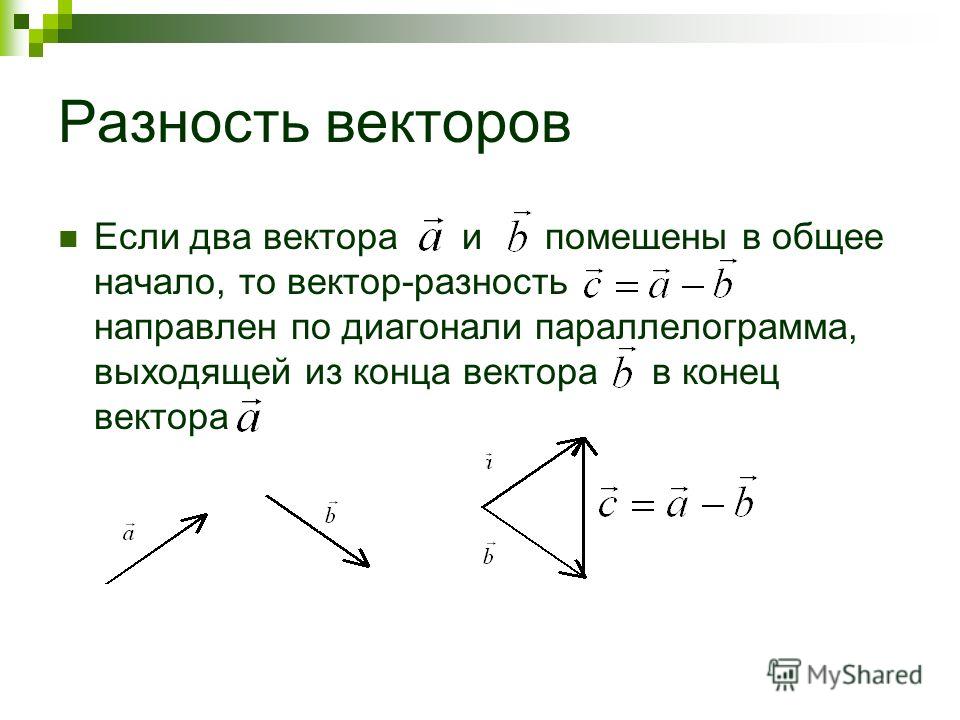 Нам нужно будет взять один вектор и найти, какие другие векторы, сложенные вместе, дают его. В большинстве случаев это включает в себя определение перпендикулярных компонентов одного вектора, например, x — и y -компоненты, или компоненты север-юг и восток-запад.

Например, мы можем знать, что общее перемещение человека, идущего по городу, составляет 10,3 квартала в направлении 29,0°29,0° размером 12{«29» «.» 0°} } {} к северу от востока и хотите узнать, сколько кварталов нужно было пройти на восток и на север. Этот метод называется нахождением компонентов (или частей) смещения в восточном и северном направлениях, и это процесс, обратный процессу, применяемому для нахождения полного смещения. Это один из примеров нахождения компонентов вектора. В физике есть много приложений, где это может оказаться полезным.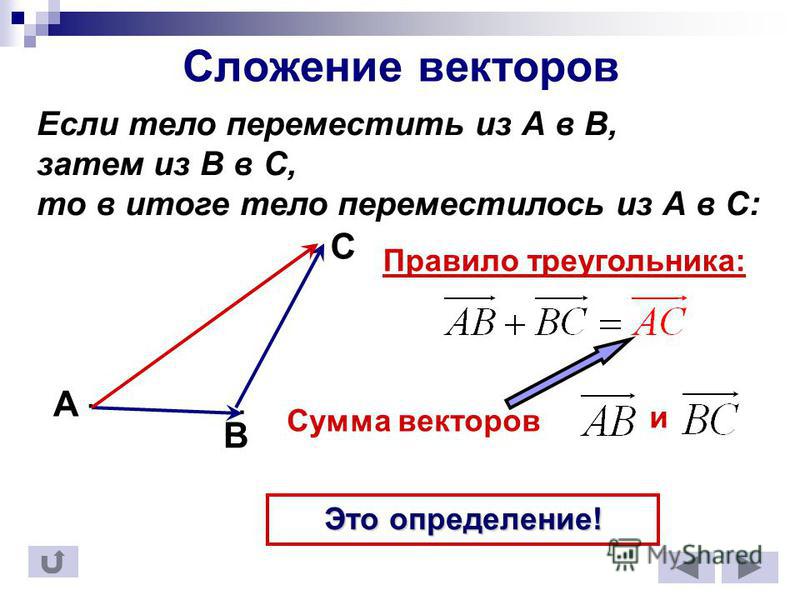 Мы скоро увидим это в Projectile Motion и многое другое, когда рассмотрим заставляет в динамике: законы движения Ньютона. Большинство из них включают поиск компонентов вдоль перпендикулярных осей (например, север и восток), так что задействованы прямоугольные треугольники. Аналитические методы, представленные в разделе «Сложение и вычитание векторов: аналитические методы», идеально подходят для поиска компонентов вектора.

PhET Explorations: Maze Game

Узнайте о положении, скорости и ускорении в Arena of Pain . Используйте зеленую стрелку, чтобы переместить мяч. Добавьте больше стен на арену, чтобы усложнить игру. Постарайтесь достичь цели как можно быстрее.

Рисунок 3.25 Игра «Лабиринт»

• Печать
• Поделиться

Вот как работает векторное вычитание

Вот как работает векторное вычитание

Яна Руссик

24 февраля 2021

Онлайн-обучение

,

Математика

0006 ,

Тригонометрия

Вектор — это термин, используемый для определения любых отрезков прямой с указанной начальной и конечной точками.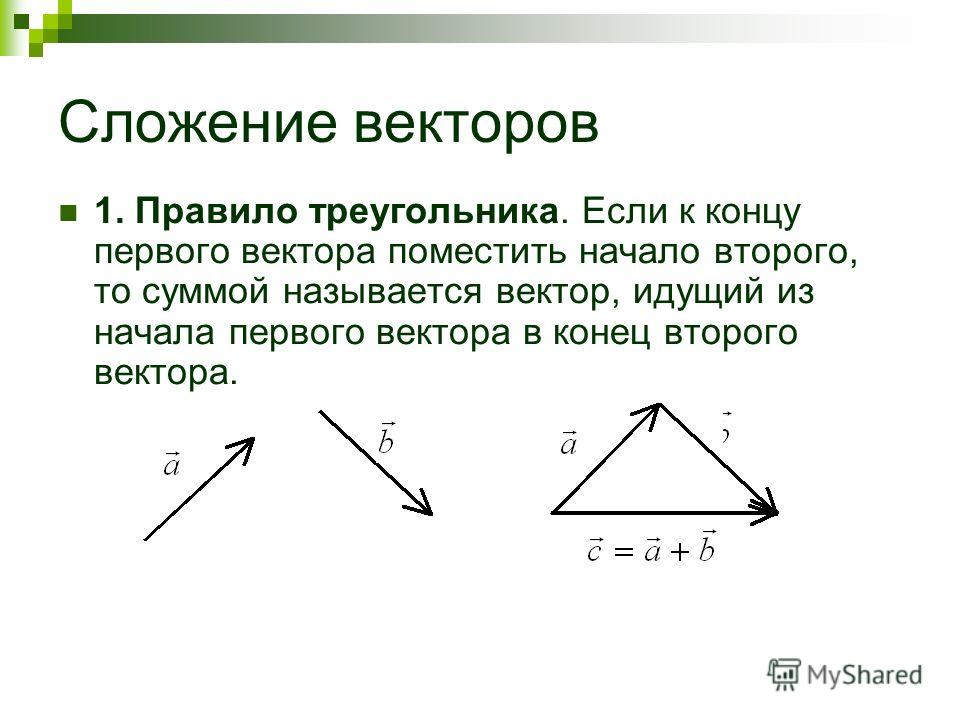 Все векторы нарисованы под углом и имеют заданное направление. Научиться вычитать векторы полезно, когда вам нужно увидеть, сколько должен пройти один вектор, чтобы добраться до другого.

Вычитание векторов — это процесс вычитания координат одного вектора из координат второго вектора.

См. пример ниже. Координаты вектора a отмечены как (3,3), а координаты вектора b как (1, 2).

При вычитании векторов необходимо взять первую векторную величину и вычесть вторую величину. Давайте вычтем вектор b из вектора a:

Ваши результирующие векторные координаты для этого конкретного примера (2, 1).

Сложение векторов, величина и направление

Каждый вектор имеет форму стрелки и имеет величину и направление. Фактическая длина стрелки, расстояние, пройденное от одной координаты до другой, является величиной. Направление вектора — это угол, на который он указывает.

При сложении векторов вы соединяете хвост вектора (конечные координаты) с головой вектора (начальные координаты).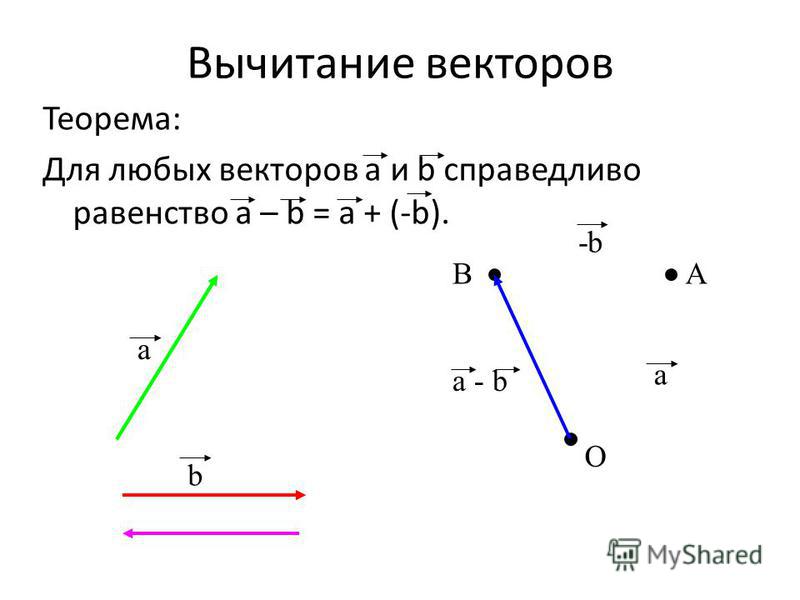

См. пример ниже. Начальными точками являются (4, 4) и (2, 3), а конечной точкой является (6, 7)

Из этого примера мы можем видеть, что величина результирующего вектора и направление результирующего вектора отличаются от исходных точек.

Разбивка векторного вычитания

При вычитании векторов необходимо изменить направление вычитаемого вектора. Это указывает на то, что длина одного вектора вычитается из другого вектора. См. пример ниже. Вектор v показан идущим в противоположном направлении, чтобы показать, что он вычитается из длины вектора u. Когда вы меняете направление вектора, вы превращаете его в отрицательный вектор.

На рисунке ниже показаны координаты (-6,1), вычтенные из (4, -2). Давайте сделаем этот процесс вычитания векторов:

Вы можете видеть, что, поскольку мы вычитаем x-значение -6 из 4, два минуса компенсируются. Это как если бы вы взяли абсолютное значение числа, что означает, что вы удалили все его отрицательные значения и превратили его в положительное.