Примеры решения заданий контрольной работы № 1 Матрицы и определители
Сумма (разность) определяется только для матриц одинаковой размерности. Пусть
. Тогда .
При умножении матрицы А на число нужно все элементы матрицыА умножить на это число.
Если , то.
Произведением матрицы на матрицуназывается матрица, элементы которой находятся по формуле. В общем случае
Пусть ,.
Имеем:, где
следовательно
.
Определителем второго порядка называется число, равное . (1.1)
Примеры.
1) ; 2).
Определителем третьего порядка называется число, равное сумме произведений элементов
его первой строки на их алгебраические
дополнения.
Аналогично определяются определители более высоких порядков.
Вычислим определитель, разложив его по элементам первой строки:
.
Определители третьего порядка можно вычислить и по правилу треугольников (правилу Саррюса) по схеме:
. (1.3)
Пример.
Системы линейных уравнений
Метод Крамера
Пример. Решить систему линейных уравнений по формулам Крамера
.
Вычислим определитель системы
Вычислим определители D1, D2, D3, заменяя в
определителе D элементы
первого, второго и третьего столбцов
соответственно элементами столбца из
свободных членов.
.
Таким образом,
, х2=,.
Итак,
х1=1, х2=6, х3=5.
Метод обратной матрицы
Определение. Матрица А называется невырожденной, если D=det А0.
Каждая невырожденная матрица А имеет обратную , причем для матрицытретьего порядка с элементами:обратная матрицаимеет вид:
, (1.4)
где А11, А12 ,…, А33 – алгебраические дополнения соответствующих элементов матрицы, располагаемые по столбцам в новой матрице.
Пример
.
Имеем: А=,Х=,Н=.
, .
Для нахождения обратной матрицы А-1 вычисляем все алгебраические дополнения элементов матрицы А:
, ,,
, ,,
, ,.
Составляем обратную матрицу (1.4):
.
Тогда
.
Таким образом, х1=1, х2=6, х3=5.
Метод Жордана-Гаусса последовательного исключения переменных
Пример. Решить систему методом Жордана-Гаусса. Найти общее, частное и базисное решение системы.
Составляем расширенную матрицу системы и проводя элементарные преобразования над строками матрицы исключаем переменные в соответствующих этой матрице системах линейных уравнений. В результате преобразований исходная матрица сводится к трапецеидальному виду. Преобразуем
расширенную матрицу системы:
Преобразуем
расширенную матрицу системы:Поясним сделанные преобразования:
Первую строку умножим последовательно на (- 2), (-3), (-4) и прибавим ко второй, третьей и четвертой строкам соттветственно.
Вторую строку умножаем на (-1), (-2) и прибавим к третьей и четвертой строке соответственно.
Поменяем местами вторую и четвертую строчку.
Вторую строку умножаем на 2 и на (-3) и прибавим к первой и третьей строке соответственно. Удаляем четвертую – нулевую строку.
Третью строку умножаем на на (-1) и на (-3) и прибавляем ко второй и первой строке соответственно.
Используя последнюю матрицу, эквивалентную исходной, получаем равносильную систему уравнений следующего вида:
х1++1,2х4 = 1
х2+ +0,4х4 = 3
х3+
−1,4х4 =− 2.
Переменныех1, х2, х3назовём базисными, переменную х4 − свободной. Полагая х4=0, непосредственно находим базисное решение: х1
=1, х2=3, х3=−2.При х4=5, получим частное решение: х3=5, х2=1, х1=−5. При х4= t, где t R, получим общее решение системы:х1=1-1,2 t
х2=3-0,4 t
х3=-2+1,4 t.
Колосова А.А., Степанов В.Е. Матрицы и определители, решение задач
- формат exe
- размер 1.06 МБ
- добавлен 25 сентября 2011 г.
В книге кроме необходимых теоретических сведений, формул и типовых
задач описана работа с математическими web-сервисами, которые
позволяют получить полное решение задач со всеми промежуточными
преобразованиями.
Смотрите также
- формат doc
- размер 1.99 МБ
- добавлен 15 июня 2009 г.
Данные методические указания предназначены студентам гуманитарного факультета заочной формы обучения. Они содержат задания по всем темам программы. В конце приведены образцы решения задач. ОмГТУ 2001 Содержание: -Матрицы и определители -Системы линейных уравнений -Построение графиков функций -Предел и непрерывность функций -Вычисление производной
- формат pdf
- размер 1.86 МБ
- добавлен 06 сентября 2011 г.
Учебное пособие. — М.: Изд-во Экономика, 2010. — 384 c. -(Высшее образование). В сборник включены задачи по следующим разделам высшей математики: матрицы и определители, системы линейных уравнений, аналитическая геометрия, линейная алгебра, математический анализ, дифференциальные уравнения, ряды.
- формат htm, doc, gif, jpg, html
- размер 2.63 МБ
- добавлен 05 декабря 2011 г.
Учебно-практическое пособие. — Ижевск: ГОУ ВПО ИЖГТУ. Матрицы и действия над ними. Определители квадратных матриц. Обратная матрица. Решение простейших матричных уравнений. Системы линейных алгебраических уравнений и их исследование. Понятие ранга матрицы. Линейные пространства. Вектор. Базис. Линейный оператор и собственные вектора. Векторная алгебра. Приложение линейной алгебры к задачам аналитической геометрии. Уравнения прямой в пространстве….
- формат doc
- размер 651.03 КБ
- добавлен
12 мая 2009 г.

Учебно-практическое пособие. — М.: МГУТУ, 2004. -96 с. Аннотация. Аналитическая геометрия. Элементы линейной алгебры. Координаты. Определители. Решение систем линейных уравнений (метод Крамера). Матрицы. Основные свойства и операции. Решение уравнений. Ранг матрицы. Исследование системы m линейных уравнений с n неизвестными. Решение системы уравнений методом Гаусса. Векторы. Основные операции над векторами. Скалярное произведение. Векторное произ…
- формат djvu, pdf
- размер 5.04 МБ
- добавлен 09 ноября 2011 г.
Учебное пособие. — Новосибирск, НГТУ, 2001. — (97+93)с. В первую часть учебного пособия включены задачи по темам «Комплексные числа», «Матрицы и определители», «Линейные пространства», «Системы линейных уравнений», «Евклидовы и унитарные пространства», «Квадратичные формы». Во вторую часть работы включены задачи по теме «Линейные операторы в линейных пространствах». Приводятся методические разъяснения и даются практические советы к решению задач…
Во вторую часть работы включены задачи по теме «Линейные операторы в линейных пространствах». Приводятся методические разъяснения и даются практические советы к решению задач…
- формат pdf
- размер 202.04 КБ
- добавлен 24 февраля 2009 г.
Линейная алгебра (Матрицы, Действия над матрицами, Определители, Свойства определителей, Обратная матрица, Решение систем линейных уравнений, Модель Леонтьева многоотраслевой экономики) Аналитическая геометрия (Уравнение прямой, Угол между прямыми, Различные уравнения, Пересечение прямых, Расстояние от точки до прямой) Предел (Числовая последовательность, Предел последовательности, Понятие функции, Предел функции, Замечательные пределы) Теория…
- формат pdf
- размер 389.41 КБ
- добавлен
25 апреля 2009 г.

Раздел 1. Числовые последовательности Раздел 2. Предел функции Раздел 3. Производная и график функции. Раздел 4. Матрицы, определители, системы линейных алгебраических уравнений
- формат pdf
- размер 72.36 МБ
- добавлен 11 октября 2009 г.
Содержание: 1. Матрицы и определители 2. Системы линейных уравнений 3. Векторная алгебра 4. Аналитическая геометрия на плоскости 5. Аналитическая геометрия в пространстве 6. Функции и пределы 7. Производная и ее применение 8. Неопределенный интеграл 9. Определенный интеграл 10. Комплексные числа 11. Функции нескольких переменных
- формат pdf
- размер 1.45 МБ
- добавлен 26 апреля 2010 г.
/ В.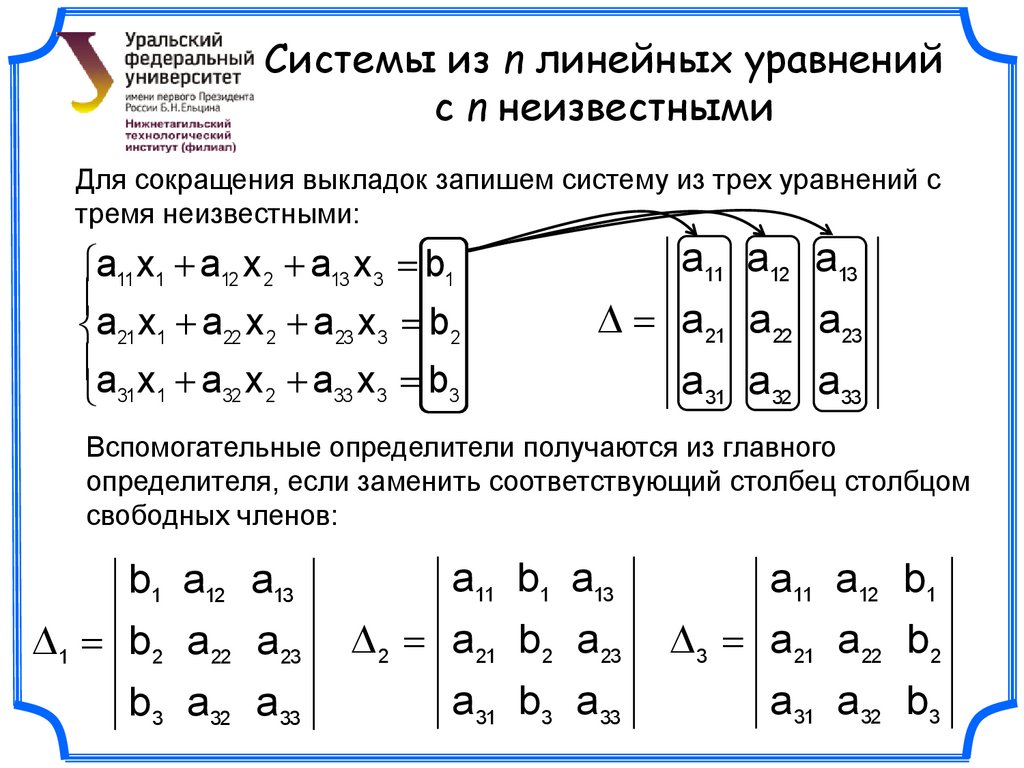 К. Пчельник, Е. А. Сетько, И. И. Ревчук. -Гродно. ГрГУ, Матрицы и определители. Аналитическая геометрия на плоскости и в пространстве: пособие. 2007, — 164с. Пособие содержит краткие теоретические сведения по матричной алгебре, аналитической геометрии на плоскости и в пространстве, примеры решения задач, задачи для самостоятельного решения и задания для контрольной работы. Матрицы и определители. Системы линейных уравнений. Собственные вект…
К. Пчельник, Е. А. Сетько, И. И. Ревчук. -Гродно. ГрГУ, Матрицы и определители. Аналитическая геометрия на плоскости и в пространстве: пособие. 2007, — 164с. Пособие содержит краткие теоретические сведения по матричной алгебре, аналитической геометрии на плоскости и в пространстве, примеры решения задач, задачи для самостоятельного решения и задания для контрольной работы. Матрицы и определители. Системы линейных уравнений. Собственные вект…
- формат pdf
- размер 1.94 МБ
- добавлен 01 февраля 2010 г.
Математика ч.1 УМК решение задач. Матрицы. векторная алгебра. мат. анализ, анал. геометрия 229 стр.
Примеры задач на определитель матрицы
Об «Примере задач на определение матрицы»
Примеры задач на определитель матрицы :
Здесь мы рассмотрим несколько примеров задач, чтобы понять решение определителей с использованием свойств.
Чтобы узнать свойства определителей, посетите страницу «Свойства определителей».
Примеры задач на детерминант матрицы – вопросы
Вопрос 1 :
Докажите, что
Решение:
Сначала разложим на множители «a» из 1 -й -й строки, «b» из 2 -й -й строки и c из 3 -й -й строки.
Теперь нам нужно умножить столбцы 1, 2 и на a, b и c соответственно.
Вычтем 2 -й -й -й ряд из 1-го -го -го ряда и вычтем 3 -й -й ряд из 2-го -го -го ряда.
= х 2 (c 2 х 2 + x 4 + B 2 x 2 ) + x 2 (0 + A 2 x 2 )
= x 2 (C 2 x 2 + x 4 + B 2 x 2 ) + x 2 (0 + A 2 x 2 )
= x 4 C 2 + x 6 + + C 2 + x 6 + + C 2 + x 6 +. б 2 x 4 + a 2 x 4
б 2 x 4 + a 2 x 4
= x 4 (c 2 + x 2 + b 2 + a 2 )
Следовательно, оно делится на x 4 .
Вопрос 2:
Если A, B, C все положительны и являются P TH , Q TH и R TH Условия G.P.
n th член Г.П.
a n = ar n-1
a = p th термин Г.П = 9-0 p-30 9 1 0008 B = Q TH Срок G.P = AR Q-1 -(2) C = R TH Срок G.P = AR R-1 -(3) используя свойства определителей, запишем их в виде суммы двух определителей. Во втором определителе добавим столбец 1 st и 3 rd . В первом столбце определителя 1 и совпадают. Во втором столбце определителя 1 и 2 совпадают. = log a (0) + log r (0) = 0 Следовательно, доказано. Вопрос 3: Найдите значение , если x, y и z ≠ 1 Решение: . Расширение вышеупомянутого определителя, мы получаем = 1 [1 — log z y log y z] — log x y[log y x — log z x log y z] + log x z[log y 90 x4z log z x] Используя свойства логарифмов = [1 — log y y] — log x ylog y x + log x ylog z x log y z + log x zlog y xlog z y — log x zlog z x = [1 — log y y] — log y y + log z ylog y z + log y zlog z y — log z z = [1 — 1] — 1 + log y y + log z z — 1 = — 1 + 1 + 1 — 1 = 0 Следовательно, ответ равен 0. Вопрос 4 : Если A = Решение : |A |A | = 1/4 det (A k ) = (1/4) k , если k = 1 det (A 1 ) = (1/4) 1 , если k = 2 det (A 2 ) = (1/4) 2 , если к = 3 дет (А 3 )=(1/4) 3 Найдя сумму, получим = (1/4) + (1/4) 2 + (1/4) 3 + ………… ……n членов Сумма геометрического ряда S n = a(r n — 1) / (r — 1) a = 1/4, r = 1/4 S n = (1/4)((1/4) n — 1) / ((1/4) — 1) = (1/4)((1/4) n — 1) / (-3/4) = (-1/3) ((1/4) n — 1) = (1/3)(1 — (1/4) n ) Следовательно, доказано. Мы надеемся, что после изучения вышеизложенного материала учащиеся поняли, что такое «Задачи на детерминант матрицы». Помимо материалов, приведенных в разделе «Примеры задач на детерминант матрицы», если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь. Пожалуйста, присылайте свои отзывы на [email protected] Мы всегда ценим ваши отзывы. ©Все права защищены. onlinemath5all.com Матрицы представляют собой двумерное расположение чисел в строках и столбцах, заключенное в пару квадратных скобок или, можно сказать, матрицы не что иное, как прямоугольное расположение чисел, выражений и символы, расположенные в столбцах и строках. Приложения матриц и определителей в основном в области науки и техники. Представление матрицы: любая матрица размера m × n представляется в виде \(A=\left[\begin{array}{ccc}a_{11} & \cdots & a_{1 n} \\ \vdots & \ddots & \vdots \\ a_{m 1} & \cdots & a_{m n}\end{массив}\right]_{m \times n}\). Его также можно представить как \(\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}} \) где 1 ≤ i ≤ m и 1 ≤ j ≤ n. Детерминанты в математике признаются масштабным коэффициентом матриц. Их можно рассматривать как функции расширения и сжатия матриц. Детерминанты используют квадратную матрицу в качестве входных данных и выдают одно число в качестве результата. Для всех квадратных матриц \(X=\left[x_{ij}\right]\) порядка n×n определитель может быть указан как скалярное значение, которое может быть действительным или комплексным числом, где \(x_ {ij}\) — (i,j)-й элемент матрицы X. Определитель обозначается обозначением det(X) или |X|. Пример матриц и определителей: Рассмотрим матрицу как: \(A=\begin{bmatrix}3&\ \ 5\\ Тогда его определитель представляется в виде: \(\left|A\right|=\begin{vmatrix}3&\ \ 5\\ Матрицы и детерминанты имеют множество применений в научной сфере и применимы к практическим задачам реальной жизни. Применение матриц и детерминантов следующим образом: Решение системы линейных уравнений можно найти с помощью обратной матрицы. Пусть уравнения: \(a_1x + b_1y + c_1z = d_1\) \(a_2x r+ b_2y + c_2z = d_2\) \(a_3x + b_3y + c_3z = d_3\) Эти уравнения могут быть представлены с помощью матрицы как следует \(\begin{bmatrix} a_{1}x +b_{1}y+c_{1}z\\ a_{2}x +b_{2}y+c_{2}z \\ a_{ 3}x +b_{3}y+c_{3}z \end{bmatrix}= \begin{bmatrix} d_{1}\\ d_{2}\\ d_{3} \end{bmatrix}\) Кроме того, это можно записать как \(\begin{bmatrix} a_{1} & b_{1} &c_{1} \\ a_{2}& b_{2} & c_{2}\\ a_{ 3} & b_{3} & c_{3} \end{bmatrix} \begin{bmatrix} x \\ y\\ z \end{bmatrix}= \begin{bmatrix} d_{1} \\ d_{2} \\ d_{3} \end{bmatrix}\) Далее эту систему можно записать как AX = B где матрица A содержит коэффициенты неизвестных переменных. \(A = \begin{bmatrix} a_{1} & b_{1} &c_{1} \\ a_{2}& b_{2} & c_{2}\\ a_{3} & b_{3 } & c_{3} \end{bmatrix}\) Матрица X — это матрица-столбец, содержащая неизвестные переменные. \(X = \begin{bmatrix}x\\y\\z \end{bmatrix}\) Матрица B также является матрицей-столбцом и содержит константы. 9{-1}\) не существует. В этом случае |А| = 0, поэтому вам придется вычислить (adj A)B. В зависимости от количества решений система уравнений называется непротиворечивой или непротиворечивой. Как проверить непротиворечивость уравнений Чтобы проверить непротиворечивость уравнений, выполните следующие действия: Шаг 1: Запишите данную систему уравнений в виде матричного уравнения AX = B Шаг 2: Найдите расширенную матрицу [A, B] системы уравнений. Шаг 3: Найдите ранг A и ранг [A, B], применяя только элементарные операции со строками. Операции со столбцами применять не следует. Шаг 4: Если в системе уравнений n неизвестных и ρ(A) = ρ([A|B]) = n, то система AX = B совместна и имеет единственное решение. Если в системе AX = B ρ(A) = ρ([A| B]) < n неизвестных n, то система совместна и имеет бесконечно много решений и этих решений. Если ρ(A) ≠ ρ([A| B]), то система AX = B несовместна и не имеет решений. Детерминанты можно использовать для быстрого решения линейных уравнений с одной переменной, линейных уравнений с двумя переменными, когда переменных больше двух. Важно понимать свойства определителей. Выше мы видели, как можно использовать матрицы для решения системы линейных уравнений. Мы можем распространить описанный выше метод на системы любого размера. Мы не можем использовать тот же метод для нахождения обратных матриц больше 2×2. Мы будем использовать систему компьютерной алгебры, чтобы найти инверсию больше 2 × 2. Давайте рассмотрим пример линейного уравнения с тремя переменными. Решите систему с помощью матричных методов. \(\begin{matrix} Предположим, нам нужно найти уравнение прямой, проходящей через две точки \( (x_1, y_1)\) и \( ( х_2, у_2)\) \(\begin{bmatrix} Пример: Найти уравнение прямой, проходящей через (-1, 3), (3, -5) с помощью определителей . Решение: Мы знаем формулу \(\begin{bmatrix} \(\begin{bmatrix} Итак, уравнение прямой 2x + y – 1 = 0 Площадь параллелограмма, натянутого на a и b, равна величине a×b. \(a\times{b}=\begin{bmatrix} Теперь представьте, что a и b лежат в плоскости так, что \(a_3 = b_3 = 0.\) Используя правила вычисления определителей, мы видим, что в этом случае векторное произведение упрощается до \( a\times{b}=\begin{bmatrix} Следовательно, площадь параллелограмма ∥a×b∥ является абсолютной величиной определителя \(\begin{bmatrix} Предположим, что \((x_1, y_1), (x_2, y_2 )\) и \(( x_3, y_3 )\) — три точки треугольника. Теперь площадь треугольника будет равна: Чтобы найти площадь треугольник в детерминантной форме, мы используем формулу, приведенную ниже: \(A={1\over{2}}\begin{bmatrix} Объем параллелепипеда, натянутого на векторы aa, bb и cc, представляет собой абсолютную величину скалярного тройного произведения (a×b)⋅ в. \((a\times{b}).c=\begin{bmatrix} Пример 1: Проверка на непротиворечивость и решение: x + 2y + z = 7, 2x – y + 2z = 4, x + y – 2z = -1 Число ненулевых строк равно 3. ρ(A) = ρ([A|B ]) = 3. Система совместна и имеет единственное решение. С 1-го ряда, х+2у+г = 7 —(1) Со 2-го ряда, 5у = 10 —-(2) у = 2 С 3-го ряда, -15з = -30 —-(3) з = 2 8 Прикладывая значение y и z в (1), получаем x+2(2)+2 = 7 x+6 = 7 x = 7-6 x = 1 Решение: x = 1, y = 2 и z = 2 Матрицы находят множество применений в научной сфере и применимы к практическим задачам реальной жизни. Надеюсь, эта статья о применении матриц и определителей была информативной. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас! В. Ответ 1 Применение матриц и определителей следующее: Q.2 В чем разница между матрицей и определителями? Ответ 2 A Матрицы — это двумерное расположение чисел в строках и столбцах, заключенное в пару квадратных скобок, или, можно сказать, матрицы — это не что иное, как прямоугольное расположение чисел, выражений, символов, которые расположены в столбцах и строках. В математике определитель — это скалярное значение, являющееся функцией элементов квадратной матрицы. Это позволяет охарактеризовать некоторые свойства матрицы и линейного отображения, представляемого матрицей. Q.3 Каково применение определителей? Ответ 3 Детерминанты используются при решении линейных уравнений, непротиворечивости системы, объеме параллелепипеда, площади треугольника, применении определителей в бизнесе, технике, информатике, физике и применении определителей в реальных life Q.4 Какие области применения матриц? Ответ 4 Детерминанты могут проявляться в любой области, которая может решить проблемы с (а) множеством переменных, которые (б) взаимодействуют значимо. Это практически вся наука, инженерия, большие данные, анализ данных, бизнес-расчеты и так далее. Не всем, кто работает над этими вещами, нужны детерминанты, но многие люди во всех этих областях определенно использовали детерминанты. Q.5 Каково применение матриц в технике? Ans.5 Матрицы могут быть решены в приложениях, связанных с физикой, а также при изучении электрических цепей, квантовой механике и оптике, с помощью матриц, расчете выходной мощности батареи, преобразовании электрической энергии резистором в другую полезной энергии, эти матрицы играют роль в расчетах, с помощью матриц проблема, связанная с законом Кирхгофа напряжения и силы тока, может быть легко решена.


Применение матриц и определителей с примерами

7&\ \ 9\end{bmatrix}_{2\times2}\)
7&\ \ 9\end{vmatrix}_{2\times2}\) В основном они используются в области науки и техники.
В основном они используются в области науки и техники.
Приложение 1: Решение системы линейных уравнений 
Приложение 2: Непротиворечивость системы  Система уравнений считается непротиворечивой, если она имеет решение.
Система уравнений считается непротиворечивой, если она имеет решение.
\displaystyle{\left.\begin{matrix}{x}+{2}{y}-{z}={6}\\{3}{x}+{5 }{y}-{z}={2}\\-{2}{x}-{y}-{2}{z}={4}\end{matrix}\right.}\\
{\ displaystyle{A}{\left(\begin{matrix}1 & 2 & -1\\3 & 5 & -1\\-2 & -1 & -2\end{matrix}\right)}, \displaystyle{ X} = {\ left (\ begin {matrix} {x} \\ {y} \\ {z} \ end {matrix} \ right)}, \ text {and} \ displaystyle {C} = {\ left ( \begin{matrix}{6}\\{2}\\{4}\end{matrix}\right)}}\\ 9{-{{1}}}{C}}\\
={\left(\begin{matrix}5,5 & -2,5 & -1,5\\-4 & 2 & 1\\-3,5 & -1,5 & -0,5 \end{matrix}\right)}{\left(\begin{matrix}{6}\\{2}\\{4}\end{matrix}\right)}\\
={\left(\begin {matrix}{22}\\{-16}\\{-16}\end{matrix}\right)}\\
\text{ Итак, решение } \displaystyle{x}={22}, \displaystyle {y}=-{16}\text{ и }\displaystyle{z}=-{16}.
\end{matrix}\)
Пусть (x, y) любая точка на прямой.
Мы видим, что (x, y), \((x_1, y_1)\) и \((x_2, y_2)\) находятся на одной строке.
Значит, площадь треугольника, образованного этими тремя точками, равна нулю.
x & y & 1\\
x_1 & y_1 & 1\\
x_2 & y_2 & 1
\end{bmatrix} = 0\)
x & y & 1\\
x_1 & y_1 & 1\\
x_2 & y_2 & 1
\end{bmatrix} = 0\)
Подстановка значений двух точек.
x & y & 1\\
-1 & 3 & 1\\
3 & -5 & 1
\end{bmatrix}=0\)
x(3 x 1 – (-5) x 1) – y((-1) x 1 – 3 x 1) + ((-1) x (-5) – 3 x 3) = 0
x(3 + 5) – y(- 1 – 3) + (5 – 9) = 0
8x + 4y – 4 = 0
4 (2x + y – 1) = 0
2x + y – 1 = 0 Мы можем написать векторное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\) и \(\vec{b} =b_1\hat{ i}+b_2\hat{j}+b_3\hat{k}\) в качестве определителя.
Мы можем написать векторное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\) и \(\vec{b} =b_1\hat{ i}+b_2\hat{j}+b_3\hat{k}\) в качестве определителя.
\hat{i} & \hat{j} & \hat{k}\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{bmatrix}\)
a_1 & a_2\\
b_1 & y_2
\end{bmatrix}\)
a_1 & a_2\\
b_1 & y_2
\end{bmatrix}\)
\(A = ½ [x_1 ( y_2 – y_3 ) + x_2 ( y_3 – y_1 ) + x_3 ( y_1 – y_2 ) ]\)
x_1 & y_1 & 1\\
x_2 & y_2 & 1\\
x_3 & у_3 & 1
\end{bmatrix}\) Мы можем написать скалярное тройное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\)
Мы можем написать скалярное тройное произведение \(\vec{a} =a_1\hat{i}+a_2\hat{j}+a_3\hat{k}\)
\(\vec{b} = b_1\hat {i}+b_2\шляпа{j}+b_3\шляпа{k}\) и \(\vec{c} =c_1\шляпа{i}+c_2\шляпа{j}+c_3\шляпа{k}\) как определитель
c_1 & c_2 & c_3\\
a_1 & a_2 & a_3\\
b_1 & b_2 & b_3
\end{bmatrix}\)
Применение определителей в инженерии 

Применение детерминантов в компьютерных науках 
Применение определителей в физике 
Применение детерминантов в реальной жизни 

Компьютеры запускают марковское моделирование на основе стохастических матриц, чтобы моделировать события, начиная от азартных игр и прогнозирования погоды и заканчивая квантовой механикой. 1 Каковы применения матриц и определителей?
1 Каковы применения матриц и определителей?