Матрица (математика) — Wikiwand
- ВведениеМатрица (математика)
- История
- ВведениеСистемы линейных уравненийЛинейные преобразования
- ОпределенияПрямоугольная матрицаКвадратная матрицаВектор-строка и вектор-столбецЭлементарные преобразования матрицРанг матрицы
- ОбозначенияТранспонированная матрицаДиагональная матрицаДругие диагонали матрицыЕдиничная матрицаНулевая матрица
- Операции над матрицамиСложение матрицУмножение матрицы на числоУмножение матрицУмножение вектора на матрицуКомплексное сопряжениеТранспонирование и эрмитово сопряжениеМинорыСледОпределитель (детерминант)Перманент
- Связанные понятияЛинейные комбинацииЛинейная зависимость
- СвойстваМатричные операции
- Примеры
- Квадратная матрица и смежные определения
- Кольцо матриц
- Матрицы в теории групп
- См.
 также
также - Примечания
- Литература
Уважаемый Wikiwand AI, давайте упростим задачу, просто ответив на эти ключевые вопросы:
Перечислите основные факты и статистические данные о %d0%9c%d0%b0%d1%82%d1%80%d0%b8%d1%86%d0%b0 (%d0%bc%d0%b0%d1%82%d0%b5%d0%bc%d0%b0%d1%82%d0%b8%d0%ba%d0%b0)?
Кратко изложите эту статью для 10-летнего ребёнка
ПОКАЗАТЬ ВСЕ ВОПРОСЫ
Ма́трица — математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля (например, целых, действительных или комплексных чисел), который представляет собой совокупность строк и столбцов, на пересечении которых находятся его элементы. Количество строк и столбцов задает размер матрицы. Матрицу можно также представить в виде функции двух дискретных аргументов. Хотя исторически рассматривались, например, треугольные матрицы[1], в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими.
Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае количество строк матрицы соответствует числу уравнений, а количество столбцов — количеству неизвестных. В результате решение систем линейных уравнений сводится к операциям над матрицами.
Для матрицы определены следующие алгебраические операции:
- сложение матриц, имеющих один и тот же размер[⇨];
- умножение матриц подходящего размера (матрицу, имеющую n{\displaystyle n} столбцов, можно умножить справа на матрицу, имеющую n{\displaystyle n} строк)[⇨];
- в том числе умножение матрицы на вектор-столбец и умножение вектор-строки на матрицу (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы)[⇨];
- умножение матрицы на элемент основного кольца или поля (то есть скаляр)[⇨].
Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют модуль над соответствующим кольцом (векторное пространство над полем).
Доказано, что каждому линейному оператору, действующему в n{\displaystyle n}-мерном линейном пространстве, можно сопоставить единственную квадратную матрицу порядка n{\displaystyle n}; и обратно — каждой квадратной матрице порядка n{\displaystyle n} может быть сопоставлен единственный линейный оператор, действующий в этом пространстве.[2] Свойства матрицы соответствуют свойствам линейного оператора. В частности, собственные числа матрицы — это собственные числа оператора, отвечающие соответствующим собственным векторам.
То же можно сказать о представлении матрицами билинейных (квадратичных) форм.
В математике рассматривается множество различных типов и видов матриц. Таковы, например, единичная, симметричная, кососимметричная, верхнетреугольная (нижнетреугольная) и т. п. матрицы.
п. матрицы.
Особое значение в теории матриц занимают всевозможные нормальные формы, то есть канонический вид, к которому можно привести матрицу заменой координат. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают дополнительными свойствами, например, устойчивостью.
как математика помогает определять тип людей — Что почитать на vc.ru
Отрывок из книги «Десять уравнений, которые правят миром, и как их можете использовать вы» Дэвида Самптера, которую выпустило издательство МИФ.
18 916 просмотров
Сначала я подумал, что это электронное письмо — спам. Оно начиналось с приветствия: «Мистер Самптер:», а в мире мало реальных людей, которые используют двоеточие в начале письма. Даже когда я прочитал текст — просьбу комитета по предпринимательству, науке и транспорту Сената США в Вашингтоне, округ Колумбия, о беседе со мной, — я оставался скептиком.
Странным показался уже сам факт, что просьба пришла в форме электронного письма. Не знаю, чего стоило ожидать, но я с подозрением отнесся к соседству длинного и подробного названия комитета и неформального обращения за помощью. Не сходилось.
Однако всё было правильно. Комитет Сената действительно хотел побеседовать со мной. Я отправил короткий положительныи ответ, и через несколько дней мы общались по скайпу с людьми из республиканской части комитета.
Они желали узнать о компании Cambridge Analytica, которую Дональд Трамп нанял для обращения к избирателям в соцсетях и которая предположительно собирала данные о десятках миллионов пользователей Facebook. В СМИ уже имелись две стороны истории Cambridge Analytica.
Одна сторона — блестящее представление Александра Никса, тогдашнего CEO, который заявлял, что использует алгоритмы в политических кампаниях для микротаргетинга. Другая — разоблачитель Крис Уайли с крашеными волосами, который утверждал, что помогал Никсу и его компании создать инструмент для «психологической войны». Впоследствии Уайли сожалел о своих действиях, которые позволили избрать Трампа, а Никс создавал свой бизнес в Африке, опираясь на свой «успех».
Впоследствии Уайли сожалел о своих действиях, которые позволили избрать Трампа, а Никс создавал свой бизнес в Африке, опираясь на свой «успех».
В 2017 году, за год до скандала, я детально исследовал алгоритм, который использовала Cambridge Analytica, и пришёл к заключению, противоречащему обеим версиям событий — и Никса, и Уайли. Я сомневался, что компания могла повлиять на президентские выборы в США.
Она, конечно, пыталась, но я обнаружил, что методы, которые, по их словам, использовались для таргетинга избирателей, были с изъяном. Мои заключения привели к странной ситуации, когда я оспаривал оба имеющихся варианта изложения.
Вот почему комитет Сената желал поговорить со мной. Больше всего республиканцы из администрации Трампа весной 2018 года хотели узнать, что делать с грандиозным скандалом вокруг рекламы в социальных сетях.
Прежде чем мы сможем помочь сенаторам, нам нужно понять, как нас видят создатели соцсетей. Для этого мы будем рассматривать людей как наблюдения (так делают и компании) и начнём с самых активных и важных: подростков.
Эта группа желает увидеть как можно больше и как можно быстрее. Каждый вечер можно наблюдать, как они — либо вместе на диване, либо (всё чаще) в одиночестве в спальне — быстро щелкают и листают странички на своих любимых платформах в соцсетях: Snapchat и Instagram.
Через окошко своих телефонов они могут видеть невероятные картины мира: гномов, падающих со скейтбордов; пары, идущие на свидания «правда или действие»; собак, играющих в Fortnite; маленьких детей, сующих руки в пластилин PlayDoh; девочек-подростков, стирающих макияж; или «сцепленные» истории из текстовых диалогов между воображаемыми студентами колледжа. Они перемежаются сплетнями о знаменитостях, крайне редкими реальными новостями и, конечно, регулярной нескончаемой рекламой.
Внутри Instagram, Snapchat и Facebook создаётся матрица наших интересов. Это набор чисел в виде таблицы, где в строках — люди, а в столбцах — типы «постов» или «снимков», на которые они нажимают. В математике мы представляем таблицу подростковых кликов в виде матрицы, которую обозначим M.
Каждое число в матрице показывает, сколько раз подросток кликнул по конкретному типу постов. Например, Мэдисон посмотрела 8 постов о еде, по 6 о косметике и Кайли Дженнер, ни одного о ютьюбере Пьюдипае и видеоигре Fortnite и 2 публикации о рэпере Дрейке.
Просто глядя на эту матрицу, мы можем получить хорошее представление о том, что за человек Мэдисон. Попробуйте представить её себе, а потом потратьте несколько секунд, чтобы вообразить некоторых других персонажей, которых я ввёл здесь, используя в качестве ориентиров просмотренные ими снимки. Не беспокоийтесь. Это не настоящие люди. Вы можете быть сколь угодно категоричными.
В матрице есть ещё несколько человек, похожих на Мэдисон. Например, Сэм любит косметику, Кайли Дженнер и еду, но проявляет незначительный интерес к другим категориям. Есть и люди, которые резко отличаются от Мэдисон. Джейкоб, как и Лорен, предпочитает Пьюдипая и Fortnite.
Уравнение рекламы — математический способ автоматически определять тип людей. Оно имеет следующую форму:
Оно измеряет корреляцию между различными категориями снимков. Например, если люди, которые обычно ставят лайк Кайли Дженнер, также ставят лайк и косметике, то r (косметика, Кайли) будет положительным числом. В этом случае мы говорим, что существует положительная корреляция между Кайли и косметикой. Но если люди, которые ставят лайки Кайли, обычно не ставят их Пьюдипаю, r (Пьюдипай, Кайли) будет отрицательным числом, и мы назовем это отрицательной корреляцией.
Чтобы понять, как работает уравнение 7, разберем его шаг за шагом начиная с M (i,x). Это число в строке i и столбце x нашей матрицы M. Мэдисон 6 раз просматривала посты о косметике, поэтому M(Мэдисон, косметика) = 6: у нас строка i = Мэдисон, а столбец x = косметика.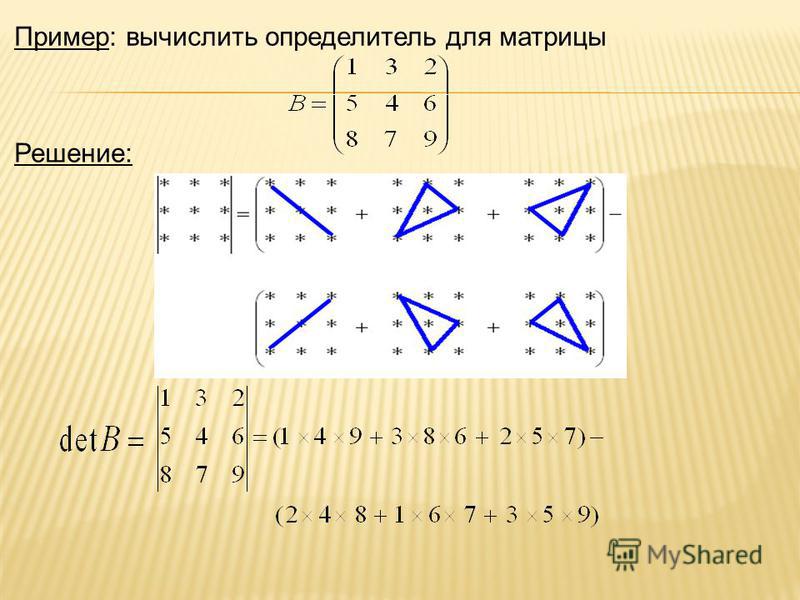
В общем случае каждый раз, когда мы смотрим на число в строке i и столбце x матрицы, то видим M(i,x). Взглянем на Ḿ(х). Эта величина — среднее число постов в категории x, приходящееся на одного пользователя. Например, среднее число просмотренных публикаций о косметике для наших подростков таково:
Ḿ(косметика) = (6+6+0+0+9+6+7+3+0+4+7+0)/12 = 4.
Если мы вычтем среднюю заинтересованность в косметике из общего числа публикаций, просмотренных Мэдисон, то получим:
M(i,x) – Ḿ(х) = 6–4 = 2.
Это говорит нам, что Мэдисон интересуется косметикой выше среднего. Аналогично, вычислив
M(i,y) – Ḿ(y) = 6–5 = 1, если i = Мэдисон, а y = Кайли.
А теперь переходим к мощной интересной идее, лежащей в основе уравнения 7: если мы перемножим (M(i,x) – Ḿ(х)) · (M(i,y) – Ḿ(y)), то определим те интересы, которые, как правило, у людей общие. Для Мэдисон мы получаем:
Для Мэдисон мы получаем:
Это говорит нам о том, что между её интересом к Кайли и косметике существует положительная корреляция.
Для Тайлера взаимоотношения между косметикой и Кайли отрицательные: (6 – 4) ∙ (1 – 5) = 2 ∙ (–4) = –8. Он проявляет интерес только к первой. Для Джейкоба величина снова положительна: (0 – 4) ∙ (0 – 5) = (–4) ∙ (–5) = 20, так как ему не нравятся ни первая, ни вторая (см. рис. 7).
Обратите внимание на один нюанс. И у Джейкоба, и у Мэдисон положительное значение, хотя у них противоположные взгляды на Кайли и косметику. Однако их взгляды предполагают, что Кайли и косметика коррелируют между собой, хотя Джейкоб вообще никогда не смотрел ни на ту, ни на другую. Поведение Тайлера в социальной сети не соответствует такой закономерности.
Мы можем произвести расчёты для каждого из подростков и сложить все такие величины. Получится сумма:
Знак Σi указывает, что мы берём сумму по всем двенадцати тинейджерам. Сложив все произведения, где перемножены отношения подростков к косметике и к Кайли, получим:
2–8+20–16+10+8+6+2+20+0+9+16=69.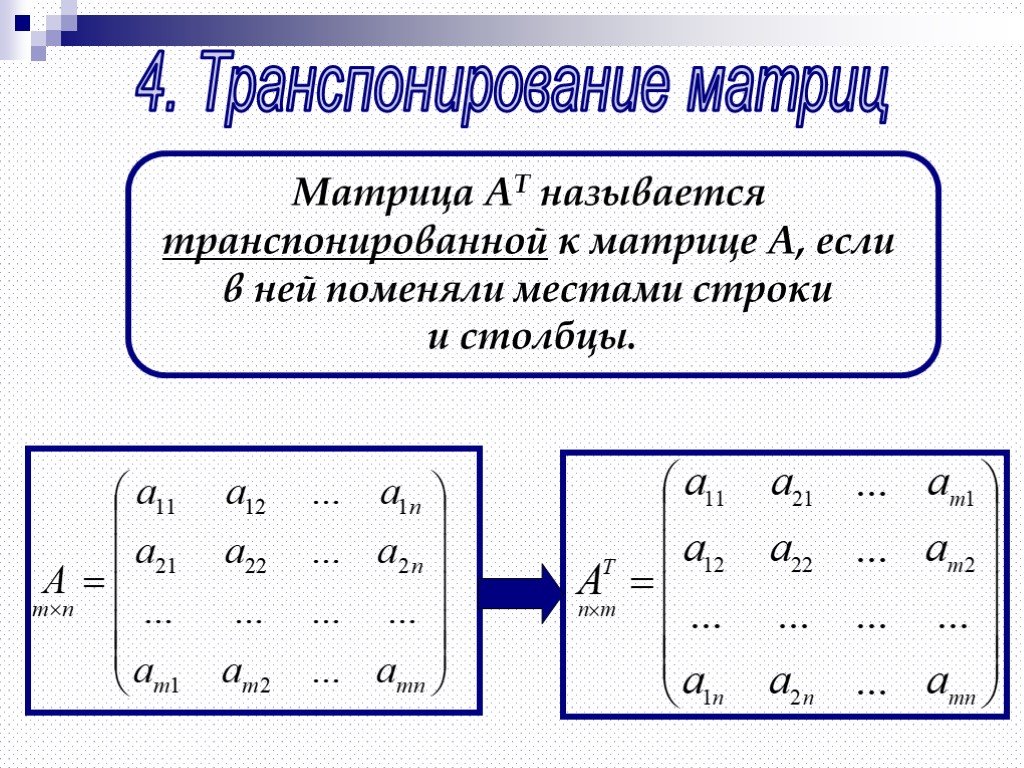
Бoльшая часть слагаемых положительна: это показывает, что дети имеют схожее отношение к Кайли и косметике. Среди тех, кто вносит свой положительный вклад в сумму, — Мэдисон и Джейкоб: 2 и 20 соответственно. Исключения — Тайлер, которому не нравится Кайли, и Райан, которому не нравится косметика; зато Кайли Дженнер по душе. Именно эта пара дала слагаемые –8 и –16.
Рис. 7. Иллюстрация к вычислению корреляции между Каили и косметикои
Математики не любят больших чисел вроде 69. Мы предпочитаем, чтобы они были меньше, лучше между 0 и 1, так их удобно сравнивать. Для этого мы добавим в уравнение 7 знаменатель (нижнюю часть дроби). Я не стану подробно разбирать это вычисление, но если мы подставим все наши числа, то получим:
Мы получили одно единственное число 0,51, которое измеряет корреляционную зависимость между косметикой и Кайли. Значение 1 показывало бы идеальную корреляцию между этими двумя типами постов, значение 0 говорило бы об отсутствии связи. Так что реальное значение 0,51 даёт нам среднюю корреляцию между любовью к косметике и к Кайли Дженнер.
Так что реальное значение 0,51 даёт нам среднюю корреляцию между любовью к косметике и к Кайли Дженнер.
Я понимаю, что провёл уже довольно много вычислений, но мы нашли только одно из пятнадцати важных чисел, отражающих предпочтения подростков! Нам бы хотелось узнать корреляцию не только между косметикой и Кайли, но и между всеми категориями: еда, косметика, Кайли, Пьюдипай, Fortnite и Дрейк.
К счастью, мы уже в курсе, как вычислить один коэффициент корреляции с помощью уравнения 7, — остаётся только подставлять в это уравнение каждую пару категорий. Именно это я сейчас и сделаю. Получится то, что известно под названием корреляционной матрицы, которую мы обозначим как R.
Если вы посмотрите на пересечение строки «Кайли» и столбца «Косметика», то увидите найденное нами ранее число 0,51. Точно так же заполняются и остальные строки матрицы — для всех пар категорий.
Например, Fortnite и Пьюдипай дают корреляцию 0,71. Но есть и такие пары, как Fortnite и косметика, которые дают коэффициент –0,74, то есть коррелируют отрицательно. Это означает, что геймеры, как правило, не особо интересуются косметикой.
Это означает, что геймеры, как правило, не особо интересуются косметикой.
Корреляционная матрица группирует людей по типам. Когда я просил вас представить себе этих подростков и не стесняться быть категоричными, я предлагал вам самим построить такую матрицу. Корреляция Кайли/косметика относит к одному типу таких подростков, как Мэдисон, Алисса, Эшли и Кайли, а корреляция Пьюдипай/Fortnite относит к другой группе Джейкоба, Райана, Моргана и Лорен. А вот Тайлер и Мэтт не вполне подходят под такую простую категоризацию.
В мае 2019 года я спрашивал Дуга Коэна, специалиста по данным из Snapchat, о той информации о пользователях, которую они хранят в корреляционных матрицах. «Ну, это почти всё, что вы делаете в Snapchat, — отвечал он. — Мы смотрим, как часто наши пользователи разговаривают в чатах с друзьями, сколько у них полос общения, какими фильтрами пользуются, как долго разглядывают карты, в скольких групповых чатах сидят, сколько времени тратят на просмотр контента или когда читают истории своих друзей. И мы смотрим, как эти действия коррелируют друг с другом».
И мы смотрим, как эти действия коррелируют друг с другом».
Данные анонимны, поэтому Дуг не знает, чем занимаетесь конкретно вы. Но такие корреляции позволяют Snapchat категоризировать пользователей — от «одержимых селфи» и «документалистов» до «див макияжа» и «королев фильтров», если пользоваться внутренней терминологией компании.
Как только компания узнаёт, что привлекает определённого пользователя, она даёт ему это в большом количестве. Слушая, как Дуг описывает свою работу по привлечению людей, я не мог не прокомментировать: «Погодите! Я, как родитель, стараюсь, чтобы мои дети пользовались телефоном меньше, а вы трудитесь, чтобы повысить их вовлеченность!».
Дуг парировал, слегка уколов конкурентов: «Мы не просто стараемся максимизировать время, проведённое в приложении, как традиционно делал Facebook. Мы следим за уровнем участия, смотрим, как часто пользователи возвращаются. Мы помогаем им общаться с друзьями».
Snapchat не претендует на то, чтобы мои дети проводили у них всё свое время, но компания желает, чтобы они снова и снова возвращались. И по личному опыту могу сказать, что это работает.
И по личному опыту могу сказать, что это работает.
Матрицы — SAT II Math II
Все ресурсы SAT II Math II
2 диагностических теста 130 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 3 Следующая →
SAT II Math II Помощь » Математические отношения » Матрицы
Умножьте:
Возможные ответы:
Правильный ответ:
Объяснение:
Произведение матрицы 2 x 2 и матрицы 2 x 1 является матрицей 2 x 1.
Умножить каждую строку в первой матрице на матрицу-столбец путем умножения элементов в соответствующих позициях, а затем добавить произведения следующим образом:
\
Сообщить об ошибке
Умножить:
5
4 Ответы: Правильный ответ:
Объяснение:
Произведение матрицы 2 x 2 и матрицы 2 x 1 является матрицей 2 x 1.
Умножить каждую строку в первой матрице на матрицу-столбец путем умножения элементов в соответствующих позициях, а затем добавить продукты следующим образом: значения матрицы определено ли выражение?
Возможные ответы:
Выражение определено для всех значений , указанных в других ответах.
Правильный ответ:
Объяснение:
Чтобы произведение матриц было определено, необходимо и достаточно, чтобы количество столбцов в было равно количеству строк в .
содержит два столбца. Из вариантов только
есть две строки, что делает его правильным выбором.
Сообщить об ошибке
Вычислить:
Возможные ответы:
Правильный ответ:
6
Объяснение:
Чтобы вычесть две матрицы, вычтите элементы в соответствующих положениях:
Отчет о ошибке
Оценка:
Возможные ответы:
. 0018
0018
Объяснение:
Определитель матрицы равен
.
Substitute :
Report an Error
Give the determinant of the matrix
Possible Answers:
Correct answer:
Объяснение:
Определитель матрицы равен
.
Заменитель:
Отчет о ошибке
Умножение:
Возможные ответы:
Правильный ответ:
Объяснение:
Произведение матрицы 2 x 2 и матрицы 2 x 1 является матрицей 2 x 1.
Умножить каждую строку в первой матрице на матрицу-столбец путем умножения элементов в соответствующих позициях, а затем сложить произведения следующим образом:
Сообщить об ошибке
Let .
Дать.
Возможные ответы:
не определено.
Правильный ответ:
не определено.
Объяснение:
содержит три строки и два столбца; так как количество строк не равно количеству столбцов, не является квадратной матрицей и, следовательно, не имеет обратной.
Сообщить об ошибке
Определить матрицу .
Для какого из следующих значений матрицы определено выражение?
I:
II:
III:
Возможные ответы:
II и II только
I и II. и только III
Правильный ответ:
Только I
Объяснение:
Для того, чтобы сумма матрицы была определена, необходимо и достаточно чтобы и иметь одинаковое количество строк и одинаковое количество столбцов. имеет три строки и два столбца; из трех вариантов только (I) имеет одинаковые размеры.
имеет три строки и два столбца; из трех вариантов только (I) имеет одинаковые размеры.
Сообщить об ошибке
Пусть и будет единичной матрицей 2 x 2.
Пусть.
Что из следующего равно ?
Возможные ответы:
Правильный ответ:
Объяснение:
Единичная матрица 2 x 2 – это .
, или, эквивалентно,
,
SO
Вычтите элементы в соответствующих позициях:
Сообщайте о ошибке
← Предыдущий 1 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 33 Уведомление
Все ресурсы SAT II Math II
2 диагностических теста
130 практических тестов
Вопрос дня
Карточки
Учитесь по концепции
Знакомство с матрицами — Math Insight
Матрицу можно рассматривать просто как обобщение вектора, где мы
расположить числа как в строках, так и в столбцах. Давайте сохраним количество
строки и столбцы произвольны, пусть $m$ будет количеством строк, а $n$
количество столбцов. Назовем такую матрицу $m \times n$
матрица и записать ее как
\начать{выравнивать*}
А=
\левый[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots и а_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\конец{массив}
\верно].
\конец{выравнивание*}
Например, матрица $3 \times 2$
\начать{выравнивать*}
Б=
\левый[
\begin{массив}{rr}
4 и -3\\
7 и 9\\
-5& 0
\конец{массив}
\верно],
\конец{выравнивание*}
и матрица $4 \times 7$
\начать{выравнивать*}
С=
\левый[
\begin{массив}{рррррр}
9 и -9 и -8 и 1 и 4 и -3 и -3\\
7 и -1 и 7 и -3 и -5 и -2 и 9\\
11 и 1 и 8 и -5 и -5 и 0 и -2\\
9 и -2 и -8 и -1 и 3 и 10 и 0
\конец{массив}
\верно].
\конец{выравнивание*}
Давайте сохраним количество
строки и столбцы произвольны, пусть $m$ будет количеством строк, а $n$
количество столбцов. Назовем такую матрицу $m \times n$
матрица и записать ее как
\начать{выравнивать*}
А=
\левый[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots и а_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\конец{массив}
\верно].
\конец{выравнивание*}
Например, матрица $3 \times 2$
\начать{выравнивать*}
Б=
\левый[
\begin{массив}{rr}
4 и -3\\
7 и 9\\
-5& 0
\конец{массив}
\верно],
\конец{выравнивание*}
и матрица $4 \times 7$
\начать{выравнивать*}
С=
\левый[
\begin{массив}{рррррр}
9 и -9 и -8 и 1 и 4 и -3 и -3\\
7 и -1 и 7 и -3 и -5 и -2 и 9\\
11 и 1 и 8 и -5 и -5 и 0 и -2\\
9 и -2 и -8 и -1 и 3 и 10 и 0
\конец{массив}
\верно].
\конец{выравнивание*}
Расположение матрицы в строках и столбцах нужно не только для того, чтобы она выглядела красиво. Структура матрицы позволяет нам определить фундаментальную операцию над матрицами: умножение.
Это умножение составляет основу линейной алгебры.
В частности, это умножение матриц позволяет матрицам представлять линейные преобразования (или линейные функции)
которые преобразуют векторы в другие векторы.
(Простым примером линейного преобразования является поворот вектора.)
Другое использование матриц связано с вычислением их определителя.
Структура матрицы позволяет нам определить фундаментальную операцию над матрицами: умножение.
Это умножение составляет основу линейной алгебры.
В частности, это умножение матриц позволяет матрицам представлять линейные преобразования (или линейные функции)
которые преобразуют векторы в другие векторы.
(Простым примером линейного преобразования является поворот вектора.)
Другое использование матриц связано с вычислением их определителя.
Векторы как матрицы
Концепция матриц настолько мощна, что во многих случаях
мы делаем нашу жизнь проще, рассматривая вектор как
специальный тип матрицы. Сравнивая вектор, такой как $\vc{x}=(1,5,3)$, с матрицей, сначала кажется, что разница между векторами и матрицами
что векторы имеют только одну строку, а матрицы имеют несколько строк.
Однако есть один важный поворот (буквально), который не очевиден при записи векторов в форме $\vc{x}=(1,5,3)$ . Когда мы рассматриваем векторы как матрицы, мы на самом деле рассматриваем их как
повернутая версия стандартной формы, написание
$n$-мерный вектор как матрица-столбец $n \times 1$
\начать{выравнивать*}
\vc{х} =
\левый[
\начать{массив}{с}
х_1\\
х_2\\
х_3\\
\vdots\\
х_n
\конец{массив}
\верно].

 0018
0018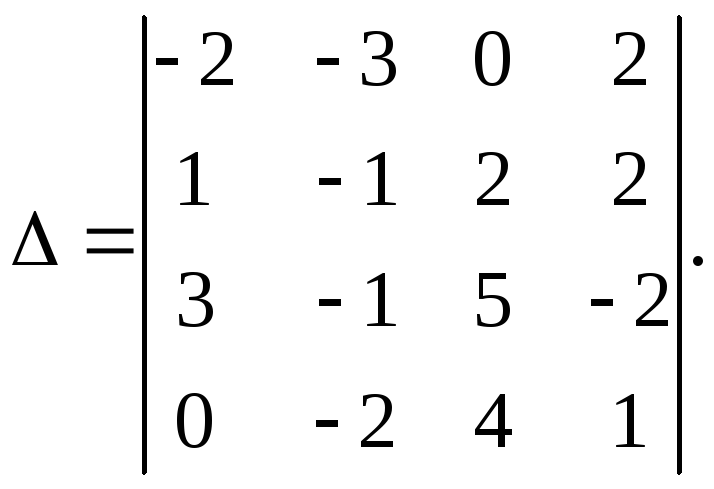
 имеет три строки и два столбца; из трех вариантов только (I) имеет одинаковые размеры.
имеет три строки и два столбца; из трех вариантов только (I) имеет одинаковые размеры. Давайте сохраним количество
строки и столбцы произвольны, пусть $m$ будет количеством строк, а $n$
количество столбцов. Назовем такую матрицу $m \times n$
матрица и записать ее как
\начать{выравнивать*}
А=
\левый[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots и а_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\конец{массив}
\верно].
\конец{выравнивание*}
Например, матрица $3 \times 2$
\начать{выравнивать*}
Б=
\левый[
\begin{массив}{rr}
4 и -3\\
7 и 9\\
-5& 0
\конец{массив}
\верно],
\конец{выравнивание*}
и матрица $4 \times 7$
\начать{выравнивать*}
С=
\левый[
\begin{массив}{рррррр}
9 и -9 и -8 и 1 и 4 и -3 и -3\\
7 и -1 и 7 и -3 и -5 и -2 и 9\\
11 и 1 и 8 и -5 и -5 и 0 и -2\\
9 и -2 и -8 и -1 и 3 и 10 и 0
\конец{массив}
\верно].
\конец{выравнивание*}
Давайте сохраним количество
строки и столбцы произвольны, пусть $m$ будет количеством строк, а $n$
количество столбцов. Назовем такую матрицу $m \times n$
матрица и записать ее как
\начать{выравнивать*}
А=
\левый[
\begin{массив}{cccc}
а_{11} и а_{12} и \ldots и а_{1n}\\
a_{21} & a_{22} & \ldots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\конец{массив}
\верно].
\конец{выравнивание*}
Например, матрица $3 \times 2$
\начать{выравнивать*}
Б=
\левый[
\begin{массив}{rr}
4 и -3\\
7 и 9\\
-5& 0
\конец{массив}
\верно],
\конец{выравнивание*}
и матрица $4 \times 7$
\начать{выравнивать*}
С=
\левый[
\begin{массив}{рррррр}
9 и -9 и -8 и 1 и 4 и -3 и -3\\
7 и -1 и 7 и -3 и -5 и -2 и 9\\
11 и 1 и 8 и -5 и -5 и 0 и -2\\
9 и -2 и -8 и -1 и 3 и 10 и 0
\конец{массив}
\верно].
\конец{выравнивание*} Структура матрицы позволяет нам определить фундаментальную операцию над матрицами: умножение.
Это умножение составляет основу линейной алгебры.
В частности, это умножение матриц позволяет матрицам представлять линейные преобразования (или линейные функции)
которые преобразуют векторы в другие векторы.
(Простым примером линейного преобразования является поворот вектора.)
Другое использование матриц связано с вычислением их определителя.
Структура матрицы позволяет нам определить фундаментальную операцию над матрицами: умножение.
Это умножение составляет основу линейной алгебры.
В частности, это умножение матриц позволяет матрицам представлять линейные преобразования (или линейные функции)
которые преобразуют векторы в другие векторы.
(Простым примером линейного преобразования является поворот вектора.)
Другое использование матриц связано с вычислением их определителя.

 также
также