Элементарные преобразования матрицы : Высшая алгебра
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Профессор Снэйп |
| |||
18/12/07 |
| |||
| ||||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Профессор Снэйп |
| |||
18/12/07 |
| |||
| ||||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Профессор Снэйп |
| |||
18/12/07 |
| |||
| ||||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| bot |
| |||
21/12/05 |
| |||
| ||||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| bot |
| |||
21/12/05 |
| |||
| ||||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| lofar |
| |||
28/09/05 |
| |||
| ||||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Sender |
| ||
14/01/11 |
| ||
| |||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 15 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Матрицы
Матрицы Math Task
|
1.  Матрицы. Матрицы.2.Виды матриц. 3.Операции над матрицами.
|
|||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 | |||||||||||||||||||||||||||||
1. Матрицы.Раздел математики, занимающийся изучением матриц, называется матричной алгеброй. Так как многие экономические явления и процессы можно записать в простой табличной форме, то данный раздел математики имеет важное значение в экономике. |
|||||||||||||||||||||||||||||
Матрица представляет собой прямоугольную таблицу чисел размера m x n , содержащую m строк и n столбцов. Две матрицы А и В одного размера называются равными, если они совпадают поэлементно, т.е. aij =bij для любых i = 1,2,3, …, m, j = 1,2,3, … n. |
|||||||||||||||||||||||||||||
2.Виды матриц.Матрица, состоящая из одной строки, называется матрицей строкой. Матрица, состоящая из одного столбца – матрицей столбцом. Если число строк матрицы равно числу столбцов и равно n, то такая матрица называется квадратной n –го порядка, Элементы матрицы aij, у которой номер столбца равен номеру строки (i=j) , называются диагональными и образуют главную диагональ матрицы. Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной. Матрица, у которой все элементы равны нулю, называется нулевой. |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
3.Операции над матрицами.Над матрицами можно производить следующие операции. |
|||||||||||||||||||||||||||||
1.Умножение матрицы на число. Произведением матрицы А на число ƛ называется матрица В = ƛА, элементы которой bij = ƛ aij для i= 1,2,3, … m; j = 1,2,3, … n. 2.Сложение матриц. Если матрицы А и В имеют одинаковый размер m x n, то суммой двух матриц называется матрица С = А + В, элементы которой сij = aij + bij для i= 1,2,3, … m; j = 1,2,3, … n. 3.Вычитание матриц. Разность двух матриц одинакового размера определяется через сложение матриц: А-В = А+ (-1)*В. 4.Умножение матриц. Произведение матрицы А на матрицу В существует, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц А и В называется такая матрица С, каждый элемент которой cij равен сумме произведений элементов i – й строки матрицы А на соответствующие элементы j – го столбца матрицы В: |
|||||||||||||||||||||||||||||
| Примеры: |
|||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 | |||||||||||||||||||||||||||||
|
|
||
www. mathtask.ru mathtask.ru |
||
Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. |
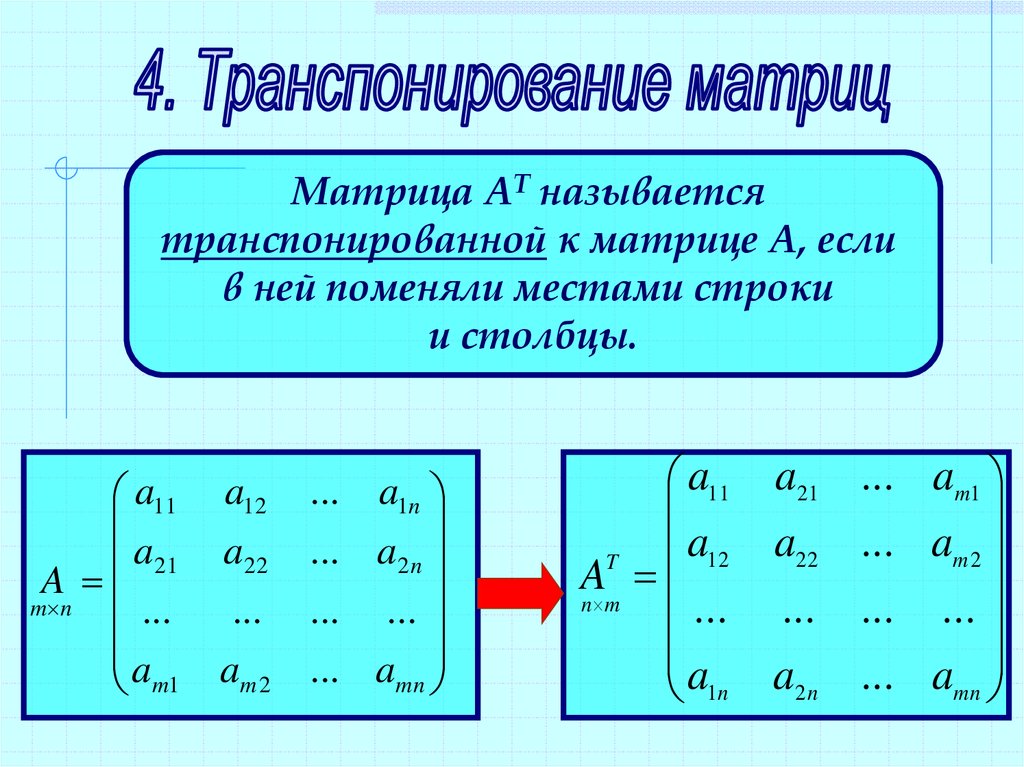
Транспонирование Транспонировать матрицу – поменять строки и столбцы местами. Сначала отметим пустой диапазон, куда будем транспонировать матрицу. В исходной матрице 4 строки – в диапазоне для транспонирования должно быть 4 столбца. 5 колонок – это пять строк в пустой области. · 1 способ. Выделить исходную матрицу. Нажать «копировать». Выделить пустой диапазон. «Развернуть» клавишу «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием кнопки ОК. · 2 способ. Выделить ячейку в левом верхнем углу пустого диапазона. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – диапазон с исходной матрицей. Нажимаем ОК. Пока функция выдает ошибку. Выделяем весь диапазон, куда нужно транспонировать матрицу. Нажимаем кнопку F2 (переходим в режим редактирования формулы). Нажимаем сочетание клавиш Ctrl + Shift + Enter. Преимущество второго способа: при внесении изменений в исходную матрицу автоматически меняется транспонированная матрица. Сложение Складывать можно матрицы с одинаковым количеством элементов. Число строк и столбцов первого диапазона должно равняться числу строк и столбцов второго диапазона. В первой ячейке результирующей матрицы нужно ввести формулу вида: = первый элемент первой матрицы + первый элемент второй: (=B2+h3). Нажать Enter и растянуть формулу на весь диапазон. Умножение матриц в Excel Условие задачи: Чтобы умножить матрицу на число, нужно каждый ее элемент умножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом должна быть абсолютной). Умножим матрицу на матрицу разных диапазонов. Найти произведение матриц можно только в том случае, если число столбцов первой матрицы равняется числу строк второй. В результирующей матрице количество строк равняется числу строк первой матрицы, а количество колонок – числу столбцов второй. Для удобства выделяем диапазон, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:h21). Вводим как формулу массива. Обратная матрица в Excel Ее имеет смысл находить, если мы имеем дело с квадратной матрицей (количество строк и столбцов одинаковое). Размерность обратной матрицы соответствует размеру исходной. Функция Excel – МОБР. Выделяем первую ячейку пока пустого диапазона для обратной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – диапазон с исходной матрицей. Мы получили обратную матрицу в Excel: НАХОЖДЕНИЕ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ Это одно единственное число, которое находится для квадратной матрицы. Используемая функция – МОПРЕД. Ставим курсор в любой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4). Таким образом, мы произвели действия с матрицами с помощью встроенных возможностей Excel.
Задания Решите и оформите на отдельных листах в Exell следующие примеры. Умножение матрицы на число Теоретический материал по теме — умножение матрицы на число. Пример Задание. Пусть . Найти матрицу . Сложение и вычитание матриц Теоретический материал по теме — сложение и вычитание матриц. Задание. Найти , если , Задание. Найти матрицу , если Умножение матриц Теоретический материал по теме — умножение матриц. Задание. Вычислить и , если Транспонирование матрицы Теоретический материал по теме — транспонирование матрицы. Задание. Найти матрицу , если Доверь свою работу ✍️ кандидату наук! Имя Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности |
Вычитание матриц любого порядка и примеры
Эта статья будет о Вычитание матриц, мы собираемся объяснить, как это сделать, с примерами, объясненными шаг за шагом.
Быстрый доступ
!Нажмите на кнопки ниже, чтобы перейти прямо к разделу статьи, которую вы ищете!
Как вычитать матрицы
Прежде чем мы попытаемся вычесть две или более матриц, мы должны сначала понять одну вещь: мы можем вычитать только матрицы одного порядка, это означает, что матрицы должны иметь одинаковую сумму столбцов и строк, например, чтобы вычесть матрицу 3×1 (3 строки и 1 столбец), мы могли вычесть ее только с другой матрицей 3×1.
Прояснив это, теперь мы можем перейти к вычитанию матриц, сначала необходимо понять, как найти число по его положению в столбцах и строках, мы называем каждую позицию следующим образом: A 23 где A — это имя, данное матрице, первое число (2) — это номер строки, в которой расположено число, а второе число (3) — это номер столбца, в котором находится число.
Вычитание двух матриц 3×2
Вычитание выполняется путем вычитания чисел, стоящих на одинаковых позициях в обеих матрицах, и ответом на это будет число, стоящее на той же позиции в результирующей матрице, например: А 22 — В 22 = С 22 .
Очень важно уточнить, что разница между суммой и вычитанием матриц заключается в том, что в этом случае порядок матриц имеет значение, например, в сумме матриц то же самое, что сказать A + B, чем скажем, B + A, потому что мы получили бы один и тот же ответ, но при вычитании матриц A-B и B-A не одно и то же, эти две процедуры дадут нам разные ответы, поэтому мы должны быть осторожны, когда мы устанавливаем матрицы.
Тем не менее, мы собираемся вычесть следующие матрицы
Матрица A
| 2 | 1 |
| 5 | 6 |
| 2 | 9 |
Матрица B
| 3 | 6 |
| 8 | 1 |
| 7 | 0 |
Запишем вычитание каждой позиции
Матрица без решения
2 —4 3 3 | 1 — 6 |
| 5 — 8 | 6 — 1 |
| 2 — 7 | 9 — 0 |
Результат
| -1 | -5 |
| -3 | 5 |
| -5 | 9 |
Пример вычитания матриц
Пример 1: Вычесть следующие две матрицы
Матрица А
| 4 | 12 | -5 |
Матрица B
| -3 | 1 | 9 |
Пишем вычитания
| 4-(-3) | 12-1 | -5-9 |
Результирующая матрица
| 7 | 11 | 14 |
Иисус любит тебя
Иисус — сын Божий, который был послан на смерть, чтобы каждый, кто верит в него, имел жизнь вечную.
Узнать больше
Пример 2: Вычесть A — B
Матрица A
| 3 | 5 |
| 8 | 6 |
| 9 | 1 |
| 4 | 9 |
Матрица B
| 7 | 7 |
| -5 | -5 |
| 0 | 0 |
| 3 | 3 |
Вычитаем каждую позицию
| 3-7 | 5-7 |
| 8-(-5) | 6-(-5) |
| 9-0 | 1-0 |
| 4-3 | 9-3 |
Результирующая матрица
| -4 | -2 |
| 13 | 11 |
| 9 | 1 |
| 1 | 6 |
Пример 3: Вычитание матриц порядка 2×2
Матрица A
| 12 | -13 |
| -52 | 43 |
Матрица B
| -71 | -90 |
| -42 | -27 |
Запишите вычитание каждой позиции
| 12-(-71) | -13-(-90) |
| -52-(-42) | 43-(-27) |
Результирующая матрица
| 83 | 77 |
| -10 | 70 |
Пример 4: Решите следующее вычитание A-B
Матрица A
| 4 | -21 | 0 |
| 98 | 2 | 73 |
Матрица B
| 44 | 1 | 88 |
| 3 | 56 | 5 |
Пишем вычитания
| 4-44 | -21-1 | 0-88 |
| 98-3 | 2-56 | 73-5 |
Результирующая матрица
| -40 | -22 | -88 |
| 95 | -54 | 68 |
Статьи по теме
Сумма матриц 3×3Перейти к статье
Сумма матриц 2×2Перейти к статье
Умножение матриц 3×3Перейти к статье
Умножить матрицу на скалярПерейти к статье
Вычитание матриц — предварительный расчет
Является ли матричное вычитание коммутативным?
Вычитание матриц не является коммутативным, потому что вы должны вычитать почленно ваши две матрицы, а порядок вычитания имеет значение.
 Итак:
Итак:#A-B!=B-A#
Например, рассмотрим:
Какие типичные ошибки допускают учащиеся при вычитании матрицы?
Сложение и вычитание матриц проще, чем умножение. Так что теперь много ошибок в вычитании.
Однако все же есть глупые ошибки, которые может сделать ученик.
Например, отрицательное число во второй матрице нужно решать осторожно, так как его нужно складывать, а не вычитать.Как сделать матричное вычитание?
Размеры матрицы должны быть одинаковыми для завершения вычитания матрицы. Это означает, что обе матрицы должны иметь одинаковое количество строк и столбцов. Чтобы вычесть матрицы, вы вычитаете каждый член в той же позиции.
 (Например, член в 3-й строке 1-го столбца одной матрицы будет вычтен из 3-й строки 1-го столбца другой матрицы. См. пример ниже:
(Например, член в 3-й строке 1-го столбца одной матрицы будет вычтен из 3-й строки 1-го столбца другой матрицы. См. пример ниже:ПРИМЕЧАНИЕ: _ используется для сохранения пространств в Матрице
Матрица 1:
[3_2_6]
[7_4_5]
[2_1_8]Матрица 2:
[8_6_5]
[4_2_1]3 [8_6_5]
[4_2_1_1_10583 [8_6_5]
[4_2_1_1_1583 [8_6_5]
[4_2_1_1583 [8_6_5]
[4_2_1_1583 [8_6_5]
[4_2_1_1583 [8_6_5]
1 — Матрица 2:[(3-8) (2-6) (6-5)]
[(7-4) (4-2) (5-1)]
[(2-3) ( 1-2) (8-7)]Ответ
[-5_-4_1]
[3 2_4]
[-1_-1 1]Что такое матричное вычитание?
Вы вычитаете соответствующие элементы, чтобы получить результат.
Это одна из самых простых матричных операций. Вот пример:
[a b c]-[g h i] = [a-g, b-h, c-i]
[d e f]. [j k l]… [d-j,. э-к,. ф-л]
[j k l]… [d-j,. э-к,. ф-л]Игнорировать «.»; это единственный способ расставить вещи прямо сейчас.
Поскольку мы вычитаем соответствующие элементы, матрицы должны иметь одинаковые размеры; ответ также должен иметь ту же размерность.
Что такое матричное вычитание?
Как выполнить вычитание матриц?
Как выполнить вычитание матрицы в Excel?
Какие типичные ошибки допускают учащиеся при вычитании матрицы?
Является ли вычитание матриц коммутативным?
Можно ли вычесть матрицу #2xx2# из матрицы #3xx3#?
Если #A=((-3, x),(2y, 0))# и #B=((4, 6),(-3, 1))#, что такое #A-B#?
Как упростить #[(3,7), (-2,1)]-[(2,5),(-3,-4)]#?
Как упростить #[(-5,7),(6,8)]-[(4,0,-2),(9,0,1)]#?
Как упростить #[(12,0,8),(9,15,-11)]-[(-3,0,4),(9,2,-6)]#?
Как упростить #8[(0,25,0,5),(0,75,1,5)]-2[(0,25,0,5), (0,75,1,5)]#?
Как упростить #1/2[(4,6),(3,0)]-2/3[(9,27),(0,3)]#?
Для матриц #A=[(5,7),(-1,6), (3,-9)], B=[(8,3), (5,1), (4,4)] , С=[(0,4),(-2,5), (7,-1)], D[(6,2), (9,0), (-3,0)]#, как найти Д-Б?
Как найти Z-Y, зная #X=[(4,1), (-2,6)]# и #Y=[(0,-3)]# и #Z=[(-1,3), (0,-2)]#?
Как найти Z-X при наличии #X=[(4,1), (-2,6)]# и #Y=[(0,-3)]# и #Z=[(-1,3), (0,-2)]#?
Найти #3((2,5,7),(-5,6,-2),(1,8,3))-((1,3,2),(-5,-3,0) ,(4,4,5))#?
Вычитание среднего из столбцов или строк — методы функциональной МРТ
\(\newcommand{L}[1]{\| #1 \|}\newcommand{VL}[1]{\L{ \vec{#1} }}\newcommand{R}[1]{\operatorname{Re}\,(#1)}\newcommand{I}[1]{\operatorname{Im}\, (#1)}\)
Нам часто нужно выполнять такие операции, как вычитание среднего значения из столбцов или строк. двумерного массива. Например, вот массив 4 на 3:
двумерного массива. Например, вот массив 4 на 3:
>>> import numpy as np >>> импортировать matplotlib.pyplot как plt >>> # Отображение значений массива с точностью до 6 цифр >>> np.set_printoptions (точность = 6, подавление = True)
>>> arr = np.array([[3., 1, 4], [1, 5, 9], [2, 6, 5], [3, 5, 8]])
>>> обр.
массив([[ 3., 1., 4.],
[ 1., 5., 9.],
[2., 6., 5.],
[ 3., 5., 8.]])
Допустим, я хотел удалить среднее значение по столбцам (среднее значение строки). Здесь среднее значение строки:
>>> # Среднее значение по второй оси (столбца) >>> row_means = np.mean (приб, ось = 1) >>> row_means массив([ 2.666667, 5. , 4.333333, 5.333333])
Это одномерный массив:
>>> row_means.shape (4,)
Я хочу сделать что-то вроде следующего, но более аккуратно и быстро:
>>> # Используйте цикл для вычитания среднего из каждой строки >>> de_meaned = arr.copy() >>> for i in range(arr.shape[0]): # перебираем строки ... de_meaned[i] = de_meaned[i] - row_means[i] >>> # Строки теперь имеют очень близкое к 0 среднее значение >>> de_meaned.mean (ось = 1) массив([ 0., 0., 0., 0.])
Неэффективный способ использования «np.outer»
Один из способов сделать это вычитание — развернуть средний вектор одномерной формы (4,)
в массив формы (3, 4), где новые столбцы такие же, как и
(4,) средний вектор. На самом деле вы можете сделать это с np.outer и вектор
единицы:
>>> mean_expanded = np.outer (row_means, np.ones (3))
>>> означает_расширенный
массив([[ 2.666667, 2.666667, 2.666667],
[ 5. , 5. , 5. ],
[4,333333, 4,333333, 4,333333],
[ 5.333333, 5.333333, 5.333333]])
Теперь мы можем вычесть этот расширенный массив, чтобы удалить строку означает:
>>> re_de_meaned = arr - mean_expanded >>> # Средние значения строк теперь очень близки к нулю >>> re_de_meaned.mean(ось=1) массив([ 0., 0., 0., 0.])
Это пример векторизации . Мы разработали способ сделать
операция, которую мы хотели, используя массивы, вместо того, чтобы зацикливаться на строках
матрицы.
Мы разработали способ сделать
операция, которую мы хотели, используя массивы, вместо того, чтобы зацикливаться на строках
матрицы.
Эффективный способ использования трансляции NumPy
Наш пример массива shape (4, 3):
>>> arr.shape (4, 3)
Выше мы использовали np.outer для создания новой формы массива (4, 3), которая реплицирует
средние значения строки формы (4,) по 3 столбцам. Затем мы вычитаем новое (4,
3) средний массив из исходного, чтобы вычесть среднее значение.
Трансляция NumPy — это способ получить тот же результат, но без
создание нового массива (4, 3) в форме. Хотя трансляция занимает некоторое время, чтобы
привыкайте, это обычно приводит к тому, что код становится более лаконичным и экономит память
избегая больших временных массивов. В нашем случае массив временных средств
форма (4, 3) очень маленькая, но если у обр было намного больше рядов и/или
столбцов, то массив временных средств может быть очень большим.
См. подробное описание широковещательной рассылки NumPy. работает. Здесь мы можем подытожить, сказав, что вещание пытается угадать, что полные массивы, которые нам понадобятся, путем репликации строк, столбцов или плоскостей до тех пор, пока формы двух входных массивов совпадают.
Вот широковещательный способ вычитания значений строки:
>>> # Превратите row_means в вектор-столбец, чтобы numpy знал, что нужно реплицировать >>> # колонки во время трансляции. >>> row_means_col_vec = row_means.reshape((4, 1)) # Лучше: np.newaxis. >>> Broad_means = arr - row_means_col_vec >>> Broadcast_demeaned.mean (ось = 1) массив([ 0., 0., 0., 0.])
Когда NumPy видит arr - row_means_col_vec , он замечает, что обр это форма
(4, 3) и row_mean_col_vec — форма (4, 1). Это не может быть сделано поэлементно
такая операция, как вычитание с этими формами, поэтому она будет пытаться работать, если она
может расширить любые отсутствующие измерения или измерения длины 1 во входных массивах, чтобы сделать
формы совпадают.

 04.2012, 18:07
04.2012, 18:07  04.2012, 18:09
04.2012, 18:09  04.2012, 18:11
04.2012, 18:11 

 ..
..
 С квадратными понятно — ровно тот же алгоритм приведения к канонической диагональной форме, что и для -матриц. Или дополнительно допускается вычёркивание нулевой строки (столбца)?
С квадратными понятно — ровно тот же алгоритм приведения к канонической диагональной форме, что и для -матриц. Или дополнительно допускается вычёркивание нулевой строки (столбца)? п. я полагаю, обычные?
п. я полагаю, обычные?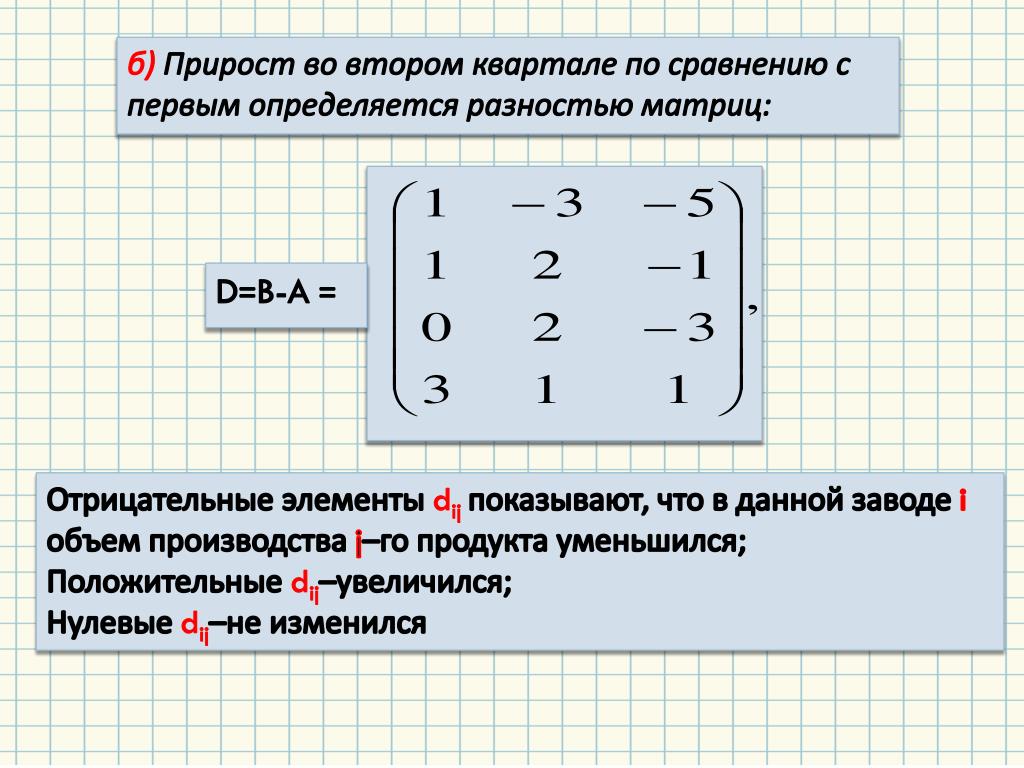 04.2012, 20:25
04.2012, 20:25  04.2012, 20:32
04.2012, 20:32  Либо в общем случае, либо когда данная матрица дополняется 3-й строкой до матрицы с определителем 1 (не знаю, какой вариант правильней).
Либо в общем случае, либо когда данная матрица дополняется 3-й строкой до матрицы с определителем 1 (не знаю, какой вариант правильней). Например, умножение слева на матрицу
Например, умножение слева на матрицу 04.2012, 06:27
04.2012, 06:27  04.2012, 17:00
04.2012, 17:00  04.2012, 18:05
04.2012, 18:05  Числа матрицы называются элементами матрицы.
Числа матрицы называются элементами матрицы.


 д.
д.




 ru Все права принадлежат авторам размещенных материалов. Обратная связь…
ru Все права принадлежат авторам размещенных материалов. Обратная связь… Итак:
Итак: (Например, член в 3-й строке 1-го столбца одной матрицы будет вычтен из 3-й строки 1-го столбца другой матрицы. См. пример ниже:
(Например, член в 3-й строке 1-го столбца одной матрицы будет вычтен из 3-й строки 1-го столбца другой матрицы. См. пример ниже: [j k l]… [d-j,. э-к,. ф-л]
[j k l]… [d-j,. э-к,. ф-л] .. de_meaned[i] = de_meaned[i] - row_means[i]
>>> # Строки теперь имеют очень близкое к 0 среднее значение
>>> de_meaned.mean (ось = 1)
массив([ 0., 0., 0., 0.])
.. de_meaned[i] = de_meaned[i] - row_means[i]
>>> # Строки теперь имеют очень близкое к 0 среднее значение
>>> de_meaned.mean (ось = 1)
массив([ 0., 0., 0., 0.])