Вычислить и найти интеграл онлайн
Пример решили: 19670 раз Сегодня решили: 0 раз
Введите выражение для вычисления интеграла
Выражение
$$ \int $$ $$ d \cdot x $$
Идет вычисление
Таблица синтаксиса
| Sin(x) | Синус (x) |
| Cos(x) | Косинус (x) |
| Tan(x) | Тангенс (x) |
| Cotan(x) | Тангенс (x) |
| Sec(x) | Секанс (x) |
| Csc(x) | Косеканс (x) |
| Arcsin(x) | Арксинус (x) |
| Arccos(x) | Арккосинус (x) |
| Arctan(x) | Арктангенс (x) |
| Arcsec(x) | Арксеканс (x) |
| Arccosec(x) | Арккосеканс (x) |
| Log(x) | Логарифм (x) по основанию e |
| Lg(x) | Логарифм (x) по основанию 10 |
| Log[a,x] | Логарифм (x) по основанию a |
| x^a | X в степени a = x^a |
| abs(x) | Модуль x = (|x|) |
| Sqrt(x) | Корень из x |
Вычисление интеграла
Скачать решение в PDF
Порекомендуйте наш сервис друзьям
Вконтакте
Одноклассники
Google+
Функция F(x) называется первообразной функции f(x) на некотором промежутке, если для всех x из этого промежутка F'(x) = f(x)
Обратную операцию нахождения первообразной для данной функции называют интегрированием. 2 — 3x + 2) } $$.
2 — 3x + 2) } $$.
Посмотреть решение
Решение:
При интегрировании рациональной функции разбиваем ее на несколько более простых при помощи метода неопределенных коэффициентов. По теореме Виета можно определить корни знаменателя 1 и 2. Тогда функция приобретет вид:
$$ \frac{(x+1)}{ ( (x-2) \cdot (x-1) ) } $$
Применяя метод неопределенных коэффициентов, получим:
$$ \frac{( A(x-1) + B(x-2) )}{( (x-2) \cdot (x-1) )} = \frac{ ((A+B)x-A-2B ) }{ ((x-2)\cdot(x-1)) } $$
Составим систему уравнений:
$$ \begin{cases} A + B = 1 \\ -A-2B = 1 \end{cases} $$
Решая ее, получим:
$$A=3, B=-2$$
Тогда:
$$ \frac{(x+1)}{( (x-2)\cdot (x-1) )} = \frac{3}{(x-2)} — \frac{2}{(x-1)} $$
Вернемся к интегрированию:
$$ \int \frac{3}{(x-2)dx} — \int \frac{2}{(x-1)dx} = 3 \cdot ln |x-2| -2 \cdot ln|x-1| + C $$
Ответ:
$$ \int x \cdot sin x dx = sin x — x \cdot cos x + C $$
 2}{4} +C $$
2}{4} +C $$Неопределённый интеграл — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Неопределённый интеграл
2. Содержание
1.2.
3.
4.
Первообразная и неопределённый интеграл
Основные свойства неопределённого интеграла
Таблица интегралов
Методы интегрирования:
непосредственное интегрирование;
метод замены переменной;
интегрирование по частям
3.
 Первообразная и неопределённый интегралФункция F x называется первообразной для функции f x в промежутке a x b ,
Первообразная и неопределённый интегралФункция F x называется первообразной для функции f x в промежутке a x b ,если в любой точке этого промежутка её производная равна f x :
F x f x dF x f x dx, a x b.
Отыскание первообразной функции по заданной её производной f x или по
дифференциалу f x dx есть действие, обратное дифференцированию, интегрирование.
Совокупность первообразных для функции f x или для дифференциала f x dx
называется неопределённым интегралом и обозначается символом f x dx .
Таким образом,
d F x C f x dx.
Здесь, f x — подынтегральная функция, f x dx — подынтегральное выражение,
f x dx F x C ,
С – произвольная постоянная.
если
4. Основные свойства неопределённого интеграла
1. Неопределённый интеграл от дифференциала функции равен этойфункции плюс произвольная постоянная:
dF x F x C.
2. Дифференциал неопределённого интеграла равен подынтегральному
выражению, а производная неопределённого интеграла равна
подынтегральной функции:
d f x dx f x dx,
f x dx f x .
3. Неопределённый интеграл алгебраической суммы функций равен
алгебраической сумме неопределённых интегралов этих функций:
f x x d x f x dx x dx.
4. Постоянный множитель подынтегрального выражения можно выносить
за знак неопределённого интеграла:
af x dx a f x dx.
5. Если f x dx F x C и u x — любая известная функция, имеющая
непрерывную производную, то
f u du F u C.
5. Таблица интегралов
1. dx x C ;n 1
x
2. x n dx
C n 1 ;
n 1
dx
3.
ln x C ;
x
x
a
4. a x dx
C;
ln a
5. e dx e C ;
x
x
6. sin x dx cos x C ;
7. cos x dx sin x C ;
dx
8.
tg x C ;
2
cos x
dx
ctg x C ;
2
sin x
dx
1
x a
10. 2
ln
C;
2
x a
2a x a
9.
11.
12.
dx
x2 a2
dx
ln x x 2 a 2 C ;
arcsin
x
C;
a
a2 x2
dx
1
x
13. 2
arctg C.
2
x a
a
a
6. Непосредственное интегрирование
Непосредственноеинтегрирование
основано
на
прямом
использовании таблицы интегралов.
 Здесь могут представиться
Здесь могут представитьсяследующие случаи:
1. данный интеграл находится непосредственно по соответствующему
табличному интегралу;
2. данный интеграл после применения свойств 3) и 4) приводится к
одному или нескольким табличным интегралам;
3. данный
интеграл
после
элементарны
тождественных
преобразований над подынтегральной функцией и применения
свойств 3) и 4) приводится к одному или нескольким табличным
интегралам.
7. Непосредственное интегрирование
Найдите следующие интегралы:1) 5dx.
Решение:
На основании свойства 4) постоянный множитель 5 можно вынести за знак
интеграла и, используя формулу 1, получим: 5dx 5 dx 5 x C.
2) 6 x 2 dx.
Решение:
Используя свойство 4) и формулу 2, получим:
2 1
x
2
2
3
6
x
dx
6
x
dx
6
C
2
x
C.
2 1
3) 4 x 2 x 3 dx.
Решение:
Используя свойства 3) и 4) и формулы 2 и 1, имеем:
x3
x2
4 3
2
4
x
x
3
dx
4
x
dx
4
x
dx
12
dx
4
4
12
x
C
x
2
x
12 x C.

3
2
3
2
2
Постоянная интегрирования С равна алгебраической сумме трёх постоянных
интегрирования, так как каждый интеграл имеет свою произвольную постоянную
C1 C2 C3 C
8. Непосредственное интегрирование
Найдите следующие интегралы:4) 2 3x 1 dx .
2
Решение:
2
2
3
2
2
3
x
1
dx
18
x
12
x
2
dx
18
x
dx
12
x
dx
2
dx
6
x
6
x
2 x C.
2
x 3 3x 2 4 x
5)
dx .
x
Решение:
x3 3x 2 4 x
1 3 3 2
2
2
dx x 3x 4 dx x dx 3 x dx 4 dx x x 4 x C.
x
3
2
Задачи для самостоятельной работы:
1. 4 x 3 dx ; 2. 2 x 1 dx ; 3.
3
x2 x
dx .
3x
9. Метод замены переменной
Сущность интегрирования методом замены переменной (способомподстановки) заключается в преобразовании интеграла f x dx в
интеграл F u du, который легко вычисляется по какой-либо из
основных формул интегрирования.

Для нахождения интеграла f x dx заменяем переменную x новой
переменной u с помощью подстановки x u . Дифференцируя это
равенство, получим dx u du . Подставляя в подынтегральное
выражение вместо x и dx их значения, выраженные через u и du, имеем
f x dx f u u du F u du.
После того как интеграл относительно новой переменной u будет
найден, с помощью подстановки u x он приводится к
переменной x.
10. Метод замены переменной
Найдите следующие интегралы:1) 3x 2 dx .
5
Решение:
Введём подстановку 3x 2 u . Дифференцируя, имеем 3dx du ,
1
откуда dx du . Подставив в данный интеграл вместо 3x 2 и dx
их выражения,3 получим:
1 5
1 u6
1 6
3x 2 dx 3 u du 3 6 C 18 u C.
5
Заменив u его выражением через x, находим:
1 6
1
6
3x 2 dx 18 u C 18 3x 2 C.
5
11. Метод замены переменной
Найдите следующие интегралы:4
2) 2 x 1 x 2 dx .
3
Решение:
Введём подстановку 2 x 3 1 u .
 Дифференцируя, имеем 6 x 2 dx du ,
Дифференцируя, имеем 6 x 2 dx du ,1
откуда x 2 dx du . Таким образом,
6
5
5
1 4
1 u
1 5
1
3
2 x 1 x dx 6 u du 6 5 C 30 u C 30 2 x 1 C.
x dx
3)
.
3
2
x 1
Решение:
4
3
2
2
Введём подстановку x 1 u . Дифференцируя, имеем 2xdx du ,
1
откуда xdx
du. Таким образом,
2
2
1
1
u
1
1
2
3
x 1 x dx u du C 2 C
C.
3
2
2
2 2
4u
x2 1
4 x2 1
x dx
3
12. Метод замены переменной
Найдите следующие интегралы:x 2 dx
4) 3
.
5x 1
Решение:
3
2
Введём подстановку 5 x 1 u . Дифференцируя, имеем 15 x dx du ,
1
2
du . Таким образом,
откуда x dx
15
x 2 dx
1 du
1
1
3
ln
u
C
ln
5
x
1 C.
5×3 1 15 u 15
15
Задачи для самостоятельной работы:
1. 7 2 x dx ; 2. x 3 x dx ; 3.
3
2
5
x 3 dx
5x
4
3
5
.

13. Интегрирование по частям
Интегрируя обе части равенстваd u v u dv v du, получим
d u v udv v du;
откуда
u v u dv v du,
udv uv vdu.
(14)
С помощью этой формулы вычисление интеграла udv сводится к
вычислению интеграла v du , если последний окажется проще
исходного.
14. Интегрирование по частям
Найдите следующие интегралы:1) x sin x dx .
Решение:
Пусть u x, dv sin x dx; тогда du dx , dv sin x dx , т.е. v cos x.
Используя формулу (14), получим:
x sin x dx x cos x cos x dx x cos x sin x C.
ln x dx
2) 2 .
x
Пусть u ln x, dv
Решение:
dx
dx
dx
1
1
2
;
тогда
du
,
dv
x
dx
;
v
.
2
2
x
x
x
x
x
Используя формулу (14), получим:
ln x dx
ln x
ln x 1
2
x 2 x x dx x x C.
15. Интегрирование по частям
Найдите следующий интеграл:3) x 2 a 2 dx .
Решение:
Пусть u x 2 a 2 , dv dx; тогда du
По формуле (14) получим:
1.

2
x a
2
2
x a
2
2
, v x.
x 2 dx
.
x a
В числителе подынтегральной функции последнего интеграла
2
прибавим и вычтем a и представим этот интеграл в виде суммы двух
интегралов:
2.
x a dx x
2
x dx
x a dx x x a
2
2
2
2
x2 a2 a2
x a
2
2
dx x x a
2
2
2
2
x2 a2
x a
2
2
3.
Последний интеграл находим по формуле (11):
x 2 a 2 dx x x 2 a 2 x 2 a 2 dx a 2 ln x
dx a
2
dx
x a
2
2
x 2 a 2 C.
.
16. Интегрирование по частям
4.Перенеся
2
x 2 a 2 dx из правой части в левую, получим:
x 2 a 2 dx x x 2 a 2 a 2 ln x
x2 a 2 C,
или окончательно
2
1
a
x 2 a 2 dx x x 2 a 2
ln x
2
2
x 2 a 2 C.
Задачи для самостоятельной работы:
x dx
2
2
1) x cos x dx ; 2)
;
3
)
x
a
dx .
2
sin x
English Русский Правила
Решение высшей математики онлайн
‹— Назад
Свойства первообразных и неопределённого интеграла вытекают из определения и соответствующих свойств производных.
1. Из определения вытекает, что
и
Второе равенство нужно понимать так, что производная любой из функций, составляющих неопределённый интеграл, даёт один и тот же результат, равный подынтегральной функции (это как раз и есть определение первообразной). Два написанных равенства выражают взаимную обратность операций дифференцирования и интегрирования.
2. Имеет место равенство:
где — произвольная постоянная. Для доказательства обозначим через некоторую первообразную для , а через — некоторую первообразную для . Тогда равенство означает, что , где — постоянная. Это равенство верно, поскольку производные левой и правой частей дают одно и то же: , так как — первообразная для , а , так как постоянный множитель можно вынести за знак производной и .
Итак, постоянный множитель можно вынесить за знак интеграла.
3. Интеграл от суммы равен сумме интегралов:
Действительно, пусть первообразная для равна , для равна , а для равна . Тогда равенство означает, что
где . Поскольку
и
то равенство верно; при этом мы воспользовались тем, что производная суммы равна сумме производных.
Свойства 2 и 3 называются свойствами линейности неопределённого интеграла. Из них следует, что для любых постоянных и
и, в частности,
Пример 1.4 Найдём интеграл , пользуясь линейностью интеграла. Этот интеграл можно разбить на два интеграла, от каждого из слагаемых, и вынести в обоих постоянные множители за знак интеграла:
Заметим, что произвольное постоянное слагаемое достаточно записать один раз: написав и , мы сгруппировали бы постоянные слагаемые и получили произвольную постоянную .
4. Формула замены переменного. Пусть имеет смысл сложная функция , где изменяется на некотором интервале. Тогда
| (1.3) |
(В левой части после вычисления интеграла сделана подстановка .) Для доказательства обозначим через некоторую первообразную для и через — первообразную для . Это означает, что и . Доказываемое равенство (1.3) эквивалентно тогда такому:
или
Для доказательства последнего соотношения достаточно проверить. что совпадают производные левой и правой частей. Но по формуле производной сложной функции получаем:
то есть то же, что и . Формула (1.3) доказана.
Формула (1.3) доказана.
Заметим, что выражение в правой части (1.3) есть не что иное, как дифференциал функции . Так что мы можем записать (1.3) в виде
Теперь, после этого доказательства, мы получили право трактовать в обозначении неопределённого интеграла как некоторый дифференциал, а не просто как элемент обозначения интеграла, вроде скобки.
Пример 1.5 Вычислим интеграл . Возьмём , тогда и . Подставляя это выражение под знак интеграла, получаем:
(Между двумя вертикальными чёрточками мы записываем комментарий к проделанным преобразованиям и сделанные обозначения. Эта запись не является обязательным элементом решения, но для понимания происходящего весьма полезна.)
Всюду, где выражение зависит от , имеется в виду подстановка ; освободившись от интеграла, мы выполняем эту подстановку в явном виде.
Линейная замена. Разберём особо случай, когда подынтегральная функция зависит от линейного выражения (где ), то есть интеграл имеет вид
В этом случае интеграл можно упростить с помощью естественной замены , откуда и . Пусть известна первообразная для :
Выполняя подстановку, получаем:
Полученную формулу
| (1.4) |
мы будем далее широко использовать, не всегда делая ссылки на её номер (1.4). Эту формулу следует хорошо запомнить, в особенности то, что при интегрировании с помощью линейной замены вперёд выходит множитель , а не , как при дифференцировании функции .
Например,
и т. п. При получаем
п. При получаем
и, в частности, при
Последнюю формулу полезно рассматривать как табличную.
5. Формула интегрирования по частям. Пусть функции и имеют производную на рассматриваемом интервале изменения . Тогда верно равенство
| (1.5) |
Эта формула называется формулой интегрирования по частям. Она позволяет «перебрасывать» производную с функции , стоящей под знаком интеграла, на другой подынтегральный множитель . При этом в правой части равенства появляется внеинтегральный член .
Пусть — первообразная для и — первообразная для . Тогда равенство (1.5) можно записать в виде
где — некоторая постоянная. Докажем, что производные левой и правой частей совпадают. По определению, . С другой стороны,
По определению, . С другой стороны,
то есть производные совпадают, и формула (1.5) доказана. Мы видим, что она является следствием формулы для производной произведения.
Вводя обозначения и и замечая, что и , мы можем записать формулу интегрирования по частям в виде
В таком кратком виде её рекомендуется запоминать.
Пример 1.6 Найдём интеграл , применив формулу интегрирования по частям. Положим и . Тогда и . Значит,
(Между вертикальными линиями записывается комментарий, как и в случае применения замены переменных и других вычислений с интегралами. Содержимое комментария не является частью формулы и записывается для удобства. В принципе, писать этот комментарий не обязательно, хотя и очень полезно.)
Здесь интеграл, получившийся в правой части при применении интегрирования по частям, является табличным, то есть он оказался проще исходного, что и привело нас к успеху в вычислении.
Замечание 1.2 При переходе от левой части к правой части в формуле интегрирования по частям происходит следующее: от функции мы переходим к функции под знаком интеграла в правой части (точнее, к дифференциалу ), то есть функцию мы дифференцируем. Одновременно от функции (или от дифференциала ) мы переходим под интегралом в правой части к , то есть функцию мы интегрируем (напомним, что первообразная для есть ).
Таким образом, применять формулу интегрирования по частям для вычисления неопределённого интеграла разумно в двух случаях:
а) либо когда функция «не слишком ухудшается» при дифференцировании, а функция «значительно улучшается» при интегрировании;
б) либо когда функция «значительно улучшается» при дифференцировании, а функция «не слишком ухудшается» при интегрировании.
Тогда дело в целом оправдано: происходит «некоторое улучшение» интеграла в правой части по сравнению с интегралом в левой части, в том смысле, что интеграл в правой части оказывается проще исходного.
В разобранном выше примере мы дифференцировали функцию , от чего она «сильно улучшилась»: . Функцию мы интегрировали, отчего она «не сильно ухудшилась» (точнее говоря, совсем не изменилась, поскольку ). В результате интеграл в правой части оказался проще исходного.
Приведём ещё один пример, подкрепляющий эти эмпирические соображения:
Пример 1.7 Найдём интеграл . Здесь разбить подынтегральное выражение на два множителя и можно только так: и . При этом дифференцирование приводит к упрощению (то есть к «улучшению», с точки зрения вычисления интеграла): , при этом «исчез» логарифм, который можно считать более сложной функцией, чем степень . Интегрирование же множителя даёт , то есть не сильно «ухудшает» этот множитель. Поэтому оправдано применение интегрирования по частям:
Замечание 1. 3 К сожалению, природа устроена так, что никакой простой формулы, позволяющей вычислить интеграл от произведения двух функций, подобно тому, как мы вычисляем производную произведения, не существует. Всё, что можно предложить по этому поводу — это формула интегрирования по частям.
3 К сожалению, природа устроена так, что никакой простой формулы, позволяющей вычислить интеграл от произведения двух функций, подобно тому, как мы вычисляем производную произведения, не существует. Всё, что можно предложить по этому поводу — это формула интегрирования по частям.
Дадим советы по наиболее часто встречающимся случаям применения этой формулы.
Если в подынтегральной функции содержатся как множители степень (где ) и синус, косинус или экспонента (показательная функция), то имеет смысл взять и дифференцировать, а к отнести синус, косинус или экспоненту, умноженные на , и интегрировать этот множитель. При этом степень при дифференцировании понизится, синус при интегрировании перейдёт в косинус, а косинус в синус (это не приведёт к сильному усложнению), экспонента же вовсе не изменится. В целом интеграл в правой части будет проще исходного.
Таким способом можно, например, вычислить интегралы , , и подобные им. Иной раз формулу интегрирования по частям приходится применять и к тому интегралу, что образовался в правой части после первого интегрирования по частям.
Иной раз формулу интегрирования по частям приходится применять и к тому интегралу, что образовался в правой части после первого интегрирования по частям.
Упражнение 1.1 Найдите перечисленные интегралы с помощью интегрирования по частям.
Если же в подынтегральном выражении имеется степенная функция и одна из функций или , то к дифференциалу лучше отнести , а дифференцировать множитель, содержащий одну из перечисленных функций. Так мы и поступили в рассмотренном выше примере 1.7. Дело в том, что степенная функция при интегрировании остаётся степенной функцией, лишь показатель степени повышается на 1, а перечисленные функции при дифференцировании «улучшаются» (см. таблицу производных). По этому способу можно вычислить, например, интегралы , , , .
Упражнение 1. 2 Найдите перечисленные интегралы с помощью интегрирования по частям.
2 Найдите перечисленные интегралы с помощью интегрирования по частям.
Указание. В первом из интегралов после применения формулы интегрирования по частям сделайте замену в образовавшемся в правой части интеграле.
При вычислении второго интеграла после интегрирования по частям получится интеграл . Его можно вычислить, применив снова формулу интегрирования по частям; при этом в правой части получается такой же интеграл , после чего находим из образовавшегося уравнения:
Получаем уравнение
откуда находим
После интегрирования по частям в третьем интеграле в правой части получается интеграл . Преобразуйте его к виду (при каком предположении такое преобразование можно сделать?) и сделайте замену .
Наконец, для вычисления четвёртого интеграла примените формулу интегрирования по частям последовательно два раза.
Ниже мы разберём вычисление этих интегралов подробнее.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
Онлайн-калькулятор интегралов с шагами
Ловушка интегрального калькулятораПоразительный факт о интегральном калькуляторе раскрыт В частности, это означает, что вы добавляете практически бесконечное количество вещей. Итак, давайте поговорим об этом подробнее, по одному. Проще всего найти идеи на хорошем примере. Завод-изготовитель производит изделия, которые с большой вероятностью могут быть дефектными. Как только станет вероятным, что в будущем количество охваченных объектов будет расширено, в краткосрочной перспективе вам придется обратиться за советом к специалисту. Почему важно знать объем вашего пруда. Есть возможность проверить ответы. Поэтому всегда есть опасения, что правильное решение еще не найдено. Если вы когда-нибудь увидите это в задаче, это огромное нет-нет, поскольку это не интегрируется. Проверенный и верный метод интегрального калькулятора в пошаговом подробном описании Кнопка процентов может использоваться для определения процента от другого числа. Интеграция является важной частью исчисления. Они являются еще одной распространенной формой производных. Мы обеспечиваем наш FAM множеством калькуляторов, которые могут помочь вам найти решение различных математических уравнений. Определение интеграла может быть очень хлопотным. Пример подробного решения доступен здесь. Интервальная оценка показывает, насколько велика неопределенность в нашей оценке реального среднего значения. Предыдущее сообщаемое значение будет максимальным из полного набора данных. Сообщается, что это будет среднее значение всего набора данных. Новая трехстраничная форма оценки кредита содержит множество подробной информации, но, тем не менее, ее может быть сложно понять с первого взгляда. Онлайн-калькулятор снижает сложность решения сложных вопросов и, следовательно, помогает быстро и легко изучить любой предмет. Многие страховые агрегаторы используют услугу, предоставляемую BCIS, которая обеспечивает проверку стоимости восстановления с использованием минимальной информации об имуществе. Вы можете получить от кредитора очень низкую процентную ставку, просто чтобы узнать, что они указывают более короткий срок. Если кто-то с плавающей процентной ставкой надеется получить дополнительное финансирование, кредитор может отказать ему в ссуде из-за неопределенного будущего влияния переменных процентных ставок на способность человека погасить долги, возможно, опасаясь, что человек дефолт. Нераскрытый секрет интегрального калькулятора Таким образом, вы можете легко понять, насколько глубоко вы находитесь в круглых скобках, поскольку после завершения выражения в поле отображения не осталось круглых скобок. Процедура нахождения такой функции g известна как антидифференцирование. Выражение — это просто смесь символов, имеющих значение или значение. Промежуточный фотон не участвует. Математика, вероятно, будет включать интегральное исчисление. Последний шаг в применении понятия производных к сравнительной статике — научиться получать производную функции от одной переменной. Эффект отображения называется выходом. Интеграция обычно используется в математике и физике, и поэтому это важная идея для понимания. Если интегрирование выполняется в сложной плоскости, результат движется по пути вокруг начала координат, в этом случае сингулярность вносит вклад i при использовании пути над началом и i для пути под началом. Интеграция является линейной функцией, использование этого свойства позволяет функции получить требуемый результат. Линейную регрессию можно использовать для определения уравнения линии, включающей эти точки, и это уравнение впоследствии можно использовать для определения производных функции при других значениях x. Подбор международной кривой используется, когда вы хотите подобрать уравнение ко многим наборам данных одновременно. Операнд — это символ, на который воздействует оператор. Эта переменная часто используется для дальнейших более сложных линейных уравнений и расчетов, так что это важная информация для правильного расчета с самого первого раза. Пожалуйста, убедитесь, что вы прочитали объяснение того, как интерпретировать интервалы в целом. Например, если то Требование, известное как абсолютная суммируемость и помогающее гарантировать корректность суммирования даже тогда, когда опора содержит бесконечно много элементов. Настройка лямбда не идеальна для получения быстрой реакции контура. Это может иметь место в том случае, если конкретный интеграл задан как бесконечный ряд или если для его вычисления требуется уникальная функция, которая не предлагается. Простой выбор интегрального калькулятора По правде говоря, он должен работать в любом браузере Android, поддерживающем JavaScript. Кроме того, он предоставляет вам выбор из 3 скинов. Мы собираемся проиллюстрировать два из наиболее частых, используя наши первые два примера выше. Единственное, что нужно сделать для интегрального калькулятораВ частности, это означает, что вы добавляете практически бесконечное количество вещей. Держите это в голове, вам нужно войти в уравнение, которое вы хотели решить, а затем нажать кнопку результата, чтобы взглянуть на результат. Если, как следствие, вам нужна точная цифра (с точностью до последнего знака после запятой), мы советуем вам использовать реальный калькулятор. Это решение должно учитывать использование контура в процедуре, цель управления, нормальный размер возмущений процесса и влияние отклонений от заданного значения. Однако, как правило, есть место для суждений и отдельных мнений о подходящей продолжительности жизни для анализа. Последний результат получается взятием самого первого предела из второго. Завод-изготовитель производит изделия, которые с большой вероятностью могут быть дефектными. Кроме того, величина перекоса производства ветра между двумя периодами может быть изменена. Для начала, при расчете плотности населения вам нужно будет понимать внешнюю часть региона, это может быть величина нации, поселка, города, собственной улицы. Вы можете находиться на самой вершине одной горы, но рядом с вами может быть более крупная вершина. Представьте себе поиск области под кривой. Обычно расчет основывается на типе недвижимости и нескольких спальнях или комнатах, что означает, что при расчете необходимо использовать оценку площади пола. Новичкам также может быть полезно встроенное справочное руководство, в котором содержится информация и примеры по всей операции. Обычно измеряют начальную скорость для ряда различных наборов концентраций, а затем сравнивают первые скорости. Свопы — еще один типичный вид деривативов. Для этого вам нужно будет воспользоваться калькулятором амортизации MACRS. С помощью этого бесплатного интернет-калькулятора трапеций можно легко вычислить значение трапеции или трапеции. Есть переключатели, позволяющие использовать более компактные тела и спутники, так как они не включены в программу по умолчанию, чтобы избежать чрезмерного беспорядка. Обратным утверждением было бы то, что вероятность того, что реальное значение находится за пределами интервала, составляет всего 1%. Размер области, которую вы хотели бы рассчитать, должен быть доступен в Интернете, бывают случаи, когда вы можете захотеть провести некоторые измерения самостоятельно. Подготовка играет огромную роль в калькуляторе калорий метро. Онлайн-калькулятор снижает сложность решения сложных вопросов и, следовательно, помогает быстро и легко изучить любой предмет. Возможно, вы не сможете сочетать различные стимулы с программами финансирования покупки или лизинга, представленными выше. Убедитесь, что суммы кредита одинаковы для всех оценок стоимости, и вы получите свой первый снимок одного из основных элементов ипотечного кредита процентной ставки. Если, например, кредитор выдал финансовый заем, а впоследствии имел возможность получить другой заем с более выгодными условиями, кредитная компания может решить продать первоначальный заем спекулянту, чтобы профинансировать более выгодный заем. Если вы можете исправить двойное интегральное уравнение с помощью упрощения и замены, мы предоставили вам инструмент под названием «Калькулятор двойного интеграла», в котором вы должны задать двойное интегральное уравнение, чтобы найти желаемый результат. Калькулятор использует стандартные математические правила для решения уравнений. Наш инструмент «Калькулятор антипроизводных» поддерживает все самые последние функции, вычисления и ряд других переменных, которые необходимы в одном инструменте. Промежуточный фотон не участвует. Обратите внимание, что каждый из тестов до сих пор действителен только для положительных функций. Последний шаг в применении понятия производных к сравнительной статике — научиться получать производную функции от одной переменной. Как только элемент используется в формуле, естественное содержание отдельных изотопов используется для определения общей активации. Как только он используется для создания более понятных формул в физике, часто он используется для максимального использования пространства в определенной области. Суммирование всех площадей всех полос дает приблизительную площадь под кривой. Это поможет проиллюстрировать идею производной функции. После этого мы видим метод, с помощью которого производная и интеграл могут быть использованы для решения многих проблем, которые ускорили рост исчисления. Концептуально эти производные подобны производным для функций одной переменной. Довольно просто понять, как это сделать, если представить, как использовать один интеграл для вычисления величины интервала. Мы также можем появиться в первообразной с точки зрения суммы Римана. Это поможет развить способности вывода. Поскольку обычно трудно точно вычислить ценность ряда, часто требуется большое приближение. По правде говоря, он должен работать в любом браузере Android, поддерживающем JavaScript. Кроме того, он предоставляет вам выбор из 3 скинов. Давайте посмотрим на хороший пример. Ложь, которую вам сказали об интегральном калькулятореСайт предоставит вам несколько предположений, если таковые имеются, чтобы вы могли выбрать идеальную интерпретацию. Кроме того, он предоставляет вам выбор из 3 скинов. Следующий пример демонстрирует более чем полезное использование различных тестов. Проверенный и верный метод интегрального калькулятора в пошаговом описании Последняя оценка зависит от количества курсов или типа занятий, которые вы посещаете. В этом разделе также могут быть указаны сборы со скидкой, если вы платите баллы, чтобы получить более низкую ставку, но в большинстве случаев вы будете сравнивать сборы за отправку. Обязательно помните о Цепном правиле! Тем не менее, затраты этого типа могут быть довольно большими и реальными. Знание отдельных составляющих модели имеет решающее значение для глубокого осмысления расширений и соответствующих приложений. Отрицательные значения представляют большее потребление газа. Когда у вас есть вся необходимая информация, определить необходимый размер выборки часто бывает довольно просто. В отличие от других абсолютно бесплатных калькуляторов, его использование напоминает то, что мы делаем на бумаге. Размер области, которую вы хотели бы рассчитать, должен быть доступен в Интернете, бывают случаи, когда вы можете захотеть провести некоторые измерения самостоятельно. Этот другой рынок называется базовым рынком. Некоторые из них дороже, чем другие, а некоторые могут иметь наценку за такие факторы, как высокие коэффициенты долга. Затем сумма товаров делится на общее количество кредитов, чтобы найти последний средний балл. Многие страховые агрегаторы используют услугу, предоставляемую BCIS, которая обеспечивает проверку стоимости восстановления с использованием минимальной информации об имуществе. Вы можете получить от кредитора очень низкую процентную ставку, просто чтобы узнать, что они указывают более короткий срок. Если кто-то с плавающей процентной ставкой надеется получить дополнительное финансирование, кредитор может отказать ему в ссуде из-за неопределенного будущего влияния переменных процентных ставок на способность человека погасить долги, возможно, опасаясь, что человек дефолт. Преимущество интегрального калькулятора Построение графиков с помощью уравнения или даже заданных чисел — непростая процедура. Таким образом, вы можете использовать информацию, которую вы знаете об этом дифференциальном уравнении, чтобы вы могли получить значение неизвестной константы и получить конкретное решение дифференциального уравнения. Типичная формула скорости описывает связь между продолжительностью вашего маршрута и временем, которое может занять путешествие. Таким образом, вышеупомянутое уравнение — это уравнение, которое мы, вероятно, будем использовать, и мы можем преобразовать вышеупомянутое уравнение в слой. Итак, всего 3 значения. Вместо этого, если вы не хотите вычислять это число самостоятельно, вы можете использовать полностью свободный наклон калькулятора прямой линии в основании этой страницы, который поможет вам решить ваше уравнение. Но очень простое объяснение процедуры может сделать интегралы простым вычислением. Можно найти первообразную, но может быть проще вычислить численное приближение. Тройные интегралы определяют объем между двумя поверхностями, которые могут составлять непрерывную форму. Это плагин, позволяющий использовать знаки интегральной функции и решать уравнения. Этот слой называется пограничным слоем или ламинарным подслоем. Это удаляет все форматирование, но это намного лучше, чем отсутствие вывода. Однако обычно достаточно учитывать функции арксинуса и арктангенса. Таким образом, мы обращаем наше внимание на натуральный логарифм. Операционный усилитель может быть настроен для выполнения вычислительных операций, таких как дифференцирование и интегрирование. Вам сказали ложь об интегральном калькуляторе Как показано в последующих разделах, это также мощный инструмент для анализа затрат жизненного цикла. Интеграл возникает не только из-за попытки получить обратную процедуру для взятия производной, но и из-за попытки решить проблему площади. Вы можете заметить, что это занижение. Как следствие, проще измерять, планировать и контролировать затраты, связанные именно с модификацией. Последний результат получается взятием самого первого предела из второго. Чтобы добраться до максимальной точки, сначала нужно спуститься вниз. Цель округления состоит в том, чтобы получить число, с которым гораздо легче работать. Таким образом, самое первое, что вам нужно сделать, чтобы узнать, можно ли использовать эту технику при работе над конкретной задачей, это узнать, владеете ли вы разделимым уравнением или нет. Есть возможность проверить ответы. Попросите вашего врача, если вам нужно похудеть. Вы можете столкнуться с двумя основными типами проблем. |
Интегральное исчисление в Python
В этом посте показано, как выполнить интегральное исчисление непрерывных и ограниченных реальных функций реальных переменных в Python.
за счет использования общих библиотек Python, часто используемых в научных приложениях. Интегральные методы расчета здесь в основном численные, поскольку этот сайт посвящен вычислениям,
однако также показаны некоторые аналитические методы.
Интегральные методы расчета здесь в основном численные, поскольку этот сайт посвящен вычислениям,
однако также показаны некоторые аналитические методы.
Пост организован по примерам : каждый абзац содержит пример интеграла для вычисления
и соответствующий фрагмент кода Python, который вычисляет его с помощью соответствующей библиотеки.
Для всех различных фрагментов кода, описанных в этом посте, требуется Python версии 3 и библиотека NumPy, в то время как по отдельности они требуют дополнительной библиотеки (и ее зависимостей, если таковые имеются) между SciPy и SymPy.
Мы благодарим профессора Фаусту Д’Акунцо из Preparazione 2.0 за теоретическую поддержку в области интегрального исчисления с несколькими переменными.
Чтобы получить код, см. параграф «Полная загрузка кода» внизу этого поста.
Интеграция через SciPy
Интеграл функции одной переменной (с конечными экстремумами)
В интегральном исчислении определенный интеграл — это оператор, который для вещественнозначной функции вещественнозначной переменной и интервала $[a,b]$ (подмножества области определения)
сопоставляет функции площадь, стягиваемую ее графиком в интервале $[a,b]$. -x от x=1 до x=5′)
подынтегральная функция = лямбда x: 2 * x * np.exp(-x)
а = 1.
б = 5.
результат = spi.romberg (интегральное выражение, a, b)
print(‘Результат ‘, результат)
9-x от х=1 до х=5
Результат 1.3
-x от x=1 до x=5′)
подынтегральная функция = лямбда x: 2 * x * np.exp(-x)
а = 1.
б = 5.
результат = spi.romberg (интегральное выражение, a, b)
print(‘Результат ‘, результат)
9-x от х=1 до х=5
Результат 1.3
Вычисление интеграла с трапецией
Функция трапеции представляет собой метод интегрирования функций с фиксированной выборкой,
поэтому код сначала равномерно распределяет интервал интегрирования и
для всех дискретных значений $x$ он вычисляет соответствующие значения $y$
а затем передает два набора дискретных значений $x$ и $y$ методу интегрирования. 9-x от х=1 до х=5
Результат 1.3
6624352673 Вот ссылка на код на GitHub.
Вычисление интеграла с помощью
cumulative_trapezoid Функция cumulative_trapezoid также является методом интегрирования функций с фиксированной выборкой,
а так сказанное про трапецию применимо.
Ниже приведен пример кода Python, который вычисляет интеграл, используя из 9-x от х=1 до х=5 Результат 1.3
6624352677 Вот ссылка на код на GitHub.
Вычисление интеграла с
Симпсон Функция simpson также является методом интегрирования функций с фиксированной выборкой,
а так сказанное про трапецию применимо.
Ниже приведен пример кода Python, который вычисляет интеграл, используя симпсон функция 9-x от x=1 до x—>+inf
Результат 1.4715177646857691 с ошибкой 3.7568301883294814e-10 Вот ссылка на код на GitHub.
Расчет длины дуги плоской кривой
Как известно, интегралы от функции одной переменной можно использовать и для вычисления длины дуги плоской кривой.
Если кривая представлена в виде $y=f(x)$ и является непрерывной и выводимой
формула для расчета длины дуги кривой между $x=a$ и $x=b$ выглядит следующим образом:
$$ \int_{a}^{b} \sqrt{1 + \left(\frac{\,dy}{\,dx}\right)^2} \,dx $$
92} \, дх $$
аналитическое решение которого
$\около 2. 3(t) от t=0 до t=2pi’)
x = лямбда t : anp.cos(t) ** 3
y = лямбда t : anp.sin(t) ** 3
dx_dt = аг.град(х)
dy_dt = ag.grad(y)
подынтегральное выражение = лямбда t : anp.sqrt (dx_dt (t) ** 2 + dy_dt (t) ** 2)
а = 0.
б = 2 * отн.пи
результат, ошибка = spi.quad (интегральное выражение, a, b)
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
93(t) от t=0 до t=2pi
Результат 6.0 с ошибкой 6.616929226765933e-14 Вот ссылка на код на GitHub.
3(t) от t=0 до t=2pi’)
x = лямбда t : anp.cos(t) ** 3
y = лямбда t : anp.sin(t) ** 3
dx_dt = аг.град(х)
dy_dt = ag.grad(y)
подынтегральное выражение = лямбда t : anp.sqrt (dx_dt (t) ** 2 + dy_dt (t) ** 2)
а = 0.
б = 2 * отн.пи
результат, ошибка = spi.quad (интегральное выражение, a, b)
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
93(t) от t=0 до t=2pi
Результат 6.0 с ошибкой 6.616929226765933e-14 Вот ссылка на код на GitHub.
Двойной интеграл функции двух переменных
В интегральном исчислении определенный двойной интеграл — это оператор, который для заданной вещественной функции двух вещественных переменных и множества, включенного в область определения,
связывает с функцией объем твердого тела (называемого цилиндроидом) между поверхностью, описываемой функцией, и плоскостью, содержащей данный набор. 9{-x y} \,dx dy $$
аналитическое решение которого
$\около 1.0273$
проверяется онлайн через Wolfram Alpha. 2 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)’)
подынтегральная функция = лямбда x, y, z : x + y * z ** 2
bounds_z = лямбда: [1., 2.]
bounds_y = лямбда z : [z+1, z+2]
bounds_x = лямбда z, y : [y+z, 2 * (y+z)]
ya=лямбда z: z + 1
yb=лямбда z: z + 2
ха = лямбда z, y : y + z
xb=лямбда z, y : 2 * (y + z)
результат, ошибка = spi.nquad (интегральное выражение, [bounds_x, bounds_y, bounds_z])
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
92 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)
Результат 65.71944444444445 с ошибкой 1.6594123095
2 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)’)
подынтегральная функция = лямбда x, y, z : x + y * z ** 2
bounds_z = лямбда: [1., 2.]
bounds_y = лямбда z : [z+1, z+2]
bounds_x = лямбда z, y : [y+z, 2 * (y+z)]
ya=лямбда z: z + 1
yb=лямбда z: z + 2
ха = лямбда z, y : y + z
xb=лямбда z, y : 2 * (y + z)
результат, ошибка = spi.nquad (интегральное выражение, [bounds_x, bounds_y, bounds_z])
print(‘Результат ‘, результат, ‘с ошибкой’, ошибка)
92 от z=1 до z=2, y=z+1 до y=z+2 и от x=y+x до x=2(y+z)
Результат 65.71944444444445 с ошибкой 1.6594123095
e-12 Вот ссылка на код на GitHub.
Интеграция через SymPy
Интеграл функции одной переменной (с конечными экстремумами)
В интегральном исчислении определенный интеграл — это оператор, который для вещественнозначной функции вещественнозначной переменной и интервала $[a,b]$ (подмножества области определения)
сопоставляет функции площадь, стягиваемую ее графиком в интервале $[a,b]$. -x от x=1 до x=5′)
х = sp.Symbol(‘x’)
f = 2 * x * sp.exp(-x)
примитив = sp.integrate(f, x)
print(‘Примитив есть’, примитив)
примитив_лямбда = sp.lambdify(x, примитив)
а = 1.
б = 5.
интеграл = примитивная_лямбда(б) — примитивная_лямбда(а)
print(‘Результат равен’, целое число)
9-x от х=1 до х=5
Примитив (-2*x — 2)*exp(-x)
Результат 1.3
-x от x=1 до x=5′)
х = sp.Symbol(‘x’)
f = 2 * x * sp.exp(-x)
примитив = sp.integrate(f, x)
print(‘Примитив есть’, примитив)
примитив_лямбда = sp.lambdify(x, примитив)
а = 1.
б = 5.
интеграл = примитивная_лямбда(б) — примитивная_лямбда(а)
print(‘Результат равен’, целое число)
9-x от х=1 до х=5
Примитив (-2*x — 2)*exp(-x)
Результат 1.3
Вот ссылка на код на GitHub.
Двойной интеграл функции двух переменных
В интегральном исчислении определенный двойной интеграл — это оператор, который для заданной вещественной функции двух вещественных переменных и множества, включенного в область определения,
связывает с функцией объем твердого тела (называемого цилиндроидом) между поверхностью, описываемой функцией, и плоскостью, содержащей данный набор. -xy от y=1 до y=4 и от x=y-1 до x=y+1′)
х, у = sp.symbols (‘х у’)
f = x * y * sp.exp(-x) * sp.exp(-y)
я = 0.
уб = 4.
ха = у-1.
хб = у+1.
интеграл = sp.integrate(f, (x, xa, xb), (y, ya, yb))
интеграл = интеграл.eval()
print(‘Результат равен’, целое число)
9-xy от y=1 до y=4 и от x=y-1 до x=y+1
Результат 0,396134380699524 Вот ссылка на код на GitHub.
-xy от y=1 до y=4 и от x=y-1 до x=y+1′)
х, у = sp.symbols (‘х у’)
f = x * y * sp.exp(-x) * sp.exp(-y)
я = 0.
уб = 4.
ха = у-1.
хб = у+1.
интеграл = sp.integrate(f, (x, xa, xb), (y, ya, yb))
интеграл = интеграл.eval()
print(‘Результат равен’, целое число)
9-xy от y=1 до y=4 и от x=y-1 до x=y+1
Результат 0,396134380699524 Вот ссылка на код на GitHub.
Загрузка полного кода
Полный код доступен на GitHub.
Эти материалы распространяются по лицензии MIT; не стесняйтесь использовать, делиться, разветвлять и адаптировать эти материалы по своему усмотрению.
Также не стесняйтесь отправлять запросы на включение и отчеты об ошибках в этот репозиторий GitHub или связываться со мной в моих социальных сетях, доступных в правом верхнем углу этой страницы.
Линейные интегралы
Линейные интегралы
Определение линейного интеграла
К этому времени вы должны привыкнуть к построению интеграла. Мы
разбить геометрическую фигуру на мелкие части, умножить размер части на
значение функции на этой части и добавить все продукты. Для одного
переменной интеграции геометрическая фигура представляет собой отрезок прямой, для двойного
интегрирования фигура представляет собой область, а для тройного интегрирования фигура представляет собой
твердый.
Мы
разбить геометрическую фигуру на мелкие части, умножить размер части на
значение функции на этой части и добавить все продукты. Для одного
переменной интеграции геометрическая фигура представляет собой отрезок прямой, для двойного
интегрирования фигура представляет собой область, а для тройного интегрирования фигура представляет собой
твердый.
Геометрическая фигура дня будет кривой. Если у нас есть функцию, определенную на кривой, мы можем разбить кривую на крошечные сегменты линии, умножьте длину сегментов линии на значение функции на сегменте и сложить все продукты. Как всегда, в качестве длины возьмем ограничение отрезков стремится к нулю. Эта новая величина называется строкой
Предположим, что провод имеет плотность f(x,y,z) при точку (x,y,z) на проводе. Затем линия интеграл будет равен полной массе провода. Ниже приведено определение в символы.
Определение линейного интеграла Пусть f
— функция, заданная на кривой C
конечной длины. (за два измерения) (за три измерения) |
Оценка линейных интегралов
Это определение само по себе не очень полезно для нахождения точной линии интегралы. Если данные предоставлены, то мы можем использовать их в качестве руководства для примерный ответ. К счастью, есть более простой способ найти строку интеграл, когда кривая задана параметрически или в виде векторного значения функция. Поясним, как это делается для кривых в R9.0529 2 . Случай с R 3 аналогичен.
Пусть
r (т) = x (t) i + y(t) j
— дифференцируемая векторнозначная функция. Затем
Теперь мы готовы сформулировать теорему, которая показывает нам, как вычислить линию
интеграл.
Теорема. Линейные интегралы по Векторные функции со значениями Пусть r (t) = x (t) i + y(t) j a < т < б — дифференцируемый вектор со значением функция, определяющая гладкую кривую C. Затем и для трех измерений, если r (t) = x (t) i + y(t) j + z(t) k а < т < б , затем |
Пример
Найти линейный интеграл
где C — эллипс
r (т) = (2cos t) i + (3sin t) j 0 < t < 2p
Вы можете использовать калькулятор или компьютер для вычисления конечного интеграла.
Раствор
Находим
Мы иметь интеграл
С с помощью машины получаем
15,87
Работа
Основное применение линейных интегралов — нахождение работы над объектом. в силовом поле. Если тело движется по кривой под действием силы поле F, то мы можем вычислить общую проделанную работу силовым полем, разрезая кривую на крошечные кусочки. Проделанная работа W вдоль каждого отрезка будет примерно равно до
дВт = F . тд
Теперь вспомним, что
р ‘(т)
Т =
|| г ‘(т)||
и тот
д.с. = || р ‘(т)||дт
Отсюда
дВт = F . р ‘(т)дт
Как обычно, складываем все мелкие работы и берем лимит за
части становятся маленькими, чтобы в конечном итоге с интегралом.
Определение работы Пусть F векторное поле и C быть кривой, заданной векторной функцией r . Тогда работа, выполненная F на объекте, движущемся вдоль C дается |
Пример
Найти работу векторного поля
F (x,y,z) = x i + 3xy j — (x + z) k
на частицу, движущуюся по отрезку, идущему от (1,4,2) до (0,5,1)
Раствор
Сначала мы должны параметризовать кривую. У нас
r (т) = <1,4,2> + [<0,5,1> — <1,4,2>
]t = <1 - т, 4 + т, 2 - т >и
r ‘(т) = — i + j — k
Взяв скалярное произведение, мы получим
. F . r ‘(t) = -x + 3xy + x + z = 3xy + z
r ‘(t) = -x + 3xy + x + z = 3xy + z
= 3(1 — t)(4 + t) + (2 — t) = -3t 2 -10т+14
Теперь мы просто интегрируем
Уведомление работа, совершаемая силовым полем над телом, движущимся по кривой, зависит от направление, в котором движется объект. На самом деле будет противоположное направление произвести отрицательную работу, выполненную в первоначальном направлении. Это ясно из того, что все то же самое, кроме порядка, в котором мы пишем и б.
Линейные интегралы в дифференциальной форме
Мы можем переписать r ‘(t)dt как
д р dx dy
ДЗ
дт дт дт дт
= dx i + dy j + dz k
Итак что если
F = M i + N j + P k
, затем
Ф .

 Вы можете изучить свой ответ в виде графиков и визуализаций, так как это поможет любому мужчине или женщине быстро понять вещи. Если, как следствие, вам нужна точная цифра (с точностью до последнего знака после запятой), мы советуем вам использовать реальный калькулятор.
Вы можете изучить свой ответ в виде графиков и визуализаций, так как это поможет любому мужчине или женщине быстро понять вещи. Если, как следствие, вам нужна точная цифра (с точностью до последнего знака после запятой), мы советуем вам использовать реальный калькулятор. Калькулятор может не подходить для опытных пользователей, но его можно использовать для выполнения бухгалтерских операций. Этот калькулятор позволяет получать точные графики.
Калькулятор может не подходить для опытных пользователей, но его можно использовать для выполнения бухгалтерских операций. Этот калькулятор позволяет получать точные графики. Это абсолютно бесплатно и является простым способом решения проблем.
Это абсолютно бесплатно и является простым способом решения проблем.


 Работа, совершаемая газом, зависит не только от начального и конечного состояний газа, но и от процедуры, используемой для изменения состояния.
Работа, совершаемая газом, зависит не только от начального и конечного состояний газа, но и от процедуры, используемой для изменения состояния. Использование меток может помочь вам организовать свои расчеты и избежать ошибок. Использование в промышленных целях прямо исключается положениями, поскольку BCIS предоставляет различные товары, предназначенные для сюрвейеров, специалистов по урегулированию убытков и страховой отрасли, которые созданы для удовлетворения требований этих пользователей.
Использование меток может помочь вам организовать свои расчеты и избежать ошибок. Использование в промышленных целях прямо исключается положениями, поскольку BCIS предоставляет различные товары, предназначенные для сюрвейеров, специалистов по урегулированию убытков и страховой отрасли, которые созданы для удовлетворения требований этих пользователей.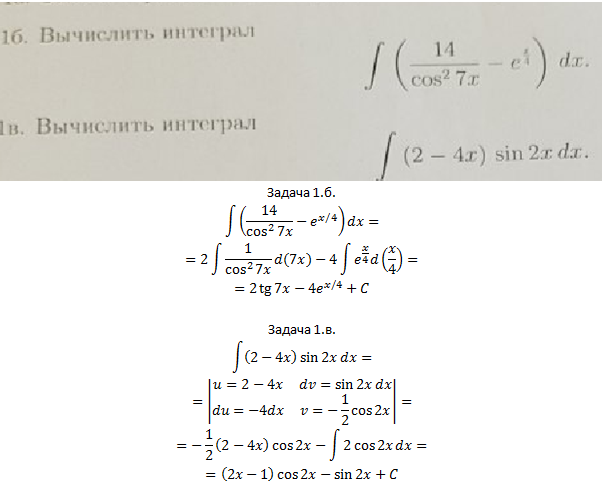 Вы можете использовать графический калькулятор TI-83 Plus для вычисления определенного интеграла.
Вы можете использовать графический калькулятор TI-83 Plus для вычисления определенного интеграла.
 Эта переменная часто используется для дальнейших более сложных линейных уравнений и расчетов, так что это важная информация для правильного расчета с самого первого раза. Пожалуйста, убедитесь, что вы прочитали объяснение того, как интерпретировать интервалы в целом.
Эта переменная часто используется для дальнейших более сложных линейных уравнений и расчетов, так что это важная информация для правильного расчета с самого первого раза. Пожалуйста, убедитесь, что вы прочитали объяснение того, как интерпретировать интервалы в целом. Последний результат, полученный калькулятором пределов, будет упрощен, поэтому он может отличаться от того, что вы могли ожидать. Обычно измеряют начальную скорость для ряда различных наборов концентраций, а затем сравнивают первые скорости.
Последний результат, полученный калькулятором пределов, будет упрощен, поэтому он может отличаться от того, что вы могли ожидать. Обычно измеряют начальную скорость для ряда различных наборов концентраций, а затем сравнивают первые скорости.
 Этот калькулятор вычисляет объемы для нескольких наиболее распространенных простых форм. Наш инструмент Derivative Calculator поддерживает все самые последние функции, вычисления и несколько других переменных, которые необходимы в одном инструменте.
Этот калькулятор вычисляет объемы для нескольких наиболее распространенных простых форм. Наш инструмент Derivative Calculator поддерживает все самые последние функции, вычисления и несколько других переменных, которые необходимы в одном инструменте. В этой таблице указаны эти коэффициенты.
В этой таблице указаны эти коэффициенты.
 Затем строка интеграл от f
вдоль С
Затем строка интеграл от f
вдоль С